An online tool for calculation of free-energy balance for the renal inner medulla

Abstract

Concentrating models of the renal inner medulla can be classified according to external free-energy balance into passive models (positive values) and models that require an external energy source (negative values). Here we introduce an online computational tool that implements the equations of Stephenson and colleagues (Stephenson JL, Tewarson RP, Mejia R. Proc Natl Acad Sci USA 71: 1618–1622, 1974) to calculate external free-energy balance at steady state for the inner medulla (http://helixweb.nih.gov/ESBL/FreeEnergy). Here “external free-energy balance” means the sum of free-energy flows in all streams entering and leaving the inner medulla. The program first assures steady-state mass balance for all components and then tallies net external free-energy balance for the selected flow conditions. Its use is illustrated by calculating external free-energy balance for an example of the passive concentrating model taken from the original paper by Kokko and Rector (Kokko JP, Rector FC Jr. Kidney Int 2: 214–223, 1972).

the mammalian kidney concentrates urine by generating an axial osmolality gradient along the corticomedullary axis. This gradient has been documented both in the outer medulla and in the inner medulla (IM) (1). The basis of the axial osmolality gradient in the outer medulla is widely accepted to be countercurrent multiplication or related processes dependent on active transport of NaCl in the thick ascending limb of Henle's loop (10, 12). In contrast, the concentrating process in the IM remains a point of controversy, because the ascending limb of Henle's loop in this region appears to be incapable of substantial active salt transport.

A widely recognized hypothesis to explain the axial gradient in the IM is the passive countercurrent mechanism of Stephenson (14) and Kokko and Rector (8). The principle of this proposed mechanism is that mixing of a high NaCl stream (the descending limb of Henle) and a high urea stream (collecting duct) in the inner medullary interstitium can produce an increase in urine osmolality by virtue of the entropic increase owing to the mixing (14). As a consequence, the concentrating process can theoretically occur spontaneously (decreasing free energy). However, other mechanisms are possible as described by Knepper, Chou, and Layton (5), including a role for renal pelvic contractions in providing energy for the inner medullary concentrating process (6).

Stephenson, Tewarson, and Mejia (16) provided a theoretical formalism for calculation of external Gibbs free-energy requirements for urinary concentration based on “free-energy flows” of the individual streams going into and out of the IM (including both renal tubule segments and vasa recta). Calculations using this formalism can be useful as a way of determining whether energy flows across the boundaries of the IM are such that the passive model could be the sole explanation for the overall concentrating function of the IM (positive external free-energy balance) or whether another source of energy is required (negative external free-energy balance).

Here, we have created a software tool called the Renal Inner Medulla Free-Energy Calculator, written in Java, to carry out both mass balance and external free-energy balance calculations for the IM at steady state. This allows the user to consider simultaneously the constraints of mass balance and energy balance on the concentrating process, providing an indicator of whether a given concentrating state requires a free-energy input or can occur spontaneously.

MATERIALS AND METHODS

Software implementation.

The Renal Inner Medulla Free-Energy Calculator was written in Java (Java Development Kit 6 Update 26; Oracle) using NetBeans IDE 7.0 as an integrated development environment. The web application of the calculator was developed using a Java Applet for presentation. The web application was implemented using Apache Tomcat 7.0.12 hosted by the NIH Biowulf cluster (http://biowulf.nih.gov/). The program can be accessed at http://helixweb.nih.gov/ESBL/FreeEnergy.

To run the web version of the calculator, a user needs the Java SE Runtime Environment Version 6 (http://www.java.com/en/download/) and JavaScript enabled in a web browser. The web version of the calculator has been tested on multiple operating systems and web browsers as follows: operating systems: Microsoft Windows XP (version 5.1.2600), Microsoft Windows 7 (version 6.1.7600), and Mac OS X 10.6.4 (10F569); web browsers (Macintosh and Windows): Firefox 4, Chrome 17, and Safari 5.

Model assumptions.

We assume that the kidney is functioning at steady state. The model is set up to calculate mass and energy balance explicitly for the IM using flow streams at the outer-inner medullary junction (OIJ). However, the calculations would be exactly the same for other boundaries, including the corticomedullary border, giving balances for the entire medulla. Multiple individual tubules and blood vessels enter and exit the IM at the OIJ. The radial organization of tubules and blood vessels in the IM has also been shown to be essential for hypertonic urine formation (19). To handle this complexity, we use the standard assumptions of 1) lumping similar tubules and blood vessels into a single stream and 2) uniform concentrations and flows in all descending and ascending tubules and blood vessels. The free-energy expression assumes that salts can be represented by an equivalent number of nonionic particles because of strict electroneutrality requirements, another standard assumption in kidney physiology.

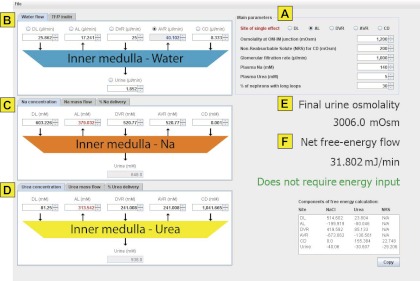
The input page is shown in Fig. 1. Default values are set for rat IM and are based on values modified from Fig. 2 of a paper by Kokko and Rector (8) (i.e., data set “adjusted vasa recta concentrations” in Table 1, column 3, see results). The following general data can be modified (Fig. 1A): site of single effect, osmolality at the OIJ, nonreabsorbable solute concentration (NRS) for flow into the inner medullary collecting duct (IMCD), glomerular filtration rate, plasma Na concentration, plasma urea concentration, and percent of nephrons with long loops. The single effect site specifies what flow stream at the OIJ can differ from the specified osmolality allowing the IM as a whole to concentrate the urine stream. “Nonreabsorbable solute” is included to account for the osmotic effect of solutes in the collecting duct other than urea and NaCl. The percent of nephrons with long loops must be specified because these loops of Henle are the only ones that cross the OIJ.

Fig. 1.

Screen shot of user interface showing default values. A: main parameters. B: water flow and TF/P inulin. C: Na concentration, Na mass flow, and %Na delivery. D: urea concentration, urea mass flow, and %urea delivery. E: final urine osmolality output. F: net free-energy flow output.

Fig. 2.

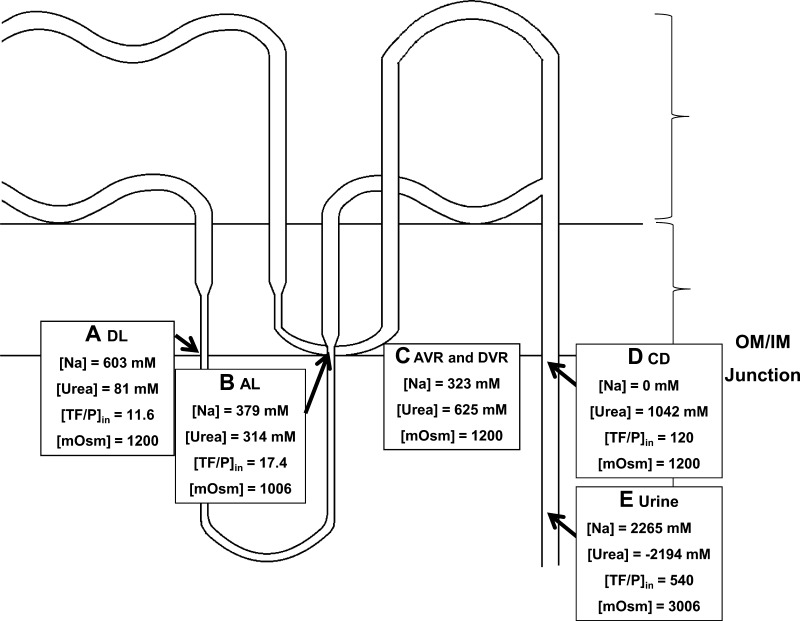
Modified redrawing of Fig. 2 of the original Kokko-Rector paper in simplified form. A: descending limb (DL) values. B: ascending limb (AL) values. C: interstitial values. D: collecting duct values at the outer-inner medullary junction (OIJ). Xs, nonreabsorbable solute, i.e., solutes in the collecting duct other than urea and NaCl viz. all salts, including potassium, ammonium, and organic molecules. E: urine values. Brackets denote concentration. OM, outer medulla; IM, inner medulla; TF/P, tubular fluid-to-plasma concentration ratio.

Table 1.

Table of values for different models considered

Variable	Kokko-Rector	Modified Kokko-Rector	Adjusted Vasa Recta Concentrations	Adjusted Collecting Duct Urea
Site of single effect	AL	AL	AL	AL
Osmolality at OM-IM junction, mosmol/kgH2O	1,200.0	1,200.0	1,200.0	1,200.0
Nonreabsorbable solute for CD, mosmol/kgH2O	200.0	200.0	200.0	200.0
Glomerular filtration rate, μl/min	No value	1,000.0	1,000.0	1,000.0
Plasma Na, mM	No value	140.0	140.0	140.0
Plasma urea, mM	No value	5.0	5.0	5.0
Nephrons with long loops, %	No value	30.0	30.0	30.0
Site to calculate volume in mass balance	No value	AVR	AVR	AVR
Water flow, μl/min
DL	No value	25.9	25.9	25.9
AL	No value	17.2	17.2	17.2
DVR	No value	25.0	25.0	25.0
AVR	No value	40.1	40.1	40.1
CD	No value	8.3	8.3	8.3
Urine	No value	1.9	1.9	1.9
TF/P inulin
DL	11.6	11.6	11.6	11.6
AL	17.4	17.4	17.4	17.4
DVR	No value	40.0	40.0	40.0
AVR	No value	24.9	24.9	24.9
CD	120.0	120.0	120.0	120.0
Urine	540.0	540.0	540.0	540.0
Na concentration, mM
DL	603.2	603.2	603.2	603.2
AL	379.0	379.0	379.0	379.0
DVR	No value	322.6	520.8	639.0
AVR	No value	322.6	520.8	639.0
CD	No value	0.0	0.0	320.9
Urine	No value	2,264.7	648.5	1,128.4
Na mass flow, nmol/min
DL	No value	15,600.7	15,600.7	15,600.7
AL	No value	6,535.0	6,535.0	6,535.0
DVR	No value	8,064.5	13,019.3	15,974.2
AVR	No value	12,936.2	20,884.0	25,624.0
CD	No value	0.0	0.0	2,673.8
Urine	No value	4,194.0	1,200.9	2,089.7
Na delivery, %
DL	No value	11.1	11.1	11.1
AL	No value	4.7	4.7	4.7
DVR	No value	5.8	9.3	11.4
AVR	No value	9.2	14.9	18.3
CD	No value	0.0	0.0	1.9
Urine	No value	3.0	0.9	1.5
Urea concentration, mM
DL	81.3	81.3	81.3	81.3
AL	313.5	313.5	313.5	313.5
DVR	No value	625.0	241.0	12.0
AVR	No value	625.0	241.0	12.0
CD	1041.7	1,041.7	1,041.7	420.0
Urine	937.5	−2,194.0	937.5	7.7
Urea mass flow, nmol/min
DL	No value	2,101.3	2,101.3	2,101.3
AL	No value	5,405.9	5,405.9	5,405.9
DVR	No value	15,625.0	6,025.2	300.0
AVR	No value	25,063.9	9,664.9	481.2
CD	No value	8,680.5	8,680.5	3,500.0
Urine	No value	−4,062.9	1,736.2	14.2
Urea delivery, %
DL	No value	42.0	42.0	42.0
AL	No value	108.1	108.1	108.1
DVR	No value	312.5	120.5	6.0
AVR	No value	501.3	193.3	9.6
CD	No value	173.6	173.6	70.0
Urine	No value	−81.3	34.7	0.3
Final urine osmolality, mosmol/kgH2O	1,800.0	3,006.0	3,006.0	3,006.0
Net free-energy flow, mJ/min	No value	0.0	31.8	−12.1

AL, ascending limb; OM, outer medulla; IM, inner medulla; CD, collecting duct; AVR, acending vasa recta; DL, descending limb; DVR, descending vasa recta.

The user can modify the water flow rate in each structure (Fig. 1B) either in terms of absolute flow rate (for the aggregate of all relevant nephrons) or tubular fluid-to-plasma concentration ratio (TF/P) inulin, representing the flow in terms commonly used in micropuncture studies. TF/P inulin represents the aggregate filtered load of water for the relevant nephrons (aggregate glomerular filtration rate) divided by the absolute flow rate for a given structure. The user clicks on a given option button to indicate the flow that is to be calculated from the other five flows to achieve overall mass balance for water. All solutions are assumed to be dilute.

Next, the user can modify the concentrations for Na or urea (in mM) in the streams entering and leaving the IM (Fig. 1, C and D). For Na mass balance, the role of the anion is taken into account as described below. The Na or urea values can be represented alternatively as mass flow rate or percent delivery vs. the aggregate filtered load for the represented nephrons. Values are entered for all structures at the OIJ, and the concentration, mass flow, and percent delivery of Na and urea in the final urine are calculated to achieve overall mass balance. Note that, when the user modifies Na (or urea) values in a particular structure other than the site of single effect, the complementary urea (or Na) values will be automatically calculated to match osmolality at OIJ.

Once all of the mass balances have been set as described above, the program calculates osmolalities and free-energy flows for all the streams (Fig. 1, E and F, respectively). The osmolalities are given by the equation:

$$\text{Osm}=\left[\text{Na}\right]\times 1.86+\left[\text{urea}\right]\times 0.96+\left[\text{NRS}\right]$$

where the brackets denote concentration. This equation uses the osmotic coefficients for NaCl (13) and urea (7).

The free-energy calculation follows Stephenson et al. (16):

$$\frac{\Delta \text{G}}{\Delta t}={\displaystyle \sum _{i,k}}\left[{\left(F_{ik}{\mu }_{ik}\right)}_{x=\mathrm{L}}-{\left(F_{ik}{\mu }_{ik}\right)}_{x=0}\right]$$

where ΔG/Δt is the change in Gibbs free energy per change in time, F_ik is the axial molar flow rate, and μ_ik is the chemical potential (in Joules) of the kth solute (k = 0: Na⁺, k = 1: Cl⁻, k = 2: urea) in the ith tube [i = 0: descending limb, i = 1: ascending limb, i = 2: descending vasa recta (DVR), i = 3: ascending vasa recta (AVR), i = 4: collecting duct, see Fig. 1]. Assuming ideality of solution,

$${\mu }_{ik}={\mu }_{0k}+\text{RT}\ln {\text{c}}_{ik}$$

where R is the ideal gas constant = 8.31 J mol/K, T is the absolute temperature in Kelvin, and c is the unitless concentration (i.e., divided by a reference concentration), they obtained:

$$\frac{\Delta \text{G}}{\Delta t}=\text{RT}{\displaystyle \sum _k}\left[{\text{F}}_{\text{U}k}\text{In}\left(\frac{{\text{c}}_{\text{U}k}}{{\text{c}}_{0k}}\right)-{\displaystyle \sum _i}{\left[{\text{F}}_{ik}\text{In}\left(\frac{{\text{c}}_{ik}}{{\text{c}}_{0k}}\right)\right]}_{x=0}\right]$$

where F_Uk is the collecting duct outflow rate, c_Uk is the outflow concentration of the kth solute, and c_0k is the reference concentration of the kth solute flowing into the medulla. The choice of the reference values is arbitrary because these terms cancel when steady-state mass balance holds.

RESULTS

To illustrate the use of the software, we used values from Fig. 2 of the original Kokko-Rector paper (8) describing the passive concentrating model for the IM. Figure 2 of this paper is drawn de novo based on the original. Table 1 shows the values from this figure in the first column labeled “Kokko-Rector.” [Note that Table 1 and Figs. 2–5 report the Na and urea concentrations (in mM) rather than the total osmolalities of NaCl and urea as shown in the original paper.] The first thing that was evident is that mass balance was not fully specified in Fig. 2 of the original paper because it did not include flows in the vasa recta. The next column of Table 1 (labeled “modified Kokko-Rector”) shows a complete set of values using the Kokko-Rector values as a basis. A file containing these values can be downloaded at http://helixweb.nih.gov/ESBL/FreeEnergy/sample_data.html and be inserted into the program using the “File” tab followed by “Load data.” Among the data added were values for the AVR and DVR, which were not taken into consideration in the original mass balance. This is important because the AVR furnishes the pathway by which water reabsorbed from the IMCD and descending limb is removed from the IM (20). Thus, even if the DVR and AVR are completely in equilibrium, the vasa recta produce a net loss of solute from the IM, not accounted for in the original model. In the modified Kokko-Rector model (column 2 of Table 1 and Fig. 3, data set “modified Kokko-Rector model” accessible at http://helixweb.nih.gov/ESBL/FreeEnergy/sample_data.html), we used the Na and urea values listed in Fig. 2 of the Kokko-Rector paper for the interstitium at the inner-outer medullary junction as the values for the DVR and AVR. When the mass balances were solved with the modified Kokko-Rector model, the urea concentration in the urine was calculated to be −2,194 mM to satisfy mass balance for urea. Because this is physically impossible, it was apparent that the Kokko-Rector model with the additional values assumed in column 2 is untenable.

Fig. 5.

Free-Energy Calculator results for modified Kokko-Rector values with no net urea secretion. A: descending limb values. B: ascending limb values. C: AVR and DVR values. D: collecting duct values at OIJ. Urea delivery in the inner medullary collecting duct (IMCD) was lowered to a level that requires no net secretion, that is, a percent delivery of 70%. E: urine values. Here, the urine osmolality was calculated to be 3,006 mosmol/kgH₂O. However, the inner medullary free-energy balance for this condition is negative and is thus inconsistent with a passive concentration of the inner medulla, i.e., it would require an energy input.

Fig. 3.

Free-Energy Calculator results for nominal Kokko-Rector values. A: descending limb values. B: ascending limb values. C: ascending (AVR) and descending vasa recta (DVR) values. In the original paper, the mass balance for the vasa recta was not fully specified. To represent the Kokko-Rector model, we assigned the interstitial concentrations assigned in the original paper to both AVR and DVR. D: collecting duct (CD) values. E: urine values. To achieve steady-state mass balance, the urea concentration was calculated to be −2,194 mM, a physically impossible value. Therefore, the nominal Kokko-Rector values were incompatible with mass balance in the inner medulla.

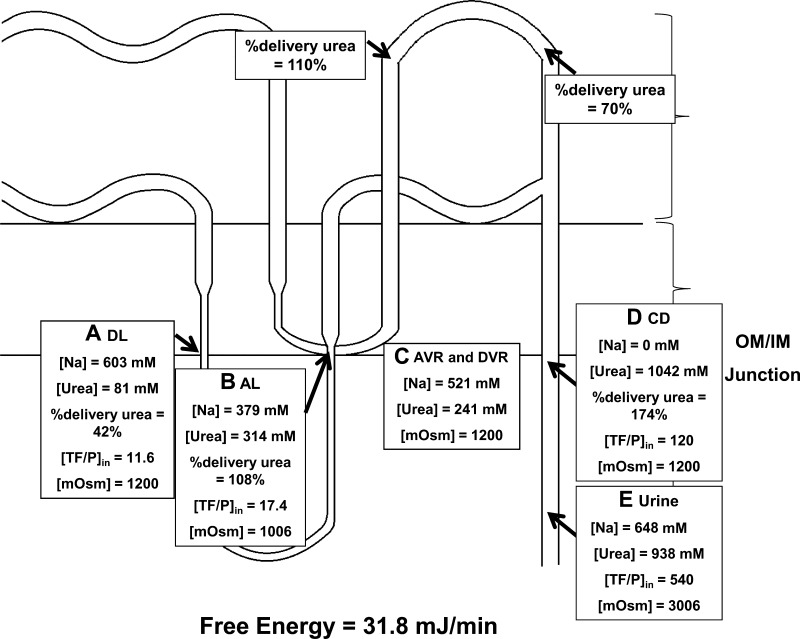
To repair the mass balance, it was necessary to adjust the values assumed for the interstitium and vasa recta by lowering the urea concentration and increasing the Na concentration. This alteration would produce more NaCl loss and less urea loss from the IM (column 3 of Table 1 and Fig. 4, data set adjusted vasa recta concentrations accessible at http://helixweb.nih.gov/ESBL/FreeEnergy/sample_data.html). We were able to match the final urinary urea concentration of the Kokko-Rector model of 938 mM by lowering the AVR and DVR urea concentration from 625 to 241 mM with a concomitant increase in the Na concentration from 323 to 521 mM. This gave a viable model that satisfied mass balance requirements and fit the Kokko-Rector conditions with the above exceptions. This set of conditions gave a positive free-energy balance (31.8 mJ/min) compatible with concentration entirely by passive processes inside of the IM.

Fig. 4.

Free-Energy Calculator results for modified Kokko-Rector values with adjusted vasa recta concentrations. A: descending limb values. B: ascending limb values. C: ascending and DVR values. The Kokko-Rector value of 938 mM urea in the final urine could be obtained by lowering the AVR and DVR concentration of urea from 625 to 241 mM with a concomitant increase in the Na concentration from 323 to 521 mM. The inner medullary free-energy balance for this steady state was calculated to be 31.8 mJ/min, consistent with a passive mechanism. D: collecting duct values at OIJ. The Kokko-Rector values for urea converted to percent delivery for urea are 174% of the filtered load of urea at the beginning of the inner medullary collecting duct. This requires extensive net urea secretion before the inner medullary collecting duct at sites outside of the inner medulla. E: urine values.

Thus, the passive model as described in column 3 of Table 1 is a feasible explanation of the concentrating processes in the IM given the inputs assumed. However, examination of the percent delivery values for urea in the collecting duct at the OIJ raises a new issue. This value is 174% of the filtered load of urea, implying net urea secretion upstream from this site. The usual explanation for a high mass flow rate of urea in the distal nephron comes from the work of Lassiter et al. (11), viz. urea that is reabsorbed from the IMCD is recycled by uptake into the loops of Henle. However, in this model, the percent delivery of urea out of the ascending limb of Henle's loop is only 108%. This represents only the long-loop ascending limb. This value is insufficient alone to explain the percent delivery of 174% in the collecting duct. Therefore, for the passive model to function in the Kokko-Rector formulation, one must assume that there is substantial urea secretion in the nephron external to the IM, i.e., in either the short loop nephrons or long loop nephrons at sites outside of the IM, but proximal to the outer medullary collecting duct. This could be achieved if there is a large amount of active or passive urea secretion in one or more nephron segments. Passive secretion could occur in the outer medullary vascular bundles (17) effectively transferring urea from the AVR exiting the IM to the short-loop descending limbs with which they are interspersed in the bundles (9). Micropuncture studies by Lassiter et al. (11) show a urea percent delivery of 110% in the early distal tubule, which nominally falls short of the amount required by the passive model (>174%). Active urea secretion of a magnitude that would account for 174% of the filtered load in the collecting ducts has not been demonstrated experimentally in isolated perfused proximal tubules (2, 4), thick ascending limbs (3), or cortical collecting ducts (3). However, urea transport has not been assessed in the isolated distal convoluted tubule.

To determine the effect of lowering the urea delivery to the IMCD to a level that could be explained without the postulated urea secretion, we reran the program with the urea concentration in the collecting duct at the OIJ reduced to 420 mM to give a percent urea delivery of 70% (a value predicted if there is no secretion of urea outside of the IM, see column 4 of Table 1 and Fig. 5, data set “adjusted collecting duct urea” accessible at http://helixweb.nih.gov/ESBL/FreeEnergy/sample_data.html). This value is consistent with the measured percent delivery in the late distal tubule in the study of Lassiter et al. (11). In this case, the concentration of solutes in the IM required a free-energy input (ΔG/Δt of −12.1 mJ/min) and thus the passive model does not hold under these conditions. Thus, we conclude that the Kokko-Rector model requires an additional component, namely urea secretion in some segment upstream from the collecting duct.

DISCUSSION

We have described web-based software to calculate mass balance and external free-energy balance in the renal IM. Free energy is an important constraint tied directly to any physiological process, and particularly to the production of the corticomedullary osmolality gradient. Because there is currently no consensus on how solutes are concentrated in the urine in renal IM, external free-energy balance calculations are a powerful way of classifying alternative mechanisms. Specifically, when the net external free-energy balance is positive, a passive process is feasible. If it is negative, an additional input of energy is required. The free-energy balance can be related to mechanisms of entropy creation in the medulla (18). Based on the work of Stephenson and colleagues (15, 16), the free energy may be expressed as a function of concentration and flow rates for each of the sites entering and exiting the renal IM.

Users can employ the Renal Inner Medulla Free-Energy Calculator to simultaneously consider changes in multiple factors, such as concentrations and flow rates, which influence the free-energy balance. The complicated interactions between these variables, for instance, the steps required to assure mass balance for a set of putative flow rates and solute concentrations, require a computational approach. Previously, calculations were carried out informally (“back of the envelope”), which were cumbersome due to the interlinked nature of the equations. Our program allows users to explore the whole of flow, concentration, and solute parameter space and map out, efficiently and accurately, the free-energy requirements implied by a particular choice of these values. A side benefit of this work is that we draw attention once again to the papers describing the mathematical formalism of the free-energy balance in the renal IM (15, 16, 18), which have been largely forgotten in recent literature. It is important to emphasize that the Free-Energy Calculator does not make assumptions about the mechanism involved in generating the osmolality gradient within the IM. Based on our software, the user can determine: 1) if a choice of flow rates and concentrations is admissible (in the sense that it is consistent with mass balance), 2) the magnitude of the net external free-energy balance implied by that choice, and 3) whether the physiological mechanism must be passive or active for a given set of flows and concentrations.

We illustrated the use of the Renal Inner Medulla Free-Energy Calculator tool using values from the original Kokko-Rector paper (8). The concentrations and flow rates from the original Kokko-Rector paper were underspecified for calculation of mass balance and free energy. However, using the Free-Energy Calculator, we could easily modify the Kokko-Rector model to obtain a set of conditions compatible with a purely passive concentrating model. Among the necessary adaptations was that the urea concentration in the AVR and DVR at the junction of the outer medulla and IM must be low (Fig. 4). The Free-Energy Calculator cannot address possible mechanisms for lowering urea concentration in the inner medullary vasa recta. We also found that, for successful adaptation of the Kokko-Rector model, there must be net urea secretion in the nephron before the IMCD at sites outside of the IM. Thus, use of the Free-Energy Calculator tool described here provides valuable assistance for the analysis of medullary concentrating mechanisms and for formulation of new experimental hypotheses. For advanced users, the calculations can be performed to evaluate mass and energy balance for the entire medulla by replacing all values associated with OIJ with those from the corticomedullary border.

GRANTS

This work was supported by the Intramural Budget of the National Heart, Lung, and Blood Institute (Project Z01-HL-001285). Funding from Vitreous State Lab and The Catholic University of America is gratefully acknowledged.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: R.L.V., A.S., J.Z., M.A.K., and T.P. conception and design of research; R.L.V., A.S., J.Z., M.A.K., and T.P. performed experiments; R.L.V., A.S., J.Z., M.A.K., and T.P. analyzed data; R.L.V., A.S., J.Z., M.A.K., and T.P. interpreted results of experiments; R.L.V., A.S., M.A.K., and T.P. prepared figures; R.L.V., A.S., M.A.K., and T.P. drafted manuscript; R.L.V., A.S., M.A.K., and T.P. edited and revised manuscript; R.L.V., A.S., J.Z., M.A.K., and T.P. approved final version of manuscript.