Determining Degradation and Synthesis Rates of Arabidopsis Proteins Using the Kinetics of Progressive ¹⁵N Labeling of Two-dimensional Gel-separated Protein Spots

Abstract

The growth and development of plant tissues is associated with an ordered succession of cellular processes that are reflected in the appearance and disappearance of proteins. The control of the kinetics of protein turnover is central to how plants can rapidly and specifically alter protein abundance and thus molecular function in response to environmental or developmental cues. However, the processes of turnover are largely hidden during periods of apparent steady-state protein abundance, and even when proteins accumulate it is unclear whether enhanced synthesis or decreased degradation is responsible. We have used a ¹⁵N labeling strategy with inorganic nitrogen sources coupled to a two-dimensional fluorescence difference gel electrophoresis and mass spectrometry analysis of two-dimensional IEF/SDS-PAGE gel spots to define the rate of protein synthesis (K_S) and degradation (K_D) of Arabidopsis cell culture proteins. Through analysis of MALDI-TOF/TOF mass spectra from 120 protein spots, we were able to quantify K_S and K_D for 84 proteins across six functional groups and observe over 65-fold variation in protein degradation rates. K_S and K_D correlate with functional roles of the proteins in the cell and the time in the cell culture cycle. This approach is based on progressive ¹⁵N labeling that is innocuous for the plant cells and, because it can be used to target analysis of proteins through the use of specific gel spots, it has broad applicability.

The growth and development of plant tissues is associated with an ordered succession of cellular processes that are dictated by the appearance and disappearance of proteins and the transcripts that encode them (1–4). The ratio of the synthesis and degradation rates of these molecules, whether they are in quasi-steady state or are rapidly changing in abundance, defines both the net turnover rate and the abundance of each (5). The control of the kinetics of these processes is central to how plants can rapidly alter specific protein abundance and thus molecular function to respond to environmental or developmental cues.

Genome wide analysis of Arabidopsis mRNA turnover rates has confirmed that knowledge of transcript decay rates can provide insights into diverse biological processes (6). For example, the number of introns and sequence elements in the 3′-untranslated region and subcellular localization of the encoded protein affect the turnover rate of transcripts in Arabidopsis (6). Analysis of plant proteome synthesis and degradation has lagged considerably from our understanding of these processes in the transcriptome.

Many methods have been developed to measure protein turnover in other organisms. Some are direct measurements of endogenous proteins using isotope labeling methods including both radioactive and stable isotope labeling (5, 7–10), whereas others use stable or transient transgenic techniques and a range of tags and markers (11, 12). The clearest advantage of isotope labeling approaches is that the tags are very subtle with little or no impact on cellular processes and allow the fully functional proteins being assessed to be produced and distributed within cells in a normal context. The advent of mass spectrometry as a key tool in proteomics has provided a means to use enrichment of the natural abundance of stable isotopes to provide mass rather than radio decay signals to track the synthesis of new proteins. The ratio between light and heavy isotopes and the degrees of enrichment provided by mass spectrometry provides a powerful means to measure synthesis and degradation rates of individual proteins (5, 13).

Stable isotope labeling using individual amino acids (SILAC)¹ has proven highly successful in mammalian cell culture systems (14). SILAC has also been used to measure protein turnover in yeast but required the use of auxotrophic mutants (5). However, this approach is problematic in plants that actively synthesize all of their amino acids de novo, which dilutes and mixes the label between amino acids and leads to inefficient incorporation into proteins (15, 16). Alternatively, ²H₂O, ¹⁸O, ¹⁵N, or ¹³C can be used to label whole plants and de novo synthesis tracked by the increase in the mass of the resulting proteins (9, 17). Deuterium oxide has been used to study labeling at the protein and amino acid levels (8, 9). The advantage of deuterium labeling is that it rapidly enters cellular compartments and equilibrates with the water environment. However, ²H₂O is not biologically benign, and multicellular organisms are limited in the percentage of deuterium oxide they tolerate (8, 9, 18).

An increasing range of studies are using saturation or partial ¹⁵N labeling in steady-state experiments in plants as a means to perform quantitative proteomic studies (19–21). However, its use to measure protein synthesis rates is still uncommon for a variety of reasons. First, there are informatics and technical hurdles to combine identification and quantification of proteins and their labeling state to calculate turnover rate. Second, a variety of factors including differences in the labeling of amino acids, changes in incorporation rates over time and the range of turnover rates provide a heterogeneous response and complicate data interpretation. Here we have sought to overcome these obstacles and provide a data processing approach to measure kinetics of changes in ¹⁵N incorporation of peptides from in-gel digestions of separated protein spots.

EXPERIMENTAL PROCEDURES

Arabidopsis Suspension Cell Growth and Nitrogen Source Test

Arabidopsis cell suspension was cultured in growth medium (1× Murashige and Skoog medium without vitamins, 3% (w/v) sucrose, 0.5 mg/liter naphthalene acetic acid, 0.05 mg/liter kinetin, pH 5.8) at 22 °C under continuous light conditions and light intensity of 90 μmol m⁻² s⁻¹ with orbital shaking at 120 rpm. Cultures were maintained in 250-ml Erlenmeyer flasks by the inoculation of 20 ml of 7-day-old cells into 100 ml of new medium. The same growth medium without nitrogen (no ammonium nitrate or potassium nitrate) was used for the nitrogen source experiments. Ammonium nitrate (1.65 g/liter), potassium nitrate (1.9 g/liter), or both were added to the growth medium without nitrogen for the different nitrogen source media tested. Fresh weight, dry weight, and sucrose and nitrate concentrations were measured by collecting 5 ml of cell culture from different media each day for comparison. The cells were collected using vacuum filtration onto filter paper.

Comparison of Proteome Pattern in ¹⁴N and ¹⁵N Media by Two-dimensional Fluorescence Difference Gel Electrophoresis (DIGE)

Ammonium-¹⁵N nitrate-¹⁵N (1.69 g/liter) and potassium nitrate-¹⁵N (1.92 g/liter) (98% ¹⁵N; Sigma) were added to growth medium without nitrogen as the ¹⁵N growth medium. Seven-day-old cells were washed with no nitrogen growth medium three times before transfer to ¹⁴N or ¹⁵N medium. After 7 days of growth, these ¹⁴N and ¹⁵N cells where subcultured again. Fresh cells (0.1 g) were collected for analysis from 7-day-old cells that had been subcultured in this manner in three successive, weekly cycles in either ¹⁴N or ¹⁵N growth medium. Total proteins were extracted using methanol and chloroform (2). Protein was dissolved in lysis solution (8 m urea, 40 mm Tris base, 4% (w/v) CHAPS), and concentration was measured by Amido Black (22). A 75-μg protein aliquot of each sample was precipitated using 9 volumes of cold acetone and stored overnight at −20 °C. Precipitated protein was pelleted by centrifugation of samples at 20,000 × g for 15 min, and pellets were dried at room temperature for 5 min. Protein (25 μg) from each sample was combined to make a DIGE reference standard for labeling with the fluorescent dye Cy2, whereas 50 μg of protein from each sample was labeled with either fluorescent dye Cy3 or Cy5. All of the samples were combined and added to rehydration solution (8 m urea, 2% (w/v) CHAPS, 0.5% (v/v) IPG buffer, 18 mm DTT, 0.001% (w/v) bromphenol blue) to make a final volume of 450 μl. Triplicate biological samples were separated by IEF pH 3–10 nonlinear (24 cm; GE Healthcare) according to the manufacturer's instructions. After completing IEF, the strips were then transferred to an equilibration solution (6 m urea, 50 mm Tris base, 2% (w/v) SDS, 26% (v/v) glycerol, 0.001% (w/v) bromphenol blue, 65 mm DTT) and incubated in the dark for 15 min at room temperature with shaking. The strips were then transferred to the same solution omitting DTT but including iodacetamide (135 mm) and incubated for a further 15 min at room temperature in the dark with shaking. After a brief rinse in 1.5 m Tris-HCl (pH 8.0), 1% SDS, the strips were transferred to 12% (w/v) polyacrylamide gels and overlaid with 1.2% (w/v) agarose. The second dimension SDS-PAGE was run in the dark at 50 mA/gel for 6 h in a glycine buffer system. The proteins were visualized on a Typhoon laser scanner (GE Healthcare), and image comparison was performed using the DECYDER software package (version 6.5; GE Healthcare).

Amino Acid ¹⁵N Incorporation Measurement by GC-MS

Seven-day-old cells in ¹⁴N medium were washed three times with no nitrogen media and then transferred to ¹⁵N medium. The cells (5 ml) were collected by vacuum filtration at the 0.5-, 8-, 48-, 96-, and 168-h time points for the first experiment and at the 0.5-, 8-, 24-, 48-, 72-, 96-, 120-, 144-, and 168-h time points for the second experiment. Fresh cells (0.1 g) were snap frozen in liquid nitrogen and stored at −80 °C. A 500-μl volume of methanol metabolite extraction medium (20 parts methanol:1 part 0.2 mg/ml ribitol stock solution:2 parts H₂O) was added to each sample, vortexed, and heated at 65 °C in a thermomixer for 30 min at 1400 rpm. The tubes were then centrifuged at 14,000 rpm for 10 min, the supernatant was collected, and 60 μl of each sample was dried overnight by rotary evaporation in a SpeedVac (Savant). Dried samples were derivatized with 20 μl of methoxylamine hydrochloride (20 mg/ml) at 30 °C for 90 min. Then 20 μl of MBTSTFA was added, and the samples were shaken (750 rpm) while being incubated at 85 °C for 60 min. Finally, 10 μl of an Alkanes mix was added as a retention time marker. The lists of the m/z values used for each derivatized amino acid, the formula used for ¹⁴N and ¹⁵N qualifier ions (Q ion), and the natural theoretical distribution of the unlabeled and labeled components follow (Table I). The GC-MS settings and ¹⁴N to ¹⁵N ratio calculation were based on protocols published previously (23). For amino acids containing two nitrogen atoms, glutamine and asparagine, the qualifier ions included both the M⁺¹ and M⁺² peaks.

Table I. Isotope contributions of amino acids.

Amino acids	Q ion formula	14N Q ion	15N Q ion	15N Q ion 2	Isotope contribution (%)	Isotope contribution 2 (%)
Aspartic acid	C18H40NO4Si3	418	419		0.363
Alanine	C14H32NO2Si2	302	303		0.266
Valine	C13H30NO2Si2	288	289		0.255
Leucine	C14H32NO2Si2	302	303		0.266
Isoleucine	C14H32NO2Si2	302	303		0.266
Glycine	C10H24NO2Si2	246	247		0.221
Methionine	C13H30NO2SSi2	320	321		0.255
Serine	C20H46NO3Si3	432	433		0.386
Proline	C19H24NO4	330	331		0.22
Threonine	C18H42NO3Si3	404	405		0.363
Cysteine	C17H40NO2SSi3	406	407		0.359
Phenylalanine	C17H30NO2Si2	336	337		0.299
Glutamic acid	C22H48NO4Si3	432	433		0.409
Glutamine	C19H43N2O3Si3	431	432	433	0.378	0.173
Asparagine	C18H41N2O3Si3	417	418	419	0.367	0.149

Whole Protein and Individual Protein Abundance Change Measurement DIGE

A 10-ml volume of cell suspension was collected at 0, 24, 96, and 168 h (six replicates). Half of each sample was used for fresh and dry weight measurements, whereas the other 5 ml was used for protein measurement. The cells (500 mg of fresh weight) were collected at time points 0, 24, 96, and 168 h. Half of the samples (three replicates) were vortexed with Qiagen tissue lysis beads (5 mm) and boiled in 1× sample buffer for 5 min and then centrifuged at 10,000 × g for 10 min. The supernatant was collected and separated with one-dimensional SDS-PAGE on Bio-Rad Criterion precast gels (10–20% (w/v) acrylamide, 1 mm Tris-HCl, 18-well comb gels). Gel electrophoresis was performed at 20 mA/gel for 5 h. The proteins were visualized by colloidal Coomassie Brilliant Blue G250 staining. The entire lane was selected and quantified using ImageJ. Proteins from the remaining half of the samples were precipitated with the methanol/chloroform method described above. The pellets were then dissolved in lysis buffer, and the concentrations were measured by an Amido Black method (22). Because the ImageJ and Amido Black methods gave similar protein abundance levels, the values were averaged to represent total protein abundance change at time points 0, 24, 96, and 168 h.

Seven-day-old ¹⁴N medium growth cells were washed three times with no nitrogen media and then transferred to ¹⁵N medium. A 5-ml volume of cell culture was collected by vacuum filtration at 0, 24, 96, and 168 h in triplicate. Total protein was extracted, and protein measurements were determined as described previously. Standards for Cy2 labeling were made by mixing equal amounts of protein from each sample. A total of six DIGE gels were made: Gel 1 standard (Cy2), 0A (Cy3) and 24A (Cy5); Gel 2 standard (Cy2), 24B (Cy3) and 96A (Cy5); Gel 3 standard (Cy2), 96B (Cy3) and 168A (Cy5); Gel 4 standard (Cy2), 168B (Cy3) and 0B (Cy5); Gel 5 standard (Cy2), 24C (Cy3) and 168C (Cy5); and Gel 6 standard (Cy2), 0C (Cy3) and 96C (Cy5). Image analysis was as previously mentioned. The abundance of each spot at a particular time point was an averaged value and normalized by dividing by the abundance of the protein at the 0 time point.

Preparative Two-dimensional Gel Electrophoresis and In-gel Trypsin Digestion

Whole protein samples (700 μg) at time points 0, 24, 96, and 168 h were precipitated using nine times their volume of cold acetone at −20 °C overnight. The proteins were pelleted by centrifuge 20,000 × g for 15 min and dried at room temperature for 5 min. The samples were added to rehydration solution (8 m urea, 2% (w/v) CHAPS, 0.5% (v/v) IPG buffer, 18 mm DTT, 0.001% (w/v) bromphenol blue) to a final volume of 450 μl. They were first separated by IEF pH 3–10 nonlinear (24 cm; GE Healthcare) according to the manufacturer's instructions. After the first dimension, IEF strips were then transferred separately to an equilibration solution (6 m urea, 50 mm Tris base, 2% (w/v) SDS, 26% (v/v) glycerol, 0.001% (w/v) bromphenol blue, 65 mm DTT) and incubated for 15 min at room temperature with shaking. The strips were then transferred to the same solution omitting DTT but including iodoacetic acid (135 mm) and incubated for a further 15 min at room temperature with shaking. After a brief rinse in 1.5 m Tris-HCl, 1% SDS (pH 8.0), the strips were transferred horizontally onto 12% (w/v) polyacrylamide gels and covered with 1.2% (w/v) agarose. Two-dimensional gels were run at 50 mA/gel for 6 h. The proteins were visualized by colloidal Coomassie Brilliant Blue G250 staining. The same 120 protein spots from 0-, 24-, 96-, and 168-h gels were cut and in-gel digestion by trypsin according to the method described by Taylor et al. (24), with only a quarter of the trypsin amount used to decrease the effect of trypsin peaks on data interpretation.

Mass Spectrometry Analysis of the Digested Spots

Peptides were analyzed with an UltraFlex III MALDI-TOF/TOF mass spectrometer (Bruker Daltonics). In-gel digested peptides were reconstituted with 5 μl of 5% ACN (v/v), 0.1% (v/v) TFA. Two μl of each sample was spotted onto a MTP 384 MALDI target plate and mixed with 2 μl of spotting matrix (90% ACN, 10% saturated α-cyano-4-hydroxycinnamic acid in TA90 (90% ACN, 0.01% TFA)). Dried spots were overlaid with 10 μl of cold washing buffer (10 mm NH₄H₂PO₄, 0.1% TFA) and allowed to stand for 10 s before removal by pipette. The spots were analyzed at 50–85% laser intensity with up to 1200 shots for MS analysis per spot. Ions between 700 and 4000 m/z were selected for MS/MS experiments using 3% additional laser power. Masses corresponding to trypsin autolysis were excluded from analysis. Tandem mass spectrometry data were analyzed using Biotools (Bruker Daltonics) and an in-house Arabidopsis database comprising ATH1.pep (release 9) from the Arabidopsis Information Resource and the Arabidopsis mitochondrial and plastid protein sets (33,621 sequences; 13,487,170 residues), using the Mascot search engine version 2.1.04 and utilizing error tolerances of ±1.2 Da for MS and ±0.6 Da for MS/MS; “Max Missed Cleavages” set to 1; variable modifications of oxidation (Met), carbamidomethyl (Cys), and deamidated (Asn and Gln). Only protein matches with more than two peptides and with ion scores greater than 37 were used for analysis (p < 0.05). For all 120 spots, the 0- and 24-h time points were used for both MS and MS/MS analyses for protein IDs, whereas only the MS data were analyzed for 96 and 168 h. Search results were exported to comma saprated value format for each spot. Identifications are outlined in supplemental Table 1. Spectral data (supplemental Data 2) are available for download from the ProteomeCommons Tranche network (ProteomeCommons.org) using hash codes (2DZyjPUwvskRQQDr5+RNbT+e2xS7Mm4JleiiaNXXrWMGT++RrpLjBYqOVhCJCqXpS619dJT9K7T4H6vsrGKBf2YxJEYAAAAAAAACWQ==).

The false discovery rate cutoff ion score was calculated by concatenation of all the MS/MS spectra from gel spot analysis at the 0- and 24-h time points and analyzed against a combined forward/reverse ATH1.pep (release 9) database. Of the peptide ions selected for quantification by Isodist, 428 (95%) had an ion score greater than 22 (false discovery rate < 10%), and a small set of 25 peptides used for the subsequent MS analysis had an ion score of <22. These 25 peptides with ion score of <22 were assessed in two ways. First, all 22 peptides matched to proteins in gel spots with more than five peptides and protein scores with false discovery rates of <95%. Second, upon manual inspection, all of the empirical data aligned well with predictions based on Isodist calculations for partial labeling of the matched peptide sequence. Retrospective analysis of the degradation and synthesis rates of the proteins that incorporated the use of these ions showed no noticeable difference between means and S.D. with or without inclusion of the intensity of these lower scoring MS ions.

Isodist Measurement of Relative Isotope Abundance

To calculate heavy label incorporation and the relative abundance of natural abundance (NA) and heavy labeled (H) peptide populations, MALDI-TOF/TOF MS data were exported to mzXML files (CompassXport 3.0 (Bruker)) and were subsequently converted to text files using the ProteomeCommons.org IO Framework 6.21 (http://proteomecommons.org/current/531/). Text files were then parsed using a script written in Mathematica 7.0 (Wolfram Research) for further analysis. Isotopic envelopes were fitted using a two population model consisting of natural abundance and ¹⁵N-labeled fractions with the open source program Isodist (http://williamson.scripps.edu/isodist/) as previously described (25). Briefly, five iterations were allowed per round of fitting to calculate the abundance (amplitude) of the natural abundance (¹⁴N) form of the peptide, abundance of ¹⁵N-labeled population, ¹⁵N incorporation level, Gaussian peak width, mass error, and base line. The results from Isodist were then parsed with another Mathematica script, and spectra were generated by overlaying experimental and calculated data with these images then exported as PDF files for manual inspection. Only peptides with good signal-to-noise were considered further. All of the data on a peptide by peptide basis are provided in supplemental Table 2. Spectra from Isodist (supplemental Data 3) are available for download from the ProteomeCommons Tranche network (ProteomeCommons.org) using hash codes (ufWHF3kYYqD7xqMt1YraUK6B3loQ0O+ZR1Ly4CBMrtHLA2Lp1l77CfdlrQH90T2rkdzMXZXhGw7C4hVcJrXETm9GnfYAAAAAAAACmA==).

Calculations

Amino Acid Half-lives

The half-lives of amino acids were calculated by first dividing the amino acids into sets based on time points around H/(H + L) = 0.5. These were the 0.5–8-, 8–24-, 24–48-, and 48–72-h ranges. The final value shown for each amino acid is an average of data from these time points.

Protein Degradation Rate

We first calculated protein-specific degradation rates (K_D) in a manner similar to that previously described (26, 27). Briefly, for a given time point t, abundance levels of NA (A₁₄) and isotopically labeled (A₁₅) samples were determined using Isodist and then used to calculate relative isotope abundance (RIA) of NA samples at each time point. For time point 0, the RIA is equal to 1.

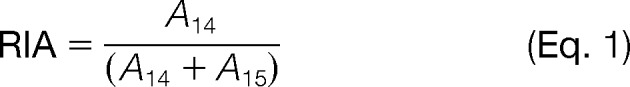The first order (i.e. protein degradation as a function of protein concentration) rate constant (K_D) was first calculated in a manner similar to that previously described (26, 27). The fraction of natural abundance isotope remaining at time point t, was natural log-transformed, and a linear regression used to calculate K_loss. K_D was then calculated by subtracting K_dilution, which is the growth rate of the cell culture system and was also acquired by linear regression. In our system, K_dilution was 0.232.

As an alternative, we can represent the ratio of heavy isotope to light isotope (R) as calculated by Isodist from experimental data, in terms of a series of factors to determine degradation rate: 1) the fold change in protein abundance (FCP), which can be measured; 2) the amount of protein degradation (D) that we wanted to derive; and 3) the amount of the NA protein before transfer to ¹⁵N-enriched medium (i.e. time 0) represented by abundance (A). Thus, we derived Equation 3, which is an approach similar to that of Jayapal et al. (28).

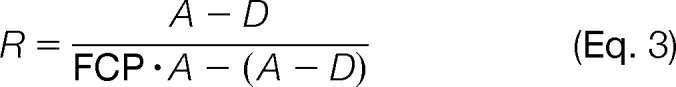For time point t, relative to time point 0, FCP was calculated by multiplying the total cellular protein abundance fold change of the cell culture with the individual protein abundance fold change from the DIGE analysis. Hence, if a protein abundance does not change, FCP = 1, whereas if it doubles, then FCP = 2. P_deg (the fraction of natural abundance protein present at time point 0 that is remaining at time point t) could thus be calculated using only two parameters, FCP and R.

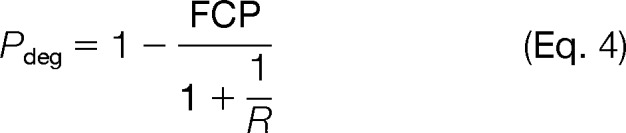In a manner analogous to Jayapal et al. (28), K_D can then be calculated by the natural log of NA protein remaining (1 − P_deg).

We then used Equation 5 to calculate K_D in two different ways. First, we used linear regression to define K_D as a rate constant, assuming first order kinetics. Second, we calculated K_D for each protein at each time point and then averaged these values, which allows us to consider proteins for which simple kinetics do not apply.

Protein Synthesis Rate

Because of the availability of quantitative protein abundance data at each time point from the DIGE analysis, we could also calculate protein-specific synthesis rates (K_S). Presuming equal degradation rates between ¹⁴N and ¹⁵N samples, as others have previously reported (29–31), we deduced that the change in abundance of a ¹⁵N-labeled protein (dA₁₅/dt) is the difference between K_S and K_D multiplied by the protein abundance.

Upon integration

When t = 0, because there were no ¹⁵N proteins, A₁₅ = 0 and so Constant = K_S. Thus,

and then the relationship between K_S and K_D is as follows.

By substitution of Equation 5 into Equation 9,

The change in the abundance of a protein was thus a combination of the ¹⁵N (A₁₅) and ¹⁴N (A·P_deg) protein abundance changes. To represent this, we derived the following equations.

K_S, the average rate of synthesis of a protein to a time point was solved by combining Equations 5, 10, and 12

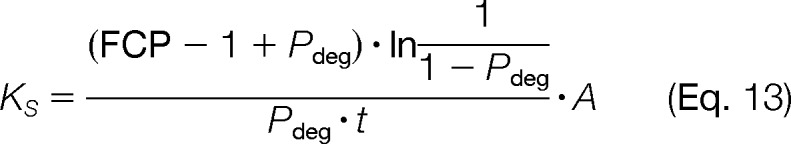To account for increasing cell amounts through time, the relative cell numbers (i.e. the increase in total protein in the cell culture) were averaged between t = 0 and a time point t. The synthesis rate constant (K_S/A) was then normalized across all data by dividing by the relative cell number.

RESULTS

Arabidopsis Cell Culture Growth in ¹⁵N Labeling and Labeling of Proteins

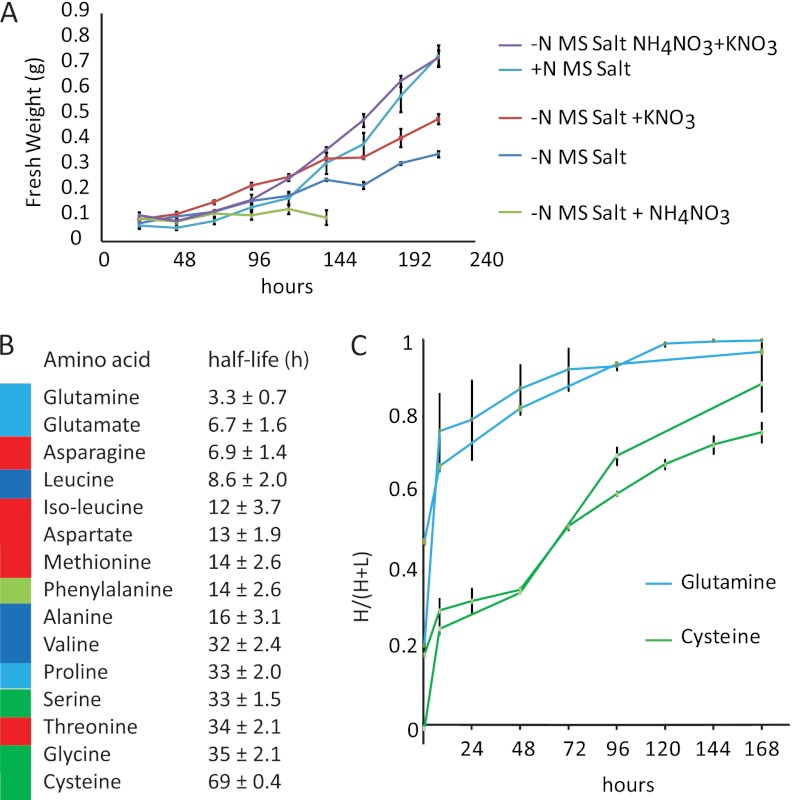
Arabidopsis cell cultures have been used for steady-state ¹⁵N labeling experiments to determine abundance changes in a variety of experiments (15, 16, 32). One of these reports noted that nearly complete labeling with ¹⁵N was possible in 2 weeks of culturing of cells when 19 mm 98% K¹⁵NO₃ was used to replace all nitrogen sources in the cell medium (15). In our laboratory, a rapidly growing Arabidopsis cell culture is used for a wide range of experiments, but the medium contains two nitrogen sources for optimal growth: 18.8 mm KNO₃ and 20.6 mm NH₄NO₃. To assess the impact of nitrogen source on growth, we measured changes in fresh weight of culture over 216 h (9 days). When cells were transferred to medium without a nitrogen source (−N MS salt medium), there was a doubling of fresh mass of cells over 9 days, whereas in premixed media containing both sources of nitrogen, cell mass increased 7-fold over the 9 days. When −N MS salt medium was supplemented with either KNO₃ alone or NH₄NO₃ alone, substantially lower growth was recorded than with both nitrogen sources in the premixed media. Co-supplementation of both nitrogen sources into −N MS salt media provided growth equivalent to the premixed media (Fig. 1A). We therefore decided to retain the use of two nitrogen sources in our experiments, through the use of 98% K¹⁵NO₃ and 98% ¹⁵NH₄¹⁵NO₃ supplementation of −N MS salts.

Fig. 1.

Growth rate and amino acid pool labeling over time of Arabidopsis cell culture. A, cell culture growth rate in media with different sources of N. B, ¹⁵N incorporation rate into different amino acids. The colors show amino acids in different synthesis pathway families. C, kinetics of incorporation as proportion of ¹⁵N (H) compared with both ¹⁵N and natural abundance (H + NA) into the amino acids with the fastest (Gln) and slowest (Cys) ¹⁵N incorporation rates.

There was no apparent difference in total cell yield from cell flasks whether these nitrogen sources were at natural abundance (99.6% ¹⁴N, 0.4% ¹⁵N) or ¹⁵N enriched (2% ¹⁴N, 98% ¹⁵N). To assess whether growth in 98% ¹⁵N influenced the steady-state proteome of the cell culture, total protein was extracted from cells cultured in two successive 7-day cycles in ¹⁴N or ¹⁵N medium. Fluorescence difference gel electrophoresis using Cy dyes was used to look for significant differences in the protein profiles (supplemental Fig. 1). No significant differences were observed in statistical analysis of three biological replicates. Tandem mass spectrometry of the two samples revealed only matches to ¹⁴N-containing peptides from the ¹⁴N-labeled cells and only matches to ¹⁵N-containing peptides from the ¹⁵N-labeled cells (supplemental Data 1).

Dynamics of ¹⁵N Labeling of Amino Acids

To determine how rapidly ¹⁵N labeled the amino acid pools in the cells, we performed GC-MS analysis of hot methanol (23) extracts derivatized with MBTSTFA and quantified the half-life of ¹⁴N-containing amino acids following the movement of washed cells from ¹⁴N medium to ¹⁵N medium (Fig. 1B). Although we could not detect all of the amino acids using this method, we could reproducibly observe 15 amino acids and show that the half-lives of these pools are between 3 and 70 h (Fig. 1B and supplemental Fig. 2). As expected, glutamine and glutamate were the most rapidly labeled with ¹⁵N, with nearly 70% incorporation within the first 24 h. Most of the other amino acids followed with half-lives within 24 h, but the most difficult pools to label rapidly were the amino acids derived from 3-phosphoglycerate, namely serine, glycine, and cysteine (Fig. 1C). This plant cell culture is not photosynthetically active, so photorespiratory glycine and serine were not a complicating factor in assessing ¹⁵N incorporation. Although ¹⁵N labeling of amino acids showed a steady increase over time, none appeared to obey a simple standard curve (supplemental Fig. 2). This complicated pattern may arise from the multiple sources of amino acids for protein synthesis, including de novo amino acid synthesis from the ¹⁵N-enriched inorganic nitrogen sources, scavenged from the degradation of proteins, and/or different subcellular amino acids pools (33, 34). At 8 h the calculated average ¹⁵N incorporation of the amino acid pool was 43.6% (this number was calculated based on the measured ¹⁵N incorporation of 15 free amino acids and the known proportion of each of these amino acid in Arabidopsis proteins). A lag followed between 8 and 24 h, perhaps because of the degradation of proteins at natural abundance levels of nitrogen producing amino acids. At 24, 96, and 168 h, the ¹⁵N incorporation in the total pool was 52.7, 86.7 and 90.5%, respectively.

Dynamics of ¹⁵N Labeling of Proteins

Based on these amino acid data, we chose three time points for analysis of incorporation of labeled amino acids into proteins, namely 24 h (1 day), 96 h (4 days), and 168 h (7 days). Three independent sets of flasks were transferred to ¹⁵N medium, sampled at the times indicated, and snap frozen; proteins were extracted from each sample and quantified. Substantial growth occurred over these time periods, with the total protein in each flask rising from 1 at 0 h, to 1.05 ± 0.10 at 24 h, 1.97 ± 0.11 at 96 h, and 6.02 ± 0.23 at 168 h based on Amido Black protein assays and quantification of Coomassie staining on one-dimensional gels (data not shown). Visual inspection of Coomassie-stained gels loaded on a protein basis showed that most protein spots were present at similar abundance across all time points (supplemental Fig. 3). To determine quantitatively whether protein profiles were changing relative to the total extracted protein amount, we performed an integrated DIGE experiment with the 12 samples on IEF/SDS-PAGE gels (supplemental Fig. 4). Approximately 20% of the protein spots were statistically observed to change in abundance, and the changes observed were all <2-fold between time points, indicating a relatively steady-state system for each protein relative to the size of the proteome as a whole (supplemental Table 1).

A set of 120 protein spots, matched across a typical gel from each time point, was excised from each time point and digested with trypsin (supplemental Fig. 5). The 480 samples were analyzed by MALDI-TOF/TOF. For the 0- and 24-h time points, a set of 10–20 MS/MS spectra were obtained from each sample to identify the proteins and define the parent mass of ions matching to peptides from each protein that could be used as proteotypic peptides across the time series. In total, 108 proteins were identified with 648 peptides (supplemental Table 1). For the 96- and 168-h time points, whereas both MS and MS/MS data were obtained, only MS spectra were pursued. We had previously found that identification of MS/MS spectra from the partially incorporated spectral envelopes observed at later time points was extremely poor, so we concentrated on analysis of high quality MS spectra for quantification purposes at 96 and 168 h.

Raw data were analyzed with Isodist (25), a program that uses Fourier transform convolution and least squares to fit calculated distributions to our experimental data set. Using the combined peptide identifications at 0- and 24-h time points, the relative abundance of the NA and the ¹⁵N-labeled H peptide ion envelopes were calculated. Only good fit, high intensity spectra were chosen for further analysis and incorporation into the measurements made. Full data sets used are provided online as supplemental Data 3. Fig. 2A shows typical examples of two peptides and the MS spectra showing the lighter, natural abundance ion envelope (NA), and the heavier (H) ion envelope of peptides derived from the ¹⁵N enriched pool of amino acids. The MAB1 (At5g50850) peptide (LALPQIEDVR) has a relatively slow synthesis rate. There is little evidence of peptides from the ¹⁵N pool after 24 h, but by 96 h a significant H peptide envelope is found. The TRIP-1 (At2g46280) peptide (DHTPTLWFADNGER) has a relatively fast synthesis rate, with an abundant H peptide envelope already at 24 h and few NA peptides remaining by 96 h, suggesting that a significant turnover of the original ¹⁴N protein was likely to have occurred. It is evident from both examples that although the NA peptides have a defined and constant mass, the mass envelope of the H peptides changes during the course of the experiment (Fig. 2A). This is due to the increased labeling of the amino acid pools over time. Combining all of the peptide spectra used in our analysis, we have made frequency histograms of the % ¹⁵N in the heavy spectral envelope. At 24 h, this averaged at 68% and then rose to ∼90% by 96–168 h (Fig. 2B). Interestingly, at the 24-h time point, this is slightly higher than the value predicted from the level of incorporation seen in the amino acid pools by GC-MS (Fig. 1, B and C, and supplemental Fig. 2). This would suggest either a small systematic error in our measurements, Isodist fitting, or GC-MS calculations or the presence of a pool of nonincorporating amino acids at the early stage in the cells that do not participate in protein synthesis. When all of the peptides for these two sample proteins were considered, it was clear there was a high degree of correlation between the NA/(H + NA) ratios for peptides derived from the same protein at a given time point giving confidence in these ratios at the protein level (Fig. 2C).

Fig. 2.

Analysis of ¹⁵N incorporation into peptides of specific Arabidopsis cell culture proteins. A, examples of theoretical prediction and actual MS fit at 0, 24, 96, and 168 h (theoretical prediction, red; actual, blue) for single peptides derived from MAB1 (At5g50850) and TRIP-1 (At2g46280). B, histogram of calculated ¹⁵N partial labeling averages for peptides at 24, 96, and 168 h following ¹⁵N addition. In total, 336, 381, and 344 peptides are used for the distributions at each time point. C, average ratio of ¹⁴N only (NA) to ¹⁵N containing (H) + ¹⁴N only peptides (NA/(H + NA)) for all the MAB1 and TRIP-1 peptides at 24, 96, and 168 h. The error bars show the standard deviation.

Calculation and Comparison of K_D Rates for Proteins

A first consideration to the strategy of stable isotopic tracers in protein turnover studies is the speed with which the amino acid pools are replaced with labeled versions (35). We specifically considered whether a significant amount of newly synthesized protein might have contributed to the NA envelope in the early time points before the amino acid pools had incorporated sufficient ¹⁵N. Such an accumulation would have adversely affected our calculations (see “Experimental Procedures”). Our analysis, based on GC-MS data, determined that this effect would be small to negligible on the H/NA ratio: <6% in sample calculations of peptides at 24 h for peptides >8 amino acids in length (92% of the peptides examined) and negligible for all peptides examined at the 96- and 168-h time points. Our analysis further indicated that even this 6% effect on H/NA had a less than 0.5% effect on the final K_D calculations.

Using the H to NA peptide ratio information, the increase in total protein abundance in the cell culture through time, and the DIGE data for individual proteins (supplemental Table 1), the K_D for each protein could be determined (supplemental Table 2). As outlined under “Experimental Procedures,” three different methods were used to compare our approach with others recently published. First, we have calculated values using steady-state assumptions and linear regression (27). Second, we have used regression with our modified K_D calculation, which allows us to correct for changes in protein abundance during the course of the experiment. With this alternative method of calculating K_D, we can avoid the steady-state assumption, which is likely not appropriate for many proteins in our cell culture system. In this respect, our analysis is similar to a recent study using a dual labeling strategy of SILAC and iTRAQ to correct for changes in protein abundance in log growing bacteria (28). For the two regression methods, R values for the first order kinetics fit of the data varied, 76 of the 84 proteins met the thresholds defined by Yee et al. (27), and 42 of the 84 proteins met the thresholds defined by Jayapal et al. (28). However, given that a significant number of proteins do not have simple first order kinetics of degradation (26, 35), we used a third method: while still correcting for protein abundance changes, we averaged the K_D values calculated at each time point (5, 26). Sample calculations using these latter equations for the two peptides shown as examples in Fig. 2A are provided in supplemental Data 4. For a protein to have a K_D calculated, we required quantitation data from at least three peptide(s) over two time points for inclusion in the data set.

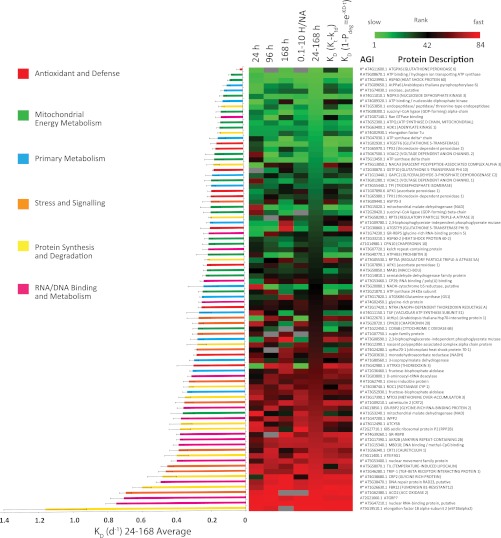
To compare data from each time point, we ranked K_D across the 84 proteins for which we had sufficient numbers of peptide identifications to make a K_D calculation. These ranks are shown in Fig. 3 as a heat map to compare the ranks for the 24-, 96-, and 168-h data sets. It was clear from these data that there was general agreement on protein rank in K_D calculations at different time points, with the majority of the green, low numbered ranks at the top of the heat map, and the majority of the red, high numbered ranks, at the bottom. We were conscious that small numbers of peptides with more extreme H/NA ratios could potentially bias the analysis because they were likely to be the most error prone measurements. We thus combined all the data for peptides with H/NA within the more restricted 2 orders of magnitude range of 0.1–10, which was ∼65% of the peptide data set, and compared a combined rank of K_D against the ranks for each time point and the average of all three time points. Again there was general agreement in this restricted data set of the slow and fast degrading proteins. Using this averaging approach, we obtained similar K_D rankings to when we used either of the regression methods (27, 28). Notably, our K_D average was most similar to the second regression method, in which iTRAQ labels were used to account for changes in protein abundance (28). In an analogous manner, we used FCP, thereby negating the necessity of a steady-state assumption. Although the heat map shows the rank of K_D across methods, the actual values of the K_D average analysis are graphed on the left of the heat map (K_D by all methods are provided in supplemental Table 2C). The data show a preponderance of RNA/DNA binding, metabolism proteins, and protein synthesis and degradation machinery proteins with rapid K_D and the majority of the mitochondrial energy metabolism and central metabolism category members with slow K_D. At the extremes of this distribution, elongation factor 1Bα had a K_D average of nearly 1.2 d⁻¹ (per day), whereas the K_D average of glutathione peroxidase 6 was less than 0.02 d⁻¹. There are examples of protein isoforms like fructose-bisphosphate aldolases (At3g52930 and At2g36460), which have very similar degradation rates, whereas others like mitochondrial malate dehydrogenases (At3g15020 and At1g53240) differed significantly in K_D.

Fig. 3.

Degradation rate of proteins in Arabidopsis cell culture. The bar graph shows the average degradation rate (K_D). The colors of the bars represent functional categories of protein sets. Heat map shows the ranked degradation rate within the 24-, 96-, and 168-h time series in the first through third columns, ranked degradation rate for spectra with a H/NA ratio between 0.1 and 10 (fourth column), and average degradation rate for all data for each protein (fifth column). The last two columns show K_D acquired by the first and second regression methods used (27, 28). # and * represent proteins that meet the regression thresholds set in Ref. 27 and Ref. 28, respectively.

Calculation and Comparison of K_S Rates for Proteins

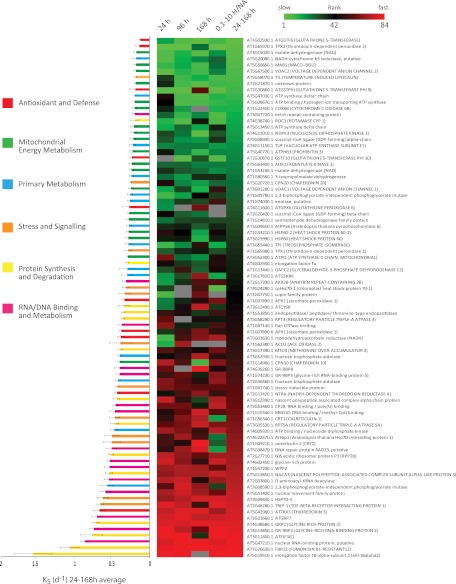
Although many reports that consider degradation in steady-state assume synthesis rate equals degradation rate, in our case we have information on changes in protein abundance and the degradation rates at different time points. Therefore we calculated K_S and assessed its relationship to K_D. Using a similar approach to that of K_D, we explored the impact of time points, the removal of data with high and low H/NA ratios (0.1–10), and an average of K_S over all time points. Although there was variation for a number of proteins, overall there were clear sets of rapidly synthesized proteins and slowly synthesized proteins (Fig. 4). There was a clear group of mitochondrial proteins with a slow and consistent synthesis rate (Fig. 4, green bars). Notably K_S for mitochondrial energy components was more consistent than the K_D observed for this category in Fig. 3. Proteins in the RNA/DNA binding and metabolism, protein synthesis and degradation, and the stress and signaling categories dominated the list of proteins with high K_S values.

Fig. 4.

Synthesis rate of proteins from Arabidopsis cell culture. The bar graph shows the average relative synthesis rate (K_S). The colors of bars present functional categories of proteins. The heat map shows the ranked synthesis rate within the 24-, 96-, and 168-h time series the first through third columns, ranked synthesis rate for spectra with a H/NA ratio between 0.1 and 10 (fourth column), and average synthesis rate for all data for each protein (fifth column).

Comparison of K_D and K_S Rates for Proteins with Each Other and with Functional Classification and mRNA Data

To explore whether the apparent variation in K_D and K_S for a given protein at different time points was biologically meaningful rather than simply noise in a steady-state system, we performed hierarchical clustering of the heat map of ranked data for 24, 96, and 168 h using a Pearson correlation coefficient method (supplemental Figs. 6 and 7). For both K_D and K_S, this showed a series of defined clusters of proteins. To determine whether K_D or K_S were simply reflections of decreasing/increasing protein abundances, we compared these clusters with total protein abundance at the different time points. We arranged the normalized abundance data from the DIGE analysis as a heat map in the same order as the clusters of ranked K_D and K_S. These comparisons show that the clusters apparent in K_D and K_S rank are unlikely to simply reflect changes that could be observed in total protein abundance, but rather they indicate independent variations of protein turnover that underlie the abundance of proteins in the cell culture. The K_D of mitochondrial energy proteins was typically considered low based on the data in Fig. 3, but the ranks for these proteins clearly clustered with faster ranked K_D in the 24-h data and decreased rank over time. In contrast, many of the stress-induced proteins and RNA/DNA-binding proteins had K_D ranks that increased over time (supplemental Fig. 6). A related trend was also apparent in K_S (supplemental Fig. 7). Mitochondrial components had fast K_S ranks at 24 h but lowered their rank at 96 h and 168 h, whereas components in RNA/DNA binding and antioxidant defense had ranks that increased over time to have faster relative K_S in the later time points.

As the cell culture is growing over time, the relationship between K_D and K_S for proteins is critical to maintain the total abundance of a protein in the proteome. We explored the veracity of this relationship in several ways. First, scatter plots of average K_D and K_S values were generated using the data from Figs. 3 and 4. This showed a positive relationship between the two parameters with a fair to moderate correlation over a range of parametric and nonparametric methods (r = 0.39–0.76, n = 84, supplemental Fig. 8). When proteins were divided into the six functional categories of Figs. 3 and 4, it was apparent that there was a better positive correlation for protein synthesis and degradation (r = 0.52–0.9, n = 15, supplemental Fig. 8) and antioxidant and defense (r = 0.62–0.79, n = 11 supplemental Fig. 8), although there was no correlation for mitochondrial energy, primary metabolism, or stress and signaling (supplemental Fig. 8). Second, in an effort to determine whether K_D and K_S were linked through time, we combined and clustered the K_D and K_S ranked data sets together over the three time points (supplemental Fig. 9). This shows that there were only a relatively small number of proteins with strong correlation between K_D and K_S across the time points. The best cases of correlation were for the cytosolic proteins: ATHIP1 (At4g22670), ROC1 (At4g38740), and GSTF9 (At2g30870), and somewhat more weakly the mitochondrial proteins: CPN10 (At1g14980), succinyl-CoA ligase (At2g20420), ATP synthase δ (At5g47030), and ATP synthase β (At5g08670).

Because K_S is dependent on mRNA abundance and half-lives and this information was available for the same Arabidopsis cell culture (6), we considered the correlations between these data sets based on the whole set of 84 proteins and the six functional categories of proteins analyzed here (supplemental Fig. 10). The correlation between protein relative abundance and mRNA half-life was most apparent in the antioxidant and defense (r = 0.58–0.87, n = 8) and stress and signaling (r = 0.47–0.60, n = 10) categories. There was less consistency in the correlation between K_D and K_S with RNA half-life. Using microarray data from untreated cell culture, we also considered correlations between protein abundance, synthesis/degradation rates, and raw mRNA hybridization abundance. We found higher correlation of RNA hybridization with K_S rates than with protein abundance alone, but only for the RNA/DNA and protein synthesis and degradation component groups. However, we also found that K_D was often better correlated with RNA hybridization than protein abundance for these same functional groups, indicating the potential importance of protein degradation rate in understanding the size and dynamics of the RNA pool involved in transcription and translational processes.

DISCUSSION

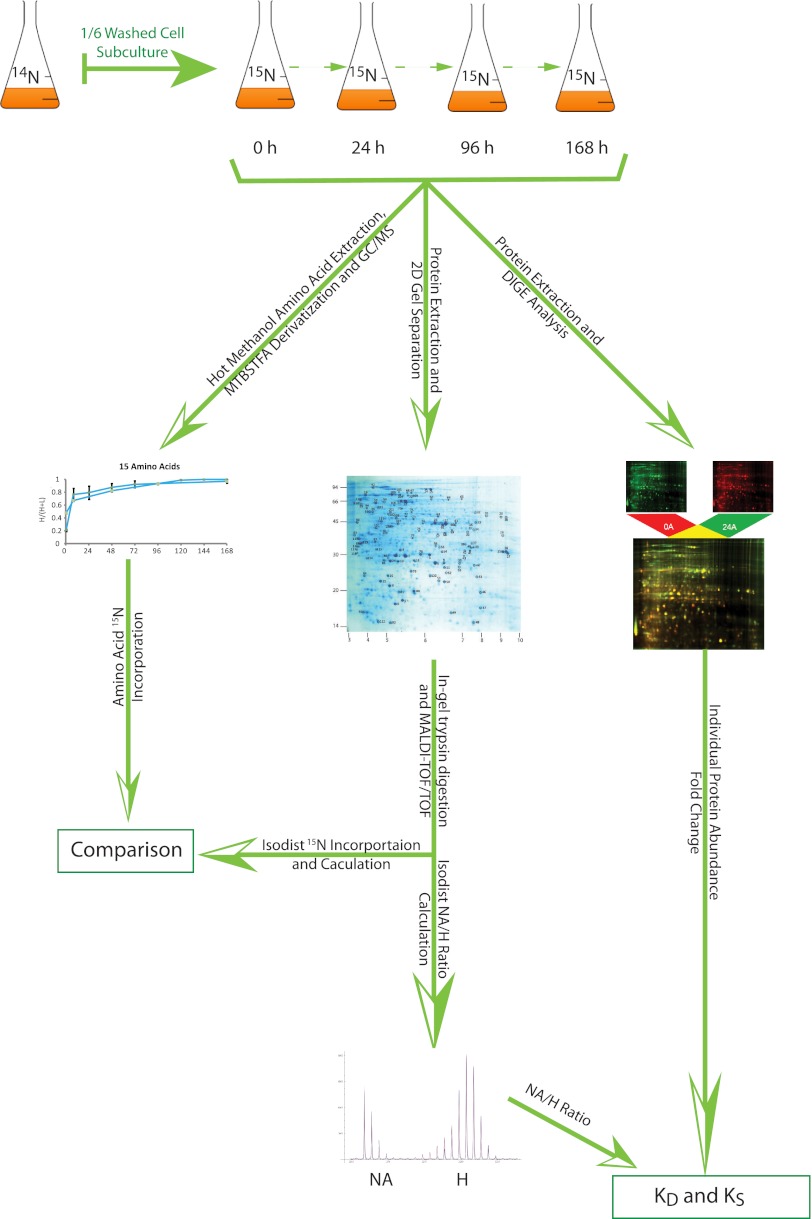
Developing methodology to measure protein synthesis and degradation rates requires a complex series of choices and compromises to evaluate the ease and transferability of the method alongside its veracity, accuracy, and its underlying assumptions of protein dynamics. As reviewed recently by Hinkson and Elias (35), a good method needs first to allow a protein of unaltered sequence to reach maturity and attain normal subcellular localization and protein-protein association. As a secondary consideration, we believe that a method that allows targeted analysis of proteins of interest would be of benefit. The combination of ¹⁵N labeling and analysis of gel-separated protein spots provides the framework for these two considerations. The use of gel-separated samples also provides simplification of mass spectra to maximize its interpretability. Choice of method must also consider if simple first order kinetics are followed (i.e. if protein degradation as a function of protein concentration is constant). Additionally, it must be determined whether a steady-state system (one in which K_D and K_S are equal, where cellular protein concentration is constant, and where it is cell growth that is responsible for any net changes to protein abundance (35)) applies. Using the key features of this workflow (Fig. 5) and the methods and assumptions in calculating K_D and K_S, we consider the benefits and limitations of our chosen approach.

Fig. 5.

Workflow and data assembly to determine K_D and K_S for Arabidopsis proteins.

The Value of Partial ¹⁵N Labeling over Other Choices for Stable Isotope Assessment of Plant Protein Turnover

Several strategies have been employed for measuring protein turnover in cells. The SILAC strategy with ¹³C-labeled amino acids has been widely used to measure protein turnover rates (5, 7, 10). However, this strategy is not well suited to fully labeling plant cells for multiple reasons. First, because plants are autotrophic and can synthesize all the amino acids, diluting and mixing SILAC label complicates analysis (16). Second, it is likely that the labeled carbon skeletons from amino acids such as lysine and arginine (which are routinely used in SILAC labeling experiments) are likely to only partially label certain amino acids, and this could not readily be anticipated or accounted for in a quantitative model. Third, because all amino acids are not transported equally between tissues, such an approach will be further complicated for use in whole plants (36). Another strategy was demonstrated in a recent paper where a heavy water method was used to measure tag-linked expressed proteins in Arabidopsis seedlings (9). However, heavy water is toxic to organisms including plants and altered the transcriptome pattern in plants (9), so this approach may alter cell physiology and in vivo proteome-wide turnover rates. ¹⁵N labeling had already been successfully used in labeling Arabidopsis cell culture and plants (15, 19, 21). Our DIGE results demonstrate that quantitative ¹⁵N labeling does not change the proteome profile, which is consistent with other reports in plants (19, 21, 32). Hence, this strategy is probably the most nonintrusive way to investigate the proteome dynamics without changing physiological conditions in plant cells. The nitrogen assimilation process in plants is well studied, and the machinery has relatively little discrimination against ¹⁵N incorporation (37). We can monitor the incorporation of ¹⁵N from amino acids into proteins, and based on peptides with 10–20 nitrogen atoms, we can clearly distinguish natural abundance and enriched ion envelopes within the mass spectrum in our data, even with only 50% ¹⁵N incorporation. This approach reduces the chance of interference and noise from other peptides or background in the calculation and also allows the relatively rapid assessment of turnover rate after the switch to ¹⁵N (<24 h). This contrasts with the longer periods of time that would be needed to make a calculation from peptides with a much higher incorporation level. Therefore we consider that this method has potential for measuring changes in degradation rate induced by environmental or developmental factors. Interestingly, levels as low as 6% ¹⁵N label have been successfully used to measure differences in protein levels (19), so the prospects for even lower partial labeling strategies to measure protein degradation could be explored in the future to further reduce the time needed to make degradation calculations.

Value of Gel-based Separation and MALDI Analysis for ¹⁵N-based Turnover Analysis

A potential limitation in the use of progressive versus steady-state ¹⁵N labeling is the increased complexity of the mass spectra. For a peptide containing 20 nitrogen atoms, this progressive labeling strategy will create an increasingly complex isotopic envelope (M to M⁺²⁰) that needs to be interpreted and quantified as NA and ¹⁵N-enriched populations. Undertaking this analysis in complex mixtures of peptides is extremely difficult because it greatly increases the chances of overlapping peaks and interference between the isotopic envelopes of different peptides. The two-dimensional gel separation we employed greatly reduces the complexity of the peptide pattern because usually peptides from only one protein are present in each spectrum. Additionally, by using MALDI-TOF/TOF MS, we generated singly charged spectra, which were easier to assign to an NA and heavy-labeled envelope of ions. This is inherently less complex than spectra generated using ESI because of the multiple charge states that exist in ESI for peptides. Moreover, the two-dimensional gel spot approach facilitated an independent measurement of abundance changes using quantitation of fluorescent dye binding across the time points in the experiment. These data were essential to account for the effect of relative differences in protein abundance during the 7 days of cell culture growth. The added advantage of using two-dimensional gels is that this technique can be used in the future by researchers to focus on gel-separated spots of interest. For example, proteins identified by antibodies raised to specific proteins or post-translational modifications of proteins (e.g. phosphorylation, oxidation, or glycosylation) or in native complexes (e.g. two-dimensional blue native PAGE/SDS-PAGE) or hydrophobic proteins in diagonal gels (e.g. benzyldimethyl-n hexadecylammonium/SDS-PAGE or Tricine/Tris SDS-PAGE) can be targeted for analysis using the combination of gels and progressive ¹⁵N labeling.

Important Considerations in the Isodist Analysis and Calculations of K_D and K_S

A critical decision we faced was how to define the abundance of existing and newly synthesized peptides in a population. When cells are transferred from NA to ¹⁵N-enriched media, assimilation of the ¹⁵N into amino acids begins, but the incorporation rate in amino acid pools for protein synthesis is very small in the first few hours (Fig. 1 and supplemental Fig. 2). Thus, even peptides containing a small number of ¹⁵N amino acids should be considered as newly synthesized, even though the masses of these peptides overlap with the NA ion envelope. Tools to quantify enrichment in peptide populations like Mascot Distiller (Matrix Sciences) presume that a system is at steady state and rely on the user to define the incorporation ratio. However, in our case this was not viable because we wanted to calculate the incorporation ratio from the spectra and aimed to assess many hundreds of spectra. We used a program called Isodist that incorporates a least squares fitting algorithm to determine both the extent of labeling for the defined labeling pattern of a given species and the relative amounts of different species in a mixture (25). Hence it will fit theoretical spectral envelopes based on a defined peptide sequence and provide both the abundance of the two populations and the degree of incorporation.

RIA has been used as the only factor to measure protein turnover in steady-state systems (5, 27). However, the abundance of individual proteins over time has to be considered in growing and non-steady-state systems like our Arabidopsis cell culture. The ratio between the NA and the ¹⁵N-enriched populations is determined by the change in total protein abundance, the rate of degradation of the NA population, and the rate of increase in the ¹⁵N enriched population. An important aspect of defining these variables (which has often been neglected) is that the newly synthesized proteins also experience a degradation process that needs to be accounted for when solving for K_D and K_S.

In our calculations, we discovered that the variation in ¹⁵N incorporation across all peptides and proteins at the same time point was very low (Fig. 2 and supplemental Table 2). So this meant that the effects of different amino acid turnover rates on our calculations were not significant. However, to directly assess this issue, we considered the GC-MS data on amino acids incorporation rates and the isotope ratios of peptides that contained a large percentage of amino acids with either a slower (Gly, Cys, Thr, Ser, and Pro) or faster (Gln, Glu, Asn, Leu, and Asp) ¹⁵N incorporation rate. We compared seven peptides enriched for lower turnover amino acids with 13 peptides enriched for higher turnover amino acids. We examined peptides where amino acids were enriched with either high or low incorporation rates. Of this smaller subset of peptides, the effect on K_D or K_S was found to be very small: 5–9% different from the average for all peptides that matched to these proteins. This implies that the effect of amino acid composition on our calculations for a single peptide is quite small and will be further reduced when K_D and K_S are calculated at the protein level.

Although the peptide to peptide variation at a given time point was small to insignificant, we found the variation in K_D and K_S for several proteins across time points was significant. In other reports a significant variation in K_D has led to proteins being discarded from analysis, because they fail to reach regression thresholds on the assumption of simple first order kinetics of degradation. For example, Jayapal et al. (28) reported that ∼50% of observed proteins did not follow simple first order kinetics in log-grown bacteria. The data on proteins that have a poor correlation and therefore do not appear to strictly adhere to simple first order kinetics could be argued to be due to experimental error and/or inadequate sampling; alternatively the variation in K_D could be the result of biological events. If the latter is the case, then clearly reporting the K_D and investigating the biological meaning is of interest. Also, even if a good regression fit is lacking, average K_D or K_S values and standard deviations can place proteins in a relative list of degradation and synthesis rates as shown in Figs. 3 and 4. In a similar manner, other researchers have reported K_D values through the use of average values across time points in yeast and mammals (5, 26). In fact, a range of studies over decades in growing systems have observed a range of examples of proteins that do not follow simple first order degradation kinetics. From early studies in tobacco cells, it was apparent that protein degradation rate can change with time in plants (38). Although simple first order kinetics models are often used in mammalian systems, even in chicken muscle, a simple single exponential decay has not been observed (39). Those authors suggested this variability was at least in part due to changes in protein metabolism resulting from circadian rhythms. In a recent review of protein degradation analysis, Hinkson and Elias (35) note that biphasic kinetics with rapid early turnover rates have been reported for many decades. They purport that variability in protein stabilities should be expected for cells to tune degradation as a means of regulating the proteome; moreover, high initial degradation rates can partially result from proteolysis of mistranslated and/or misfolded proteins (40). Perhaps an even more exciting direction will be the assessment of which protein complexes or even entire organelles are turned over as units. Hence, there is a significant body of evidence suggesting that limiting the analysis to proteins abiding by simple first order degradation kinetics in complex systems will limit the ability to draw meaningful biological conclusions.

Biological Insights from K_D and K_S Calculations

We found in our data set that by including calculations for proteins that did not follow simple first order degradation kinetics, we could uncover functional groupings of proteins that could be linked to K_D and its variability. In general, mitochondrial proteins have low K_D, whereas cytosolic and nuclear proteins were more unstable and have higher K_D values. These differences in observed degradation rates may be due to inherent differences in rates of the degradation pathways in the cytosol and organelles (41, 42) or the combination of location and the functional roles of the proteins. Such differences may benefit the plant cell, allowing stable mitochondrial proteins to ensure a steady supply of energy, whereas the dynamics of the nuclear and cytosolic proteomes can guarantee a quick response to the environment. Also, the timing of changes in K_D and K_S across the cell culture cycle differed for cytosolic and mitochondrial proteins. Note the relatively faster K_D and K_S of mitochondrial proteins in the first 24 h during the lag phase and a clear lowering of the rank of K_D and K_S for mitochondrial proteins during rapid growth compared with cytosolic proteins (supplemental Figs. 7 and 8). This could indicate that mitochondrial turnover is highest soon after cell division but is slower during the expansion and aging of cells. It would also correlate with the known early induction of mRNA for mitochondrial components during plant cell development and the apparent cessation of mitochondrial biogenesis in older cells (6).

Across the six functional categories, the RNA/DNA binding and metabolism, protein synthesis and degradation, and stress and signaling categories had higher degradation and synthesis rates than the other three categories (Figs. 3 and 4). The stress and signaling category had higher average degradation and synthesis rates than any of the others (Figs. 3 and 4). This is consistent with the reports on functional categories of protein in yeast and mammalian cell lines (11, 12). Surprisingly, even though relative protein abundances were fairly static over the 7 days of culture, many proteins did not appear to have tight links between their K_D and K_S rates at a given time point (supplemental Fig. 10). One set of exceptions were the subunits of the mitochondrial ATP synthase that were linked in synthesis and degradation, which likely reflects the fact that as a multi-subunit complex, the mitochondrial ATP synthase is restricted by stoichiometry (43) to maintain a tight link of K_D and K_S at all time points.

A range of specific proteins and their turnover rates were also of special interest. One of the five fastest K_D values recorded was for the ethylene biosynthesis enzyme, ACC (1-aminocyclopropane carboxylic acid) oxidase. The rapid turnover of proteins in this pathway has been known for some time (44, 45). This rapid degradation is needed to quickly slow the rate of ethylene synthesis after its peak (44), and the degradation process is actively regulated as a means of manipulating ethylene signaling in plants (46). We identified several translational initiation factors known to be responsible for initiation of programmed cell death triggered as a response to Pseudomonas syringae infection (At1g26630 FBR12) and in brassinosteroid signaling in plants (At2g46280 TRIP-1) as among the most rapidly degrading proteins. Rapid degradation of these proteins may aid their signaling roles by ensuring they are tightly transcriptionally controlled in plant cells. A temperature-induced lipocalin TIL1 (At5g58070) is known to be associated with the plasma membrane and be involved in prevention of lipid peroxidation during temperature changes (47). Its rapid degradation rate identified here might indicate that it is damaged during this role and needs to be rapidly replaced to maintain its function. GRP (glycine-rich RNA-binding) family proteins including GRP2, GRP7, and GRP8 had relatively fast degradation and synthesis rates (Figs. 3 and 4). GRP7 is the most well studied GRP family protein; its mRNA is known to oscillate in response to circadian rhythm (48), plant innate immunity (49), and flowering time (1). A high degradation rate of GRPs could be a mechanism for plants to more quickly and efficiently respond to environmental changes.

At more than 39-fold slower than ACC (1-aminocyclopropane carboxylic acid) oxidase, glutathione peroxidase 6 was the slowest K_D recorded at less than 0.02 d⁻¹. This protein is commonly observed to be induced transcriptionally by oxidative and environmental stress (50, 51). Its relative stability makes sense to ensure antioxidant defense during stress. A similar explanation can be made for the slow turnover of HSP60 (At3g23990) involved in protein stabilization (∼0.08 d⁻¹) and for glutathione S-transferases (At2g30860) involved in detoxification of cells (∼0.20 d⁻¹). The underlying basis of relative protein stability in plants is largely unexplored but is vital for engineering of plants with enhanced traits to meet the demands of the future.

Conclusions

Using a combination of two-dimensional electrophoresis, MALDI-TOF/TOF, and ¹⁵N isotopic labeling, we have developed a method to follow the progressive ¹⁵N labeling of plant cells under non-steady-state conditions to calculate K_D and K_S. The ability of this technique to be targeted, by use of gels and prior knowledge of the spots of interest, and the use of methods to assess data that does not meet simple first order kinetic assumptions opens many options for expanding its use for the study of protein dynamics in plants.