Two mechanisms for transducer adaptation in vertebrate hair cells

Abstract

Deflection of the hair bundle atop a sensory hair cell modulates the open probability of mechanosensitive ion channels. In response to sustained deflections, hair cells adapt. Two fundamentally distinct models have been proposed to explain transducer adaptation. Both models support the notion that channel open probability is modulated by calcium that enters via the transduction channels. Both also suggest that the primary effect of adaptation is to shift the deflection-response [I(X)] relationship in the direction of the applied stimulus, thus maintaining hair bundle sensitivity. The models differ in several respects. They operate on different time scales: the faster on the order of a few milliseconds or less and the slower on the order of 10 ms or more. The model proposed to explain fast adaptation suggests that calcium enters and binds at or near the transduction channels to stabilize a closed conformation. The model proposed to explain the slower adaptation suggests that adaptation is mediated by an active, force-generating process that regulates the effective stimulus applied to the transduction channels. Here we discuss the evidence in support of each model and consider the possibility that both may function to varying degrees in hair cells of different species and sensory organs.

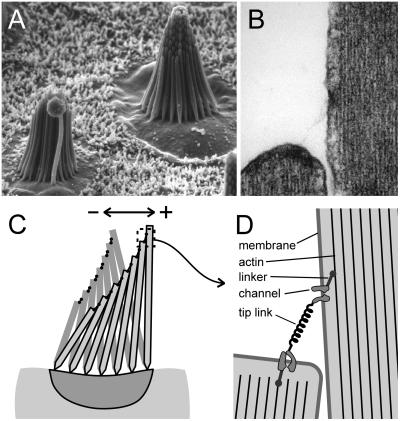
The ability to sense sound and head position has proven advantageous for vertebrate animals. For these two purposes evolution has devised a common solution: the mechanosensory hair bundle. This organelle, exquisite in form and function, crowns the apical surface of the sensory hair cells in the inner ears of vertebrates. Hair bundles comprise a staircase array of 20–300 microvilli, called stereocilia, that range in height from a few to tens of micrometers (Fig. 1A). The stereocilia contain a rigid core of cross-linked actin filaments (1–3) and do not bend under normal conditions. Their actin cores taper at the base where they insert into the cuticular plate, thus deflections cause them to pivot instead (4). The stereocilia, ensheathed by the cell membrane, are held together by three sets of extracellular links that extend laterally in a symmetrical manner. A fourth set of links, called tip links, extends from the tip of one stereocilium to the side of its adjacent, taller neighbor along the bundle's axis of symmetry (Fig. 1 B and D; ref. 5). The tip links are ≈10 nm in diameter and ≈150 nm long (6, 7). Deflection of the hair bundle toward the tallest stereocilia gates cation-selective transduction channels (Fig. 1 C and D). With a short latency (≈10 μsec at mammalian temperatures) the channels open and generate a receptor current of hundreds of picoamperes that is carried primarily by potassium and calcium ions (8–10). Transduction channels probably are located at either end of the tip links, and based on single-channel conductance estimates of ≈100 pS, some hair cells may have >200 functional channels.

Figure 1.

Ultrastructure and function of sensory hair bundles. (A) Scanning electron micrograph (×2,500) of two hair bundles in the sensory macula of the bullfrog saccule. The bundles have a morphological axis of polarity defined by the graded heights of the stereocilia (Right) and the eccentric placement of the kinocilium (Left), such that the tallest stereocilia are at the positive edge. These bundles are about 8 μm tall and contain 50–60 stereocilia. (B) Transmission electron micrograph (×50,000) of the tip of a stereocilium and its adjacent, taller neighbor. Note the fine filamentous tip link extending between the two stereocilia. At each end is an electron-dense plaque between the membrane and the actin core. The tip link is 150–200 nm in length; stereocilia are ≈400 nm in diameter. (C) Schematic diagram of a hair bundle. Note that the taper at the base of the stereocilia allow them to pivot rather than bend. In this view a bundle deflection to the left is consider a negative stimulus that allows transduction channels to close and a deflection to the right is positive and causes them to open. (D) Schematic diagram illustrating the gating spring model for transduction. The tip link may be the morphological correlate of the gating spring. When the bundle is deflected in the positive direction the tip links stretch, which would in turn pull directly on the channels and cause them to open.

Transduction Model

Taken together, the following evidence supports a model for hair cell mechanoelectric transduction that is now widely accepted (Fig. 1D). The short latency of the response argues against activation of a second-messenger cascade and favors direct activation of a mechanically sensitive channel. Bundle deflection parallel to the sensitive axis is posited to stretch elastic “gating springs,” which pull directly on the channels (9). Direct channel gating was supported by experiments of Howard and Hudspeth (11) who found that hair bundle stiffness decreased as the channels opened. This finding implicated a direct gating mechanism in series with the gating springs. The discovery of tip links (5) oriented along the sensitive axis suggested that these fine extracellular filaments are the morphological correlates of the gating spring. Furthermore, Assad et al. (6) found that brief exposure to the calcium chelator, 1,2-bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetate (BAPTA), concurrently abolished transduction and tip links. Using the same manipulation, Zhao et al. (12) went on to show that if the hair cells were allowed time to recover for 12–24 h, transduction and tip links returned with the same time course. Detailed analysis of quick-freeze, deep-etch electron micrographs of tip-link structure has revealed at least two helical strands with 2–3 branches at their insertion into the stereocilia membrane (13). If there is a transduction channel for each branch, there may be up six channels per tip link.

Calcium Metabolism

Experiments with Ca²⁺-sensitive dyes in the patch pipette have demonstrated that transduction channels have a significant Ca²⁺ permeability, channels can be located at either end of tip links, and the concentration rises rapidly in the tips of the stereocilia when channels open (14–16). As discussed in the next section, the Ca²⁺ concentration near the transduction channels has a pronounced feedback effect on the channel open probability. Knowledge of calcium metabolism within the tips of the stereocilia is critical for understanding transduction and adaptation.

Calcium that enters the tips may meet four possible fates: it can diffuse down the stereocilia, bind to mobile buffers that diffuse away, bind to fixed buffers, or be extruded by calcium pumps in the stereocilia membranes. Models indicate that all four mechanisms are required to account for the fluorescence transients that follow transduction channel opening (17). The Ca²⁺ buffers in stereocilia have not yet been identified but may be a protein such as calbindin or calretinin (18, 19), and the effective endogenous buffer concentration is equivalent to 0.1–0.4 mM BAPTA (20). Recent work on Ca²⁺ extrusion from the stereocilia has focused on the plasma membrane Ca²⁺ ATPases (PMCA). Immunocytochemistry and quantitative immunobloting indicated that the stereocilia may contain up to 2,000 molecules/μm² of a PMCA, enough to account for an outward pump current of several picoamperes (21). Further implicating PMCA is the finding that mice with a mutation or a targeted deletion of the gene for PMCA2 are deaf and have vestibular deficits (22, 23).

Despite the efforts of the hair cell to maintain low levels of Ca²⁺, the concentration may rise as high as 50 μM within close proximity to the transduction channels where it can act to modulate transducer adaptation.

Adaptation

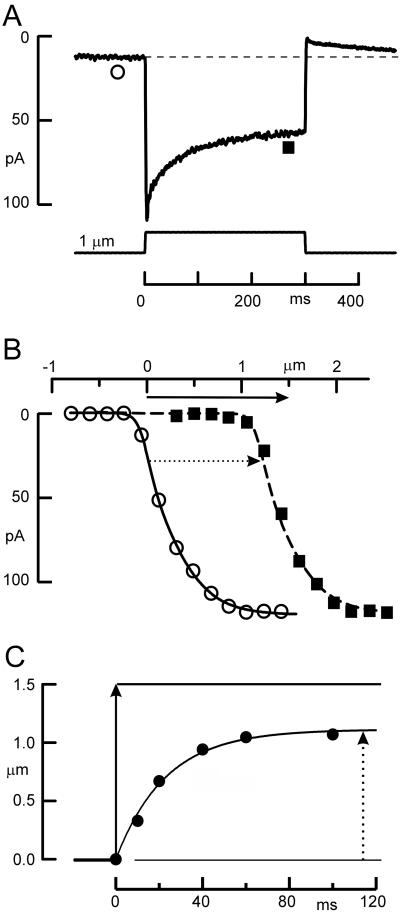
In response to a sustained bundle deflection, the hair cell receptor current declines or adapts, through closure of the transduction channels (Fig. 2A). The decline in current could occur in three ways: by a decrease in slope sensitivity of the channels, so that a larger deflection is needed to open more channels; by an inactivation so that the number of channels available to be opened is reduced; or by shifting the stimulus-response [I(X)] relationship without a reduction in sensitivity. Hair cell adaptation has been found to be primarily associated with a shift of the I(X) relation, whereby the hair cell moves the relation in the direction of the applied stimulus, thus bringing the channel open probability back toward the resting value (Fig. 2 B and C) (9, 24, 25).

Figure 2.

Properties of adaptation in a mouse utricular type II hair cell. (A) Transduction current evoked by deflecting the hair bundle with a stiff probe mounted on a bimorph stimulator. The current declines in response to a step deflection. When the bundle is returned to its rest position there is an overshoot that eventually returns to its initial level. ○, ■, Time points at which the I(X) curves in B were acquired. (B) The I(X) relation shifts in the direction of the applied stimulus. These data were taken from a family of transduction currents (not shown). ○, The peak currents plotted vs. bundle deflection beginning from a resting bundle position. ■, An I(X) relation that was measured near the end of 300-msec, 1.5-μm bundle deflection similar to that shown in A. The solid arrow indicates the magnitude of the adapting step and the dotted arrow indicates the magnitude of the I(X) shift (1.2 μm in this case). (C) Magnitude of the I(X) shift as a function of time. The position of I(X) curves such as those in B were measured at several time points after the onset of a 1.5-μm deflection. Fitting these data with an exponential function indicated that the curve shifted with a time constant of 23 msec. Solid arrow indicates magnitude of the stimulus; dashed arrow shows final magnitude of the I(X) shift. Data were replotted from figure 5 in ref. 25.

However, adaptation is not complete: the shift of the I(X) curve is not as large as the sustained bundle deflection that evokes it, so the receptor current does not return all of the way to the resting level (Fig. 2 A and C). The extent of adaptation is 60–80%, that is, adaptation shifts the I(X) curve by 60–80% of the magnitude of the bundle deflection (25, 26). Thus the major component of the receptor current signals phasic bundle deflections whereas the remaining nonadapted component signals more tonic stimuli.

Calcium inside the tips of the stereocilia has been found to affect both the speed and extent of adaptation considerably. To investigate its role, the concentration in the tips has been manipulated a number of ways, each with measurable effects. A decrease in extracellular Ca²⁺ decreases Ca²⁺ flux through the transduction channels and slows the rate of adaptation, measured either as the rate of shift of the I(X) curve or the decline in receptor current (9, 24, 25, 27–29). An increase in the concentration of a calcium buffer within the cell causes Ca²⁺ to be more rapidly bound once it enters and slows the rate of adaptation (16, 29). Depolarizing the hair cell reduces the driving force for Ca²⁺ influx, reduces Ca²⁺ entry, and reduces or abolishes adaptation (28).

The precise site of action for Ca²⁺ is not clear but it must be within ≈1 μm of the transduction channels. If Ca²⁺ entry is reduced by depolarization, adaptation is slowed; upon repolarization, Ca²⁺ enters the bundle and adaptation proceeds within 1–2 msec. Thus, Ca²⁺ must find the adaptation control site very near the transduction channel (28). Furthermore, Ca²⁺ buffers with slow binding kinetics, like EGTA, have little effect on adaptation, whereas BAPTA, which has more rapid kinetics, has a significant effect on adaptation rate and extent (29). The interpretation is that BAPTA binds Ca²⁺ before it has time to diffuse to its site of action (20).

Initial descriptions of adaptation characterized it as one mechanism with a single exponential time course. Time constants were reported that ranged between 3 and 100 s of msec (24, 25, 28, 29). Recent work suggests that adaptation may have two different mechanisms, with one as fast as 0.3 msec (30). The latter is more prominent for small deflections, but saturates with larger ones where the slower process dominates. Two distinct models for adaptation have been proposed; one involves a mechanical adjustment of tension on the gating spring (31), and the other involves Ca²⁺ binding directly to a site at or near the channel that alters the relation between tension and open probability (29, 32). In the following sections we consider the evidence for each model and consider the possibility of these acting simultaneously in the hair cell.

The Active Motor Model.

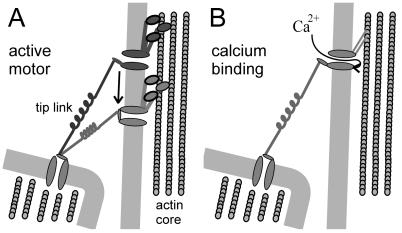
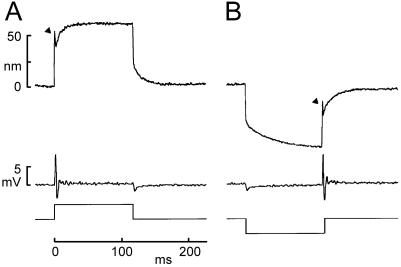
This model proposes that in response to a maintained bundle deflection the hair cell actively adjusts the tension in each gating spring to return it toward its resting level (Fig. 3A). Howard and Hudspeth (31) used a flexible glass stimulus probe to measure the mechanical correlates of adaptation in bullfrog saccular hair cells. An applied force caused a rapid bundle deflection that was followed by an additional, slower deflection (Fig. 4). The latter had the same time course as adaptation (≈30 msec). This slow deflection occurred for forces parallel to the bundle's axis of sensitivity, but did not occur for forces directed perpendicular to that axis. When adaptation of the receptor current slowed or disappeared during prolonged recording, the slow deflection did as well. Because these bundle relaxations had the same time course as adaptation, Howard and Hudspeth (31) proposed that the mechanical relaxation might be the result of a movement of the upper tip-link attachment point along the side of the stereocilium. Thus, the model suggests that an active motor complex—probably in the vicinity of the upper tip-link insertion—is continuously trying to “climb up” the stereocilium to increase tension in the tip link. In response to a positive deflection, tension in the tip link increases and opens channels. As adaptation proceeds, the motor slips down the side of the stereocilium, tip-link tension decreases, the channels begin to close, and the bundle relaxes forward. In response to a negative deflection, tip-link tension decreases and closes channels. In this case the motor complex climbs up the stereocilium, restores tension to the tip link, and pulls the bundle in the negative direction. At steady state, the rate of motor slipping equals the rate of climbing and the steady-state tension maintains 10–20% of the channels in the open conformation. The slipping and climbing of adaptation motors can be measured as a shift of the I(X) curve in the direction of the applied stimulus. To view this in terms of a shift of the upper attachment point for a single tip link, the geometrical gain of the bundle must be taken into account (≈0.12 for bullfrog hair cells). For example, a positive deflection of 0.5 μm would stretch the gating spring by about 60 nm, and a subsequent slippage of 48 nm would allow ≈80% of the channels to close. Because the cores of the stereocilia are composed of actin of the proper polarity, it has been suggested that a myosin motor could be a suitable mechanoenzyme to power transducer adaptation in hair cells.

Figure 3.

Schematic diagrams illustrating the two models for hair cell adaptation. (A) The active motor model proposes that when the bundle is deflected in the positive direction, the motor cannot resist the increased tension and slips down the stereocilium, reducing tension and allowing channels to close. In addition, Ca²⁺ entry through open channels accelerates the rate of slipping. Conversely, when the bundle is deflected in the negative direction, the reduced tension allows the motor to climb and restore tension to reopen channels. (B) The calcium-dependent closure mechanism proposes that when the channels open calcium enters the stereocilia and binds to a site on or near the channel protein. Bound Ca²⁺ promotes a closure of the channel. When deflected in the negative direction, the Ca²⁺ concentration falls and reduces the inhibition of the channel.

Figure 4.

The “twitch” and subsequent slow relaxations of the hair bundle during maintained force steps. (A) The positive force stimulus in this experiment caused a quick forward deflection of ≈50 nm (arrowhead), a rapid twitch back of ≈10 nm, and then a relaxation forward of ≈25 nm. The receptor potential recorded simultaneously (middle trace) showed a transient depolarization, and then an oscillation during and after the twitch. (B) A negative force evoked a quick negative deflection and slower negative relaxation. The twitch was not observed until the bundle was returned to the rest position (arrowhead) and was associated with an oscillation. [Reprinted with permission from ref. 52. (Copyright 1996, Society for Neuroscience).]

This simple model has three basic tenants. First, it suggests that adaptation is a mechanical process that adjusts tension in the physiologically defined gating spring by moving one end. Second, by correlating the gating spring with the tip link, it predicts that the morphologically defined, electron-dense attachment of the tip link also moves during adaptation. Third, it suggests a protein of the myosin family as the leading candidate for the adaptation motor. Work during the past decade has supported all three of these tenants.

To study the mechanical basis of adaptation, Assad and Corey (33) systematically measured adaptation rates for positive and negative bundle deflections. Based on these measurements and the previously measured bundle stiffness they developed a quantitative model that described the active, force-producing properties of the adaptation motor. They found that reducing calcium entry (by depolarizing the hair cell) reduced both climbing and slipping rates, but reduced slipping more. The difference in rates allowed for a simple test of the model: it predicted that depolarization would cause a decrease in calcium entry, which would allow the adaptation motors to climb up the stereocilia and thus increase tension on the channels. The added tension was expected to increase the channel open probability to ≈80% and therefore shift the I(X) curve by ≈120 nm, both of which were confirmed experimentally. Based on the geometry of the bundle (see Fig. 1) an increase in tip-link tension was predicted to pull an unrestrained bundle in the negative direction. The expected position change with depolarization, of ≈100 nm, was in close agreement with that actually measured by using high-resolution video microscopy (33). A final validation of the model was derived from an experiment in which the bundle movement caused by depolarization was abolished when tip links were cut with BAPTA, suggesting that tip links convey the tension that produces the bundle movement (6). Thus, this model accurately predicted movement of the bundle and supported a mechanical basis for adaptation.

On the other hand, morphological correlates of adaptation have been more difficult to obtain. Video microscopy with a resolution of 30–40 nm showed no gross movement of the stereocilia or cuticular plate during adaptation, thus the focus was shifted to smaller-scale molecular rearrangements (34). Thus far, it has not been possible to resolve the predicted changes (10–20 nm) in the position of the electron-dense plaques. On the other hand, cutting tip links with BAPTA should relieve tension and allow motors to climb even in an undeflected bundle. Indeed, BAPTA treatment was followed by an upward movement of the plaques by 50–70 nm, as measured from transmission electron micrographs (34).

A growing body of evidence supports the involvement of myosin in hair cell adaptation. First, using isolated frog stereocilia with the membranes removed, Shepherd et al. (34) showed that chicken muscle myosin II could move along the actin cores at a rate of 1–2 μm/sec toward tips—the same direction as that predicted for the adaptation motor. Second, blockers of the ATPase cycle such as ADPβS, which arrest myosin while strongly bound to actin, block adaptation when dialyzed into the hair-cell cytoplasm (35). Similarly, phosphate analogs that arrest myosin while weakly bound should inhibit myosin force production and apparently cause release of resting tension on channels (36).

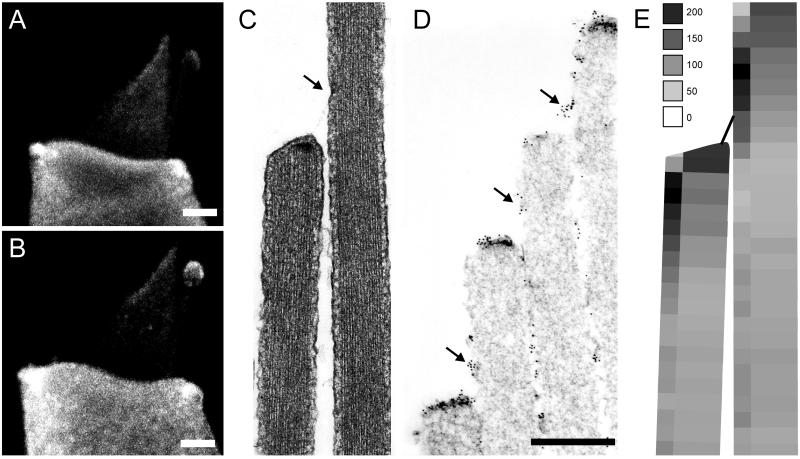
The myosin gene superfamily contains dozens of members, organized into 15 classes, eight of which occur in vertebrates. Identification of hair cell myosins has followed two strategies. Gillespie et al. (37) used vanadate trapping of adenine nucleotides to identify three putative myosins within stereocilia, of molecular masses 120, 160, and 230 kDa. The 120-kDa protein was labeled with an antibody to a myosin type Iβ, and this antibody particularly labeled the tips of stereocilia. Solc et al. (38) used degenerate PCR to amplify fragments of most myosins expressed in the hair-cell epithelium and found 10 different myosins from six different classes (I, II, V, VI, VII, and X). Interestingly, two of these myosins (VI and VIIa) cause inherited deafness in mice and/or humans when mutated (39, 40). The myosin-Iβ was cloned in full, and an antibody was raised against the tail domain (38). An extensive antibody study found that myosins Iβ, VI, and VIIa all are expressed by the hair cells, and all are in the stereocilia as well as elsewhere in the cells (41). These have molecular masses of approximately 120, 160, and 230 kDa, respectively. Recently, a myosin XV also has been discovered in stereocilia (42). Of all these myosins, however, only myosin Iβ is concentrated in the tips of stereocilia (Fig. 5 A and B) (41). Because localization with light microscopy cannot determine the relation of a myosin to the tip links, and because myosins might naturally climb to the tips of stereocilia unless otherwise prevented, the location of myosin Iβ was determined more precisely with ImmunoGold electron microscopy (43, 44). Myosin Iβ immunoreactivity was indeed associated with both end of the tip links, where it may link the channels to the actin cores (Fig. 5 C–E) (44).

Figure 5.

Myosin Iβ immunoreactivity in bullfrog hair cells. (A and B) Immunofluorescence of single dissociated cells shows myosin Iβ in the cell body and also in the hair bundle where it is especially concentrated at the tips of stereocilia. The kinocilium also shows fluorescent label. (Scale bar = 2 μm.) (C) Transmission electron micrograph (×30,000) showing a longitudinal section of two adjacent stereocilia. The arrow indicates the tip-link insertion and the electron-dense plaque, the presumed site of the adaptation motors. (D) Immunogold electron microscopy localizing myosin Iβ at both ends of tip links. (Scale bar = 500 nm.) (E) Summary of myosin Iβ distribution in the tips of stereocilia. Gold particles marking the antibody were counted and averaged over many stereocilia in six bundles, and their density is indicated as particles/μm² of surface membrane. The greatest density is within ≈200 nm of either end of the tip link. [Reprinted with permission from ref. 44 (Copyright 1998, Society for Neuroscience).]

Like most myosins, myosin Iβ has binding sites for regulatory light chains such as calmodulin. Three calmodulin molecules bind to myosin Iβ and confer a calcium dependence to the myosin activity (45, 46). Calmodulin is in stereocilia, especially concentrated at the tips (3, 47), and antagonists of calmodulin block adaptation* (49). It may be that calmodulin mediates the Ca²⁺ sensitivity of adaptation (49, 50).

Ca²⁺-Dependent Closure Model.

The rate of adaptation depends on the Ca²⁺ concentration inside the tips of stereocilia. With high extracellular Ca²⁺, and low or slow internal calcium buffer, adaptation can become quite fast, with a time constant as short as 0.3 msec (16). This speed is probably too fast to be mediated by a tension adjustment system that requires an ATPase cycle of myosin. For instance, the calculated 1- to 2-μm/s climbing rate of the adaptation motor and a myosin step size of 8 nm suggest an ATPase cycle time of 4–8 ms. A fast time constant is still compatible with a myosin motor if Ca²⁺ rapidly causes the myosin to release tension, for instance if Ca²⁺ reversibly causes the lever domain of myosin to become more compliant (50). However, such a mechanism could account only for a limited shift of the I(X) curve—perhaps 0.1 μm given the myosin lever dimensions and the bundle geometry—and fast adaptation can cause more shift than that.

To explain a rapid “twitch” in bundle movement, Howard and Hudspeth (11) proposed that Ca²⁺ binding directly to an intracellular site on the channel could shift the energetics of channel opening, such that the channel with calcium bound requires more force to reach the same open probability. That is, calcium entry would tend to close the channel (Fig. 3B). In an extension of this model, in which the energy of one of the two closed states is affected by Ca²⁺, Crawford et al. (29) suggested that Ca²⁺ binding is responsible for the adaptive shift of the I(X) curve. Although their initial model cannot explain adaptation to large deflections (33), a later model, in which calcium changes the “set point” of the channel, accounts for adaptation of up to 0.8 μm (32).

These two models—one in which Ca²⁺ relaxes tension and allows channel closure, and the other in which Ca²⁺ causes the channel to shut even with the same tension—have quite different predictions for the mechanical behavior of a hair bundle during adaptation. In the motor model, a force that opens channels would quickly move the bundle a certain amount determined by the force and the stiffness of the bundle. Bundle stiffness is determined by two springs in parallel: the stereocilia pivot stiffness and the gating spring stiffness. If myosin motors slip to allow channel closure, the gating spring relaxes, which could be seen as a decrease in stiffness (chord stiffness but not slope stiffness). The bundle would move forward with the time course of adaptation. On the other hand, if adaptation happens because Ca²⁺ causes the channel to shut, the small movement of the channel's gate slamming shut would tighten the gating spring (Fig. 3E), in essence increasing the stiffness and pulling the whole bundle backward.

Which behavior is seen with adaptation? In fact, both positive and negative going movements have been observed, with different time courses (refs. 11, 31, 51, and 52; R. Fettiplace, personal communication). Fig. 5A shows a rapid forward movement (arrowhead), followed by a quick hook back—the twitch—and then a slower and larger forward relaxation. Both the twitch and the slower relaxation depend on Ca²⁺, becoming slower and smaller when Ca²⁺ is reduced. The termination of force allows the bundle to move back, but no twitch is seen on the return, at least after large deflections. On the other hand, a negative force evokes a slow negative relaxation of the bundle, and then a twitch is seen when termination of force allows the bundle to move forward toward the rest position.

These two mechanical behaviors, which are separable by time course and stimulus polarity, suggest that both proposed mechanisms of adaptation may be occurring in hair cells. The calcium closure might be fast (0.3–5 msec), and cause the quick twitch; a myosin slipping would be slower (10–100 msec) and may cause the slow relaxation. A careful analysis of the time course of adaptation in turtle hair cells has found that two time constants are needed to fit the transduction current. Moreover, they depend differently on external Ca²⁺ and internal buffer concentration, further indicating their separability (32). Comparison with a model of Ca²⁺ diffusion in stereocilia suggests that the fast phase is controlled at a Ca²⁺ binding site that is 20–50 nm from the site of Ca²⁺ entry and may be the channel itself (32). The slow phase is controlled at a more distant site, 150–200 nm from the site of entry, which corresponds well with the location of myosin Iβ. Wu et al. (32) did not speculate about molecular mechanisms of the two components, but it will be interesting to find out which parts of the transduction complex correspond to each phase.

Future Directions

How can we resolve the relative contribution of these two mechanisms to transducer adaptation in hair cells? Both the channel and the motor have measurable mechanical correlates of their activity, which can be recorded together with the receptor current. High-speed and high-resolution mechanical measurements, with concurrent voltage-clamp recording, could better clarify which way the bundle moves when fast or slow adaptation occur.

Ultimately, we need to test individual proteins for involvement in adaptation. At present, the only putative components of the transduction apparatus that have been cloned are myosin Iβ and calmodulin—a remarkably meager portfolio in comparison to, say, phototransduction. Cloning the transduction channel would provide an important tool to study the calcium-binding form of adaptation. Even with candidates in hand, testing function is problematic for components of the hair-cell transduction assembly: unlike voltage-gated ion channels, none of the proteins involved in transduction or adaptation are likely to display interesting behavior outside of their native environment. Instead, they must be disrupted in the intact hair cell and assayed physiologically to understand their function.

Although costly and time consuming, targeted gene deletion is one approach. Unfortunately, attempts to knock out myosin Iβ were found to be embryonic lethal (P. G. Gillespie, personal communication). To circumvent developmental complications one strategy would be to use hair cell-specific promoters, such as those for the α9 acetycholine receptor (53) and Math1 (54), to drive expression of exogenous gene constructs in hair cells only. An alternative approach is to introduce dominant-negative fragments of candidate genes into hair cells by using adenoviral vectors (55). This approach offers several advantages: disruption of a single gene product in the fully developed system; ease of viral construction and delivery; identification of infected cells using green fluorescent protein; and the ability to study negative controls (uninfected cells) in the same tissue.

Recently the possibility of engineering drug sensitivity into endogenous proteins has been raised. Gillespie et al. (48) have designed a myosin Iβ construct that has a point mutation (Y61G) in its ATP binding pocket. Assays for ATPase activity and in vitro motility demonstrated that this construct behaved normally in the presence of dinucleotides and trinucleotides. However, introduction of bulky dinucleotide analogs arrested the activity of mutant, but not wild-type, myosin Iβ. Whether this construct alters transducer adaptation in sensory hair cells remains to be seen.

Abbreviations

BAPTA

bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetate

I(X)

stimulus-response.