Motor Control is Decision-Making

Abstract

Motor behavior may be viewed as a problem of maximizing the utility of movement outcome in the face of sensory, motor and task uncertainty. Viewed in this way, and allowing for the availability of prior knowledge in the form of a probability distribution over possible states of the world, the choice of a movement plan and strategy for motor control becomes an application of statistical decision theory. This point of view has proven successful in recent years in accounting for movement under risk, inferring the loss function used in motor tasks, and explaining motor behavior in a wide variety of circumstances.

Introduction

While adjusting your chair at a dinner party, you bump the table. Out of the corner of your eye, you see what appears to be a wine glass tipping over. What should you do? In recent years, it has been recognized that such questions can be answered by considering the planning and control of movements within the framework of decision-making under risk. In typical decision-making tasks, the subject (human, primate, rat or pigeon) is given two or more options from which to choose. The optimal choice (Figure 1) depends on prior knowledge (e.g., of the probability of various outcomes), uncertain sensory information (e.g., of the values of the options), uncertainty of the outcome after selection of an option (i.e., the consequences may be stochastic), and the costs/benefits of any outcomes that may occur. In a purely sensory decision task, these elements are codified as the prior distribution (prior knowledge of the probability P(S) of various states of the world S), the likelihood function (the probability P(D|S) of obtaining the sensory data D that you have given a particular state of the world) and a loss function (L(C,S), determining the loss to the decision-maker of choice C in world state S).

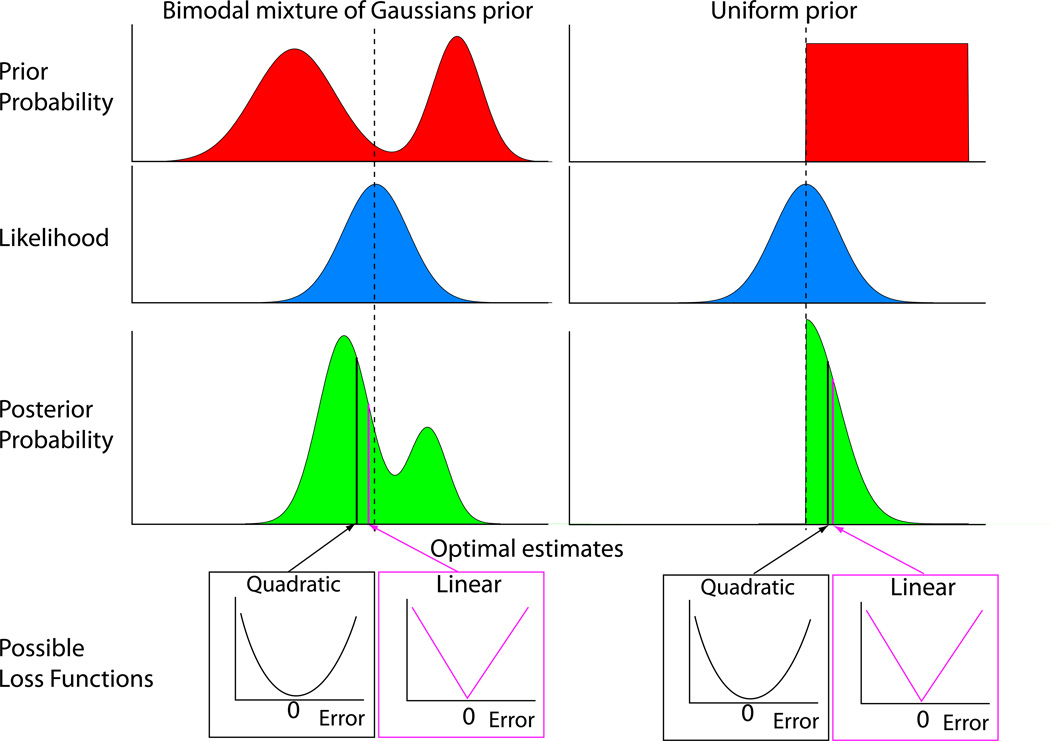
Figure 1.

The optimal choice depends on the prior, likelihood and loss function. In this schematic we consider pointing to the location of a target in one dimension. The top row shows two different possible priors (red curves) for target locations that might be imposed by task conditions, a mixture of two Gaussians (left) or a uniform prior over limited range (right). When the target is seen, the noisy sensory data specify a likelihood (blue curves). In this case the visual location of the target has been corrupted by Gaussian noise. The posterior probability (green curves) is the point-wise product of the prior and the likelihood (renormalized so that the area under the curve is one). The final decision depends on the loss function. Two possible loss functions are shown, one in which the loss increases quadratically (black curve) and the other in which it increases linearly (magenta) with error. The optimal estimate, shown by the arrows and lines on the posterior, depends on all three components.

For the tipping wine glass, all of these elements are present, so that the choice of a movement plan (where to move, what grasp to adopt, how to control the ongoing movement) constitutes a decision under risk. You have prior information about where the wine glass is located, how full it is, and how tipping wine glasses behave (which specifies the time constraint under which you are operating). The peripherally viewed wine glass presents you with noisy information about its current location and how fast it is tipping over. There is additional uncertainty due to the variability in motor responses, which will be exaggerated due to the need for a rapid reach. There are potential costs (e.g., failing in the reach and splashing the wine on your dinner partner’s clothes) and benefits (e.g., managing to catch the glass in time, and be able to drink the wine that didn’t spill).

Here, we will review recent research that considers movement planning and control from the standpoint of optimal decision-making under risk. We will review the elements that act together in motor decision-making. These include the role of loss functions, how the sensorimotor system responds to motor errors, the role of optimal control, the effect of sensory uncertainty, and ways in which motor decisions are suboptimal in ways analogous to suboptimality in cognitive decision tasks. For other recent reviews of motor behavior as decision-making, see [1–5].

Loss functions and optimality

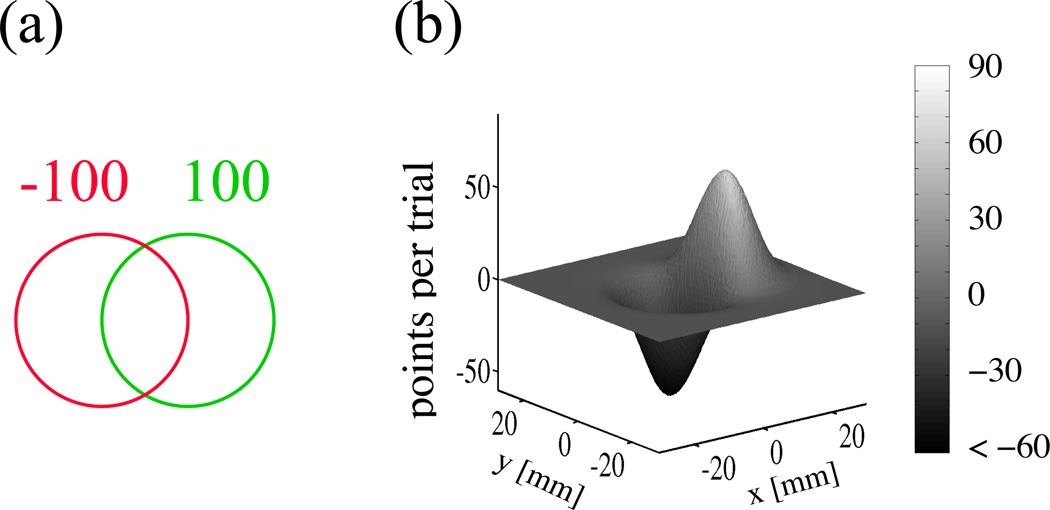
The choice of a movement plan should depend on the consequences of the movement. A loss function specifies the cost associated with the outcome of an action and is central to many theories of sensorimotor control. Several studies have shown that when participants perform movements with an explicit loss function they can be close to optimal in maximizing their reward. For example, in one study subjects were required to perform a rapid reach at a display consisting of a green target circle and a partially overlapping red penalty circle [6] (Figure 2a). Subjects were told that points were awarded if a reach landed within the target and deducted if a reach landed within the penalty region, and within any set were told how many points were associated with the target and penalty. Given motor variability for these speeded reaches, any choice of intended endpoint can result in a penalty and/or missed target. Given the measured covariance of movement endpoints for speeded reaches to a single target, it is simple to determine the probabilities of each outcome (hitting the target, penalty, both or neither) for any choice of aimpoint, and hence the expected gain (negative of the expected loss) in terms of average points per trial (Figure 2b). The results were surprising: Participants chose aim points that maximized expected gain. That is, within measurement error, humans were optimal at the task of reaching under risk.

Figure 2.

(a) In a rapid reaching task, subjects are awarded points (as indicated) for landing in the green target and penalties for landing in the red penalty region. (b) A typical gain landscape reflecting the, expected gain as a function of aimpoint. The expected gain takes into account subjects’ motor variability.

Unlike the simple reaches under risk in which the cost of a movement depends only on the final state, costs can often accrue over the entire movement. This is particularly true of path planning, in which the cost of a path over a landscape depends on the route taken. When planning such a path under risk, humans are not always able to maximize gain. For example, when subjects were required to reach to a goal by moving across a two-dimensional surface in which different regions had different costs per cm travelled, subjects’ behavior was suboptimal [7]. The choice of route resulted in 30% less income, on average, than the optimal path. However, behavior has been shown to be qualitatively similar to optimal behavior for more naturalistic loss functions. For example, the approach angle for a precision grasp tends to align with the maximal uncertainty of the position of the object to be grasped, thus minimizing the probability of unstable grasp [8]. Also, grip aperture widens when sensory uncertainty is increased by viewing the object to be grasped in peripheral vision [9]. Similarly, when reaching around an obstacle there is a trade-off between the cost of a circuitous path and the risk of bumping into the obstacle, so that clearance (minimum distance to the object) increases when sensory information is poor or motor uncertainty is increased [10].

The cost of time

In planning a movement such as a reach, the movement plan can encode where the reach will land on average (the aimpoint) and the expected duration. This specification of duration is an important component of such motor decisions because of the speed-accuracy tradeoff: movements that allow more time are spatially more accurate. Humans can optimize the duration of a movement; when an explicit loss function is imposed on movement duration (analogous to Figure 2 in time), such that one range of durations receives a reward and another range a penalty, mean movement durations are optimal in the sense of maximizing expected gain [11]. Similarly, subjects appear to optimize when they choose to initiate a movement, taking their speed-accuracy tradeoff (faster movements are less accurate) into account. In two studies [12–13], participants had a fixed total amount of time to make a reaching movement and they could choose how to split this time between an initial pre-movement viewing time and the remaining time to carry out the movement. This situation leads to a trade-off with earlier movement initiation leading to increased sensory uncertainty but smaller motor variability, and the converse for later movement initiation. In both studies, human performance was optimal in the sense that subjects chose the initiation time that maximized the probability of hitting the target. Humans also trade off the amount of time fixating the object of a reach and the goal where that object will next be placed based on the acuity requirements of each sub-task [14].

Many everyday tasks require a planned sequence of movements (such as reaching and grasping a wine glass and subsequently bringing it to one’s mouth). Surprisingly, motor decisions concerning planned sequences of movements under risk turn out to be suboptimal. When subjects have a fixed time within which to try to sequentially hit two targets, each associated with a different reward, there is a tradeoff in the time allocated to each movement, and performance is suboptimal [15]. Subjects spend too much time on the first reach even when hits on the second target are far more valuable than on the first. Such suboptimal behavior is resistant to training, and moreover, having an imposed time constraint itself comes at a cost of movement accuracy [16]. That is, there is no single speed-accuracy-tradeoff function; a fast reach is more accurate when carried out without a time constraint than when it is chosen to satisfy a time constraint.

Time can be costly for reasons independent of the motor system. For example, when using a sequence of eye movements to search for a target in a complex visual display, working memory is used to remember previously viewed locations. However, the quality of this memory decays over time. A recent study demonstrated a tradeoff between memory and motor effort in a cognitively difficult visual search task [17]. Participants were required to find a set of targets that shared the same attribute but on some trials the targets only became visible after a motor act such as a fixed delay after saccade or on a mouse click. When the motor task had low effort, subjects reduced the cost of working memory by increasing exploration so as to revisit previously fixated targets whereas when motor costs were high they relied more on memory to reduce motor costs.

In general, the value of a reward also depends on how long you expect to wait for the reward. In cognitive decision-making tasks, this discount function specifies how the value of future rewards decay with delays, ranging from minutes to weeks, in receiving the reward. Recently, it has been proposed that the motor system also uses such a temporal discounting of reward but with a discounting time period that is a fraction of a second. That is, the duration of a saccade can be thought of as delaying the reward of placing one’s gaze on target. Such a model can explain several aspects of saccade dynamics such as faster saccades to more rewarding targets [18].

Estimating the loss function

In several of the studies discussed thus far, the loss function for the task, specified by the reward for hitting a target, was imposed by the experimenter. What loss function is used by subjects when the loss function is not specified? How are errors scored in determining accuracy, and how does accuracy trade off with other costs, such as effort? If we consider the choice between making two movements both missing a target by 2 cm or the first by 1 cm and the second by 3 cm, a loss function specifies which choice is better. For example, if the loss function is quadratic in error, then the first choice is more desirable (loss 8 vs. 10). However, if the loss is linear in absolute error, then both are equally good (4 vs. 4). And, if the loss function is proportional to the square root of error, then the second choice is better (2.83 vs. 2.73). Therefore, the loss function for accuracy may be estimated by asking subjects to choose between different distributions of errors. The results of such a motor-decision task showed that for small errors the loss function was proportional to squared error, but rose less steeply for larger errors [19]. Such a loss is robust to outliers in comparison with a quadratic loss function. Similarly, to estimate the loss function that trades off effort and variability, subjects were asked to produce a target amount of total force using two fingers [20]. This is another “motor decision” as to what combination of forces to use to accord with the constraint of total force production. Increasing the force produced by a finger incurs a cost both because of the increased effort and the resulting increased variability (motor variability increases with the strength of the motor command). However, by varying the target force and the combination of fingers used, it is possible to disentangle the two potential contributions to the loss function. The results demonstrated that both effort and variability contribute to the choice of how to distribute force across the pair of fingers, with much higher weight given to reducing overall effort.

Interpretation of and response to error

A key aspect of decision-making in sensorimotor control is how to interpret and respond to errors. This is a huge area of research. Here, we highlight a few recent studies that emphasize error-interpretation as a decision-making problem. In particular, given an error, how should I assign the credit for that error across different body segments or back in time to different actions? The results of these studies can been formalized in a Bayesian model in which the relative allocation of credit to internal or external sources [21] or, during a bimanual task, to the left or right arm [22], can be assigned based on both a prior shaped by previous experience as well as on the source that is most consistent with the error. In addition, the way errors of different magnitudes lead to change in the motor command can also be understood as being optimal in a Bayesian framework in which small errors are interpreted as likely due to variability, requiring no adaptive response, but large errors may indicate a miscalibration that needs to be remedied [23].

Not only must errors be interpreted, they can also be controlled by selecting our actions. In a series of studies, it has been shown that subjects may adopt different strategies to reduce errors. For example when throwing an object, not only is it important to select the correct average hand position and velocity for the release but improvements in performance can be achieved by controlling the covariance between components of their action, for example releasing early if the velocity is high and late if it is low [24].

Optimal feedback control

While most of the studies described so far deal with discrete actions, most tasks involve continuous generation of complex trajectories. The concept of maximizing expected gain generalizes easily to the framework of optimal control in which a loss function is specified over the entirety of the movement so that the controller itself is organized so as to minimize loss. Typical costs penalize a mixture of effort and inaccuracy. The form of the optimal solution to minimizing this cost in the face of uncertainty arising from sensory and motor variability is to learn a feedback rule that generates the motor command as a function of the best estimate of the current state of the motor system, thereby setting up an optimal feedback controller. The beauty of this approach is that the feedback rules now specify the entire control strategy and how the trajectory will unravel and compensate for internal noise and external perturbations. The feedback rules rely on estimating the state, which is not a trivial task. Sensory noise and time delays require an estimation process that optimally combines sensory information with predictive information based on the outgoing motor command to estimate the state (an example of such an estimator is the Kalman filter). The framework of optimal feedback control has seen development both in the underlying theory [25] as well as experimental validation. For example, the theory is able to account for detailed aspects of trajectory generation and the response to perturbations [26] as well as how co-variation of effectors is tuned so as to push variability into task-irrelevant dimensions while preserving accuracy in task-relevant dimensions [27]. The framework has also been successfully applied to complex full-body movement such as balancing on a snowboard [28].

Bayesian approaches to uncertainty

As we pointed out in the Introduction, an optimal Bayesian approach to movement planning and control combines prior knowledge of the probability of various states of the world and uncertainty both in sensory data and in the outcome of the movement plan itself. Several recent studies examine how these elements combine to affect the choice of movement plan.

In one study, subjects were asked to point at a target with the unseen hand in a virtual display and, at reach initiation, the display of hand position was extinguished [29]. The finger position was displayed briefly at the halfway point in the reach with varied sensory uncertainty (using a noisy visual display) and displaced laterally from true finger position by a random amount (a prior distribution of displacement that had a mean of 1 cm and standard deviation of 0.5 cm). Landing points were consistent with a model in which subjects combine the sensory likelihood about the amount of finger displacement with a prior distribution in a Bayesian fashion. However, another study showed in a similar experiment that when the sensory likelihoods are measured, although the results were qualitatively consistent with a Bayesian model (i.e., estimates regressed more to the mean of the prior with increasing sensory uncertainty), they were quantitatively suboptimal, inconsistent with optimal Bayesian movement planning that maximized expected gain given prior information and uncertain sensory signals [30].

Suboptimal behavior may result from a Bayesian computation in which the subject uses a different prior distribution than exists naturally in the environment or than imposed by the experimenter. Thus, it is important to develop methods to estimate the prior distribution adopted by the subjects. In sensory research, techniques have been developed to estimate sensory priors by analyzing perceptual bias [31]. An analogous technique has been developed for estimating the covariance of a prior on sensory-motor transformations across the class of linear transformations (scaling, rotation, shear and reflection, [32]). Humans also behave as if they also have a prior expectation of the consequences of movement. For example, in one study [33] subjects performed a speeded reach at a payoff-penalty display (as in Figure 2). At reach initiation, the target-penalty display was replaced with a large pattern, and mid-way through the reach the pattern randomly began to drift slowly leftward, rightward, or remained stationary. The drift affected reach trajectories, nudging the reach laterally in the direction of visual drift, through a visuomotor reflex known as the manual following response (MFR). Since there was insufficient time to compensate for the MFR, this setup effectively increased movement uncertainty, making it anisotropic (in particular, the covariance was elongated horizontally). Performance was suboptimal (in contrast to the study [6] reviewed in Loss functions and optimality), but was effectively optimal for an ideal performance model that assumed that motor noise was isotropic. In effect, subjects behaved as if they had overwhelmingly strong prior knowledge that movement uncertainty of endpoints in this speeded reaching task would be isotropic. Thus, viewing movement planning and control as a decision-making task enables the researcher to uncover assumptions made by the participant in carrying out the task.

Risk sensitivity: Prospect Theory in motor control

In sensorimotor control subjects appear to maximize expected gain and this principle has been used to explain behavior in tasks in which uncertainty arises from variability of the perceptual or motor system. This contrasts with a large number of studies in economic decision-making where deviations from such optimality have been observed. For example, when offered a choice of a lottery that involves either a 50:50 gamble of winning $0 or $100 or a sure bet of $45, most people choose the sure bet even though it has a mean reward lower than the gamble. Prospect theory [34] suggests that such deviations from what might appear optimal can due to a nonlinear relation between reward (such as dollars) and the subjective value of that reward, and between the probability of an outcome and the subjective weight applied to that outcome. The shape of these relations determines how subjects will choose which of two lotteries they would prefer to play. Moreover, the value relation can be highly asymmetric in terms of gains and losses (typically people are loss averse). Simple shapes of the relation can also be interpreted as sensitivity not only to the mean reward (or cost) but also to the variance of the reward—that is, risk sensitivity. Subjects may be willing to accept a lower mean reward if it either reduces their variance (risk aversion, as in the previous lottery example) or increases their variance (e.g., the typical risk-seeking behavior seen in lotteries involving losses). Several recent studies using sensorimotor tasks find that participants do not maximize expected reward and are consistent with sensitivity to risk as well as expected reward. In the reaching-under-risk task (Figure 2a), the uncertainty in the outcome of the movement arises from intrinsic variability in the actions [35]. When comparing standard economic choices such as a choice of lotteries with the equivalent motor task, subjects behave in a more risk-seeking manner in the motor task [36]. This result can be interpreted within the framework of Prospect Theory. In lottery choice tasks, participants overweight small probabilities (expecting rare events to be more probable than they are) and underweight large ones (expecting highly probable events to be less probable than they are); the opposite pattern is seen in the equivalent motor choice task.

Evidence of decision-making in motor behavior

While the field of decision-making has tended to focus on the mechanisms underlying simple perceptual decisions, studies in this field have focused less on the interaction of the motor system with the evolving decision-making process. Similarly, in the work we have reviewed so far, we have shown how movement planning and control can be viewed as a decision-making problem. However, there are clear examples of behavior in which the motor system can betray the internal decision-making process for a purely perceptual decision (for a review see [37]). Recently, studies have started to link the dominant theory of decision-making—the drift-diffusion model—with the motor system. In the drift-diffusion model, when making a decision between two alternatives, evidence is accumulated in favor of one alternative over the other. Evidence is modeled as draw from a Gaussian distribution with a mean that depends on the stimulus. A bound is associated with each choice (a negative and a positive bound) and when the accumulated evidence crosses a bound the associated choice is made. This model can explain both the probability of making a correct choice and the time to choice as a function of task difficulty. However, whenever we make a perceptual decision that leads to an action, because of time delays in perception and the enacting of that decision, there is further evidence in the processing pipeline (around 250 ms) that cannot be used to make the decision but that could still be processed. A recent study showed that indeed this information is processed and, having hit one of the bounds for the initial decision, a new change-of-mind bound is created. If this bound is subsequently crossed then the decision is reversed, leading to a change of mind and an appropriately altered movement trajectory [38]. Moreover, even before the movement is initiated the medium and long-latency reflex gains in the motor system (as measured by the stretch reflex) track the evolving decision process with an almost linear relation between reflex gain and the accumulated evidence [39], suggesting there can be a continuous flow of information from the decision to the motor system. Indeed, MEG studies show that signals in motor cortex build up gradually in decision-making tasks [40].

Conclusion and outlook

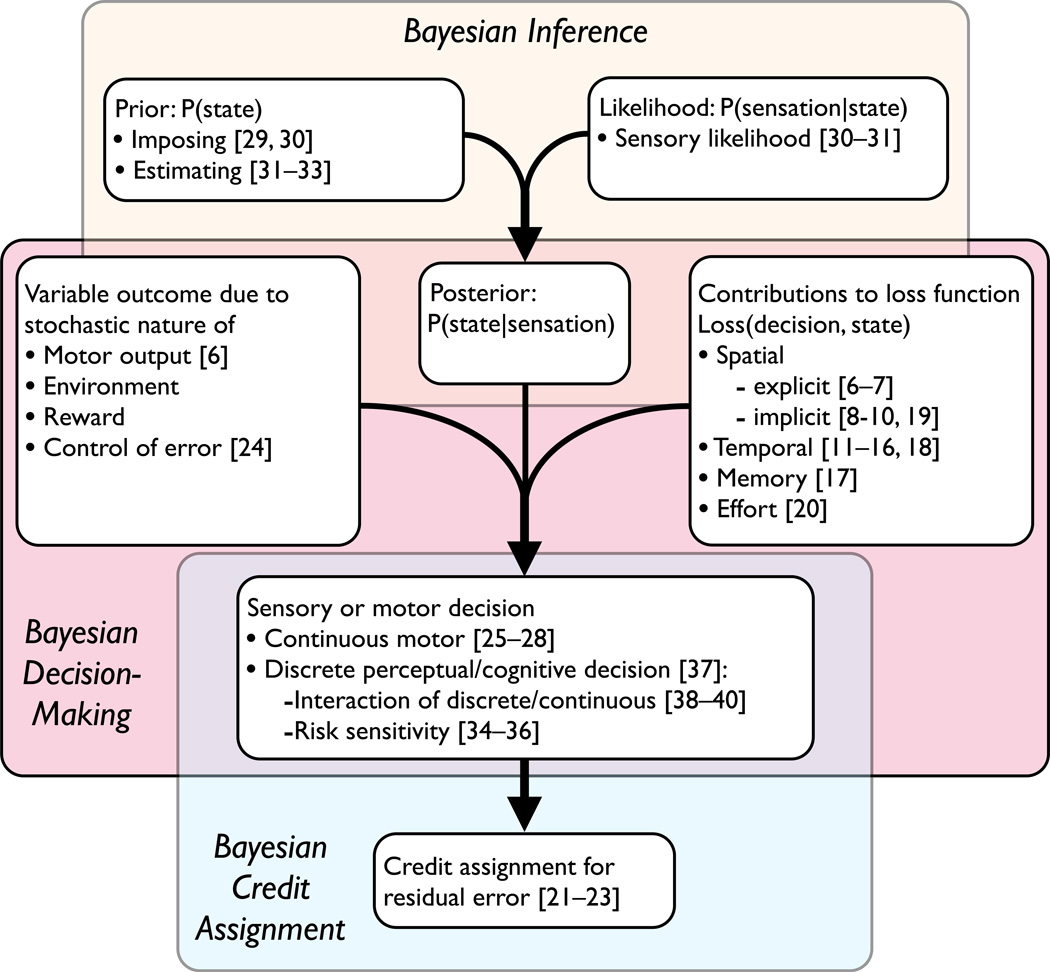
Viewing movement planning and control as a problem of statistical decision theory has proven a useful viewpoint for understanding motor behavior. In this view, visuo-Page motor planning, control and adaptation proceed in three stages (Figure 3). First, prior knowledge and noisy sensory signals are combined to produce a posterior distribution. In the second stage, for both sensory decisions and motor tasks, the posterior is combined with knowledge of the loss function as well as any downstream uncertainty (in the motor output, environment, or expected reward) to produce a sensory estimate or decision or a movement plan. In the third and final stage, residual error is interpreted, e.g., to adapt the motor system for subsequent movements. We predict that substantial progress in modeling movement will result as researchers get a better handle on the loss functions and models of sensory and motor uncertainty adopted in natural movement tasks.

Figure 3.

Three stages of sensory and motor decisions: Bayesian inference, decision-making and credit assignment. We cross-reference the primary focus of the articles we have surveyed to the elements of sensory/motor decision processes.

Highlights.

Movement planning and control may be viewed as a form of decision-making

Movement is thus influenced by prior knowledge, sensory and motor uncertainty, and the loss function

Recent research indicates movement plans can be near optimal

Response to movement error may also be viewed relative to an ideal performance model