Evolutionary shift dynamics on a cycle

Abstract

We present a new model of evolutionary dynamics in one-dimensional space. Individuals are arranged on a cycle. When a new offspring is born, another individual dies and the rest shift around the cycle to make room. This rule, which is inspired by spatial evolution in somatic tissue and microbial colonies, has the remarkable property that, in the limit of large population size, evolution acts to maximize the payoff of the whole population. Therefore, social dilemmas, in which some individuals benefit at the expense of others, are resolved. We demonstrate this principle for both discrete and continuous games. We also discuss extensions of our model to other one-dimensional spatial configurations. We conclude that shift dynamics in one dimension is an unusually strong promoter of cooperative behavior.

1. Introduction

The impact of population structure on ecological and evolutionary dynamics is a topic of great interest (Wright, 1943; Slatkin, 1981; Nowak & May, 1992; Barton, 1993; Durrett & Levin, 1994; Hassell et al., 1994; Dieckmann et al., 2000; Hauert & Doebeli, 2004; Rousset, 2004; Nowak et al., 2010a). Spatial and social structure can promote the evolution of cooperation (Nowak & May, 1992; Nakamaru et al., 1997; Killingback & Doebeli, 1996; van Baalen & Rand, 1998; Mitteldorf & Wilson, 2000; Le Galliard et al., 2003; Nowak, 2006b; Traulsen & Nowak, 2006; Szabó & Fáth, 2007; Helbing & Yu, 2009; Tarnita et al., 2009a), though this effect depends on the underlying details of the evolutionary process (Wilson et al., 1992; Taylor, 1992; Nowak et al., 1994; Hauert & Doebeli, 2004; Ohtsuki et al., 2006; Lion & van Baalen, 2008; Roca et al., 2009a; Korolev & Nelson, 2011; van Veelen et al., 2012).

Evolutionary graph theory provides an elegant framework for studying the effect of fixed population structure on evolutionary dynamics (Lieberman et al., 2005; Santos & Pacheco, 2005; Ohtsuki et al., 2006; Taylor et al., 2007; Szabó & Fáth, 2007; Santos et al., 2008; Roca et al., 2009b; Fowler & Christakis, 2010; Perc & Szolnoki, 2010). In this framework, individuals are located at the nodes of a graph. Interaction and reproduction occur along edges. The one-dimensional cycle is a particularly simple graph topology for which many results can be obtained analytically (Ohtsuki & Nowak, 2006; van Veelen & Nowak, 2012). More generally, there may be two different graphs, one for interaction and one for replacement (Ohtsuki et al., 2007). There are also various approaches for studying the effect of dynamical population structure on social evolution, where individuals can adjust their social ties either at random (Wu et al., 2010b) or depending on game actions and payoffs (Skyrms & Pemantle, 2000; Pacheco et al., 2006a,b; Fu et al., 2008; Antal et al., 2009; Helbing & Yu, 2009; Tarnita et al., 2009a; Perc & Szolnoki, 2010; Poncela et al., 2009; Fehl et al., 2011; Rand et al., 2011).

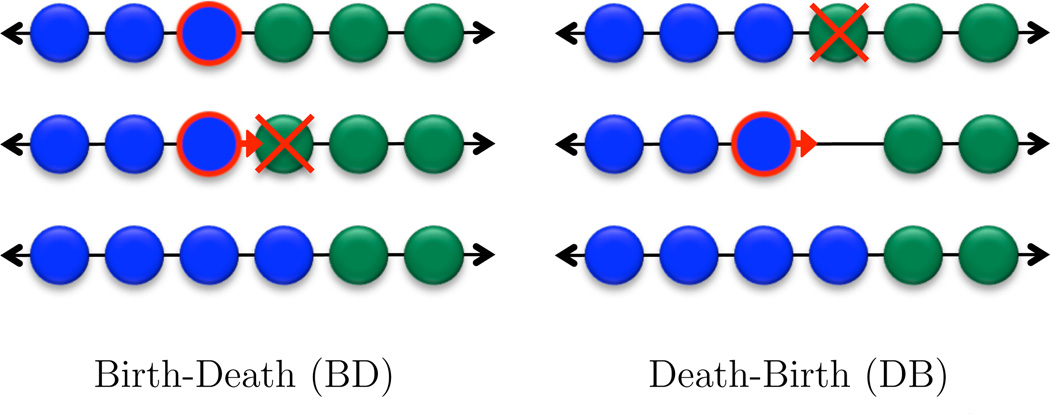
In any evolutionary model, the “update rule” determines how reproduction occurs. One particular rule is called “Birth-Death” (BD) updating. Here an individual is chosen for reproduction (proportional to payoff) and the offspring replaces a randomly chosen neighbor (in the replacement graph). Another rule is called “Death-Birth” (DB) updating. Here a random individual dies and the neighbors compete for the empty site proportional to their payoff. Different update rules can lead to different evolutionary outcomes (Ohtsuki & Nowak, 2006; Ohtsuki et al., 2006).

Here we introduce a new rule, which we call “shift” updating. One individual is chosen for reproduction. The offspring is placed next to the parent. Elsewhere one individual dies. The individuals shift around to redistribute themselves evenly in space. Shift updating is particularly simple in one dimension, which is the topic of this paper. Generalizations to higher dimensions or more complicated graphs are possible and will be studied in subsequent papers.

We find that shift updating is an unusually strong promoter of cooperative behavior, compared to other update rules that have been studied previously. For shift updating, the abundance of cooperators increases primarily because cooperators reproduce deep inside clusters. The clusters then expand according to the shift rule. In contrast, for other update rules such as BD and DB, a cooperator cluster can only expand through reproduction of cooperators that are located near the boundary between cooperators and defectors (Ohtsuki & Nowak, 2006, 2008). But there cooperators can be at a disadvantage relative to the nearby defectors who exploit them.

Shift updating is inspired by cellular reproduction. The idea is that a cell divides and subsequently the population readjusts to accommodate the new cell. A particular example is the organization of epithelial layers in human tissue. The human colon, for instance, contains crypts where cell division leads to a movement of cells along the crypt. It has been argued that this architecture reduces the rate of cancer initiation (Nowak et al., 2003; Michor et al., 2004b). Another example is microbial colonies growing on a at surface. In such colonies, since existing individuals are generally fixed in place, competition dynamics occur primarily at the expanding one-dimensional circumference of the colony (Hallatschek et al., 2007; Hallatschek & Nelson, 2010; Korolev et al., 2010; Nadell et al., 2010). As new offspring arise, the colony boundary expands in a manner similar to the shift dynamic we consider here. We note, however, that each of these biological systems differs in certain ways from our model. In the human colon model of Nowak et al. (2003), cells are arranged in a directed line segment, with stem cells at one end, rather than a cycle. In growing microbial colonies, the boundary is always increasing in size, whereas our model holds population size fixed.

Our paper is organized as follows. Section 2 formally presents our model of evolutionary shift dynamics. Section 3 provides general formulas for fixation probability. Section 4 examines the case of constant selection, showing that evolution in this model neither amplifies nor suppresses selection. We then turn to evolutionary games in Section 5. We obtain simple closed-form results in two cases: the large population limit (Section 5.1) and the weak selection limit (Section 5.2). In each case we obtain the result that, for sufficiently large population sizes, evolution favors the type that maximizes whole-population payoff. Section 6 introduces the possibility of mutation, and shows how this weakens the spatial benefit to cooperation. In Section 7 we turn to continuous games. Using the adaptive dynamics approach (Nowak & Sigmund, 1990; Hofbauer & Sigmund, 1990; Dieckmann & Law, 1996; Metz et al., 1996), we study how the shift dynamics model affects the long-term evolutionary trajectories of continuous traits. Finally, in Section 8 we compare the results obtained from the shift rule with other update rules on the cycle.

2. Model

We consider a cycle with N positions, each occupied by a single individual. In each time-step, each individual is assigned a fecundity (reproductive rate). Fecundities may be constant, depending only on the individual’s type—a case we explore in Section 4. For most of this work, however, we consider fecundities to be determined through game interactions with neighbors, as we discuss in Section 5.

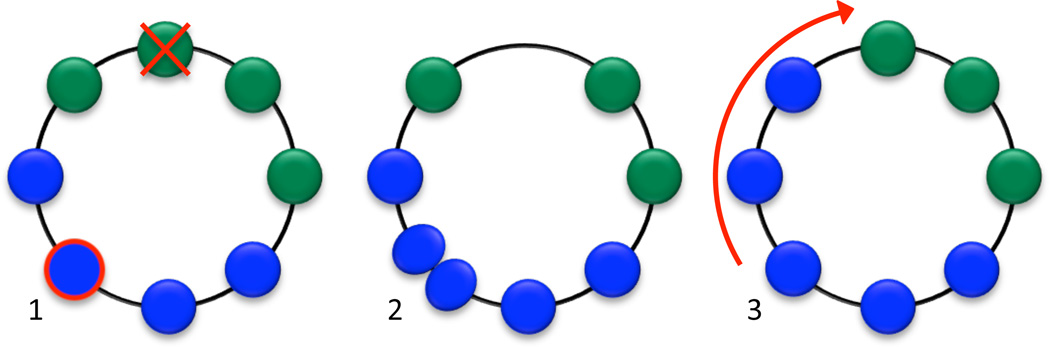
After fecundities are determined, an individual is chosen for reproduction, with probability proportional to fecundity. Another individual is chosen for death at random, with uniform probability. The new individual appears in a position neighboring the parent, and the remaining individuals shift around the cycle until the position of the deceased individual is filled. Since the cycle has rotational symmetry, it does not matter in which direction the birth and shifts occur. It may happen that the parent is itself chosen for death, in which case the new offspring simply replaces the parent. This update rule is illustrated in Figure 1.

Figure 1.

Shift dynamics on a cycle. (1) First, an individual is chosen to reproduce with probability proportional to fecundity, and an individual is chosen for death with uniform probability. (2) The new offspring appears adjacent to the parent. (3) The remaining individuals shift along the cycle until the position of the deceased individual is filled. It does not matter which direction the reproduction and shifts occur—the resulting state is the same (up to a rotation of the cycle).

Though this model could be applied to any number of competing types, we focus here on competition between two types A and B. For the majority of this work we assume that offspring always inherit the type of their parent; the exception is Section 6, where the possibility of mutation is added.

3. Fixation probability

We quantify evolutionary success using the fixation probabilities ρ_A and ρ_B (Nowak et al., 2004; Nowak, 2006b). Here, ρ_A denotes the probability that, starting from a population with one A and (N − 1) B, type A will eventually occupy all N positions. ρ_B denotes the analogous probability with the roles of A and B reversed. We say that selection favors A if ρ_A > ρ_B.

We observe that, absent mutation, any population founded by one individual of one type and (N − 1) individuals of the opposite type will always consist of two “clusters”, each comprised of only one type. In other words, the two types remain spatially segregated. The state of the evolutionary system can therefore be completely characterized by the number k of A individuals.

Because of this, the fixation probability of A can be expressed as (Taylor et al., 2004; Nowak, 2006a)

$${\rho }_A={\left(1+{\displaystyle \sum _{j=1}^{N-1}{\displaystyle \prod _{k=1}^j\frac{p_k^{-}}{p_k^{+}}}}\right)}^{-1}.$$ (1)

Here $p_k^{+}$ (resp., $p_k^{-}$) denotes the probability that the number of As will increase (resp., decrease) in the next evolutionary step, when there are currently k individuals of type A. We can express these probabilities as

$$p_k^{+}=\frac{\text{total fecundity of }A’\mathrm{s}}{\text{total fecundity of population}}\times \frac{N-k}{N}$$

$$p_k^{-}=\frac{\text{total fecundity of }B’\mathrm{s}}{\text{total fecundity of population}}\times \frac{k}{N}.$$

Using these expressions, we can simplify the ratio $p_k^{-}/p_k^{+}$ to

$$\frac{p_k^{-}}{p_k^{+}}=\frac{\text{average fecundity of }B’\mathrm{s}}{\text{average fecundity of }A’\mathrm{s}}.$$

Substituting into (1) yields the formula

$${\rho }_A={\left(1+{\displaystyle \sum _{j=1}^{N-1}{\displaystyle \prod _{k=1}^j\frac{g_k}{f_k}}}\right)}^{-1}.$$ (2)

Here f_k (resp., g_k) denotes the average fecundity of A’s (resp., B’s), when the number of A individuals is k.

Combining the above arguments with the analysis of Taylor et al. (2004), we can express the ratio ρ_A/ρ_B as

$$\frac{{\rho }_A}{{\rho }_B}={\displaystyle \prod _{j=1}^{N-1}\frac{f_k}{g_k}.}$$ (3)

4. Constant selection

We first consider constant selection. We suppose type B has constant fecundity 1, and A has constant fecundity 1 + r. Thus f_k = 1 + r and g_k = 1 for each k.

In this case, the birth and death probabilities of each individual are exactly the same as they would be in the well-mixed Moran (1958) process. In other words, this particular spatial structure has no effect on evolutionary dynamics when selection is constant. Using (2), we can express the fixation probability of A as

$${\rho }_A=\frac{1-r^{-1}}{1-r^{-N}}.$$

Since this is the same fixation probability as would be found in the Moran process, we conclude that the shift model is neither an amplifier nor a suppressor of selection, in the language of Lieberman et al. (2005).

5. Discrete games

We now turn to evolutionary games. We begin with the case of two competing types, A and B, who interact according to the game matrix

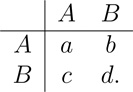(4)

Individuals play this game with each neighbor. For each individual, we retain the average of the two payoffs obtained from the neighbors.

This average payoff must then be transformed into fecundity (reproductive rate). For this, we consider a positive, differentiable, increasing function F(x), and a real number δ > 0 quantifying the intensity of selection. The mapping from payoff to fecundity is given by π ↦ F (δπ). Specific examples of payoff-to-fecundity mappings are the linear map π ↦ 1 + δπ (with the constraint δπ > −1; see Nowak et al., 2004; Ohtsuki et al., 2006) and the exponential map π ↦ e^δπ (Traulsen et al., 2008). Wu et al. (2010a) provide further discussion of payoff-to-fecundity mappings. Unless otherwise specified, the results presented here are independent of the particular choice of F(x).

In general, the expressions (2) and (3) for ρ_A and ρ_A/ρ_B do not reduce to closed-form expressions when considering evolutionary games. However, for two important cases, we can obtain simple conditions for which type is favored. These cases are the large population regime, N ≫ 1, and the weak selection regime, Nδ ≪ 1.

5.1. Large populations

For large population size, the condition for A to be favored is simply a > d. In other words, A must obtain a higher payoff from other A’s than B’s do from other B’s. This result can be interpreted as saying that, in the large population limit, only same-type interactions matter.

This result is intuitive: when population size is large, most individuals reside in the interiors of the two segregated clusters. Thus most A’s have payoff a, and most B’s have payoff d. Since, according to (2), the evolutionary dynamics depend on the average fecundities of the two types, the success of the two types depends predominantly on the same-type payoffs a and d.

We state this result in the following theorem, the proof of which appears in Appendix A.

Theorem 1. For any positive, differentiable, increasing payoff-to-fecundity mapping F(x), and any selection intensity δ > 0, we have: if a > d, then

$$\mathit{\text{if}}a<d,\mathit{\text{then\hspace{1em}}}\begin{array}{cc}\underset{N\to \infty }{\text{lim}}{\rho }_A>0,\hfill & \underset{N\to \infty }{\text{lim}}{\rho }_B>0;\hfill \\ \underset{N\to \infty }{\text{lim}}{\rho }_A=0,\hfill & \underset{N\to \infty }{\text{lim}}{\rho }_B>0.\hfill \end{array}$$

Thus A is favored (ρ_A > ρ_B) in the large population limit if and only if a > d. In short, evolution favors the type that maximizes the whole-population payoff.

As an example, for any Prisoner’s Dilemma (c > a > d > b), Snowdrift (c > a > b > d), or Stag Hunt (a > c ≥ d > b) game, the cooperative strategy is favored over the non-cooperative strategy as long as population size is sufficiently large.

This result readily extends to multiplayer games (Gokhale & Traulsen, 2010) played with nearest neighbors on the cycle (van Veelen & Nowak, 2012). For such games, strategy A is selected over strategy B in large populations if and only the payoff to A interacting with other A’s exceeds the payoff to B interacting with other Bs. Thus, as in two-player games, selection favors the type that obtains the higher payoff from its own kind.

5.2. Weak selection

For weak selection, Tarnita et al. (2009b) proved that to every population structure is associated a “structure coefficient” σ, which is independent of the game played in the population (see also Nowak et al., 2010a; Tarnita et al., 2011). For any particular pairwise game of the form (4), A is favored over B (ρ_A > ρ_B) if and only if

$$\sigma a+b>c+\sigma d.$$ (5)

The value of σ quantifies the relative importance of same-type versus opposite-type interactions for evolutionary success in a given structure.

In Appendix B we compute the structure coefficient for shift dynamics on a cycle of size N, obtaining

$$\sigma =\frac{N-1}{h_{N-1}}-1.$$ (6)

Here h_N is the Nth harmonic number:

$$h_N={\displaystyle \sum _{k=1}^N\frac{1}{k}.}$$

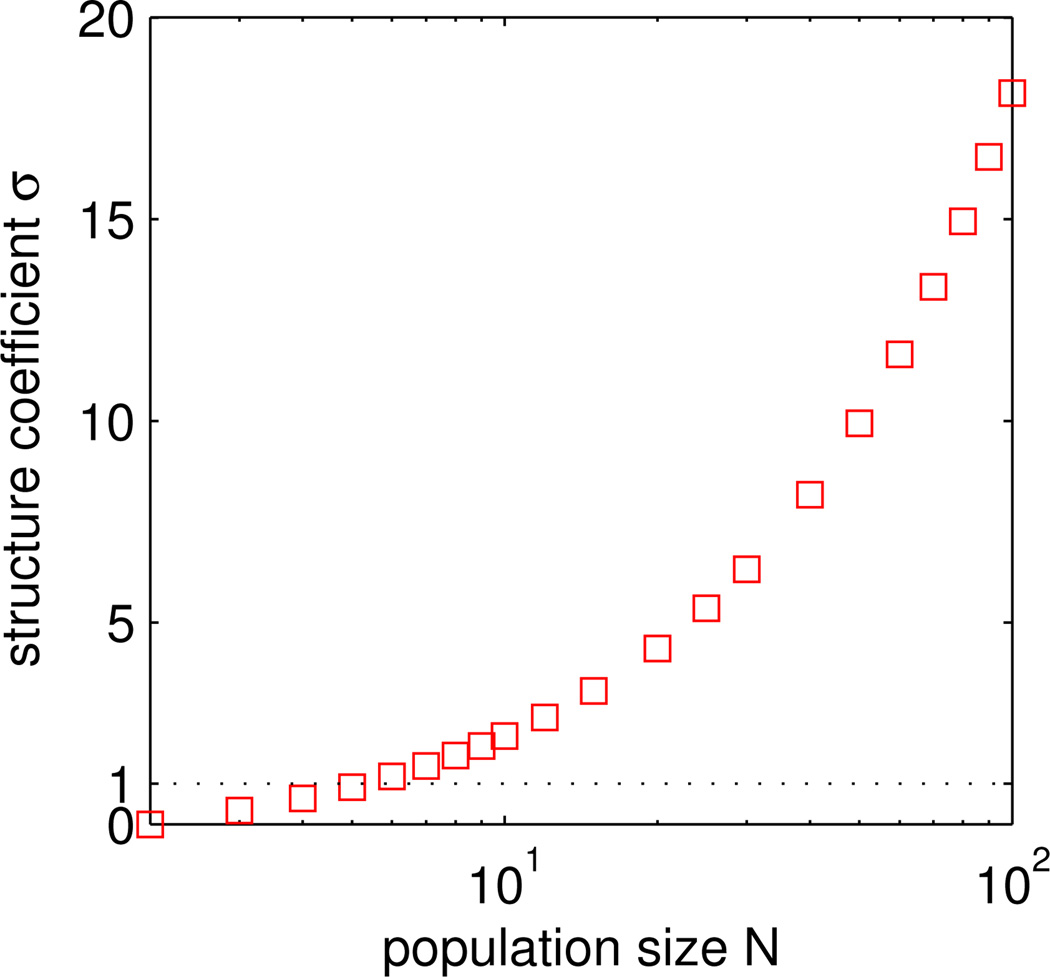
The harmonic number h_N can be approximated as γ + ln N, where γ ≈ 0:577 is the Euler-Mascheroni constant. The value of σ therefore grows asymptotically as N/ln N, as shown in Figure 2. This growth reflects the fact that same-type interactions grow increasingly important as N increases.

Figure 2.

The structure coefficient σ for the shift rule, as a function of the population size N, according to (6). A logarithmic scale is used for the horizontal axis. For N = 2 we have σ = 0. The value of σ exceeds one for N ≥ 6. Asymptotically, as N increases, σ increases as N/ln N.

We observe from (6) that σ = 0 for a population of size two. This is because the only relevant state in the N = 2 case consists of one individual of each type. Consequently, selection favors whichever type obtains a higher payoff from the other—b versus c in the payoff matrix (4). For populations of size six or larger, the value of σ exceeds 1, indicating that cooperative strategies are aided by the population structure.

6. Mutation

We can also analyze how mutation affects evolutionary success under shift dynamics. We incorporate mutation into our model by supposing that, whenever a new individual is born, that individual has probability u of having a mutation. An offspring with a mutation has an equal chance of being born as either of the two competing types.

With nonzero mutation, the evolutionary process is ergodic. This means there is a stationary distribution of states to which the time-averaged behavior of the evolutionary process converges. We consider type A to be favored if it has greater than 50% abundance in this stationary distribution, following Antal et al. (2009).

Before continuing, we adopt the following notation: We index the individuals in the population by the integers modolu N (thus i = −1 and i = N − 1 refer to the same individual). We designate individual 0 as a focal individual (by symmetry, this choice does not affect the results). The type of individual i will be denoted s_i ∈ {A, B}. The fecundity of individual i will be denoted F_i. For simplicity, we assume that the payoff-to-fecundity function F(x) satisfies F(0) = F′ (0) = 1, though our results hold for any positive, differentiable, increasing function F(x).

In the limit of weak selection, Nowak et al. (2010b, Appendix A) showed that, if death probabilities are constant over all states (as they are in our shift model), type A is favored over type B if and only if

$${\langle \frac{\partial b_0}{\partial \delta }\rangle }_{\underset{s_0=A}{\delta =0}}>0.$$ (7)

Above, b₀ is the reproduction probability (per time-step) of the focal individual. The notation ${\langle \rangle }_{\underset{s_0=A}{\delta =0}}$ indicates an expectation over the stationary distribution of states of the neutral (δ = 0) process, conditioned on the focal individual being of type A. The partial derivative in (7) is also assumed to be taken at δ = 0.

For the shift model in particular, the left-hand side of condition (7) can be expanded as

$${\langle \frac{\partial b_0}{\partial \delta }\rangle }_{\underset{s_0=A}{\delta =0}}={\langle \frac{\partial }{\partial \delta }\frac{F_0}{{\displaystyle {\sum }_{i=0}^{N-1}{F}_i}}\rangle }_{\underset{s_0=A}{\delta =0}}=\frac{1}{N}{\langle \frac{\partial F_0}{\partial \delta }\rangle }_{\underset{s_0=A}{\delta =0}}-\frac{1}{N^2}{{\displaystyle \sum _{i=0}^{N-1}\langle \frac{\partial F_i}{\partial \delta }\rangle }}_{\underset{s_0=A}{\delta =0}},$$ (8)

using the fact that F_i = 1 for all i when δ = 0.

We now restrict our attention to the additive Prisoner’s Dilemma game, with payoff matrix

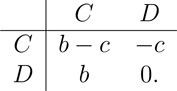(9)

We will use this game to compute the structure coefficient σ for the shift model with arbitrary mutation rate u. This value of σ can then be used to obtain success conditions for any 2 × 2 game, using relation (5).

For this game, using F′(0) = 1, we have

$${\langle \frac{\partial F_i}{\partial \delta }\rangle }_{\underset{s_0=C}{\delta =0}}=-c{\langle s_i\rangle }_{\underset{s_0=C}{\delta =0}}+\frac{b}{2}{\langle s_{i-1}+s_{i+1}\rangle }_{\underset{s_0=C}{\delta =0}}.$$ (10)

We obtain the quantities ${\langle s_i\rangle }_{\underset{s_0=C}{\delta =0}}$ using the method of stationary identity-by-descent probabilities (Rousset & Billiard, 2000; Taylor et al., 2007; Antal et al., 2009; Tarnita et al., 2009a; Allen et al., 2012b). Specifically, we compute the probabilities q_k that two individuals located k positions apart on the cycle are identical-by-descent (IBD). Two individuals are IBD if no mutations have occurred in either of their lineages since they diverged from their common ancestor. These probabilities can be obtained using the coalescent method, in which the evolutionary process is traced backwards through time. In Appendix C we use this method to derive recurrence relations for the q_k, k = 0;…,N − 1. Though these recurrence relations do not appear to have a general closed-form solution, the q_k can be obtained numerically, for any combination of N and u, using Gaussian elimination.

Since mutation is equally likely to result in either type, the IBD probabilities q_k are related to the quantities ${\langle s_i\rangle }_{\underset{s_0=C}{\delta =0}}$ by

$${\langle s_i\rangle }_{\underset{s_0=C}{\delta =0}}=\frac{1+q_i}{2}.$$

Thus (10) can be rewritten as

$${\langle \frac{\partial F_i}{\partial \delta }\rangle }_{\underset{s_0=C}{\delta =0}}=\frac{b-c}{2}+\frac{1}{2}\left(-c{q}_i+\frac{b}{2}(q_{i+1}+q_{i-1})\right).$$

Combining with (7) and (8), we obtain the result that C is favored if and only if

$$-c+b{q}_1-(-c+b\overline{q})>0.$$

Here q₁ is the probability that two nearest neighbors are IBD. The quantity

$$\overline{q}=\frac{1}{N}{\displaystyle \sum _{k=0}^{N-1}{q}_k}$$

is the average IBD probability of two randomly chosen individuals. We conclude that cooperation is favored in the Prisoner’s Dilemma under weak selection if and only if

$$\frac{b}{c}>\frac{1-\overline{q}}{q_1-\overline{q}}.$$ (11)

This condition can be interpreted as a form of Hamilton’s rule. Many studies of inclusive fitness theory (e.g. Rousset & Billiard, 2000; Rousset, 2004; Taylor et al., 2007) use

$$R=\frac{q_1-\overline{q}}{1-\overline{q}}$$

as a formula for relatedness between neighbors; with this definition, condition (11) becomes equivalent to bR > c.

We note, however, that the condition for successful cooperation takes this simple form only because the shift rule is a “global update rule”, a term that we define and discuss in Section 8.2. For other update rules that do not possess this property, including BD and DB (defined above and in Figure 3), the condition for successful cooperation cannot be written as bR > c with R representing relatedness; see Nowak et al. (2010b).

Figure 3.

Two update rules introduced by Ohtsuki & Nowak (2006). For Birth-Death updating, at each time-step, an individual is chosen to reproduce, with probability proportional to fecundity. The new offspring displaces a neighbor of the parent, chosen randomly with uniform probability. For Death-Birth updating, in each time-step, an individual is chosen to die, with uniform probability. This death leaves a vacancy. The neighbors of this vacant site then compete for the opportunity to reproduce. One of them is chosen, with probability proportional to fecundity, and the offspring of the chosen neighbor fills the vacant site.

Combining (11), and (5), we can express the structure coefficient for the shift rule as

$$\sigma =\frac{1+q_1-2\overline{q}}{1-q_1}.$$ (12)

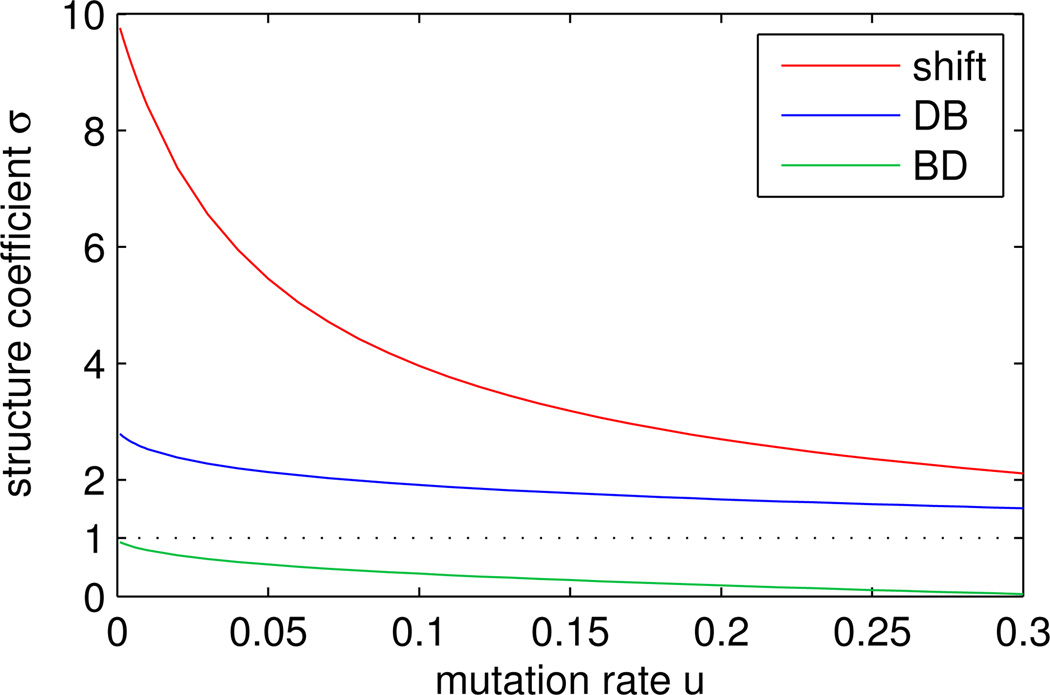
The dependence of σ on u is illustrated in Figure 6.

Figure 6.

The structure coefficient σ as a function of mutation rate u for shift, DB, and BD updating on a cycle of size N = 50. In each case, mutation hinders cooperative strategies by diluting assortment between cooperators. We note, however, that the σ-value for the shift rule, even for the relatively high mutation rate of u = 0.15, exceeds the maximum possible σ-value for DB.

7. Continuous games

We can also consider continuous games. In this case, an individual’s strategy or trait value is represented by a real number (or, for multivariate traits, a vector). The payoff to an individual of trait value x interacting with a partner of trait value y is given by the value of a payoff function G(x; y).

For continuous games, the course of evolution can be studied by considering the long-term trajectory of the trait value x, as it evolves through a sequence of invasion and fixation events. We assume that mutation in x is both rare and incremental. These assumptions allow us to apply the adaptive dynamics approach (Nowak & Sigmund, 1990; Hofbauer & Sigmund, 1990; Dieckmann & Law, 1996; Metz et al., 1996). We also assume that the payoff function G is positive and differentiable in both arguments, and that each individual’s fecundity is equal to the average payoff from interacting with both neighbors.

Though adaptive dynamics is traditionally formulated for well-mixed populations, a recent study (Allen et al., 2012a) has extended the adaptive dynamics approach to a broad class of structured population models. This class includes the shift dynamics model considered here. Under the above assumptions, this work derived the following equation for expected evolutionary trajectories under any model in this class:

$$\dot{x}=\frac{N_e(N-1)}{2}uv\left(\frac{\partial }{\partial x\prime }{|}_{x\prime =x}G(x\prime ;x)+\frac{\sigma -1}{\sigma +1}\frac{\partial }{\partial x\prime }{|}_{x\prime =x}G(x;x\prime )\right).$$

Here,

• N is population size,

• N_e is an effective population size (discussed below),

• u is the mutation probability per birth,

• v is the variance in the distribution of mutational steps,

• σ is the structure coefficient.

The effective population size N_e for a particular model is obtained by comparing the fixation probability of a trait with constant selective advantage to the analogous fixation probability in the baseline Wright-Fisher model. Since for constant selection, fixation probabilities in the shift model are the same as those in the Moran process (see Section 4), the effective population size for the shift model is equal to that of the Moran process, which is N/2.

The expected evolutionary trajectory of the trait value x under the shift model is therefore given by

$$\dot{x}=\frac{N-1}{2}uv\left(\frac{\partial }{\partial x\prime }{|}_{x\prime =x}G(x\prime ;x)+\left(1-\frac{2h_{N-1}}{N-1}\right)\frac{\partial }{\partial x\prime }{|}_{x\prime =x}G(x;x\prime )\right).$$ (13)

We observe that, as N → ∞, the equation for expected evolutionary trajectories (13) approaches

$$\dot{x}=\frac{N-1}{2}uv\left(\frac{\partial }{\partial x\prime }{|}_{x\prime =x}G(x\prime ;x)+\frac{\partial }{\partial x\prime }{|}_{x\prime =x}G(x;x\prime )\right)\equiv \frac{N-1}{2}uv{\nabla }_{x}G(x;x).$$

This implies that, as N → ∞, evolutionary trajectories perform gradient ascent on the average population payoff G(x; x). In other words, evolution acts to optimize the payoff of the whole population. This stands in stark contrast to evolution in well-mixed or otherwise structured populations, in which social dilemmas can cause whole-population payoff to evolve downward, possibly even leading to extinction of the population (Gyllenberg & Parvinen, 2001).

Equation (13) for adaptive dynamics with the shift model can readily be extended to multivariate (vector-valued) traits and more general mutation schemes (Allen et al., 2012a). An important open question is to understand how shift dynamics affect the possibility of evolutionary branching (Geritz et al., 1997; Dieckmann & Doebeli, 1999; Doebeli & Dieckmann, 2003; Doebeli et al., 2004), in which multiple trait values coexist and evolve in different directions.

8. Comparison to other update rules

In their study of evolutionary games on cycles Ohtsuki & Nowak (2006) considered a number of update rules, all of which had the feature that individuals remain fixed in place until they are replaced or updated. Of the update rules they considered, two in particular have been extensively studied in subsequent research: the death-birth (DB) rule and the birth-death (BD) rule. We define and illustrate these update rules in Figure 3.

8.1. Conditions for success in evolutionary games

Different update rules can lead to strikingly different outcomes for evolutionary games. For example, for the additive Prisoner’s Dilemma game (9), cooperation is never favored under BD updating. For DB updating, cooperation is favored on a large cycle if b/c > 2. In contrast, for the shift rule, cooperation is favored on a large cycle whenever b > c.

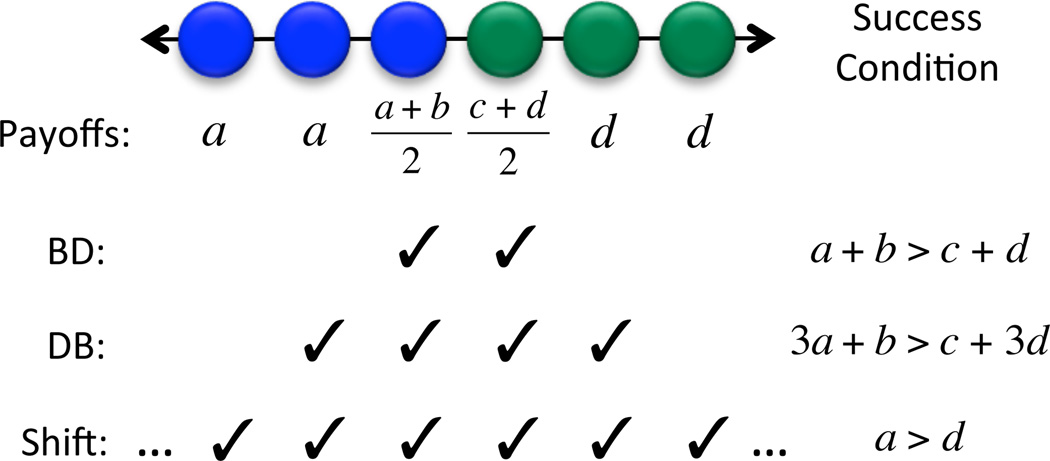
We can understand the different outcomes of these rules by examining the dynamics of clusters—connected chains of individuals who share a common type. For all three update rules (BD, DB, and shift), if there is no further mutation after an initial mutant is introduced, then the population will be comprised of two clusters until one type reaches fixation. The update rules differ in the the mechanisms by which these clusters expand or contract (Figure 4):

• For BD updating, clusters change size only if an individual at an boundary (where the two types meet) is selected to reproduce. Thus evolutionary success is determined by the payoffs of individuals at cluster boundaries. To see whether type A is favored in the general evolutionary game (4), we compare the payoff of an A individual at a boundary, (a + b)/2, to that of a B individual at a boundary, (c + d)/2, yielding the condition a + b > c + d.

• For DB updating, for a cluster to change size, an individual an a boundary must be selected to die. Competition then occurs between the two neighbors of this now-vacant site. We observe that one of these neighbors is at a boundary, while the other is in the interior of its respective cluster. Thus evolutionary success is determined by comparing the payoffs of an individual at a boundary versus another of the opposing type in a cluster interior. There are therefore two relevant comparisons, a versus (c + d)/2, and (a + b)/2 versus d. Combining these linearly (which is meaningful for weak selection or exponential payoff-to-fecundity map) yields the condition 3a + b > c + 3d.

• For shift updating, changes in cluster size can result from any reproduction event, not just those at or near boundaries. Thus evolutionary success depends on the payoffs of all individuals. For large populations, in a generic state of the evolutionary process, most individuals reside in a cluster interior. This implies the success condition a > d.

Figure 4.

Cluster expansion under different update rules. Payoffs are given in terms of the entries of the game matrix (4). The check marks indicate the individuals whose payoffs matter for cluster expansion. For Birth-Death (BD) updating, success is determined by comparing the payoffs of individuals at cluster boundaries. For Death-Birth (DB) updating, an individual at an interface must be compared to an individual of an opposing type in a cluster interior. For shift updating, success depends on the payoffs of all individuals. If the population size is large then most individuals have payoff a or d. These comparisons lead to the success conditions shown at right, which are valid in the limit of large population size, for the exponential payoff-to-fecundity mapping π ↦ e^δπ with any selection strength δ > 0.

Though the above calculations are heuristic, the conditions they yield are correct in the limit of large population size, for the exponential payoff-to-fecundity mapping π ↦ e^δπ with any selection strength δ > 0. If instead a linear payoff-to-fecundity mapping is used, the conditions for BD and shift remain the same, while the condition for DB becomes nonlinear and varies with the selection strength; see van Veelen & Nowak (2012).

8.2. Local vs. global updating

The shift rule is a global update rule, in the terminology of Nathanson et al. (2009). This means that the birth and death probabilities of an position i depend only on its fecundity, F_i, and the total fecundity of the population, ${\displaystyle {\sum }_{j=1}^N{F}_j}$ (using the notation introduced in Section 6). In contrast, BD and DB are local update rules, meaning that the birth and/or death probabilities of position i also depend on the fecundities of i’s neighbors. Local update rules may induce additional forms of local interaction, beyond those represented by the game. For example, under BD updating, for example, it is disadvantageous to be located adjacent to a high-fecundity individual, for then one is more likely to be displaced during the next transition.

For global update rules, the structure coefficient σ quantifies the degree of spatial assortment between like types arising from the evolutionary dynamics; see (12) and related formulas obtained by Nathanson et al. (2009). For local update rules, the value of σ is also affected by any additional local interactions induced by the update rule.

8.3. Dependence on population size

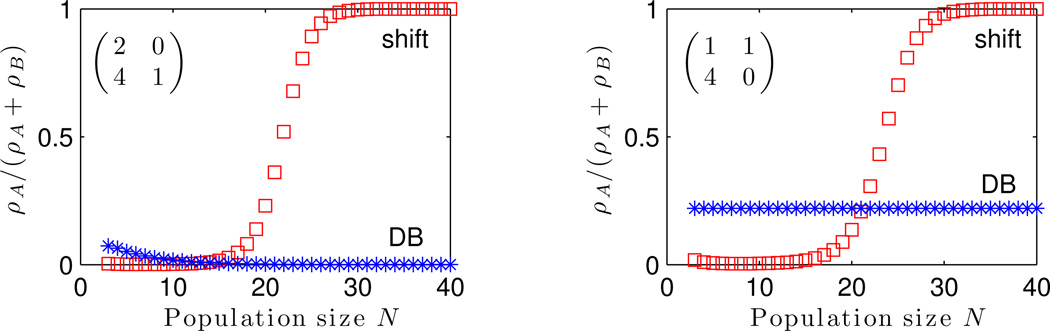
Combining (3) with previous analyses of the DB process on the cycle (Ohtsuki & Nowak, 2006; van Veelen & Nowak, 2012), we can see how the success of cooperation varies with the game matrix, update rule, and population size. Figure 5 illustrates this for a Prisoner’s Dilemma and a snowdrift game. In each case, for sufficiently large N, shift dynamics favor the type that maximizes the whole-population payoff, as guaranteed by Theorem 1. The same is not necessarily true for DB updating. However, for small populations, DB can sometimes favor cooperative behaviors more than shift does.

Figure 5.

The success of cooperative strategies on the cycle for shift and death-birth updating, as a function of population size N. On the left is a Prisoner’s Dilemma, on the right is a Snowdrift game. We use the exponential payoff-to-fecundity mapping, π ↦ e^δπ, with selection strength δ = 1. In each case, for sufficiently large N, shift dynamics favor the strategy that maximizes whole-population payoff (while the same is not necessarily true for DB). However, for small population sizes, DB provides a larger benefit to cooperation compared to the shift rule in the examples shown here.

8.4. Dependence on mutation rate

In previous work (Allen et al., 2012b), we investigated how nonzero mutation rates affect success in spatial evolutionary games under the DB and BD update rules. We found that mutation tends to weaken the spatial benefit to cooperation, by diluting the clustering between cooperators.

For shift dynamics, we find the same qualitative effect: the structure coeffiecient σ—and hence the success of cooperative strategies—decreases with u (Figure 6).

9. Variations on the one-dimensional model

Our main result—that that selection favors A over B, in the large population limit, if and only if a > d—depends on two qualitative features of our model. First, due to one-dimensional geometry, the population is typically composed of clusters of like cells. Thus, in a typical configuration of a large population, most A’s receive payoff a and most B’s receive payoff d. Second, since shift is a global update rule (see Section 8.2), selection favors the type with the larger average payoff, which is type A if and only if a > d.

These two basic features—one-dimensional geometry and global updating—are also shared by a number of variants of our model, including the following:

• Changing cycle size: One can consider variations in which birth and death events are decoupled, so that the total population size varies stochastically. The cycle expands with each division and contracts with each death. One can then study the evolutionary dynamics conditioned on non-extinction of the population. To prevent the population size from growing arbitrarily large, a density limitation can be introduced so that division rates decrease as the population grows.

• Empty sites: One can also consider a cycle of fixed size in which some sites may be empty. A death results in an empty site, and empty sites are filled by reproduction (with shifts). Again, the dynamics can be studied conditioned on non-extinction of the population.

• Chains with endpoints: Instead of a cycle, one can consider a linear chain of cells. Shits might occur in both directions, or they might occur in only one direction, as in the colon cancer model of Nowak et al. (2003). There are also different conventions for cell death: one might suppose death affects random cells within the chain, or only cells that are shifted past the end of the chain (which again corresponds to the colon cancer model of Nowak et al., 2003).

• Cell stacking: One might suppose that sometimes, instead of appearing to the side of the parent and shifting other cells aside, a newly created cell may stack on top of its parent. It is possible to incorporate such stacking into our model while maintaining one-dimensional spatial geometry. For example, one could suppose that each cell plays the game with all other cells in the same or in neighboring stacks. A newly created cell can join its parent’s stack or initiate a new stack to either side of the parent (resulting in shifts). Stacks shift as a single unit, and disappear when their last cell dies.

Since the above variations maintain one-dimensional geometry and global updating, the argument at the beginning of this section applies in principle to them as well. Thus we expect the result that selection favors A, in the large population limit, if and only if a > d to hold for these variations. We caution, however, that the correctness of this argument may depend on certain details of how these variations on the model are implemented (for example, how game payoffs are calculated in the presence of empty sites, whether stacks are allowed to grow indefinitely, etc.).

10. Outlook for higher dimensions

So far we have considered only one-dimensional spatial geometry. One may also ask to what extent shift dynamics can promote cooperation in two- or three-dimensional space. This question is made complicated by the fact that there are a number of different update rules that can be considered higher-dimensional analogues of the shift rule.

We have studied a number of higher-dimensional analogues of shift dynamics in preliminary simulations. These include

1. Lattice-structured populations in which shifts occur in a randomly chosen direction from the reproducer,

2. Populations structured as a regular graph, in which shifts occur along a randomly determined path from the reproducer,

3. Populations located in continuous space, in which physical forces push cells away from their neighbors.

In our preliminary simulations of models based on (i) and (ii), we have observed only a weak spatial benefit to cooperative strategies. We traced this weakness to the fact that spatial clusters of cooperators are often disrupted by shifts arising from reproductions elsewhere. In contrast, for continuous-space models (iii), our simulations show only a minimal disruption effect, and consequently, a strong spatial benefit to cooperation. We hope to present these results in future work.

11. Discussion

We have studied a new update rule of spatial evolution. Offspring do not replace their parents’ neighbors, but shift them aside. Shift updating is a strong promoter of cooperation in one dimensional models. In the limit of large population size, social dilemmas are avoided entirely: selection favors the type that maximizes the payoff of the whole population. Here natural selection favors what is good for the population.

Our work may have implications for social evolution in microbes (Crespi, 2001; Velicer, 2003; Fiegna et al., 2006; Santorelli et al., 2008; Gore et al., 2009; Damore & Gore, 2011). While microbial colony evolution differs in important ways from our shift model, the two systems share the feature that reproductions do not necessarily co-occur with death of a neighbor (Hallatschek et al., 2007). This lack of direct spatial competition between neighbors is what enables the unusually high degree of success for cooperators in our model. Thus the spatial benefit to cooperation in microbes may be stronger than traditional evolutionary game theory models suggest (see, for example, Gore, 2010). Since cooperative dilemmas in microbes have been shown to favor the evolution of multicellular clumping (Koschwanez et al., 2011), models with shift dynamics may be useful in understanding evolutionary transitions from unicellularity to multicellularity (Maynard Smith & Szathmáry, 1997; Grosberg & Strathmann, 2007; Knoll, 2011).

Shift dynamics may also be relevant in somatic evolution, including cancer development (Moolgavkar & Knudson, 1981; Wysocki et al., 1986; Nowak et al., 2002; Michor et al., 2004a; Boland & Goel, 2005; Michor et al., 2005; Wodarz & Komarova, 2005; Iwasa et al., 2006; Merlo et al., 2006; Beerenwinkel et al., 2007; Gatenby & Gillies, 2008; Jones et al., 2008; Meza et al., 2008; Attolini & Michor, 2009; Bozic et al., 2010; Durrett & Moseley, 2010; Yachida et al., 2010). Spatial tumor structure, including with shift-type dynamics (Nowak et al., 2003; Michor et al., 2004b), has been shown to significantly affect the waiting time to cancer (Komarova, 2006; Martens et al., 2011). While somatic evolution of cancer is typically not viewed through the lens of game theory, there are opportunities for cancer cells to cooperate by sharing resources or inuencing the tumor microenvironment (Axelrod et al., 2006; Bidard et al., 2008; Nadell et al., 2010). Spatial evolution with shift dynamics may promote cooperation among neighboring cells in healthy or cancerous tissue.

We emphasize, however, that toy models of shift dynamics, such as the model considered here, may overlook important features of spatial evolution in microbial colonies and somatic tissues. One particularly interesting consideration is that the spatial geometry may change through time. For example, an initially two-dimensional colony or tissue may become three-dimensional as cells layer on top of one another. Incorporating these spatial dynamics into future models can provide a closer interplay between theory and experiment, and may reveal further nuances in how spatial structure affects cooperative behavior in cells.

• We investigate a new model of one-dimensional spatial evolution among cells

• When a cell divides, it does not replace a neighbor, but shifts neighbors aside

• We find a very strong benefit to cooperative strategies

• For large populations, selection maximizes whole population fitness

Appendix A. Evolutionary games in the large population limit

This appendix provides the proof of Theorem 1, which states that, for any game matrix

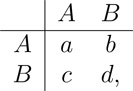fecundity function F, and selection intensity δ > 0, if a > d then

$$\text{and if}a<d,\text{then\hspace{1em}}\begin{array}{cc}\underset{N\to \infty }{\text{lim}}{\rho }_A>0,& \underset{N\to \infty }{\text{lim}}{\rho }_B=0,\\ \underset{N\to \infty }{\text{lim}}{\rho }_A=0,& \underset{N\to \infty }{\text{lim}}{\rho }_B>0.\end{array}$$

Though we consider only two-player games, the extension to multiplayer games (Gokhale & Traulsen, 2010; van Veelen & Nowak, 2012) is straight-forward.

Proof. We begin by calculating payoffs in each state. We adopt the shorthand notation ${\varphi }_{YZ}^X$ for the fecundity of a type X individual interacting with types Y and Z, with X, Y, Z ∈ {A, B}. So, for example, ${\varphi }_{AA}^A=F(\delta a)$ and

$${\varphi }_{AB}^B=F\left(\delta \frac{c+d}{2}\right).$$

Suppose there are k cooperators a population of size N ≥ 3. We first calculate the average payoff to A’s:

• For k ≥ 2, there are two A’s that have one neighbor of each type, and the rest of the A’s have two A neighbors. The average payoff to A’s is

  $$f_k=\frac{1}{k}[2{\varphi }_{AB}^A+(k-2){\varphi }_{AA}^A].$$ (A.1)

• For k = 1, the lone A has payoff $f_1={\varphi }_{BB}^A$.

Now we calculate the average payoff to B’s:

• For k ≤ N − 2, there are two B’s that have one neighbor of each type, and the rest of the B’s have two B neighbors. The average payoff to B’s is

  $$g_k=\frac{1}{N-k}[2{\varphi }_{AB}^B+(N-k-2){\varphi }_{BB}^B].$$ (A.2)

• For k = N − 1, the lone B has payoff $g_{N-1}={\varphi }_{AA}^B.$

For the remainder of the proof we restrict to the case a > d; the case a < d will follow by interchanging the roles of A and B. Note that since F is increasing, a > d implies ${\varphi }_{AA}^A>{\varphi }_{BB}^B$.

Turning first to the fixation probability ρ_A, we observe that that, according to equation (2) of the main text, lim_N→∞ ρ_A > 0 if and only if

$$\underset{N\to \infty }{\text{lim}}{\displaystyle \sum _{j=1}^{N-1}{\displaystyle \prod _{j=1}^k\frac{g_k}{f_k}<\infty .}}$$ (A.3)

We will show that this limit converges by establishing the following two bounds on g_k/f_k:

• Bound 1 : There exists an M ≥ 1 such that g_k/f_k ≤ M for all N ≥ 1 and 1 ≤ k ≤ N − 1.

• Bound 2 : There exists a r, 0 < r < 1, and integers K₁ ≥ 1, K₂ ≥ 2 (independent of N and k) such that for all N ≥ 1, K₁ < k ≤ N − K₂ implies g_k/f_k < r.

Once these two bounds have been established, we show that the limit (A.3) converges—and thus lim_N→∞ ρ_A > 0—by the following argument:

$$\underset{N\to \infty }{\text{lim}}{\displaystyle \sum _{j=1}^{N-1}{\displaystyle \prod _{j=1}^k\frac{g_k}{f_k}<}}\underset{N\to \infty }{\text{lim}}\left({\displaystyle \sum _{j=1}^{K_1}{M}^j+}{\displaystyle \sum _{j=K_1+1}^{N-K_2}{M}^{K_1}{r}^{j-K_1}+}{\displaystyle \sum _{j=N-K_2+1}^{N-1}{M}^{K_1+j-(N-K_2)}{r}^{N-K_1-K_2}}\right)<\underset{N\to \infty }{\text{lim}}{\displaystyle \sum _{j=1}^{N-1}{M}^{K_1+K_2-1}{r}^{j-K_1-K_2}}=M^{K_1+K_2-1}{r}^{-K_1-K_2}{\displaystyle \sum _{j=1}^{\infty }{r}^j<\infty .}$$

The third line above uses the facts that M ≥ 1 (hence M^x is nondecreasing in x) and r < 1 (hence r^x is decreasing in x).

For Bound 1, we simply let

$$M=\text{max}\left\{\frac{\text{max}\{c,d\}}{\text{min}\{a,b\}},1\right\}.$$

To establish Bound 2, we define

$$r=\frac{2{\varphi }_{BB}^B+{\varphi }_{AA}^A}{2{\varphi }_{AA}^A+{\varphi }_{BB}^B},$$

which is less than 1 since ${\varphi }_{AA}^A>{\varphi }_{BB}^B$. We define K₁ and K₂ by

$$\begin{array}{c}{K}_1=\text{max}\left\{\lfloor 6\frac{|{\varphi }_{AB}^A-{\varphi }_{AA}^A|}{{\varphi }_{AA}^A-{\varphi }_{BB}^B}\rfloor ,1\right\},\\ K_2=\text{max}\left\{\lceil 6\frac{|{\varphi }_{AB}^B-{\varphi }_{BB}^B|}{{\varphi }_{AA}^A-{\varphi }_{BB}^B}\rceil ,2\right\},\end{array}$$

where ⌊ ⌋ and ⌈ ⌉ respectively denote the oor function (the greatest integer less than or equal to the argument) and the ceiling function (the least integer greater than or equal to the argument). These values of K₁ and K₂ are chosen so that

$$k>K_1\Rightarrow \frac{2}{k}|{\varphi }_{\text{AB}}^A-{\varphi }_{AA}^A|<\frac{1}{3}({\varphi }_{AA}^A-{\varphi }_{BB}^B)$$ (A.4)

and

$$k\le N-K_2\Rightarrow \frac{2}{N-k}|{\varphi }_{AB}^B-{\varphi }_{BB}^B|<\frac{1}{3}({\varphi }_{AA}^A-{\varphi }_{BB}^B).$$ (A.5)

Therefore, if K₁ < k ≤ N − K₂, then applying (A.1), (A.2), (A.4), and (A.5), we have

$$\frac{g_k}{f_k}=\frac{{\varphi }_{BB}^B+\frac{2}{N-k}({\varphi }_{AB}^B-{\varphi }_{BB}^B)}{{\varphi }_{AA}^A+\frac{2}{k}({\varphi }_{AB}^A-{\varphi }_{AA}^A)}<\frac{{\varphi }_{BB}^B+\frac{1}{3}({\varphi }_{AA}^A-{\varphi }_{BB}^B)}{{\varphi }_{AA}^A-\frac{1}{3}({\varphi }_{AA}^A-{\varphi }_{BB}^B)}=r,$$

as required in the statement of Bound 2. This completes the proof that lim_N→∞ ρ_A > 0.

To show that lim_N→∞ ρ_B = 0, we look at the ratio of fixation probabilities ρ_B/ρ_A. Combining formula (3) from the main text with Bounds 1 and 2 yields

$$\frac{{\rho }_B}{{\rho }_A}={\displaystyle \prod _{k=1}^{N-1}\frac{g_k}{f_k}<M^{K_1+K_2-1}{r}^{N-K_1-K_2}.}$$

The right-hand side above converges to zero as N → ∞, since r < 1. Therefore, lim_N→∞ ρ_B/ρ_A = 0: Since ρ_A is bounded between 0 and 1, ρ_B must converge to zero.

Appendix B. Evolutionary games with weak selection

In this appendix we calculate the value of the structure coefficient σ for the shift model. Since the value of σ is independent of the evolutionary game, its value can be computed by considering any particular game (Tarnita et al., 2009b). We consider the additive Prisoner’s Dilemma game:

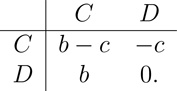The value of σ is also independent of the choice of the fecundity function F (Tarnita et al., 2009b). This is because the values F(0) and F′(0) suffice to determine fixation probabilities under weak selection (Wu et al., 2010a). We therefore use the linear payoff-to-fitness mapping π ↦ 1 + δπ (that is, we choose F(x) = 1 + x).

The formulas for the average payoffs f_k and g_k, obtained in Appendix A, simplify greatly in this case, due to the additivity of the game and linearity of F. For each k = 1;…, N − 1, the average payoffs to cooperators and defectors, respectively, simplify to

$$\begin{array}{c}{f}_k=1+\delta \left[-c+b\frac{k-1}{k}\right]\\ g_k=1+\delta \frac{b}{N-k}.\end{array}$$

Applying (main text, 3), we compute the ratio ρ_C/ρ_D as

$$\frac{{\rho }_C}{{\rho }_D}={\displaystyle \prod _{k=1}^{N-1}\frac{1+\delta \left[-c+b\frac{k-1}{k}\right]}{1+\delta \frac{b}{N-k}}}\approx 1+\delta {\displaystyle \sum _{k=1}^{N-1}\left[-c+b\left(1-\frac{1}{k}-\frac{1}{N-k}\right)\right]}=1+\delta \left[-c(N-1)+b(N-1)-b{\displaystyle \sum _{k=1}^{N-1}\left(\frac{1}{k}+\frac{1}{N-k}\right)}\right]=1+\delta [-c(N-1)+b(N-1)-2b{h}_{N-1}].$$

The approximation in the second line above is valid in the weak selection regime Nδ ≪ 1.

Using this result, cooperation is favored in the sense ρ_C/ρ_D > 1 if and only if

$$\frac{b}{c}>\frac{N-1}{N-1-2h_{N-1}}.$$ (B.1)

The value of the structure coefficient σ can be obtained from the critical benefit-to-cost ratio (b/c)* by

$$\sigma =\frac{{(b/c)}^{*}+1}{{(b/c)}^{*}-1}.$$

Substituting the right-hand side of (B.1) for (b/c)* we calculate:

$$\sigma =\frac{N-1}{h_{N-1}}-1.$$

Appendix C. Identity-by-descent probabilities

To obtain recurrence relations between the IBD probabilities q_k, we consider the evolutionary process backwards in time. The reverse of a single time-step in the model can be described as follows:

• Two pairs of neighboring individuals are chosen at random (the same pair can be chosen both times).

• A new individual appears between the first pair of individuals (this is the reverse of a death).

• The second pair of individuals fuse together (this is the reverse of a birth).

If the same pair is chosen twice, then a new individual appears and instantly fuses with one of the two neighbors (this is the reverse of an individual reproducing and dying in the same time-step). In each fusion event, one individual is randomly designated the parent, and the other is designated the offspring.

In the neutral (δ = 0) process, the two neighboring pairs are chosen independently with uniform probability, and the designations of parent and offspring occur with equal probability for the two fusing individuals.

We introduce mutation into this reverse-evolutionary process by supposing that, with each fusion event, the offspring has probability u of being a mutant (thus destroying any identity by descent with any other individual).

Consider two individuals, labeled α and β, alive in the current state of the system. α and β are IBD if and only if

1. Neither α nor β is a new offspring, and α and β were IBD in the previous state,

2. α is a new offspring, α’s parent was IBD to β in the previous state, and α was born without a mutation, or

3. β is a new offspring, β’s parent was IBD to α in the previous state, and β was born without a mutation.

We must also incorporate the possibility that the distance between α and β may change over the course of a time step, due to shifts. To this end, consider two positions i and j in the current state of the system, where i and j are integers modulo N. (We emphasize that i and j represent positions, in contrast to α and β above, which represent individuals.) Using our description of the reverse process, we can say that the current occupants of i and j are IBD if and only if

1. An appearance occurs in between one of the pairs (i, i + 1),…, (j − 1, j), and

   1. A fusion occurs in one of the pairs (i + 1; i + 2),…,(j − 2, j − 1), and positions i and j are IBD in the previous time-step.

   2. A fusion occurs in one of the pairs (j + 1, j + 2),…, (i − 2, i − 1), and positions i and j + 1 are IBD in the previous time-step.

   3. A fusion occurs in one of the pairs (i, i + 1) or (j − 1, j), positions i and j are IBD in the previous time-step, and neither of the current occupants of i or j is a new mutant offspring.

   4. A fusion occurs in one of the pairs (i − 1, i) or (j, j + 1), positions i and j + 1 are IBD in the previous time-step, and neither of the current occupants of i or j is a new mutant offspring.

2. An appearance occurs in between one of the pairs (j, j + 1),…,( i − 1, i), and

   1. A fusion occurs in one of the pairs (i + 1, i + 2),…,(j − 2, j − 1), and positions i and j − 1 are IBD in the previous time-step.
   2. A fusion occurs in one of the pairs (j + 1, j + 2), …, (i − 2, i − 1), and positions i and j are IBD in the previous time-step.
   3. A fusion occurs in one of the pairs (i, i + 1) or (j − 1, j), positions i and j − 1 are IBD in the previous time-step, and neither of the current occupants of i or j is a new mutant offspring.
   4. A fusion occurs in one of the pairs (i − 1; i) or (j, j + 1), positions i and j are IBD in the previous time-step, and neither of the current occupants of i or j is a new mutant offspring.

Special consideration must also be given to the case in which i and j are neighboring positions, and thus their occupants may fuse during a reverse time-step.

Noting that the stationary IBD probabilities depend only on relative, rather than absolute positions, we use the above case-by-case analysis to obtain the following recurrence relations between the stationary IBD probabilities q_k:

$$q_0=1,$$

$$q_1=\frac{1}{N^2}[(N-1)(1-u)q_0+(1-u+(N-1)(N-1-u))q_1+(N-1-u)q_2],$$

$$q_k=\frac{1}{N^2}[(N-k)(k-u)q_{k-1}+(k(k-u)+(N-k)(N-k-u))q_k+k(N-k-u)q_{k+1}]\text{ for }2\le k\le N-2,$$

$$q_{N-1}=\frac{1}{N^2}[(N-1-u)q_{N-2}+(1-u+(N-1)(N-1-u))q_{N-1}+(N-1)(1-u)q_N],$$

$$q_N=1.$$

Though these relations do not appear to admit a general closed-form solution, numerical values of q_k can be obtained for arbitrary u, N and k via Gaussian elimination.