The spatial and temporal representation of a tone on the guinea pig basilar membrane

Abstract

In the mammalian cochlea, the basilar membrane's (BM) mechanical responses are amplified, and frequency tuning is sharpened through active feedback from the electromotile outer hair cells (OHCs). To be effective, OHC feedback must be delivered to the correct region of the BM and introduced at the appropriate time in each cycle of BM displacement. To investigate when OHCs contribute to cochlear amplification, a laser-diode interferometer was used to measure tone-evoked BM displacements in the basal turn of the guinea pig cochlea. Measurements were made at multiple sites across the width of the BM, which are tuned to the same characteristic frequency (CF). In response to CF tones, the largest displacements occur in the OHC region and phase lead those measured beneath the outer pillar cells and adjacent to the spiral ligament by about 90°. Postmortem, responses beneath the OHCs are reduced by up to 65 dB, and all regions across the width of the BM move in unison. We suggest that OHCs amplify BM responses to CF tones when the BM is moving at maximum velocity. In regions of the BM where OHCs contribute to its motion, the responses are compressive and nonlinear. We measured the distribution of nonlinear compressive vibrations along the length of the BM in response to a single frequency tone and estimated that OHC amplification is restricted to a 1.25- to 1.40-mm length of BM centered on the CF place.

von Békésy (1) discovered that sound-induced stapes movement causes a wave of basilar membrane (BM) displacement to travel from the base of the cochlea to the apex because of a pressure difference set up across the cochlear partition. The length of the BM is graded in stiffness, and the cochlear partition can be modeled as a series of weakly coupled sections, each section comprised of a rigid mass connected to the sides of the cochlea by springs that decrease in stiffness toward the apex (2). The BM will resonate when the mechanical impedance caused by the stiffness of the springs cancels that caused by the mass of the section (1). At a point just basal to the resonant place, a peak of displacement will occur on the BM. At a point just apical to the resonant place, the BM impedance is insufficient to maintain a pressure difference across the cochlear partition, and the traveling wave dies out. The location of the displacement peak depends on stimulus frequency, so that each segment of the BM is tuned to a characteristic frequency (CF). von Békésy measured BM movement under postmortem conditions and found that the mechanical responses were broadly tuned and insensitive. Subsequent measurements made from sensitive cochleae in vivo have revealed that, in fact, BM displacement responses are sharply tuned and very sensitive at low sound-pressure levels (3–6).

Contributions from the electromotile outer hair cells (OHCs) (7–10) appear to be essential for cochlear sensitivity and frequency tuning (11, 12). Many current models of cochlear function include OHC-mediated feedback that amplifies BM motion at the CF to compensate for the energy dissipation that would occur through viscous damping (13–15). However, for the amplification of BM motion to take place, OHC feedback must occur at the appropriate phase of BM displacement (14, 16) and at the appropriate place along the length of the BM.

When in Each Cycle of Vibration Do OHCs Boost BM Displacement?

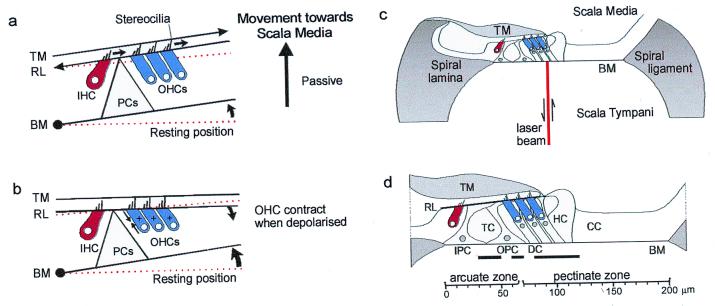
In a simple model of hair cell excitation (17), the BM hinges about its attachment to the spiral lamina. When the BM moves toward scala media, shearing between the tectorial membrane (TM) and the reticular lamina causes hair bundles to be deflected in the depolarizing direction toward the tallest row of stereocilia (Fig. 1a). In studies of excised cochleae (18, 19), electrical depolarization of the OHCs, which mimics the effects of excitatory hair-bundle deflection, induces somatic contractions that cause the BM and the reticular lamina to be drawn together (Fig. 1b). These findings support (14) and form the basis of (16) mechanical models of BM tuning comprising two resonant masses, e.g., represented by the BM and the reticular lamina coupled through the OHCs. However, the phase relationship between BM motion and the OHC forces must be appropriate for these models to provide frequency-dependent amplification of BM displacement. Amplification will not occur if the two resonant masses move in phase or if OHC forces are delivered in phase with the BM movement. By introducing a phase lead of 90° between the force generated by the OHCs and the passive movement of the BM, the OHCs would provide a properly timed force to enhance the BM's motion (14, 20). To deduce when in each cycle of vibration OHCs contribute to BM displacement, we investigated how different regions across the width of the BM move in response to tones at, below, and above the CF. Measurements were also made postmortem when OHCs make no active contribution to the mechanical properties of the BM (3, 11, 21).

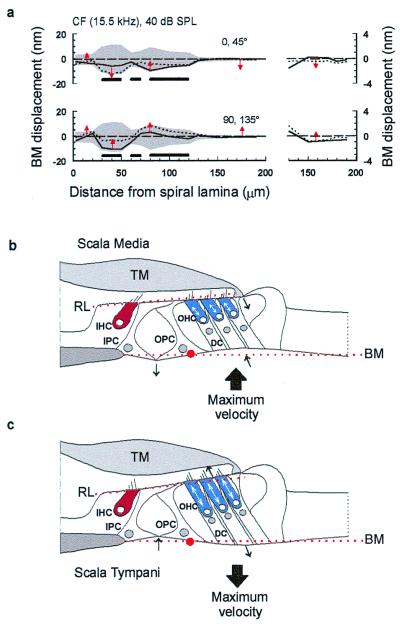
Figure 1.

(a) A model of hair cell excitation without OHC motility according to Davis (17) (see text for details). (b) OHCs contract when depolarized and the BM is drawn to the reticular lamina. (c) Experimental arrangement with laser diode beam. (d) Transverse section through the organ of Corti in the 15.5-kHz region based on measurements made in vivo and from histological sections: scale bar referenced to the bony edge of the spiral lamina. Solid horizontal bars indicate the following regions across the BM width with respect to the bony edge of the spiral lamina: 30–50 μm (junction of inner and outer pillar cells), 60–70 μm (near midpoint of OPC base), 80–120 μm (Deiters' cells). TM, tectorial membrane; IHC, inner hair cell; OHC, outer hair cell; HC, Hensen cell; CC, Claudius cell region; PCs, pillar cells; IPC, inner pillar cell; OPC, outer pillar cell; DC, Deiters' cell; RL, reticular lamina; TC, tunnel of Corti. Experiments were performed on deeply anaesthetized pigmented guinea pigs (180–300 g, 0.06 mg atropine sulfate s.c., 30 mg/kg pentobarbitone i.p., 4 mg/kg Droperidol i.m.; 1 mg/kg Phenoperidine i.m.), which were tracheotomized, artificially respired, and with core temperatures maintained at 37°C. Modified from Nilsen and Russell (22).

Amplification of BM Vibrations Is Greatest in the Organ of Corti Region

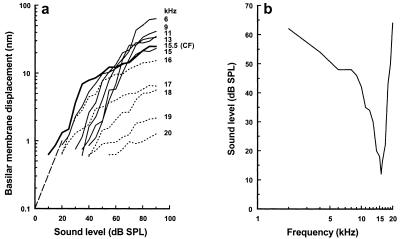
The basal turn of the cochlea was exposed in guinea pigs that were under deep neuroleptanalgesia, and an opening was made in the scala tympani (22) (Fig. 1c). Through this opening, the beam of a displacement-sensitive laser-diode interferometer was focused onto the BM, forming a spot 5 μm in diameter. Tone-evoked BM displacements can be measured through the interaction of light within the laser diode and reflections from the surface of the BM. Measurements at up to 15 different locations across the width of the BM were made from nine animals in response to the CF of the recording site (22). Tones of varying sound pressure level (SPL), expressed in dB (dB relative to 2 × 10⁻⁵ Pa), were used in the experiments. The position of each measurement location was determined with respect to the outer edge of the spiral lamina (0 μm being where the edge of the BM joins the spiral lamina). These locations were related later to the structural elements of the cochlear partition in histological sections of the measurement site (Fig. 1d). Locations of particular interest are indicated with horizontal bars in Fig. 1d and are used in subsequent figures as a reference. We determined the CF of the measurement location by constructing displacement-level functions for different frequency tones (Fig. 2a) and by deriving an iso-response frequency tuning curve (Fig. 2b). For frequencies close to the CF, displacement-level functions are typically saturating curves with steeply sloping regions at low levels and strongly compressive regions at high levels (3–6). The slope of the steep region is close to unity for frequencies half an octave or more below the CF and becomes progressively shallower as the frequencies approach and exceed the CF. This nonlinear behavior of the displacement-level functions is attributed to feedback from the OHCs, which increases as the tone frequency approaches the CF (2).

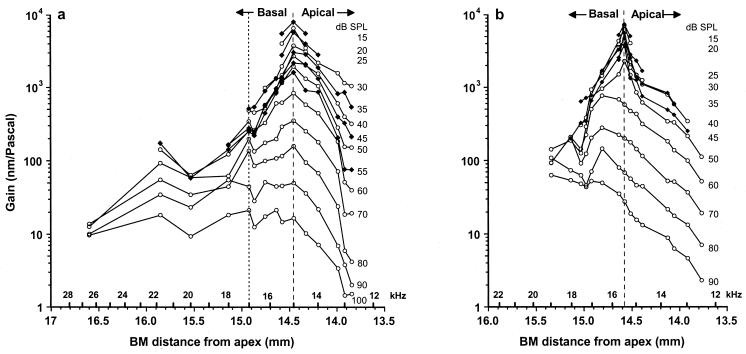
Figure 2.

(a) BM displacement as a function of sound level for frequencies between 6–20 kHz recorded from the 15.5-kHz place. Solid lines, below CF; thick line, at CF; dotted lines, above CF. Dashed line indicates slope of 1. (b) Iso-response tuning curve derived from the displacement-level functions in a. Response criterion: 0.7 nm [BM displacement at the detection threshold of the compound action potential (CAP) for a 15.5 kHz tone. Recording location: 100 μm from the spiral lamina. From Nilsen and Russell (22), with permission from Nature Neuroscience (Copyright 1999).

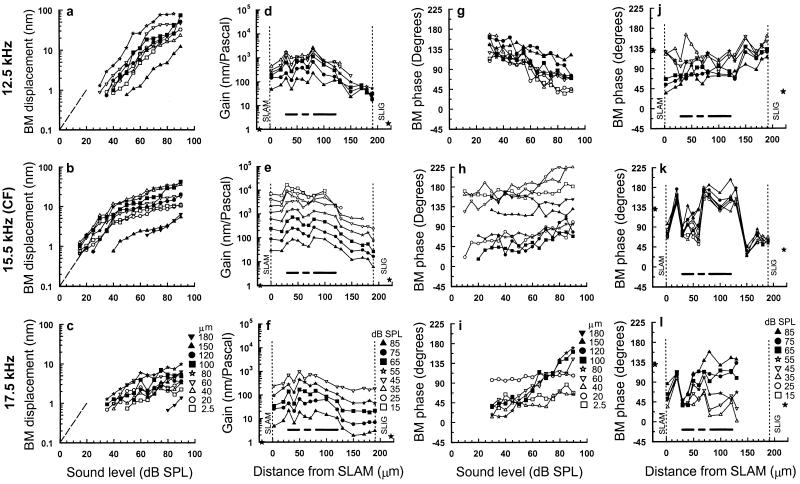
The differences in displacement-level functions measured across the width of the BM (Fig. 3 a–c) are revealed in iso-level gain profiles (Fig. 3 d–f). The gain of BM displacement is calculated by dividing the displacement magnitude by the sound pressure at which the measurements are made. The degree of compression is reflected in the separation between the gain profiles at successive levels, so that the greater the separation the stronger the compression. It can be seen that the greatest compression occurs in response to frequencies at and above the CF. In all three profiles (Fig. 3 d–f), the greatest gain occurs beneath the organ of Corti. In response to CF tones, there are peaks of gain at the junction between the feet of the inner and outer pillar cells and in the Deiters' cell region (indicated by horizontal bars in Fig. 1d). These peak regions are separated by a node of minimum gain near the outer pillar cell foot (indicated by the middle bar in Fig. 1d). These characteristics are not clearly apparent in the gain profiles obtained at 12.5 kHz and 17.5 kHz. Displacement measurements were also made on the spiral lamina and the spiral ligament themselves, at locations that were 20 μm from the edges of the BM in a postmortem preparation (Fig. 4e). Vibrations were not detected above the measurement noise floor of 0.5 nm for CF tones below 90 dB SPL. The gains calculated from measurements made above 90 dB SPL (0.7 for the spiral lamina and 1.2 for the spiral ligament, at 95 dB SPL) are plotted as stars in Fig. 3 d–f.

Figure 3.

(a–c) BM displacement-level functions in response to 12.5 kHz, 15.5 kHz (CF), and 17.5 kHz tones for different locations across the width of the BM. The locations are measured from the edge of the spiral lamina (symbols shown in c). Dashed line indicates slope of 1. (d–f) BM gain (nanometers/Pascal) in response to 12.5-kHz, 15.5-kHz (CF), and 17.5-kHz tones as a function of measurement location across the width of the BM for stimulus levels between 15 and 85 dB SPL (symbols shown in f). The solid stars represent BM gain of vibrations measured on the spiral lamina attachment (SLAM) (0.7) and spiral ligament attachment (SLIG) (1.7) at 95 dB SPL from a postmortem preparation. (g–i) BM phase as a function of the stimulus level of 12.5-kHz, 15.5-kHz (CF), and 17.5-kHz tones for different measuring locations across the width of the BM (symbols shown in i). (j–l) BM phase in response to 12.5-kHz, 15.5-kHz (CF), and 17.5-kHz tones as a function of measurement location across the width of the BM for stimulus levels between 15–85 dB SPL (symbols shown in l). The solid stars represent BM phase of vibrations measured on the SLAM and SLIG at 95 dB SPL from a postmortem preparation. The vertical dashed lines represent the inner SLAM and outer SLIG of the BM. Horizontal bars as in Fig. 1d; BM width: 190 μm; CAP threshold at CF: 12 dB SPL; 0 dB loss after opening cochlea to expose the BM; measurement noise floor 0.7 nm. b, e, h, and k are from Nilsen and Russell (22), with permission from Nature Neuroscience (Copyright 1999).

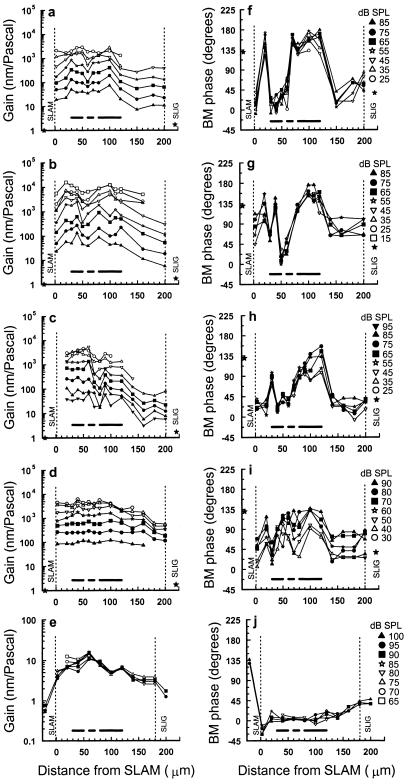
Figure 4.

BM responses as a function of measurement location across the width of the BM at different stimulus levels (symbols for each preparation shown on the right), measured under different recording conditions. (a and b) BM gain (nanometers/Pascal) and (f and g) BM phase measured from sensitive preparations with no perceptible loss in sensitivity, CF = 15.5 kHz (a and f), 18 kHz (b and g). (c) BM gain and (h) BM phase measured from a preparation with a 10-dB loss of sensitivity in initial preparation, CF = 16 kHz. (d) BM gain and (i) BM phase measured from a preparation with a 15- to 20-dB loss of sensitivity in initial preparation, CF = 18.25 kHz. The solid stars represent BM gain and phase of vibrations measured on the SLAM (0.7) and SLIG (1.7) at 95 dB SPL from the postmortem preparation in e. (e) BM gain and (j) BM phase measurements made 1.5–4 h postmortem near the 15.5-kHz location of the BM. The vertical dashed lines represent the inner spiral lamina attachment (SLAM) and outer spiral ligament attachment (SLIG) of the BM. Horizontal bars as in Fig. 1d.

Different Regions Across the BM Width Respond at Different Phases to CF Tones

To see how different regions across the width of the BM move in relation to each other, we measured the phase of BM displacement relative to the stimulus tone as a function of both measurement location and sound level. For frequencies below the CF (Fig. 3g), responses to low-level tones typically (3–6) phase lead those to high-level tones. At the CF and above (Fig. 3 h and i), the responses of low-level tones phase lag those of high-level tones. However, measurements within about 40 μm of the spiral lamina are relatively independent of level for frequencies at and above CF, whereas those about 60–100 μm from the spiral lamina (close to the OHCs) appear to be particularly sensitive to sound level. Signal-to-noise levels in phase measurements made at frequencies above the CF and close to the spiral ligament are low, and this makes it difficult, and sometimes impossible (Fig. 3l), to determine the phase of BM displacement in this region. The phase-level functions shown in Fig. 3 g–i are reexpressed in Fig. 3 j–l to show the variation of phase with distance from the spiral lamina. In response to 12.5 kHz tones, there is no clear variation in phase with location across the width of the BM, only a systematic phase lead of about 45° from the spiral lamina to the spiral ligament. However, phase varies strikingly with location for CF tones. The BM near the attachment to the spiral lamina, beneath the outer pillar cell foot and close to the spiral ligament, have similar phases and lag the BM regions beneath the inner pillar cell foot and Deiters' cells by up to 135°. Above CF, the phases of BM responses measured close to the inner pillar cells are similar to those measured at the CF in that they are relatively independent of level (Fig. 3l). However, in the region around the outer pillar cell and OHC/Deiters' cell complex, the phase is highly level dependent.

Phase measurements made from the spiral lamina and spiral ligament are represented as stars in Fig. 3 j–l and are measured from the postmortem preparation (Fig. 4j). Vibrations measured from the spiral ligament are in phase with those of the adjacent BM, an indication that these vibrations are driven by the BM or by pressure differences between the scala tympani and scala media. Vibrations measured from the spiral lamina have phases different from that of the adjacent BM but are the same for all frequencies, an indication that these vibrations are caused by conduction through the bones of the skull or fluids of the cochlea.

Thus, for frequencies at the CF and above, the pattern of vibration across the BM width has several modes but a single mode for frequencies below the CF.

Cochlear Sensitivity and Ambient Noise Influence BM Displacement Measurements

In Fig. 4, we show four examples of variations in gain and phase with location across the BM width that were measured under different recording conditions in response to CF tones. These figures reveal that BM displacement measurements can be influenced by 10- to 20-dB losses in sensitivity during exposure of the BM and by ambient noise. By comparison with the laser Doppler velocitometers that are commonly used to make BM measurements (4–6), BM displacements measured with a self-mixing effect interferometer are vulnerable to low-frequency vibrations, such as those caused by building noise, heartbeat, and respiration, which can be difficult to minimize. Thus at best, the measurement noise floor in our experiments is about 0.4–0.8 nm, whereas the noise floor of laser Doppler measurements is typically two orders of magnitude less than this (4–6). The data in Fig. 3 and Fig. 4 a and b are from sensitive cochleae that were prepared without a perceptible loss in sensitivity and that were obtained under relatively stable recording conditions. The data in Fig. 4c were also collected under similar recording conditions, but a 10-dB loss in sensitivity was incurred during initial preparation. The data shown in Fig. 4d were obtained after a 15- to 20-dB sensitivity loss during initial preparation. In preparations where the loss in sensitivity is <10 dB, the gain and phase profiles across the width of the BM are distinctive and similar to those shown in Fig. 3 for CF tones. In the least sensitive of the preparations shown in Fig. 4d, BM displacement gain is still greatest over the organ of Corti but without a distinct minimum in the region of the outer pillar cell foot. The phase pattern is also disrupted in that the point of flexion near the junction between the inner and outer pillar cells appears to have moved closer to the spiral lamina, and the outer pillar cell and the OHC/Deiters' cell complex move together. However, the inner pillar cell and the OHC/Deiters' cell complex still phase lead the flexion point and the spiral ligament by up to 90°. Postmortem, when the contribution of OHC feedback is absent, responses to CF tones were detected only above the 0.5-nm noise floor when the sound level was increased above 65 dB SPL. The displacement-level functions are linear and without compression regardless of the measurement location and frequency (Fig. 4e). Across the BM width, the largest gains are measured beneath the outer pillar cell feet (Fig. 4e; note scale change) and thus resemble responses that have been recorded from insensitive living preparations (4). The phase of BM vibrations varies progressively across the BM width, with vibrations measured close to the spiral ligament leading those near the spiral lamina by about 45° (Fig. 4j). This variation of phase across the BM width is similar to that measured from sensitive cochleae for frequencies below the CF (Fig. 3 g and j).

Within the limitations of our measurements, vibration patterns across the BM width in response to CF tones are similar in sensitive cochleae, and any differences can be attributed largely to variations in preparation sensitivity and ambient noise levels.

Visualizing the Relative Movement of Different Regions Across the Width of the BM

We visualized the way different regions across the width of the BM vibrate in relation to one another by plotting the product of the magnitude and cosine of the phase angle (measured relative to the sound source) of the displacement. This provides the instantaneous transverse vector of BM displacement as a function of location across the width of the BM. The solid and dotted lines in Fig. 5a plot [D*cos(θ (t))] at 45° intervals across the BM width for 15.5 kHz, CF tones at 40 dB SPL, where D is the magnitude of BM displacement and θ is the phase. The gray shaded area plots the envelope of the BM displacement and is widest, and BM displacement is therefore greatest, in the region of the organ of Corti. As can be seen in Fig. 3, the envelope in this region is bilobed, with peaks of displacement at the junction between the inner and outer pillar cell feet and beneath the Deiters' cells. These are separated by a minimum displacement near the center of the outer pillar cell base. Thus, through interaction with other elements in the organ of Corti, OHCs appear to limit the movement of the outer pillar cells while permitting Deiters' cells and the junction between the pillar cell feet to move more freely with respect to each other.

Figure 5.

(a) Displacement across the width of the BM as a function of time for a 40-dB SPL CF tone (based on data from Fig. 3). The gray shaded area plots the envelope of the BM displacement. The solid and dotted lines plot the BM displacement at successive 45° intervals, i.e., 0°, solid; 45°, dotted. The arrows indicate the instantaneous direction of BM motion in the transverse plane; horizontal bars as in Fig. 1d. (Right) Expanded view of the region spanning from 130 μm from the spiral lamina to the edge of the spiral ligament. Modified from Nilsen and Russell (22). (b and c) A simple model of BM vibration. OHCs are proposed to generate positive (cell-body shortening) forces during maximum BM velocity toward scala media (b) and negative (cell body lengthening) forces during maximum BM velocity toward scala tympani (c). The model is also proposed to account for the spatial variation in the magnitude and phase of the displacements we have measured in response to CF tones across the width of the BM. Red dotted lines, resting positions of the basilar membrane (BM) and the reticular lamina (RL); red dot, base of the outer pillar (OPC) foot which acts as a point of flexion; TM, tectorial membrane; IHC, inner hair cell; IPC, inner pillar cell; OHC, outer hair cell; DC, Deiters' cell. Arrows indicate the direction of movement. See text for explanation.

OHCs Boost the Vibrations of the BM at the Time of Maximum BM Velocity

The arrows in Fig. 5a indicate the instantaneous direction of BM motion and show that as the regions beneath the Deiters' cells and inner pillar cells move farthest into the scala media or scala tympani, the region adjacent to the spiral ligament, which is driven remotely by the OHCs, crosses its resting position and is thus moving with maximum velocity (Fig. 5a). In Fig. 5 b and c, these observations are interpreted in terms of OHC contraction (7–10) when the OHCs are depolarized by displacements toward scala media (23) and elongation when the OHCs are hyperpolarized by displacements toward scala tympani. Accordingly, we propose that OHCs boost the vibrations of the BM by achieving their maximum length changes and changes in force generation (24, 25) at the time of maximum BM velocity (14–16).

We propose a simple model to account for the spatial variation in the displacement magnitude and phase that we have measured in response to CF tones across the width of the BM (Fig. 5 b and c). When the BM undergoes excitatory displacements toward scala media (Fig. 5b), the OHCs contract with a lead of 90°, thereby drawing the BM and the reticular lamina together. In this configuration, the outer pillar cell behaves as a rigid strut (26, 27) extending from a broad foot via an articulated joint. The outer pillar cell resists the contractions of the OHCs so that when the BM is pulled up toward the scala media, the foot of the outer pillar cell rotates slightly and pushes the joint between itself and the inner pillar cell downwards toward the scala tympani. The reticular lamina seesaws about a fulcrum at the apex of the tunnel of Corti to provide a lever ratio of 4:1 in favor of the OHCs. Upward swings of the proximal edge of the reticular lamina draw up the inner pillar cell, and the region of the BM immediately underlying it, toward the scala media. The proposed tilting of the reticular lamina upward (as the BM moves toward and away from the scala media) and downward (as the BM moves toward and away from the scala tympani; Fig. 5c) would tend to amplify further shear displacement between the reticular lamina and the tectorial membrane and hence amplify the angular rotation of the inner hair cell (IHC) and OHC hair bundles.

The basis of the 90° phase lead is unknown and could, in fact, be a 270° phase delay between OHC depolarization and shortening of the OHC body because of two components. A delay of 180° could be introduced if OHC length changes were driven by potentials in the extracellular spaces surrounding the OHCs rather than by intracellular potentials in the OHCs themselves (28, 29). A further 90° delay could be introduced by a TM resonance (30) tuned to a frequency half an octave below that of the BM.

In summary, the BM beneath the Deiters' cells and OHCs vibrates with a greater magnitude and phase lead of approximately 90° compared with the BM regions beneath the bases of the outer pillar cells and adjacent to the spiral ligament. This complex vibration is not seen postmortem when amplification attributable to the OHCs is lost, resulting in a reduction in the gain of BM vibration in the Deiters' cell region by about 65 dB (5, 6).

In many respects, our measurements resemble the behavior of Kolston's three-dimensional model of cochlear mechanics (31). In particular, both the model and our measurements exhibit a bilobed displacement pattern across the width of the BM. The model also predicts that the motion beneath the Deiters' cells phase leads that of the pillar cells by about 90°. However, in the model, the inner and outer pillar cells are treated as a single element. Thus, the model does not reveal the more complex phase behavior of the BM indicated by our measurements and which we have interpreted as being caused by a flexion point at the junction between the two pillar cell bases. The model also does not predict the phase lead of about 90°, which we have measured between the region of the BM beneath the Deiters' cells and that adjacent to the spiral ligament.

Comparisons with Other Measurements

Several studies investigating mechanically and electrically evoked radial movements of the BM and organ of Corti reveal that the phase and magnitude of these movements are complex and vary with measurement position (32–36).† In excised cochlea segments, electrically evoked organ of Corti displacements are greatest in the region of the OHCs and are smaller in the IHC region (33). Measurements of BM stiffness (36) show the BM region around the outer pillar cell foot to be stiffer than surrounding regions. In accordance with this, measurements from the excised cochlea reveal a striking decrease in movement amplitude between the inner OHC row and the pillar cells (33). Thus, there are some strong similarities between the electrically evoked responses recorded in vitro and those we report here for in vivo BM movements measured in response to CF tones.

In vivo measurements of acoustically driven BM movements in the horseshoe bat Rhinolophus (32) and electrically driven BM movements in the guinea pig cochlea reveal that the arcuate and pectinate zones move 180° out of phase (35), with the outer pillar cell foot moving as much as, or more than, the OHC region (35). These latter findings (35) differ from those reported here where the phase difference between the outer pillar cell foot and the OHC region is only about 90° with CF tone stimulation, and the OHC region moves more than the outer pillar cell foot. Interestingly, Kolston's model (31) predicts these differences in the response of the cochlear partition to local electrical and acoustic stimulation. Furthermore, our proposal that the reticular lamina tilts about a fulcrum at the apex of the tunnel of Corti is supported by direct observations of just such a motion in response to electrical stimulation of the organ of Corti in an isolated preparation (37).

Recent reports of the radial pattern of BM motion evoked by CF tones in guinea pigs measured with laser Doppler interferometery (38)‡ without using reflective beads reveal that the BM vibrates most near the feet of the outer pillar cells. In the most sensitive preparations and at low sound levels, the region of the BM between the outer pillar cell and the spiral lamina leads the region between the outer pillar cell and the spiral ligament by about 30°. In a recent report (39) where multiple large (25 μm) reflective beads were attached to the BM near the base of the chinchilla cochlea, it was reported that there is little variation in the phase of BM motion radially across the width of the BM. Thus, although there is very good agreement between single point measurements on the BM using self-mixing interferometry and laser Doppler interferometry and indeed for measurements along the length of the BM (see below), there are significant differences between measurements that have been made across the width of the BM.§

Where Along the Traveling Wave Is Energy Introduced?

A number of modeling studies have suggested that energy is introduced at a point in the BM traveling wave basal to the CF place and that the active element extends over several millimeters (11, 43, 44). This proposal is attractive because the traveling wave would pass through the active region before reaching the CF, thereby directly stimulating the OHCs, which could then feed energy back to boost the displacement of the adjacent CF region. The location and extent of the BM region responsible for amplifying the traveling wave can be obtained by measuring the spatial representation of the nonlinear responses to a pure tone along the BM. Spatial representations of pure tones on the BM have been constructed from the responses of auditory afferent nerve fibers in sensitive cochleae. However, these indirect measurements of excitation pattern were confined to low frequencies (45–47). We have measured the distribution along the BM of nonlinear compressive vibrations to 15- and 15.5-kHz tones in the 12.5- to 27-kHz region of the guinea pig cochlea in vivo.

Self-mixing interferometry has considerable drawbacks for making spatial measurements. It is essential to focus and maximize the signal in terms of both sensitivity and intensity at each measurement location. If these conditions are obeyed, it is possible to plot a surface profile of the BM. If the beam is not focused, it is still reflected from this surface but from a broad diffuse spot. It is essential to adhere to these requirements and to check for repeatability of measurement. Therefore, data acquisition is slow. It is necessary to repeat all measurements if the recording conditions change and to abandon measurements if ambient noise cannot be controlled or if the sensitivity of the animal decreases by more than 5 dB during the measurements. Thus measurements are slow to perform, and our success rate is low.

BM Displacements in Response to a Tone Are Amplified Most at the Tone's Frequency Place

In response to a tone (15 kHz, Fig. 6a; 15.5 kHz, Fig. 6b), the gains of displacement were measured at up to 15 different locations along the length of the BM for sound levels 15–100 dB SPL. The exact location of each measurement point with respect to the apex of the cochlea was determined by using lesion studies (48) and a function relating the CF of a point along the BM to its distance from the apex (49). At each recording site, we determined the CF and used this to estimate the distance of the measurement point from the apex of the cochlea. Thus, the spatial distribution of the tone was obtained along the length of the BM. This was achieved for a varying number of measurement sites in six preparations. For low levels of the tone, the maximum gain and spread of excitation are centered on the tone's frequency place (Fig. 6 a and b, dashed lines). The gain of BM displacement declines progressively with sound level at the frequency place, being 1,000 times greater at 15 than at 100 dB SPL, when presumably the vibrations of the BM are dominated by the passive properties of the cochlear partition. The gain also decreases rapidly with distance from the frequency place. There is a sharp cutoff in the apical extent of the response to the tone near the 12.5-kHz place, when the acoustic impedance of the BM becomes dominated by its mass and the BM appears unable to sustain either pressure differences between the scalae vestibuli and tympani or any OHC forces that attempt to boost its motion at 15.5 kHz. A decline in gain also occurs with distance in the basal direction, so that at about 0.7 mm from the frequency place of the tone, the gain is reduced to about 10% of its value at the frequency place. This is presumably because OHC forces generated at the 15.5-kHz place are ineffective against the stiffness-dominated acoustic impedance of the BM at locations basal to the 15.5-kHz place.

Figure 6.

The gain of BM displacements in response to 15-kHz (a) and 15.5-kHz tones (b) measured at 15 positions along the BM over a range of intensities from 15 to 100 dB SPL. Data from a and b are from separate preparations. Dashed line indicates the CF location. In a, frequency positions to the right of the dotted line (12.5–17 kHz) are from one preparation and those on the left (17–27 kHz) are each from separate preparations. Data in a modified from Nilsen and Russell (48).

The “Panoramic” Tuning Curve Peak Shifts Toward the Cochlea Base at High SPLs

According to the measurements shown in Fig. 6a, the peak response to the 15-kHz tone remains almost stationary in its location on the BM for levels below about 80 dB SPL. The peak response from another preparation shown in Fig. 6b moves toward the base of the cochlea when the level exceeds 55 dB SPL, in accord with the shift at high levels in the tuning curve peak of cochlear responses to a frequency about half an octave below the CF (50, 51). Differences between the two preparations in the SPL threshold for the basal-ward shift in the peak are not caused by differences in sensitivity but represent variability between preparations that may be caused by differences in their susceptibility to intense tones. Differences between preparations in the threshold for the half-octave shift, although not as marked as those in Fig. 6 a and b, may be observed in other preparations (6, 11, 39).

BM Phase Measurements Indicate That the CF Place Is the Point of Resonance for a CF Tone

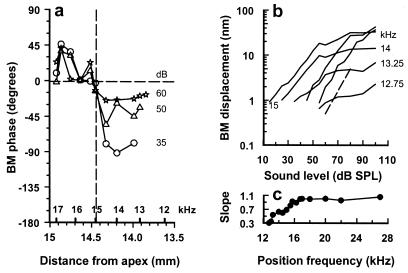
The phase of displacement evoked by responses to low-level 15 kHz tones is plotted relative to that of a higher-level (70 dB SPL) 15-kHz tone (Fig. 7a) for the preparation shown in Fig. 6a. It can be seen that at the 15-kHz place, the phase is relatively independent of sound level. For locations just basal to the 15-kHz place, the low-level responses lead those of the high-level responses. For locations apical to the 15-kHz place, the phase of low-level responses strongly lag those of the high-level responses. Accordingly, the 15-kHz place behaves as a point of resonance on the BM. Observations from this preparation and others show that in response to 15-kHz tones, level-dependent phase changes are not evident in BM regions more basal than the 17-kHz place. This may indicate that feedback from OHCs located basal to the 17-kHz location is unlikely to contribute to boosting BM responses to 15-kHz tones. Similar findings were obtained for the preparation shown in Fig. 6b for 15.5-kHz tones.

Figure 7.

(a) The phase of BM displacement evoked by responses to low-level 15-kHz tones plotted relative to that of a higher-level (70 dB SPL) 15-kHz tone at different positions along the BM. Vertical dashed line indicates 15-kHz (CF) location. (b) BM displacement-level functions in response to a 15-kHz tone measured over a range of frequency positions about the 15-kHz point. Dashed line indicates a slope of 1. (c) The slope of the initial region of the displacement-level function as a function of frequency position. Modified from Russell and Nilsen (48).

OHC Feedback Is Restricted to a Limited Region Extending Apical and Basal to the CF Site

In a linear system, the slopes of input–output functions are 1 dB/dB. In systems with feedback that changes as a function of stimulus level, response-level functions can grow at less than 1 dB/dB. This is the case in the cochlea where for CF tones and for sound levels just above the response threshold of auditory fibers the slopes of BM displacement-level functions lie between 0.8 and 0.5 dB/dB. For sound levels above about 40 dB SPL, the displacement-level functions become strongly compressive with slopes of about 0.2 dB/dB. We found that for locations between the 12.5-kHz and 16.5-kHz places on the BM, 15-kHz displacement-level functions were nonlinear and compressive and, therefore, were subject to nonlinear amplification from the OHCs. The slopes and magnitude at which the displacement saturated decreased as the measuring point was moved apical to the 15-kHz point and toward lower frequencies (Fig. 7b). At locations basal to the 16.5-kHz place, where amplification is greatly reduced, the steep slopes of the displacement-level functions become unity (Fig. 7c). We thus suggest that the 1.25-mm long section of the BM between the 12.5- to 16.5-kHz regions is the source of mechanically active elements contributing to the amplification of the 15-kHz place. On a similar basis, we estimated that a 1.4-mm-long section of the BM contributed to the 15.5-kHz place. The extent and location of the nonlinear region of BM displacement reported here is in agreement with estimates of the distribution of the cochlear amplifier based on noise-induced lesions of the BM (52). Our estimate is somewhat less than that of the extent of the cochlear amplifier in the basal turn of the guinea pig cochlea based on power dissipation and modeling of the cochlea (53). It is also less than the 2.0- to 3.5-mm estimates of the cochlear amplifier based on the spatial extent of the compressive region in the basal region of the chinchilla cochlea (39).

Conclusions

In conclusion, we propose that OHCs boost the vibrations of the BM by achieving their maximum length changes and changes in force generation (24, 25) at the time of maximum BM velocity (14, 16). We find that compressive nonlinear displacements of the BM in response to 15- and 15.5-kHz tones are restricted to a 1.25- to 1.40-mm region extending both apical and basal to the frequency place of the tone on the BM. If this nonlinearity reflects OHC-mediated feedback to the cochlear partition, no more than about 500 OHCs (48) contribute to the displacement of the 15- and 15.5-kHz frequency places on the BM.

Abbreviations

BM

basilar membrane

TM

tectorial membrane

IHC

inner hair cell

OHC

outer hair cell

CF

characteristic frequency

SPL

sound pressure level

SLAM

spiral lamina attachment

SLIG

spiral ligament attachment