Abstract
Previous findings suggest the posterior parietal cortex (PPC) contributes to arm movement planning by transforming target and limb position signals into a desired reach vector. However, the neural mechanisms underlying this transformation remain unclear. In the present study we examined the responses of 109 PPC neurons as movements were planned and executed to visual targets presented over a large portion of the reaching workspace. In contrast to previous studies, movements were made without concurrent visual and somatic cues about the starting position of the hand. For comparison, a subset of neurons was also examined with concurrent visual and somatic hand position cues. We found that single cells integrated target and limb position information in a very consistent manner across the reaching workspace. Approximately two-thirds of the neurons with significantly tuned activity (42/61 and 30/46 for left and right workspaces, respectively) coded targets and initial hand positions separably, indicating no hand-centered encoding, whereas the remaining one-third coded targets and hand positions inseparably, in a manner more consistent with the influence of hand-centered coordinates. The responses of both types of neurons were largely invariant with respect to the presence or absence of visual hand position cues, suggesting their corresponding coordinate frames and gain effects were unaffected by cue integration. The results suggest that the PPC uses a consistent scheme for computing reach vectors in different parts of the workspace that is robust to changes in the availability of somatic and visual cues about hand position.
Keywords: arm, eye, coordinates, reference frames, transformations
arm movement planning requires the specification of a vector that defines the direction and distance the hand must move to acquire a target (“reach vector”). The location of a seen target is defined initially in a retinotopic frame of reference (“eye centered”). The location of a seen hand can also be defined in this frame in addition to the hybrid trunk/arm frame defined by the proprioceptors (“body-centered coordinates”). Although not required for movement planning, mapping hand and target positions into a common reference frame would facilitate computation of reach vectors. The nature of this common reference frame(s), however, remains enigmatic. For example, behavioral studies have provided support for both eye- and body-centered planning of reaches (Crawford et al. 2004; Flanders et al. 1992; Henriques et al. 1998; Khan et al. 2007; McGuire and Sabes 2009; McIntyre et al. 1998). Neurophysiological studies are generally supportive of these findings with evidence for eye-centered (Batista et al. 1999; Buneo et al. 2002, 2008; Cohen and Andersen 2002), body-centered (Lacquaniti et al. 1995), and mixed or intermediate representations of reach-related variables (Batista et al. 2007; Buneo et al. 2002; Chang and Snyder 2010; McGuire and Sabes 2011; Stricanne et al. 1996). In addition, a recent study by Pesaran et al. (2006) suggests reaches may be encoded in some areas with the use of a relative rather than absolute position code that may be flexibly switched depending on task demands.
Neurophysiological studies of the posterior parietal cortex (PPC) and dorsal premotor cortex (PMd) suggest reach vectors are computed from target and hand position signals encoded at least in part in eye-centered coordinates (Batista et al. 1999; Buneo et al. 2002; Chang et al. 2009; Chang and Snyder 2010; McGuire and Sabes 2011; Pesaran et al. 2006). However, in these studies initial hand positions were generally varied along a limited portion of the achievable workspace of the arm. Thus it is unclear whether this scheme is limited to positions most frequently visited by the hand and eye during natural behaviors (Graziano et al. 2004) or whether this scheme generalizes to a larger range of workspace positions. In addition, because initial hand positions in these previous studies were always associated with a concurrent visual stimulus, it is unclear the extent to which the representation of hand position depends on visual vs. somatic (proprioceptive and/or efference copy) cues. The integration of these signals is highly relevant to both position coding and reach planning (Sober and Sabes 2003, 2005).
Thus our goals were 1) to examine the integration of target and hand position signals in PPC neurons over a large range of the workspace of the arm, 2) to probe the modalities contributing to the representation of hand position, and 3) to characterize the separability of single-cell responses using singular value decomposition (Pesaran et al. 2006, 2010). We found that the coding of target and hand position information by single cells was very consistent across the reaching workspace. In addition, providing visual cues about the starting position of the hand did not appreciably change the manner in which hand position was encoded by individual neurons. These findings suggest that the PPC uses a consistent scheme for computing reach vectors in different parts of the workspace and that concurrent vision does not strongly influence the representation of hand position in this area when visual and proprioceptive signals are spatially congruent. In addition, the presence of both separable and inseparable neurons provides additional support for the idea that the PPC is involved in transforming reaching-related variables into signals appropriate for directing motor behavior.
METHODS
Behavioral Paradigm
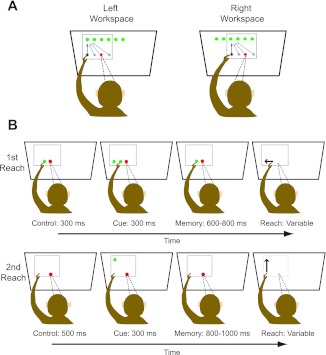
Figure 1A shows the basic behavioral paradigm. Monkeys made reaching movements from an array of horizontally arranged starting positions to an array of horizontally arranged targets (located above or below the array of initial hand positions). Either a 3 × 3 or a 4 × 4 arrangement of starting and target positions was used in a given session, with 5 trials being performed for each combination, resulting in a total of either 45 or 80 trials performed in each workspace. The reach targets were touch-sensitive buttons that were 3.7 cm in diameter and set 7.5 cm apart (18°) on a vertically oriented Plexiglas board. To actuate the buttons and move between positions on the board, the animals had to pull their hand away from the surface and then place it back again once the target was reached. Because of the large range of starting positions and target positions employed in this study (see below), movements involved changes in both shoulder angle and, to a lesser extent, elbow angle. However, since targets were constrained to lie on a surface, limb movements involved minimal variation along the depth axis.
Fig. 1.
Behavioral paradigm. A: arrangement of targets and starting positions in each workspace. Reaches were made from each of 3–4 starting positions to each of 3–4 targets. Initial hand positions were always in the same (middle) row, and targets were either above or below the array of starting positions. In this plot, only required reaches to the upper leftmost target are illustrated. B: sequence of events on a single trial. Two reaches were performed: on no hand vision trials (shown), the first reach served to define the initial hand location for the second reach in such a way that somatic and visual information were never simultaneously available. The sequence of events was identical on concurrent hand vision trials, except that a visual stimulus was present at the starting position after completion of the first reach.
Movements were made with the left arm by one animal (Cky) and the right arm by the other (Dnt); in both cases, the arm used was contralateral to the recording chamber. The position of the hand was indicated by the actuation of the push buttons and was therefore expressed in board coordinates during data acquisition. Note that we did not record arm or hand kinematics in this study. As a result, we were unable to distinguish among various extrinsic and intrinsic coordinate frames associated with the limb (e.g., arm endpoint coordinates vs. joint-based coordinates).
Eye position was monitored using the scleral search coil technique. The eye coil was calibrated so that its signal corresponded to known fixation positions on the reaching board. As a result, these signals were also expressed in board coordinates during data acquisition. Given that gaze, hand, and target position were all initially expressed in the same coordinate system, their relative positions could be easily computed as required for data analysis.
The initial hand positions and target positions were sampled in two different workspaces (randomly interleaved) that corresponded to different horizontal gaze positions separated by 36° of visual angle. Adjacent targets and hand positions within each workspace were separated by 18° of visual angle. Thus hand positions were studied over a range of 90° with respect to the head/body between the two workspaces. Note that because gaze covaried with the reaching workspace, corresponding targets and hand positions in the two workspaces were identical in eye- and hand-centered coordinates but different in body-centered coordinates (by 36°).
Two variants of the basic behavioral paradigm were used in this study. In one variant (no hand vision), responses were studied in a task where haptic, proprioceptive, and efference copy-related information could be used to localize the initial hand position but where visual cues about hand position were not concurrently available, having been provided only in the past (i.e., they were remembered cues). In the second variant (concurrent hand vision), somatic and visual cues about hand position were both simultaneously available. The details of the two tasks are described below.
No hand vision task.
Experiments were performed in total darkness with the exception of the reach and fixation position cues. On a given trial, animals performed a sequence of two reaches to remembered visual targets (Fig. 1B). The purpose of the first reach was to define the initial hand location for the second reach in such a way that somatic and visual information were never simultaneously available. At the beginning of a trial, the fixation point and an initial hand position were cued visually by the illumination of LEDs that were set within each pushbutton. A red LED instructed the animals where to direct and maintain their gaze, and a green LED instructed the animals where to direct and maintain their hand position. After these positions were acquired, a target was briefly illuminated (300 ms). After the offset of the target, a variable delay period ensued, lasting from 500 to 800 ms. At the end of this delay period, the visual stimuli indicating the initial hand position and fixation position were extinguished, cueing the animal to reach to the target, which then became the initial hand location for the second reach. Animals were required to maintain this new starting position for 500 ms, after which the trial proceeded as for the first reach, with the exception that the delay period was slightly longer (600–1,000 ms) and the “go” signal was the extinguishing of the fixation position only.
To summarize, in this experiment animals performed a sequence of two reaches to memorized target locations, one within the row of starting positions and a second to the row of targets either above or below the row of starting positions. Starting positions and initial target locations were always in the middle row of the target array. The row of final target locations varied on a cell-by-cell basis and depended on the response field of the cell, which had been established previously using a standard center-out reaching task with fixation. Data analysis focused exclusively on activity occurring during the planning and execution of the second reach, i.e., a 400-ms epoch centered on movement onset.
Given the manner in which the starting position for the second reach was cued, and with the recording room being totally dark, animals never had concurrent visual and somatic information at that location and in fact experienced a delay of several hundred milliseconds between somatic and visual cues. Delays of this length should have affected reach planning in this task, because the removal of visual information has been shown to affect the variability of both reaching movements and saccadic eye movements at delays as short as 500 ms (McIntyre et al. 1998; Ploner et al. 1998; Rolheiser et al. 2006). To further ensure that the animals could not see their hand during the planning and execution of the second reach additional steps were also taken. First, LED intensity was adjusted to a level high enough that the animals could identify cued target locations but low enough so that target illumination could not provide visual cues about the starting position of the hand. As an added measure, at the end of each trial the room lights were briefly illuminated, thereby preventing dark adaptation. These combined measures were sufficient to prevent illumination of the hand or any portion of the arm as a result of target illumination.
Concurrent hand vision task.
A subset of neurons was concurrently tested with vision of the hand at the starting position for the second reach. Given the substantial increase in the number of trials that would have been required to run this task with the no hand vision task in both workspaces, data were collected in only one workspace, although trials with and without vision were randomly interleaved. In this task the sequence of events was identical to that shown in Fig. 1B except that at the completion of the first reach, the LED corresponding to the starting position was illuminated and remained illuminated throughout the delay period, providing constant visual information about the starting position. At the end of the delay period, this LED and the one indicating the fixation point were extinguished, cueing the second reach.
Neurophysiology
All experimental procedures were conducted according to the “Principles of Laboratory Animal Care” (NIH Publication No. 86-23, Revised 1985) and were approved by the California Institute of Technology Institutional Animal Care and Use Committee. Single-cell recordings were obtained from one hemisphere of two adult rhesus monkeys (right hemisphere for monkey Cky; left hemisphere for monkey Dnt) using standard neurophysiological techniques. Activity was recorded extracellularly with varnish-coated tungsten microelectrodes (impedance ∼1–2 MΩ at 1 kHz; Frederick Haer, Bowdoinham, ME). Single action potentials were isolated from the amplified and filtered (600–6,000 Hz) signal via a time-amplitude window discriminator (Plexon, Dallas, TX). Spike times were sampled at 2.5 kHz.
The activity of 134 neurons was recorded in 2 animals. Of these neurons, 109 (69 from monkey Cky and 40 from monkey Dnt) were modulated by hand position and/or target position in at least one workspace and were analyzed further (see ANOVA below). A subset of neurons (26) was examined in the no hand vision task in both workspaces and the concurrent hand vision task in at least one workspace. Recordings were obtained from both the surface cortex adjacent to the intraparietal sulcus (IPS) and the medial bank of the sulcus. Note that the surface recordings were more caudal (∼3 mm) to those reported by Buneo et al. (2002, 2008). The mean recording depth was 3.2 mm (±1.81) from the estimated point of entry into the brain. The median depth was 3.15 mm, meaning approximately equal numbers of cells were recorded from the surface cortex near the bank of the IPS and from the bank of the IPS.
Data Analysis
Peristimulus time histograms of the mean firing rates of single neurons were constructed for each target location by smoothing the spike train with a Gaussian kernel (σ = 50 ms). The Pearson product-moment coefficient was used to assess the degree of scalar correlation between the firing rates of single cells and the population of cells in each workspace. In addition, a three-factor ANOVA (α = 0.05) was used to assess the dependence of firing rate on target location, hand location, and workspace. A separate three-factor ANOVA was performed to assess the effects of target location, hand location, and vision in a given workspace. T-tests (α = 0.05) were used to assess differences in the recording depths of groups of cells that differed from each other on functional grounds.
Singular value decomposition.
Singular value decomposition (SVD) was used to assess whether responses were separable or inseparable (Pena and Konishi 2001; Pesaran et al. 2006, 2010). In this experiment, if responses are separable, the implication is that the experimental variables (target and hand position) are combined in a manner similar to a gain field representation (Andersen et al. 1985; Chang et al. 2009; Pesaran et al. 2006). If the responses are inseparable, the implication is that the response field shifts as one or the other variable is changed. A field that shifts by an amount that is approximately equal to the change in hand or target position would technically be consistent with either a coding of hand position in target-centered coordinates or a coding of target position in hand-centered coordinates (Pesaran et al. 2006). For simplicity, however, we have used the latter interpretation here and throughout the results. For this analysis, average responses associated with the different combinations of reach variables were first arranged as two-dimensional (2-D) matrices, such as those shown in Figs. 4 and 5, and were then subjected to SVD. Responses were considered to be separable if the first singular value was significantly larger than the singular values obtained when trial conditions were randomized (randomization test, α = 0.05). More specifically, we randomly rearranged the data in each matrix 1,000 times and subjected each “shuffled” matrix to SVD. The first singular values from each shuffled matrix were accumulated into a vector, which was then sorted in ascending order. This sorted vector (n = 1,000) formed the reference distribution for determining statistical significance. If the first singular value obtained from the original unshuffled matrix was greater than 95% of the singular values in this distribution, the responses were considered separable.
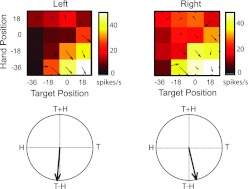
Fig. 4.
Example posterior parietal cortex (PPC) neuron (recorded at a depth of 0.85 mm) with inseparable responses that coded for the reach vector (T−H). Top: response fields (color maps) and superimposed vector fields are based on mean firing rates during the perireach epoch for the neuron shown in Fig. 3. Response fields are plotted as a function of starting hand position and target position (in degrees of visual angle). Bottom: corresponding field orientations derived from the vector fields (see methods for details). T, target position; H, hand position.
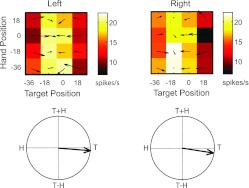
Fig. 5.
Example PPC neuron (recorded at a depth of 4.43 mm) with separable responses that coded for the reach target. Figure conventions are as described in Fig. 4 legend.
Field orientations.
To further probe the contribution of target and hand position signals to each response field, we calculated the field orientation, as previously described (Buneo et al. 2002; Pesaran et al. 2006, 2010). For separable neurons, the field orientation describes the relative directions and strengths of the gainlike effects of target and hand position. For inseparable neurons, the field orientation describes the degree to which a response field shifts as hand or target position is varied. A gradient (vector field) was first computed from each 2-D response matrix using an approximate numerical method (Matlab; The MathWorks). The angles of the individual gradient vectors were then doubled (to prevent cancellation for symmetrically shaped response fields) and the vectors summed. This resultant (the field orientation vector) allows for a simple, graphical depiction of the tuning of a neuron to the experimental variables. More specifically, due to the angle-doubling procedure, field orientations in this experiment could be expressed in terms of their dependence on target position, initial hand position, target + initial hand position, and target − initial hand position (see Figs. 4 and 9). Target − initial hand position is the difference between the target and initial hand position and can also be interpreted as the target position in hand-centered coordinates. Target + initial hand position does not have similarly intuitive meaning, although it should be noted that relatively few cells have field orientations that tend to point in this direction (see results).
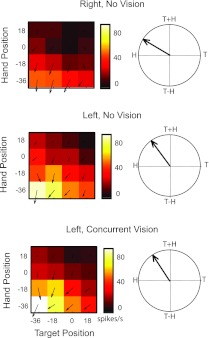
Fig. 9.
Example PPC neuron in the no hand vision and concurrent hand vision tasks. This neuron was recorded at a depth of 2.75 mm, close to the juncture of superficial and deep cortex. Color maps and vector fields for the right and left workspaces (top and middle, respectively) and 2 visual conditions in the same workspace (middle and bottom, respectively) are shown. Other figure conventions are as described in Figs. 4 and 5.
Although an ANOVA was initially used to assess the presence of statistically significant responses to the experimental variables, we also assessed significance using the field orientations. A field orientation vector was considered to be significantly tuned if this vector was greater in length than the distribution of vectors obtained when the trial conditions were randomized (randomization test, α = 0.05). The randomization procedures were similar to those described above for assessing the significance of the first singular values obtained from SVD. Once significance was assessed, orientation vectors were normalized by magnitude for plotting purposes.
Vector correlation.
Neurons that are inseparable according to the SVD analysis and that have field orientations consistent with target − initial hand position can be considered to be hand centered. Neurons with separable responses, however, could be eye centered, hand centered, or body centered. For these neurons, we probed the extent to which these neurons were consistent with body-centered coordinates using a vector correlation method. This method involved correlating the vector fields computed for the left and right workspaces (see Field Orientations above). The basic premise behind this approach is that neurons that are consistent with eye-centered or hand-centered coordinates should have response fields that are well correlated, because targets and hand positions were identical in eye and hand coordinates in the two workspaces, whereas body-centered neurons should be relatively poorly correlated. Note that more definitive statements regarding eye- vs. hand-centered coordinates can be made if eye position is varied to the same extent as target and hand position, an approach that has been taken by Pesaran et al. (2006, 2010) to study the reference frames of neurons in PMd. This approach was precluded by the goals of the present study, which were directed at characterizing responses over a large portion of the workspace while also probing the sensory modalities contributing to hand position coding.
In general, vector correlation provides information about the degree of relatedness of two response fields. Although similar information can be obtained by cross-correlating the scalar response fields, this procedure requires shifting the fields with respect to one another, which can lead to progressively nonoverlapping response fields and progressively fewer data to correlate (Buneo 2011). Although numerous measures of vector correlation have been defined in the literature, we employed the method of Hanson et al. (1992), which was originally developed for the analysis of geographic data. This method provides a correlation coefficient that is analogous to the scalar correlation coefficient. In addition, it determines the degree of rotational or reflectional dependence and scaling relationship between the sets of vectors. Rotational dependence describes the degree of rotation (clockwise or counterclockwise) needed to best align the sets of vectors with respect to one another, whereas reflectional dependence means the two sets of vectors are better described by a reflection about a fixed axis. If x and y refer to the components of one set of vectors and u and v to the components of the second set, the vector correlation can be computed as follows (Hanson et al. 1992):
| (1) |
where
| (2) |
| (3) |
and where σx, σy, σu, and σv represent the variances of x, y, u, and v and σxu, σyv, σxv, and σyu represent the four component covariances. A scale factor (β) can also be computed as
| (4) |
and an angle of reflection/rotation (phase angle, θ) as
| (5) |
The correlation coefficient ρ ranges from −1 to 1, with 1 representing a perfect rotational relationship, −1 representing a perfect reflectional relationship, and 0 representing no relationship (Hanson et al. 1992). Importantly, the correlation represents the degree of relatedness of the two sets of vectors after accounting for the rotational (or reflectional) dependence. Thus it is possible to have large phase angles with correlations close to 1 (in the case of rotation) or −1 (in the case of reflection). The phase angle θ ranges from −180° to 180° and describes the angle or rotation or reflection needed to best superimpose the two sets of vectors, whereas the scale factor β describes the gain relationship between the two vector fields.
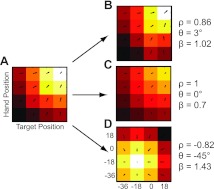
Figure 2 shows example vector correlations derived from idealized neural responses. The values of ρ, θ, and β shown were obtained by correlating the vector field in Fig. 2A with those in Fig. 2, B–D. The field in Fig. 2B was designed to have the same tuning structure as the neuron in Fig. 2A, but with added noise that was proportional to firing rate (Fano factor =1). As a result, the field was expected to be well correlated with a small phase angle and a scale factor near unity and does in fact exhibit those properties. The scalar field in Fig. 2C is identical to the one in Fig. 2A except for a multiplication by 0.7, and the corresponding vector correlations reflect these properties. Last, the scalar field in Fig. 2D was simulated to have a peak response that was shifted by −36° along the target and hand position axes. This is the shift expected of body-centered cells in the present experiment (see below). Importantly, here the correlation is best described as a reflectional relationship (negative correlation), rather than a rotational (positive) one.
Fig. 2.
Example vector correlations. A–D: idealized scalar response fields (color maps) with corresponding vector fields superimposed. Data are plotted as a function of starting hand position and target position (in degrees of visual angle). For the scalar fields, lighter colors represent higher firing rates. Corresponding vector fields converge toward the highest response. ρ, θ, and β represent the vector correlation coefficient, phase angle, and scale factor, respectively, obtained by correlating the vector field in A with those in B–D.
Simulations.
In this experiment, PPC neurons with separable responses that are eye or hand centered would be expected to have vector correlation coefficients close to 1 and phase angles close to 0°. The expected distribution of vector correlations for a body-centered population of neurons is not as intuitively apparent. Therefore, to compare observed vector correlations with those expected of a body-centered population, we used a simulation approach. In this simulation, we produced a population of body-centered and body/hand-centered neurons with a distribution of field orientations similar to those observed in the population. To produce this distribution, neurons were assumed to encode one of the following combinations of variables: 1) target location in body-centered coordinates and hand-centered coordinates (Eq. 6 below), 2) hand location in body-centered coordinates and target in hand-centered coordinates (Eq. 7), and 3) target location and hand location in body-centered coordinates (Eq. 8). Responses were simulated as either sigmoidal or Gaussian functions of the experimental variables, and the choice of function as well as the peak target location, hand location, and reach vector were randomly determined. Only multiplicative interactions between the variables were simulated. Thus, for Gaussian fields, firing rates (fr) were described by the following:
| (6) |
| (7) |
| (8) |
where TB and HB represent the target and hand position in body-centered coordinates, respectively, and TB − HB represents a reach vector (equivalent to target in hand coordinates, TH). Our observations regarding these simulated responses (see results, Effects of Workspace) appear to be relatively insensitive to the width of the Gaussians. In addition, these observations did not appear to depend on whether the functions of hand position were modeled using combinations of Gaussian and sigmoidal functions, or only sigmoidal functions.
Neural responses were simulated for one workspace (left or right) at random. We then produced a second set of responses for the other workspace, shifted by −36°. This is the shift that would be expected if the neurons were body centered in the current experiment, because targets and hand positions differed by this amount in body-centered coordinates. Once the shifted responses were generated, we calculated the vector correlations (ρ, θ) in the same manner as for the real neural data and compared the distribution of parameters with those from the real data.
RESULTS
Effects of Workspace
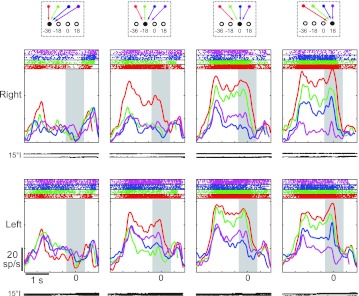
Effects of workspace were examined with the no hand vision task. This task revealed that the activity of single neurons was generally quite similar between the two workspaces. Figure 3 shows perievent time histograms and rasters for a neuron, aligned to movement onset (peak at time 0). Each column shows the activity for one target location in visual coordinates, with different colored lines representing different starting positions (and therefore different movement vectors). For this cell, activity was largest for movements that began at the far left portion of each workspace (−36°) and ended at the lower right (18°). This preference was observed at movement onset as well as throughout the preceding memory period. In addition, the preference was present in both workspaces. The absolute firing rate of this cell also appeared to differ somewhat between workspaces, appearing relatively higher in the right workspace.
Fig. 3.
Peristimulus time histograms from a single neuron for all targets in both workspaces (right and left, rows). Data are aligned at movement onset. Gray rectangle illustrates the analysis window used in this study. Each column shows responses for a given target location in visual coordinates; colors represent different starting positions. Traces illustrate horizontal (top) and vertical (bottom) eye position traces. Average movement times over all 4 starting positions and targets were 249 ± 106 ms. Average reaction times were 272 ± 100 ms. sp/s, Spikes/s.
Figure 4 depicts mean firing rates during the 400-ms-long perireach epoch for the same cell. Activity is represented as a response matrix where firing rates (color) are plotted as a function of initial hand position and target position. Here again, it can be observed that the combination of hand position and target position for which this cell responded best was the same in each workspace. That is, the cell was most active when the initial hand position was located 36° to the left of fixation and the horizontal location of the target was 18° to the right (white squares, bottom right of each map). SVD indicated that the responses of this cell were inseparable in both workspaces. In addition, the field orientations in each workspace indicated that the cell was tuned to the difference between targets and hand positions. Thus the responses of this neuron were consistent with a coding in hand-centered coordinates. As in Fig. 3, the color maps also suggest that firing rates differed between the two workspaces (right > left). This effect was relatively small, and as a result, the corresponding vector fields show only weak evidence of scaling. This was borne out by the vector correlation analysis, which indicated that the scale factor (β = 0.94) was not significantly different from unity (randomization test, P < 0.05). Thus, overall, the responses of this neuron were consistent with hand-centered coordinates and showed little evidence of a workspace-dependent modulation.
Figure 5 shows the responses of another neuron with somewhat different characteristics. Like the neuron in Fig. 4, this one showed similar tuning in both workspaces; this can be appreciated from both the response fields and the field orientations. In contrast to the previous cell, however, responses were best described as separable rather than inseparable in both workspaces (SVD; randomization test on first singular value, P < 0.05). In both workspaces, the field orientations were tuned to target position. Close examination of the response fields indicates that activity was greatest for target positions between −18° and 0°. This neuron did not demonstrate a significant main effect of workspace (ANOVA, P > 0.05), and the scale factor (β) derived from the vector correlation analysis was also not statistically significant (randomization test, P > 0.05). The cell did, however, demonstrate a significant interaction between workspace and hand position; this effect is evident in the slightly stronger tuning with hand position in the right workspace, particularly for targets located at −18°. Note that due to the experimental design, such workspace effects could arise due to changes in eye position, changes in limb position with respect to the body, or both phenomena.
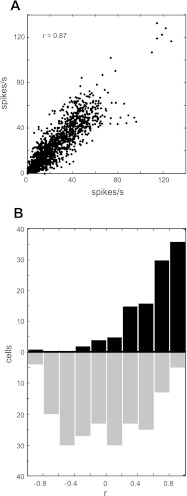
In the present experiment, most neurons (86/109) exhibited either main effects of workspace or interaction effects between workspace and target/hand position (3-factor ANOVA, P < 0.05). Despite these workspace-dependent effects, responses were still largely similar between workspaces at the population level. Figure 6A shows a scatter plot of the activity from all cells. Each point corresponds to the mean firing rate of one cell for the same combination of target and hand position in the two workspaces. Activity for the right workspace is plotted on the abscissa and activity for the left workspace on the ordinate. Activity was highly correlated across the population (r = 0.87). In addition, Fig. 6B shows a bar plot of the scalar correlation coefficients obtained by correlating the activity for corresponding locations in the two workspaces on a cell by cell basis. This plot shows activity was moderately to highly correlated between workspaces for the majority of neurons. Thus, in general, activity was very well correlated between workspaces at both the single-cell level and across the population.
Fig. 6.
Scalar correlations for the population. A: scatter plot of firing rates for corresponding movement vectors in the left (ordinates) and right workspaces (abscissa). Data for all cells are shown. B. distribution of coefficients for correlations performed on a cell-by-cell basis (solid bars) and distribution of correlation coefficients obtained for 200 random pairings of cells (shaded bars).
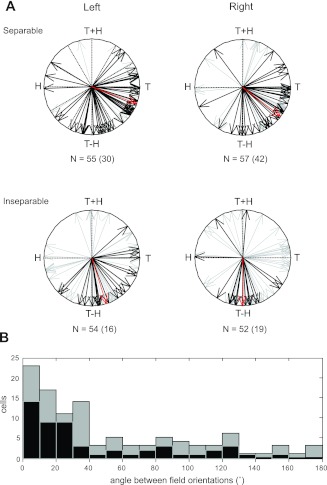
The manner in which target and hand position information were integrated in each workspace was also very similar across the population. Figure 7A shows the distributions of field orientations for neurons with separable (top) and inseparable responses (bottom). Data from both workspaces are shown, with the most strongly tuned neurons (those with a statistically significant randomization test, P < 0.05) indicated in black. The distributions of separable and inseparable responses were very similar in the two workspaces; this can be best appreciated from their corresponding mean vectors (red), which have very similar orientations, as well as from the histogram of angular differences between field orientations in the two workspaces (Fig. 7B). Neurons with separable responses were more common in both workspaces, and these neurons demonstrated a large range of field orientations, including those that were primarily target related (vectors pointing toward “T”) and primarily target − hand related (“T−H”), as well as those with properties that were intermediate between these two. Inseparable responses exhibited a more limited range of orientations, tending toward target − hand related. Thus, although a range of responses was observed, these responses were generally consistent between workspaces, in terms of both their separability and field orientations, i.e., only eight neurons changed their representation between workspaces (from separable to inseparable or vice versa).
Fig. 7.
Response field orientations for all neurons (n = 109). A: black vectors indicate the best-tuned neurons according to a permutation test. Numbers indicate the number of neurons in each plot, with the number of best-tuned neurons in parentheses. Red vectors represent the mean of the black vectors in each plot. B: angle between field orientations in the left and right workspaces for all neurons.
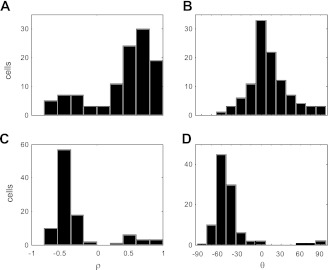
A key question concerns the nature of the separable neurons. As discussed in methods, these neurons could be consistent with eye-, hand-, or body-centered coordinates. To distinguish between body-centered coordinates and the other two reference frames, we simulated the responses of a population of neurons coding targets in body- and/or hand-centered coordinates in both workspaces (see methods). From these simulated responses, we then produced corresponding vector fields and correlated them, and we then compared these correlations with those obtained from the population of recorded neurons. Figure 8 shows the results of these analyses. Because corresponding target and hand positions in the two workspaces were identical in eye coordinates in this experiment, vector fields derived from a population of eye- and hand-centered cells would be expected to be highly and positively correlated between the two workspaces with small phase angles (θ). Figure 8, A and B, shows that for the recorded neurons, correlations were generally strong and positive with phase angles largely clustered between ±30 degrees. In contrast, our simulations predicted that a population of body-centered and body/hand-centered cells would be expected to show moderate to high degrees of negative correlation, implying a reflectional relationship between the vector fields in the two workspaces (Fig. 8, C and D). This reflection is a direct consequence of the response field shifts expected of separable, body-centered neurons in this experiment. It should be noted that some recorded neurons did show properties consistent with body-centered coordinates (small bump in the bar plot at ∼ρ = −0.5), which may reflect the contribution of somatosensory signals to the representation in this area (Caminiti et al. 1991; Ferraina et al. 2009; Lacquaniti et al. 1995; McGuire and Sabes 2011; Scott et al. 1997). Overall, however, individual response fields in this task appeared to be more consistent with a coding of reach-related information in hand- and eye-centered coordinates, rather than body-centered or intermediate hand- and body-centered coordinates.
Fig. 8.
Vector correlations between workspaces. A: distribution of coefficients for the population. B: rotational/reflectional dependencies for the population. C: distribution of coefficients for the simulated population of body-centered neurons. D: distribution of rotational/reflectional dependencies for the simulated population.
Positional Modulation
The results presented above are consistent with previous suggestions that the PPC is involved in transforming target and hand position signals in eye-coordinates into a reach vector in hand-centered coordinates (Buneo and Andersen 2006; Buneo et al. 2002). If the separable cells are coding in eye coordinates, and if this encoding persists even in the absence of hand vision, it suggests that an eye-centered code for hand position may be constructed from somatically derived limb position information that is transformed, via combination with head and eye position signals, into eye coordinates. Previous work strongly suggests that neurons are modulated by both eye and limb position signals in reach-related areas of the PPC (Buneo et al. 2002; Chang et al. 2009; Cohen and Andersen 2000). The fact that many neurons showed workspace-dependent effects (3-factor ANOVA, P < 0.05), even though the coding schemes of individual neurons were largely similar between workspaces, suggests the presence of positional modulation in these neurons. Because the presence of such modulation seems to be a prerequisite for a body- to eye-centered transformation, we looked for evidence of this phenomenon in the present data set.
Positional modulation would be most easily identifiable in neurons with response fields that are nearly identical in shape in the two workspaces. In these cases, position effects would manifest simply as a “gain modulation” of the underlying response field (Andersen et al. 1985). A single-cell example of this phenomenon can be seen in Fig. 5, where the responses of the neuron were higher in the left vs. right workspace but the overall structure of the response field was virtually identical between workspaces. It is important to reiterate that changes in limb position with respect to the head/body and changes in eye position were confounded in this study. As a result, such positional modulation could be attributed to changes in limb positions/configurations between workspaces, changes in eye position between workspaces, or both effects. Nevertheless, given the importance of any positional modulation for the coordinate transformation scheme being proposed here, we quantified the significance of these effects. This was done using the parameter β that was derived from our vector correlation analysis. This parameter describes the scale factor or gain that best describes the relationship between vector fields. For reasons discussed above, we limited our analysis to those neurons with strong correlations (ρ > 0.6) and low rotational/reflectional dependencies (−30° > θ < 30°), i.e., those cells with response fields that were the most similar in shape between workspaces. We then determined the significance of the corresponding scale factors. Of the 40 neurons that were tested, 16 (40%) demonstrated a significant difference in scale between workspaces (randomization test, P < 0.05). Assuming this subset of neurons is representative of the rest of the population, this analysis suggests that a substantial number of neurons in this study were modulated by eye and/or limb position signals, consistent with previous findings in the superior parietal lobule (Chang et al. 2009; Cisek and Kalaska 2002; Ferraina et al. 2009; Johnson et al. 1996; Lacquaniti et al. 1995; Scott et al. 1997). This positional modulation is likely the source of the workspace-dependent effects identified by our ANOVA.
Visual Modulation
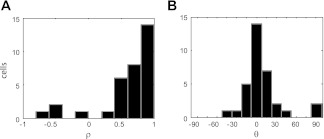
Allowing hand vision did not generally alter the responses of PPC neurons in this study. A three-way ANOVA of responses in the no hand vision and concurrent hand vision conditions identified main and/or interaction effects of vision in only 18% (6/33) of the cases. Figure 9 shows a cell that was tested in both workspaces without vision of the hand as well as with hand vision in the left workspace. A comparison of the no-vision response fields (top and middle, left) reveals that the target and hand location associated with the peak response was largely the same in the two workspaces (−36° for both), although the magnitude of the response differed greatly between the workspaces. The response fields suggest a strong influence of hand and/or eye position in this cell, and the field orientations indicate that the manner in which this information was integrated with information about target position was also similar between workspaces. Somewhat surprisingly then, allowing hand vision throughout the trial did not substantially alter the responses of this cell. That is, although this cell demonstrated significant main effects of hand and target position as well as a significant hand-target interaction, it did not demonstrate main effects of vision or an interaction between vision and hand/target position (3-factor ANOVA, P < 0.05). This absence of visual modulation can also be readily observed in the response fields: the concurrent and no-vision maps for the left workspace appear virtually identical in shape and scale.
The findings described above were representative of the population. Figure 10 shows the vector correlations obtained by comparing responses in the same workspace during the no hand vision and concurrent hand vision tasks. Data from all neurons tested in at least one workspace are shown. Figure 10 shows that for these comparisons, correlations between responses were generally very strong and positive, with phase angles strongly peaked at 0°. This indicates that the shapes of the response matrices were relatively unaffected by the presence of visual input. To assess changes in scale between the no hand vision and concurrent hand vision tasks, we again focused on the parameter β derived from the vector correlation (see above). As with our analysis of workspace effects, we focused on cells with strong correlations (ρ > 0.6) and small phase angles (−30° > θ < 30°), i.e., cells with response fields that were most similar in shape in the no hand vision and concurrent hand vision tasks. Of 22 possible comparisons, we found 5 instances where the vector fields in the no hand vision and concurrent hand vision conditions were significantly different in scale (randomization test, P < 0.05). Thus, although some cells did show a change in activity in the presence of vision, this affect appeared to manifest largely as a change in the overall firing rate that did not alter the coordinate frames or gain fields of these cells.
Fig. 10.
Vector correlations between the no hand vision and concurrent hand vision tasks (same workspace). A: distribution of correlation coefficients for the population. B: rotational/reflectional dependencies for the population.
Trends with Recording Depth
As described in methods, cells were recorded at depths ranging from 0 to 6.95 mm. This raises the question as to whether the various functional classifications described in this paper, e.g., separable vs. inseparable and movement vector related vs. target related, could be explained by differences in the recording depth. We found no difference in the mean depths of separable and inseparable neurons in either workspace (t-test, P < 0.05). We also found no difference in the mean depths of cells that were predominantly movement vector related vs. target position related (t-test, P < 0.05). Regarding sensitivity to visual modulation, the six cells that were shown to have significant effects of vision by the ANOVA were recorded at a mean depth of 4.33 mm. The five cells that showed significant visual gain effects by the randomization test were recorded at a mean depth of 4.92. Taken as a group, these visually sensitive cells were recorded at locations that were significantly deeper than the rest of the population (t-test, P < 0.05).
DISCUSSION
We examined the effects of workspace and hand vision on the integration of target and hand position signals in the PPC. Within each workspace we found both inseparable and separable responses (although the latter were more common) for initial hand position and target position. For most cells, however, responses were generally consistent between the two workspaces. Although small differences in response magnitude were occasionally observed with and without vision of the initial hand position, responses were otherwise unaffected by the presence or absence of visual hand position cues, in agreement with recent findings showing an insensitivity of parietal reach-related activity to proprioceptive vs. visual targets (McGuire and Sabes 2011). Assuming that hand-centered coordinates would be an appropriate coordinate frame for representing parameters of reaching movements, these findings suggest that the PPC uses a consistent scheme for computing reach vectors in different parts of the workspace and that hand vision does not strongly influence this computation.
In this experiment eye position was not varied over the same number of locations as hand and target position, an approach that was used by Pesaran et al. (2006) to identify the reference frames of reach-related activity in PMd and PRR. As a result, we cannot say definitively whether target positions and hand positions were encoded in eye coordinates for the separable cells, although the vector correlation analysis is consistent with this idea. In addition, previous studies of coordinate frames in this area using a more complete matrix of eye, hand, and target positions are also consistent with an eye-centered coding of target position (Pesaran et al. 2006).
In this study separable cells were more commonly encountered. This is in agreement with Pesaran et al. (2006), who found that cells coding targets and hand positions separably were more common in MIP/PRR. We found no differences in depth of recording in terms of the relative numbers of neurons encoding targets and hand positions separably vs. inseparably. The similarities between superficial and deep recordings in the present study may be partly due to the fact that recordings in superficial cortex were made very close to the bank of the IPS, to sample responses in surface cortex as well as within the bank of the IPS. The caudal placement of the recording sites and the large number of separable cells suggests that the recordings were largely made in PRR. Cells recorded more anteriorly on the surface in area 5d have been found to code predominantly in hand coordinates; i.e., the population is largely inseparable for variations of hand position (Bremner and Andersen 2010).
Neural Mechanisms of Visual and Somatic Cue Integration
The integration of visual and proprioceptive cues by PPC neurons was previously examined in a task where the unseen limb was passively varied between two positions in the horizontal plane (Graziano et al. 2000). During these experiments, visual information was also manipulated by using a fake monkey arm that was placed in positions that were either congruent or incongruent with an animal's real arm. In agreement with previous investigations of area 5 (Georgopoulos et al. 1984; Lacquaniti et al. 1995), nearly one-half of the neurons in this area were modulated by changes in the position of the unseen real arm, an effect attributed to somatic (mainly proprioceptive) signals. Although few cells responded to manipulations of the seen arm only, 27% of the cells were reported to respond to both the seen and unseen arm, an effect that was statistically significant at the population level.
In the present study, we found that ∼18% of PPC neurons were concurrently modulated by visual and somatic cues, with this modulation manifesting largely as a change in magnitude of responses, rather than a change in the coordinate frame or gain fields used to encode hand and target position. Although these results were largely consistent with those of Graziano et al., methodological differences between the two studies may account for the slightly differing results. In Graziano et al. (2000), animals were not required to make a perceptual judgment based on the available sensory cues. As a result, it is unclear if the fake arm was perceived by the animals as a visual signal regarding the position of their limb. This was likely not the case in the present study, which involved varying available sensory cues in a more veridical situation. In addition, in the study by Graziano et al. (2000), animals were not required to actively maintain their limb position and in fact had their limbs passively placed in position by the investigators. Consequently, the contribution of motor processes to position coding was not addressed in this experiment. This is in contrast to the present experiment, which required the production and sustained maintenance of motor output in the presence of varying sensory cues. It is well known that the integration of sensory and motor cues is highly context dependent (Kording and Wolpert 2004; Scheidt et al. 2005; Sober and Sabes 2003; Vetter and Wolpert 2000; Wolpert et al. 1995); thus the small differences in the number of bimodal neurons may simply represent a neural correlate of this context dependency. Last, in the present study, a visual cue about limb position was available in both the concurrent and no hand vision tasks, although in the latter case this cue was presented in advance of the somatic cue. This may also have contributed to the slightly differing results between the two studies.
The fact that relatively few neurons in the present study were modulated by visual cues at the starting position suggests that vision did not contribute strongly to the representation of limb position in this experiment. Vision could be more important in representing limb position in other contexts, however, as suggested by the theory of optimal cue integration (Angelaki et al. 2009). In this framework, motor and sensory signals are weighted according to their relative reliability, which can vary with context. The combination of tactile, proprioceptive, and force feedback experienced during the actuation of pushbuttons in this experiment, as well as the continuous motor output, likely provided a very reliable estimate of hand position. As a result, visual signals may not have been weighted very strongly in this task (relative to somatic cues), contributing to the relatively small differences between the no hand vision and concurrent hand vision response fields (Fig. 10). In other contexts, vision might provide a more reliable estimate than somatic cues, e.g., during the maintenance of limb positions in free space, and might therefore be weighted more strongly, manifesting as stronger modulation in the presence of limb vision.
Coordinate Transformations for Reaching
Initial psychophysical experiments designed to investigate sensorimotor transformations for reaching supported a scheme where visually derived target information is transformed into body-centered coordinates and compared with the body-centered position of the hand (Flanders et al. 1992). Subsequent neurophysiological studies of the PPC and PMd, areas thought to be involved in coordinate transformations, have expanded this viewpoint. Neurons in the PPC and PMd have been shown to encode reach targets in eye-centered coordinates (Batista et al. 1999; Buneo et al. 2002; Cohen and Andersen 2000; Pesaran et al. 2006) as well as in both eye- and hand/body-centered coordinates (Batista et al. 2007; Buneo et al. 2002; Chang and Snyder 2010; McGuire and Sabes 2011). In addition, many cells in PMd have been shown to encode the position of the hand in eye coordinates (Pesaran et al. 2006). Together, these findings suggest that the PPC and PMd are involved in integrating target positions in eye coordinates with limb position signals represented (at least in part) in eye coordinates to derive a desired hand displacement vector (Buneo and Andersen 2006; Buneo et al. 2002). Recent transcranial magnetic stimulation (TMS), imaging, and clinical studies in humans are consistent with this view (Beurze et al. 2006, 2007, 2010; Khan et al. 2007; Vesia et al. 2008).
In the present study, the responses of most neurons were consistent when compared between the two workspaces, where targets and hand positions were the same in eye-centered coordinates but different in body-centered coordinates. The fact that this was observed even in the absence of hand vision suggests that the aforementioned scheme is likely robust to changes in the availability of somatic and visual cues about hand position. This is similar to recent reports showing that the coding scheme used by individual PPC neurons was invariant with respect to target modality (McGuire and Sabes 2011). The present findings do not imply, however, that body-centered information is not represented in this area or that it is not used in coordinate transformations for reaching, because previous studies have provided evidence for body-centered coding of reach variables in the PPC (Lacquaniti et al. 1995; McGuire and Sabes 2011). Instead, the use of body-centered and eye-centered information in coordinate transformations may be contextual. For example, in the presence of reliable visual cues about the hand and target, hand position may be remapped from body- to eye-centered coordinates to determine the reach vector. The responses of neurons in PMd are consistent with such a transformation (Pesaran et al. 2006), although it remains to be seen whether the PPC contains enough neurons encoding the hand position in eye coordinates to also participate in this computation. In contrast, when visual cues are absent or unreliable, targets may be remapped from eye- to body-centered coordinates and then compared with the body-centered hand location to derive the motor error (Buneo and Soechting 2009). The former scheme may have certain benefits with respect to proprioceptive biases and sensory delays (Tuan et al. 2009). Eye and limb position gain fields, such as those described in PMd and the PPC (Buneo et al. 2002; Chang et al. 2009; Pesaran et al. 2006), would play an important role in both scenarios.
GRANTS
This work was supported by the J. G. Boswell Foundation, the Sloan-Swartz Center for Theoretical Neurobiology, National Eye Institute Grant R01 EY005522, and NIH T32 NS007251-15.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
Author contributions: C.A.B. and R.A.A. conception and design of research; C.A.B. performed experiments; C.A.B. analyzed data; C.A.B. and R.A.A. interpreted results of experiments; C.A.B. prepared figures; C.A.B. and R.A.A. drafted manuscript; C.A.B. and R.A.A. edited and revised manuscript; C.A.B. and R.A.A. approved final version of manuscript.
ACKNOWLEDGMENTS
We thank Kelsie Pejsa, Nicole Sammons, and Viktor Shcherbatyuk for technical assistance, Janet Baer and Janna Wynne for veterinary care, Tessa Yao for administrative assistance, and Bijan Pesaran and Lindsay Bremner for helpful discussions.
REFERENCES
- Andersen RA, Essick GK, Siegel RM. Encoding of spatial location by posterior parietal neurons. Science 25: 456–458, 1985 [DOI] [PubMed] [Google Scholar]
- Angelaki DE, Gu Y, DeAngelis GC. Multisensory integration: psychophysics, neurophysiology, and computation. Curr Opin Neurobiol 19: 452–458, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batista AP, Buneo CA, Snyder LH, Andersen RA. Reach plans in eye-centered coordinates. Science 285: 257–260, 1999 [DOI] [PubMed] [Google Scholar]
- Batista AP, Santhanam G, Yu BM, Ryu SI, Afshar A, Shenoy KV. Reference frames for reach planning in macaque dorsal premotor cortex. J Neurophysiol 98: 966–983, 2007 [DOI] [PubMed] [Google Scholar]
- Beurze SM, de Lange FP, Toni I, Medendorp WP. Integration of target and effector information in the human brain during reach planning. J Neurophysiol 97: 188–199, 2007 [DOI] [PubMed] [Google Scholar]
- Beurze SM, Toni I, Pisella L, Medendorp WP. Reference frames for reach planning in human parietofrontal cortex. J Neurophysiol 104: 1736–1745, 2010 [DOI] [PubMed] [Google Scholar]
- Beurze SM, Van Pelt S, Medendorp WP. Behavioral reference frames for planning human reaching movements. J Neurophysiol 96: 352–362, 2006 [DOI] [PubMed] [Google Scholar]
- Bremner LR, Andersen R. Multiple reference frames for reaching in parietal area 5d. Soc Neurosci Abstr 752/PP11, 2010 [Google Scholar]
- Buneo CA. Analyzing neural responses with vector fields. J Neurosci Methods 197: 109–117, 2011 [DOI] [PubMed] [Google Scholar]
- Buneo CA, Andersen RA. The posterior parietal cortex: sensorimotor interface for the planning and online control of visually guided movements. Neuropsychologia 44: 2594–2606, 2006 [DOI] [PubMed] [Google Scholar]
- Buneo CA, Batista AP, Jarvis MR, Andersen RA. Time-invariant reference frames for parietal reach activity. Exp Brain Res 188: 77–89, 2008 [DOI] [PubMed] [Google Scholar]
- Buneo CA, Jarvis MR, Batista AP, Andersen RA. Direct visuomotor transformations for reaching. Nature 416: 632–636, 2002 [DOI] [PubMed] [Google Scholar]
- Buneo CA, Soechting JF. Motor psychophysics. In: Encyclopedia of Neuroscience, edited by Squire LR. Oxford: Elsevier, 2009, p. 1041–1045 [Google Scholar]
- Caminiti R, Johnson PB, Galli C, Ferraina S, Burnod Y. Making arm movements within different parts of space: the premotor and motor cortical representation of a coordinate system for reaching to visual targets. J Neurosci 11: 1182–1197, 1991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang SW, Papadimitriou C, Snyder LH. Using a compound gain field to compute a reach plan. Neuron 64: 744–755, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang SW, Snyder LH. Idiosyncratic and systematic aspects of spatial representations in the macaque parietal cortex. Proc Natl Acad Sci USA 107: 7951–7956, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cisek P, Kalaska JF. Modest gaze-related discharge modulation in monkey dorsal premotor cortex during a reaching task performed with free fixation. J Neurophysiol 88: 1064–1072, 2002 [DOI] [PubMed] [Google Scholar]
- Cohen YE, Andersen RA. A common reference frame for movement plans in the posterior parietal cortex. Nat Rev Neurosci 3: 553–562, 2002 [DOI] [PubMed] [Google Scholar]
- Cohen YE, Andersen RA. Reaches to sounds encoded in an eye-centered reference frame. Neuron 27: .647–652, 2000 [DOI] [PubMed] [Google Scholar]
- Crawford JD, Medendorp WP, Marotta JJ. Spatial transformations for eye-hand coordination. J Neurophysiol 92: 10–19, 2004 [DOI] [PubMed] [Google Scholar]
- Ferraina S, Brunamonti E, Giusti MA, Costa S, Genovesio A, Caminiti R. Reaching in depth: hand position dominates over binocular eye position in the rostral superior parietal lobule. J Neurosci 29: 11461–11470, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flanders M, Helms-Tillery SI, Soechting JF. Early stages in a sensorimotor transformation. Behav Brain Sci 15: 309–362, 1992 [Google Scholar]
- Georgopoulos AP, Caminiti R, Kalaska JF. Static spatial effects in motor cortex and area 5: quantitative relations in a two-dimensional space. Exp Brain Res 54: 446–454, 1984 [DOI] [PubMed] [Google Scholar]
- Graziano MS, Cooke DF, Taylor CS. Coding the location of the arm by sight. Science 290: 1782–1786, 2000 [DOI] [PubMed] [Google Scholar]
- Graziano MS, Cooke DF, Taylor CS, Moore T. Distribution of hand location in monkeys during spontaneous behavior. Exp Brain Res 155: 30–36, 2004 [DOI] [PubMed] [Google Scholar]
- Hanson B, Klink K, Matsuura K, Robeson SM, Willmott CJ. Vector correlation: review, exposition, and geographic application. Ann Assoc Am Geogr 82: 103–116, 1992 [Google Scholar]
- Henriques DY, Klier EM, Smith MA, Lowy D, Crawford JD. Gaze-centered remapping of remembered visual space in an open-loop pointing task. J Neurosci 18: 1583–1594, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson PB, Ferraina S, Bianchi L, Caminiti R. Cortical networks for visual reaching: physiological and anatomical organization of frontal and parietal lobe arm regions. Cereb Cortex 6: 102–119, 1996 [DOI] [PubMed] [Google Scholar]
- Khan AZ, Crawford JD, Blohm G, Urquizar C, Rossetti Y, Pisella L. Influence of initial hand and target position on reach errors in optic ataxic and normal subjects. J Vis 7: 8.1–8.16, 2007 [DOI] [PubMed] [Google Scholar]
- Kording KP, Wolpert DM. Bayesian integration in sensorimotor learning. Nature 427: 244–247, 2004 [DOI] [PubMed] [Google Scholar]
- Lacquaniti F, Guigon E, Bianchi L, Ferraina S, Caminiti R. Representing spatial information for limb movement: role of area 5 in the monkey. Cereb Cortex 5: 391–409, 1995 [DOI] [PubMed] [Google Scholar]
- McGuire LM, Sabes PN. Heterogeneous representations in the superior parietal lobule are common across reaches to visual and proprioceptive targets. J Neurosci 31: 6661–6673, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGuire LM, Sabes PN. Sensory transformations and the use of multiple reference frames for reach planning. Nat Neurosci 12: 1056–1061, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntyre J, Stratta F, Lacquaniti F. Short-term memory for reaching to visual targets: psychophysical evidence for body-centered reference frames. J Neurosci 18: 8423–8435, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pena JL, Konishi M. Auditory spatial receptive fields created by multiplication. Science 292: 249–252, 2001 [DOI] [PubMed] [Google Scholar]
- Pesaran B, Nelson MJ, Andersen RA. Dorsal premotor neurons encode the relative position of the hand, eye, and goal during reach planning. Neuron 51: 125–134, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pesaran B, Nelson MJ, Andersen RA. A relative position code for saccades in dorsal premotor cortex. J Neurosci 30: 6527–6537, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ploner CJ, Gaymard B, Rivaud S, Agid Y, Pierrot-Deseilligny C. Temporal limits of spatial working memory in humans. Eur J Neurosci 10: 794–797, 1998 [DOI] [PubMed] [Google Scholar]
- Rolheiser TM, Binsted G, Brownell KJ. Visuomotor representation decay: influence on motor systems. Exp Brain Res 173: 698–707, 2006 [DOI] [PubMed] [Google Scholar]
- Scheidt RA, Conditt MA, Secco EL, Mussa-Ivaldi FA. Interaction of visual and proprioceptive feedback during adaptation of human reaching movements. J Neurophysiol 93: 3200–3213, 2005 [DOI] [PubMed] [Google Scholar]
- Scott SH, Sergio LE, Kalaska JF. Reaching movements with similar hand paths but different arm orientations. II. Activity of individual cells in dorsal premotor cortex and parietal area 5. J Neurophysiol 78: 2413–2426, 1997 [DOI] [PubMed] [Google Scholar]
- Sober SJ, Sabes PN. Flexible strategies for sensory integration during motor planning. Nat Neurosci 8: 490–497, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sober SJ, Sabes PN. Multisensory integration during motor planning. J Neurosci 23: 6982–6992, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stricanne B, Andersen RA, Mazzoni P. Eye-centered, head-centered, and intermediate coding of remembered sound locations in area LIP. J Neurophysiol 76: 2071–2076, 1996 [DOI] [PubMed] [Google Scholar]
- Tuan MT, Soueres P, Taix M, Girard B. Eye-centered vs body-centered reaching control: a robotics insight into the neuroscience debate. In: IEEE International Conference on Robotics and Biomimetics (ROBIO2009), Guilin, China, 2009 [Google Scholar]
- Vesia M, Yan XG, Henriques DY, Sergio LE, Crawford JD. Transcranial magnetic stimulation over human dorsal-lateral posterior parietal cortex disrupts integration of hand position signals into the reach plan. J Neurophysiol 100: 2005–2014, 2008 [DOI] [PubMed] [Google Scholar]
- Vetter P, Wolpert DM. Context estimation for sensorimotor control. J Neurophysiol 84: 1026–1034, 2000 [DOI] [PubMed] [Google Scholar]
- Wolpert DM, Ghahramani Z, Jordan MI. An internal model for sensorimotor integration. Science 269: 1880–1882, 1995 [DOI] [PubMed] [Google Scholar]