Putting ion channels to work: Mechanoelectrical transduction, adaptation, and amplification by hair cells

Abstract

As in other excitable cells, the ion channels of sensory receptors produce electrical signals that constitute the cellular response to stimulation. In photoreceptors, olfactory neurons, and some gustatory receptors, these channels essentially report the results of antecedent events in a cascade of chemical reactions. The mechanoelectrical transduction channels of hair cells, by contrast, are coupled directly to the stimulus. As a consequence, the mechanical properties of these channels shape our hearing process from the outset of transduction. Channel gating introduces nonlinearities prominent enough to be measured and even heard. Channels provide a feedback signal that controls the transducer's adaptation to large stimuli. Finally, transduction channels participate in an amplificatory process that sensitizes and sharpens hearing.

It takes work to open an ion channel. A voltage-sensitive cation channel associated with the action potential, for example, opens after the performance of a certain amount of electrical work in the form of gating-charge movement through the transmembrane electrical field. The gating of a ligand-activated channel, such as the receptor for a neurotransmitter, is mediated by the chemical work done on ligand binding. Finally, a mechanically activated channel, such as the transduction channel of a hair cell, opens or closes in response to mechanical work done by sound or acceleration.

Statistical thermodynamics describes the requirement for work in channel gating. If the internal-energy content of a two-state channel is E_O in the open state and E_C in the closed state, the equilibrium probabilities of these two configurations, respectively p_O and p_C, are related by the Boltzmann equation

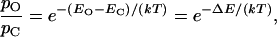1

in which k is the Boltzmann constant and T the temperature. ΔE is the channel's change in energy on opening—the work done in gating the channel. This equation may be rearranged to yield the channel's open probability at equilibrium,

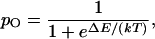2

which explicitly relates channel gating to the associated energy difference.

Gating of Mechanically Sensitive Channels

In hair cells of the inner ear and lateral-line system, mechanical stimulation supplies the work necessary to open transduction channels. When sound sets the cochlea's basilar membrane into resonant motion, the tectorial membrane communicates force to the mechanoreceptive hair bundles. In a semicircular canal or lateral-line organ, angular acceleration or water flow displaces a cupula that transmits force to the bundles. Finally, in the otolithic organs, the utriculus and sacculus, linear acceleration acts on otolithic membranes that convey force to the bundles.

In response to external force, a hair bundle pivots at its base. This deflection in turn affects the tension in elastic elements, termed gating springs (1), that affect the open probability of the mechanoelectrical transduction channels (reviewed in refs. 2–4). Each gating spring is probably a tip link, a filament interconnecting adjacent stereocilia (5, 6), or the cytoskeleton associated with its insertions (3). The channel's open probability is

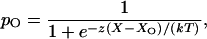3

in which X represents the hair bundle's displacement from its resting position, and X₀ is the displacement at which the open probability is one-half. z is the single-channel gating force, a measure of mechanical sensitivity. If the gating spring is Hookean, z = γκd, in which κ is the spring's stiffness and d is the distance by which the spring shortens when the channel opens. The term γ denotes the geometric projection factor relating gating-spring extension to hair-bundle displacement; moving the bundle's top by a distance X extends the tip link by an amount γX (7).

A hair bundle's mechanical properties may be understood from analysis of the balance of forces within the bundle. In a resting hair bundle (Fig. 1A), contiguous stereocilia are pulled toward one another by the intervening tip link, which therefore bears tension at rest (6, 8). The actin-filled rootlet of each stereocilium, however, acts as a flexional spring that resists stereociliary deflection (9, 10). At equilibrium, the hair bundle is strained internally like a strung bow: the tension in the tip link produces a torque on the stereocilium equal and opposite that exerted by the stereociliary pivots. If the N transduction channels are arranged in parallel and if we disregard a relatively minor term reflecting channel opening at rest,

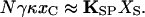4

Here x_C is the extension of the gating spring with the channel closed, K_SP the combined stiffness of the stereociliary pivots, and X_S the distance that the bundle moves when the tip links are disconnected (6, 7, 11).

Figure 1.

Mechanical behaviors of a hair bundle. Although a bundle may contain from ≈20 to >300 stereocilia, it is represented here by only two. The sizes of various constituents are distorted for the sake of clarity; in reality, a stereocilium (black) is <1 μm to ≈100 μm in length, a tip link (pink) is ≈150 nm long, a channel (yellow) is <10 nm in diameter, and its gate (orange) moves by ≈4 nm. The actual movements of a hair bundle are far smaller than illustrated: a robust stimulus (60 dB sound-pressure level) deflects the bundle only ±10 nm, half the thickness of the stereociliary outline depicted here, whereas a threshold stimulus moves the bundle less than one-tenth that far. (A) Resting strain. The stereocilia extend initially straight from the apical surface of a hair cell. When a tip link joins contiguous processes, however, it draws the stereociliary tips together and cocks the bundle in the negative direction to its resting position. The tension in the tip link then balances the strain in the actin-filled pivots at the stereociliary bases. (B) Gating compliance. Application to a hair bundle of a positively directed force (green arrow) extends the tip link. When a channel opens (curved orange arrow), the associated tip link shortens, and the tension in the link falls. Relaxation of the tip link acts like an external force in the positive direction, causing the bundle to move still further (red arrow). (C) Adaptation. A positive stimulus force (green arrow) initially deflects the hair bundle, opening a transduction channel. A Ca²⁺ ion (red) that enters through the channel interacts with a molecular motor, probably myosin Iβ, and causes it to slip down the stereocilium's actin cytoskeleton (orange arrow). Slackening of the tip link fosters a slow movement of the bundle in the positive direction (dashed red arrow). The reduced tension in the tip link then permits the channel to reclose. (D) Amplification. When a hair bundle is deflected by the positive phase of a sinusoidal stimulus (upper green arrows), channel opening facilitates bundle movement (upper red arrow). A Ca²⁺ ion (red) that enters through the transduction channel binds to a cytoplasmic site on or associated with the channel, promoting its reclosure. As the channel shuts, the increased tension in the tip link exerts a force that moves the bundle in the negative direction (lower red arrow), enhancing the effect of the negatively directed phase of a stimulation (lower green arrows). When the ion is extruded by a membrane Ca²⁺ pump, or Ca²⁺-ATPase (orange arrow), the hair bundle is primed to repeat the cycle.

It is possible to estimate the values of the foregoing parameters experimentally. For a large hair bundle from the bullfrog's sacculus, electron-microscopic examination indicates that γ ≈ 0.14 (7, 12). Both ultrastructural (6, 12) and mechanical measurements (7) indicate that N ≈ 50. When Ca²⁺ chelators sever tip links, a hair bundle moves in the positive direction to the equilibrium position of the stereociliary pivots; for cells originally in a medium containing 4 mM Ca²⁺, X_S ≈ 130 nm (6). Stiffness measurements in the absence of tip links or orthogonal to them indicate that K_SP ≈ 200 μN⋅m⁻¹ (13, 14); determinations of the hair bundle's total stiffness then imply that κ ≈ 700 μN⋅m⁻¹ (14). Analysis of bundle properties during channel gating indicate that d ≈ 4 nm (7, 15; but see ref. 16). Finally, calculations from the foregoing results suggest that z ≈ 0.6 pN and x_C ≈ 7 nm for hair bundles exposed to 4 mM Ca²⁺.

When a hair bundle is deflected by mechanical stimulation, the shearing motion between contiguous stereocilia produces a force that in each tip link affects the gating of the attached channel (Fig. 1B). The external force, F_HB, required to hold the hair bundle at a particular position is given by (3, 11)

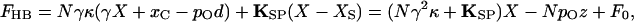5

in which F₀ is an offset term such that F_HB is zero at the bundle's resting position. This relation includes a critically important negative term that associates a decrease in the applied force with an increase in the channel open probability p_O. When a transduction channel opens, the associated tip link relaxes by the distance d (Fig. 1B). The force exerted by the link, which pulls the hair bundle in the negative direction at rest, therefore declines on opening by κd—equivalent to exerting a positive force on the bundle. Measured at the bundle's top, the ensemble of channels can produce a force as great as Nγκd. The system thus displays positive feedback: a stimulus that moves a hair bundle in the positive direction opens transduction channels, whose opening in turn promotes additional positive movement. As we shall see below, nature has evidently exploited this characteristic to do useful work.

The hair bundle's stiffness may be calculated from the foregoing expression to be

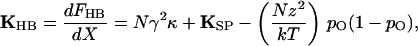6

in which the open probability depends on bundle displacement as described by Eq. 3 (7, 11). The stiffness (Fig. 2A) is nearly constant for displacements well in the negative direction, for which p_O ≈ 0, or positive direction, for which p_O ≈ 1. Each increment in the force exerted on the hair bundle, ΔF_HB, accordingly produces an approximately constant change in bundle position, ΔX:

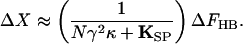7

Over the range of displacements in which the channels gate, though, the stiffness declines. At the position where half the channels are open, X₀, the stiffness reaches its minimal value, and the bundle's sensitivity to stimulus force peaks:

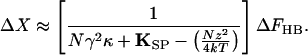8

This effect, known as gating compliance, has been observed experimentally in hair cells of the frog's sacculus (7) and probably in those of the teleost lateral-line organ (17), mammalian cochlea (18), and mammalian vestibule (19). The hair bundle's mechanical nonlinearity can account for distortion products (20), the illusory tones heard when sinusoidal stimuli of two or more frequencies are presented concurrently. These distortions seem to be an ineluctable price paid for the advantages—speed and sensitivity—associated with the direct transduction of mechanical stimuli.

Figure 2.

Gating of ion channels. (A) Gating of a mechanically sensitive ion channel. The large plot relates hair-bundle displacement (X) to the external force applied to the bundle (F_HB). As a result of gating compliance, channel gating is highly sensitive over a narrow range of forces. The green lines portray the linear relations expected if the channels were to remain closed (top line), open (bottom line), or both in equal numbers (middle line). The curve was obtained by numerically solving a transcendental equation, the inverse of Eq. 5; the parameter values were n = 35, γ = 0.14, κ = 1200 μN⋅m⁻¹, d = 4 nm, z = 0.67 pN, and K_SP = 200 μN⋅m⁻¹. The plot at the left represents the Boltzmann relation between displacement and the channel's open probability (Eq. 3); the displacement axis is identical to that in the principal graph. The graph at the bottom displays the dependence of the channel's open probability on hair-bundle force; the force axis accords with that in the main plot. Note the steepness of this relation, in comparison both to that of a Boltzmann curve and especially to that of the corresponding plot for an electrically activated channel in B. (B) Gating of an electrically sensitive ion channel. The large graph relates membrane potential (V_M) to the charge applied to the membrane (Q_M). As a consequence of gating capacitance, the membrane potential is less responsive to charge over the range of potentials in which channels open and close. The green lines portray the linear relations expected if the channels were to remain closed (left line), open (right line), or both in equal numbers (center line). The curve was obtained by numerically solving a transcendental equation, the inverse of Eq. 12; the numerical values were those provided in the text, with Q₀ = −30 fC. The plot at the left represents the Boltzmann relation between membrane potential and the channel's open probability (Eq. 11); the voltage axis is identical to that in the principal graph. The graph at the bottom displays the dependence of the channel's open probability on the charge applied to the membrane; the charge axis accords with that in the main plot. To facilitate comparison, the four open-probability plots in A and B were scaled such that each extends from p_O = 0.01 to p_O = 0.99.

Note that gating compliance could actually render the hair bundle's stiffness negative over a certain range of displacements (4, 15) if

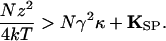9

Because the final term is substantially smaller than the penultimate one, the definition of z allows this relation to be restated as

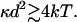10

If the stiffness were locally negative, the unrestrained hair bundle would be bistable (4), residing at either of two stable points flanking the negative-slope region. Under these circumstances, the bundle could nevertheless transduce small stimuli if thermal noise were sufficient to surmount the energy barrier separating the two states, a phenomenon termed stochastic resonance (21). Moreover, if supplemented with an energy source to bias its operation into the unstable region, such a hair bundle would potentially be capable of producing active oscillations.

Comparison of Electrically and Mechanically Sensitive Channels

It is interesting to contrast the behavior of a mechanically stimulated ion channel with that of a channel responsive to electrical stimuli. Consider, for example, a member of the well-studied superfamily of voltage-activated Na⁺, Ca²⁺, and K⁺ channels. When the charge on the interior surface of the cell's membrane becomes more positive, such a channel opens as one or more gating moieties undergo a rearrangement equivalent to the movement of ζ charges through a transmembrane potential V_M. The open probability in this instance is

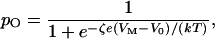11

in which e is the elementary charge and V₀ is the potential at which the open probability is one-half (reviewed in ref. 22).

As a voltage-activated channel progresses from one configuration to another, say from the closed to the open state, it exchanges a certain amount of energy with the environment in the form of charge displacement across the membrane. For any membrane potential, the total membrane charge, Q_M, comprises that deposited on the lipid bilayer, Q_B, and the gating charge, Q_G, associated with the opening and closing of an ensemble of N channels:

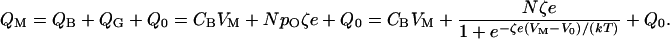12

Here C_B represents the capacitance caused by the lipid bilayer, whose value per unit area is typically ≈10 mF⋅m⁻². Q₀ is an offset term such that Q_M is zero when the membrane is electrically unpolarized. It follows that the system's capacitance, C_M, is not constant (23), for

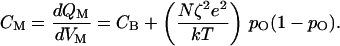13

The final term represents gating capacitance, the increase in the membrane's capacitance because of the movement of gating moieties, whose magnitude depends on the open probability and hence on the membrane potential.

The impact of the gating charge on neural signaling may be appreciated by examining the relation between the charge applied to the membrane and the ensuing membrane potential (Fig. 2B). For extreme hyperpolarization, during which p_O ≈ 0, or depolarization, during which p_O ≈ 1, each increment of charge, ΔQ_M, produces an essentially constant voltage change, ΔV_M:

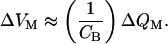14

Over the range of potentials at which the channels gate, however, the membrane capacitance increases. The voltage therefore changes less per unit of charge deposited on the membrane. At the potential V₀, the midpoint of the gating range, the responsiveness reaches its minimal value,

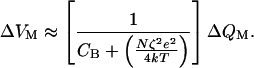15

The capacitive load imposed by gating can be substantial. Consider an isopotential, spherical neuron 10 μm in diameter. Suppose that this cell is endowed at the modest density of ≈40 μm⁻² with identical voltage-sensitive channels, each with an effective gating charge of 12e (24). The maximal capacitance contributed by channel gating then equals that caused by the membrane bilayer! After an excitable cell has reached threshold for firing of an action potential, the capacitive cost imposed by channel gating is repaid by the far larger current supplied through ion channels.

Gating capacitance also has considerable impact on the speed of neural signaling. An organism is likely to enjoy a selective advantage if its nervous system operates with particular rapidity. Speed is important in neural computation, which consists of integrating synaptic inputs until the threshold is reached for initiating an action potential. In addition, the propagation velocity of the action potential determines how quickly information may be moved between cells in the nervous system. When ionic current flows through activated synaptic receptors, gating capacitance slows synaptic potentials and thus the approach to threshold. Moreover, after an action potential has been initiated in an axon, gating charge diminishes the rate at which longitudinal current can depolarize successive increments of the axonal membrane. This effect on propagation is great enough that an excessive density of channels in the membrane of an unmyelinated fiber would actually retard the signal (23, 25).

The energetic cost of gating is shared by electrically and mechanically activated channels (Fig. 2). The symmetry in the descriptions of the two gating mechanisms is broken, however, by the nature of the relevant independent parameters, charge and force, and the dependent parameters, voltage and displacement. This distinction introduces a critical difference in the signs of the final terms in the denominators of Eqs. 8 and 15. The gating of voltage-activated channels increases membrane capacitance and therefore constitutes negative feedback that acts to retard change in the membrane potential. The gating of force-activated channels, by contrast, decreases hair-bundle stiffness and thus provides positive feedback that promotes bundle motion. The distinct behaviors of the two types of channel are apparent from the dependence of channel open probability on the respective inputs, electrical charge and mechanical force (Fig. 2). By broadening the relation between charge and open probability, gating capacitance desensitizes electrically activated cells. Gating compliance, on the other hand, narrows the relation between force and open probability and thereby enhances sensitivity in mechanically responsive cells.

Gating compliance is an intrinsic property of direct mechanoelectrical transduction that natural selection may well have heightened to increase the ear's sensitivity. A hair bundle's responsiveness to force improves as the denominator of Eq. 8 approaches zero. Sensitivity could be enhanced by increasing the single-channel gating force, z, either by augmenting κ, the stiffness of the gating spring, or by increasing d, the distance by which the spring shortens on channel opening. From the evolutionary perspective, the former change might be effected by mutations that produce a gating-spring protein that is more rigid in extension. If d represents the “swing” of the channel's gate, the moiety that obstructs the ion-conducting pore, its magnitude would be constrained by the size of the channel molecule. If the gate were to evolve a lever-like extension, however, the value of d might increase without disrupting channel structure (3).

Adaptation

The hair cell's great sensitivity poses a problem: how might the mechanoreceptor's response be prevented from saturating in the presence of large static stimuli? In other words, if mechanoelectrical transduction is direct, without the intervention of a second messenger between the detection of force and the opening of channels, how can the transducer's sensitivity be adjusted? The answer to these questions involves a novel form of sensory adaptation (reviewed in refs. 26–29).

When a hair bundle from the frog's sacculus is deflected in the positive direction, an initial surge of inward transduction current rapidly depolarizes the hair cell. Within milliseconds, however, the response declines, following an approximately exponential time course to a plateau (30–32). Negative stimulation elicits similar adaptation; an immediate decrease in the transduction current and the associated hyperpolarization are followed by a gradual return toward the resting state. The association of adaptation with mechanical relaxation of the hair bundle (7, 8, 13, 33) initially hinted that the process is mediated by a physical readjustment of tension in the gating springs. It was accordingly hypothesized that the position of each tip link's upper insertion is adjusted during adaptation (13, 33): the link's insertion slides downward in response to positive stimulation (Fig. 1C) and climbs upward after negative stimuli. In view of the actin cytoskeleton of stereocilia, a protein of the myosin family was proposed as the motor to drive adaptation.

Several lines of evidence now buttress this model for adaptation. Along with at least three other myosin isoforms, hair bundles contain myosin Iβ (34, 35), which is concentrated near the ends of each tip link (36, 37). The number of myosin molecules present in a stereocilium (34) could easily account for the forces produced by the adaptation motor (8). Whole-cell dialysis of hair cells indicates that the adaptation motor is inhibited by ATP depletion (38) and by phosphate analogs (39), both characteristics of myosin. Adaptation is regulated by Ca²⁺ (31, 32), which readily traverses the transduction channel (40, 41), accumulates in the stereociliary cytoplasm (42) and is extruded by Ca²⁺ pumps (43). The Ca²⁺ sensor for adaptation appears to be calmodulin (44), which occurs at a high concentration near stereociliary tips (45, 46) and can occupy the light-chain binding sites on myosin Iβ (47, 48). Finally, the biochemical properties of myosins I (reviewed in ref. 49) accord with the activity of the adaptation motor. During steady-state ATP turnover, these mechanoenzymes characteristically detach from actin more rapidly in the presence of Ca²⁺ (50), which might in the present context explain the downward slippage of the adaptation motor when a channel is open.

The effects of adaptation on channel open probability and on the hair bundle's mechanical properties can be accommodated readily by the gating-spring model (32, 51; reviewed in ref. 3). When a tip link's upper insertion moves down the stereocilium by a distance x_A, the open probability of the associated channel falls to

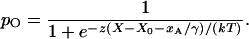16

In other words, adaptation offsets the setpoint of transduction by an amount x_A/γ, as measured atop the bundle. The force necessary to hold the bundle at displacement X correspondingly declines to

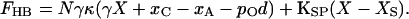17

Adaptation does not proceed to completion, though; for stimuli of small to moderate size, mechanosensitivity generally migrates ≈80% of the magnitude of an imposed bundle offset (30, 31, 51).

Adaptation serves at least four ends. Every hair cell may need the process to avoid saturation of its responsiveness by large stimuli. Next, despite irregularities in hair-bundle growth and in the operation of the conductive apparatus that delivers stimuli to a hair cell, adaptation situates a bundle in a sensitive region of its operating range. Because cells with especially rapid adaptation are insensitive to low-frequency stimuli, adaptation participates in high-pass filtering during the processing of sensory inputs (52). As a consequence of dissimilar rates of adaptation, cells in a single receptor organ may differ in their frequency responsiveness (37, 53). Finally, as discussed below, adaptation poises the transduction machinery so that the hair bundle is most capable of doing active mechanical work (54).

In keeping with the numerous roles of adaptation, the process is common to hair bundles in many vertebrates. As detailed above, adaptation is prominent in hair cells of the amphibian sacculus. Adaptation also occurs in the amphibian utriculus, where cells of disparate bundle morphology display strikingly different rates (53). The corresponding process in reptiles, termed slow adaptation (55, 56), resembles adaptation in the frog but is not thought to be mediated by a mechanical readjustment of the hair bundle (57). In mammals, adaptation has been documented electrophysiologically in hair cells of the murine cochlea and utriculus (28, 58, 59). In addition, the mechanical relaxation of the hair bundle associated with adaptation occurs in both organs (19, 60).

Amplification

Most of the foregoing discussion treats the hair bundle as a passive structure that is deflected by stimuli. As is apparent from the mechanical correlates of adaptation, however, a hair cell is also capable of actively producing forces. This means that a hair bundle can do work against an external load with energy provided by the hair cell itself. This capacity raises two important questions: what purpose is served by active hair-bundle work, and what cellular motor accomplishes it?

Active hair-bundle movement may underlie the phenomenon of cochlear amplification (reviewed in refs. 61–63). Despite the damping effects of fluid in the inner ear, the cochlea acts as a resonator with a high quality factor; this behavior implies the presence in the ear of an active process that counters viscous dissipation (64). A large body of research (reviewed in ref. 63) indicates that a mechanical amplifier confers on the inner ear four linked properties: enhanced mechanical sensitivity, sharpened frequency selectivity, metabolic vulnerability, and the ability to produce spontaneous otoacoustic emissions. These features are clearly present in cochleas, the hearing organs of reptiles, birds, and mammals. Moreover, the primitive auditory receptor organs of amphibians display similar characteristics; those of fishes have not been tested. The phenomenon of electromotility or voltage-driven change in the length of an outer hair cell is believed to constitute the active process in the mammalian cochlea (reviewed in refs. 65, 66, but see ref. 67). Because electromotility seems not to occur in nonmammalian tetrapods, however, there must be an additional active process in these animals. The resemblance of mammalian audition to that in other vertebrates (reviewed in ref. 63) may alternatively imply the existence of a ubiquitous active process, present in all tetrapods and perhaps supplemented by electromotility to permit the higher-frequency hearing of mammals.

In addition to the slower motions associated with adaptation (32, 68), hair bundles can evince several types of active mechanical behavior. Some bundles display spontaneous oscillations (9, 13) that are severalfold as great as expected for the thermal vibration of passive bundles of the stiffness measured (69). The narrow frequency spectra of these movements (68) suggest that they reflect the operation of a tuned mechanical oscillator. Active motions of a second type are evoked by abruptly deflecting a hair bundle with a flexible fiber. In hair cells of the turtle's cochlea, this stimulus elicits damped mechanical oscillations (9). When maintained in saline solution containing 4 mM Ca²⁺, stimulated hair cells from the frog's sacculus produce abrupt twitches (13, 54). If the Ca²⁺ concentration is reduced to the level normally found in endolymph, however, the response becomes slower and more resonant (54, 70). Damped oscillatory responses also occur in the short hair cells of the avian cochlea (Fig. 3), which are specialized for mechanical amplification (reviewed in refs. 62, 63, 71). Rapid, active hair-bundle movements have not been reported from the inner ears of fishes or mammals.

Figure 3.

Mechanically evoked response of a hair bundle from the chicken's cochlea. A damped sinusoidal oscillation of the hair bundle (Upper) ensues from stimulation of a short hair cell situated roughly one-quarter of the distance along the cochlea from its apex. This active mechanical response resembles those recorded earlier from hair cells of the turtle's cochlea and the frog's sacculus, but is severalfold as large and occurs at a higher frequency of ≈235 Hz. An epithelial preparation of the basilar papilla was maintained at room temperature in an oxygenated archosaur saline solution including 1 mM Ca²⁺. The tip of a flexible glass fiber, with a stiffness of 680 μN⋅m⁻¹ and a response time constant of 30 μs, was attached to the bundle's top; stimulation was accomplished by abruptly displacing the fiber's base by 400 nm for 120 ms (Lower). The response represents the output of a dual photodiode onto which an image of the fiber's tip was projected. (×1,000.)

Perhaps the most interesting responses occur in anuran hair cells kept in a two-compartment experimental chamber, so that their apical surfaces may be bathed in artificial endolymph while their basolateral membranes are exposed to a perilymph-like medium. Under these conditions, which resemble those found in the intact ear, many bundles display spontaneous oscillatory motions at frequencies of 5–40 Hz and with amplitudes up to 40 nm or occasionally even more (72). When a sinusoidal force is exerted on such a bundle by a flexible fiber, the stimulus can entrain the bundle's motion. Entrainment is most effective at the frequency of spontaneous oscillation; for progressively lower or higher frequencies, stimuli of increasing magnitude are necessary.

Power gain, an increase in the energy content of an output signal with respect to the otherwise similar input signal, provides a benchmark for amplification. Analysis of the work done by hair bundles from the frog's ear confirms that these organelles accomplish active mechanical amplification (72). In a healthy cell, application of a sinusoidal stimulus force only a few piconewtons in amplitude can entrain the bundle's motion. During each cycle of motion, viscous drag on the bundle and the attached stimulus fiber irrecoverably dissipates an amount of energy that can be calculated from the speed of bundle motion and the system's drag coefficient. Remarkably, the average viscous dissipation often exceeds the energy supplied by the stimulus fiber. The balance of energy must come from the hair bundle, which therefore does mechanical work in such a way that it amplifies the weak stimulus.

The second important question about hair bundle-based mechanical amplification is the identity of the motor that mediates the process. Two candidates have been considered. First, the myosin-based adaptation motor might also power the active process (reviewed in ref. 26). Especially if the myosin heads do not detach from actin filaments but rock in place like those of insect flight muscle, the adaptation motor might produce bundle oscillations at frequencies into the kilohertz range. Even faster movements could arise through the interplay of the collective activity of a motor ensemble with the hair bundle's passive mechanical properties (73). The principal difficulty with this mechanism is its seeming variance with correlated mechanical and electrophysiological observations on the bullfrog's saccular hair cell (14, 54). In this preparation, positive stimulation with a flexible fiber causes hair-bundle motion in the same direction that is interrupted by a transient movement, or twitch, in the opposite direction. The initial component of motion is accompanied by inward transduction current and cellular depolarization; the twitch is associated with abrupt channel reclosure and repolarization toward the resting potential. If the adaptation motor is in series with the gating spring (reviewed in refs. 26–29), the motor must step up the stereocilium to produce a negatively directed twitch. Because such a motion increases tension in the tip link, however, it would be expected to open rather than to close transduction channels. Despite this objection, a modest relaxation of tension in the gating spring, caused for example by the adaptation motor's slippage down the stereocilium, may suffice to trigger a larger and oppositely directed movement associated with channel reclosure.

The hair-bundle twitch and related active motions may be explained by an alternative mechanism of force production in the hair bundle, fast channel reclosure owing to Ca²⁺ binding. For hair cells of the frog and turtle, the transduction channel's open probability declines with increasing Ca²⁺ concentration in the solution bathing the hair bundle (31, 52, 55). Moreover, the hair-bundle twitch accelerates as the Ca²⁺ level climbs (54, 70). These observations led to the suggestion (7, 70) that Ca²⁺ entering through an open transduction channel can combine with a site on or associated with the channel, causing it to reclose (Fig. 1D). Closure then increases the tension in the tip link, jerking the hair bundle in the negative direction. Developed to describe responses in the frog's sacculus, this model also explains channel reclosure—termed fast adaptation—in the turtle's cochlea (56, 57). In light of the similarities between the two preparations, it seems probable that measurement of the mechanical signals associated with fast channel reclosure in the turtle would yield results similar to those analyzed in the frog.

Ca²⁺-mediated channel reclosure could power active hair-bundle motions, including both spontaneous oscillations and those entrained by a stimulus force (reviewed in ref. 61). In this model (Fig. 1D), the positive phase of a sinusoidal stimulus force initiates the opening of transduction channels. The gating compliance associated with channel opening provides a positively directed force that augments the movement. As Ca²⁺ flows into the stereociliary cytoplasm, however, it promotes channel reclosure, tightens tip links, and thus causes a negatively directed force on the hair bundle. If this response occurs with an appropriate latency, it accentuates the effect of the negative phase of stimulation.

Implemented as a computational model, the foregoing scheme can account for several properties of the cochlear amplifier (74). The proposed mechanism provides an amplification of about 100-fold by comparison with the hair bundle's passive responsiveness. The amplification is strongly level dependent: threshold stimuliation evokes the greatest gain, then sensitivity falls as the stimulus grows. Finally, the amplification is sharply frequency selective. These three properties accord with the known characteristics of the cochlear amplifier (reviewed in refs. 65, 75). The model can additionally be made to produce spontaneous oscillations, which might underlie the spontaneous otoacoustic emissions that are widely associated with the inner ear's active process (reviewed in refs. 63, 76). This ability to function as a sharply tuned high-gain amplifier or as a spontaneous oscillator is intrinsic to a broad class of models, such as the present one, that display a Hopf bifurcation (73, 77).

Conclusion

The work required to open and close ion channels is an inevitable price of signaling by excitable cells. Uniquely among known sensory receptors, hair cells exploit the nonlinearity inherent in channel gating to sharpen their responsiveness to stimulation. By coupling channel gating to a power source, some hair cells have additionally developed an amplifier that augments the ear's mechanical sensitivity and frequency selectivity.