Abstract
Neurofilaments are long flexible cytoplasmic protein polymers that are transported rapidly but intermittently along the axonal processes of nerve cells. Current methods for studying this movement involve manual tracking of fluorescently tagged neurofilament polymers in videos acquired by time-lapse fluorescence microscopy. Here, we describe an automated tracking method that uses particle filtering to implement a recursive Bayesian estimation of the filament location in successive frames of video sequences. To increase the efficiency of this approach, we take advantage of the fact that neurofilament movement is confined within the boundaries of the axon. We use piecewise cubic spline interpolation to model the path of the axon and then we use this model to limit both the orientation and location of the neurofilament in the particle tracking algorithm. Based on these two spatial constraints, we develop a prior dynamic state model that generates significantly fewer particles than generic particle filtering, and we select an adequate observation model to produce a robust tracking method. We demonstrate the efficacy and efficiency of our method by performing tracking experiments on real time-lapse image sequences of neurofilament movement, and we show that the method performs well compared to manual tracking by an experienced user. This spatially constrained particle filtering approach should also be applicable to the movement of other axonally transported cargoes.
Index Terms: Axonal transport, Bayesian estimation, fluorescence microscopy, neurofilament, object tracking, particle filtering, spatial constraint
I. Introduction
The function of biological cells is critically dependent on the active and directed movement of intracellular cargoes [1]. These cargoes are very diverse, including cytosolic protein complexes, cytoskeletal polymers, ribonucleoprotein particles, and membranous organelles. One of the most powerful tools for studying the movement of these structures is fluorescence microscopy because it permits the moving structures to be observed directly in living cells [2]. To extract kinetic data from the resulting image sequences it is necessary to track large and time-varying numbers of moving objects in real-time or time-lapse movies, either in an online or offline manner.
One important example of intracellular movement is axonal transport, which is the movement of subcellular organelles and macromolecular structures along the axonal processes of nerve cells [3], [4]. An interesting feature of axons is that they are very slender cylindrical processes, just micrometers in diameter but often millimeters, centimeters, or even meters in length. Thus, axons reduce what is usually a complex three-dimensional intracellular traffic pattern to essentially a one-dimensional one, in which the cargoes move largerly forwards or backwards along the long axis of the axonal cylinder.
Among the many cargoes of axonal transport are neurofilaments, which are long flexible protein polymers measuring about 10 nm in diameter and many micrometers in length [5]. These polymers, which are major components of the axonal cytoskeleton, align parallel to the long axis of the axon andmove in an intermittent and bidirectional manner that is characterized by short bouts of forwards or backwards movement interrupted by pauses of varying duration [6], [7]. The filaments move rapidly, at average rates of about 0.5 µm/s, but their overall rate of movement is much slower because they spend most of their time pausing [7], [8], [10]. The duration of the bouts of movement and the frequency of the transitions between the moving and pausing states are highly variable and can be modeled as a stochastic process [8], [9]. To analyze the transport kinetics it is necessary to track neurofilaments in successive frames of time-lapse movies, which is a process known as video object tracking. To date, this process has been done manually, which is labor-intensive and subject to human error [11]. Thus, it is desirable to develop a fully automated tracking method to improve tracking efficiency and to eliminate the subjectivity and potential variability associated with human operation.
During the past two decades, a large number of video object tracking algorithms have been developed for diverse image-based applications including human face tracking, human gesture tracking, motion tracking, visual servoing, surveillance, biological and medical applications, etc. Generally, these algorithms can be classified into two major categories: target representation and localization, and filtering and data association. A common example of the target representation and localization approach is the mean-shift tracking algorithm [12]–[15]. The idea is to iteratively compute the mean-shift vector on the locally estimated density until converging to local maxima. Since the convergence needs only a few iterations, it is a fast and effective tracking method and has been used successfully in real-time applications such as surveillance video tracking, and video segmentation [16]. Common examples of the filtering and data association approach are methods that use the Kalman filter, extended Kalman filter, unscented Kalman filter [17], and particle filter [18], [19]. All filtering and data association algorithms generally include two steps: prediction and updating. The prediction step uses a dynamic state model to predict the possible states (e.g., position, orientation, and velocity) in each frame based on the state in the preceding frame. Then the updating step uses the latest observation to estimate the actual state from among these possible states according to Bayesian theorem. When the dynamic state model is linear, and the noise and the measurement models are both Gaussian, the posterior (i.e., updated) distribution of the state is also Gaussian, and the state estimation can be obtained using the Kalman filter [17]. When the models are nonlinear/non-Gaussian, particle filtering, based on the Monte Carlo method, is a more effective approach [19].
Video object tracking has been applied to a variety of different kinds of intracellular movement, e.g., [20], [21]. Conventional approaches in intracellular tracking consist of two major steps: detection and localization, and correspondence. In the detection and localization step, the tracked objects are localized through image denoising and segmentation. Then the key is the correspondence step, in which links are established between the tracked objects in successive frames of the video. Due to a number of factors including rapidmotion, object distortion, image noise, object merging and splitting, etc., automatic object tracking for measuring intracellular movement has been a challenge. Jaqaman et al. [22], [23] presented an algorithm, the linear assignment problem (LAP), to solve the problem of disappearing, merging, and splitting objects in the correspondence step, and Yang et al. [24] described a different approach for reliable tracking of large-scale dense antiparallel particle motion based on the Kalman filter. However, the limitation of these approaches is that they do not work well with images of low signal-to-noise ratio (SNR) [25]–[27]. To track objects in noisy image sequences, Smal et al. [27] presented a robust algorithm using particle filtering. To account for the optical blurring of diffraction-limited objects, the authors used a point-spread function (PSF) model to calculate the likelihood in the observation model. However, this method uses generic particle filtering (GPF), which is computationally expensive because a large number of observations, called particles, must be made to determine the position of the object with statistical confidence, and each observation involves the computation of a two-dimensional model. When the number of the particles increases, the total computation time adds up quickly. Kong et al. [28], [29] used a snake (also called active contours) algorithm to automatically segment and track transitions between growing, shortening, and pausing states during microtubule assembly and disassembly. Their experimental results showed that the snake algorithm did not work well when the change in the microtubule length was large and exceeded the capture range of the algorithm. To improve the tracking accuracy of this algorithm, the authors implemented a particle filtering algorithm to reinitialize the capture range based on the predicted the movements of the microtubules [30]. Unfortunately, this resulted in only a small improvement in the tracking performance (5.7%), and the computation load is still an issue. Sargin et al. [31] and Koulgi et al. [32] described different methods to track the elongation, shortening and gliding of microtubules employing an arc-emission hidden Markov model and a graphical model-based algorithm, respectively. However, like the snake algorithm, such approaches only work well for small displacements, and fail to yield reliable tracking results in the case of rapid motion.
In recent years, another notable development has been the use of kymographs for tracking cargos in video image sequences [33]–[37]. This approach involves projecting the pixel intensities in the path of the moving object onto a single line to create a linear intensity profile. This process is repeated for each frame in the video and then the resulting linear intensity profiles are “stacked” to create a two-dimensional image in which one axis represents distance along the axon and the other axis represents time elapsed. Using this approach, objects moving along the axon create diagonal trajectories in the kymograph. Compared with frame-based image sequences, the advantage of kymographs is that they represent the movement information in a single graph in which the velocities of the moving object can be obtained by measuring the slopes of the diagonal trajectories. In principle, kymograph analysis appears well suitable for the analysis of motion of neurofilaments in axons. The kymograph could be generated using a linear intensity projection along the medial axis of the axon, which defines the path of the moving objects. However, this approach can be problematic when the object moves rapidly with respect to the video frame rate because this will generate discontinuous in object trajectories in the resulting kymograph. This often occurs in videos of neurofilament transport because relatively long time-lapse intervals (4 or 5 s) between video frames must be used in order to minimize photobleaching of these faint diffraction-limited structures [7], [11]. Consequently, tracking objects that are transported rapidly but intermittently along neural axons presents a significant challenge for the kymograph method.
In this paper, we present a new approach for video object tracking in axons based on particle filtering and we show that it can be applied to the motion of a cytoskeletal polymer. The most distinctive feature of our approach is the utilization of the geometry of the axon in tracking the movement of the neurofilament. Simply put, we take advantage of the fact that axons are long narrow processes and that axonally transported cargoes can only move within them. As a result, the prior dynamic state is spatially constrained, which reduces significantly the variance of the distribution of the possible states in the next video frame. Consequently, we can reduce the number of particles to be measured without compromising the tracking accuracy. We model the path of the axon with a piecewise polynomial formulated using cubic spline interpolation. The curvature of the spline limits the possible orientations of the moving structure and constrains the trajectory. The paper is organized as follows. In Section II, we describe the experimental methods that we used to obtain the time-lapse videos of neurofilament movement for the present study. In Section III, we present the particle filtering algorithm and the formulation of our tracking problem. In Section IV, we discuss the implementation of the axon constraint in the particle filtering algorithm. In Section V, we present experimental results using actual image sequences of neurofilament movements. In Section VI, we discuss our data and summarize our conclusions.
II. Observation of Neurofilament Movement
Neurofilaments are composed of up to five distinct protein subunits called neurofilament L, M, and H (the low, medium, and high molecular weight neurofilament triplet proteins), as well as peripherin and alpha-internexin. To track the movement of neurofilaments in living cells it is necessary to label one of these proteins with a fluorescent tag. This can be done using a recombinant fluorescent fusion protein consisting of a neurofilament protein linked to a fluorescent protein such as green fluorescent protein [11]. To resolve the moving neurofilaments, we take advantage of the low neurofilament content of certain types of cultured neurons, which results in local discontinuities in the axonal neurofilament array that we call naturally occurring gaps [11]. Neurofilaments that emerge from the flanking regions can be tracked in the gaps by time-lapse imaging.
All of the experimental data used in this paper were obtained from cultures of neurons dissociated from the cerebral cortices of newborn mice and cultured on glass coverslips using the glial sandwich technique of Kaech and Banker [38], as described by Wang and Brown [39]. To visualize neurofilaments, the cells were transfected with an EGFP-mNFM plasmid construct, which encodes the codon-optimized F64L/S65T variant of green fluorescent protein attached to the amino terminus of mouse neurofilament protein M [40]. Transfection was performed by electroporation of the dissociated cells prior to plating using an Amaxa Nucleofector (Lonza Inc., Walkersville, MD). To record the neurofilament movement, the neurons were observed after 8–12 days in culture by epifluorescence microscopy on a Nikon TE300 inverted microscope (Nikon, Garden City, NY) using a 100× Plan Apo VC 1.4NA oil immersion objective. The observation medium consisted of Hibernate-E (BrainBits, Springfield, IL) supplemented with 2%[v/v] B27 Supplement Mixture, 0.3%[w/v] glucose, 1 mM L-glutamine, 37.5 mM NaCl, and 10 µg/ml gentamicin. The temperature on the microscope stage was maintained using an Air Stream incubator (Nevtek, Williamsville, VA). Silicone fluid (dimethylpolysiloxane, Sigma, 5 centistokes) was layered over the observation medium to prevent evaporation. For time-lapse imaging, the exciting light from the mercury arc lamp was attenuated 12-fold using neutral density filters, and images were acquired with one second exposures at four second intervals using a Micromax 512BFT cooled CCD camera (Roper Scientific, Trenton, NJ) and MetaMorph software (Molecular Devices, Sunnyvale, CA). Allmovieswere 15 min in length. The acquired images measured 512 × 512 pixels in area and the magnification was 0.131 µm per pixel. The average SNR of such images typically is around 7 but lowest SNR can be around 2. Examples of two time-lapse image sequences are shown in Fig. 1. To track the movement of neurofilaments manually, we recorded the position of the leading end of each filament in successive frames of the time-lapse movies using the TrackPoints drop-in within the MetaMorph software.
Fig. 1.
Two examples of neurofilament movement in axons of cultured cortical neurons. The analysis of neurofilament movement in these axons is facilitated by heir relatively low neurofilament content, which results in regions of axon that lack neurofilaments. We refer to these regions as gaps. Fluorescent filaments that move into these gaps can be tracked because of the absence of other neurofilaments. This figure shows frames excerpted from two time-lapse movies. (a)–(f) Filament moves through a gap from left to right (Movie 1) at SNR = 7.5. (g)–(k) A filament moves through a gap from left to right, overlapping with a short pausing filament in frame (j) (Movie 3) at SNR = 5.5. Scale bar = 5 µm. (a) 1.5 min. (b) 2.5 min. (c) 3.5 min. (d) 4.5 min. (e) 5.5 min. (f) 6.5 min. (g) 0 min. (h) 1.5 min. (i) 3 min. (j) 4.5 min. (k) 6 min. (l) 7.5 min.
III. Particle Filtering and Formulation of the New Tracking Approach
Due to the erratic motile behavior of neurofilaments, it is not possible to develop a linear and deterministic model that predicts their movement. Consequently, a tracking method based on such models cannot be effective. Particle filtering is a natural choice for automated tracking of such cargoes because it is based on the Bayesian estimation theory which gives an optimal solution when the dynamic behavior of the object is uncertain and consequently the measurement of the object is nondeterministic. In this section, we first introduce the GPF method and then we describe the formulation of our new spatially constrained particle filtering (SCPF) tracking method.
A. The Generic Particle Filtering Method
Let xt and zt denote the state vector of the object and the observation at time t, and z1:t denote the set of observations [z1,…,zt] representing the frames of a time-lapse movie. In the framework of Bayesian tracking, the fundamental problem is to calculate the posterior probability p(xt | z1:t) given the dynamic state model p(xt | xt−1) and the observation likelihood model p(zt | xt). Particle filtering provides an approximate solution for this nonlinear/non-Gaussian problem by implementing recursive Bayesian filtering based on the sequential Monte Carlo method. The basic strategy is to use a set of random samples (particles) with associated weights (w) to represent the required posterior probability density function (pdf) p(xt | z1:t) and to compute the estimated new object state based on these samples and weights [18], [19]. To describe the particle filtering algorithm mathematically, the posterior pdf can be expressed by a set of weighted random samples as
| (1) |
where δ(·) is the Dirac delta function, is the particle of number i at time t, and the weights are chosen using the principle of importance sampling [41], [42]. The particles can be generated from a proposal density function q(·), which we call importance density function, written as
| (2) |
The weight can be defined as
| (3) |
Most commonly, the importance density function is chosen to be the dynamic model, i.e.,
| (4) |
Thus, the particle weights can be computed directly from the observation likelihood
| (5) |
According to the minimum mean square error (MMSE) estimation, the new object state can be expressed as the posterior mean
| (6) |
In practice, we use the sampling importance resampling (SIR) algorithm to perform object tracking [18]. It consists of five steps: 1) draw the samples: , 2) calculate the weight of each sample: , 3) calculate the total weight of all the samples, 4) normalize the weight of each sample: , and 5) resample using the algorithm of the cumulative sum of weights (CSW) [19]. Here, resampling is used to eliminate the samples with low importance weights and replicate the samples with high importance ones according to the observation likelihood.
B. Formulation of a Spatially Constrained Particle Filtering Method
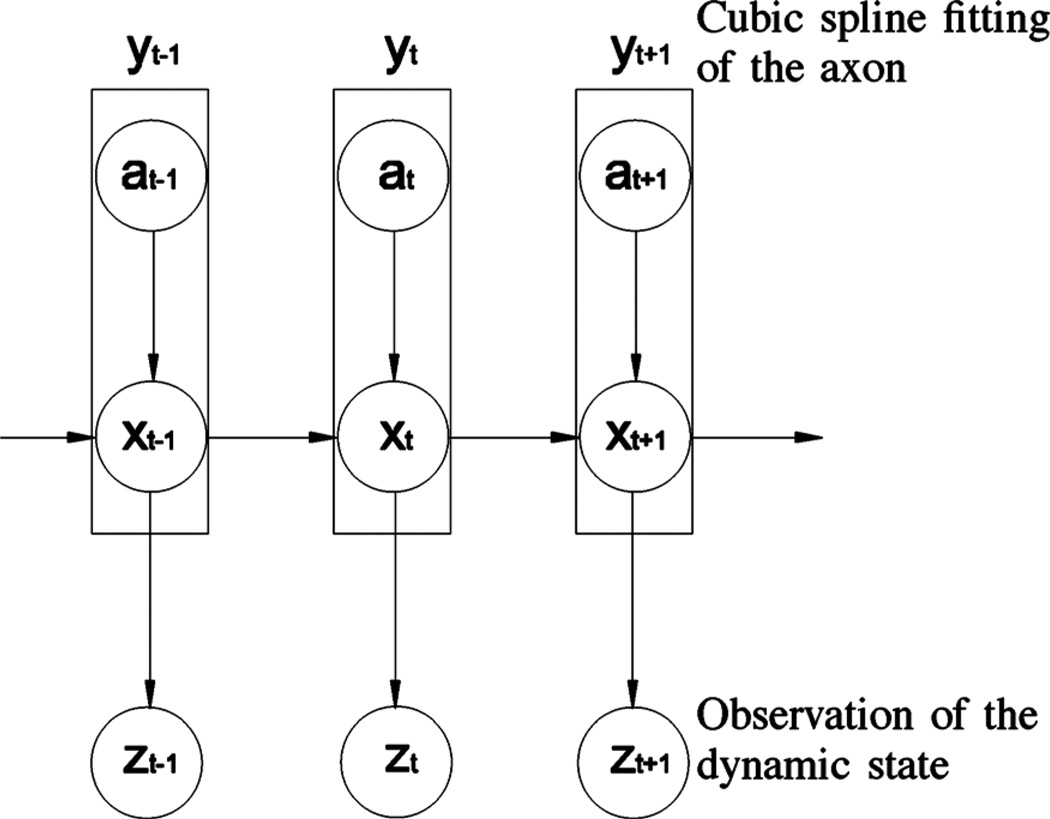
To track neurofilament movement, we need to locate neurofilaments in axons and calculate their velocities across the distance and time between successive frames of time-lapse videos. One obvious yet important characteristic of this movement is that neurofilaments are intracellular cargoes that can only move inside axons. In other words, the boundaries of the axon are a kinematic constraint on the position and orientation of the neurofilament. By introducing such a constraint in our tracking algorithm, the prior probability density function p(xt | xt−1) will have a smaller variance such that the number of particles can be significantly reduced without compromising tracking performance. To implement this spatially constrained dynamic model, we use an axon constraint state a. Then we define a compound object state at time t, yt, which represents two substates: the dynamic state xt and the axon constraint state at. The observation state zt remains the same. In terms of probabilistic dependencies, the current dynamic state is dependent upon both the previous dynamic state and the current axon constraint state. Thus the current dynamics and axon constraint states are coupled. Fig. 2 shows a graphical representation of the probabilistic dependencies among these states.
Fig. 2.
Graphical representation of the spatially constrained probabilistic model for neurofilament tracking. x represents the dynamic state, a represents the axon constraint, y represents the compound dynamic state resulting from the combination of a and x, and z represents the observation state. The dynamic state (position, orientation, and velocity) of the moving neurofilament at time t depends on the dynamic state in the prior time interval, t-1, and the constraint imposed on the position and orientation of the neurofilament by the axon at time t.
Using the product rule of probability and the conditional independent properties, we can express the prior distribution p(yt | yt−1) of the compound dynamic state at time as
| (7) |
Hence, the prior distribution when limited by the axon constraint can be described as p(xt | xt−1, at)p(at). The term p(xt | xt−1, at) shows that the current dynamic state depends on the previous dynamic state as well as the current constraint state while p(at) represents the current constraint probability, which will be described in detail in the following section.
IV. Implementation of the Axon Constraint in the Particle Filtering Algorithm
To integrate the axon constraint into GPF, the path of the axon has to be modeled such that p(at) can be determined. In the following section we present a curve fitting method to model the path of the axon.
A. Modeling the Path of the Axon
As shown in Fig. 1, the axons of cultured neurons trace a smooth curve. To model this shape, we use cubic spline interpolation to obtain a piecewise polynomial approximation of the axon path [43]. That is, the curve of interest is divided into a collection of segments connected by points called knots, and each segment is modeled by a different polynomial function using spline interpolation. Let [u, v] be any pixel position in the image coordinate system. Given the horizontal coordinate u for a given knot, the vertical coordinate v is given by the cubic spline interpolation function for each curve segment
| (8) |
where i represents the index of the knot (1, 2,…, n), c0i, c1i, c2i, and c3i are the polynomial coefficients for each segment and can be calculated using real pixel coordinates within the curve. Fundamentally, 4n coefficients have to be determined if the curve is to be divided into n − 1 segments. To derive these 4n unknowns, 4n conditions are required: the position, continuity, continuity of the first derivative, and continuity of the second derivative at the knots 2,…, n − 1 plus two boundary conditions at knots 1 and n [43]. For a natural spline, i.e., one in which the ends are not closed, the boundary conditions are to let the second derivatives at two end knots be equal to zero. Fig. 3 shows examples of two axons modeled in this way. Since the movement of the filament is constrained by the axon, we use its path to define the medial axis of the axon. To reveal the path of the filament, we perform a maximum intensity projection of the entire video sequence on a single plane [Fig. 3(c) and (d)] and then we place the knots manually [Fig. 3(e) and (f)].
Fig. 3.
Modeling the axon using cubic spline interpolation. Two examples are shown, one in panels (a), (c), and (e) and the other in panels (b), (d), and (f). These are the same axons shown in Fig. 1. (a), (b) Single frame from each video image sequence showing the moving neurofilaments within the gaps in the neurofilament array (white arrowheads). (c), (d) Maximum intensity projection of each image of the entire video sequence, revealing the paths of the moving filaments, and thus the axons, within the gaps in the neurofilament array. The blue line represents the medial axis of this projection. (e), (f) The resulting curve fit obtained by cubic spline interpolation (white line) overlaid on the image of the maximum intensity projection. The solid white points along the white lines are the knots, which are placed manually. The number of knots required to achieve a good fit depends on the extent of curvature of the axon; more knots are needed when the axon bends sharply, and fewer when it bends more gradually. Eight knots were sufficient for the axon in (e) but 14 knots were required for the axon in (f).
B. Modeling the State of the Neurofilament
In tracking applications, the elements of the dynamic state are chosen according to the motion characteristics of the object. To track the movement of an asymmetric cargo such as a neurofilament, the required elements are position, velocity, and orientation. For convenience, we model the appearance of each neurofilament by a rectangular bounding box with length (l) and width (w). This box represents the particle in the filtering algorithm. We selected the dimensions of the bounding box independently for each video sequence depending on the length of the moving filament and the degree of bending degree of the axon. For axons with sharp bends it was necessary to increase the width of the bounding box in order to sample the entire filament in all frames, whereas for straight axons a narrower box was adequate. The position, velocity, and orientation of the box at time t can be defined by the dynamic state xt = [ut, vt, θt, u̇t, v̇t, θ̇t], where [ut, vt] represents the position of the center of the box in the image coordinate system, θt represents the orientation of the box, and u̇t, v̇t, and θ̇t are the corresponding velocities. The dynamic state can be expressed in the following form:
| (9) |
where Δt is time difference between two frames, 𝒩 indicates a Normal distribution, and σu, σv, and σθ are the variances of the distribution of ut, vt, and θt, respectively. We use a Normal distribution because the importance density function has a Gaussian form [44]. Both the mean and the variance in (9) can be selected empirically. It should be noted that we use orientation in addition to position and velocity to determine the dynamic state, which is different from many tracking approaches. The orientation variable is perhaps not so important for tracking axonally transported cargoes that are globular in shape, but it is important for tracking cytoskeletal polymers such as neurofilaments because these cargoes are long asymmetric structures that change their orientation during their movement to accommodate the often tortuous path of the axon.
A consequence of using three vector elements (u, v, and θ) to determin the dynamic state is the generation of a large number of particles, which reduces the efficiency of the particle filtering tracking algorithm. Howerver, the number of particles can be reduced by constraining one or more of the vector elements. For example, if each element has 10 possibilities, the vector can produce 1000 particles in the next frame. If we reduce the number of possibilities for two elements in the vector from 10 to 1, the number of particles in this example would be reduced by a factor of 100. This is effectively what we accomplish by applying a spatial constraint in our particle filtering approach. Specifically, we constrain both the orientation and position of the bounding box to lie within the boundary of the axon as described below.
C. Modeling the Orientational Constraint
Since the neurofilament has to follow the path of the axon, the orientation of the particle must be the same as the orientation of the axon at that particular axial location. That is, the orientation θt at the time t should be the tangent of the axon curve function v(ut). Consequently the dynamic state model in (9) can be rewritten
| (10) |
and
| (11) |
We call the particle filtering algorithm imposed by this orientation constraint the OCPF.
D. Modeling the Positional Constraint
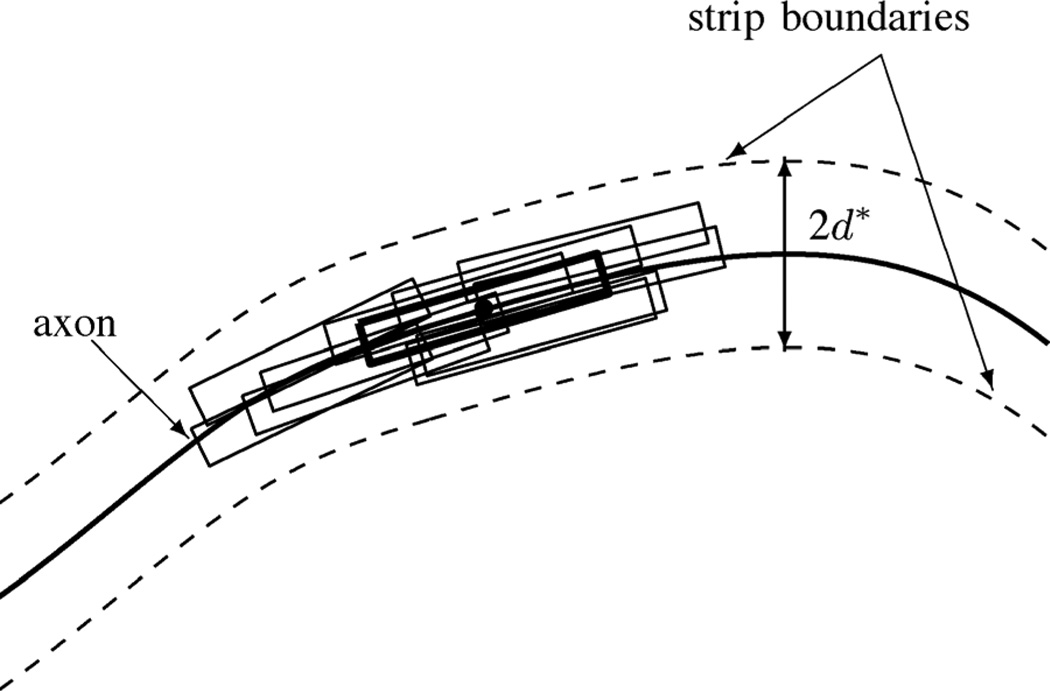
In addition to constraining the orientation of neurofilaments, axons also constrain the neurofilament position. To model this positional constraint, we confine the particles in the particle filtering algorithm to be distributed along the path of the axon as defined by the cubic spline curve fitting procedure. To allow for the fact that the cubic spline interpolation is not a perfect model of the axon path, we represent the axon by a narrow strip which has a width of 2d*, where the center line of the strip is the cubic spline of the axon (Fig. 4). d* is determined by the error of the curve fitting. If the distance (dt) of a particle from the center line at time t is less than d*, the particle is accepted. However, if dt > d*, the likelihood of the neurofilament being there is zero and the particle is rejected. This positional constraint on the motion of the neurofilament can be modeled as follows:
| (12) |
Fig. 4.
Schematic diagram of the distribution of particles within the boundaries of the axon at time t. The solid line represents the medial axis of the axon, as described by the cubic spline interpolation. The dashed lines represent the boundaries of the axon region which extend to a distance on d* either side of the medial axis. The black rectangular bounding boxes represent some particles distributed within the axon region as defined by the axon constraint. The bold black rectangular bounding box represents the particle in this example with the maximum observation likelihood, which corresponds to the location of the neurofilament. By rejecting those particles that lie outside the boundaries of the axon and that do not conform to the orientation of the axon, we reduce the number of particles required to locate the neurofilament.
Now the overall prior dynamic state can be rewritten as
| (13) |
Integrating the positional constraint expressed here in (13) with the orientational constraint expressed in (10) and (11), we use an accept–reject mechanism to sample the particles according to the following three-step process.
Step 2) Calculate the distance (dt) of perpendicular to the medial axis of the axon.
Step 3) Accept the sample as xt if dt < d*; otherwise, go to Step 1.
Now particles can be generated from the dynamic state model with both positional and orientational constraints included. We call this approach spatially constrained particle filtering (SCPF).
E. Calculation of the Observation Likelihood
According to [45], the observation likelihood p(zt | xt) at the state xt can be obtained by comparison of a histogram of the pixel intensities for the particle and for a reference model of the neurofilament
| (14) |
where
| (15) |
h(·) and ht(·) represent the histogram of the reference model and the particle, respectively; h(n; x0) and ht(n; xt) are the corresponding values in bin n of the histogram. D is called the Bhattacharyya coefficient which is a measure of the similarity of the particle and reference model histograms [15]. λ is a coefficient.
V. EXPERIMENTS
We have tested the performance of our proposed tracking method using time-lapse image sequences of neurofilament movement in cultured mouse cortical neurons obtained by fluorescence microscopy (see Section II). In this section, we present our tracking results for five image sequences in four movies, which contain one, one, one, and two image sequences, respectively. The first example illustrates the tracking accuracy and efficiency of SCPF compared with GPF, OCPF, and manual tracking by an experienced user. The tracking accuracy in noisy image sequences is also tested based on the first example. The second example illustrates the tracking accuracy when neurofilaments move rapidly. The rest three examples illustrate the robustness of the tracking approach using SCPF. We will first describe the tracking initialization and parameters, and then we will present the results of the tracking experiments.
A. Tracking Initialization and Parameters
All neurofilaments have a fixed width of about 10 nm. However, when neurofilaments are observed by fluorescence microscopy they appear to be several hundred nanometers in width due to the diffraction-limited resolution of the light microscope. Empirically, we determined that 10 pixels (about 650 nm) for the width of the rectangular box is sufficient to encompass the entire width w of the neurofilaments in our images. The length of the moving neurofilaments is highly variable and can exceed 30 µm, but the average is 5–10 µm. Thus, we set the width of the bounding boxes to 10 pixels and varied the length of the box to match the filament being tracked accordingly. The distance d* on either side of the medial axis was chosen to be five pixels.
In time-lapse movies rapidly moving structures can appear to jump from one frame to the next. To ensure that the track is not lost during such jumps, the variances (σu and σv) of the Gaussian noise for the particle distribution in the horizontal and vertical dimensions of the image were set empirically at 25 pixels and the variance of the particle orientation (σθ) was set at 0.5 rad. The intensity “signature” of the neurofilament in the observation model was represented by a 16-bin pixel intensity histogram. In the calculation of the observation likelihood, the coefficient λ was set to 20. To obtain the reference model, which defines the pixel intensity histogram for the filament, we usedmanual placement of the bounding box in a single frame of the time-lapse video image series. The tracking algorithm was programmed and interfaced using the Enthought Tool Suite and Python programming language (Enthought, Austin, TX) running on 2.1 GHz Intel Core 2 Duomachine. MetaMorph software was used to track the movement of the neurofilament manually in order to calculate the true velocity of the neurofilament. This velocity was used as the reference for calculating the tracking error in the automated particle tracking experiments.
B. Experimental Results
Experiments were conducted using GPF, OCPF, and SCPF, and their performances were evaluated and compared. Fig. 5(a) and (b) shows representative tracking results obtained using GPF with 100 and 200 particles, respectively. There are large tracking errors in both position and orientation in each frame, though the tracking performance is slightly better with 200 particles. Thus, GPF with 100 or 200 particles cannot be used to track neurofilaments in these kinds of movies. Fig. 5(c) and (d) shows the tracking results obtained using OCPF with 50 and 100 particles, respectively. As we can see in Fig. 5(c), OCPF with 50 particles shows tracking errors in some frames. Fig. 5(d) shows that the performance is improved with 100 particles, but is still not satisfactory in all frames. Fig. 5(e) shows that SCPF with only 50 particles gives the best tracking results.
Fig. 5.
Comparison of the tracking performance obtained using three particle filtering algorithms. These data correspond to frames 42, 50, 52, 55, 61, and 77 of Movie 1 with SNR = 7.5, which is the same sequence shown in Fig. 1(a)–(f) and Fig. 3(a), (c), and (e). (a) GPF with 100 particles. (b) GPF with 200 particles. (c) OCPF with 50 particles. (d) OCPF with 100 particles. (e) SCPF with 50 particles. The upper row of panels in (a)–(e) show the distribution of the particles, which are represented as rectangular bounding boxes. The bounding boxes measure 10 × 130 pixels throughout. The bottom row of panels in (a)–(e) show tracking results overlaid on the image of the moving neurofilament, with insets showing the object tracking area at higher magnification. The position of the bounding box relative to the image of the filament is an indication of the tracking performance. GPF and OCPF generate many tracking errors in position and orientation. SCPF generates more accurate tracking performance with fewer particle numbers, resulting in a more efficient tracking method.
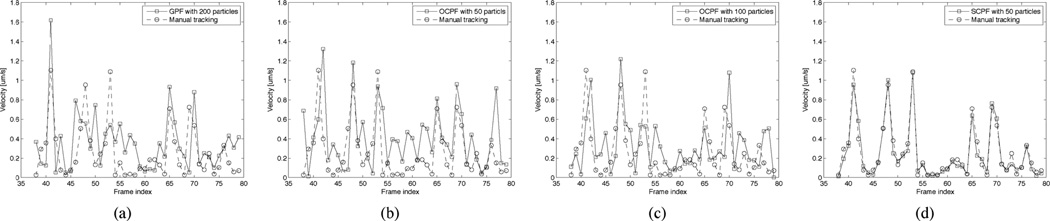
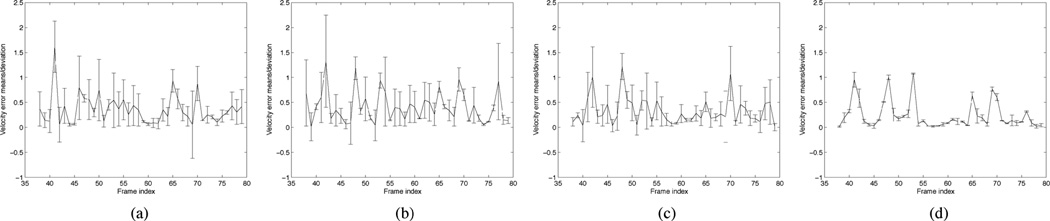
To further analyze the tracking performance of SCPF, we repeated the GPF, OCPF, and SCPF approaches 100 times in each of the above tracking experiments and then we computed for each time interval the mean and standard deviation of the tracking errors for the neurofilament velocity. The tracking error was defined as the ratio of the actual velocity (obtained by manual tracking) and the estimated velocity (obtained by automated tracking using particle filtering). Fig. 6 shows the velocities obtained using GPF with 200 particles, OCPF with 50 particles, OCPF with 100 particles, and SCPF with 50 particles compared to those obtained using manual tracking, and Fig. 7 shows the corresponding mean tracking errors. GPF with 200 particles showed large tracking errors in each frame, and OCPF with 50 particles and 100 particles also showed unsatisfactory results. The SCPF method produced the smallest tracking errors and generated velocities that were closer to that of manual tracking than the other filtering methods [Fig. 6(d) and Fig. 7(d)]. These results demonstrate that GPF is not efficient for tracking neurofilament movement in time-lapse image sequences. Tracking performance can be improved by including an orientational constraint, but it is best when both positional and orientational constraints are included.
Fig. 6.
Comparison of the estimated and actual neurofilament velocities obtained using three different particle tracking algorithms. These data were obtained using the moving neurofilament shown in Fig. 5. The open squares represent the data obtained by using particle filtering and the open circles represent the data obtained by an experienced user using manual tracking. (a) GPF with 200 particles, (b) OCPF with 50 particles, (c) OCPF with 100 particles, and (d) SCPF with 50 particles. Note that there is considerable discrepancy between the actual velocities and the estimated velocities obtained using GPF and OCPF, but good agreement with the estimated velocities obtained using SCPF.
Fig. 7.
Comparison of the tracking errors obtained using three different particle filtering algorithms. These data were obtained using the same moving neurofilament analyzed in Fig. 6 and shown in Fig. 5. The tracking error was defined as the ratio of the actual velocity (obtained by manual tracking) and the estimated velocity (obtained by automated tracking using particle filtering). The tracking procedure was repeated 100 times and then the mean and standard deviation of the tracking errors were calculated for each time interval in the image sequence. The vertical bars represent the standard deviation about the mean. (a) GPF with 200 particles, (b) OCPF with 50 particles, (c) OCPF with 100 particles, and (d) SCPF with 50 particles. Note that the tracking errors are greatest when the neurofilament moves abruptly, e.g., in frames 41, 47, 52, 53, 65, and 70. Nevertheless, SCPF generates small tracking errors compared to GPF and OCPF.
A common method to evaluate the efficiency of particle filtering methods is to calculate the number of effective particles (Neff) [42] according to the following equation [19]:
| (16) |
where is the normalized weight obtained from (5) and Ns is the total number of particles. If the weights are uniform ( for i = 1,…,Ns), then Neff = Ns, but this happens only in extreme cases. Usually, Neff < Ns. Too small an effective particle number has a negative effect on tracking accuracy and easily leads to severe degeneracy. In other words, the more effective particles an algorithm generates, the more accurate the tracking result can be.
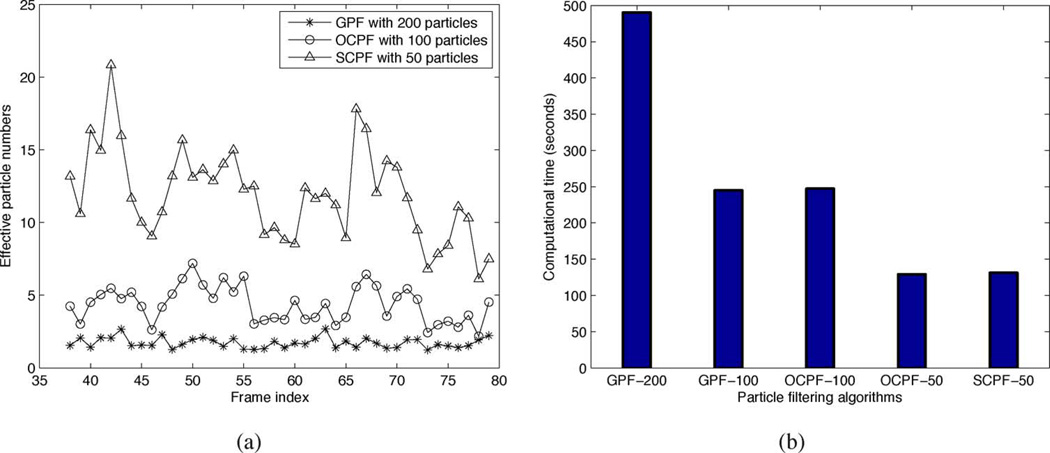
Fig. 8 shows the effective particle number and computional time for different particle filtering algorithms. Fig. 8(a) shows the effective particle number for GPF with 200 particles, OCPF with 100 particles, and SCPF with 50 particles. The effective particle numbers generated by using SCPF with only 50 particles are significantly higher than those obtained by using GPF with 200 particles, and even higher than those obtained by using OCPF with 100 particles. The explanation for this is that the particles generated by the SCPF method are confined to the vicinity and shape of the axon and are thus aligned closer to the true position and orientation of the neurofilament. These results prove that the orientation constraint alone is not sufficient to improve the tracking performance.
Fig. 8.
Comparison of effective particle number and computational time generated using different particle tracking algorithms. These data were obtained using the same moving neurofilament analyzed in Figs. 7 and 6, and shown in 5. (a) Effective particle number. The asterisks, open circles and open triangles represent the data obtained using GPF with 200 particles, OCPF with 100 particles, and SCPF with 50 particles, respectively. (b) Computational time. Bars from left to right represent the computational time using GPF with 200 particles, GPF with 100 particles, OCPF with 100 particles, OCPF with 50 particles, and SCPF with 50 particles, respectively. Note that the effective particle number is much greater, and the computational time is much less, when using SCPF compared to GPF and OCPF. Thus, SCPF is a more efficient tracking method.
To further examine the efficiency of GPF, OCPF, and SCPF, we compared the time required to execute these algorithms. In all particle filtering algorithms, the computational time is determined principally by the number of particles and the evaluation of those particles according to the observation model. In this paper, we use the same observation model throughout, so the computational time is essentially proportional to the particle number. Thus the computational time of SCPF with only 50 particles is around one half of the computational time of OCPF with 100 particles, and one quarter of the computational time of GPF with 200 particles [Fig. 8(b)]. Therefore, compared with GPF and OCPF, SCPF is a more accurate and computationally efficient method for tracking neurofilament movement in axons.
Figs. 9–11 show the tracking performance for three more sequences using GPF with 200 particles, OCPF with 100 particles, and SCPF with 50 particles. GPF generated considerable tracking error that sometimes resulted in complete loss of the filament, as shown in Fig. 9(a), Fig. 10(a), and Fig. 11(a). OCPF improved the tracking performance, but still produced significant error in estimating the neurofilament position, as shown in Fig. 9(b), Fig. 10(b), and Fig. 11(b). In all three cases, SCPF generated acceptable tracking accuracy with fewer particles. These results verify the robustness of particle filtering with integrated spatial constraints for tracking neurofilaments in axons.
Fig. 9.
Comparison of the tracking performance obtained using three particle filtering algorithms. These data correspond to frames 61, 64, 71, 76, 81, and 88 of Movie 3 with SNR = 5.5, which is the same movie shown in Fig. 1(g)–(l) and Fig. 3(b), (d), and (f). (a) GPF with 200 particles. (b) OCPF with 100 particles. (c) SCPF with 50 particles. The upper row of panels in (a)–(c) shows the distribution of the particles. The bounding boxes measure 10 × 120 pixels throughout. The lower row of panels in (a)–(c) shows the tracking results overlaid on the image of the moving neurofilament, with insets showing the object tracking area at higher magnification. GPF and OCPF generate many tracking errors in position and orientation. In the example shown in (a) the tracked neurofilament is lost completely. SCPF generates more accurate tracking performance with fewer particle numbers.
Fig. 11.
Comparison of the tracking performance obtained using three particle filtering algorithms. These data correspond to frames 64, 67, 69, 77, 83, and 85 of the second sequence of Movie 4 with SNR = 2.6. (a) GPF with 200 particles. (b) OCPF with 100 particles. (c) SCPF with 50 particles. The bounding boxes measure 10 × 60 pixels throughout. The panels in (a)–(c) show the tracking results overlaid on the image of the moving neurofilament and the insets show the object tracking area at higher magnification. The position of the bounding box relative to the image of the filament is an indication of the tracking performance. The SCPF method generates more accurate tracking performance.
Fig. 10.
Comparison of the tracking performance obtained using three particle filtering algorithms. These data correspond to frames 6, 8, 10, 12, 14, and 17 of the first sequence of Movie 4 with SNR = 2.6. (a) GPF with 200 particles. (b) OCPF with 100 particles. (c) SCPF with 50 particles. The bounding boxes measure 10 × 55 pixels throughout. The panels in (a)–(c) show the tracking results overlaid on the image of the moving neurofilament and the insets show the object tracking area at higher magnification. The position of the bounding box relative to the image of the filament is an indication of the tracking performance. The SCPF method generates more accurate tracking performance.
To test the performance of the SCPF algorithm with noisy images, we artificially added white noise with different standard deviations to our existing movies to generate a range of signal-to-noise ratios. The average signal-to-noise ratio (SNR) of our time-lapse image sequences of neurofilament movement in axons is typically around 7 but can be as low as 2. Fig. 12 shows the effect of noise on the tracking performance for the neurofilament in Movie 1. We found that the SCPF algorithm performs accurately for SNR =4.2, 2.3, and 1.7, but not for SNR = 1.5. For example, note that there is good agreement between the locations of the bounding boxes and the moving neurofilament in Fig. 12(a)–(c) but not in Fig. 12(d). Thismeans that our tracking method breaks down at an SNR < 1.7. However, movies with such low SNRs are rarely encountered in our applications. Therefore, the SCPF algorithm is an effective method for tracking neurofilament polymer movement in axons using real-world time-lapse image sequences.
Fig. 12.
Influence of noise on tracking performance using SCPF with 50 particles. These data correspond to frames 42, 50, 52, 55, 61, and 77 of Movie 1. The original movie (SNR = 7.5) was degraded by artificial addition of white noise to produce a range SNRs: (a) SNR = 4.2, (b) SNR = 2.3, (c) SNR = 1.7, and (d) SNR = 1.5. The bounding boxes measure 10 × 130 pixels throughout. The panels show the tracking results overlaid on the image of the moving neurofilament, with insets showing the object tracking area at higher magnification. The position of the bounding box relative to the image of the filament is an indication of the tracking performance. Note that the tracking performance is good with SNRs as low as 1.7, but significant errors are apparent with SNR = 1.5 (note the bounding boxes in red in (d) are shifted relative to those in (a)–(c), which is most noticeable in the insets).
One alternative to the particle filtering approach for tracking object movement is kymograph analysis (see Section I). We evaluated the suitability of kymograph analysis for tracking neurofilaments in axons. We found that short or rapidly moving neurofilaments produce kymographs with discontinuous trajectories [Fig. 13(a)], which represents a challenge for kymograph-based tracking applications. In contrast, analysis of the same image sequences using the SCPF algorithm with 50 particles generated an acceptable tracking accuracy [Fig. 13(b)]. Thus, particle filtering has an advantage over kymograph analysis for time-lapse imaging applications such as ours, where the temporal sampling is not sufficient to produce continuous trajectories.
Fig. 13.
Comparison of kymograph analysis and the particle filtering tracking algorithms for a rapidly moving neurofilament. These data correspond to frames 118, 119, 129, 130, 132, and 133 of Movie 2 with SNR = 4.1. (a) Kymograph obtained for frames 111 to 181. Note that the neurofilament trajectory is not continuous from frames 118 to 119, 129 to 130, 130 to 131, and 132 to 133 due to the rapid movement and short length of this neurofilament. (b) Tracking results obtained by using SCPF with 50 particles. The bounding boxes measure 10 × 16 pixels throughout. The particle filtering algorithm generates acceptable tracking accuracy.
Another alternative to the particle filtering approach for tracking linear structures such as cytoskeletal polymers is the snake algorithm [46], [47] is an active contour model that has been used to track microtubule growth and shrinkage in cells. In the snake algorithm, a capture range is first defined by encircling the tracked object with a snake curve. Then, the snake curve allowed to converge on the likely contour of the tracked object using a force balance function. To implement the snake algorithm for video object tracking, the tracked object must always be contained within the capture range [28], [29]. Fig. 14 shows the tracking performance for Movie 3 from frame 56 to frame 65 using the snake algorithm. The capture range is initialized manually in the first frame and then tracking results were used to determine the location in the subsequent frames. Fig. 14(a) shows the initial capture ranges (red ellipses) and Fig. 14(b) shows the neurofilament contours (red curves) generated by the snake algorithm. The algorithm exhibits a large tracking error in most frames and loses the filament completely in frame 65. The reason why the snake algorithm does not work for tracking moving neurofilaments in such movies is that these structures move too far within many time-lapse intervals and are thus not always contained within the required capture range. Particle filtering can be used to reinitialize the capture range based on the predicted movements [30]. But this approach is more complicated and not necessary for our application because we only need to know the neurofilament location, not its contour. Our data indicate that particle filtering alone, without the snake algorithm, is sufficient to track neurofilament movement in axons, and that SCPF provides a computationally efficient implementation of this approach.
Fig. 14.
The tracking performance obtained using the snake algorithm. These data correspond to frames 56, 57, 60, 62, 64, and 65 of Movie 3 with SNR = 5.5. (a) The initial capture ranges, which are represented by the red ellipses. (b) The tracking performance, which are represented by the red lines. The snake method generates many tracking errors.
VI. Discussion and Conclusion
The nonlinear and erratic motile behavior of neurofilaments in axons presents a challenge for automated tracking algorithms. Particle filtering is a natural solution to this problem due to its superior performance in dealing with nonlinear and uncertain motion. However, the main drawback of GPF methods is that they are computationally intensive because a large number of total particles must be generated in order to obtain a small number of effective particles. In this paper, we have presented a new SCPF method for tracking the movement of axonal neurofilaments. This method takes advantage of the fact that neurofilament motion is confined within the boundaries of the axon, which is a long and narrow structure. This confinement imposes kinematic constraints on the possible orientation and position of the moving neurofilament within the field of view. To facilitate the integration of these two constraints into the particle filtering algorithm, we use cubic spline interpolation to model the path of the axon. The position of the particles is constrained to lie within a narrow strip defined by this path, and their orientation at any given location is constrained to a direction tangential to the curvature of the axon path at that point. Together, these two constraints function to increase the number of effective particles, and therefore reduce the uncertainty of the dynamic state model. To test this, we compared SCPF with GPF, as well as with OCPF, in which only the orientational constraint is considered. Our results prove that the SCPF method is substantially more efficient than either GPF or OCPF. Thus, it is necessary to take both positional and orientational constraints into consideration to achieve optimal tracking efficiency. In addition, the SCPF method is more effective for tracking neurofilaments than other available tracking methods including kymograph analysis and the snake algorithm. This approach should also be applicable to the movement of other axonally transported cargoes, including cytoskeletal polymers, membranous organelles, and cytosolic protein complexes.
The SCPF algorithm presented here is robust for high quality image sequences of neurofilament movement in which there is no focus drift, minimal photobleaching, and little overlap with other moving structures. In reality, however, we often obtain movies which are not ideal in these respects. Focus drift can be eliminated to a great extent with focusing feedback loops such as Nikon’s Perfect Focus System (Nikon Instruments, Melville, NY), but photobleaching is unavoidable when using fluorescent fusion proteins, and neurofilaments can often overlap with each other when there aremultiplemoving filaments in the same movie. In addition to these problems, neurofilaments can sometimes exhibit folding and unfolding behaviors while pausing between bouts of movement. Finally, when long exposures are required to image the moving filaments, there can be significant motion blurring during bouts of fastmovement. For our tracking method to be maximally useful it must be capable of addressing these issues, and this is where our future efforts will be directed.
Acknowledgments
The work of L. Yuan, Y. F. Zheng, and J. Zhu was supported by grants to Y. F. Zheng from the National Science Foundation. The work of L. Wang and A. Brown was supported by grants to A. Brown from the National Institute for Neurological Disorders and Stroke and from the National Science Foundation.
Contributor Information
Liang Yuan, Email: yuanl@ece.osu.edu, Department of Electrical and Computer Engineering, The Ohio State University, Columbus, OH 43210, USA.
Yuan F. Zheng, Email: zheng@ece.osu.edu, Department of Electrical and Computer Engineering, The Ohio State University, Columbus, OH, 43210 USA.
Junda Zhu, Email: zhuj@ece.osu.edu, Department of Electrical and Computer Engineering, The Ohio State University, Columbus, OH 43210, USA.
Lina Wang, Email: wang.1095@osu.edu, Department of Neuroscience, The Ohio State University, Columbus, OH, 43210 USA.
A. Brown, Email: brown.2302@osu.edu, Department of Neuroscience, The Ohio State University, Columbus, OH, 43210 USA.
References
- 1.Bray D. Cell Movements: From Molecules to Motility. 2nd ed. New York: Garland Science; 2000. [Google Scholar]
- 2.Goldman RD, Spector DL. Live Cell Imaging: A Laboratory Manual. 2nd ed. New York: Cold Spring Harbor Laboratory; 2009. [Google Scholar]
- 3.Brown A. Slow axonal transport. In: Squire LR, editor. New Encyclopedia of Neuroscience. vol. 9. Oxford, U.K.: Academic; 2009. pp. 1–9. [Google Scholar]
- 4.Brown A. Axonal transport of membranous and non-membranous cargoes: A unified perspective. J. Cell Biol. 2003;vol. 160(no. 6):817–821. doi: 10.1083/jcb.200212017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Perrot R, Berges R, Bocquet A, Eyer J. Review of the multiple aspects of neurofilament functions, and their possible contribution to neurodegeneration. Mol. Neurobiol. 2008;vol. 38(no. 1):27–65. doi: 10.1007/s12035-008-8033-0. [DOI] [PubMed] [Google Scholar]
- 6.Brown A. Slow axonal transport: Stop and go traffic in the axon. Nat. Rev. Mol. Cell Bio. 2000;vol. 1:153–156. doi: 10.1038/35040102. [DOI] [PubMed] [Google Scholar]
- 7.Wang C, Ho L, Sun D, Liem R, Brown A. Rapid movement of axonal neurofilaments interrupted by prolonged pauses. Nature Cell Biol. 2000;vol. 2:137–141. doi: 10.1038/35004008. [DOI] [PubMed] [Google Scholar]
- 8.Brown A, Wang L, Jung P. Stochastic simulation of neurofilament transport in axons: The stop and go hypothesis. Mol. Biol. Cell. 2005;vol. 16(no. 9):4243–4255. doi: 10.1091/mbc.E05-02-0141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jung P, Brown A. Modeling the slowing of neurofilament transport along mouse sciatic nerve. Phys. Biol. 2009;vol. 6(no. 4):046002:1–046002:15. doi: 10.1088/1478-3975/6/4/046002. [DOI] [PubMed] [Google Scholar]
- 10.Trivedi N, Jung P, Brown A. Neurofilaments switch between distinct mobile and stationary states during their transport along axons. J. Neurosci. 2007;vol. 27(no. 3):507–516. doi: 10.1523/JNEUROSCI.4227-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Brown A. Live-cell imaging of slow axonal transport. Methods Cell Biol. 2003;vol. 71:305–323. doi: 10.1016/s0091-679x(03)01014-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Comaniciu D, Ramesh V, Meer P. Kernel-based object tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2005 Mayvol. 25(no. 5):564–577. [Google Scholar]
- 13.Fukunaga K, Hostetler L. The estimation of the gradient of a density function, with application in pattern recognition. IEEE Trans. Inf. Theory. 1975 Jan.vol. 21(no. 1):32–40. [Google Scholar]
- 14.Cheng Y. Mean shift, mode seeking, and clustering. IEEE Trans. Pattern Anal. Mach. Intell. 1995 Aug.vol. 17(no. 8):790–799. [Google Scholar]
- 15.Comaniciu D, Ramesh V, Meer P. Real-time tracking of nonrigid objects using mean shift. Proc. IEEE Conf. Comput. Vis. Pattern Recognit.; Hilton Head, SC. 2000. pp. 142–149. [Google Scholar]
- 16.Comaniciu D, Meer P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002 Mayvol. 24(no. 5):603–619. [Google Scholar]
- 17.Bar-Shalom Y, Li XR, Kirubarajan T. Estimation With Application to Tracking and Navigation. New York: Wiley; 2001. [Google Scholar]
- 18.Arulampalam S, Maskell S, Gordon N, Clapp T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002 Feb.vol. 50(no. 2):174–188. [Google Scholar]
- 19.Ristic B, Arulampalam S, Gordon N. Beyond the Kalman Filter: Particle Filters for Tracking Applications. Boston, MA: Artech; 2004. [Google Scholar]
- 20.Meijering E, Smal I, Danuser G. Tracking in molecular bioimaging. IEEE Signal Process. Mag. 2006 Mayvol. 23(no. 3):46–53. [Google Scholar]
- 21.Sbalzarini IF, Koumoutsakos P. Feature point tracking and trajectory analysis for video imaging in cell biology. J. Struct. Biol. 2005;vol. 151(no. 2):182–195. doi: 10.1016/j.jsb.2005.06.002. [DOI] [PubMed] [Google Scholar]
- 22.Jaqaman K, Loerke D, Mettlen M, Kuwata H, Grinstein S, Schmid S, Danuser G. Robust single-particle tracking in live-cell time-lapse sequences. Nature Methods. 2008;vol. 5(no. 8):1212–1221. doi: 10.1038/nmeth.1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jaqaman K, Danuser G. Computational image analysis of cellular dynamics: A case study based on particle tracking. Cold Spring Harb Protoc. 2009 doi: 10.1101/pdb.top65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yang G, Matov A, Danuser G. Reliable tracking of large scale dense antiparallel particle motion for fluorescence live cell imaging. Proc. IEEE Conf. Comput. Vis. Pattern Recognit.; San Diego, CA. 2005. pp. 9–17. [Google Scholar]
- 25.Cheezum WF, Walker WH, Guilford MK. Quantitative comprison of algorithms for tracking single fluorescent particles. Biophys. J. 2001;vol. 81(no. 4):2378–2388. doi: 10.1016/S0006-3495(01)75884-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Carter BC, Shubeita GT, Gross SP. Tracking single particles: A user-friendly quantitative evaluation. Phys. Biol. 2005;vol. 2(no. 1):60–72. doi: 10.1088/1478-3967/2/1/008. [DOI] [PubMed] [Google Scholar]
- 27.Smal I, Draegestein K, Galjart N, Niessen W, Meijering E. Particle filtering for multiple object tracking in dynamic fluorescence microscopy images: Application to microtubule growth analysis. IEEE Trans. Med. Imag. 2008 Jun.vol. 27(no. 6):789–803. doi: 10.1109/TMI.2008.916964. [DOI] [PubMed] [Google Scholar]
- 28.Kong KY, Marcus AI, Giannakakou P, Wang MD. Computer assisted analysis of microtubule dynamics in living cells. Proc. 27th Annu. Int. Conf. Eng. Med. Biol. Soc.; Shanghai, China. 2005. pp. 3982–3985. [DOI] [PubMed] [Google Scholar]
- 29.Kong KY, Marcus AI, Giannakakou P, Wang MD. Cellular imaging data analysis: Mircotubule dynamics in living cell. Proc. IEEE Int. Conf. Image Process; Atlanta, GA. 2006. pp. 2545–2548. [Google Scholar]
- 30.Kong KY, Marcus AI, Giannakakou P, Wang MD. Using particle filter to track and model microtubule dynamics. Proc. IEEE Int. Conf. Image Process; San Antonio, TX. 2007. pp. 517–520. [Google Scholar]
- 31.Sargin ME, Altinok A, Rose K, Manjunath BS. Deformable trellis: Open contour tracking in bio-image sequence. Proc. IEEE Int. Conf. Acoustics, Speech, Signal Process.; Las Vegas, NV. 2008. pp. 561–564. [DOI] [PubMed] [Google Scholar]
- 32.Kougli P, Sargin ME, Rose K, Manjunath BS. Graphical model-based tracking of curvilinear structures in bio-image sequences. Proc. IEEE Int. Conf. Pattern Recognit.; Istanbuk, Turkey. 2010. pp. 2596–2599. [Google Scholar]
- 33.Zhang K, Osakada Y, Xie W, Cui B. Automated image analysis for tracking cargo transport in axons. Microsc. Res. Tech. 2011;vol. 74(no. 7):605–613. doi: 10.1002/jemt.20934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Smal I, Grigoriev I, Akhmanova A, Niessen WJ, Meijering E. Microtubule dynamics analysis using kymographs and variable-rate particle filters. IEEE Trans. Image Process. 2010 Jul.vol. 19(no. 7):1861–1876. doi: 10.1109/TIP.2010.2045031. [DOI] [PubMed] [Google Scholar]
- 35.Stepanova T, Smal I, Haren J, Akinci U, Liu Z, Miedema M, Limpens R, Ham M, Reijden M, Poot R, Grosveld F, Mommaas M, Meijering E, Galjart N. History-dependent catastrophes regulate axonal microtubule behaviour. Curr. Biol. 2010;vol. 20(no. 11):1023–1028. doi: 10.1016/j.cub.2010.04.024. [DOI] [PubMed] [Google Scholar]
- 36.Welzel O, Boening D, Stroebel A, Reulbach U, Klingauf J, Kornhuber J, Groemer T. Determination of axonal transport velocities via image cross- and autocorrelation. Eur. Biophys. J. 2009;vol. 38:883–889. doi: 10.1007/s00249-009-0458-5. [DOI] [PubMed] [Google Scholar]
- 37.Racine V, Sachse M, Salamero J, Fraisier V, Trubuil A, Sibarita J. Visualization and quantification of vesicle trafficking on a three-dimensional cytoskeleton network in living cells. J. Microsc. 2007;vol. 225(no. 3):214–228. doi: 10.1111/j.1365-2818.2007.01723.x. [DOI] [PubMed] [Google Scholar]
- 38.Kaech S, Banker G. Culturing hippocampal neurons. Nat. Protoc. 2006;vol. 1(no. 5):2406–2415. doi: 10.1038/nprot.2006.356. [DOI] [PubMed] [Google Scholar]
- 39.Wang L, Brown A. A hereditary spastic paraplegia mutation in kinesin-1A/KIF5A disrupts neurofilament transport. Mol. Neurodegenerat. 2010;vol. 5(no. 52) doi: 10.1186/1750-1326-5-52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Yan Y, Jensen K, Brown A. The polypeptide composition of moving and stationary neurofilaments. Cell Motil. Cytoskeleton. 2007;vol. 64(no. 4):299–309. doi: 10.1002/cm.20184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bergman N. Ph.D. dissertation. Linkoping, Sweden: Linkoping Univ.; 1999. Recursive Bayesian Estimation: Navigation and Tracking Applications. [Google Scholar]
- 42.Doucet A, Godsill S, Andrieu C. On sequential Monte Carlo methods for Bayesian filtering. Stat. Comput. 2000;vol. 10(no. 3):197–208. [Google Scholar]
- 43.Burden R, Faires J. Numerical Analysis. Pacific Grove, CA: Brooks/Cole Publishing Company; 1997. [Google Scholar]
- 44.Ghosh S, Manohar C, Roy D. A sequential importance sampling filter with a new proposal distribution for state and parameter estimation of nonlinear dynamical systems. Proc. R. Soc. A. 2008;vol. 464(no. 2089):25–47. [Google Scholar]
- 45.Perez P, Hue C, Vermaak J, Gangnet M. Color-based probabilistic tracking. Proc. 7th Eur. Conf. Comput. Vis.; Copenhagen, Denmark. 2002. pp. 661–675. [Google Scholar]
- 46.Kass M, Witkin A, Terzopoulos D. Snakes: Active contour models. Int. J. Comput. Vis. 1987;vol. 1:321–331. [Google Scholar]
- 47.Xu C, Prince JL. Snakes, shapes, and gradient vector flow. IEEE Trans. Image Process. 1998 Mar;vol. 7(no. 3):359–369. doi: 10.1109/83.661186. [DOI] [PubMed] [Google Scholar]