Optimal Link Removal for Epidemic Mitigation: A Two-Way Partitioning Approach

Abstract

The structure of the contact network through which a disease spreads may influence the optimal use of resources for epidemic control. In this work, we explore how to minimize the spread of infection via quarantining with limited resources. In particular, we examine which links should be removed from the contact network, given a constraint on the number of removable links, such that the number of nodes which are no longer at risk for infection is maximized. We show how this problem can be posed as a non-convex quadratically constrained quadratic program (QCQP), and we use this formulation to derive a link removal algorithm. The performance of our QCQP-based algorithm is validated on small Erdős-Renyi and small-world random graphs, and then tested on larger, more realistic networks, including a real-world network of injection drug use. We show that our approach achieves near optimal performance and out-perform so ther intuitive link removal algorithms, such as removing links in order of edge centrality.

1. Introduction

Infectious diseases are a major burden on human health, resulting in more than 10 million deaths annually and accounting for 23% of the global disease burden [1]. These impacts arise from ongoing epidemics of infectious diseases, such as HIV/AIDS and tuberculosis, as well as from sudden global outbreaks of emerging infectious diseases, such as SARS, H1N1 influenza, and avian influenza. Various interventions have been developed to control infectious disease epidemics, such as vaccination, treatment, quarantining, and behavior change programs (e.g., social distancing, partner reduction). However, the implementation of these interventions is often constrained by limited budgets, time, and personnel. Therefore, decisions must be made as to how to allocate these scarce resources most efficiently.

The structure of the contact network through which an infectious disease spreads influences the evolution of an epidemic and thus has major implications for epidemic control strategies. For example, certain individuals, or certain links between individuals, may play a particularly important role in the spread of disease based on their positions in the network, and should therefore be given special consideration in an epidemic control policy. Various papers have explored the importance of network structure in controlling the spread of disease, primarily in the context of vaccination [2, 3, 4, 5, 6]. Generally, these analyses find that vaccination algorithms that make use of network structure perform better than those that do not. For example, Miller et al. found that an algorithm vaccinating nodes with the greatest number of unvaccinated neighbors outperformed a vaccination strategy based simply on node degree [4].

For many infectious diseases, such as HIV, tuberculosis, and SARS, a vaccine is not available. Prevention measures instead focus on behavior change so that individuals can reduce their chance of acquiring infection by reducing contact with infected individuals. In this paper, we investigate how to prevent the spread of disease by changing contact patterns as opposed to the vaccination approach more commonly used in the literature. In particular, given a limited number of links that can be removed in the contact network and knowledge of which nodes are initially infected, we seek to isolate (quarantine) the portion of the network containing the infected nodes from the rest of the network, while leaving the minimum number of susceptible nodes connected to infected nodes through some path in the network. The limit on the number of links that can be removed reflects the resource limitations encountered by public health institutions.

Except for very specific settings (e.g., hospitals, schools), it is unlikely that prevention efforts could intervene on links at the level of individual interactions. Instead, nodes are likely to represent cities, communities, or clusters of individuals with links representing the high-level interactions between them. While networks of individuals may consist of thousands of nodes or more, these high level networks are likely to be much smaller. An analysis of global airline networks found that 95% of global air travel was associated with a subgraph of 500 airports [7, 8]. Wylie et al. described a network of injection drug users in terms of their injection habits among 49 residential hotels in Winnipeg, Canada [9]. Youm et al. described a network of 77 neighborhoods in Chicago and the potential for the spread of HIV through sexual and needle-sharing relationships between neighborhoods [10]. Kao et al. constructed a network of livestock movement in Great Britain to investigate the potential for the spread of foot and mouth disease [11]. In these contexts, the link removal problem might then be one of deciding which flights to cancel in order to prevent the spread of respiratory diseases through a network of cities connected by air travel; or it might involve changing the structure of a city's outreach and harm reduction programs in order to prevent interactions between geographically disparate clusters of injection drug users and the potential spread of bloodborne diseases; or determining how to limit the movement of livestock between farms to prevent the spread of zoonotic diseases within the livestock population.

In order to determine which links to remove, we formulate a mathematical optimization problem based on two-way graph partitioning. The objective is to minimize the number of susceptible nodes connected to any infected nodes via any path, i.e., minimize the number of susceptible nodes at risk for infection. We show that this can be equivalently posed as a (non-convex) quadratically constrained quadratic program (QCQP), and we present a method for generating feasible, near-optimal solutions based on techniques described by Aspremont and Boyd [12]. We demonstrate that our quarantining method performs well on small Erdős-Renyi and small-world random graphs as compared to optimal solutions found by exhaustive search. We also test our approach on larger, more realistic graphs, where a brute-force approach to determine an optimal solution is no longer computationally feasible.

Only a few studies have examined the problem of link removal for the control of infectious diseases. Roy and Saberi [13] and Omic et al. [14] explored techniques that modify network structure to make a network more resistant to the spread of disease. Marcelino et al. [8] examined the effects of breaking links ranked by edge centrality or other metrics to slow the spread of disease in an airline network. All of these studies take a preventative approach to controlling infectious diseases, seeking to modify the network structure to make the network robust to the spread of infection before an infectious agent is introduced. In contrast, our approach is reactive, seeking to modify the network after an infection begins to spread and taking into account knowledge of the infection state of nodes in the network. Carlyle [15] developed an integer programming formulation to solve for an optimal quarantining of individuals based on their suspected infection status. However, that study focused specifically on finding geographically feasible partitions and did not incorporate resource constraints in its formulation.

The remainder of this paper proceeds as follows. In Section 2, we show how the quarantining problem can be formulated as a QCQP. Section 3 describes how to analyze this QCQP and obtain feasible, near-optimal solutions through the use of a semidefinite programming approximation. We validate the performance of our algorithm in Section 4 by testing it on various random and small-world networks and then demonstrate its applicability to more realistic networks in Section 5. In Section 6, we discuss directions for future work and offer some concluding thoughts.

2. Problem Formulation

We consider the case of a disease spreading over a contact network in which disease control efforts focus on breaking links in the network. Link dissolution might result from prevention efforts aimed at promoting safer behaviors within interactions (e.g., condom use, hand washing) or from efforts that eliminate interactions completely (e.g., partner reduction, social distancing, quarantining). We assume that it is known which nodes are initially infected. Given no resource constraints, the simple solution would be to isolate these infected nodes from the rest of the population by breaking all of their links. However, it is likely that resources are limited and this constrains the number of links that can be broken in the contact network. For example, public health departments operate with limited budgets and must decide how to invest these scarce resources for the greatest public benefit. Furthermore, in the case of a rapidly spreading infection, there may be a limited amount of time in which to implement a quarantining policy and there may not be enough time to isolate all infected individuals before their close contacts also become infected. Therefore, we wish to determine which links to break such that we quarantine infected nodes from as much of the rest of the (susceptible) population as possible, given a constraint on the number of links that can be removed.

We model the population as a network with N nodes. We denote the set of nodes susceptible to the disease by $\mathcal{S}$ and the set of nodes infected with the disease by $\mathcal{I}$. Let $N_S=\mid \mathcal{S}\mid$ and $N_I=\mid \mathcal{I}\mid$. In our analysis, a node i must either be susceptible ($i\in \mathcal{S}$) or infected ($i\in \mathcal{I}$): thus, N_S + N_I = N. Nodes are connected by links, described by an adjacency matrix A, where the entry a_ij = 1 if there is a link between i and j. We assume that links are undirected, meaning that a_ij = 1 implies a_ji = 1. For any $i\in \mathcal{S}$, if there is a path $i\leftrightarrow j$ in A for any $j\in \mathcal{I}$, then we say that i is at risk for infection.

For a given network A, our goal is to identify, for some integer K, which K links to remove in order to minimize the number of susceptible nodes at risk for infection (and therefore, minimize the number of susceptible nodes quarantined with the infected nodes). We can think of this as a partitioning problem: we assign nodes to one of two sets, ${\mathcal{Q}}_1$ and ${\mathcal{Q}}_{-1}$, such that there are at most K links between the two sets. These K links represent the links that should be broken to completely isolate the two sets of nodes from each other. We assign all infected nodes to ${\mathcal{Q}}_1$; any susceptible node assigned to ${\mathcal{Q}}_{-1}$ will therefore not be at risk for infection once the K links are broken. Our problem is then to maximize the number of susceptible nodes assigned to ${\mathcal{Q}}_{-1}$ (or equivalently minimize the number of susceptible nodes assigned to ${\mathcal{Q}}_1$) subject to the link constraint, K.

To formalize the problem, we first define a set assignment variable, x ∈ {−1, 1}^N, where x_i = 1 if node i is assigned to set ${\mathcal{Q}}_1$ and x_i = −1 if node i is assigned to set ${\mathcal{Q}}_{-1}$. We can compute the number of links connecting the two sets, ${\mathcal{Q}}_1$ and ${\mathcal{Q}}_{-1}$, from the assignment variable x ∈ {−1, 1}^N and the adjacency matrix A by noting that

$$a_{ij}-a_{ij}{x}_i{x}_j=\{\begin{array}{cc}2a_{ij},\hfill & \text{if}{x}_i\ne x_j\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

Summing over all (i, j) pairs, we can compute the total number of links between sets, k, from the following expression

$$\sum _{(i,j)}{a}_{ij}-a_{ij}{x}_i{x}_j=1^{T}A1-x^{T}Ax=4k.$$

Thus, for a given A, the constraint that no more than K links connect the two sets is satisfied for any x for which 1^T A1 − x^T Ax ≤ 4K.

Our problem can then be expressed as the minimization of the size of |{i | x_i = 1}| = |${\mathcal{Q}}_1$| over the set assignment variable, x ∈ {−1, 1}^N, satisfying the link constraint and assigning all infected nodes to ${\mathcal{Q}}_1$. This is written as the optimization problem, P0:

$$\begin{array}{cc}\hfill \underset{x}{\text{minimize}}& \mid {\mathcal{Q}}_1\mid \hfill \\ \hfill \text{subject to}& 1^{T}A1-x^{T}Ax\le 4K\hfill \\ \hfill & x_i\in \{-1,1\}\text{for}i=1,\dots ,N\hfill \\ \hfill & x_i=1\text{if}i\in \mathcal{I}.\hfill \end{array}$$

2.1. Quadratically Constrained Quadratic Program Formulation

Solving P0 requires searching over the set assignment of all susceptible nodes, a space of size 2^N_S, which grows exponentially in the number of susceptible nodes, N_S. We therefore transform P0 to an equivalent problem that can be solved using established optimization techniques. Instead of minimizing the number of nodes assigned to the set ${\mathcal{Q}}_1$, we can instead think of finding a set assignment which minimizes a partition cost function, where partitions that group many susceptible nodes with infected nodes are more costly than those that separate susceptible nodes from infected ones. Let W_ij be the cost of assigning nodes i and j to the same set, and −W_ij the cost of assigning these nodes to different sets. For a given set assignment, x, the partition cost is then ${\sum }_{(i,j)}{W}_{ij}{x}_i{x}_j=x^{T}Wx$. The assignment costs, W_ij, are determined by the states of nodes i and j:

$$W_{ij}=\{\begin{array}{cc}\alpha ,\hfill & \text{if}i\in \mathcal{I},j\in \mathcal{S}\text{or}i\in \mathcal{S},j\in \mathcal{I}\hfill \\ -\beta ,\hfill & \text{if}i,j\in \mathcal{I}\hfill \\ 0,\hfill & \text{for}i,j\in \mathcal{S}\hfill \end{array}\phantom{\}}$$

where α, β ≥ 0. The term α is the cost of having susceptible nodes with infected nodes in the same set. The term −β represents the benefit of putting infected nodes together in the same set. (Note that −β is a negative cost, in other words, a cost savings, and therefore reduces the objective value in the minimization problem). We include no cost of assigning susceptible nodes to the same or different sets.

We will show that, with appropriately chosen values of α and β, a solution to the problem P1

$$\begin{array}{cc}\hfill \underset{x}{\text{minimize}}& x^{T}Wx\hfill \\ \hfill \text{subject to}& 1^{T}A1-x^{T}Ax\le 4K\hfill \\ \hfill & x_i^2=1,\text{for}i=1,\dots ,N\hfill \end{array}$$

is also a solution of the original optimization problem, P0. The problem P1 is a quadratically constrained quadratic program (QCQP). Though generally non-convex, there are heuristic solution methods for solving such problems [12].

To prove the equivalence of P0 and P1, we first show that any solution to the QCQP, P1, is a feasible set assignment for the original problem, P0. We prove this by showing that any feasible set assignment in the original problem has a lower partition cost than any set assignment feasible in the QCQP but not in the original problem. We then show that a solution to the QCQP also minimizes |${\mathcal{Q}}_1$|. We prove this by showing that the partition cost is increasing in the number of susceptible nodes assigned to ${\mathcal{Q}}_1$.

We start with some definitions. For any set assignment, x, we denote the number of infected and susceptible nodes assigned to ${\mathcal{Q}}_1$ by $u_I=\mid \{i\in \mathcal{I}\mid x_i=1\}\mid$ and $u_S=\mid \{i\in \mathcal{S}\mid x_i=1\}\mid$, respectively. The numbers of infected and susceptible nodes assigned to ${\mathcal{Q}}_{-1}$ are N_I − u_I and N_S − u_S, respectively. In terms of u_I and u_S, we can write the partition cost, x^T Wx, as

$$\begin{array}{cc}\hfill g(u_I,u_S)& =-u_I^2\beta +2\alpha u_I{u}_S-{(N_I-u_I)}^2\beta +2\alpha (N_I-u_I)(N_S-u_S)+2\beta (N_I-u_I)u_I-2\alpha (N_I-u_I)u_S-2\alpha u_I(N_S-u_S)\hfill \\ \hfill & =-4\beta u_I^2+8\alpha u_S{u}_I+(4N_I\beta -4N_S\alpha )u_I-4N_I\alpha u_S-N_I^2\beta +2N_S{N}_I\alpha .\hfill \end{array}$$ (1)

2.1.1. Feasibility

We will first show that an optimal solution to P1, x*, is also a feasible set assignment for the original problem, P0. Let $\mathcal{F}=\{x\in {\{-1,1\}}^N\mid 1^{T}A1-x^{T}Ax\le 4K,x_i=1\forall i\in \mathcal{I}\}$ be the set of feasible set assignments in the original problem, P0, and ${\mathcal{F}}^{\prime }=\{x\in {\{-1,1\}}^N\mid 1^{T}A1-x^{T}Ax\le 4K\}$ be the set of feasible set assignments in P1. Note that $\mathcal{F}\subset {\mathcal{F}}^{\prime }$.

Assume that x* is a solution for P1 (and therefore x* ∈ $x^{\ast }\in {\mathcal{F}}^{\prime }$), but suppose that x* is not a feasible set assignment to the original problem, $x^{\ast }\notin \mathcal{F}$. Let $u_I^{\ast }=\mid \{i\in \mathcal{I}\mid x_i^{\ast }=1\}\mid$ and $u_S^{\ast }=\mid \{i\in \mathcal{S}\mid x_i^{\ast }=1\}\mid$. Because $x^{\ast }\notin \mathcal{F}$, it is the case that $1\le u_I^{\ast }\le (N_I-1)$ (i.e., not all infected nodes are assigned to the same set). Also suppose that there exists a feasible set assignment for the original problem, $y\in \mathcal{F}$. Note that $y\in {\mathcal{F}}^{\prime }$ also since $\mathcal{F}\subset {\mathcal{F}}^{\prime }$. Let $u_I=\mid \{i\in \mathcal{I}\mid y_i=1\}\mid$ and $u_S=\mid \{i\in \mathcal{S}\mid y_i=1\}\mid$. From the feasibility constraints, under y, all the infected nodes must be assigned to ${\mathcal{Q}}_1$, which means that u_I = N_I. The partition cost of y is therefore

$$\begin{array}{cc}\hfill y^{T}Wy& =g(N_I,u_S)\hfill \\ \hfill & =-4\beta N_I^2+8\alpha N_I{u}_S+(4N_I\beta -4N_S\alpha )N_I-4N_I\alpha u_S-N_I^2\beta +2N_S{N}_I\alpha \hfill \\ \hfill & =4N_I\alpha u_S-2N_I{N}_S\alpha -N_I^2\beta \hfill \\ \hfill & \le 4N_I\alpha N_S-2N_I{N}_S\alpha -N_I^2\beta ,\text{for}{u}_S\in \{0,\dots ,N_S\}\hfill \\ \hfill & =2N_I{N}_S\alpha -N_I^2\beta .\hfill \end{array}$$

Comparing the partition cost of x* and y, we have

$$\begin{array}{cc}\hfill x^{\ast T}W{x}^{\ast }-y^{T}Wy& =g(u_I^{\ast },u_S^{\ast })-g(N_I,u_S)\hfill \\ \hfill & \ge g(u_I^{\ast },u_S^{\ast })-(2N_I{N}_S\alpha -N_I^2\beta )\hfill \\ \hfill & =-4\beta {\left(u_I^{\ast }\right)}^2+8\alpha u_S^{\ast }{u}_I^{\ast }+(4N_I\beta -4N_S\alpha )u_I^{\ast }-4N_I\alpha u_S^{\ast }\hfill \\ \hfill & =h(u_I^{\ast },u_S^{\ast }).\hfill \end{array}$$

We note that $h(u_I^{\ast },u_S^{\ast })$ is a concave quadratic function with minima at the extrema of the domain, $u_I^{\ast }\in \{1,\dots ,N_I-1\}$ and $u_S^{\ast }\in \{0,\dots ,N_S\}$. Let β > N_Sα. For each of the domain extrema, we have

$$\begin{array}{cc}\hfill h(1,0)=h(N_I-1,N_S)& =4(N_I-1)\beta -4N_S\alpha \hfill \\ \hfill & >4(N_I-1)N_S\alpha -4N_S\alpha ,\text{for}\beta >N_S\alpha \hfill \\ \hfill & =4N_S(N_I-2)\alpha \hfill \\ \hfill & \ge 0,(\text{for}{N}_I\ge 2)\hfill \end{array}$$

$$\begin{array}{cc}\hfill h(1,N_S)=h(N_I-1,0)& =4(N_I-1)\beta -4N_S(N_I-1)\alpha \hfill \\ \hfill & >4(N_I-1)N_S\alpha -4N_S(N_I-1)\alpha ,\text{for}\beta >N_S\alpha \hfill \\ \hfill & =0\hfill \end{array}$$

from which we can conclude that $h(u_I^{\ast },u_S^{\ast })>0$ for all $u_I^{\ast }\in \{1,\dots ,N_I-1\}$ and $u_S^{\ast }\in \{0,\dots ,N_S\}$ if β > N_Sα. If this condition on β is satisfied, for any $x^{\ast }\in {\mathcal{F}}^{\prime }$ but $x^{\ast }\notin \mathcal{F}$ and any $y\in \mathcal{F}$, then x*^TWx* > y^TWy. This contradicts our original assumption that x* is an optimal solution to P1. Thus if x* is a solution to P1, then x* must also be a feasible set assignment to the original problem P0, $x^{\ast }\in \mathcal{F}$ as long as we set β > N_Sα.

2.1.2. Optimality

We now show that an optimal solution to P1 is also an optimal solution to the original problem, P0. Assume that x* is an optimal solution to P1, minimizing x^TWx. We have already shown that this implies that $x^{\ast }\in \mathcal{F}$, with u_I(x*) = N_I. Thus, x* minimizes the objective function

$$\begin{array}{cc}\hfill x^{\ast }& =\text{arg}\underset{x\in \mathcal{F}}{\text{min}}{x}^{T}Wx\hfill \\ \hfill & =\text{arg}\underset{x\in \mathcal{F}}{\text{min}}g(N_I,u_S\left(x\right))\hfill \\ \hfill & =\text{arg}\underset{x\in \mathcal{F}}{\text{min}}4N_I\alpha u_S\left(x\right)-2N_I{N}_S\alpha -N_I^2\beta .\hfill \end{array}$$

Note that the objective function is strictly increasing in u_S(x). Since x* minimizes the objective function, this implies that u_S(x*) ≤ u_S(x) for any $x\in \mathcal{F}$.

Now assume that x* is not an optimal solution to the original problem, P0. That is, there exists some solution $y\in \mathcal{F}$ for which fewer nodes are assigned to ${\mathcal{Q}}_1$. Since all infected nodes are assigned to ${\mathcal{Q}}_1$, it must be that fewer susceptible nodes are assigned to ${\mathcal{Q}}_1$ under y as compared to x*. But this means that u_S(y) < u_S(x*) and since $\mathcal{F}\subset {\mathcal{F}}^{\prime }$, y is also a feasible solution to P1. Thus we have another feasible solution to P1, y, for which y^TWy < x*^TWx*, which implies that x* is not an optimal solution to P1, contradicting our first assumption. Therefore, an optimal solution to the QCQP formulation, P1, must also be an optimal solution to the original problem, P0.

3. Problem Solution

In this section, we describe how we solve the non-convex QCQP, P1, formulated in the previous section. We first relax the QCQP to a convex optimization problem via a semidefinite relaxation. The resulting semidefinite program (SDP) provides a lower bound on the objective function of the original problem, P1. Additionally, through heuristic methods, the solution of the SDP can be used to generate feasible points that often achieve objective function values close to the optimal value of the original problem. These solutions provide feasible partition assignments (given the link removal constraint) of the nodes into two sets, those that can be saved from infection and those that cannot.

Using the relationship x^TWx = Tr(Wxx^T), we can rewrite P1 as

$$\begin{array}{cc}\hfill \underset{x}{\text{minimize}}& \mathbf{Tr}\left(WX\right)\hfill \\ \hfill \text{subject to}& 1^{T}A1-\mathbf{Tr}\left(AX\right)\le 4K\hfill \\ \hfill & X_{ii}=1,\text{for}i=1,\dots ,N\hfill \\ \hfill & X=x{x}^T\hfill \end{array}$$

We can find a lower bound on the objective function of the QCQP using the semidefinite program (SDP) relaxation of the original non-convex problem [12]. For the SDP relaxation, we relax the last equality constraint X = xx^T to the positive semidefinite constraint $X\underset{-}{\succ }x{x}^T$. We can write the SDP relaxation, P2, as:

$$\begin{array}{cc}\hfill \underset{x,X}{\text{minimize}}& \mathbf{Tr}\left(WX\right)\hfill \\ \hfill \text{subject to}& 1^{T}A1-\mathbf{Tr}\left(AX\right)\le 4K\hfill \\ \hfill & X_{ii}=1,\text{for}i=1,\dots ,N\hfill \\ \hfill & \left[\begin{array}{cc}\hfill X\hfill & \hfill x\hfill \\ \hfill x^T\hfill & \hfill 1\hfill \end{array}\right]\underset{-}{\succ }0\hfill \end{array}$$

where the last constraint is $X\underset{-}{\succ }x{x}^T$ written in terms of the Schur complement. An optimal solution X to P2 provides a bound on the objective function of P1, since Tr(WX) ≥ Tr(Wxx^T) = x^TWx for $X\underset{-}{\succ }x{x}^T$.

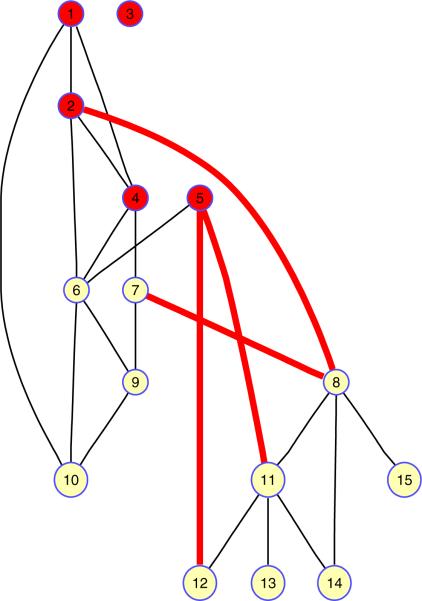
In addition to providing a bound on the objective function, we can also obtain “ good” feasible set assignments from the SDP relaxation [12]. We first note that the solutions X and x from P2 form the covariance matrix X − xx^T. If we consider the random variable y ~ N(x, X − xx^T), y is then the solution to the original problem, P1, on average. We can sample this distribution, keeping the sample value which results in the minimum cost. In order to ensure that this process yields feasible solutions satisfying the binary constraint ($y_i^2=1$), we calculate the sign of y. Using this technique, we obtain an approximation to the optimal solution of the original QCQP. The final output of this method is the binary classification vector y, where a node i is assigned to the set ${\mathcal{Q}}_1$ if y_i = 1 and to the set ${\mathcal{Q}}_{-1}$ if y_i = −1 . To quarantine the nodes in ${\mathcal{Q}}_1$ from the nodes in ${\mathcal{Q}}_{-1}$, we simply remove all links across the two sets. An example of the result of the method is depicted in Figure 1.

Figure 1.

Links to be removed (denoted by heavy lines), as determined by the QCQP approach for a network of 15 nodes with 5 initially infected nodes (denoted by dark shading) and a link removal constraint of K = 4. In this example, 6 nodes are saved from infection by link removal.

4. Validation over small-scale random networks

We validate the QCQP approach by first comparing its performance on small networks (~ 15 nodes) to the optimal quarantining partition found through exhaustive search over all possible partitions of the network. We test the QCQP approach on two standard models of random networks: Erdöos-Renyi random networks and small-world networks. For a given set of random networks, we consider two performance metrics: first, the fraction of networks, Θ, for which the QCQP approach saves the same number of susceptible nodes from infection as the optimal partition, which provides a measure of how often our method identifies an optimal partition; and second, the fraction of susceptible nodes saved from infection under both the optimal partition and the QCQP approach, the comparison of which describes the extent of the sub-optimality of the QCQP approach. Using these metrics, we establish performance bounds for our method on these networks and characterize its performance as a function of network structure. In Section 5, we apply the QCQP approach to larger, more realistic networks, where exhaustive search to identify the optimal solution is no longer computationally feasible.

4.1. Erdős-Renyi Random Graphs

We begin by considering Erdős-Renyi random graphs of 15 nodes with 5 initially infected nodes. Such graphs are formed by randomly connecting each pair of nodes with a probability p [16, 17]. As p increases, the random network becomes more connected, making the problem of separating infected nodes from susceptible ones more difficult. We evaluated the performance of the QCQP approach as a function of p. For a given probability p, we randomly generated 5,000 different random graphs, with the infected nodes randomly distributed throughout each network. For each graph, we computed the number of susceptible nodes saved from infection by the QCQP approach and in the true optimal partition (found by exhaustive search), given a range of link removal constraints, K.

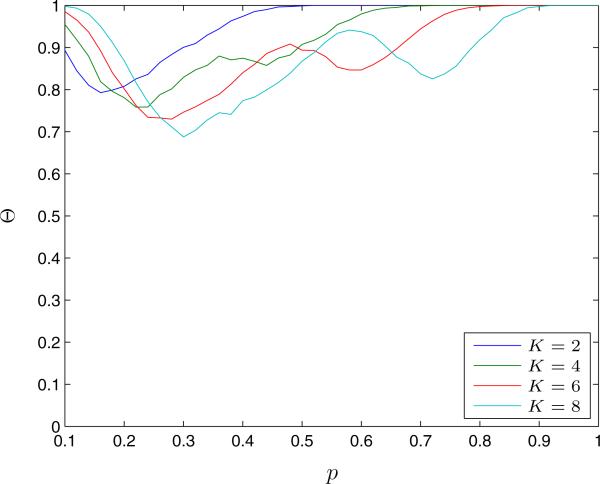
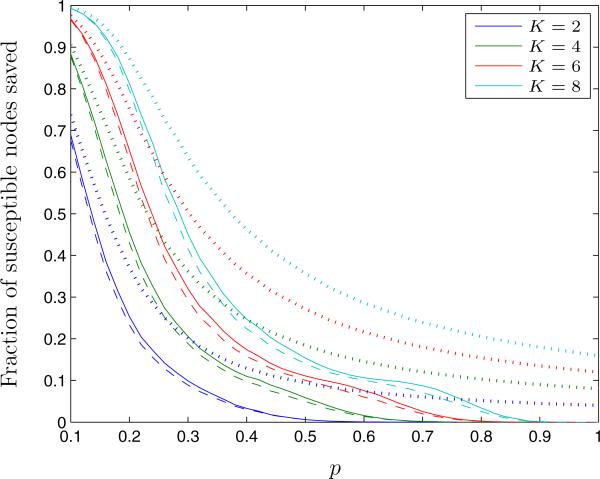
We first compute Θ, the fraction of graphs for which the QCQP approach saves the same number of susceptible nodes from infection as the optimal solution (Figure 2). For all tested values of K and p, the QCQP approach provides the optimal solution at least 70% of the time. We also observe that for a given link constraint, K, the QCQP approach finds an optimal partition more frequently for low and high values of p. This is likely due to the varying difficulty of the partitioning problem. At small values of p, the network is sparsely connected, so it may be feasible to completely separate all susceptible nodes from infected nodes, which the QCQP approach does well. As p increases, the network becomes more connected and the problem becomes more difficult due to the increasing number of links resulting in a greater diversity of viable quarantining options. Once p is large enough, the connectedness of the graph makes it unlikely that even the optimal solution will isolate many susceptible nodes given the link constraint. We see this illustrated in Figure 3, which compares the average fraction of susceptible nodes in the network saved from infection under both the optimal partition and the QCQP approach. We see that even though the QCQP approach does not always identify an optimal partition, it still saves nearly as many susceptible nodes from infection as the optimal partition. In fact, for p = 0.3 and K = 8, even when the QCQP approach does not identify the optimal partition (30% of the time), we calculate that it still saves 72% (IQR: 67% – 80%) as many susceptible nodes as the optimal partition, on average. We also plot the upper bound provided by the SDP solution on the fraction of susceptible nodes saved. Though this bound is not tight, it tracks the general trend of the optimal solution.

Figure 2.

The fraction of Erdős-Renyi random graphs, Θ, for which the QCQP approach finds an optimal partition (as confirmed by exhaustive search) as a function of the link probability p and for different link removal constraints K. Evaluated over 5,000 random networks of 15 nodes with 5 infected nodes.

Figure 3.

The fraction of susceptible nodes saved from infection under the optimal partition (solid line) and the QCQP approach (dashed line) in Erdős-Renyi random graphs, as a function of the link probability p and for different link removal constraints K. The performance bound derived from the SDP is shown for each case (dotted line). Evaluated over 5,000 random networks of 15 nodes with 5 infected nodes.

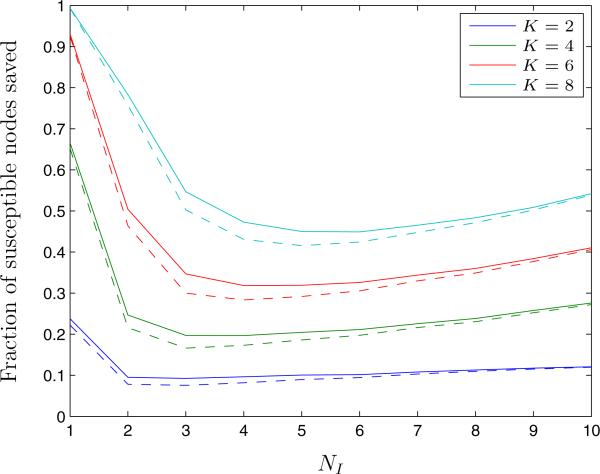
We also considered how performance of the QCQP approach varies with the prevalence of disease in the network. We varied the number of infected nodes from 1 to 10 out of the 15 total nodes in the network (Figure 4). The QCQP approach generally tracks the optimal solution in the number of susceptible nodes saved for all prevalence levels. The QCQP performs worst, as compared to the optimal solution, for between 2 to 5 infected nodes. Therefore, considering a prevalence of 5 infected nodes out of 15 appears to be representative of the QCQP algorithm performance.

Figure 4.

The fraction of susceptible nodes saved from infection under the optimal partition (solid line) and the QCQP approach (dashed line) in Erdős-Renyi random graphs, as a function of the number of infected nodes in the network, N_I. Evaluated over 5,000 random networks of 15 nodes with link formation probability, p = 0.3.

4.2. Small-World Networks

We next explored the effects of network structure and regularity on the performance of the QCQP approach by evaluating it on small-world networks. We again considered networks of 15 nodes with 5 initially infected nodes. We formed small-world graphs by first initializing a lattice network of neighborhood size of 2, where each node is connected to its two nearest neighbors (i.e., a ring). We then re-wired each link with a probability q. This process results in a network with many local connections and a few long-range connections [17, 18]. As q increases, the network changes from a structured network to a random network.

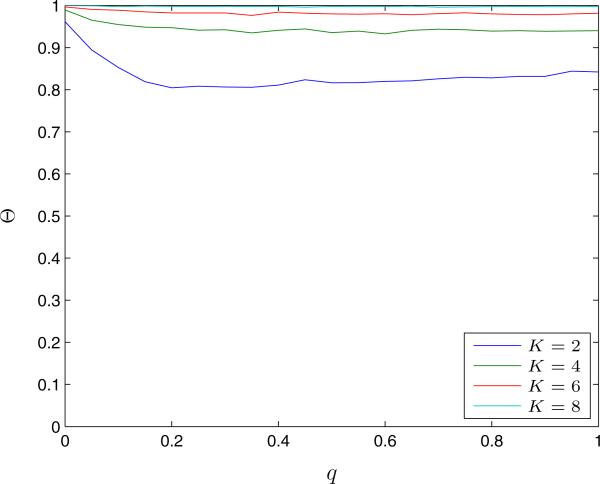
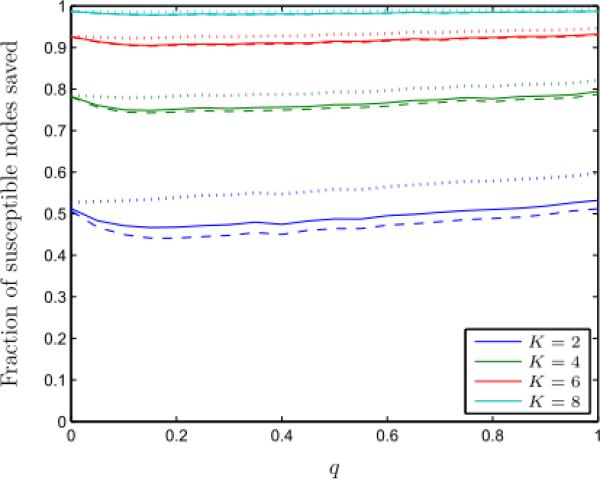
We randomly generated 5,000 sample small-world graphs for a given q and computed the same performance parameters described in Section 4.1. We find that the QCQP approach identifies an optimal partition more than 80% of the time (Figure 5). We also observe that the QCQP approach is nearly always optimal for structured networks (i.e., for small q). As q increases and the network becomes more random, the frequency of optimality of the QCQP approach decreases slightly, eventually reaching a plateau at a minimum level of optimality that depends on K, but no longer varies with q. This is likely due to the regularity of the degree distribution of the small-world network, since most nodes will have a degree close to the original neighborhood size of the network. Figure 6 shows the fraction of susceptible nodes saved from infection in the small-world networks for both the optimal partition and the QCQP approach as a function of the re-wiring probability q and for different link removal constraints K. Similar to the case of the Erdős-Renyi random graphs, we find that even when the optimal solution is not found by the QCQP approach, nearly as many infections may be prevented. For q = 0.2 and K = 2, when the QCQP does not identify the optimal solution (20% of the time), we compute that the QCQP approach still saves 62% (IQR: 50% – 75%) as many susceptible nodes as the optimal partition, on average. Again the performance bound provided by the SDP follows the same trends as the optimal solution and is always within 30% of the optimal value for these networks.

Figure 5.

The fraction of small-world graphs, Θ, for which the QCQP approach finds an optimal partition (as confirmed by exhaustive search) as a function of the re-wiring probability, q, and for different link removal constraints, K. Evaluated over 5,000 sample small-world graphs of 15 nodes with 5 infected nodes.

Figure 6.

The fraction of susceptible nodes saved under the optimal partition (solid line) and QCQP approach (dashed line) in small-world graphs as a function of the re-wiring probability, q, and for different link removal constraints, K. The performance bound derived from the SDP is shown for each case (dotted line). Evaluated over 5,000 sample small-world graphs of 15 nodes with 5 infected nodes.

5. Performance over Realistic Networks

We next applied the QCQP approach to more realistic networks, much larger than the small 15-node networks considered previously. For realistically sized networks, an exhaustive search for the optimal partition is no longer computationally possible. We therefore present results on the fraction of susceptible nodes saved from infection under the QCQP approach as a function of the number of links that can be removed, K. For context, we compare the performance of the QCQP approach to myopic algorithms that remove links in order of different measures of link significance, similar to the approaches evaluated by [3, 4, 5, 8].

5.1. Computation Time

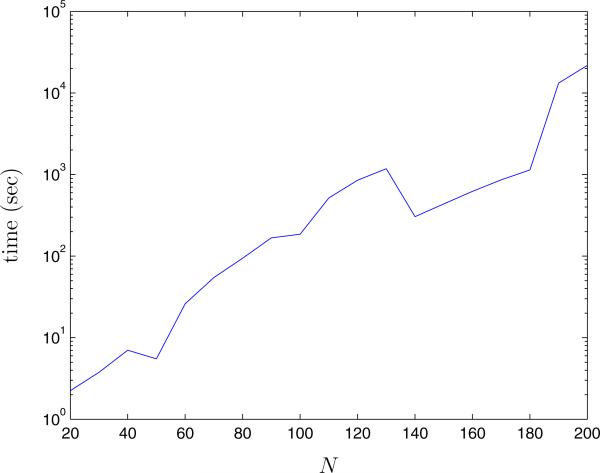
Because we have formulated the link removal problem in terms of a semidefinite program, the QCQP approach can be applied to networks as large as SDP solvers will allow. For ease of computation, we solved the SDP in Matlab using the disciplined convex programming package CVX [19, 20]. The interior-point algorithms called by CVX have been shown to have computation times scaling as a polynomial of the problem size (which in our case is N+ 1, where N is the number of nodes in the network), with some potential savings in computation time through the exploitation of problem sparsity or structure [21, 22]. This polynomial growth is reflected in Figure 7, where we plot the computation time of the QCQP approach as a function of network size for random networks with link formation probability p = 0.3, an infection prevalence of 10%, and a link removal constraint of K = 10. Computation times were measured using CVX version 1.21 in Matlab 7.11 on a 64-bit Intel Xeon 2.33 GHz processor. We tested the algorithm on networks up to 200 nodes. Larger problems could potentially be solved using more sophisticated large-scale optimization algorithms [23, 24, 25].

Figure 7.

Computation time (in seconds) of the QCQP algorithm as a function of the network size, N. The QCQP algorithm was applied to random networks of size N with link formation probability p = 0.3, a link removal constraint of K = 10 and a fixed 10% prevalence of infection. Simulations were done with a 64-bit Intel Xeon 2.33 GHz processor with 8 GB of RAM .

5.2. Measures of Link Significance

Different metrics can be used to measure the significance of a link in the spread of disease over a network. One commonly used measure is edge centrality, which measures of the importance of a link in maintaining the connectivity of the network. For a given link, e, its edge centrality is given by

$$c\left(e\right)=\sum _{(i,j)}\frac{\sigma (i,j\mid e)}{\sigma (i,j)},$$ (2)

where σ(i, j|e)/σ(i, j) is the fraction of shortest paths between nodes i and j passing over link e. This measure captures the importance of a link to the overall connectivity of the network, but does not reflect how important that link may be in maintaining paths between infected and susceptible nodes. To measure this, we introduce a susceptible-infected (SI) edge centrality measure which for a given link, e, is given by

$$c_{si}\left(e\right)=\sum _{(i,j)\in \mathcal{I}\times \mathcal{S}}\frac{\sigma (i,j\mid e)}{\sigma (i,j)},$$ (3)

where we only sum over paths that connect infected nodes to susceptible ones.

In addition to edge centrality measures, which are global indices that must be calculated over the entire network, we also compare the QCQP approach against a local measure of link importance. “Bridgeness” estimates the importance of a link in maintaining network connectivity using only the clique sizes of the link and the nodes it connects [26]. The clique size of a link or node is the maximal completely connected set containing that link or node [17]. For a given link, e, connecting nodes i and j, its bridgeness is given by

$$b\left(e\right)=\frac{\sqrt{S_i{S}_j}}{S_e}$$ (4)

where S_i, S_j and S_e are the clique sizes of nodes i and j and link e, respectively. Because bridgeness only requires local information, it can be efficiently calculated for very large networks by computing the index for each link in parallel.

We implemented link removal algorithms based on each of these three link significance indices (standard edge centrality, SI edge centrality, and bridgeness). To account for the influence of a link's removal on the importance of the remaining links in the network, we sequentially removed links and recomputed the index after each removal.

5.3. Finite Scale-Free Networks

To evaluate the performance of the QCQP approach for more realistically sized networks, we applied the algorithm to scale-free networks. Many real-world networks have been found to have scale-free degree distributions, where the probability that a node has k links is proportional to k^−γ. Such networks have the property that a few nodes have a very large number of links (acting as highly connected hubs), while most nodes have very few. In real-world networks, ranging from citation networks to the world wide web, the exponent γ has been found to be between 2.1 and 3 [27, 28, 29]. Scale-free networks have been extensively studied in the context of epidemics due to the ease with which diseases spread over such configurations and the importance of targeting hubs in control efforts [5, 30, 31, 32].

We randomly generated 500 networks of 150 nodes using the configuration model [17, 33, 34], where each node is assigned a random number of links sampled from the desired degree distribution. Links between nodes are then randomly matched together. We sampled from a power law distribution with γ = 2.1, truncated at k ≥ 150, since any given node cannot have more connections than nodes in the network. Truncating the degree distribution for a finite population size may cause deviations from the analytical results derived on large, near-infinite scale-free networks (see [31, 32]); however, the finite scale-free networks that we generated still exhibited the important characteristic of having a small number of nodes with many connections and a large number with few connections. This network formation process resulted in an average of 215 total links over the 150 nodes. In each network, 15 nodes were initially infected. The fraction of susceptible nodes saved from infection, averaged over 500 networks, is shown in Figure 8 as a function of the number of links removed K under the QCQP approach and by removing links by order of edge centrality, c(e), SI edge centrality, c_si(e), and bridgeness, b(e), measures.

Figure 8.

Average fraction of susceptible nodes saved from infection in finite scale-free networks with degree distribution ~ k^−2.1 as a function of the number of links removed, K, using the QCQP approach (solid line), the SI edge centrality measure (dashed line), the standard edge centrality measure (dotted line), and the bridgeness index (circle label). The performance bound derived from the SDP is also shown (cross label).

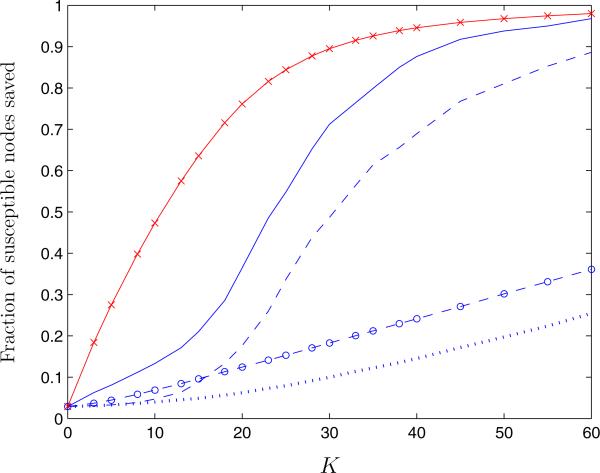
Of all the algorithms, the QCQP approach saves the greatest fraction of susceptible nodes for any given K. Removing links only in order of edge centrality or bridgeness ignores the infection pattern in the network, and thus performs poorly in separating susceptible nodes from infected ones. The SI edge centrality measure incorporates knowledge of infection status by only considering paths between infected and susceptible nodes and thus performs better than edge centrality alone. For both the QCQP approach and the removal of links in order of SI edge centrality, the fraction of susceptible nodes saved follows an S-shaped curve in K, indicating that there is a critical number of links that must be removed before a substantial fraction of the network can be successfully separated from the infected nodes.

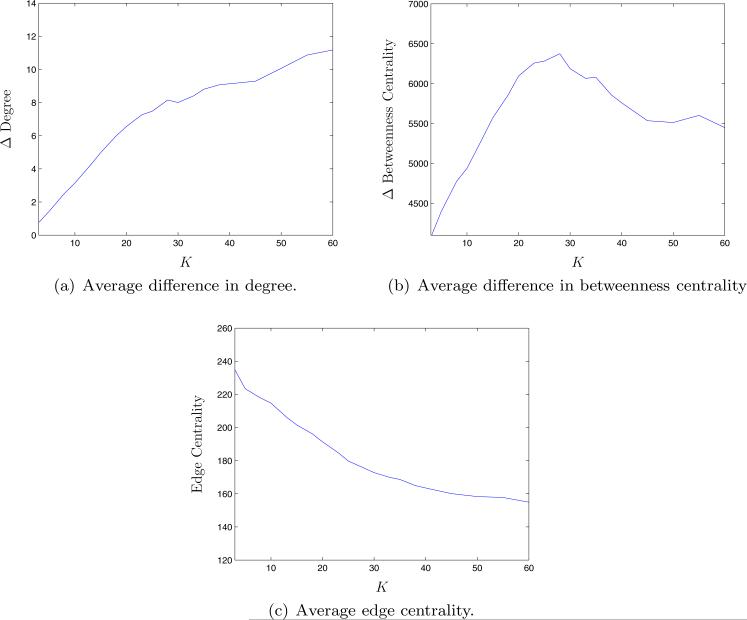
To gain qualitative insight into the QCQP algorithm, we explored how the characteristics of the links removed in these finite scale-free networks vary as K increases. For a given K, for each link removed by the QCQP approach, we computed the difference in degree and betweenness-centrality of the two nodes connected by that link, as well as the edge centrality of the link itself (Figure 9). If resources are scarce and only a few links can be removed, the algorithm removes links connecting nodes of similar degree and betweenness-centrality. We also find that the algorithm first removes links with high edge centrality, as we might expect. As more links can be removed, the method then starts to remove links between low-degree nodes and high-degree hubs, with an increasing difference in betweenness-centrality. The difference in betweenness-centrality of removed links peaks around K = 30, which is the inflection point on the QCQP performance curve.

Figure 9.

Average characteristics of links removed by the QCQP algorithm as a function of the number of links removed, K, in finite scale-free networks of 150 nodes with degree distribution ~ k^−2.1.

Though we see these qualitative trends in the links removed for this set of real-world networks, it is important to emphasize that the specific set of links removed in the QCQP approach depends on the actual network and the set of infected nodes. Previous work on the optimal control of infectious diseases over networks has often focused on vaccinating nodes rank ordered by degree or betweenness centrality [3, 4, 5]. Analogously, we considered removing links in order of edge centrality, but found performance to be greatly reduced. Though the QCQP approach does remove links with relatively high edge centrality first, it also accounts for the connectivity patterns between infected and susceptible nodes, which is something that a simple metric such as edge centrality or even the modified SI edge centrality metric cannot account for.

5.4. Network of Residential Hotels in Winnipeg, Canada

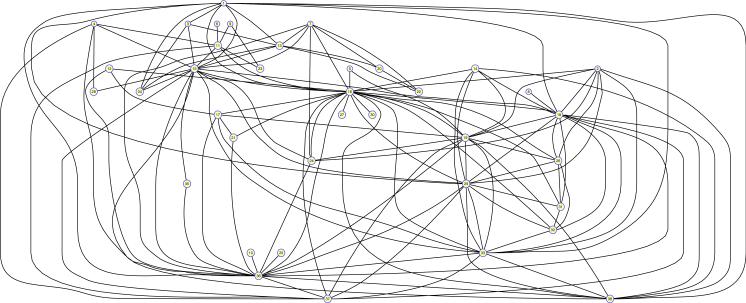
To demonstrate the applicability of the QCQP approach in a real-world setting, we applied it to a network dataset of residential hotels in downtown Winnipeg, Canada, that are sites of injection drug use and needle sharing [9]. Bloodborne diseases such as HIV and hepatitis C spread rapidly through needle sharing. Understanding the connectivity patterns in these behaviors and identifying critical areas for intervention are important for policies aimed at preventing the further spread of disease and improving injection drug user (IDU) health. The original dataset consisted of a survey of 435 IDUs and 49 residential hotels where they injected drugs. We generated a network of these 49 hotels, where two hotels were connected if at least one IDU reported injecting at both locations. This resulted in a network with 128 links and a large connected component of 38 nodes (Figure 10). Given a particular infection pattern (where a hotel can be considered “infected” if the prevalence of its residents exceeds a given threshold), our algorithm can identify critical inter-hotel links that should be targeted by local harm reduction programs and public health campaigns aimed at preventing the spread of bloodborne diseases.

Figure 10.

Connectivity pattern of the large connected component of 38 residential hotels in Winnipeg, Canada.

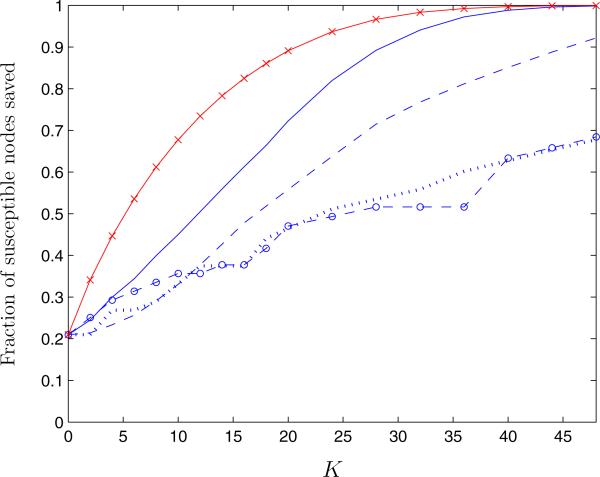
We randomly assigned 5 hotels to be initially infected and generated 5,000 infection patterns. We computed the average fraction of susceptible nodes saved from infection over these 5,000 networks as a function of the number of links removed, K, under the QCQP approach and also by removing links by order of edge centrality and bridgeness measures (Figure 11). Because the network is not fully connected, about 20% of susceptible nodes are not at risk for infection even if no links are removed (K = 0). As K increases, the fraction of susceptible nodes saved from infection increases smoothly under all four link removal algorithms. As in the case of finite scale-free networks, the QCQP approach saves the greatest fraction of susceptible nodes for a given K. In fact, the QCQP approach is able to fully separate infected nodes from susceptible nodes if more than 45 links are removed (30% of total links), while removing 45 links in order of SI edge centrality saves only 90% of susceptible nodes and in order of standard edge centrality or bridgeness only 67%, on average.

Figure 11.

Average fraction of susceptible nodes saved from infection in a residential hotel network of injection drug use as a function of the number of links removed, K, using the QCQP approach (solid line), the SI edge centrality measure (dashed line), the standard edge centrality measure (dotted line), and the bridgeness index (circle label). The performance bound derived from the SDP is also shown (cross label).

Though we cannot compare these approaches to the optimal solution, the bound provided by the SDP offers some context for their performance. The difference between the performance achieved by the QCQP approach and the upper bound on the fraction of susceptible nodes that can be saved provides a worst-case bound on the suboptimality of the QCQP algorithm. In the case of the Winnipeg hotel network, using the SDP bound, we can say that the QCQP approach is guaranteed to be within a factor of 0.6 of the optimal value, though in reality it is likely to be much closer.

The difference in performance between the QCQP approach and removal of links in order of edge centrality or bridgeness, which ignores the infection pattern, increases with the number of links removed. For a given K, this difference represents the value of information of knowing the infection status of nodes in the network. For example, for K = 20, the QCQP approach saves about 50% more susceptible nodes than the algorithms that ignore the infection pattern. The value (in health benefits and averted costs of infection) of saving 50% more susceptible nodes then represents how much a decision maker should be willing to invest in disease surveillance to acquire knowledge of the infection pattern in this particular contact network.

6. Discussion

We have described a novel approach to the quarantining problem for preventing the spread of infectious diseases. Unlike previous work on epidemic prevention, which focuses on the vaccination of nodes in a network, we examine the problem of link removal to stop a disease from spreading. Using an approach based on quadratically constrained quadratic programming and semidefinite programming, we show how to near-optimally isolate susceptible nodes from infected ones, given a constraint on the number of links that can be removed. This provides important insights into the real-life problem of how to contain the spread of a disease when faced with resource limitations. For example, applying the QCQP approach to a network of residential hotels used as sites for injection drug use can help identify targets for reducing needle sharing where public health initiatives and harm reduction programs would best prevent the spread of disease.

Validating the approach over small networks, we found that the optimal partition was identified at least 70% of the time, though performance was much higher for regular networks with low connectivity. While the QCQP approach did not always identify the optimal partition, it did save nearly as many susceptible nodes from infection. Furthermore, we found that the QCQP approach is more efficient in identifying critical links than other measures of link significance, such as edge centrality and bridgeness. This in part because the QCQP approach takes into account the infection status of the nodes in the network. The increase in the number of infections prevented by the QCQP approach as compared to removing links according to standard edge centrality or bridgeness measures represents the value of knowing the infection status of the nodes in the network. This could could help decision makers estimate the worth of disease surveillance in their particular network structures.

Even when compared against measures of link significance that account for the infection pattern in the network, such as the SI edge centrality measure, the QCQP approach is still more efficient. This is because it holistically identifies a set of K links, rather than greedily considering removing one link at a time, and because it explicitly formulates the problem in terms of the true objective; that is, as a minimization of the number of susceptible nodes at risk for infection. This is contrast to previous work that makes use of intuitive measures, such as edge centrality, to guess which links in the network are critical. Though edge centrality does correlate with a link being critical in maintaining the connectivity of the network (or in maintaining paths between susceptible and infected nodes in the case of SI edge centrality), an algorithm removing links by edge centrality seeks to greedily minimize the maximum edge centrality in the network, which does not necessarily minimize the number of susceptible nodes at risk for infection. In addition, because the QCQP approach is formulated in an optimization framework, additional constraints and/or competing objectives can be explicitly incorporated.

The QCQP approach relies upon solving a semidefinite program. Generic SDP solvers make use of interior-point methods, which are polynomial time algorithms, so the computation time scales quite rapidly as the size of the problem grows. Using basic computational resources, we were able to apply the QCQP algorithm to networks of up to 200 nodes. The QCQP approach could potentially be extended to larger networks by exploiting the specific structure of the link removal problem, such as sparsity in the adjacency matrix A, to improve efficiency and by leveraging more sophisticated large-scale and distributed optimization algorithms to facilitate scalability [23, 24, 25].

Future work could introduce considerations of the dynamics of the spread of an epidemic over time. For example, future projects could consider the following formulation: in each time step, only a certain number of links can be removed, and the number of infected nodes evolves via the contact network according to some disease transmission process. Given such a scenario, how should the limited link-removal resources be utilized dynamically over time to minimize the spread of the disease across the network? The QCQP approach can be used as a starting point in this line of research, although other optimization techniques such as dynamic programming could also be incorporated. The results of such a study could have interesting implications for real-life epidemic response, where limited resources must be deployed in response to an evolving epidemic.

Highlights.

Removing links from a contact network may prevent the spread of disease.

We developed an optimization algorithm for identifying critical links.

Achieves near optimal performance on small networks.

Outperforms other link removal algorithms.

May be used to strategically target disease prevention efforts in a contact network.