Rigorous A-Posteriori Assessment of Accuracy in EMG Decomposition

Abstract

If EMG decomposition is to be a useful tool for scientific investigation, it is essential to know that the results are accurate. Because of background noise, waveform variability, motor-unit action potential (MUAP) indistinguishability, and perplexing superpositions, accuracy assessment is not straightforward. This paper presents a rigorous statistical method for assessing decomposition accuracy based only on evidence from the signal itself. The method uses statistical decision theory in a Bayesian framework to integrate all the shape- and firing-time-related information in the signal to compute an objective a-posteriori measure of confidence in the accuracy of each discharge in the decomposition. The assessment is based on the estimated statistical properties of the MUAPs and noise and takes into account the relative likelihood of every other possible decomposition. The method was tested on 3 pairs of real EMG signals containing 4–7 active MUAP trains per signal that had been decomposed by a human expert. It rated 97% of the identified MUAP discharges as accurate to within ±0.5 ms with a confidence level of 99%, and detected 6 decomposition errors. Cross-checking between signal pairs verified all but 2 of these assertions. These results demonstrate that the approach is reliable and practical for real EMG signals.

I. Introduction

The process of estimating the firing patterns of multiple simultaneously active motor units (MUs) from an EMG signal is referred to as EMG decomposition. A number of automatic and computer-aided methods have been developed [1]–[15]. EMG decomposition is used to study the neural control of movement [16]–[25], diagnose neuromuscular disorders [26], [27], and characterize MU architecture [28], [29].

EMG decomposition is possible in signals in which MUs have distinct motor-unit action potentials (MUAPs) and regular firing patterns. However, because of background noise, MUAP shape and firing variability, and obfuscation when MUAPs superimpose, the true composition of the signal is not always obvious. Therefore, in order to know whether the results obtained by decomposition are scientifically valid, it is important to have a way to assess their accuracy.

The accuracy that can be achieved in decomposing a particular signal depends both on the characteristics of the signal and on the capability of the algorithm. If a signal is too complex, or if the MUAPs are too similar, it might not be possible to determine the true composition with complete certainty. Algorithmic performance can be tested using signals whose true composition is already known [30]. However, there is no way to be sure that the same performance seen with test signals can necessarily be expected for new signals with different characteristics.

Assessment of decomposition accuracy for a signal whose true composition is not already known must be based on evidence provided by the signal itself. Is the decomposition self consistent? Is it physiologically plausible? Does it fully account for all the activity in the signal? Many decomposition algorithms provide indices or graphical representations in this regard to characterize the consistency of the MUAP waveforms, the regularity of the firing patterns, and the fit between the estimated MUAP trains and the signal [1], [6], [9], [14], [31]. These representations can provide convincing evidence that the decomposition is plausible, but they do not constitute a rigorous proof that it is correct and complete.

In this paper we use statistical decision theory in a Bayesian framework to integrate all the evidence provided by the signal into a rigorous statistical assessment of decomposition accuracy. The approach involves computing the posterior probability that the given decomposition is correct, based on the estimated statistical properties of the MUAPs and noise and taking into account the relative likelihood of every other possible decomposition. The analysis is tolerant of a certain amount of abnormal or anomalous activity, which often occurs in real signals. If it is very unlikely that any other set of firing patterns could have produced the signal, then the given decomposition can be accepted as correct with a high degree of confidence. Otherwise it cannot. The final result of this aposteriori (AP) analysis is an objective measure of confidence in the accuracy of each discharge in the decomposition.

In this paper, we consider only single-channel, time-invariant signals of limited complexity, which includes many signals recorded with millimeter-sized electrodes during low-force, constant, isometric contractions. For signals with clearly distinguishable, regularly firing MUAPs and few anomalies, the AP analysis can provide a statistically sound estimate of decomposition accuracy. We refer to these as “good” signals—signals that an experienced human operator would be able to decompose with a high degree of subjective confidence. The AP analysis now provides a way to document that confidence objectively. Of equal importance, if the MUAPs or firing patterns are ambiguous, the AP analysis will indicate that ambiguity. The analysis thus serves a similar function for EMG decomposition that confidence intervals and tests of statistical significance do for other measurements: to provide a solid justification for further inferences where there is reasonable certainty and a safeguard against faulty inferences where there is reasonable doubt.

II. Overview

A. Notation

Waveforms are represented as continuous functions of time: s(t). Each waveform is defined over a particular interval and is assumed to equal zero outside that interval. The interval is indicated when the waveform is first introduced using the notation s(t₀ : t₁). In particular, the equation s(t₀ : t₁) = f (t) means that s(t) = f (t) for t₀ ≤ t < t₁ and s(t) = 0 otherwise. Although equations involving waveforms are given in continuous time, it is assumed that computations involving them are actually done in discrete time with sampling rate f_s, that sampling-theoretic interpolation is used for time shifts that are non-integer multiples of the sampling interval 1/f_s [32], and that the waveform energy ||s||² is calculated as a sum of squared sample values. The use of continuous-time notation merely simplifies the presentation by hiding the bookkeeping details associated with discrete indexing. The equations and pseudocode are not necessarily optimized for computational efficiency. In general, variables associated with the given decomposition are marked with a tilde: ${\stackrel{\sim }{t}}_{ij}$, variables estimated by the algorithm are marked with a hat: ${\hat{t}}_{ij}$, and the corresponding true values are unmarked: t_ij.

B. Problem statement and assumptions

We are given an EMG signal s(0 : l_s) and a set of estimated firing times $\tilde{T}$:

$$\stackrel{\sim }{T}=\{{\stackrel{\sim }{t}}_{ij}:j=1,\dots ,{\stackrel{\sim }{n}}_i,i=1,\dots ,{\stackrel{\sim }{n}}_u\}$$ (2.1)

where l_s is the length of the signal, ${\stackrel{\sim }{t}}_{ij}$ is the jth estimated firing time of MU i, ñ_i is the estimated number of firings of MU i, and ñ_u is the estimated number of active MUs. We refer to such a set of firing times as an annotation of s(t).

We assume that $\stackrel{\sim }{T}$ provides a reasonably accurate description of the true composition of s(t). Specifically, we assume that the ñ_u MUs specified by $\stackrel{\sim }{T}$ are all valid, and that therefore the true composition of s(t) can be written as follows:

$$s(0:l_s)=\sum _{i=1}^{{\stackrel{\sim }{n}}_u}\sum _{j=1}^{n_i}{w}_{ij}(t-t_{ij})+z(t)$$ (2.2)

where t_ij, j = 1, …, n_i are the true firing times of MU i, w_ij (−l_w : l_w) is the MUAP waveform of the jth discharge of MU i, l_w is the MUAP half width, which, for simplicity, we assume is the same for all MUAPs and is known a-priori, z(0 : l_s) is the background noise, and any other MUAP trains that are present in s(t) but not included in $\stackrel{\sim }{T}$ are treated as part of the background noise.

The problem is to determine how accurately the firing times specified in $\stackrel{\sim }{T}$ correspond to the true firing times. The true firing times are not known, and will be treated, in a Bayesian sense, as random variables. We assume that $\stackrel{\sim }{T}$ is accurate enough to provide reasonably accurate estimates of the statistical characteristics of the MUAP waveforms, firing behavior, and noise.

C. Posterior probability

Our assessment of the accuracy of $\stackrel{\sim }{T}$ will be based on the posterior probability $P\left(\stackrel{\sim }{T}\right|s)$. This is the probability that the times in $\stackrel{\sim }{T}$ are the true firing times, given all the evidence contained in s(t). By Bayes’ rule, $P\left(\stackrel{\sim }{T}\right|s)$ can be written as follows:

$$P(\stackrel{\sim }{T}\mid s)=\frac{P(s\mid \stackrel{\sim }{T})P(\stackrel{\sim }{T})}{{\sum }_{T}P(s\mid T)P(T)}$$ (2.3)

where T is an arbitrary annotation, P(s|T) is the probability that if the MUs discharged as in T they would have produced s(t), and P(T) is the probability that the MUs would have discharged as in T in the first place [33]. The former factor depends on the statistical characteristics of the MUAP waveforms and background noise, and the latter on the statistical characteristics of the MU firing behavior.

An essential component of (2.3) is the normalization, which involves summing over all possible annotations T. This is challenging because of the large number of possible annotations. One approach is to consider that each MU can either discharge or not discharge in each discrete sampling interval [34]. This gives2^ñ_ul_sf_spossible annotations, where f_s is the sampling rate. This is too many possibilities to consider in a practical algorithm.

We take a more pragmatic approach and partition s(t) into active and inactive segments. An active segment is a segment in which the signal rises significantly above the level of the background noise. Based on our experience with “good” EMG signals that have been adequately high-pass filtered, we assume that every true MU discharge results in an active segment—in other words, that there is a negligible chance of two or more MUAPs superimposing in a such a way that their sum cannot be distinguished from the background noise. We further assume that the active segments are short enough, and the MU interdischarge intervals long enough, that each active segment contains at most only one discharge of any given MU. Under these assumptions, MU discharges only occur during the active segments, and in a particular active segment each MU can either discharge or not discharge. This gives a total of 2^ñ_un_a possible “segment-wise” annotations, where n_a is the number of active segments. This number is still quite large, but, as we will show, the problem can be factored in such a way that each annotation does not have to be considered in its entirety.

We represent a segment-wise annotation by the set X = {x₁,...,x_na}, where ${\mathbf{x}}_k=[x_{k1},\dots ,x_{k{n}_{\stackrel{\sim }{u}}}]\in {[0,1]}^{{\stackrel{\sim }{n}}_u}$ denotes the MU combination that discharges in active segment k, with x_ki = 1 if MU i discharges in the segment and 0 if it doesn’t. Analogous to $P\left(\stackrel{\sim }{T}\right|s)$, the posterior probability of the segment-wise annotation $\tilde{X}$ that corresponds to $\stackrel{\sim }{T}$ is

$$P(\stackrel{\sim }{X}\mid s)=\frac{P(s\mid \stackrel{\sim }{X})P(\stackrel{\sim }{X})}{{\sum }_{X}P(s\mid X)P(X)}$$ (2.4)

where P(s|X) and P(X) are the shape- and firing-time related probabilities analogous to P(s|T ) and P(T). To compute $P\left(\stackrel{\sim }{X}\right|s)$ rigorously would still require consideration of all the different possible firing times within each active segment. Again we take a pragmatic approach. For computing $P\left(\stackrel{\sim }{X}\right|s)$ we assume that within each active segment the firing times for a particular MUAP combination are those that give the best fit between the MUAPs and the signal. Then we separately estimate how likely those times are to be correct.

By itself, the value of $P\left(\stackrel{\sim }{X}\right|s)$ does not convey what one generally thinks of as the accuracy of the annotation. For example, if there is uncertainty about only one active segment, then $P\left(\stackrel{\sim }{X}\right|s)$ could be close to 0.5, even though the rest of the annotation is highly confident. We will therefore also use the AP framework to compute the marginal posterior probabilities of the individual discharges, i.e., $P\left({\stackrel{\sim }{x}}_{ki}\right|s)$. This is the probability that the annotation of active segment k is correct with respect to MU i, given all the evidence in the signal. It can be thought of as a level of confidence in the accuracy of this particular annotation.

III. Estimation of Statistical Parameters

We assume that the given annotation $\stackrel{\sim }{T}$ is accurate enough to provide reliable estimates of the statistical properties of the true MUAP waveforms, firing behavior, and background noise. This is not unreasonable if s(t) is a “good” signal as described in the Introduction and if $\stackrel{\sim }{T}$ is the result of a reasonably competent decomposition. If $\stackrel{\sim }{T}$ does not provide good statistical estimates, then the mismatch between the signal and the statistical model will tend to undermine confidence in $\stackrel{\sim }{T}$, discouraging overestimation of its accuracy.

We assume that the statistical characteristics of the MUAPs and noise are time invariant and follow known distributions. We typically analyze signals in 5 second intervals because this is long enough to obtain reasonably accurate estimates of the statistical parameters, but short enough that the parameters are not likely to change significantly during the interval. Since any errors in $\stackrel{\sim }{T}$ are likely to produce outlying sample values that could bias the estimates, we use robust methods to exclude outliers.

A. Firing statistics

The intervals between the successive discharges of a steadily firing MU during a constant force contraction have a stationary probability distribution that is very close to normal, with a standard deviation between about 10 and 25% of the mean [35]. If the true distribution is not exactly normal, the differences are not likely to be statistically distinguishable over relatively short signals (≤ 5 s.). For the sake of simplicity we assume that the intervals are independent both within and between trains. Therefore the probability density that successive discharges of MU i occur at times t₁ and t₂ is approximated by

$$p_{Ii}(t_1,t_2)\approx \frac{1}{\sqrt{2\pi }{\widehat{\sigma }}_{Ii}}exp\frac{-{(t_2-t_1-{\widehat{\mu }}_{Ii})}^2}{2{\widehat{\sigma }}_{Ii}^2}$$ (3.1)

where û_Ii and ${\widehat{\sigma }}_{Ii}^2$ are the estimated mean and variance. The probability density of the first and last partial intervals at the beginning and end of the signal are given by hazard functions [36]. For convenience we also use the notation p_Ii to refer to these intervals by defining

$$p_{Ii}(t_1,t_2)\approx \frac{1}{2{\widehat{\mu }}_{Ii}}\text{erfc}\frac{t_2-t_1-{\widehat{\mu }}_{Ii}}{\sqrt{2}{\widehat{\sigma }}_{Ii}}$$ (3.2)

when t₁ = 0 or t₂ = l_s.

For each MU i, û_Ii and ${\widehat{\sigma }}_{Ii}^2$ are estimated as the mean and variance of the intervals ${\stackrel{\sim }{t}}_{ij+1}-{\stackrel{\sim }{t}}_{ij},j=1,\dots ,{\stackrel{\sim }{n}}_i-1$, with intervals lying outside 0.5 to 1.5 times the median value excluded as likely outliers, based on the expected regularity of MUs in “good” signals.

B. MUAP waveforms

Under the assumption of stationarity, each MU has a mean MUAP waveform that does not change throughout the signal. These mean waveforms are estimated as follows:

$${\widehat{w}}_i(-l_w:l_w)=\underset{j=1,\dots ,{\stackrel{\sim }{n}}_i}{\text{med}}s(t-{\stackrel{\sim }{t}}_{ij}),i=1,\dots ,{\stackrel{\sim }{n}}_u$$ (3.3)

where l_w is the MUAP half-width and med is the ensemble median.

C. MUAP variability and background noise

In the AP analysis, we will assess the probability that a particular combination of MUAPs x = [x₁,...,x_ñu] produced a given active segment s_k (t) in terms of the energy of the residual signal:

$$e^2={\Vert s_k(t)-\sum _{i=1}^{{\stackrel{\sim }{n}}_u}{x}_i{\widehat{w}}_i(t-a_i)\Vert }^2$$ (3.4)

where x_i indicates the occurrence of MUAP i and a_i indicates its offset within the segment. The background noise contributes to the residual energy at each sampling interval. By the central limit theorem, the net contribution is approximately normally distributed, with a mean and variance proportional to the length of the segment. Each MUAP also contributes to the residual energy due to its shape variability. We assume that this contribution also has an approximately normal distribution, with a mean and variance that depend on the MUAP, but not on the length of the segment. Thus the probability density of the residual noise is approximated as

$$p_{E\mathbf{x}}(e^2)\approx \frac{1}{\sqrt{2\pi }{\widehat{\sigma }}_{E\mathbf{x}}}exp\frac{-{(e^2-{\widehat{\mu }}_{E\mathbf{x}})}^2}{2{\widehat{\sigma }}_{E\mathbf{x}}^2}$$ (3.5)

where

$${\widehat{\mu }}_{E\mathbf{x}}=l_k{\widehat{\mu }}_z+\sum _{i=1}^{{\stackrel{\sim }{n}}_u}{x}_i{\widehat{\mu }}_{Ei},\text{and}{\widehat{\sigma }}_{E\mathbf{x}}^2=l_k{\widehat{\sigma }}_z^2+\sum _{i=1}^{{\stackrel{\sim }{n}}_u}{x}_i{\widehat{\sigma }}_{Ei}^2$$ (3.6)

with μ̂_z and ${\widehat{\sigma }}_z^2$ being the mean and variance of the energy of the background noise per unit time, l_k the length of the active segment, and μ̂_Ei and ${\widehat{\sigma }}_{Ei}^2$ the mean and variance of the residual energy contributed by MUAP i.

The parameters of the background noise are estimated by finding all the segments of the signal that lie at least l_w away from any estimated firing time ${\stackrel{\sim }{t}}_{ij}$ and then computing

$${\widehat{\mu }}_{Ez}=\underset{k}{\text{mean}}\frac{e_k^2}{l_k},\text{and}{\widehat{\sigma }}_{Ez}^2=\underset{k}{\text{mean}}\frac{{(e_k^2-l_k{\widehat{\mu }}_{Ez})}^2}{l_k}$$ (3.7)

where $e_k^2$ is the energy of the kth such segment, l_k is its length, segments with energy greater than 3 times the median value are excluded, and it is assumed that there are enough segments to obtain reliable estimates.

The MUAP variability parameters are estimated by first computing the residual over the entire signal based on $\tilde{T}$:

$$r(0:l_s)=s(t)-\sum _{i=1}^{{\stackrel{\sim }{n}}_u}\sum _{j=1}^{{\stackrel{\sim }{n}}_i}{\widehat{w}}_i(t-{\stackrel{\sim }{t}}_{ij}).$$ (3.8)

Then for each MU i, all the residual segments of length 2l_w that contain only a single discharge of MU i and no discharges of any other MUs are found, and the parameters are estimated as follows:

$${\widehat{\mu }}_{Ei}=\underset{k}{\text{mean}}{e}_k^2-2l_w{\widehat{\mu }}_{Ez},\text{and}{\widehat{\sigma }}_{Ei}^2=\underset{k}{var}{e}_k^2-2l_w{\widehat{\sigma }}_{Ez}^2$$ (3.9)

where $e_k^2$ is the residual energy of the kth segment, segments with energy greater than 3 times the median value are excluded, each parameter is replaced by 0 if its formula yields a negative value, and it is assumed that there are enough segments to obtain reliable estimates.

D. Anomalous events

Real EMG signals can contain extraneous events such as noise spikes, doublets, recruitment, and de-recruitment that fall outside the expected behavior of the statistical model. Because it is difficult to be certain about the true nature of such events, they will be classified as anomalies and their interpretation left to the investigator. To this end we assume that there is a small probability P_A that a given active segment or a given inter-discharge interval involves an anomalous event. P_A can also be thought of as the limit beyond which it is safer to assume that an event falls outside the statistical model rather than within it. Since it is difficult to assign a meaningful value to P_A a-priori, this value is left as a user-specifiable parameter. Our experience shows that the precise value of P_A is not critical for the confident recognition of anomalous events in otherwise “good” signals.

If an active segment involves an anomalous event, we assume that the value of the residual energy is unpredictable and can range as high as the energy of the largest MUAP. Thus the probability density that the residual energy takes on any particular value is

$${\lambda }_E=\frac{1}{\underset{i}{max}{\left|\right|{\widehat{w}}_i(t)\left|\right|}^2}.$$ (3.10)

Likewise, we assume that the length of an anomalous inter-discharge interval can range as high as the length of the signal. The probability density that the interval takes on any particular value is

$${\lambda }_I=\frac{1}{l_s}.$$ (3.11)

IV. Computing the Posterior Probability

In this section we present an algorithm for computing the segment-wise posterior probability $P\left(\stackrel{\sim }{X}\right|s)$ given by (2.4).

A. Segmentation

The threshold for an active segment is based on the size of the smallest MUAP specified in $\stackrel{\sim }{T}$. Any MUAPs smaller than this are treated as part of the background noise and not included in the analysis. The times of activity are given by $T_a=\{t:t\in \stackrel{\sim }{T}\text{or}\left|s_t\right|>{\theta }_s\}$ , where ${\theta }_s={0.6\text{min}}_i{\text{max}}_t\left|{\hat{w}}_i\right(t\left)\right|$ , with the factor 0.6 chosen to allow for some degree of destructive superposition. The signal is partitioned into active segments such that s(t) is in an active segment if min_{t′ ∈Ta}|t − t′| ≤ l_w.Let $s_k(-l_k:l_k)=s(t-{\overline{t}}_k)$be the kth active segment, where ${\overline{t}}_k$ is the midpoint and l_k is the half length. Let n_a be the number of active segments.

B. Firing-related part

To simplify computing the firing-related part of the posterior probability, we approximate the MU firing times by the times of the active segment in which they occur. Thus the approximate firing times of MU i are given by

$${\widehat{t}}_{ij}=\underset{{\overline{t}}_k}{argmin}\mid {\overline{t}}_k-{\stackrel{\sim }{t}}_{ij}\mid ,j=1,\dots ,{\widehat{n}}_i.$$ (4.1)

For convenience, we augment these times with ${\hat{t}}_{i0}\equiv 0$ and ${\hat{t}}_{i{\hat{n}}_i+1}\equiv l_s$ . These approximate times are sufficiently accurate for computing the firing interval probabilities as long as the intervals are relatively long compared to the active segment lengths. Under the assumption that the firing intervals are independent within and between MUAP trains, the firing-dependent terms in the AP probability (2.4) can be written as

$$P(X)=\prod _{i=1}^{{\stackrel{\sim }{n}}_u}\prod _{j=0}^{{\widehat{n}}_i}{P}_{Ii}({\widehat{t}}_{ij},{\widehat{t}}_{ij+1})$$ (4.2)

where

$$p_{Ii}(t_1,t_2)=(1-P_A)p_{Ii}(t_1,t_2)+P_A{\lambda }_I.$$ (4.3)

Note that P_A λ_I is the probability that the interval is anomalous.

C. Shape-related part

Since the shapes of the active segment are independent of one another, the shape-related terms in the AP probability (2.4) can be written:

$$P(s\mid X)=\prod _{k=1}^{n_a}P(s_k\mid {\mathbf{x}}_k).$$ (4.4)

Let $\mathbf{a}=[a_1,\dots ,a_{{\stackrel{\sim }{n}}_u}]$, where $a_i\equiv t_{ij}-{\overline{t}}_k\in [-l_k,l_k]$, represent the offsets of the MUAPs within active segment k. In theory, P(s_k|x_k) involves a summation over all possible values of a. To reduce the number of computations, we assume that P(s_k|x_k) can be approximated using the MUAP alignments that provides the best fit to s_k(t):

$$P(s_k\mid {\mathbf{x}}_k)\approx (1-P_A)p_{E{\mathbf{x}}_k}\left({\Vert s_k(t)-{\sum }_i{x}_{ki}{\widehat{w}}_i(t-{\widehat{a}}_i)\Vert }^2\right)+P_A{\lambda }_E$$ (4.5)

where

$$\widehat{\mathbf{a}}=\underset{\mathbf{a}}{argmin}{\Vert s_k(t)-{\sum }_i{x}_{ki}{\widehat{w}}_i(t-a_i)\Vert }^2$$ (4.6)

which can be computed using the algorithm in [37]. This approximation is generally adequate to distinguish feasible MUAP combinations from ones that are negligibly likely.

D. Normalization factor

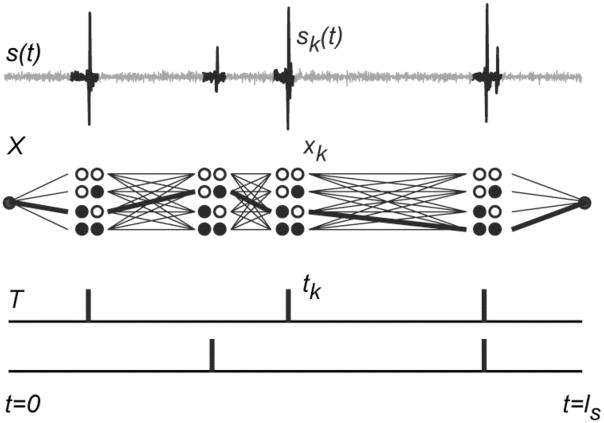
If one thinks of each possible value of x_k, i.e., each possible combination of MUAPs that could discharge during active segment k, as a node, as in Fig. 1, then each segment-wise annotation X corresponds to a path that connects to one node for each active segment. Each path has an associated likelihood P(s|X)P(X) that corresponds to one term in the denominator of (2.4).

Fig. 1.

Schematic representation of the factors involved in the calculation of the normalization factor. The signal s(t) is segmented into active segments s_k(t). For each active segment there are 2^n_u possible MUAP combinations x_k (sets of circles, each set here showing the 4 possible combinations of 2 different MUAPs). A segment-wise annotation X (heavy line) is equivalent to a path through this trellis and corresponds to a specific firing pattern T. The likelihood of the annotation is the product of shape-dependent factors associated with each active segment and firing-time-dependent factors associated with the firing pattern. Computing the normalization factor requires summing the likelihoods of all possible paths.

For a given path X, let ${\overleftarrow{t}}_{\mathrm{ki}}$ denote the most recent discharge time of MU i up to and including active segment k, i.e.,

$${\overleftarrow{t}}_{ki}=\{{\overline{t}}_{k^{\prime }}:k^{\prime }\le k,x_{k^{\prime }i}=1,x_{k^{\prime }+1i}=\cdots =x_{ki}=0\}$$ (4.7)

with ${\overleftarrow{t}}_{\mathrm{ki}}\equiv 0$ if x_1i = ··· = x_ki = 0. We define the set of the indices of the most recent discharge times of all the MUs at active segment k as the state of path X at active segment $k:{\mathbf{q}}_k\left(X\right)=[q_{k1},\dots ,q_{k{\stackrel{\sim }{n}}_u}]$, where ${\overleftarrow{t}}_{\mathrm{ki}}={\overline{t}}_{q_{\mathrm{ki}}}$ for all i. We note that the sum of the likelihoods of all the paths that have the same state q at active segment k can be factored into the product of two terms:

$$\sum _{X:{\mathbf{q}}_k(X)=\mathbf{q}}P(s\mid X)P(X)=Q_k(\mathbf{q})Q_k^{\prime }(\mathbf{q})$$ (4.8)

where Q_k (q) involves a summation over all the possible ways to arrive at the state and $Q_k^{\prime }(\mathbf{q})$ involves a summation over all possible ways to leave it.

The values of Q_k can be computed iteratively in the following way. At active segment k − 1, each element of q can have the possible values 0, …, k − 1. At active segment k, each MU i can either discharge, in which case q_ki = k, or not discharge, in which case q_ki = q_k−1i. Thus the values of Q_k can be computed as follows:

$$Q_0([0,\dots ,0])\leftarrow 1\text{for}k=1,\dots ,n_a\text{for}\mathbf{q}\in {\{0,\dots ,k\}}^{{\stackrel{\sim }{n}}_u}{Q}_k(\mathbf{q})\leftarrow 0\text{for}\mathbf{x}\in {\{0,1\}}^{{\stackrel{\sim }{n}}_u}\text{for}\mathbf{q}\in {\{0,\dots ,k-1\}}^{{\stackrel{\sim }{n}}_u}{\mathbf{q}}^{\prime }\leftarrow {[(1-x_i)q_i+x_{i}k]}_{i=1,\dots ,{\stackrel{\sim }{n}}_u}{Q}_k({\mathbf{q}}^{\prime })\leftarrow Q_k({\mathbf{q}}^{\prime })+Q_{k-1}(\mathbf{q})P(s_k\mid \mathbf{x})\prod _{i=1}^{{\stackrel{\sim }{n}}_u}{P}_{Ii}^{x_i}({\overline{t}}_{q_i},{\overline{t}}_{q_i^{\prime }})$$ (4.9)

The normalization factor D is given by a sum over all the states at the last active segment:

$$D=\sum _{\mathbf{q}\in {\{0,\dots ,n_a\}}^{{\stackrel{\sim }{n}}_u}}{Q}_{n_a}(\mathbf{q})\prod _{i=1}^{{\stackrel{\sim }{n}}_u}{P}_{Ii}({\overline{t}}_{q_i},l_s).$$ (4.10)

Note that D can also be computed by starting at the end of the signal and working backwards to the beginning. In this case the path state equals the set of nearest discharge times occurring at or after ${\overline{t}}_k$. The computation involves a set of factors similar to the Qs, but representing backward sums from the end of the path. Let us call these factors R_k (q).

E. Pruning

The time needed to compute the normalization factor grows exponentially with the number of MUs. This time can be reduced significantly by pruning nodes and paths that have only a negligible probability of being correct. In computing the shape-related probabilities, if a lower bound on the residual energy can be determined for a particular MUAP combination x:

$$e_b^2\le \underset{\mathbf{a}}{min}{\Vert s_k(t)-{\sum }_i{x}_i{\widehat{w}}_i(t-a_i)\Vert }^2$$ (4.11)

and if $p_{E\mathbf{x}}(e_b^2)<P_A{\lambda }_E$, then P(s_k|x) can be approximated by P_A λ_E without having to compute the minimum residual energy itself. We do not yet have an efficient way to compute this bound.

In computing the factors Q_k (q), it is only necessary to keep track of those states q that make a non-negligible contribution to the overall likelihood. Unfortunately, a state with a relatively small Q_k may turn out to be on a path that has a high overall likelihood, but this may not be known until much later along the path. We only keep track of states for which Q_k (q) > (P_A λ_E)² max _q′Q_k (q′), but there are probably better criteria. The effect of pruning can be checked by comparing the normalization factors computed in the forward and reverse directions. If they are not equal, then some paths with appreciable likelihood must have been pruned. If they are equal, then the pruning was almost certainly benign.

V. Firing Time Accuracy

In determining the shape-related part of the AP probability we assumed that the offsets of the MUAPs within each active segment were those that gave the best fit. In this section we consider the accuracy of that assumption.

For a given active segment s_k and a given set of MUs x that includes MU i, the probability density of the offset of MUAP i is

$$p(a)={\int }_{\mathbf{a}}{p}_{E\mathbf{x}}\left({\Vert s_k(t)-{\sum }_{i^{\prime }}{x}_{i^{\prime }}{\widehat{w}}_{i^{\prime }}(t-a_{i^{\prime }})\Vert }^2\right)\delta (a_i-a)d\mathbf{a}$$ (5.1)

where δ is the Dirac delta function. Note that since p_Ex is nonlinear, the peaks of p(a) can be much narrower than one sampling interval of s(t). The level of certainty about the accuracy of a particular value ã can be expressed in terms of the likelihood that the true value is within a particular interval ±θ_t ofã. This probability can be written as:

$$P(\mid \stackrel{\sim }{a}-a\mid <{\theta }_t)=\frac{I_1}{I_1+I_2}$$ (5.2)

where

$$I_1={\int }_{\stackrel{\sim }{a}-{\theta }_t}^{\stackrel{\sim }{a}+{\theta }_t}p(a)da,\text{and}{I}_2={\int }_{-l_k}^{l_k}p(a)da-I_1$$ (5.3)

with l_k being the segment half-width. Calculating this probability involves summation over all possible offsets of all the MUAPs. Instead, we compute a lower bound (see Fig. 2). First we approximate p(a) heuristically by the conditional probability given that all the other MUAPs are at their optimal offsets:

$$p(a)\approx \widehat{p}(a)=p_{E\mathbf{x}}(f(a))$$ (5.4)

where

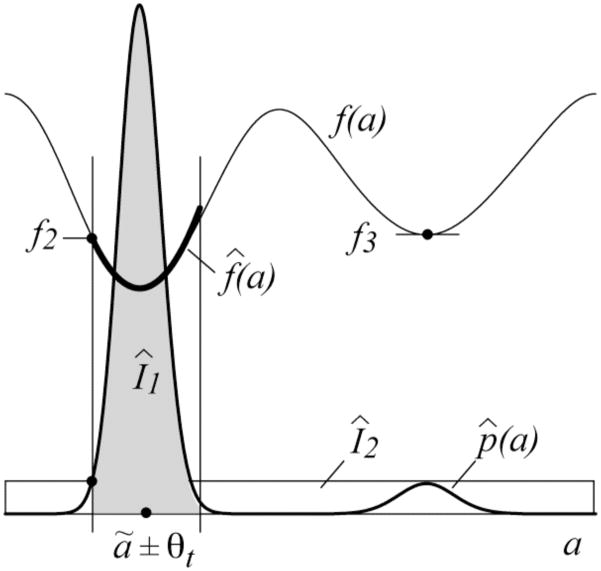
Fig. 2.

Quantities involved in the bound on the firing-time accuracy.

$$f(a)=\underset{\mathbf{a}:a_i=a}{min}{\Vert s_k(t)-{\sum }_{i^{\prime }}{x}_{i^{\prime }}{\widehat{w}}_{i^{\prime }}(t-a_{i^{\prime }})\Vert }^2$$ (5.5)

For a particular value of a, f (a) can be computed using the algorithm in [37].

The highest peak in p̂ (a) occurs at a = â_i, where

$$\widehat{\mathbf{a}}=\underset{\mathbf{a}}{argmin}{\Vert s_k(t)-{\sum }_i{x}_{i^{\prime }}{\widehat{w}}_{i^{\prime }}(t-a_{i^{\prime }})\Vert }^2.$$ (5.6)

In the vicinity of â_i, f (a) can be approximated by

$$f(a)\approx \widehat{f}(a)=f({\widehat{a}}_i)+4f_s^2(f_1-f({\widehat{a}}_i)){(a-{\widehat{a}}_i)}^2$$ (5.7)

where

$$f_1=max\left(f({\widehat{a}}_i-\frac{1}{2f_s}),f({\widehat{a}}_i+\frac{1}{2f_s})\right)$$ (5.8)

and f_s is the sampling rate of s(t). I₁ must include at least the mass from this main peak, so

$$i_1\le {\widehat{I}}_1={\int }_{\stackrel{\sim }{a}-{\theta }_t}^{\stackrel{\sim }{a}+{\theta }_t}{p}_{E\mathbf{x}}(\widehat{f}(a))da$$ (5.9)

which can be computed numerically. The smallest value of f (a) outside the region of interest is given by

$$f_2=min(f(\stackrel{\sim }{a}-{\theta }_t),f(\stackrel{\sim }{a}+{\theta }_t),f_3)$$ (5.10)

where

$$f_3=\underset{\begin{array}{c}\mathbf{a}:\mid a_i-\stackrel{\sim }{a}\mid >{\theta }_t\\ \mathbf{a}\text{is}\text{a}\text{local}\text{minimum}\end{array}}{min}{\Vert s_k(t)-{\sum }_{i^{\prime }}{x}_{i^{\prime }}{\widehat{w}}_{i^{\prime }}(t-a_{i^{\prime }})\Vert }^2.$$ (5.11)

The value of f₃ can be found using the algorithm in [37] by presetting the binary array that keeps track of which alignments have already been tried to prevent consideration of alignments in the vicinity of [ã − θ_t,ã + θ_t]. Since f₂ is the smallest value outside the region of interest,

$$I_2\le {\widehat{I}}_2=2p_{E\mathbf{x}}(f_2)l_k.$$ (5.12)

Therefore, the final bound, written in terms of firing times rather than offsets, and explicitly stating the conditioning terms, is

$$P\left(\mid {\stackrel{\sim }{t}}_i-t_i\mid <{\theta }_t\mid s_k,\mathbf{x}\right)\ge \frac{{\widehat{I}}_1}{{\widehat{I}}_1+{\widehat{I}}_2}.$$ (5.13)

VI. Measures of Accuracy

A. Posterior accuracy of a discharge

The AP framework makes it possible to compute the posterior probabilities of individual discharges. Specifically, the joint posterior probability that MU i discharged in s_k and that the estimated discharge time ${\stackrel{\sim }{t}}_i$ was within ±θ_t of the true firing time t_i is given by

$$P(x_{ki}=1,\mid {\stackrel{\sim }{t}}_i-t_i\mid <{\theta }_t\mid s)=\sum _{\mathbf{x}:x_i=1}P({\mathbf{x}}_k=\mathbf{x}\mid s)P(\mid {\stackrel{\sim }{t}}_i-t_i\mid <{\theta }_t\mid s_k,\mathbf{x}).$$ (6.1)

P(x_k = x|s) is the posterior probability that MUAP combination x fired during segment k given all the evidence in the signal. It can be computed as follows:

$$P({\mathbf{x}}_k=\mathbf{x}\mid s)=\sum _{\begin{array}{c}\mathbf{q}\in {\{0,\dots ,k\}}^{{\stackrel{\sim }{n}}_u}\\ {\mathbf{q}}^{\prime }\in {\{k,\dots ,n_a+1\}}^{{\stackrel{\sim }{n}}_u}\end{array}}\frac{Q_k(\mathbf{q})R_k({\mathbf{q}}^{\prime })}{P(s_k\mid \mathbf{x})}\prod _{i=1}^{{\stackrel{\sim }{n}}_u}{P}_{Ii}^{x_i}({\overline{t}}_{q_i},{\overline{t}}_{q_i^{\prime }})J(x_i,q_i,q_i^{\prime })$$ (6.2)

where Q_k (q) and R_k (q′) are the forward and backward factors of the AP normalization and $J(x_i,q_i,q_i^{\prime })=1$ if x_ik, q_i, and $q_i^{\prime }$ all equal k or all do not equal k and is 0 otherwise. J selects only those states q and q′ that occur on paths that pass through node x_k = x. The posterior probability that MUAP i discharged in active segment k without regard to the precise firing time is given by:

$$P(x_{ki}=1\mid s)=\sum _{\mathbf{x}:x_i=1}P({\mathbf{x}}_k=\mathbf{x}\mid s).$$ (6.3)

B. Rating individual discharges

The accuracy of each discharge in $\stackrel{\sim }{T}$ can be summarized using the rating system shown in Table I. Here ${\stackrel{\sim }{x}}_{ki}$ is the annotation of active segment k with respect to MU i according to $\stackrel{\sim }{T}$, and P(x_ki = 1|s) is the posterior probability that MU i discharged during the segment given all the information in the signal. The four corner ratings (Likely True Positive, etc) correspond to the basic contingencies of binary decision theory (True Positive, etc., see [30]), except that, since the true annotation is not known, “true” and “false” can only be understood in a probabilistic sense.

TABLE I.

Accuracy Rating for Annotation of MUi in Active Segment k

AP Probability P(xki = 1|s)	Annotation ${\stackrel{\sim }{x}}_{ki}$
	1	0
≥ 0.95	LTP: Likely True Positive	LFN: Likely False Negative
≥ 0.05	UP: Uncertain Positive	UN: Uncertain Negative
< 0.05	LFP: Likely False Positive	LTN: Likely True Negative

The Likely True Positive rating can be subdivided according to the level of certainty and the precision of the firing-time estimate as in Table II. For example, an LTP (0.1 ms) rating means that there is at least a 99% chance that MU i discharged within ± 0.1 ms of the time listed in $\stackrel{\sim }{T}$. In other words, one can be 99% confident that this annotation is correct at this level of precision. A precision of ±0.5 ms has been suggested as adequate for accurate calculations of instantaneous firing rates [30]. A precision of ±0.1 ms represents a higher firing-time accuracy that is often achievable for MUAPs with high signal-to-noise ratios. A precision of ±5 ms represents a lower accuracy that is achieved when a MUAP is suspected to occur within a particular active segment, but the precise firing time within the segment cannot be determined because of anomalous or residual noise. Different precisions could also be chosen.

TABLE II.

Ratings for Likely True Positives

AP Prob	Precision (θt)	Rating
≥ 0.99	± 0.1 ms	LTP (0.1 ms)
≥ 0.99	± 0.5 ms	LTP (0.5 ms)
≥ 0.99	± 5.0 ms	LTP (5 ms)
≥ 0.95	± 5.0 ms	LTP (95%)

The LTN and LFP ratings indicate probable annotation errors. The Uncertain ratings correspond to situations in which it is not possible to be certain from the information available in the signal whether the annotation is correct or not.

C. Summarizing the results

The accuracy of the entire estimated firing pattern of MU i can be summarized in terms of the percentage of discharges that are accurate at a certain level of confidence:

$$\text{Accuracy}=n_{\text{LTP}\ast }/\sum _{k=1}^{n_a}P(x_{ki}=1\mid s)\times 100\%$$ (6.4)

where n_LTP* is the number of estimated discharges that are rated likely true positives at a given level of confidence and precision and the denominator estimates the total number of true discharges. This index would be reported by stating, for example, that X% of the estimated discharge times of MU i are accurate to within ± 0.1 ms at a confidence level of 99%.

D. Unexplained activity

Another measure that reflects on the accuracy of an annotation is the amount of activity that it fails to explain. The total number of events that cannot be explained in terms of the model assumptions can be estimated by

$${\widehat{n}}_A={\sum }_k\frac{P_A{\lambda }_E}{P(s_k\mid {\stackrel{\sim }{\mathbf{x}}}_k)}+{\sum }_{ij}\frac{P_A{\lambda }_I}{P_{Ii}({\stackrel{\sim }{t}}_{ij},{\stackrel{\sim }{t}}_{ij+1})}.$$ (6.5)

If this number is small, it means that the annotation plausibly explains all the activity in the signal, except, perhaps, for a few anomalous events. In this case there is no reason to doubt the credibility of the accuracy assessment. On the other hand, a large number points to a serious discrepancy between the signal and the model assumptions and is reason to doubt the credibility of the assessment.

This number is also useful for judging whether or not the given annotation includes all the active MUs in the signal. If ${\hat{n}}_A$ is small, then one can be confident that all the MUAP trains in the signal with amplitudes > θ_s were included in the annotation. Otherwise, some MUAP trains may have been left out.

VII. Experimental Results

A. Methods

We have implemented a proof-of-concept version of the AP algorithm in Matlab and tested it on three pairs of “good” EMG signals collected during different experiments in our laboratory. The two signals in each pair were recorded from nearby sites in the same muscle, making it possible to crosscheck the decomposition results [38], [39]. The signals were recorded using monopolar needle or fine-wire electrodes (1 mm exposed conductor) during 20-second-long, low-force, isometric contractions at a sampling rate of 10 kHz. The signals are summarized in Table III, and segments of the two signals from pair 1 are shown in Fig. 3(a). The analysis software and signals are available at www.emglab.net.

TABLE III.

Summary of EMG signals

Pair	Muscle	Signal	# MUs	Mean firing rate (pps)	# Common MUs
1	BR	1.1	4	10.2	4
		1.2	6	9.4
2	TA	2.1	5	9.3	5
		2.2	7	9.2
3	BF	3.1	5	9.3	4
		3.2	5	8.7

BR=brachioradialis, TA=tibialis anterior, BF=biceps femoris.

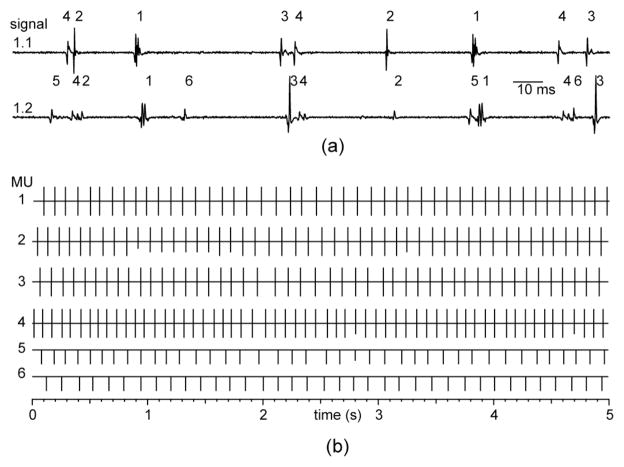
Fig. 3.

(a) Annotated segments of EMG signals from set 1. The MUAPs of the common MUs are offset in the two signals because of conduction delay between the two electrodes. (b) Estimated MU firing times for the first 5 seconds of signals 1.1 and 1.2. The times for signal 1.1 are plotted upward from the solid lines and those from signal 1.2 are plotted downward (after correction for the mean inter-signal offsets). The length of each line segment indicates the AP accuracy rating: full length = LTP (0.1 ms), 3/4 length = LTP (0.5 ms), etc.

Each signal was digitally high-pass filtered at 1 kHz and independently decomposed using the EMGlab program with manual editing [9]. For each MU that was detected in common in both signals of a pair, every discharge was classified as to whether the two annotations agreed (after mean offset correction) to within ± 0.5 ms, ±5 ms, or did not agree.

Each annotation was also divided into four 5-s intervals, and each of these was analyzed using the AP algorithm, with parameters l_w = 2.5 ms and P_A = 0.001.

B. Results

The annotations for one interval of signals 1.1 and 1.2 are shown in Fig. 3(b), with the estimated firing times from decomposition 1.1 plotted upward from the solid horizontal lines and the those from decomposition 1.2 plotted downward. MUs 1–4 were detected in both signals, and the two annotations agreed about every discharge time to within ± 0.5 ms, confirming that these times were very probably correct.

The results of the AP analyses are indicated by the lengths of the line segments, as described in the figure caption. Every estimated firing time in annotation 1.1 was rated LTP (0.1 ms). In signal 1.2, several discharges of the smaller MUAPs received LTP (0.5 ms) or LTP (5 ms) ratings.

The overall results are summarized in Table IV. The total number of annotated discharges of all the common MUs was 4678. Of these, 4658 matched the corresponding annotation of the paired signal to within ±0.5 ms. An additional 12 matched to within ±5 ms, and 8 discharges did not match. Upon manual re-inspection, the 8 unmatched discharges were found to be due to 4 decomposition errors involving small or similarly shaped MUAPs. These errors were not corrected prior to AP analysis.

TABLE IV.

Summary of results

Cross-check	AP Analysis
	LTP**	LTP*	UP	LFP
agree ±0.5 ms	4516	119	22	1
agree ±5 ms	1	6	5	0
disagree	4	0	2	2
			UN	LFN
not seen			72	3

LTP** = LTP (0.1 or 0.5 ms), LTP* = LTP (5 ms or 95%)

The AP analysis rated 4521 of the annotations as likely correct to within ±0.5 ms, and 125 as likely correct to within ±5 ms. All but 4 of these assertions were confirmed as correct by the cross-checking results. The other 4 corresponded to the decomposition errors, and would have been confirmed if the errors had been corrected. The AP analysis rated 29 annotations as uncertain, and detected 72 uncertain negative events (i.e., possible missed discharges). These all involved very small MUAPs or noise glitches. It also correctly detected 2 false positives and 2 false negatives that resulted from the decomposition errors. Thus the AP analysis detected and correctly assessed all 4 of the decomposition errors.

One LFP and one LFN rating listed in Table IV were contradicted by the cross-checking results and so must be counted as type I errors. They occurred in a single situation that involved two adjacent active segments that both had anomalous noise glitches. The AP analysis incorrectly placed one MU discharge in one segment rather than the other. This was the only case in which confident assertions of the AP analysis were found to be in error.

In summary, the results show that for the “good” signals tested here, the accuracy assessments provided by AP analysis were largely consistent with those of an experienced human operator and comparable to those obtained by cross-checking against a second channel. The analysis was cautious when it came to small MUAPs and noise glitches, but this conservatism resulted in a very low rate of type I errors: 0.04% (2 of 4650). Even though these were admittedly fairly simple signals, it has not previously been possible to “prove” the accuracy of decompositions of even simple signals like these in a statistically rigorous way.

VIII. Discussion

Reliable assessment of the accuracy of scientific measurements is essential for judging whether they are trustworthy and thus whether inferences drawn from them are based on objective reality or only wishful thinking. In the case of EMG decomposition, accuracy assessment is difficult because of the complicated nature of the EMG signal. Many decomposition methods provide numerical or graphical indications of the self-consistency of their results, for example in terms of the regularity of the estimated firing patterns [1], [6], [9], [14], [31]. This type of assessment can provide a convincing demonstration that the results are physiological plausible, but it does not prove that they are correct or complete, and so is less than fully satisfactory for investigations of motor unit firing behavior, in which complete and accurate firing patterns are required.

In a correct decomposition, the estimated MUAP trains not only match the shape of the signal, but they also exhibit regular firing patterns, similar to the way that the pieces of a correctly assembled jigsaw puzzle not only fit together but also contribute to a coherent picture. The interlocking shape and firing-time information in the EMG signal can be conveniently combined using a Bayesian framework (Fig. 1). In this paper we have shown that this framework can be used to determine not only the relative likelihood of one decomposition with respect to another, but also its absolute likelihood with respect to all possible others. This absolute likelihood—the posterior probability—can be interpreted as a level of confidence in the accuracy of the decomposition given all the information available in the signal. We used a dynamic programming approach to normalize the posterior probability, although other approaches such as Markov chain Monte Carlo methods [40] might also be possible.

The posterior probability serves two important purposes. First, it provides an objective confirmation of accuracy where accuracy is warranted. In the most clear-cut cases, it shows that a decomposition accounts for the shape of the signal to a degree consistent with the estimated levels of MUAP variability and background noise, that the estimated firing patterns possess a consistent degree of regularity, and that it is very unlikely that the MUs could have produced the signal by firing in any other way. In such cases the decomposition results can be accepted with a high degree of confidence as an accurate representation of the true MU firing behavior.

Just as importantly, the posterior probability also points out cases in which there is reason to doubt decomposition accuracy. These are cases for which there are more than one plausible explanation and it is not possible, based only on the evidence contained in the signal, to be certain which is correct. Uncertainty can arise because of excessive noise, signal complexity, intra-MUAP shape variability, firing variability, inter-MUAP shape similarity, or deviation from the model assumptions. In such cases one cannot be sure that the decomposition results are accurate.

The AP assessment is based on fairly minimal assumptions about the EMG signal and the given decomposition: the signal should not be too complex, its statistical parameters should not change with time, and the given decomposition should provide reasonably accurate estimates of those parameters. The latter assumption introduces an unfortunate circularity, since the estimated parameters are then used to assess the decomposition from which they were estimated. This should not lead to erroneous overestimation of accuracy, however. If the given decomposition is fairly accurate to begin with, the assumption is not unreasonable. If the given decomposition is not accurate, this will result in an overestimation of the signal variability, and this, in turn, will tend to blur the distinction in relative likelihood between different possible annotations and hence to reduce confidence that any one particular annotation is correct.

To streamline the computations, some conditional probabilities that involve complicated multi-dimensional integrals are approximated by their most likely values (e.g., (4.5)). These approximations preserve the approximate relative likelihoods of the alternative conditions. Within the context of the current problem, and given the robust way that the information from different sources is integrated within the Bayesian framework, these approximations do not impair the ability to reach a confident assessment.

In using the AP assessment, it must be kept in mind that the most any statistical measure can do is report the degree to which the data matches the stated assumptions. The responsibility for making sure that the assumptions are appropriate and for providing the final physiological interpretation of the results must always lie with the investigator.

A proof-of-concept implementation of the AP algorithm written in Matlab is available as an extension for the EMGlab decomposition program at www.emglab.net. It is able to assess the decomposition accuracy of 5-second-long, low-complexity signals containing up to 6 MUAP trains in a matter of minutes. Code optimization and more efficient pruning strategies can be expected to reduce this time, making it practical to analyze signals with at least 8 to 10 MUAP trains. As signal complexity increases, however, so too does the possibility that parts of the signal may fail to have a single unambiguous explanation. Beyond a certain level of signal complexity (which will depend on the strength of the contraction and the selectivity of the electrode) it will probably not be possible theoretically to demonstrate decomposition accuracy in a convincing way based only on evidence provided by the signal itself.

Biographies

Kevin C. McGill (M’84) received the B.S. and M.S. degrees from the University of Notre Dame, Notre Dame, IN, in 1975 and 1979, respectively, and the Ph. D. degree in electrical engineering from Stanford University, Stanford, CA, in 1984.

Since 1984 he has been a Biomedical Engineer with the Rehabilitation Research and Development Center, VA Palo Alto Health Care System. His research interests include neuromuscular physiology, electromyography, and signal processing.

Hamid R. Marateb (M’10) received the B.S. and M.S. degrees from Shahid Beheshti University of Medical Science and Amirkabir University of Technology, Tehran, Iran, in 2000 and 2003, respectively.

Since 2008 he has been a Ph.D. candidate in the Laboratory of Engineering of Neuromuscular Systems, Politecnico di Torino, Turin, Italy. He was a visiting researcher at Stanford University in 2009 and at Aalborg University in 2010. His research interests include intra-muscular and surface electromyography, expert-based fuzzy systems, biomedical signal processing, design of electronic systems, and non-convex optimization.