Bayesian probabilistic population projections for all countries

Abstract

Projections of countries’ future populations, broken down by age and sex, are widely used for planning and research. They are mostly done deterministically, but there is a widespread need for probabilistic projections. We propose a Bayesian method for probabilistic population projections for all countries. The total fertility rate and female and male life expectancies at birth are projected probabilistically using Bayesian hierarchical models estimated via Markov chain Monte Carlo using United Nations population data for all countries. These are then converted to age-specific rates and combined with a cohort component projection model. This yields probabilistic projections of any population quantity of interest. The method is illustrated for five countries of different demographic stages, continents and sizes. The method is validated by an out of sample experiment in which data from 1950–1990 are used for estimation, and applied to predict 1990–2010. The method appears reasonably accurate and well calibrated for this period. The results suggest that the current United Nations high and low variants greatly underestimate uncertainty about the number of oldest old from about 2050 and that they underestimate uncertainty for high fertility countries and overstate uncertainty for countries that have completed the demographic transition and whose fertility has started to recover towards replacement level, mostly in Europe. The results also indicate that the potential support ratio (persons aged 20–64 per person aged 65+) will almost certainly decline dramatically in most countries over the coming decades.

Projections of countries’ future populations, broken down by age and sex, are used by governments for social, economic, and infrastructure planning by international organizations for development planning and monitoring and global modeling, by the private sector for strategic and marketing decisions, and by academic and other researchers as inputs to social and health research.

Most population projections are currently done deterministically, using the cohort component method (1, 2). This is an age- and sex-structured version of the basic demographic identity that the population of a country at the next time point is equal to the population at the current time point, plus the number of births, minus the number of deaths, plus the number of immigrants minus the number of emigrants. It was formulated in matrix form by Leslie (3) and is described in detail in ref. (4, chap. 6).

Population projections are currently produced by many organizations, including national and local governments and private companies. The main organizations that have produced population projections for all or most of the world’s countries are the United Nations (UN) (5), the World Bank (6), and the United States Census Bureau (7), all of which use the standard deterministic approach. Among these, the UN produces updated projections for all the world’s countries every 2 y, published as the World Population Prospects, and these are the de facto standard (8). We refer to the 2010 Revision of the World Population Prospects (5) as WPP 2010.

Standard population projection methods are deterministic, meaning that they yield a single projected value for each quantity of interest. However, probabilistic projections that give a probability distribution of each quantity of interest, and hence convey uncertainty about the projections, are widely desired. They are needed for planning purposes. For example, those planning school construction may wish to be reasonably sure of building enough capacity to accommodate all students in the future. For this the relevant projection is an upper quantile of the predictive distribution of the future school population, that is relatively unlikely to be exceeded, rather than a “best guess.” Probabilistic projections are also useful for assessing change and deviations of population outcomes from expectations and also for providing a general assessment of uncertainty about future population.

The most common approach to communicating uncertainty in population projections is the scenario, or high-medium-low, approach. In this approach, a central or main projection is first produced. Then high and low values of the main inputs to the projection model, such as fertility or mortality, are postulated, and a projection is produced with the high values and another one with the low values. These high and low trajectories are viewed as bracketing the likely future values. This approach has been criticized as having no probabilistic basis and leading to inconsistencies (9, 10).

Previous approaches to producing probabilistic population projections include ex-post analysis, time series methods, and expert-based approaches (10, 11). Ex-post analysis is based on the errors in past forecasts (12–16). The time-series analysis approach uses past time series of forecast inputs, such as fertility and mortality, to estimate a statistical time series model, which is then used to simulate a large number of random possible future trajectories. Simulated trajectories of forecast inputs are combined via a cohort component projection model to produce predictive distributions of forecast outputs (9, 17). In the expert-based method (18–21), experts are asked to provide distributions for each forecast input. These are then used to construct predictive distributions of forecast outputs using a stochastic method similar to the time series method.

Our method is most closely related to the time series approach. We simulate a large number of trajectories of future values of the total fertility rate (TFR) and convert them to age-specific fertility rates using model fertility schedules. We simulate an equal number of trajectories of life expectancy at birth for females and males and convert them to age-specific mortality rates using a variant of the Lee–Carter method (22). We convert each of these trajectories to a future trajectory of all age- and sex-specific population quantities using a cohort component model. For any future population quantity of interest, the resulting set of values is viewed as a sample from the sought predictive distribution.

To simulate future values of TFR for all countries, we use the Bayesian hierarchical model of Alkema et al. (23). This accounts for several empirical regularities: The TFR starts at a high value (typically in the range 5–9) and may initially increase, but after that it declines to a level below the replacement level of about 2.1 and then increases gradually again, eventually fluctuating around replacement level. The model represents this by a random walk with a drift that is a double logistic function (24) of TFR during the declining, or demographic transition, phase and then an autoregressive model during the phase of slow recovery. There are relatively few data points for each country, and the Bayesian hierarchical model stabilizes estimation by shrinking the estimate for each country toward a world mean (25).

To simulate future values of female life expectancy at birth for all countries, we use a Bayesian hierarchical model developed by Raftery et al. (26). This represents the empirical findings that life expectancy has been increasing steadily for most countries, that it increases most quickly for countries with “middle” levels of life expectancy (around 60 y), and more slowly for countries with lower or higher levels. It uses a random walk with drift given by a double logistic function of life expectancy. This allows for an asymptotically linear rate of increase for each country, consistent with the finding that the rate of increase of maximal life expectancy over the past 150 y has been highly linear (27).

To simulate future values of male life expectancy at birth, we need to take into account the correlation between female and male life expectancies and also of the fact that the life expectancy of females is typically higher than that of males. The gap between female and male life expectancies also has outliers, often corresponding to periods of conflict, for example, in Iraq and Bosnia. We use the regression model of Lalic (28) for the gap, with an error term that has a Student’s t-distribution rather than a normal one, thus modeling the outliers explicitly.

Results

Major Population Indicators.

We show results for five countries, chosen to represent different stages of the demographic transition, continents, and sizes: Brazil, the Netherlands, Madagascar, China, and India. The results for Brazil are shown here, and those for the other countries are shown in the SI Text. We also show some aggregated population results for major regions.

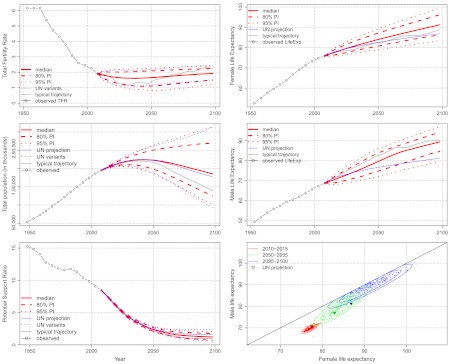
Brazil is close to completing the demographic transition in that fertility has declined below replacement level (Fig. 1, Top, Left), but it has not yet bottomed out and started to recover. Fig. 1 shows Bayesian probabilistic population projections for some of the main demographic indicators for Brazil: TFR, female and male life expectancy, total population, and the potential support ratio (PSR), defined here as the number of people aged 20–64 for each person 65 or over. The joint predictive distribution of female and male life expectancy is also shown for several future years. They are highly correlated, particularly farther into the future.

Fig. 1.

Bayesian probabilistic population projections for Brazil, 2010–2100: major population indicators. Left, Top to Bottom: total fertility rate; total population; potential support ratio (20–64 population/65+ population). Right, Top to Bottom: female life expectancy; male life expectancy; joint predictive distribution of female and male life expectancy for 2010–2015, 2050–2055 and 2095–2100. The Bayesian predictive distributions are shown in red: median—solid; 80% prediction interval—dashed; 95% prediction interval—dotted. The UN WPP 2010 projection is shown as a solid blue line. The typical trajectory is shown as a solid gray line.

Fig. 1 also includes the WPP 2010 projections with their high and low variants (5), as well as a “typical trajectory,” defined as the future trajectory for which the median absolute deviation from the median projection is the median among all the sampled future trajectories. This shows that we expect the actual outcomes to evolve less smoothly than the sequence of our median projections.

Brazil’s TFR is projected to decline slightly and then recover slowly towards replacement. Uncertainty is fairly similar to the plus or minus half a child on which the UN’s high and low variants are based. (The UN used the median projection of TFR from our method as the medium projection in its 2010 projections.) A steady increase in both female and male life expectancy is projected, with uncertainty bands that increase with the forecast horizon. In contrast, the UN’s variants do not incorporate uncertainty about mortality. We project total population to increase and then decrease, with considerable uncertainty for the distant future. The UN’s variants are similar to our 95% prediction intervals.

The potential support ratio is projected to decrease dramatically from its current level of 8.4 to 2.5 in 2050 and 1.2 in 2100. The uncertainty about the PSR is surprisingly small, with 80% prediction intervals of [2.2, 2.8] for 2050 and [0.7, 1.8] for 2100. A similarly drastic decline in PSR is projected with relatively low uncertainty for most countries, even those that have had low fertility for a long time. This has major policy implications for governments, particularly for pay as you go social security and pension systems (29–32). Our results indicate that similar issues will likely be faced by most countries, including developing ones (33, 34).

The Netherlands has completed the demographic transition, and its fertility rate has been recovering towards replacement level for the past 25 y. As seen in Fig. S1, our method projects a continuing gradual increase in TFR with uncertainty considerably smaller than that implied by the UN’s high and low variants. Our method projects a fairly flat trajectory for total population over the next century, also with much smaller uncertainty than implied by the UN variants.

Madagascar, in contrast, is still fairly early in the demographic transition, with a TFR of 4.8. Our method projects a continuing, rather slow decline of the TFR, with uncertainty somewhat greater than that implied by the UN variants (Fig. S2). Our method projects a quintupling of the population by 2100, from the current 20.7 million to 105 million. But the uncertainty is considerable, with 80% prediction interval [65,160] million. The UN variants are tighter, with low-medium-high projections of [62, 94, 139] million. Thus, if our method is well calibrated, the UN variants underestimate uncertainty for Madagascar. We found similar results for other high-fertility countries.

China’s TFR is below replacement level, and we project a slight continuing decline followed by a slow recovery, with uncertainty not dissimilar to that implied by the UN variants (Fig. S3). The total population is projected to continue rising and then to decline, with considerable uncertainty about the population in 2100, similar to that implied by the UN variants.

India is still undergoing its demographic transition, with a TFR of 2.7, and we project a continuing decline, bottoming out later in the century, with uncertainty comparable to that implied by the UN variants (Fig. S4). We project a continuing increase in total population, reaching a peak around midcentury and then starting to decline.

Age-Specific Results.

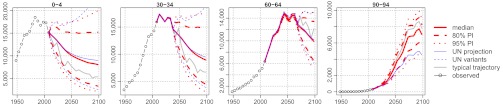
Probabilistic population projections are shown for selected age groups for Brazil in Fig. 2; the projections for all age groups are shown in Fig. S5. For each age up to age 64 or so, uncertainty is very small for the years in which the people reaching that age are already alive, and then becomes much larger for the years in which people reaching that age have not been born yet. For the former years, uncertainty is mostly due to mortality, which is low up to age 64 with little uncertainty. For the latter years, uncertainty is mostly due to fertility and is therefore substantial. The uncertainty implied by the UN variants is similar to the 95% Bayesian prediction intervals.

Fig. 2.

Bayesian probabilistic population projections for selected age groups for Brazil, 2010–2100.

The UN variants underestimate uncertainty for ages from 65 upwards, largely because they ignore uncertainty about mortality. This is particularly the case for the oldest old (80+) from 2050 onwards.

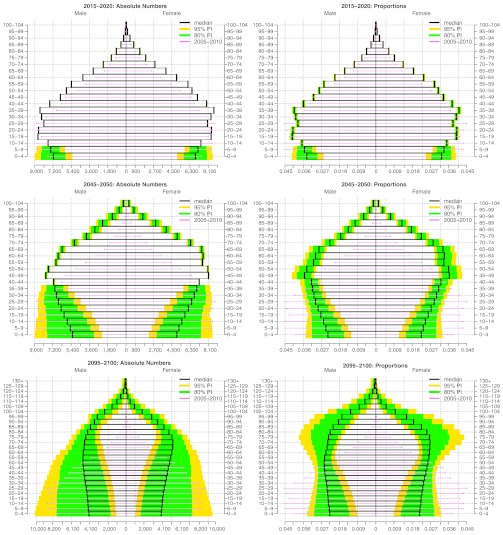
The same information is shown in a different way, by year rather than by age group, in the probabilistic population pyramids in Fig. 3. This shows uncertainty about both absolute numbers (on the Left), and the age distribution for each sex (on the Right).

Fig. 3.

Probabilistic population pyramid projections for Brazil, 2010–2100. The predictive median is shown by the black boxes. The 80% predictive intervals are shown in green and the 95% intervals in yellow. The 2005–2010 population distribution is shown by the purple horizontal lines. Left: population numbers. Right: proportions by age for each sex.

For 2015–2020 there is almost no uncertainty except for the two youngest age groups, some of whose members have not yet been born. For 2045–2050 there is considerable uncertainty about the numbers under 40, less uncertainty about the numbers over 70, and very little uncertainty about the numbers of those in the middle between 40 and 70. There is more uncertainty about the proportions between 40 and 70 than about the absolute numbers, because of uncertainty about the denominator, which is the total population.

Finally, for 2095–2100, there is considerable uncertainty about the numbers in all age groups. However, it is reasonably certain that the population will be older on average than in 2010, with lower proportions under 40 and much higher proportions 70 and older.

Aggregated Regional Results.

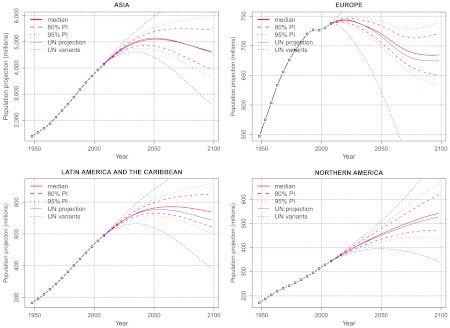
In Fig. 4 we show aggregated probabilistic population projections for four of the six major UN-defined regions of the world, compared with the current UN projections and variants (5). These aggregated results allow for some correlation between forecast errors for different countries, because projected TFR and life expectancy are assumed to be drawn from a distribution of patterns that is common to all countries. However, it does not allow for correlation between countries beyond that, and so these intervals may be too narrow.

Fig. 4.

Aggregated population projections with 80% and 95% prediction intervals, UN WPP 2010 projection and UN variants for major UN regions, 2010–2100. The probabilistic population projections are based on the assumption of statistical independence between the forecast errors of different countries.

The UN variants implicitly assume that forecast errors in the TFR are perfectly correlated across countries. In practice, cross-country correlations, when positive, are likely to be much smaller than 1 (10), and so the UN variants are likely to span too wide a range. This is particularly the case for Europe, for which TFR is lowest on average, and so the UN variants of plus or minus half a child make the largest proportional difference.

Out of Sample Validation.

To validate our method, we estimated the model based on data for the 40-y period 1950–1990 and used it to generate a predictive distribution of the full age- and sex-structured population for the 20-y period 1990–2010 for each of the 159 countries in our dataset. We then compared the resulting predictive distributions with the actual observations.

We assessed the accuracy of our point predictions using the mean absolute relative error (MARE; in %),

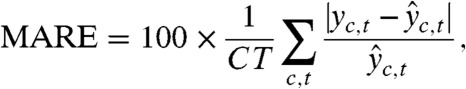where y_c,t is the observed quantity being predicted for country c and time period t, 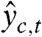is its posterior predictive median, C is the number of countries, and T the number of time periods involved in the out of sample validation. Here C = 159 and T = 4, so that the validation is based on 159 × 4 = 636 observations for each population quantity. The MARE is negatively oriented, that is, the smaller the better.

We used three criteria to assess the calibration of the prediction intervals. The standardized absolute prediction error (SAPE) is defined by

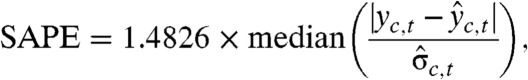where 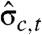is the estimated Bayesian predictive standard deviation of y_c,t. For a normal predictive distribution, the theoretical population value of this quantity is 1. Values greater than 1 suggest that the predictive distribution is underdispersed because the observations are more spread out than the predictive distribution and hence the predictive distribution underestimates the dispersion of the observations. Similarly, values of the SAPE less than 1 suggest that the predictive distribution is overdispersed.

The other two criteria are the coverages of the 80% and 95% prediction intervals, defined as the proportion of the validation sample that fall within their intervals. The closer the coverages are to their nominal values (80% and 95%), the better.

Table 1 shows the results for four major population indicators: TFR, female and male life expectancies at birth, and total population.

Table 1.

Out of sample validation of the Bayesian projections for 159 countries, 1990–2010 ^*

Quantity	MARE	SAPE	Coverage (%)
			80% PI	95% PI
Total fertility rate	0.123	1.16	72	87
Female life expectancy	0.020	0.76	83	94
Male life expectancy	0.025	0.77	83	91
Total population	0.027	1.09	73	85

^*MARE is the mean absolute relative error. SAPE is the median standardized absolute prediction error. PI refers to prediction interval. Coverage is the proportion of the 1990–2010 observations that fell within their prediction interval, in percent.

For the TFR, the MARE was 12.3%, indicating that the mean absolute error in predicting TFR was about 12% of its predicted value. The SAPE was 1.16, indicating that the observations were more spread out than the predictive distribution, by about 16%. Correspondingly, the 80% prediction intervals contained the truth 72% of the time, and the 95% prediction intervals 87% of the time.

Life expectancy was easier to predict, with MAREs under 3%. The SAPEs were 0.76 and 0.77, substantially less than 1, indicating that the observations were less spread out than the predictive distributions. However, the coverages of the prediction intervals were close to their nominal levels. Finally, total population was also accurately predicted, with a MARE of 2.7%. The predictive distributions were slightly too narrow on average, with an SAPE of 1.09. Overall, the method seems to have provided reasonably accurate and well-calibrated probabilistic projections for the 1990–2010 period.

Discussion

We have developed a Bayesian method for probabilistic population projection that provides a predictive distribution for any future population quantity of interest in a given country. It is based on Bayesian hierarchical models for the future overall fertility and mortality levels in all countries, estimated using past data for all countries. The resulting posterior predictive distributions are combined with a cohort component projection model to provide predictive distributions of any future population quantity of interest. The resulting predictive distributions were accurate and reasonably well calibrated in an out of sample calibration exercise for forecasting the most recent 20-y period.

The resulting prediction intervals for major population quantities of interest (TFR, life expectancy, total population, PSR) were for the most part fairly comparable with the UN’s (5) high and low variants for 2010–2100, even though the latter have no probabilistic interpretation. There are some notable exceptions, however. The UN’s high and low variants underestimate uncertainty about future numbers of oldest old in most countries. The UN’s variants also underestimate uncertainty about many future population quantities in countries that currently have high fertility. The UN’s variants also tend to overestimate uncertainty for low fertility countries whose fertility has bottomed out and is now recovering. These countries are mostly in Europe.

While the UN’s high, medium, and low variants were the main scenarios issued in WPP 2010, the UN also issued more realistic partially probabilistic projections that take into account uncertainty about future fertility (but not mortality) in the same way we have done here, on an experimental basis (see http://esa.un.org/unpd/wpp/P-WPP/htm/PWPP_Total-Population.htm).

A striking result is that the PSR is projected to decline drastically from its current level for most countries. While deterministic methods also project this, our results indicate that this will happen under all plausible future scenarios. While there is some uncertainty about the level the PSR will reach, large declines are essentially certain if the assumed age at retirement is kept constant.

Our method takes into account uncertainty about future overall levels of fertility and mortality, the most important determinants of future population trends. However, it does not take into account other sources of uncertainty. Foremost among these is international migration, which is becoming more important as fertility declines and stabilizes. Indeed, it has been found that international migration is the largest component of forecast errors for horizons of 10–25 y, beyond which fertility dominates (figure 2–6 in ref. 10; 35). Although our method does not take into account uncertainty about migration, our 20-y out of sample validation exercise found the projections to be reasonably well calibrated, which is somewhat reassuring.

The method also does not take into account uncertainty about the future age structure of fertility and mortality, although this is likely less important than the overall levels. Finally, it does not take into account random variation in numbers of births and deaths, given the fertility and mortality rates. However, this typically accounts for a very small proportion of overall uncertainty, except in very small populations, which are not considered here.

Incorporating these uncertainties could improve our method, albeit at the cost of greater complexity, and might alleviate its slight underestimation of uncertainty. A method to assess and incorporate uncertainty about international migration could be based on models of Cohen and colleagues (36, 37).

We have not given results for the 38 countries with generalized HIV/AIDS epidemics, containing just over 10% of the world’s population because they require special treatment. The UN uses a multistate population projection model for these countries, with HIV/AIDS as a special state (5, 38). UNAIDS has developed epidemiological models for estimating and projecting HIV/AIDS prevalence (39–41). Methods for assessing uncertainty about these quantities have also been developed (42, 43) and incorporated in UNAIDS’s current methodology (44). Combining the present uncertainty assessment methods with those used by UNAIDS for the HIV/AIDS epidemic could yield satisfactory probabilistic population projections for these countries.

Our method assumes that TFR in a country will eventually fluctuate around an equilibrium value, taken here to be the approximate replacement level of 2.1. The current UN deterministic method assumes that TFR in a country will converge to 2.1 exactly. The previous UN projections from WPP 2008 (45) assumed that TFR would converge to 1.85 exactly. Our assumption is less rigid because we assume that TFR will eventually fluctuate around an equilibrium value rather than converging to it in a deterministic way.

The equilibrium value of 2.1 is set by expert judgment since there are not yet enough data to estimate it from observations. The results seem less sensitive to the assumed equilibrium value than one might expect. For example, although we used an equilibrium value of 2.1, the average global projected value of TFR in 2100 is only 1.85. Results for longer horizons, beyond 2100, may be more sensitive to this equilibrium value.

Materials and Methods

Data.

We used the estimates of age- and sex-specific vital rates and population counts in 5-y periods from 1950 to 2010 for all countries of the world, published by the UN (5). We excluded the 38 countries with a generalized HIV/AIDS epidemic, defined by having prevalence above 1% and not being concentrated in specific subpopulations (39). This is because of the singular nature of the demographic impact of AIDS, mainly affecting young or middle-aged sexually active adults, rather than the children or old people who are primarily affected by most other causes of death. These countries may need a different projection model that explicitly takes into account AIDS mortality. This leaves 159 countries on which we based our analysis, representing 89.2% of the world’s population in 2010.

For estimating the Bayesian models for projecting fertility and mortality, we excluded small countries with populations below 100,000. However, our method does generate projections for these countries.

Probabilistic Projection of Fertility Rates.

We generated probabilistic projections of the period TFR using the Bayesian hierarchical model of Alkema et al (23), as implemented in the bayesTFR R package (46). To convert the projections of total fertility into the age-specific fertility rates required by the cohort component projection, we took percentages of age-specific fertility rates from the WPP 2010 (5), derived using the method in (38, chap. VI), and applied them throughout the projection period.

Probabilistic Projection of Female and Male Life Expectancy.

We generated probabilistic projections of the period female life expectancy at birth using the Bayesian hierarchical model of Raftery et al. (26). The model is described in more detail in the SI Text, where we also specify the prior parameter settings we used, which are given in Table S1. The resulting Bayesian hierarchical model is estimated by Markov chain Monte Carlo, yielding a large sample from the joint posterior distribution of all parameters in the model.

We generated probabilistic projections of male life expectancy conditionally on projections of female life expectancy. The resulting joint projections of female and male life expectancy need to take into account the fact that they tend to be correlated and that the life expectancy of females is almost always higher than that of males. We did this by projecting the gap, G_c,t, between the life expectancies of the two sexes in country c and time period t, using the regression model of Lalic (28), namely

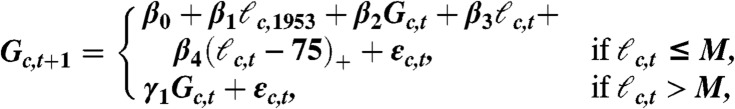[1]

where ℓ_c,t is female life expectancy for country c in time period t, M is the highest observed female life expectancy, 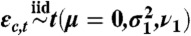if ℓ_c,t ≤ M, and 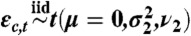otherwise.

The model of Eq. 1 represents the empirical regularities in the data on the observed gaps in a simple way. The gap in period t + 1 depends on the gap in period t, G_c,t, reflecting the fact that the gap evolves over time in a somewhat smooth way. The gap increases with female life expectancy for female life expectancy up to about age 75 and after that decreases. Finally, it accounts for outliers, such as those due to conflicts, by using Student’s t-distributed rather than normal errors. The parameter estimates are shown in Table S2. The life expectancy projections were produced using the bayesLife R package (47).

We converted the projections of life expectancy at birth into age- and sex-specific mortality rates, which were then used in the cohort-component projections. We used a modified Lee–Carter method (22), in which the mortality index of a Lee–Carter model was not projected by a random walk (as is the standard method), but was fitted to the trajectories of life expectancy at birth, as projected by the Bayesian hierarchical model.

Probabilistic Population Projections.

To produce probabilistic population projections for a given country for 2010–2100, we took a sample of 2,000 trajectories of future TFR values from their posterior predictive distribution and converted them into age-specific fertility rates. We took a sample of 2,000 trajectories of female and male life expectancy from their joint posterior predictive distribution, and converted them into age-specific mortality rates. This amounts to assuming that forecast errors in TFR and life expectancy within a country are independent, as has been previously found appropriate (48).

For each of the 2,000 combinations of fertility and mortality, we then projected the population forward from 2010 to 2100, using the standard cohort-component model (4, chap. 6). We used the same projections of net international migration as those used in WPP 2010 (5). This provides a sample of 2,000 values of any future population quantity of interest, which we used to approximate its predictive distribution.

The probabilistic population projections were produced using the bayesPop R package (49). We also used the R package bayesDem (50), which is a graphical user interface for all three R packages used, bayesTFR, bayesLife and bayesPop.