Global environmental predictors of benthic marine biogeographic structure

Abstract

Analyses of how environmental factors influence the biogeographic structure of biotas are essential for understanding the processes underlying global diversity patterns and for predicting large-scale biotic responses to global change. Here we show that the large-scale geographic structure of shallow-marine benthic faunas, defined by existing biogeographic schemes, can be predicted with 89–100% accuracy by a few readily available oceanographic variables; temperature alone can predict 53–99% of the present-day structure along coastlines. The same set of variables is also strongly correlated with spatial changes in species compositions of bivalves, a major component of the benthic marine biota, at the 1° grid-cell resolution. These analyses demonstrate the central role of coastal oceanography in structuring benthic marine biogeography and suggest that a few environmental variables may be sufficient to model the response of marine biogeographic structure to past and future changes in climate.

Biogeographic units (BUs), such as provinces or biomes, have been essential for understanding the macroecological and evolutionary processes underlying global biodiversity patterns (1–4) and are increasingly being incorporated in conservation planning (5–8). BUs are also becoming important from a global change perspective as components in models of biotic responses to global climate change in terrestrial settings (9). However, the factors that determine the biogeographic structure of benthic marine species in shallow-water habitats, where marine biodiversity is best documented and environmental changes are projected to be most severe (10–12), remain poorly understood, limiting our ability to model systems-level responses of marine biodiversity to environmental change. Here we use global datasets (Datasets S1, S2, S3, S4, and S5) to show that, in contrast to the more complex relationship between species richness and environment (13, 14), the biogeographic structure of coastal and continental shelf habitats can be predicted using just a few oceanographic parameters. This robust first-order link between specific environmental factors and large-scale biotic patterns establishes the importance of climate and oceanography in structuring marine faunas and provides important insights into modeling past and future responses of marine biogeography to global change.

We evaluate the correspondence between BUs and oceanographic variables using a model-fitting approach (Materials and Methods) to determine which oceanographic variables (individually or in combination) are most strongly correlated with biogeographic structure at both the ocean-basin and coastline scales (Table 1 and Tables S1 and S2). Our models focus on mean annual values and seasonal ranges of sea surface temperature, salinity, and productivity (hereafter TSP) because these variables have been previously hypothesized, separately or together, to affect taxonomic compositions and species richness in benthic marine systems (15–17). Biogeographic schemes for the world oceans differ mainly in the specific locations of several major provincial boundaries (1, 6, 8, 18–21). To reconcile such differences, we (i) use a recent synthesis of existing biogeographic schemes for coastal and shelf marine provinces (hereafter the Spalding scheme) as our general biogeographic framework (6) and (ii) test the robustness of our results using an independently derived biogeographic model (1) (hereafter the Valentine scheme) that was not used in the synthetic scheme (Fig. 1 A and C). We then use the taxonomic composition of bivalve mollusks, a heavily sampled and taxonomically standardized model system for marine biogeography (22, 23), to test whether (i) the correlation between spatial changes in oceanographic variables and bivalve species composition also holds at finer (1° grid cell) resolution and (ii) whether the spatial distribution of bivalve taxa can be used to reconstruct spatial patterns in oceanography.

Table 1.

Multinomial logistic regression results using temperature, salinity, and productivity means and seasonal ranges (TSP) to predict biogeographic unit (BU) membership for two biogeographic schemes by coastline and by basin

	Spalding et al. (6)			Valentine (1)
Region	AIC	% correct	No. of BUs	AIC	% correct	No. of BUs
Atlantic Basin	1574.2541	86.11	15	1554.5174	86.78	15
West Atlantic	369.4630	95.40	8	418.0608	94.92	9
East Atlantic	98.0001	100.00	8	150.0794	98.18	6
Pacific Basin	4950.5760	80.20	44	2874.1524	89.00	17
Indian Ocean	802.3963	89.66	17	124.2388	98.57	4
West Pacific	943.3720	91.48	19	206.1705	98.12	7
West Pacific Islands	543.0267	89.41	14	56.0002	100.00	5
East Pacific	129.4221	98.21	8	188.7168	97.14	9

AIC, Akaike information criterion. Percentage (%) correct is the number of 1° grid cells correctly classified into the correct BU. “No. of BUs” is the number of biogeographic units in each region. Salinity contributes more to prediction accuracy than productivity on all coastlines. Including salinity is more important for the Spalding scheme, especially in the Pacific and Indian Oceans.

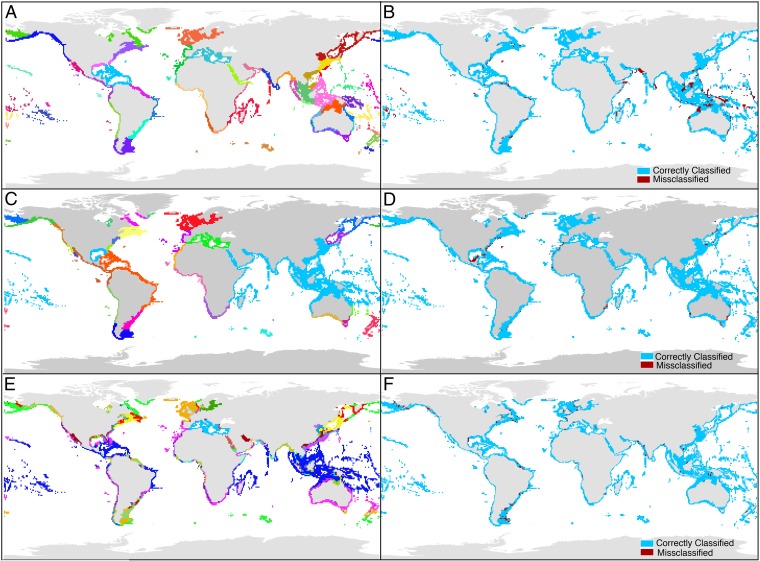
Fig. 1.

Relationships between biogeographic structure and oceanographic conditions. (A) Spalding (6) biogeographic provinces, based principally on patterns of endemism. (B) Grid cells that are classified into the correct Spalding province using TSP (blue) and misclassified (red). (C) Valentine (1) biogeographic provinces, based principally on shared species and species diversity. (D) Grid cells that are classified into the correct Valentine province using TSP (blue) and misclassified (red). (E) Oceanographic units derived for a cluster analysis of TSP. (F) Grid cells that are classified into the correct oceanographic units using bivalve occurrence data (blue) and misclassified (red).

Results and Discussion

Environmental Factors Predict BU Membership.

For both of the biogeographic schemes used here, TSP predicts BU membership with 80–89% accuracy at the ocean-basin scale and >89% accuracy along individual coastlines (Table 1, Fig. 2, Figs. S1 and S2). The greater predictive power at the coastline level most likely reflects the a priori separation of spatially disjunct areas that share similar oceanographic conditions. Overall, the predictions of BUs along each coastline using TSP are qualitatively similar between biogeographic schemes, but the prediction accuracy is higher for the Valentine scheme on coastlines where it uses fewer BUs than does the Spalding scheme (Fig. 2, Table 1). Model fits for the multinomial logistic regressions on each coastline, assessed using pseudo-R² metrics (24–27), are strong (R² = 0.88–1.00) with the exception of the Indian Ocean coastline and the West Pacific Islands in the Valentine scheme (R² = 0.67 and 0.64, respectively), which are each spatially dominated by a single province. In all cases, multinomial logistic regressions using TSP correctly predicted province membership for more cells than would be expected by chance by a margin of 23–84% (likelihood-ratio χ² test, df = 6, P < 0.001; Tables S3 and S4). For all variables, the variance inflation factor is less than 5, indicating that multicollinearity among variables is unlikely to influence these analyses (Table S5) (28).

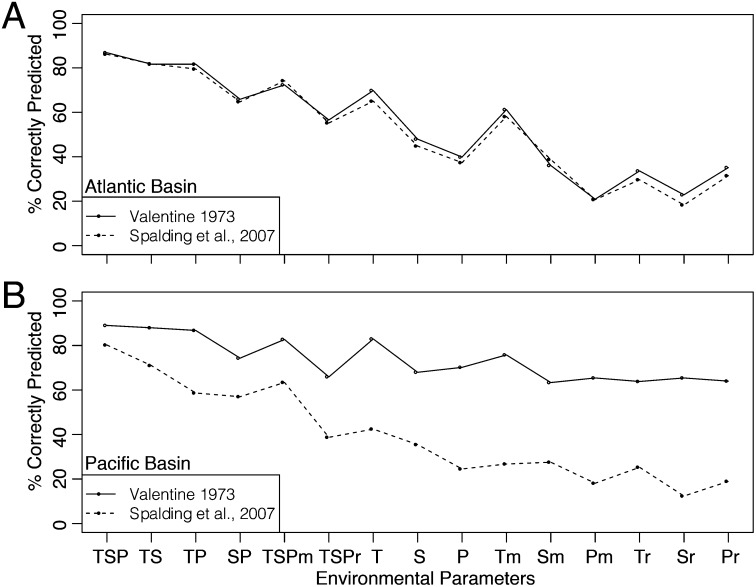
Fig. 2.

Percentage of grid cells correctly predicted by nested multinomial logistic regressions where nested sets of oceanographic variables are used to predict BU membership at the basin scale for two biogeographic schemes. T, temperature; S, salinity; P, net primary productivity; m, mean annual values only; r, seasonal ranges only. Both mean annual values and seasonal ranges are used as predictors unless otherwise specified. See Tables S4 and S5 for corresponding AIC values and for coastline-scale analyses.

The few regions with low prediction accuracy warrant further analysis of biogeographic and oceanographic patterns (Fig. 1). Spalding BUs are least related to TSP in western India and northwestern Australia (Fig. 1B); Valentine BUs are least related to TSP in the Gulf of Mexico, eastern Australia, and southeastern United States (Fig. 1D). These mismatches are not randomly distributed; grid cells near province boundaries have higher proportions of misclassification in both of the biogeographic schemes used here (χ² test, P < 0.001, Table S6). Mismatches near BU boundaries are unlikely to simply result from poor sampling because at least some occur in well-sampled regions such as the southeastern United States and eastern Australia. They also do not consistently occur more frequently in grid cells with deeper benthic environments (χ² test, Table S6), suggesting that classification of cells is robust to the distance of the habitats from surface-water environmental predictors. In some cases, these mismatches correspond to boundaries that are included in the biogeographic scheme but are not recognized in the oceanographic structure (e.g., the Central Indo-Pacific; Fig. 1 A, B, and E). In other cases, it is the precise placement of the boundary that differs between BUs and oceanographic units, suggesting boundaries that undergo episodic changes in oceanographic conditions (e.g., the northwest Indian Ocean), which are not captured by the synoptic data used here. Temporal variability in oceanographic currents may increase the permeability of biogeographic boundaries, blurring the placement of BU boundaries due to taxonomic “leakage” (29). Alternatively, the misclassification could be affected by spatially variable environmental conditions near oceanographic boundaries that are not captured in the general placement of BU boundaries (Fig. 1E). For example, strong seasonality coupled with habitat heterogeneity along western Baja California del Sur results in a unique mixture of tropical and warm temperate molluscan faunas, but the region contains few endemics and thus is not a BU in the Spalding scheme. Despite these challenges, most BU boundaries are precisely predicted by TSP (Fig. 1).

Mean annual temperature emerges as the most important single environmental predictor of biogeographic units, although the full suite of oceanographic variables (TSP) is the best-supported model and has the highest accuracy on all coastlines except the Indian Ocean and West Pacific Islands in the Valentine scheme (Fig. 2, Table 2). Mean annual values of TSP are up to 30% more informative than seasonal ranges of these values alone (median = 17.5%). Along Pacific coastlines, adding salinity and productivity data improves BU prediction by 1–36% over annual means and seasonal ranges in temperature (T) (median improvement = 16.28%). In the Atlantic, however, TSP predicts BU membership only 4–10% more accurately than temperature alone (median improvement = 8.72%) (Fig. 2, Table 2). Therefore, although temperature is always the dominant variable in structuring shallow-marine biogeography, the relative importance of temperature varies among ocean basins and between province schemes. We ran models incorporating additional variables, including nutrient concentrations and oxygen saturation, but they do not consistently improve BU prediction over TSP and have less spatial coverage because of data limitations (Materials and Methods, Table S7). Factors such as biotic interactions or carbonate saturation states of seawater may also play a role in structuring benthic biogeography, but could not be tested here owing to the lack of synoptic data on a global scale.

Table 2.

Improvement over temperature (T) data alone (annual means and seasonal range) in percent of one-degree grid-cells correctly classified when salinity (S) and productivity (P) data are added to analyses

	Spalding et al. (6)			Valentine (1)
Region	TS	TP	TSP	TS	TP	TSP
West Atlantic	7.09	6.14	9.58	3.74	1.73	4.03
East Atlantic	6.49	3.42	7.86	8.09	6.84	9.91
Indian Ocean	25.42	14.31	30.59	3.63	3.15	3.63
West Pacific	21.60	6.17	24.48	5.58	3.14	5.98
West Pacific Islands	30.69	19.47	35.99	0.62	0.47	0.78
East Pacific	16.10	6.63	17.71	12.52	3.22	14.31

Overall, these results suggest that the biogeographic structure of shallow water and continental shelf species is largely determined by the character of water masses and their boundaries, as has been reported for the surface waters of the open ocean (30–32). However, our analyses show that, in contrast to the pelagic realm (20), primary productivity plays a relatively minor role in structuring the biogeography of benthic organisms in the shallow oceans. The close coupling between oceanographic boundaries and biogeographic boundaries seen here could reflect physical barriers to dispersal owing to currents present at the boundary (29) as well as physiological challenges due to abrupt changes in environmental variables across such boundaries (33–35).

Environmental Factors Are Also Correlated with Bivalve Species Composition.

If a limited set of oceanographic variables plays a major role in shaping the biogeography of the shallow-water biota, then finer-scale analyses should also detect correlations similar to those demonstrated here for relatively large BUs. We find such correlations at the 1° grid-cell resolution for coastal and shelf-depth bivalves. At this spatial scale, compositional changes in bivalve assemblages are strongly positively correlated with changes in TSP when the data are divided into Northern and Southern Hemisphere coastlines (Mantel test r = 0.26–0.77, P < 0.001; results are robust to choice of biotic distance metric; Table S8). These results indicate that the correlation between taxonomic composition and TSP holds both at the level of regional assemblages and at the level of large-scale biogeographic units.

Bivalve Biogeographic Structure Predicts Oceanographic Structure.

Although oceanographic data can predict biogeographic structure, this does not demonstrate that biotic data can be used to reconstruct oceanographic structure, which would be valuable for analyses of coastal seas from the geological past where benthic fossil data are available but oceanographic data are scarce. To test whether bivalve taxonomic composition can predict oceanographic structure, we derived oceanographic units from a cluster analysis of TSP Euclidean distances among 1° grid cells; as temperature and salinity define water masses by determining water mass density, these factors reveal oceanographic structure (36, 37). We found that bivalve species compositions correctly predicted oceanographic unit membership with 98% accuracy in the total dataset at the maximum number of oceanographic clusters that was computationally feasible to analyze (Materials and Methods). Bivalve composition more accurately predicted oceanographic structure in the Pacific Basin than in the Atlantic Basin (Table 3). We also tested oceanographic configurations derived from the same cluster analysis that had fewer oceanographic units, and thus greater differences in TSP among the clusters, and found that bivalve biogeographic structure had higher prediction accuracy when there were fewer oceanographic units. The increase in accuracy with decreasing numbers of oceanographic units suggests that bivalve distributions are more likely to reflect large-scale oceanographic structure than smaller differences in oceanographic conditions. This likely arises in part from the range-through assumption used to determine bivalve occurrences at the 1° grid-cell resolution. This range-through protocol, necessary because the world’s shelves are not evenly sampled at the 1° grid-cell scale, places bivalves in grid cells because their geographic range encompasses those grid cells, whether or not the species has been recorded from that location. However, even though the range-through assumption potentially overestimates occurrences of many species, bivalve compositions still reconstruct oceanographic units with a high degree of accuracy. This result suggests that the oceanographic structure of ancient shallow seas can be reconstructed from the biogeographic structure of fossil benthic macrofauna, a technique more commonly used with microfossil groups (31, 38, 39).

Table 3.

Multinomial logistic regression results using bivalve species composition to predict oceanographic units (OUs)

Coastline/hemisphere	AIC	% correct	No. of OUs
West Atlantic/North	15259.1078	94.61	21
West Atlantic/South	4112.9569	85.43	10
East Atlantic/North	10463.5216	94.63	19
East Atlantic/South	776.3178	97.40	7
Indian Ocean	13617.1064	97.69	12
West Pacific/North	17425.0833	98.14	16
West Pacific/South	6732.5129	97.55	10
West Pacific Islands/North	768.0004	100.00	4
West Pacific Islands/South	1392.0002	100.00	4
East Pacific/North	7103.7724	91.36	16
East Pacific/South	1629.8629	96.21	9

AIC, Akaike information criterion. Percentage (%) correct is the number of 1° grid cells correctly classified into the correct OU. “No. of OUs” is the number of oceanographic units in each region.

Taken together, the close correspondence between oceanographic and biogeographic structure documented here suggests that oceanographic conditions play a fundamental role in determining the large-scale biogeographic structure of the world oceans, with biotic interactions and other habitat characteristics playing a less direct role. Our results also suggest that biogeographic units do not represent obligate associations of taxa, but are composed of sets of species responding in similar ways to a limited set of environmental variables. Thus, as water masses and their boundaries are altered in response to global climate change [changes in temperature and salinity are already evident (40)], the biogeographic structure of benthic marine assemblages is also likely to change. The behavior of water masses under climate change—whether they expand, contract, split, or combine—will also have important evolutionary effects in terms of creating novel combinations of selective pressures within biogeographic units and erecting or eliminating barriers to gene flow between biogeographic units. Paleontological data from past warming events suggest that tropical water masses will expand (41–43), but the long-term consequence of this expansion to global diversity remains an open question. However, because the nature of the relationship between oceanographic and biogeographic structure varies among oceans, our results suggest that biotas from different ocean basins will respond differently to the same oceanographic forcing factors.

Conclusions.

Although correlations between temperature and large-scale spatial patterns in species richness of benthic marine taxa have been documented before (15, 44, but see ref. 13), few studies have directly quantified how oceanographic variables affect the geographic structure of the benthic marine biota. We demonstrate that a few readily acquired oceanographic parameters are sufficient to predict biogeographic patterns. Such information is critical not only for modeling biotic responses to future global climate change, but also for incorporating environmental factors into macroecological and evolutionary analyses of a major global system and for providing a more rigorous framework for interpreting paleobiogeographic data. The strong correlations between TSP and biogeographic structure documented here suggest that such systems-level changes may be predictable using model-based future projections of TSP. Our results also suggest that the distribution of well-preserved benthic fossil species should be useful for reconstructing the general paleoceanographic structure of ancient shallow seas, allowing a more rigorous application of data from past warm periods onto model predictions of shelf ecosystem change in a warm future.

Materials and Methods

Oceanographic Data and Data Coverage.

The global ocean was divided into 1° grid cells, including only cells that contained (i) seafloor depths <200 m and (ii) mean annual and seasonal range data for sea-surface temperature, salinity, and net primary productivity. This protocol excluded areas with seasonal ice cover. Temperature and salinity data were obtained from the World Ocean Atlas 2009 quarter-degree grid-cell objectively averaged data set, which provides more complete coverage of coastal areas than the 1° data set (45–47). Quarter-degree cells were then averaged to achieve 1° resolution. Monthly averaged net primary productivity data were obtained from Oregon State University (48) at the one-sixth-degree cell resolution and averaged into 1° cells. Net primary productivity was calculated as a function of MODIS surface chlorophyll, MODIS sea-surface temperature, and MODIS cloud-corrected incident daily photosynthetically active radiation using the Vertically Generalized Production Model (48). This data set is available as a standard data product at http://www.science.oregonstate.edu/ocean.productivity/standard.product.php. For each variable, we calculated seasonal range as the difference between the maximum and minimum seasonal values. Annual means and seasonal ranges for TSP were available for 5,523 grid cells that could be assigned to biogeographic units and also contained data on the composition of the bivalve fauna (see below).

Assigning Grid Cells to Biogeographic Units.

The province maps from Spalding et al. (6) were obtained from that paper’s supplemental online materials (http://conserveonline.org) and province maps for Valentine (1) were manually digitized in ArcMap (49). Both were intersected with the 1° grid-cell template described above so that each grid cell had a provincial identity under each scheme. Grid cells that span neighboring provinces were assigned to the province representing the greatest area within that grid cell.

Predicting Biogeographic Structure from Environmental Variables.

We used multinomial logistic regressions to test for correspondence between oceanographic conditions and province membership at the 1° grid-cell resolution using the function “multinom” in the “nnet” package in the R programming language (50, 51). In this procedure, we used oceanographic variables as predictors of province membership as determined by Spalding et al. (6) and Valentine (1). The percentage of grid cells classified into the correct biogeographic units measured the accuracy of predicting biogeographic units from oceanographic variables. Maximum-likelihood methods were used to determine the likelihood of those province predictions and are reported here as Akaike information criterion (AIC) values. We used these AIC values to compare nested subsets of oceanographic variables within province models to determine which variables are most associated with biogeographic structure. The proportion of cells expected to be correctly classified by chance was calculated as the sum of the squared proportion of grid cells in each BU category in each region (52). Variance inflation factors were calculated using the “vif” function in the “HH” package in the R programming language (50, 53).

To further assess model fit, we used pseudo-R² metrics that compare a model using no predictors to a model using TSP as predictors. No one measure of R² is clearly a better measure of fit than another, so we calculated multiple estimators of pseudo-R² (24), using the “pR2” function in the “pscl” package of the R programming language (50, 54). Each method relies on taking two times the difference between the log-likelihood for the null (intercept only) multinomial logistic regression and the log-likelihood for the multinomial logistic regression using TSP as predictors (24).

Additional variables including dissolved oxygen, silicate, nitrate, and phosphate concentrations (55, 56) were available from the World Ocean Atlas 2009 for 3,565 1° grid cells used in this analysis, and these were also tested for their ability to predict BU membership with corresponding temperature, salinity, and productivity data as above.

Testing for Boundary Effects and Depth Effects in Mismatches Between TSP and BUs.

To test whether a grid cell’s proximity to a BU boundary contributed to its probability of being misclassified by the multinomial logistic regression, we coded grid cells by their distance from the nearest province boundary. Grid cells were then binned into two categories: “near” a province boundary and “away” from a province boundary for both biogeographic schemes. Distance cutoffs of 1°, 2°, and 3° were tested. We then tested whether the proportion of grid cells near a province boundary had a greater proportion of misclassifications than grid cells farther from the province boundary using χ² tests. We also tested whether shelf depth influenced grid-cell classification. Grid cells were binned into two categories, “shallow” and “deep,” and three depth cutoffs were tested: 20, 50, and 100 m.

Correlations Between Bivalve Composition and Environmental Factors.

We also tested whether the distribution of bivalve taxa, irrespective of clustering into provinces, is correlated with oceanographic patterns using Mantel tests between the dissimilarity in bivalve occurrences and the dissimilarity in oceanographic variables among 1° grid cells. Bivalves are a taxonomically and functionally diverse group with well-documented shallow-water distributions making them a model system for biogeography. We use a taxonomically standardized global database of occurrences for 5,460 species from 2,464 localities derived from the literature and from museum collections (22). Bivalve occurrences within each grid cell were determined by assuming that a given species is present in all grid cells contained within the total geographic range of the species. Thus, a species was counted as present wherever the box bounding its range intersected depths <200 m. Although this range-through assumption may cause species to be counted as present in cells where they do not actually occur, such errors would bias against finding strong correlations between bivalve distributions and oceanographic conditions (assuming that bivalve occurrences are in fact causally related to oceanographic conditions). Thus, this method is conservative for our purposes. We used both Jaccard and Simpson distance metrics to calculate dissimilarity in bivalve occurrences among grid cells. Oceanographic dissimilarity was calculated as the Euclidean distance between grid cells based on the z-score standardized means and seasonal ranges of temperature, salinity, and productivity.

For Mantel tests, we subdivided the data by coastline and then separated each coastline into northern and southern hemispheres (see Fig. S1 for coastline divisions). By analyzing such “hemisphere coastlines” we avoided comparing grid cells that have similar oceanographic conditions but are not connected by intervening seafloor at continental shelf depths and are thus difficult or impossible for species to disperse between. A strong positive correlation suggests that grid cells that were most similar in oceanographic variables were also most similar in their taxonomic composition. Both Pearson and Spearman correlations were calculated (Table S8).

Predicting Oceanographic Units from Bivalve Compositions.

To define oceanographic units, we used a hierarchical cluster analysis based on the Euclidean distances of z-score standardized temperature, salinity, and productivity among 1° grid cells. Clusters were defined at successively increasing similarities in 0.5 intervals to create a nested hierarchy of potential oceanographic units. In each iteration, only existing clusters containing >5% of the total grid cells were allowed to be further split to prevent situations where clusters with large differences among constituent grid cells could be reduced to single-cell units (i.e., near river outflows) while geographically large areas with smaller differences remained intact (i.e., tropical seas). Cluster analyses were performed using the “hclust” function in the “stats” package of the R programming language (43). We then asked how well bivalve occurrence data could reconstruct the oceanographic units at each level of clustering using the multinomial logistic regression analyses described above until the number of clusters become too numerous to analyze (distance = 2.5, number of clusters = 24).