Single-protein nanomechanical mass spectrometry in real time

Abstract

Nanoelectromechanical systems (NEMS) resonators can detect mass with exceptional sensitivity. Previously, mass spectra from several hundred adsorption events were assembled in NEMS-based mass spectrometry using statistical analysis. Here, we report the first realization of single-molecule NEMS-based mass spectrometry in real time. As each molecule in the sample adsorbs upon the NEMS resonator, its mass and the position-of-adsorption are determined by continuously tracking two driven vibrational modes of the device. We demonstrate the potential of multimode NEMS-based mass spectrometry by analyzing IgM antibody complexes in real-time. NEMS-MS is a unique and promising new form of mass spectrometry: it can resolve neutral species, provides resolving power that increases markedly for very large masses, and allows acquisition of spectra, molecule-by-molecule, in real-time.

Mass spectrometry (MS) – the identification of species through molecular mass measurements – is an important analytical tool in chemical and biological research. Since its first applications to organic compounds more than a half century ago^1,2, it has assumed an increasingly dominant role in the life sciences and medicine. It is now arguably the mainstay of proteomics³.

Among recent emerging areas of MS is the elucidation of the structure of complex protein assemblies^4–7. Critical to such measurements are spectrometers that are capable of high resolution in the very large mass range – above several hundred kDa – which is at or beyond the limit of many conventional MS techniques. Also essential is the development of new, delicate sample handling methods for molecular ionization/injection, enabling so-called “native” MS^4,8, to permit large molecules or molecular assemblies to be transported, intact, from the fluid phase to the vacuum phase for subsequent analysis. On these new fronts, NEMS-MS offers significant promise^9–17. NEMS are sensitive to the inertial mass of neutral particles that accrete upon them; this makes them particularly well suited to studies that require minimal ionization to avoid structural changes in the protein^4,8.

We have discussed the principles and ultimate practical limits of NEMS-based mass detection elsewhere¹⁸; here we briefly review the salient points. Upon adsorption onto a NEMS resonator, an individual analyte molecule or particle can precipitously downshift the resonant frequency of each vibrational mode [Supplementary Information]. This is the basis of the measurement. Theoretical limits to inertial mass resolution from frequency-shift detection can apparently be as small as the single-Dalton level¹⁷; indeed, recent endeavors already report mass resolution at the few hundred Dalton level¹⁵. However, central to our present work is that all measurements to date neither measure the mass of individual molecules or nanoparticles, nor can do so in real time. This is despite the impressive recent improvements in mass resolution and the detection of discrete adsorption events¹⁶. The reason for this is that the resonant frequency shift induced by analyte adsorption depends upon both the mass of the analyte and its precise location of adsorption upon the NEMS resonator.

A way out of this quandary, and first construction of NEMS-MS spectra – albeit, not in real time – has previously been achieved by employing the known position-dependent mass responsivity for a doubly-clamped NEMS resonator¹⁶. In this previous work analytes were delivered such that they accreted uniformly across the device; this foreknowledge allowed the deduction of the constituents of simple mixtures after collection of only several hundred single-molecule adsorption events. (For comparison, conventional mass spectrometry measurements typically involve measurement of ~10⁸ molecules¹⁹.) The analysis involved fitting to the statistical ensemble of measured frequency shifts by a rather complex multidimensional minimization procedure to extract the weights of each constituent, that is, to deduce the mass spectrum^16,20. These first results provided a conceptual demonstration of the potential of NEMS-MS, but the complexity of this process precluded its application to arbitrarily complex mixtures.

Here we describe an approach that enables direct determination of the mass of each arriving molecule, in real time, as it adsorbs upon the NEMS resonator²¹. It is, thereby, directly applicable to arbitrarily complex mixtures as we shall demonstrate. This approach involves no assumptions about the sample mixture, and is implemented by simultaneously tracking the resonant frequency of multiple modes of an individual NEMS resonator and then resolving the time-correlated, adsorption-induced frequency jumps in several of these modes. It is known that the resonance frequency of beams and cantilevers is affected both by the mass of the particle and its landing position. Deconvolution of mass and position is possible through information from multiple mechanical modes^22–24. Pairs of these simultaneous jumps herald a single-molecule adsorption event and are used in the analytical framework presented here to deduce the nominal values of the mass and position of adsorption of individual molecules/particles just after adsorption. Beginning with Euler-Bernoulli beam theory, we have developed a model that includes error analysis. Using the complete expression for mode shape enables direct determination of the mass and position uncertainty of each arriving molecule or particle^20,21. Our analysis provides both a numerical and a universal graphical approach (Fig. 2) to calculate the mass and position of the analyte molecule, which arrives randomly in time and position.

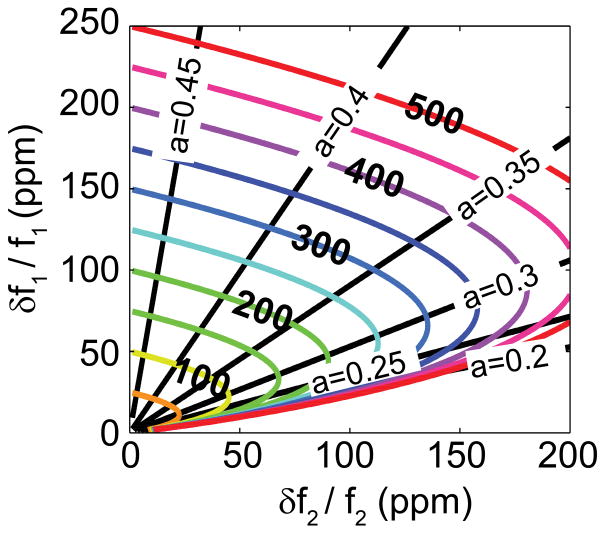
Figure 2. Transformation from experimentally obtained, time-correlated, two-mode frequency jump data to analyte mass and position-of-adsorption.

Pictured are universal mass and position contours in the correlated frequency jump |δf₁/f₁|,|δf₂/f₂| plane. The x and y axes represent the measured fractional frequency jumps, scaled in parts per million (ppm). The parametric curves displayed represent the following: i) Straight lines passing through the origin denote constant-adsorbate-position values. The beam center (a = 0.5) corresponds to the y-axis; the second mode has a node at this location. ii) Colored elliptical curves represent contours for constant adsorbate mass; these are labeled in units of m_p/M and scaled in ppm. These parametric curves hold for the first two same-plane modes of a doubly-clamped beam, and assume only Euler-Bernoulli beam theory.

Multimode Theory for Single Molecule Mass Measurements

Our approach is briefly summarized here; it is presented more fully in the Supplementary Information. A point analyte, a single molecule or particle with mass δm downshifts the resonant frequency of a nanomechanical resonator with mass M in the following way:

$$\frac{\delta f_n}{f_n}=-\frac{\delta m}{M}\frac{{\phi }_n{(a)}^2}{{\alpha }_n}$$ (1)

Here, f_n is the resonant frequency of the n^th mode and δf_n is the frequency shift for this mode. Their ratio, (δf_n/f_n), the fractional frequency shift, is proportional to the fractional mass change, δm/M. Here, φ_n denotes the mode shape for the n^th mode, and a denotes the position-of-adsorption of the molecule upon the beam (normalized to unitary beam length). The numericalconstant α_n depends on the mode number n and is of order unity (Supplementary Information).

For a symmetric NEMS doubly-clamped beam similar to the one shown in Fig. 1a, resolving the adsorbate-induced frequency shifts in the first two modes is adequate to determine the mass of the analyte molecule and its position of adsorption (Supplementary Information). The mode shapes and the position-dependent responsivities of the first two modes are shown in Fig. 1c, along with the ratio of these responsivities. The ratio of the responsivities of two arbitrary modes, G(a)≡φ_n(a)²/φ_m(a)², determines whether their simultaneous measurement is sufficient for real-time mass detection. If G is invertible, then a unique value for the position, and thus the mass of the molecule, can be obtained. Although this condition is not fulfilled for the first two modes of a doubly-clamped beam (Fig. 1c), analysis can be restricted to one half of the beam’s length due to the inherent symmetry of such a structure, and this permits determination of a unique molecular mass and adsorption position relative to the beam center (Supplementary Information).

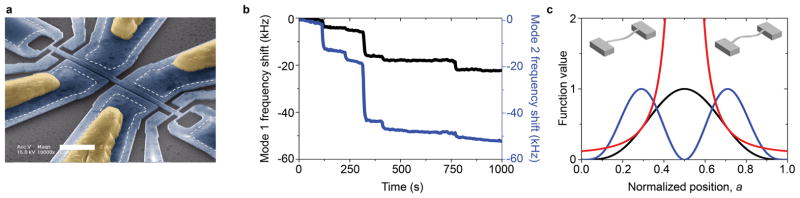
Figure 1. Multimode NEMS-based mass detection in real time.

a, Colorized electron micrograph of a representative device used in this study. The white dotted line shows the boundaries of the region beneath the suspended device that anchors it to the substrate. Yellow regions represent Al/Si gate contacts. Positioned near the ends of the beam are narrow gauges that become strained with motion of the beam and thereby enable transduction of mechanical motion into electric resistance. The white scale bar is 2 microns. b, Time-correlated resonant frequency shifts of the two modes (mode 1 (black) and mode 2 (blue)) corresponding to individual gold nanoparticles landing on the NEMS. The frequency offsets are 44.6 MHz and 105.0 MHz for the first and second modes respectively. c, Responsivities of the first two modes of a doubly-clamped beam (black=mode 1, blue = mode 2) and their ratio, G (red). Insets: Mode shapes for the first and second in-plane modes.

In this work, we shall use the first two modes of the NEMS device for mass measurements of individual protein macromolecules (IgM antibody isoforms) and individual gold nanoparticles. Each species that physisorbs onto the cooled NEMS device produces a distinct frequency shift in each of the tracked modes (the fundamental and second mode), as shown in Fig. 1b (in order to illustrate the changes better, the frequency axes in this plot are shown as frequency changes from the initial resonance frequencies at t=0). As described below, these time-correlated frequency shifts are then used to determine both the mass and position-of-adsorption for each of the newly arrived analyte molecules or particles, as well as their corresponding uncertainties.

Given the aforementioned symmetry of the mode shapes, we restrict our analysis to one half of the beam, 0<a<0.5 . For this branch, the transformation, G, from the fractional-frequency shift pair, (δf₁/f₁,δf₂/f₂), to the analyte mass-position pair (δm/M,a) is one-to-one. Figure 2 graphically represents the transformation of experimentally observed, time-correlated frequency jumps from the first two modes of a doubly-clamped beam into mass and position-of-adsorption for each arriving analyte. The real-time experimental data, i.e. frequency jumps for the two modes, are represented as fractional-frequency pairs,(δf₁/f₁,δf₂/f₂). In this representation, this transformation yields analyte position contours that appear as straight lines passing through the origin, while the deduced mass contours appear as quasi-elliptical curves.

In a noiseless measurement, each analyte landing on the NEMS would be identified as a perfectly sharp single point in the |δf₁/f₁|,|δf₂/f₂| plane. However, in practical experiments the mass and position of the analyte can only be determined up to certain confidence level that is determined by the frequency instabilities of the two separate, phase-locked modes of the NEMS resonator. These frequency fluctuations are characterized by their respective Allan deviations²⁵.

To represent the frequency instability in a single-mode measurement, the induced frequency shift in each mode is modeled as a random variable with mean value commensurate with the measured jump, and dispersion identical with that of the frequency noise. For multimode measurements, the frequency noise statistics for the separate modes are combined into a joint probability density function (JPDF) representation, JPDF_{δf1/f1,δf2/f2} (δf₁/f₁,δf₂/f₂). Using a bivariate PDF transformation²⁶, the |δf₁/f₁|,|δf₂/f₂| plane is mapped onto the (δm/M, a) plane and a joint-PDF for mass and position, JPDF_{δm, a} (δm, a), is calculated (Supplementary Information).

The JPDF of each analyte in the multimode space describes an elliptically-shaped distribution, with the length of the principal axes corresponding to the mass and position uncertainties. This two-dimensional JPDF can be projected onto either the mass or the position axis to determine the probability distribution of mass or position respectively:

$${\mathit{PDF}}_{\delta m}(\delta m)=\underset{a=0}{\overset{a=0.5}{\int }}{\mathit{JPDF}}_{\delta m,a}(\delta m,a)da$$ (2)

$${\mathit{PDF}}_a(a)=\underset{\delta m=0}{\overset{\delta m=\infty }{\int }}{\mathit{JPDF}}_{\delta m,a}(\delta m,a)d(\delta m)$$ (3)

These noise-transformation relations can be used to systematically analyze the performance of NEMS-MS experiments. For example, mass resolution as a function of analyte position-of-adsorption can be obtained (Supplementary Information, Fig. S3 and S4).

Experimental Technique for NEMS-MS

We utilize the analysis outlined above to perform mass spectrometry on individual IgM antibody isoforms and gold nanoparticles using two separate and complementary experimental systems. These systems employ distinct analyte injection/ionization schemes: electrospray ionization (ESI) and matrix assisted laser desorption ionization (MALDI). The experimental setups and their characterization are described in the Supplementary Information. The results obtained using the systems agree with each other as shown in Fig. 4a.

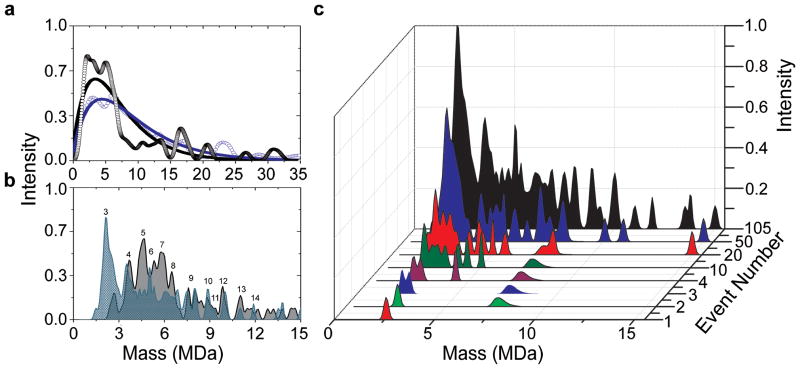
Figure 4. The evolution of a NEMS-MS spectrum in real time.

a, Mass spectra of 10nm gold nanoparticles from the ESI (blue, open circle) and the MALDI (black, open circle) setups. The solid lines represent best fits to the data with ESI (blue) d=9.8nm, σ=2.5nm and MALDI (black) d=10.7nm and σ=2.8nm. b, Mass spectra of 5nm gold nanoparticles from the MALDI setup showing results for samples prepared without glycerol (gray) and prepared with 10% glycerol (blue); the declustering effect from glycerol addition is evident. Peaks are labeled according to cluster size (e.g. the mass of 3 particles, 4 particles, 5 particles, etc.). c, Mass spectra of the ensemble of 5nm gold nanoparticles with glycerol as they arrive sequentially on the NEMS sensor. Each particle is represented as a spread in mass due to the measurement uncertainty. The event number refers to the number of particles that have accreted upon the device up to that point. The total, cumulative spectrum (black) is the additive result of 105 individually measured particles.

The NEMS resonators used in the experiments are specifically designed and optimized for the actuation and detection of the first two modes of a doubly-clamped beam. Details concerning their fabrication and measurement are presented elsewhere^27,28 and summarized in the Supplementary Information.

A colorized scanning electron microscope (SEM) image of one representative device used in the experiments is shown in Fig. 1a. The device is fabricated by CMOS-compatible, top-down processes designed for very-large-scale integration of NEMS²⁹ . Electrostatic actuation is achieved using proximal capacitive gates, and resonator motion is transduced using symmetric semiconducting piezoresistive strain gauges located near both ends of the device. Actuation and detection channels of the two modes were combined using high-frequency electronic components, and a feedback loop³⁰ was implemented through GPIB protocol. A schematic of the measurement and actuation circuit, and a summary of the device characteristics, are provided in the Supplementary Information.

The Allan deviation characterizing the frequency fluctuations of the first NEMS mode was σ_A⁽¹⁾~8×10⁻⁸, and of the second mode was σ_A⁽²⁾~1×10⁻⁷ at the chosen phase-locked loop (PLL) response time of τ_R~500 milliseconds unless noted otherwise. For measurements of the 10nm gold nanoparticles with the ESI system, obtained with a previous generation of smaller devices, these values were σ_A⁽¹⁾~3×10⁻⁶, and σ_A⁽²⁾~2×10⁻⁶, at τ_R~ 10 seconds. (A longer response time was required with the earlier generation of instrumentation used.) These frequency fluctuations yield a mass resolution of approximately 50kDa and 100kDa for these two sets of measurements, respectively. With our current, third-generation instrumentation, not yet deployed for MS, we have demonstrated sub-millisecond time resolution³¹ . The measured noise correlation between the modes was ~0.3 (~0.7 for the first generation system and devices). Figure 1b shows a snapshot of two-mode PLL data obtained during electrospray ionization of 10nm gold nanoparticles (Two-mode PLL data from the IgM run is shown in Fig. S11). Time-correlated, quasi-instantaneous frequency jumps of different heights in the two modes clearly demonstrate our ability to resolve discrete adsorption events from individual molecules or nanoparticles accreting onto the NEMS resonator. These experimentally obtained frequency jumps are subsequently used to determine the mass and position of each molecule/nanoparticle by mapping the (δf₁/f₁,δf₂/f₂) pairs onto the δm/M, a plane as previously described. Figure 3a shows the mass and position of each adsorbing particle, and their respective uncertainties, for an experiment where 5nm gold nanoparticles were delivered onto the NEMS mass sensor via MALDI. The mass spectrum is obtained by integrating the data along the position coordinate. The gold nanoparticles, as is usual in typical experimental samples, are known to have a large variance in radius (Sigma Aldrich); this translates in the very large mass spread observed (m ~ r³). If the gold nanoparticles were relatively monodisperse, the data would be expected to appear as relatively narrow bands along the mass axis. This kind of behavior is well modeled by our Monte-Carlo simulations of 5nm and 10nm gold nanoparticles – if we assume low size variance and no clustering (Fig. 3b). Note that particles (or molecules) with smaller masses will produce smaller relative frequency shifts and, in the presence of a fixed amount of frequency noise, this will appear as a larger position uncertainty. A somewhat counterintuitive feature of these spectra is the evident decrease in the position uncertainty for heavier species while the mass uncertainty remains constant. This originates from the fact that the mass resolution depends on the minimum resolvable frequency shifts – which, again, remain constant due to the frequency noise, regardless of the magnitude of the actual shifts from the arriving analytes. On the other hand, position resolution depends on the minimum resolvable angle in the (δf₁/f₁,δf₂/f₂) plane, and this improves as the magnitude of the frequency shifts become larger (see Fig. S9). The number of events observed near the center of the beam is reduced because the second mode has a node at the center, and therefore particles landing in this region produce jumps below the noise level.

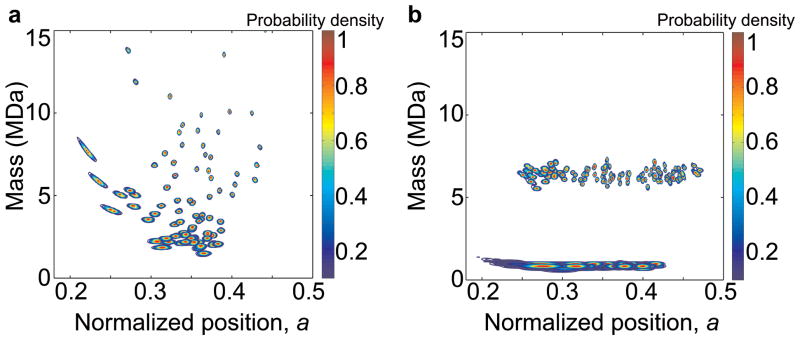
Figure 3. Joint probability distributions for analyte mass and position-of-adsorption.

a, Experimental data of 5nm gold nanoparticles from the MALDI experiment. Each analyte captured by the NEMS resonator has an error disk that reveals its uncertainty in its mass and position-of-adsorption on the NEMS resonator. b, Monte-Carlo simulations of 5 and 10nm gold nanoparticles assuming a much lower size variance (~2%, no clustering) than the actual samples (~15–20%, with clustering). These simulations reveal the respective mass “bands” that would be expected for nearly monodisperse gold nanoparticle distributions.

Gold Nanoparticle Measurements

The mass spectra of 10nm gold nanoparticles are shown in Fig. 4a for the data acquired from the ESI setup (black curve) and from the MALDI setup (blue curve). In order to more easily compare with the ESI data, the data for the MALDI curve shown here was analyzed with the same experimental mass resolution that was achieved with the ESI setup for 10nm gold nanoparticles. Also shown are the best-fit curves for each data set. For the ESI data, the best fit yielded a diameter of 9.8nm and standard deviation of 2.5nm, while the data using MALDI yields a diameter of 10.7nm and a standard deviation of 2.8nm. These values are within the experimental deviation of the vendor specifications for the gold nanoparticles. Details of our fitting protocols are given in the Supplementary Information.

We complement these 10nm gold nanoparticle measurements with MALDI-based measurements on 5nm gold nanoparticles. In these experiments two types of MALDI plates were prepared; each containing 5nm gold nanoparticles, but differing in whether glycerol was added as a separating agent (Methods). Previous studies have demonstrated that clustering effects typically exhibited by metallic nanoparticles can be mitigated by the addition of various separating agents^32–35. Figure 4b shows two distinct mass spectra for the two 5nm gold nanoparticle samples. A clear reduction in gold nanoparticle clustering is observed with the use of glycerol. To gain further insight into the observed cluster peaks, we modeled the clustering phenomena using Monte Carlo simulations; the details underlying our analyses are described in the Supplementary Information. Fig. 4c shows the accumulated mass spectra, as acquired particle-by-particle, for the 5nm gold nanoparticles

Each event in the current set of measurements provides mass of the adsorbed analyte. This contrasts with previous measurements^15,16, wherein each data point was, at best, part of a statistical ensemble – itself one bit of information convolved with the position dependence of single-mode NEMS response. Here, as is graphically displayed in Figure 4b and 5a, spectra can now be built up, particle-by-particle, as each analyte arrives. With this advance it is now possible to weigh individual molecules in real time, without the need to first collect an ensemble of identical particles. This enables straightforward analysis of complex mixtures, as exemplified in Fig. 5 which represents the first time isolated biomolecules have been weighed by a nanomechanical device.

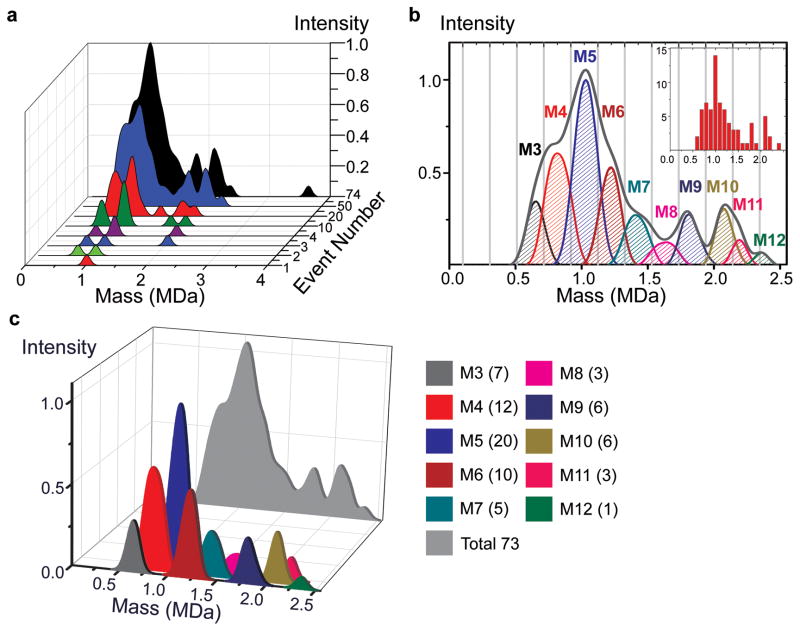
Figure 5. The nanomechanical mass spectra for Human IgM.

a, Molecule-by-molecule acquisition of the mass spectra for human IgM. Analytes accumulating at different molecular weights correspond to different isoforms of the molecule. The final spectrum shown in black is the additive result of individual mass measurements on 74 accreted molecules and has readily identifiable sharp peaks corresponding to major isoforms of IgM typically found in human serum.

b, Decomposition of the IgM spectra into different polymerization levels. Gray lines delineate the cut-off thresholds used in assigning the different forms of IgM. The most dominant form of IgM in the human serum is the pentameric form (M5) with a molecular weight of approximately 1 MDa, observed as the global maximum of the NEMS MS spectra. Subpopulations of other forms are also observed, at masses corresponding to M3, M4, and M6 through M12. Inset shows the histogram of the event masses binned according to mass resolution. The vertical axis of the inset corresponds to the number of events, while the horizontal axis is the mass in MDa.

c, Mass spectra of individual subunits are displayed quantitatively with single-molecule accuracy. Intensity peaks of different polymerized forms of IgM (M3 to M12) yield the mathematically integrated composite mass spectrum (light grey) of the IgM sample. The numbers in parenthesis in the legend show the number of measured molecules for each isoform.

Human IgM Antibody Measurements

To further demonstrate the utility of NEMS based mass spectrometry for biological species, we have obtained single-molecule NEMS-MS spectra for human IgM using ESI injection. In serum, IgM is typically found in macromolecular complexes that are assembled by the immune system. The presently-known biologically-active isoforms in serum can be tetrameric, pentameric, hexameric, or dipentameric assemblies of identical ~190kDa subunits^36–39. For the prevalent pentamer isoform, an additional small protein (the J chain) helps link the assemblage and contributes ~15kDa to the total ~960kDa mass of the complex^40,41. Our overall mass spectrum, a composite curve accumulated from 74 single particle spectra, is shown in Fig. 5a. The individual pentameric IgM complex (the highest intensity peak) is clearly visible at 1.03 ± 0.05 MDa, as is a dimerized pentameric complex (“dipentamer”) at 2.09 ± 0.05 MDa – their mass ratio very close to two, as expected. These measured values are very close to the anticipated values 0.96 MDa and 1.92 MDa⁴¹, which is remarkable considering the fact that we report mass values without any calibration other than using the nominal mask dimensions of our mass sensor (Supplementary Information).

The apparent smoothness of the mass spectra for the individual isoforms of Fig 5 arises from the fact that each single-particle/molecule event can be resolved with its own uncertainty level. Specifically, the mass spectra in Figures 4 and 5 represent information acquired from sets of 105 and 74 single-particle/molecule adsorption events, respectively. Each of these events can be represented in the mass-position plane as a continuous probability distribution. Subsequently, we obtain mass spectra for each event by projecting the individual distributions onto the mass plane. For each particle/molecule accreted, this yields a smooth Gaussian-like curve for its mass spectrum, with a width dependent on the specific mass and position of the particle. The cumulative mass spectra are then Gaussian-like mass distributions averaged by like IgM isoforms, as in the foreground of Fig 5c, or added overall to generate a composite spectrum, as in the background grey curve of Fig 5c. Alternatively, one can report the center of the mass distribution (as done in the inset of Fig. 5b), but then one loses the unique position and mass uncertainty information for each particle that is obtained with our uncertainty analysis formalism.

Figure 5b and 5c illustrate the remarkable power of single-molecule NEMS-MS to resolve spectra. Because the mass of each molecule is individually measured, and using the prior knowledge of IgM isoformal structure, each molecule can be identified based upon its mass as an IgM isoform. In a surprising reversal of the traditional situation, it is now possible to examine the underlying structure of the composite intensity curve. For instance the apparent shoulder at 0.82 MDa in the composite intensity curve is seen to arise from the presence of precisely twelve accreted macromolecular complexes. Each one is a tetramer of IgM that individually registers on the NEMS mass sensor and was separately measured as part of the ensemble of 74 molecules collected during this experiment. The legend in Fig. 5c provides the number of molecules collected for each of the subunit peaks. To identify the different IgM isoforms with our single-molecule measurements, equidistant thresholds were used between the expected mass values of adjacent species, shown as gray lines if Fig. 5b. Due to our mass measurement error, there is a small probability for some events to be misidentified when the noise level during that particular event happens to exceed the 2σ noise threshold separating two distinct species. We determine the number of potentially misidentified particles by performing a statistical analysis on the data ensemble (Supplementary Information). This analysis suggests that less than 7% of the events, that is, only ~5 of the 74 collected molecules, might be misidentified.

Our experiment reveals a sequence of IgM isoforms from trimer (N=3) up to dodecamer (N=12) within the mass range investigated (excluding the solitary event at 3.6MDa); these can originate from both physiological and experimental factors. Fragmentation and nonspecific reassembly of large macromolecular species is expected to occur in ESI systems^5,42. However it is known that IgM can also be selectively assembled by the lymphatic system into pentamer and hexamer complexes as part of an immunologically driven response to antigens ^36,37. NEMS-MS, unlike conventional MS, does not require the charging of analytes to achieve its selectivity. The ability to use neutral injection methods that capitalize on the strengths of NEMS-MS will, in future, allow direct determination of the efficiency of such immunological processes and allow monitoring them in real time and, for example, in response to potential therapies – without the confounding source of isoforms from charge-driven fragmentation.

Summary

NEMS-MS systems yield very high resolving powers in the large mass range (>500kDa) since NEMS mass resolution remains constant over the entire mass range. This is in contrast with conventional mass spectrometry systems whose resolution degrades with higher mass especially beyond mega-Dalton range. The present experiments provide the first experimental validation of real-time NEMS mass spectrometry, and demonstrate the potential of NEMS mass sensors for performing mass spectrometry on large macromolecules and nanoparticles with masses deep into the MDa range.

We have demonstrated mass spectrometry using nanomechanical devices wherein the mass of individual protein macromolecules arriving at the device are measured in real time. The work clearly demonstrates the utility of NEMS for mass spectrometry of large biomolecules and, more specifically, for native mass spectrometry. Improving the mass resolution of top-down fabricated nanomechanical devices by only one or two decades – which is attainable in the near term – offers exciting prospects for useful applications in bacterial identification, native mass spectrometry, and structural identification of large macromolecules. Recent work has dramatically improved the mass resolution of bottom-up fabricated NEMS devices^13–15 and now offers realistic potential for ultimately creating NEMS-MS spectrometers with resolution down to a few Daltons. However, much work remains: bottom-up NEMS devices and approaches have yet to demonstrate mass measurements of individual molecules, and questions remain about their compatibility with large scale integration. Ultimately, however, the ability to use VLSI and CMOS-compatible NEMS with devices providing single Dalton sensitivity will enable the possibility of measuring millions of proteins, in real-time, from a small discrete sample – like a single cell – while retaining single-protein precision over the full range of biological interest.

Methods

Human IgM solution was purchased from Sigma-Aldrich and buffer exchanged to 200mM aqueous ammonium acetate, with a final antibody concentration of approximately 1 mg/mL . A nano-electrospray ionization interface with a 20μm Pico-emitter ESI needle (from New Objective) was employed for IgM measurements. Colloidal gold nanoparticles with nominal diameters of 5nm (mean diameter = 5.1nm, variance = 19%) and 10nm (mean diameter = 10.7nm, variance = 10%) were purchased from Sigma-Aldrich. For the ESI measurements, the gold nanoparticle sample was diluted by equal amounts of methanol and introduced into the ESI needle. The NEMS device was kept at the highest vacuum chamber of a three-stage differential pumping setup, with a base pressure of 10⁻⁵ Torr before cryo-pumping takes place. Typical operation temperature for the ESI sample stage was 70 K for the gold nanoparticle samples and 140 K for the IgM samples. Cooling the NEMS device in both the ESI and MALDI setups was done to prevent captured particles from rapidly desorbing from the device surface.

The MALDI sample plates were prepared by washing the stock colloid solutions in water and, using a centrifuge, concentrating the solutions to ~5×10¹⁴ particles/ml and 1×10¹⁴ particle/ml for the 5 and 10nm gold nanoparticle samples, respectively. For each sample, 38μl of solution was drip-dried onto 3mm diameter spots on a pyrex sample plate. The glycerol samples were prepared by adding glycerol (Sigma-Aldrich) at 10% concentration to the gold nanoparticle solution prior to drying on the pyrex sample plate. After drying in air, the plate was placed inside the vacuum chamber at a distance ~0.5cm from the NEMS device. A nitrogen laser (model NL 100 from Stanford Research Systems) was focused through a lens to a spot ~50×100 μm² that illuminated the backside of the pyrex plate. The laser was operated at a wavelength of 337nm, 170μJ/pulse, 3.5ns pulse width and a repetition rate of 1Hz. The chamber was maintained at a base pressure of 10⁻⁹ Torr and the NEMS device stage was cooled to 80K.