Mapping the human phosphatome on growth pathways

Abstract

Large-scale siRNA screenings allow linking the function of poorly characterized genes to phenotypic readouts. According to this strategy, genes are associated with a function of interest if the alteration of their expression perturbs the phenotypic readouts. However, given the intricacy of the cell regulatory network, the mapping procedure is low resolution and the resulting models provide little mechanistic insights. We have developed a new strategy that combines multiparametric analysis of cell perturbation with logic modeling to achieve a more detailed functional mapping of human genes onto complex pathways. A literature-derived optimized model is used to infer the cell activation state following upregulation or downregulation of the model entities. By matching this signature with the experimental profile obtained in the high-throughput siRNA screening it is possible to infer the target of each protein, thus defining its ‘entry point’ in the network. By this novel approach, 41 phosphatases that affect key growth pathways were identified and mapped onto a human epithelial cell-specific growth model, thus providing insights into the mechanisms underlying their function.

Introduction

Phenotypic analysis of cell response after perturbations by small interfering RNAs has established itself as a powerful strategy to explore the function of entire gene families in large-scale screenings (Kiger et al, 2003; MacKeigan et al, 2005; Conrad and Gerlich, 2010; Horn et al, 2011). Using this approach, genes are connected to a function of interest, if the alteration of the cellular levels of their products perturbs a phenotypic readout associated with the function under investigation. However, this approach only provides correlative information functionally linking the interfered gene and the activation level of the phenotypic readout. Indeed, given the extensive cross-talk among different signaling pathways, the same readout alteration may be caused by perturbations of radically different branches of the cell regulatory network. By measuring multiple readouts it is sometimes possible to make educated guesses about the network node that is the most likely primary target of the induced perturbation (Jorgensen et al, 2009). However, there are a number of issues that limit this approach when applied on a large scale.

First the large number of functional (activation/inactivation) relationships between gene products that have been reported in the literature is overwhelming, even for an expert of a specific biological domain. In addition, it is often difficult to reconcile all the, sometimes conflicting, findings in different experimental systems and summarize them in a trusted signaling network, by modeling the biochemical reactions underlying signal propagation in a specific cell system. Finally, as the complexity of the model grows, it becomes practically impossible to deduce the functional outcome of network perturbations without the assistance of computable models.

Such models can be derived by a variety of different approaches (Kestler et al, 2008). A first strategy uses systems of coupled differential equations (Aldridge et al, 2006). In these models, each molecular reaction is specified using a kinetic law relating the concentrations of reactant and products. These reactions are governed by rate constants that must be estimated by optimizing the fit with a set of experimental data. Due to the large number of parameters this step can prove to be a very complex task.

An alternative approach represents signaling models as logic networks. In this case, the pathway of interest is drawn as a signed direct graph where nodes represent proteins and edges specify activatory/inhibitory relationships between them. The effect of edges is combined in logic gates (AND/OR). This strategy generally yields discrete models that are less flexible than those obtained with differential equations, yet much easier to understand and compute. Recently, methods have been developed to optimize the structure of these models against experimental data (Saez-Rodriguez et al, 2009).

Whatever the approach used biological signaling models provide detailed descriptions of a system of interest, but are necessarily limited in size due to their complexity. Conversely, large-scale perturbation screenings provide a higher level view of a larger number of proteins. In this work, we aim to bridge the gap between these two worlds in order to obtain a higher detail mapping of gene products onto complex pathways on a large scale. Our approach is based on the combination of multiparametric siRNA screening with modeling and simulation. We developed the strategy with the aim of characterizing protein phosphatases.

Phosphorylation is a pervasive post-translational modification that contributes to form regulatory switches by modulating the activity of key enzymes and promoting the formation of supramolecular complexes (Barford et al, 1998). Phosphatases work together with kinases to modulate the phosphorylation of a large number of tyrosine, serine and threonine residues on most eukaryotic proteins. We focused on protein phosphatases because of their broad yet poorly understood regulatory function in signaling pathways (Barford et al, 1998; Sacco et al, 2012). Indeed till recently protein phosphatases have been considered uninteresting housekeeping enzymes and have received less attention compared with kinases (Bardelli and Velculescu, 2005). However, evidence accumulated over the past decades have indicated that this enzyme class plays an important regulatory role and that the deregulation of the concentration or activity of specific phosphatases correlates with a variety of human disorders (Wera and Hemmings, 1995; Tonks, 2006). Approximately, 40% of protein phosphatases are implicated in tumor development, highlighting the central role of this enzyme group in growth regulation and identifying some members as new therapeutic targets (Julien et al, 2011; Liberti et al, 2012). However, the molecular mechanisms leading to tumorigenesis have been characterized only for a few of these potential oncogenes and oncosuppressors, whereas the majority of them still awaits to be placed in the intricate functional protein network underlying cell physiology.

To contribute to shed light on the involvement of phosphatases in the mechanisms regulating phosphoprotein homeostasis, we have conceived a strategy to enable the mapping of gene products onto a cell-specific growth network (Figure 1). To this end, we have characterized the perturbation of a number of key growth pathways after downregulation of 298 phosphatase (or phosphatase-related) genes by a large-scale siRNA screening coupled to automated microscopy. We report here the identification of human phosphatases (hits) that finely modulate the activities of some key node in the growth regulatory network. The change in cell state, induced by perturbing each phosphatase, was defined by monitoring the activities of pathways that regulate cell growth such as the MAP kinase (ERK and p38), mTOR, NFκB pathways and autophagy (Hennessy et al, 2005; Viatour et al, 2005; Roberts and Der, 2007; Wagner and Nebreda, 2009; Steeves et al, 2010). By combining the results of the siRNA screening with modeling and simulation, ∼67% of the protein phosphatase hits were mapped onto the growth model. Some of the hit genes, when deregulated, cause alterations in the timing of the cell cycle and therefore are new potential oncogenes or oncosuppressors.

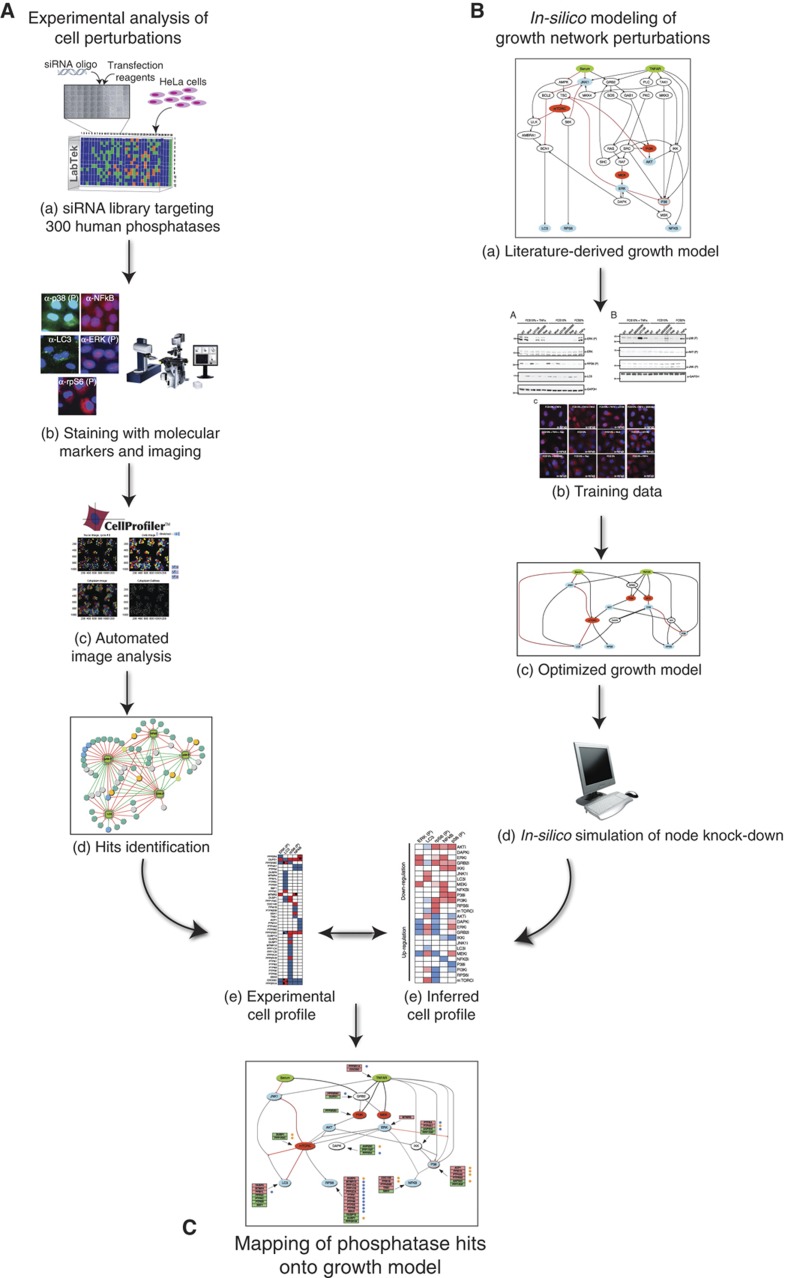
Figure 1.

Schematic illustration of a strategy to map protein phosphatases onto growth pathways. (A) We used a multiparametric siRNA phenotypic screening of the set of human genes encoding protein containing phosphatase domains or regulatory subunits to identify, by automated fluorescence microscopy and automated image analysis, genes whose downregulation modulates the activity of some key growth-associated pathways. The perturbation of the cell state by each siRNA is represented as a vector whose coordinates are the measured readouts. (B) In parallel, we assembled a literature-derived signed directed network and we simplified and optimized it by training with experimental data. The resulting logic growth model was used to infer the cell state upon perturbation of each node. (C) Finally, by matching the experimentally determined cell states with the one predicted by the pathway model, we inferred the pathway nodes that were likely to be affected by the phosphatase knock-down.

Results

Experimental strategy

To map protein phosphatases onto growth pathways, we combined experimental characterization of the cell states upon perturbation of phosphatases activity and logic modeling of pathways relevant for cell growth. The strategy involves the steps schematically summarized below and illustrated in Figure 1.

1. Perform a high-content siRNA screening of the human phosphatome to identify phosphatases (hits) whose activities modulate five readouts monitored by automated fluorescence microscopy. The cell states after inhibition of each phosphatase are represented as vectors with coordinates corresponding to the measured readout values (Figure 1Aa–e).

2. Collect from the literature and from pathway databases information describing the functional relationships between signaling proteins in the pathways of interest. This allows the assembly of a prior knowledge network which is represented as a signed directed model, where edges have sign (activating or inhibitory) and directionality (enzyme–substrate relationships). This naïve network integrates information obtained in different cellular systems under distinct experimental conditions (Figure 1Ba).

3. Optimize the model by training it against an independent set of experimental data obtained by measuring the activation of a large number of nodes under different perturbation conditions. This procedure removes connections that are not essential to explain the experimental results in the specific cell system and yields a computable model whose predictions best reproduce the experimental data set used for training (Figure 1Bb).

4. Use the optimized computable cell model to infer the changes in the measurable readouts that occur after upregulation or downregulation of the activity of each of the nodes in the network (Figure 1Bd).

5. Map the phosphatase hits on the node whose inferred network perturbation matches the one obtained experimentally in the siRNA screening (Figure 1C). The mapping procedure is based on the idea that if inhibiting a phosphatase in the siRNA screening results in the same readout values obtained when simulating the upregulation of a node in the logic model, then the phosphatase is an inhibitor of that node.

siRNA screening of the human phosphatome

To identify phosphatase genes participating in the modulation of cellular pathways underlying cell growth in HeLa cells, ∼300 known and putative protein phosphatases and regulatory subunits (phosphatome) were systematically silenced by transfecting with three different siRNA oligos for each gene (Supplementary Table S1). To monitor the ‘activation state’ of the cell upon phosphatase downregulation, five ‘sentinel proteins’ were chosen for their centrality in growth regulation pathways and for the robustness of available activation assays. The features we analyzed were the nuclear translocation of NFκB, the phosphorylation and activation of ERK, p38 and rpS6 and the formation of autophagosomes, as revealed by the appearance of LC3 dots. Forty-eight hours after transfection, the p38 and NFκB activity were analyzed in cells treated for 10 min with TNFα, whereas ERK and rpS6 phosphorylation, as well as autophagy, were monitored in untreated cells. In preliminary experiments we confirmed that, in these experimental conditions, the activation levels of each readout were intermediate between the experimentally observable minimum and maximum (Figure 2A–C). By inhibiting the activity of upstream control genes it was possible to observe either an increase or a decrease of the readouts (Supplementary Figure S1).

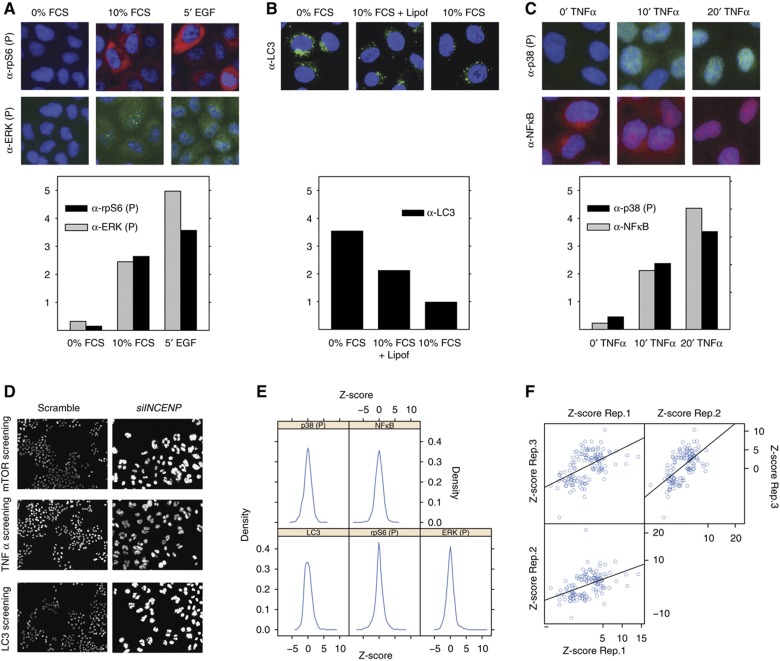
Figure 2.

Identification of phosphatase hits. Preliminary experiments were carried out to identify experimental conditions yielding intermediate readout values. (A) HeLa cells were starved for 6 h (0% FCS), induced with EGF for 5 min (5′ EGF) or left untreated (10% FCS). Cells were fixed and stained with anti-phospho ERK (FITC), anti-phospho rpS6 (TRITC) antibodies and DAPI to visualize nuclei. Cells were analyzed by indirect fluorescence microscopy coupled to automated image analysis. The ERK phosphorylation level in the nucleus (gray bar) as well as the rpS6 phosphorylation in the cytosol (black bar) were automatically measured and plotted. (B) HeLa cells were serum and amino acids deprived for 3 h (0% FCS) or left untreated (10% FCS) or transfected with an empty vector. Cells were fixed and stained with anti-LC3 antibody (FITC) and DAPI to visualize nuclei. To estimate autophagosome formation, images were analyzed by Cell Profiler and the mean LC3 intensity in the cytosol was measured and plotted as a bar graph. (C) HeLa cells were incubated with TNFα and sampled at time 0, 10 and 20 min. Cells were fixed, stained with anti-phospho p38 and anti-NFκB and visualized by indirect fluorescence microscopy. The nuclear p38 phosphorylation level (black bar) as well as the nuclear translocation of NFκB (gray bar) were measured by the Cell Profiler software and plotted. (D) HeLa cells grown on spots of siRNAs targeting the INCENP gene or a scrambled control were stained with DAPI. Images were acquired by automatic fluorescence microscopy with a × 20 objective. siRNA inhibition of the INCENP gene, causing a clear mitotic phenotype, was used as control of siRNA transfection efficiency (Neumann et al, 2010). (E) Distribution of the Z-scores of the phenotypic readouts of cells silenced in the different phosphatase genes. (F) The Z-score of each pair of three different biological replicates of phosphatase hits was plotted on the X and Y axis of a dispersion plot, respectively.

Cells were reverse transfected for 48 h by seeding and cultivating on LabTek chambers. After treatment with TNFα, cells were fixed and stained with 4′,6-diamidino-2-phenylindole (DAPI) and antibodies specific for the five ‘sentinel proteins’ or their phosphorylated forms. Images were automatically acquired and analyzed (see Materials and methods). Transfection efficiency was estimated from the appearance of polylobed nuclei (>85%) in cells silenced for the INCENP gene, which has a clear mitotic phenotype (Figure 2D; Supplementary Figure S2; Neumann et al, 2010). After statistical analysis of three biological replicas (Supplementary Table S1), protein phosphatases whose downregulation significantly affects the activation profile of the five readouts were selected as hits, as described in detail in Materials and methods. The plots in Figure 2E represent the distribution of the Z-scores of the phenotypic readouts of cells silenced in the different phosphatase genes. As expected signals in most of the interference experiments are not substantially different from the scrambled controls, while the knock-down of a few phosphatases results in a signal that is significantly higher or lower than the average (Supplementary Table S1). The experimental variation between biological replicates was analyzed by plotting the Z-scores of the phosphatase hits in each pair of the three biological replicates (Figure 2F).

The primary siRNA screen identified a total of 76 phosphatase hits for the 5 different readouts, comprising ∼30% of the human phosphatome (Supplementary Table S2). Sixty three percent correspond to genes encoding proteins with a phosphatase catalytic domain, while 20% encode regulatory subunits. The remaining 17% belong to the lipid phosphatase subgroup and was not considered further in this analysis. Figure 3A presents the results of the primary screening as a graph where phosphatase hits (circles) are linked to the phenotypes (squares) that are affected by their downregulation. In this graph, edges represent a functional relationship not a direct interaction between phosphatases and readouts. Red and green edges, respectively, connect the identified positive and negative regulators to the five sentinel proteins. Approximately 67% of the observed phenotypic perturbations by any given phosphatase were supported by two or three different phosphatase-specific oligos. Although it is possible that some of the remaining 33%, which were experimentally verified by a single oligo, may represent potential ‘off-target effects’ they were nevertheless analyzed in the secondary screening.

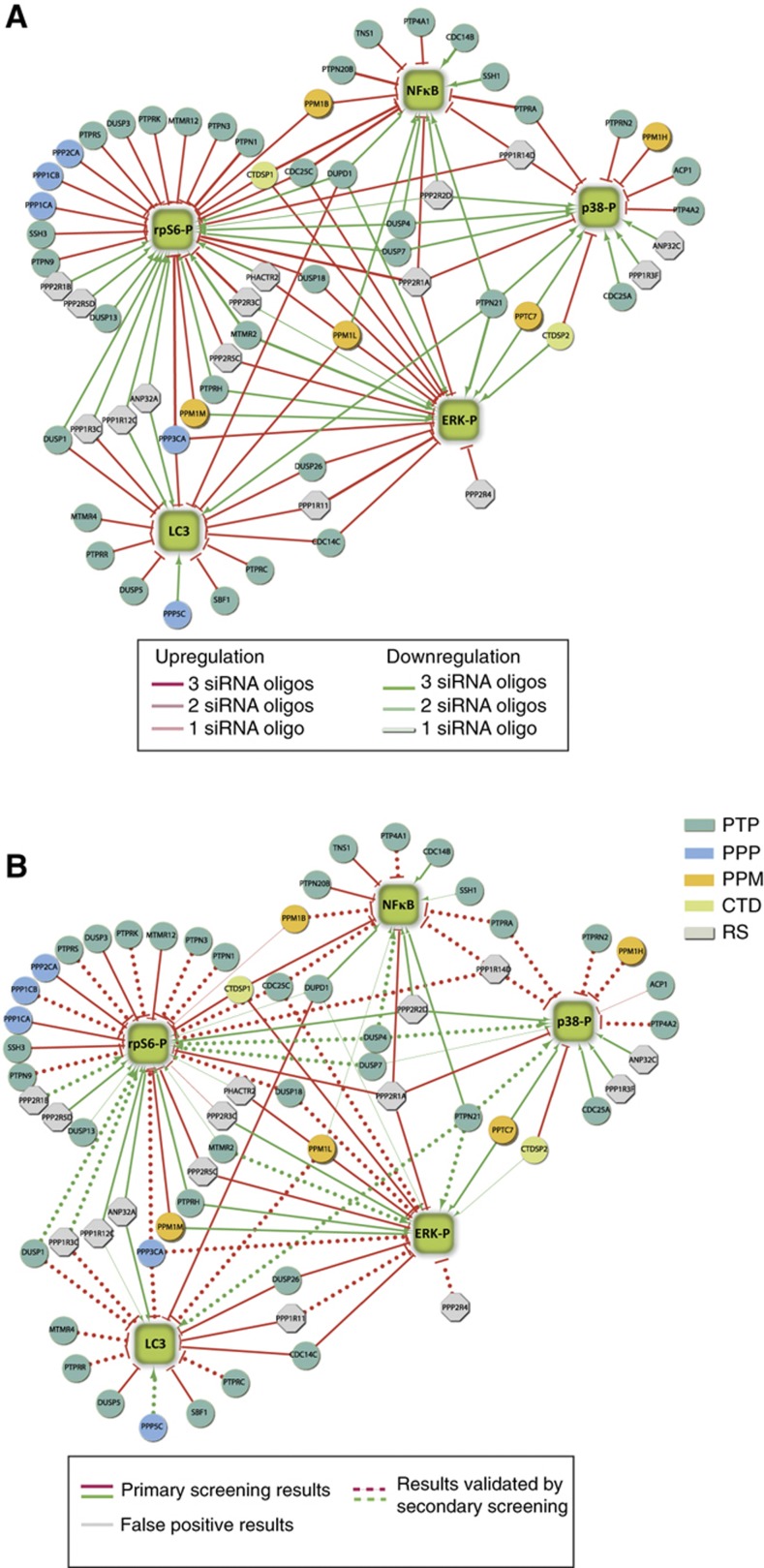
Figure 3.

Graphical representation of the siRNA screening results. (A) The results of the siRNA screening are illustrated as a graph. The green squares represent phenotypes. Phosphatases (circles) are colored according to their functional classification (Supplementary Table S1): PTP, Protein Tyrosine Phosphatases; PPP, Phosphoserine Proteine Phosphatases; PPM, Protein Phosphatase Metal dependent; CTD, Carboxy Terminal Domain phosphatases; RS, Regulatory Subunits. Edges represent a functional relationship, linking the phosphatase hits to the phenotypes that are affected by interference of phosphatase expression. Positive and negative regulators are linked to the readout by green and red edges, respectively. The three intensities of the edge colors reflect the number of different phosphatase-specific oligos that support the observation in the primary siRNA screening. (B) Illustration of the results of the secondary screening carried out with an independent shRNA library. Gray edges indicate functional relationships that were not confirmed in the secondary screening, whereas dashed edges indicate results validated by secondary screening. The experimental observations that were not retested in the secondary screening are showed as continuous edges.

siRNA screenings are often affected by a high false positive rate because of off-target effects. To increase the confidence in the identified phosphatase hits, we performed validation experiments using an independent RNA interference library (Mission® shRNA phosphatase library, Sigma). Based on the availability of predesigned shRNA oligos in the second library, 38 phosphatase hits were selected for validation and interfered by a pool of three different shRNA oligos (Supplementary Table S3; Supplementary Figure S3). Approximately 75% of the hits were confirmed by this independent approach (Figure 3B). The remaining 25%, whose phenotype was not confirmed, establishes the upper limit for false positive hits in the primary screening.

A number of known functional relationships between phosphatases and the pathways monitored in the screening were recapitulated (Supplementary Table S4). However, our approach failed to identify some known phosphatases affecting the analyzed readouts, such as the PTEN and PTPN11 phosphatases acting on mTOR and MAPK signaling, respectively (Chu and Tarnawski, 2004). The inefficiency of some siRNA oligos (data not shown) and experimental noise could explain these false negative results, a common problem in high-throughput siRNA screening (Sachse et al, 2005). However, the high rate of validation in the independent secondary screening (75%) underscores the reliability and robustness of the experimental strategy.

Logic-based modeling of cancer-associated pathways

Next we aimed at increasing the details of the functional analysis, in order to get insights into the molecular mechanisms underlying the activity of the phosphatase hits. To this end, we have first assembled a prior knowledge network by mining from the literature and from pathway databases experimental evidence linking the growth pathways analyzed in the screening. This yields an intricate and highly interconnected network (Supplementary Table S5) including 34 species and 59 stimulatory or inhibitory interactions.

This network was represented as a signed directed graph (Figure 4A) and analyzed using the CellNetOptimizer (CellNOpt) software (Saez-Rodriguez et al, 2009; Morris, 2012). CellNOpt enables the assembly of a Boolean logic model whose structure is optimized by maximizing the concordance between the model predictions and a set of experimental data used for training. As a first step, CellNOpt compresses the model by removing nodes, whose states cannot be determined with the experimental data at hand (Figure 4B). The compression therefore depends both on the topology of the network and on the design of the perturbation experiments. Essentially, this step removes: (i) nodes whose states are not affected by any of the inputs or perturbations; (ii) linear cascades of undesignated nodes (i.e., not perturbed nor measured) that impinge on a designated node.

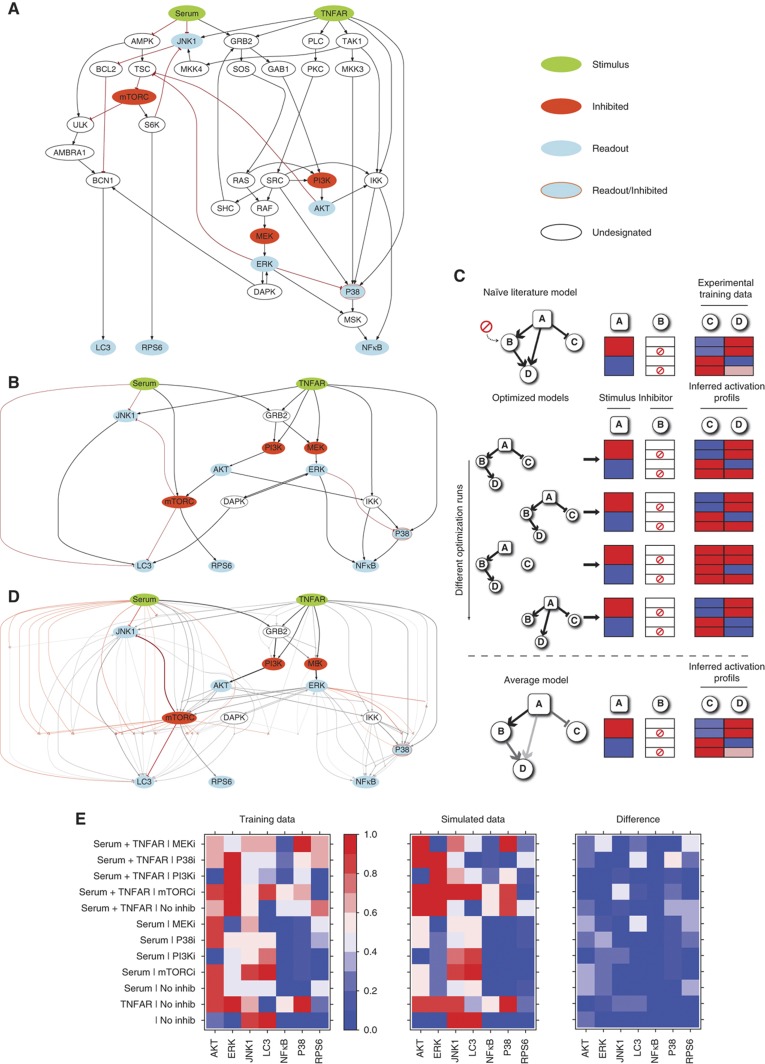
Figure 4.

Assembly and optimization of a literature-derived growth model. (A) An extensive literature and database search has been carried out to assemble a literature-derived signed directed graph modeling the cross-talk between growth pathways. The network is visualized by the graph layout routine included in the CellNOpt software. (B) The graph in (A) was automatically compressed by the CellNOpt software by applying the rules described by Saez-Rodriguez et al (2009). White ovals circled with dashed lines in (A), represents nodes, not subjected to experimental manipulation, that were part of linear cascades in which a series of undesignated nodes and edges impinged on a designated node. Such nodes were compressed by CellNOpt and consequently eliminated, as shown in (B). (C) Schematic representation of the optimization strategy of a toy network. The CellNOpt software uses a genetic algorithm to identify models whose prediction better explains the experimental results. Edges are randomly removed and connected by different combinations of AND/OR logic gates. The resulting rewired models are finally tested for their ability to reproduce the experimental results. Since different optimization runs yield models with different connections, the performance of the model is obtained by averaging the predictions of 1000 different models. (D) A graph representing the average results of 1000 optimization runs. The thickness and color intensity of each edge are proportional to the number of times it appears in the 1000 optimized models. (E) Color coded representation of the results of the experiments that were used to train the model and comparison with the average prediction of the 1000 models. The protein activation level, which ranges from 0 to 1, is represented with a gradient from blue (inactive) to red (active). The third panel uses the same color scale to display the absolute value of the difference between the data simulated from the model and the experimental data used for training.

The resulting graph is then optimized using a genetic algorithm that randomly rewires the network, in order to maximize the fit between experimental and simulated data. The end result is the removal of interactions that are not functional to explain the system response to perturbation in the specific HeLa cell context and the integration of multiple stimuli acting on the same protein node into AND/OR logic gates (Figure 4D).

The compressed model was trained and calibrated against experimental data, obtained by growing HeLa cells in 12 different experimental conditions where stimulations with serum or TNFα are combined with inhibitors targeting four nodes of the signaling network (MEK, p38, PI3 kinase and mTOR; Figure 4E). In each experimental context, the activities of seven intracellular signaling proteins were measured by western blot or immunofluorescence techniques with specific antibodies (see Supplementary Figures S4 and S5). Overall, the observed modulation of the readouts was consistent with the experimental evidence reported in the literature.

The experimental training data were normalized in the 0 to 1 range with a Hill function and used to calibrate the Boolean model by running CellNOpt 1000 times. The choice of repeating the analysis multiple times stems both from the stochastic nature of the optimization procedure and also from the fact that the training data were not sufficient to fully constrain the model (Saez-Rodriguez et al, 2009). By performing subsequent calculations on this family of 1000 models it is possible to average out the inconsistencies present in any single model (Figure 4C). Moreover, by this approach one obtains quantitative predictions even though a given node can only be on (1) or off (0) in any single model. This is important when the experimental value of a readout is close to 0.5, that is, equidistant from 0 and 1. In these cases, approximately half of the models will show inactivation and the other half activation because both situations are equiprobable in the optimization scheme. Therefore taking the average across all models will correctly show a midrange value, while any single model is distant from the true experimental value that does not show a strong activation/inactivation. In the consensus graph shown in Figure 4D, the thickness and color intensity of each edge is proportional to the number of times it appears in the 1000 optimization runs.

We used the family of 1000 logic models to compute the effect of inhibiting each of the four kinases that we had targeted with small-molecule inhibitors. This procedure essentially replicates the experimental set-up in silico and can be used to evaluate the fit between the simulated data and the experimental data used for the optimization. The activation state of a protein in a given condition is calculated as the fraction of the 1000 models in which the protein was active. The fit between the results of the in-silico simulation and the experimental data is in general high (Pearson Correlation Coefficient of 0.84), with a few exceptions, as shown in Figure 4E. As expected, the agreement increases when the predictions are carried out by averaging over a larger number of models, reaching an apparent plateau at 100 models (Supplementary Figure S6).

Mapping of phosphatase hits

The experimental data used to calibrate the HeLa cell model did not include the results of inhibiting all the nodes in the network. Moreover, the effect of upregulating the nodes is completely absent from the experimental data. This is especially relevant for the phosphatases that inhibit their target node, as their silencing should result in an upregulation of the target. However, the calibrated family of optimized models allows computing the effect of upregulating and downregulating each node (see Materials and methods). Each perturbation results in a predicted cell state defined as the calculated activity of the five sentinel proteins. By matching this signature with the experimental profile obtained in the phosphatases siRNA screening it is possible to infer the target and effect (activating/inhibitory) of each phosphatase, thus defining its ‘entry point’ in the network. For instance, if the silencing of a phosphatase results in the same cell state obtained when GRB2 is upregulated in the simulation, we can infer that the phosphatase downregulates GRB2. This ‘associated’ node is unlikely to be the direct substrate of the phosphatase since other proteins not included in our prior knowledge network may link the phosphatase with the protein in the model. The entry point of a phosphatase thus represents the node that first senses the perturbation and propagates it to the rest of the protein species in the model. This mapping strategy is especially useful for the phosphatases whose perturbation influence multiple readouts. Indeed these proteins must modulate the activity of some upstream node that serves as the branching point between multiple signaling pathways.

As a first step, to compare the simulated results with the ones measured experimentally, both experimental and inferred readout values were normalized in the 0–1 interval, as described in Materials and methods. Next, the continuous values were discretized and transformed in a categorical variable with three possible values, namely ‘downregulated’, ‘control’ and ‘upregulated’ when the normalized value fell in the 0–0.33, 0.33–0.66 and 0.6–1 ranges, respectively. Following the inhibition/activation of each protein in the growth model, the cell states can be defined as vectors with coordinates corresponding to the discretized state of each of the five sentinel proteins, represented with green (upregulated), white (control) and red (downregulated) squares in Figure 5A. According to our mapping strategy, if a phosphatase acts on a given node by inhibiting it, then its downregulation in the siRNA screening should result in a cell state similar to the one computed by the model, when the node is upregulated. Conversely, if the phosphatase has an activating effect on a network node, then we would expect that its downregulation should result in a network state comparable to the one predicted by the model after downregulation of the node. Each phosphatase is therefore matched with the upregulation or downregulation of a node that results in the most similar state vector. The distance between the state vectors is calculated as 1—the fraction of sentinel proteins with identical states.

Figure 5.

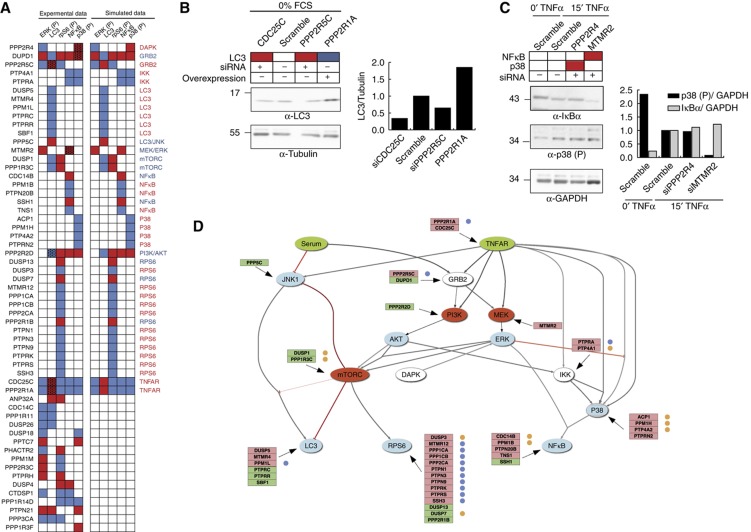
Mapping of phosphatase hits on the optimized growth model. (A) The siRNA screening results are represented as a hit map and compared with the model predictions after upregulation or downregulation of the activity of each node in the 1000 optimized models. Red and blue indicate a downregulation or an upregulation of the activity of the five sentinel proteins, respectively. (B, C) HeLa cells were transiently transfected with phosphatase coding plasmids or with an equimolar pool of vectors expressing three different oligos targeting each phosphatase. After 48 h of transfection, cells were stimulated with TNFα for 15 min (right panel) or starved for 1 h (left panel). The phosphorylation levels of p38 and ERK were measured by immunoblotting with anti-phospho p38, anti-tubulin and anti-phospho ERK. The LC3 and IκBa protein levels were monitored by immunoblotting with anti-LC3, anti-IκBα and anti-GADPH and plotted in the bar graph. (D) Protein phosphatases hits are mapped on the optimized logic model. Positive and negative regulators of the indicated nodes are represented with a green or a red background, respectively. Phosphatases with an oncogenic or oncosuppressor functions are, respectively, labeled with a yellow or blue dot.

For 35 out of 58 phosphatase hits (60%), we can identify an in-silico perturbation that has exactly the same effect (i.e., distance=0) on the five sentinel proteins as the downregulation of the phosphatase in the siRNA screening. These phosphatases were therefore mapped accordingly (Figure 5A). We also considered the possibility that some phosphatases that had a single mismatch between the experimental and the closest inferred profile could be due to false negatives in the siRNA screening or to the slightly different experimental set-up used for the screening and for the training data set. In particular, we checked whether modulation of phosphatase activity in conditions of starvation could affect LC3 levels. This turned out to be true for the PP2A scaffold PPP2R1A, its regulatory subunit PPP2R5C and the cell-cycle modulator CDC25C. This result is consistent with the mapping of the first two phosphatases onto the TNFR node and of the third onto the GRB2 node (Figure 5C, left panel). In addition, downregulation of the myotubularin-related protein MTMR2 was found to negatively affect the concentration of the NFκB inhibitor IκBα and this phosphatase was therefore mapped onto the MEK/ERK nodes, as predicted by the model (Figure 5C, right panel). Thus, a total of 41 phosphatases were mapped onto a specific node. The downregulation by siRNA of the remaining 17 phosphatase hits displayed a profile that could not be matched with the effect of perturbing any specific node. We considered the possibility that at least some of them could be explained by assuming an effect on two different nodes, and therefore simulated the effect of up/downregulating all possible pairs of nodes. This procedure allowed the mapping of three additional phosphatases (PPP3CA, DUSP4 and PPP1R14D) whose profile differed for a single readout in the simulation with single perturbations. These are respectively predicted to be an inhibitor of IKK and S6 (PPP1R14D) an activator of NFκB and S6 (DUSP4), and an inhibitor of GRB2 and LC3 (PPP3CA).

Interestingly, as illustrated in Figure 5A, some phosphatases show consistent activation profiles, even though they could not be mapped to any single node in the model (or any specific pair of nodes in the simulation with double perturbations). For instance, PPM1M and the two PP2A regulatory subunits PPP2R3C and PHACTR2 have an opposite effect on the activation of ERK and S6, while CDC14C, DUSP26 and PPP1R11 have a concordant effect on ERK activation and autophagy (Figure 5A). These patterns cannot be explained by our simulations, raising the possibility that some molecular connections were not adequately represented in our optimized logic model or that our training data were not sufficient to fully train the model (see Discussion).

To assess the reliability of our mapping, we compared experimental results and model predictions in conditions that were not used during the optimization of the model nor in phosphatase mapping. In a first experiment, we selected six hit phosphatases and we measured the activation of the sentinel proteins when the expression of the phosphatase was downregulated or upregulated in presence of serum after 10 min of incubation with TNFα Figure 6A). In principle, upregulation and downregulation may lead to activation profiles that are not necessarily inverted as this depends on the activity levels of the targeted nodes in basal conditions. However, we observed that in these conditions the activation profiles are indeed largely complementary, with the possible exception of the observed inactivation of rpS6 when PTPN21 is silenced, which is not matched by rpS6 hyper-phosphorylation when PTPN21 is overexpressed (Figure 6A, left panel). We next simulated the same experimental conditions using the model and we compared the computed activation states with the ones obtained experimentally. The inferred states are computed by setting in the model the values of the phosphatase target nodes to 1 or 0 depending on whether the phosphatase was predicted to be a positive or a negative regulator by the mapping procedure (Figure 6A, right panel). The experimental results largely confirm the predictions derived from the model. Notable exceptions are the predicted modulation of NFκB and p38 by PTP4A1 and PTP4A2, respectively, which were not observed experimentally. The experimental profiles of PTPN21 and DUSP18 had not been matched with a model prediction when using the results of the siRNA screening. Even in these different experimental conditions the profiles do not correspond to any simulation result (Figure 6A).

Figure 6.

Validation of phosphatase hits mapping prediction on the optimized growth model. (A) Comparison of phenotypes obtained after downregulation and upregulation of selected phosphatase genes. The results of the screening are represented with a color code where red and blue indicate that the phosphatase downregulates or upregulates the activation of the readout indicated on the right of the panel. Phosphatases were overexpressed (blue arrow) or silenced (red arrow) by an equimolar pool of vectors. After 48 h of transfection, cells were stimulated with TNFα for 10 min. Activation levels of the sentinel proteins were measured by immunoblotting with anti-phospho ERK, anti-GAPDH, anti-phospho p38, anti-phospho rpS6 and anti-tubulin. The nuclear translocation of NFκB was measured by indirect immunofluorescence microscopy coupled to automated image analysis in cells stained with anti-NFκB antibody. The obtained results were normalized by the Hill function to values ranging from 0 to 1 and then compared with the ones obtained by the simulation of the downregulation (red arrow) or upregulation (blue arrow) of specific nodes in the optimized model. Blue and red boxes, respectively, indicate high and low values, while intermediate values are mapped to shades of red and blue. For each measurement, the average value and standard deviation of three independent biological replicas was calculated. (B) HeLa cells were transiently transfected with plasmids encoding the indicated phosphatases or with an empty vector. After 24 h of transfection, cells were stimulated with TNFα for 10 min. Anti-V5 and anti-tubulin antibodies were used to assess transfection efficiency and as loading control, respectively. The activation level of the five sentinel proteins was analyzed either by western blot or by immunofluorescence techniques. The phosphorylation levels of RAF1, ERK, AKT, rpS6 and p38 were analyzed by immunoblotting with anti-phospho-specific antibodies and anti-tubulin. The autophagy level was assessed by revealing protein extracts with anti-LC3 antibody and anti-tubulin, as loading control. As previously described, the nuclear translocation of NFκB was measured by immunofluorescence microscopy coupled to automated image analysis. For each measurement, the average value and standard deviation of four independent biological replicas was calculated. As previously described, the obtained results were normalized by the Hill function to values ranging from 0 to 1 and reported. Source data is available for this figure in the Supplementary Information.

Source data for Figure 6A ^{(45.5KB, xls)}

Source data for Figure 6B ^{(43.5KB, xls)}

Source data for Figure 6C ^{(41KB, xls)}

In a second experiment, we checked whether the overexpression of four phosphatases, which were mapped to different positions of the signaling network (i.e., upstream and downstream of AKT and ERK), differentially affect the activity of two readouts (RAF1 and AKT activation) that were not considered in the mapping procedure. For this purpose, we selected the regulatory subunit PPP2R1A and the protein phosphatase CDC25C, mapped upstream of AKT onto the TNFR node, and the two tyrosine-specific phosphatases of regenerating liver, PTP4A1 e PTP4A2, associated with the IKK and p38 nodes, respectively (Figure 5B). As predicted, by the model and the mapping, only the overexpression of PPP2R1A and CDC25C significantly affects the phosphorylation levels of the downstream kinases AKT and RAF1, resulting in a drastic reduction of the activity of ERK, p38, rpS6 and NFκB (Figure 6B). In contrast with the results of the experiment in Figure 5C, the predicted upregulation of autophagy, upon PPP2R1A and CDC25C overexpression, was not observed in these experimental conditions. However, as shown in Figure 6B, in the presence of serum and TNFα, autophagy is severely downregulated and LC3 is barely detectable in the western analysis. In these conditions, identification of subtle modulations is extremely difficult. We confirmed in starved cells that PPP2R1A and CDC25C positively modulate autophagy (Figure 5C, left panel), confirming the reliability of our mapping. In addition, in accordance with the model prediction and its mapping on the IKK node, PTP4A1 only induces the inactivation of p38 and NFκB, which in turn is not affected by PTP4A2, which was mapped onto the p38 node. The high degree of correlation between the experimental and computed activation states, in a variety of experimental conditions, highlights the ability of the model to compute the network activation profile, after perturbing the activity of any node. In addition, the mapping procedure is robust and, once the entry node of a phosphatase has been identified, in a specific experimental condition, the effect of modifying the activity of the phosphatase in different conditions can be computed by activating or inactivating the entry node in the model simulation.

Phosphatase hits modulate cell-cycle timing

The aberrant activation of the pathways that we have considered in the growth model has been implicated in the development of several tumors. Therefore, we investigated whether our screening had preferentially identified phosphatases that are enriched for those that have already been characterized as oncogenes or oncosuppressors.

As shown in Figure 5B, the data curated in the Phosphatase Database (Liberti et al in preparation), identified 24 of the 41 mapped phosphatase hits as oncogenes or oncosuppressors, marked with yellow and blue circles, respectively. The significant enrichment (P-value <0.01 by the hyper-geometric test) of ‘cancer phosphatases’ in the hit list suggests that our screening preferentially selects proteins that have the potential to interfere with the control of cell growth.

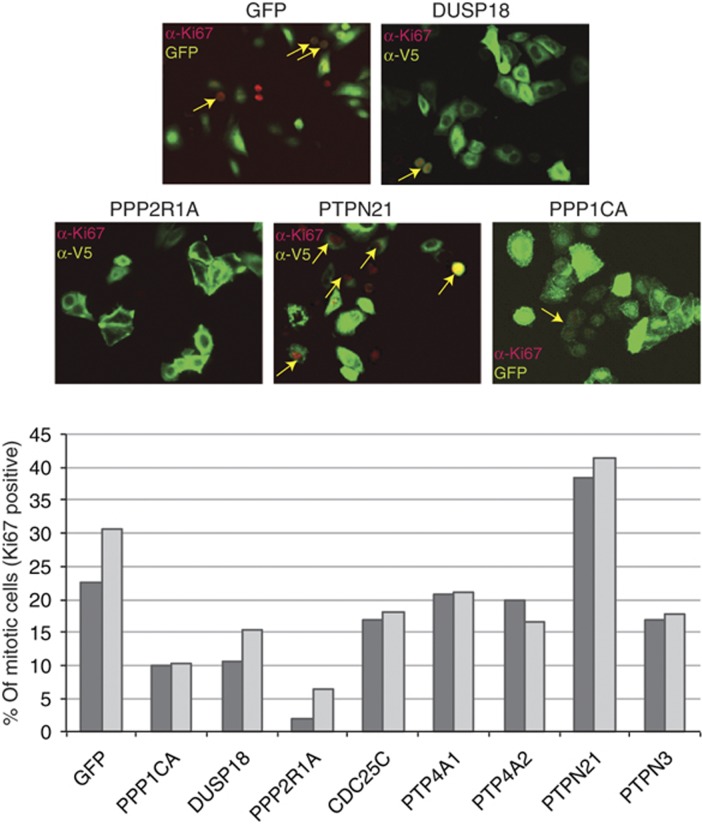
To test this hypothesis, eight phosphatase hits were overexpressed and the perturbation of cell-cycle timing was monitored by counting the percentage of transfected cells having nuclei positive for the cell proliferation marker Ki67. As shown in Figure 7, the overexpression of PTPN21, a phosphatase whose oncogenic potential has been characterized (Carlucci et al, 2010), increases the fraction of mitotic cells whereas, consistent with their reported tumor suppression function (Julien et al, 2011; Liberti et al, 2012), PPP2R1A, PPP1CA and PTPN3 negatively regulate the number of mitotic cells. Similarly, overexpression of DUSP18, which was shown in our screening to downregulate the activation of the MAPK ERK and p38 (Figure 6A), results in a decrease of the number of cells that can be labeled with the mitotic antigen antibody.

Figure 7.

Phosphatase hits affect cell-cycle timing. In HeLa cells, V5- or GFP-tagged protein phosphatases or GFP coding vector, as negative control, were overexpressed. After 24 h of transfection, cells expressing V5-tagged phosphatases were fixed, stained with anti-Ki67 and anti-V5 antibodies and analyzed by immunofluorescence microscopy coupled to automated image analysis. The percentage of transfected cells having Ki67-positive nuclei was measured. Two independent biological replicas were plotted in the bar graph.

Discussion

This work describes a novel strategy combining high-content phenotypic screenings and modeling to map proteins on a signaling network on a large scale. Our approach requires a computable signaling model, which can be assembled from the literature and subsequently optimized by training with the results of perturbation experiments (Saez-Rodriguez et al, 2009). Such a model is used to predict the effect that the activation/inhibition of upstream modulators has on a number of molecular readouts that together are used as a signature to describe the state of the cell. When the same molecular readouts are measured in an independent siRNA high-throughput screening, it is possible to bring a large number of proteins in the model by simply matching the computed and experimentally determined cell states. By this strategy the hits identified in the high-throughput screening are linked to the nodes in the model that, when perturbed in silico, result in the same cell state. We show that using this approach, it is possible to obtain mechanistic insights on a large scale without sacrificing either coverage or detail.

This novel strategy was applied to study the involvement of protein phosphatases in cell growth pathways. The results of our screening support the notion that protein phosphatases can both upregulate (40%) or downregulate (60%) signal transduction events. This observation is consistent with the current view that phosphatases do not only act to terminate signaling, but also have a prominent role in the positive regulation of signal transduction events, resulting in both oncogenic and oncosuppressor functions (MacKeigan et al, 2005; Julien et al, 2011).

Here, we show that 67% (41) of the phosphatases that were characterized as pathway modulators in our siRNA screening could be mapped onto defined nodes of our cell-specific optimized model (Figure 5). Importantly, our mapping procedure is reliable and consistent with the results of independent experiments (Figure 5). For instance, the overexpression of either PTP4A1 or PTP4A2, which were mapped on IKK and p38, respectively, only affects the activity of these downstream nodes. Conversely PPP2R1A and CDC25C, which were mapped upstream of RAF1 and AKT, have a much broader effect on cell state, drastically inhibiting the activity of ERK, p38, rpS6 and NFκB (Figure 6B) and positively modulating autophagy (Figure 5C, left panel).

Interestingly each node of our model is modulated by several phosphatases, suggesting a high level of redundancy in pathway regulation. In this scenario, it is important to consider that the scaffold model is compressed. Therefore, each of the observed phosphatase modulators may affect in a similar way the same node, by targeting different proteins that have been compressed on the same node or even proteins that do not appear in our model but modulate the activity of the node in vivo. Alternatively, the redundancy that is observed in HeLa cells may reflect a superimposition of mechanisms modulated by phosphatases that act in a tissue-specific manner in vivo. However, no clear-cut conclusion could be drawn from the analysis of phosphatases co-expression data in human tissues in the COXPRESdb database (Obayashi et al, 2008).

The measured profiles of 17 phosphatase hits could not be matched with the effect of perturbing any specific node of the model. We have considered the possibility that some of these profiles could be explained by the targeting of multiple nodes. Thus, we performed new simulations where we computed the effect of up/downregulating all the possible pairs of nodes in the model. This procedure allowed the mapping of three additional phosphatases (PPP3CA, DUSP4 and PPP1R14D). The cell states (profiles) of the remaining 14 phosphatases were either: (i) not compatible with the model, that is, they could not be reached in any of the simulated experimental conditions involving perturbation of up to two nodes or (ii) not specific to the perturbation of any node, or pair of nodes. We can contemplate a number of limitations of our model that could explain this partial failure.

1. Training data are insufficient to fully constrain the model. We observed that some of the unmatched profiles could be made compatible with the model by reinstating connections that were assigned a low weight in the model optimization procedure. For instance, three phosphatases (PPP1R11, DUSP26 and CDC14C) positively regulate both autophagosome formation and ERK phosphorylation. The link between ERK activation and autophagy was present in our literature-derived network because DAPK was described to remove the inhibitory interaction between BCL-XL and beclin (Zalckvar et al, 2009) after activation by ERK (Chen et al, 2005). However, this logic relationship is given a low weight after model optimization possibly because our training data were not adequate to support this link. In addition, the optimization procedure does not explore the addition of new nodes or edges. Thus, if the literature-derived starting model misses elements that are important to model the experimental results, these will not be tracked down during model optimization.

2. Gene regulation feedback loops. Gene expression feedback loops were not considered in the growth model. The choice was dictated by the lack of information on the regulatory circuits that are modulated by growth pathways and on their impact on the activation of the model nodes. In addition, Boolean models are inadequate to incorporate feedback loops. These simplifications do not represent a substantial limitation because the model was calibrated against experimental data, obtained by short-term network perturbations (1–2 h). However, in our mapping procedure the inferences from the signaling model were compared with the siRNA screening results, obtained by downregulating phosphatases for 48 h. This procedure would lead to incorrect inferences if the siRNA perturbation activates feedback loops involving gene transcription and causes network rewiring. Indeed extensive network rewiring can be induced by small interfering RNA, as pointed out by Jorgensen and Linding (2010). This may be responsible for our inability to map some of the phosphatase perturbations.

3. Limits of the Boolean representation. The siRNA screening results are quantitative and continuous. For comparison with the Boolean model the data are discretized. This procedure implies the somewhat arbitrary selection of threshold values. It is possible that in some cases the discretization procedure is an inadequate representation of the complexity of the regulatory network.

Our analysis reveals that multiple regulatory subunits targeting PP2A and PP1 phosphatases are essential modulators of the analyzed pathways. These observations are consistent with the current view that these two enzymes control different physiological pathways, by interacting with diverse regulatory subunits (Wera and Hemmings, 1995). Surprisingly, in our screening, the downregulation of the PP2A and PP1 catalytic subunits (PPP1CA, PPP2CA) only impairs rpS6 phosphorylation, without affecting the activity of the remaining branches of the network. This observation can be rationalized by considering that the mRNA levels of the two catalytic subunits are incompletely knocked down by siRNA (Supplementary Figure S1).

Our mapping strategy is not designed for the identification of phosphatase substrates. Nevertheless, it enables the positioning of phosphatase hits in proximity of their physiological targets. For instance, Eitelhuber et al demonstrated that PPP2R1A, which we have mapped onto the TNFR node, directly interacts with the Carma1-Bcl10-Malt1 (CBM) complex. This complex indirectly interacts with trans-membrane receptors, such as TCR or TNFR (Rawlings et al, 2006; Eitelhuber et al, 2011), leading to the PP2A-mediated dephosphorylation of Carma1 and the inactivation of NFκB. This observation is consistent with our mapping prediction, suggesting that the PPP2R1A–Carma1 interaction not only mediates NFκB inactivation, but also induces the ERK, p38 and rpS6 de-phosphorylation and, as a consequence, decreases the number of mitotic cells (Figures 5 and 6). Evidence showing that this regulatory subunit has a high frequency of mutation in human endometrial cancers and that the mutated region mediates the association with the PP2A catalytic subunit (Nagendra et al, 2011; Shih et al, 2011) underscore the physiological relevance of our observations.

Similarly, we were able to identify a model ‘entry node’ for a number of additional ‘cancer phosphatases’, whose molecular mechanism leading to tumorigenesis is still unknown (Figure 5). Indeed the statistically significant overlap between the hits of our screening and the phosphatases already implicated in cancer suggests that some of the phosphatase hits, which are not yet recognized as such, should be considered as new potential oncogenes or oncosuppressors. For example, we demonstrated that the poorly characterized DUSP18 phosphatase strongly downregulates the fraction of mitotic cells, possibly by negative modulation of the pro-proliferative MAPK ERK pathway, suggesting a novel tumor suppressor role for this phosphatase (Figure 6). However, further in-vivo experiments are required to confirm that DUSP18 as well as the other phosphatase hits are new cancer genes.

In conclusion, this study offers a genome-wide perspective on the involvement of protein phosphatases in the modulation of cell growth under TNFα stimulation, leading to the identification of new modulators of pathways that may be relevant for tumor development. To achieve this, we have developed a novel strategy to map perturbations onto complex pathways.

Multiparametric screening of cell phenotypes after small RNA interference or small molecule inhibitors are currently used to functionally characterize genes and discover new drug leads, respectively. The proposed mapping strategy is general and could be used in combination with the results of such large screenings to achieve a more detailed mechanistic description of the molecular mechanisms by which genes or small molecules determine phenotype modulation.

Materials and methods

siRNA screen

The primary siRNA screen was performed using a phosphatase library of siRNAs (Ambion) based on ENSEMBL version 27. Each phosphatase was targeted by three different oligos. For hit validation, we used a library of shRNAs (Mission® shRNA phosphatase library, Sigma) and HeLa cells were transfected with a pool of three shRNA oligos. For the primary screening, ∼10 × 10⁴ HeLa cells were seeded on LabTek chambers and reverse transfected, as previously described (Erfle et al, 2007). After 48 h, the cells were treated with different stimuli according to the analyzed molecular phenotype. In order to analyze the ERK and rpS6 phosphorylation, as well as the LC3 levels, cells were left untreated in growth medium. To induce an intermediate activation of NFκB and p38, cells were treated for 10 min with TNFα.

Subsequently, cells were fixed with 4% paraformaldehyde. After fixation, the cells were processed by immunofluorescence techniques and images corresponding to each spot of the LabTek were acquired at the HTS/HCA Facility of the Consorzio Mario Negri Sud (http://www.negrisud.it/en/research/services/htmicroscopy/) in DAPI, RFP and GFP separated channels using the automated microscopy image stationScan^R life Science (Olympus) equipped with Olympus IX81 inverted microscope, MT20E lamp, Digital camera CCD QE, motorized fast movement turret, SuperApocromatic × 20 NA 0.75 short distance objective. The experiments were carried out in three biological replicas.

Image analysis

Image analysis was performed using the open source Cell Profiler software and consisted of the following three successive steps: (i) identification of nuclei by cell nuclei segmentation in the Hoechst channel; (ii) identification of cell cytoplasm by different segmentation algorithms according to the different antibody staining; (iii) automatic measurement of several cell characteristics: cell count, perimeter, area, shape and eccentricity of cells and nuclei, signal intensity of the antibodies in the nucleus and in the cytosol. For each image, ∼100 cells were identified and analyzed. To monitor the ERK and p38 phosphorylation, for each image the mean intensity value of these two antibodies was measured in nucleus. To analyze the rpS6 phosphorylation and the autophagy level, for each image the mean intensity value of anti-phospho rpS6 and anti-LC3 was measured in the cytosolic compartment. Finally to detect the NFκB activation, for each image we measured the mean ratio between the nuclear fraction of NFκB and the cytosolic one.

Cell culture

Human epithelial carcinoma (HeLa) cells were kindly provided by Jan Ellenberg Lab and grown, as previously described (Sacco et al, 2009). HeLa cells were treated with 50 ng/ml TNFα for the prescribed time. Nutrients and amino-acid starvation was performed by incubating cells with Early Balanced Salt Solution medium. Cells were stimulated with EGF 100 ng/ml for the prescribed time. HeLa cells were lysed with RIPA buffer and analyzed by SDS–PAGE, as previously described (Sacco et al, 2009).

Immunofluorescence microscopy

HeLa cells were fixed with 4% paraformaldehyde and permeabilized with PBS1X Triton 0.1% or Digitonin 100 μg/ml for 10 min at room temperature. After 30 min of blocking solution (3% BSA PBS1X), the cells were stained with primary antibodies and appropriate secondary antibodies. Subsequently, the cells were stained with DAPI in PBS1X, 0.1% Triton for 5 min at room temperature. Images were acquired by indirect immunofluorescence on Leica microscope or Delta Vision microscope using × 20, × 40 or × 63 objectives.

Plasmids and reagents

Anti-phospho rpS6, anti-phosho ERK and anti-phospho p38 were from Cell Signaling; anti-β-tubulin, anti-NFκB, anti-GFP and anti-p62 were from Santa Cruz Biotechnology; anti-GADPH was from BD laboratories; anti-LC3 (IF) was from MBL; anti-LC3 (WB) was from Nanotools. Anti-V5 was from Invitrogen. The anti-rabbit and anti-mouse secondary antibodies were purchased from Jackson Immunoresearch. pENTR plasmids coding for protein phosphatase genes were purchased from Open Biosystem or kindly provided by Dr Stefan Wiemann. The phosphatase genes, contained in the pENTR plasmids, were cloned into pcDNA 3.1 CT-GFP Topo and pcDNA 3.2/capTEV-V5 DEST commercial destination vectors, by applying the Gateway Cloning System (Invitrogen). The small molecules kinase inhibitors (UO126, SB203580, Wortmannin and Rapamycin) were from SIGMA. HeLa cells were treated with 10 μM UO126 per 1 h, with 15 μM SB203580 per 1 h, with 200 μM Wortmannin per 2 h and were incubated with medium containing 100 μM Rapamycin per 1 h.

Statistical analysis of siRNA screening results

The data from several LabTek showed a strong positional bias. This effect was corrected by performing a 2D loess regression of the data in each array and then subtracting the estimated value from the actual value (Smyth and Speed, 2003). In order to compare data from different chambers, we calculated the Z-score of each data point with respect to all *384* points in the same chamber. We used a robust Z-score that uses the median in place of the mean and the mean absolute deviation instead of the standard deviation. We chose the median as in some cases there were extreme outliers due to artifacts in the fluorescent staining or in the image acquisition. We therefore used the median in order to have a measure as insensitive to outliers as possible. Then, to identify immunofluorescence artifacts, images corresponding to the data points with a Z-score of >15 and with a cell count of >170 were manually analyzed and ∼30 images, showing clear artifacts were removed. Moreover, in order to minimize non-specific effects due to changes in cell growth/death, we removed the images containing a number of cells in the top and bottom 2.5 percentile of the distribution of each experiment. As final value for each data point, the median of the three biological replicates was used. In order to combine the data from the three oligos against each phosphatase, we performed a χ² test by summing the squares of the three Z-scores (one for each oligo). The null hypothesis is that the vector representing the effect of the three oligos has coordinates (0, 0, 0), that is, no-effect. The values for the controls were all summed together, since in this case all the oligos are identical. We selected as hits the phosphatases with a P-value of <0.04 after the χ² test. Subsequently, we removed from the list of hits all the genes for which the P-value of the Z-score on a standard normal distribution was >0.2. This was done in order to eliminate genes that have a significant effect on a phenotype (according to the χ² test) but for which the effect is small in absolute terms, that is, the Z-score is close to 0.

Training data set normalization

The biochemical measurement of the seven signaling proteins, whose activation was measured, was scaled to a value between 0 and 1, using a Hill function (Supplementary Figure S4). The midpoint of the function was chosen so as to have a normalized value of 0.5 for the measurements obtained in experimental conditions that we consider basal. More specifically, the growth medium was considered as basal condition for the ERK, rpS6, LC3, AKT and JNK measurements, whereas stimulation with TNFα constituted the basal condition for p38 and NFκB measurement. The steepness of the Hill function was chosen after visual inspection in order to have a good dynamic response across all the range of experimental values (Hill coefficient=2).

Network model optimization

After data normalization, the literature-derived network model was subjected to 1000 runs of optimization using CellNetOptimizer (CellNOpt; www.cellnopt.org). This software tries to determine which connections in the network are significant and in which way (i.e., AND/OR) multiple inputs acting on the same node should be combined. The aim of the optimization is to minimize the difference between the experimental data and the values that can be simulated from the network model.

We then calculated the activation state of all the proteins in the network after inhibiting or activating each node. This calculation was repeated 1000 times, that is, once for each optimized model. The final value for each protein is the proportion of the 1000 optimized models in which the protein was active. For instance if the inhibition of protein A led to the activation of protein B in 120 out of 1000 models, then we express as 0.12 the activation value of B when A is inhibited. This procedure enables a quantitative prediction even when using Boolean models, which are constrained to discrete values by nature. These averaged values were compared with the training data to evaluate the goodness of the fit.

Simulating upregulation and downregulation of each node

The family of 1000 network models was used to simulate the effect of upregulating and downregulating each node on the state of the five sentinel proteins. A Boolean logic can only simulate activation or inhibition but not upregulation. Therefore, we switched to a multilevel approach. We assigned a value of 0.5 to the presence of a stimulus (Serum or TNFα) in control conditions. Upregulated and downregulated nodes were assigned a value of 1 and 0, respectively. Beside this difference in the allowed states of each node, it is necessary to choose a transfer function that relates the state of each downstream node to the states of its upstream modulators. In analogy with the Boolean approach, we used a linear transfer function. This means that the value assigned to a node corresponds to the value of the upstream node, if the edge is activatory, or 1—the value of the upstream node otherwise. Similarly to Boolean models, AND gates are computed as the minimum of the values of the incoming edges, while OR gates as the maximum. The final value for each protein in a given condition is the average of the values in the 1000 models.

Matching simulated values with the results of the siRNA screening

The results of the siRNA screening were coded with a discrete variable with three possible values ‘downregulated’, ‘control’ and ‘upregulated’ according to the results of the primary and validation screenings. Therefore, each phosphatase hit has an associated cell state vector with coordinates corresponding to the values of the five sentinel proteins coded as described above. In order to code the results of the simulation with a discrete variable, we first normalized them using a Hill function. Particularly, for the ERK and rpS6 normalization the Hill coefficient was 1.5, while for NFκB and LC3 the coefficient was 5. The Hill coefficient for the p38 normalization was 20, because this measurement was less sensitive to simulation of model perturbation. Once again the midpoint of the function was chosen so as to have a normalized value of 0.5 for the measurements obtained in basal conditions (Serum for ERK, rpS6, LC3, Serum+TNFα for p38 and NFκB). Next, the normalized values were coded as ‘downregulated’, ‘control’ and ‘upregulated’ when the value fell in the 0–0.33, 0.33–0.66 and 0.6–1 ranges, respectively.

Following this step, both the siRNA screening and the results of all the simulations are coded as a vector of five discrete variables representing the states of the five sentinel proteins (cell-state vector). Our mapping strategy relies on the assumption that if a phosphatase acts on a given protein, then its perturbation in the primary siRNA screening should result in a cell state similar to the one obtained when the protein is downregulated, if the phosphatase has an activatory effect, or upregulated otherwise. The distance between two cell-state vectors is calculated as 1—the fraction of sentinel proteins with identical states. Each phosphatase is therefore matched with the simulation resulting in the cell-state vector of minimum distance. Since in each simulation a single node is perturbed this matching allows the assignment of the phosphatase to the activation or inhibition of a specific node.

Supplementary Material

Supplementary Information

Supplementary figures S1-6, Supplementary tables S1-5