Dynamic Modulation of Cerebellar Excitability for Abrupt, But Not Gradual, Visuomotor Adaptation

Abstract

The cerebellum is critically important for error-driven adaptive motor learning, as evidenced by the fact that cerebellar patients do not adapt well to sudden predictable perturbations. However, recent work has shown that cerebellar patients adapt much better if the perturbation is gradually introduced. Here we explore physiological mechanisms that underlie this distinction between abrupt and gradual motor adaptation in humans. We used transcranial magnetic stimulation to evaluate whether neural mechanisms within the cerebellum contribute to either process during a visuomotor reach adaptation. When a visuomotor rotation was introduced abruptly, cerebellar excitability changed early in learning and approached baseline levels near the end of the adaptation block. However, we observed no modulation of cerebellar excitability when we presented the visuomotor rotation gradually during learning. Similarly, we did not observe cerebellar modulation during trial-by-trial adaptation to random visuomotor displacements or during reaches without perturbations. This suggests that the cerebellum is most active during the early phases of adaptation when large perturbations are successfully compensated.

Introduction

Maintaining the accuracy of movements is fundamental to human behavior. As such, the nervous system is constantly adapting to changes in the body and environment. Adaptation is an error-driven learning process used to account for predictable new demands. This type of learning occurs on a timescale of minutes to hours and is driven by sensory prediction errors (i.e., the difference between where you moved and where you expected to move).

The cerebellum is considered to be critically involved in the adaptation processes. Individuals with cerebellar damage are impaired at adapting reaching, walking, and eye movements (Martin et al., 1996a; Smith and Shadmehr, 2005; Morton and Bastian, 2006; Tseng et al., 2007; Werner et al., 2009; Criscimagna-Hemminger et al., 2010). Specifically, they are less able to correct their movements from one trial to the next and do not store a new sensorimotor calibration. However, a recent study showed that cerebellar patients are able to adapt reaching more normally when a perturbation is gradually introduced over many movements rather than being introduced abruptly in one movement (Criscimagna-Hemminger et al., 2010). This suggests that learning from gradual perturbations, which introduce smaller errors, might be a different process than learning from abrupt perturbations that cause large errors.

It is also known that non-invasive cerebellar stimulation can change adaptation rates in predictable ways. Direct current stimulation with the anode over the cerebellum can enhance cerebellar excitability (Galea and Celnik, 2009) and increase the adaptation rate in a reaching task (Galea et al., 2011). In walking, we have shown recently that direct current stimulation can increase or decrease the adaptation rate (Jayaram et al., 2012). This effect depended on whether the anode or cathode was placed over the cerebellum, with the former increasing the adaptation rate. It is important to note that these studies have focused on adaptations to abrupt perturbations.

Here we were interested in understanding two issues. First, is there a difference in cerebellar involvement in adaptation to abrupt versus gradual perturbations? The results from cerebellar patients suggest that cerebellar function is less critical for dealing with gradual perturbations. Second, what is the time course of cerebellar involvement in adaptation? Although previous behavioral work has clearly demonstrated cerebellar involvement in adaptation, it does not provide information about when the cerebellum is most essential to the learning process.

We addressed these questions using transcranial magnetic stimulation (TMS) to probe the strength of the cerebellar connection to primary motor cortex (M1) before, during, and after adaptation. This was done using a paired-pulse technique, in which cerebellar stimulation results in subsequent inhibition of the contralateral M1 (Meyer et al., 1994; Ugawa et al., 1995; Pinto and Chen, 2001). We have shown previously that this technique is sensitive to learning in a locomotor adaptation task (Jayaram et al., 2011) and that changes in cerebellar–M1 connectivity are proportional to the adaptive change. Cerebellar–M1 connectivity has also been observed to change in response to observing or practicing a finger sequence task compared with control conditions (Torriero et al., 2011).

Materials and Methods

Participants.

We recruited 26 participants of either sex for these experiments. Fifteen subjects (mean ± SD age, 27 ± 9 years) performed in experiment 1 and 12 subjects (mean ± SD age, 25 ± 4 years) performed in experiment 2. One participant in experiment 1 was eliminated from analysis for technical reasons [the electromyography (EMG) gain was set too high for reliable motor-evoked potential (MEP)], and one participant completed both experiments. All individuals were right handed and were screened for contraindications against TMS. Participants were given a pretest (either in a separate session or during the premovement period) to ensure that M1 could be inhibited at rest by stimulation over the cerebellum and that they were comfortable with the brain stimulation techniques. All individuals provided informed consent before the pretest. This study was approved by the Johns Hopkins Institutional Review Board and was in accordance with the Declaration of Helsinki.

Behavioral task.

Participants in both experiments performed a center-out reaching task, moving a visually displayed cursor from a central starting location through one of eight radial targets in a slicing movement (Fig. 1A). The cursor was controlled by moving a stylus on a 13” × 19” digitizing tablet (Wacom Intuos 3). The monitor was vertical, and the tablet was laid horizontally such that moving the stylus forward moved the cursor upward. We secured the stylus to the right index finger of each participant and then asked them to use finger movements to control the cursor (Fig. 1B). For a subset of these participants, to ensure activation of the target muscle during the task, we recorded EMG during the movement. Participants wore goggles with an opaque shield attached to the underside to prevent them from looking directly at their hand while moving.

Figure 1.

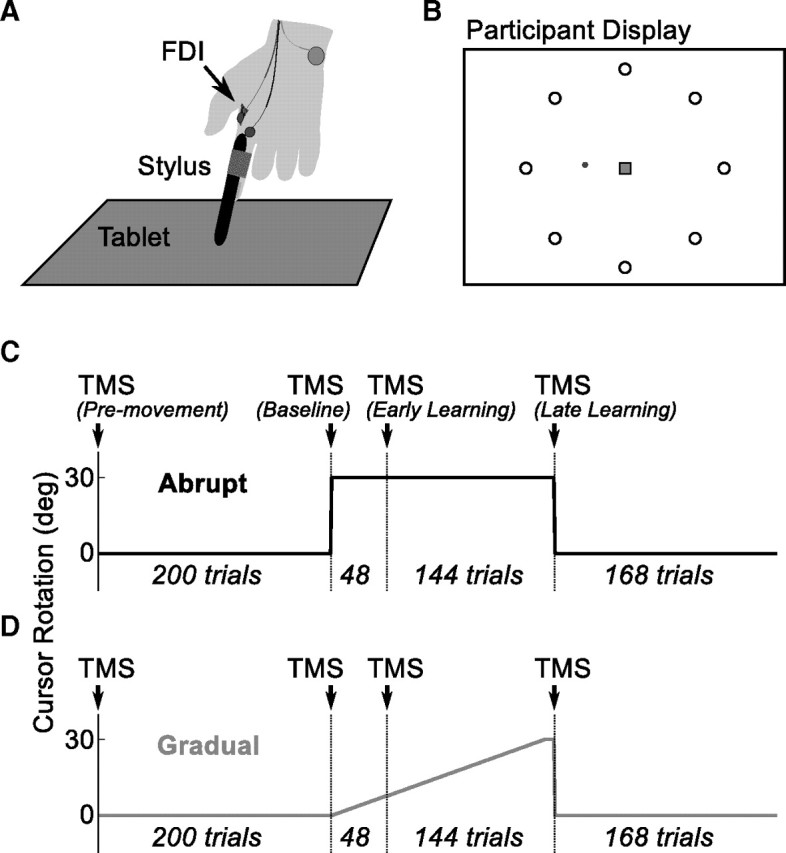
Design of behavioral task. A, Participants moved a stylus on a digitizing tablet. The stylus was secured to their index finger, and participants were asked to move their finger more than their arm. Surface EMG electrodes were placed over the FDI and used to verify activation during the behavioral task as well as measure MEPs. B, Participants performed a center-out task, moving a cursor from a central region (square) to one of eight targets (circle). C, D, Participants first received premovement TMS stimulation. Next they performed a 200 trial baseline block, followed by TMS. They then performed 192 trials with the perturbation on [shown are abrupt (C, black) and gradual (D, gray) perturbations], broken into an early and late learning blocks separated by TMS. Finally, they completed a washout block.

Data were recorded and stimuli displayed at 60 Hz by a desktop computer running MATLAB (MathWorks) with the Psychophysics Toolbox (http://www.psychtoolbox.org). Participants initiated each trial by moving the cursor to a 5 mm square in the center of the screen. One of eight radial targets was then presented, displayed as a white 3-mm-diameter circle 10 cm from the start region at an angle of 0°, 45°, 90°, 135°, 180°, 225°, 270°, or 305° from horizontal. The start of the movement was marked when the cursor left a 5 mm square region in the center of the screen. When the cursor passed the distance of the target (10 cm visually and on the tablet), online feedback of the cursor location was no longer provided. A blue 1-mm-diameter circle was presented at the 10 cm location of the cursor. The cursor remained invisible (with endpoint feedback visible) until the participant returned to within 2.5 cm of the start region (which took ∼500 ms on average) to prevent additional adaptation from occurring between trials. If participants took longer than 275 ms to complete the outward movement, a low-pitched auditory tone was delivered to indicate that the movement was too slow. If participants completed the outward movement in <175 ms, a high-pitched auditory tone was presented to indicate that the movement was too fast. Participants were instructed to try to hit the target and, as a secondary goal, try to complete the movement in the time allowed.

Target order was randomized such that every epoch of eight trials contained one presentation of each target. Epochs were grouped into blocks. Between blocks, a short rest period was provided in which we delivered TMS pulses to measure physiology (Fig. 1C, D). Participants first received a 200 trial baseline block to familiarize them with the task and movement demands. This allowed us to estimate their initial bias and error rate. After this block, participants completed two learning blocks, in which we presented a visuomotor perturbation: a rotation imposed between the movement of the stylus on the tablet and the movement of the onscreen cursor. The early learning block contained 48 trials (six epochs), and the late learning block contained 144 trials (18 epochs).

In experiment 1 (Fig. 1C), participants completed two sessions in a crossover design, with each session occurring at least 1 week apart. In the abrupt condition, we delivered a constant perturbation consisting of a 30° clockwise rotation. During the random condition, the perturbation consisted of a randomly selected visuomotor rotation of 60° clockwise, 60° counterclockwise, or 0° (veridical). The perturbation order was constrained to never be the same for more than two trials in a row. After learning, we removed the perturbation for a washout block of 168 trials (21 epochs). The random condition was a control condition, in which participants experienced large errors without learning a new stable representation.

In experiment 2 (Fig. 1D), participants again completed a two-session crossover design. During the gradual session, the perturbation was a clockwise visuomotor rotation, which initially started at 0° and increased at a rate of 0.25° on every trial, reaching a maximum of 30° clockwise just before the final epoch. As a control condition, we performed a veridical session, in which no perturbation was delivered (0° rotation). Block order was identical to experiment 1. After a baseline block (200 trials), participants completed an early learning block (48 trials) and a late learning block (144 trials), and then we removed the perturbation for a washout block of 168 trials.

EMG recording.

We used surface EMG to measure the response to TMS. Subjects sat comfortably in a chair with both arms resting on a pillow placed on their lap. The skin was treated with a mild abrasive gel and then cleaned with isopropyl alcohol to reduce impedance. EMG activity was captured through a pair of disposable surface electrodes. The active electrode was placed over the right first dorsal interosseous muscle (FDI), with the reference electrode placed on the knuckle. A ground electrode was placed over the head of the ulna. EMG signals were recorded, amplified, and filtered using a Viking IVP (Nicolet; bandwidth, 5 Hz to 1 kHz; Viasys Healthcare). Output from the Viking was sent to a CED 1401 (Cambridge Electronic Design), in which Signal software (version 4.06 or 4.08) was used to time lock the EMG response to TMS pulses and store the data for offline analysis using custom scripts in MATLAB.

TMS.

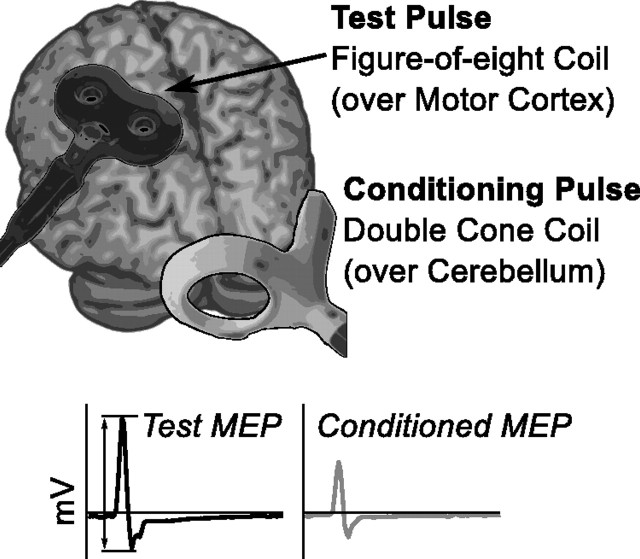
We stimulated left M1 using a 70-mm-diameter figure-of-eight coil (Bistim² stimulator; Magstim) to elicit an MEP of the right (dominant) FDI. We first located the optimal scalp location to activate this muscle and saved the position using a neuronavigation device (Brainsight; Rogue Research). The strength of the pulse was adjusted to elicit MEPs with average peak-to-peak amplitude of ∼1 mV. We assessed cerebellar excitability using a previously described protocol that measures cerebellar–M1 (brain) inhibition (CBI) (Ugawa et al., 1995; Pinto and Chen, 2001; Daskalakis et al., 2004; Galea et al., 2009). To avoid potential artifacts caused by antidromic stimulation of the pyramidal tract itself, we first assessed the brainstem threshold. We searched for MEPs by stimulating over the inion with a double-cone coil (110 mm mean diameter), with the stimulator current directed downward (Ugawa et al., 1995). We asked subjects to preactivate the FDI by lifting the index finger and searched for a stimulation intensity that evoked MEPs in 5 of 10 pulses, with an intensity cutoff of 80% of maximum stimulator output (MSO). Using this procedure, we were able to measure a threshold (<80% of MSO) in seven individuals. The intensity of cerebellar stimulation was then set at 5% less than brainstem threshold or 70% MSO. In a set of 20 TMS test stimuli (TS) over left M1, 10 (selected at random) occurred 5 ms after a TMS conditioning stimulus (CS) over the right cerebellum, centered ∼3 cm lateral to the inion (Fig. 2). For comparison, the remaining 10 TS were collected without a CS. CBI was computed as the ratio of the conditioned/unconditioned MEP. Pulses that did not result in an MEP were excluded from analysis. In a few subjects, MEPs were generated that exceeded our measurement threshold and were clipped by the EMG system. These pulses were also excluded from analysis. Because this phenomenon was biased (occurred only for large-amplitude MEPs), we minimized the effect that this would have on the computed CBI ratio by ensuring that an equal number of clipped pulses were excluded among both conditioned and unconditioned MEPs, excluding the largest unclipped MEPs when necessary to allow a balanced ratio. If >3 (of 10) pulses were clipped in any block, we excluded the subject entirely. Only one subject was removed using this criterion.

Figure 2.

Stimulating the cerebellum with TMS. We used two coils to measure CBI. A figure-of-eight coil was placed over the left M1 (to activate right FDI) and delivered stimuli to evoke a 1 mV MEP. A double-cone coil was placed over the right cerebellum, 3 cm inferior and lateral to the inion and used to deliver conditioning pulses. CBI is computed as the ratio between the peak-to-peak amplitude of the MEPs after the conditioned TS (bottom right) and the MEPs produced after the unconditioned TS (bottom left).

In a subset (6 of 14) of participants in experiment 1 and all participants in experiment 2, we performed additional measurements to explore whether changes could be detected within M1. The first measurement was MEP amplitudes with fixed stimulator output. We initially set the stimulator output at rest to generate an MEP of 1 mV and collected 10 potentials at that intensity before every CBI measurement. In this way, we can track whether excitability of M1 changes over adaptation. The next measurement was short-latency intracortical inhibition (SICI; Kujirai et al., 1993), which is a paired-pulse technique thought to reflect GABAergic inhibition (Florian et al., 2008). Here, using the same coil over M1, a subthreshold conditioning pulse was delivered 2 ms before the delivery of a suprathreshold test pulse, which was again adjusted to obtain an MEP of near 1 mV. We delivered 10 conditioned pulses and 10 test pulses and computed their ratio as the measure of inhibition. We performed this test before learning and after learning and again at the end of washout.

Data analyses.

During the behavioral task, we computed the endpoint error on every trial. This was defined as the difference between the angle between the target, the start location, and the cursor when it crossed the target distance. Trials in which the participant failed to move far enough on the first reach and then made a second, corrective reach were excluded from analysis. This occurred on ∼3% of trials, with 59% of those trials occurring during the initial baseline block when participants were unfamiliar with the task. We also measured movement time, which was the time the cursor spent traveling between the start region and the target distance. However, because we provided feedback about movement time to restrict it to a particular range, we did not analyze this data statistically.

TMS data was analyzed using repeated-measures ANOVA. Based on previous results using an adaptation task to modulate CBI (Jayaram et al., 2011), we predicted changes in the CBI ratio to occur in direct response to the presentation of the perturbation. We thus restricted our primary analysis of experiment 1 to three assessments of CBI: just before the learning period, immediately after the early learning block, and immediately after the late learning block. We thus performed a 3 × 2 repeated-measures ANOVA, with within-subject factors time and condition (abrupt or random). For experiment 2, we performed a similar ANOVA.

Results

Experiment 1

Behavior

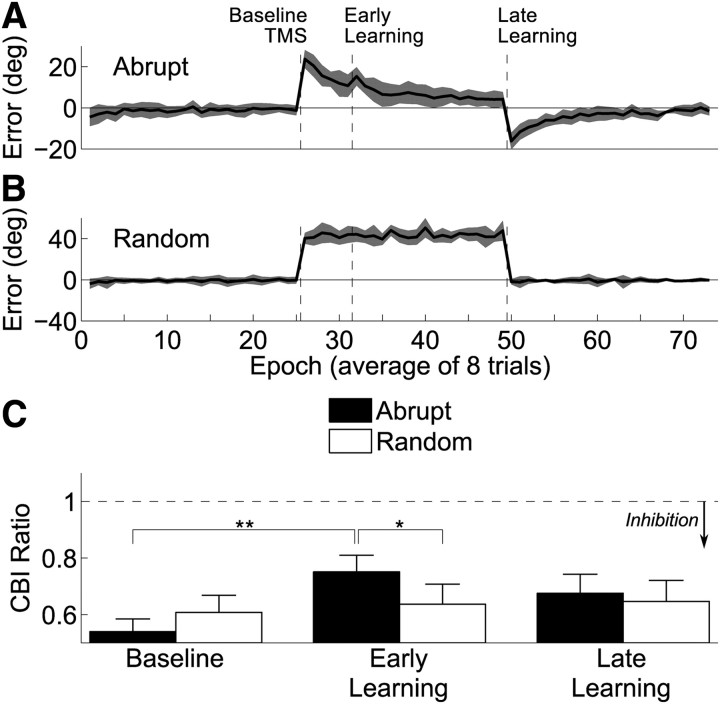
We evaluated the endpoint error as the perturbation was delivered to ensure that learning occurred. When the abrupt rotation was applied (Fig. 3A), the first epoch showed a mean ± SD error of 23.7 ± 4.4°. Across subsequent movements, the errors decayed. The first epoch in the second learning block had an average ± SD error of 15.3 ± 4.5°, and on the final learning epoch the error was 4.2 ± 3.6°. Thus, approximately half of the learning occurred during the first learning block. When the perturbation was removed, an aftereffect of −16.1 ± 4.1° (mean ± SD) was present.

Figure 3.

Results from experiment 1. A, In the abrupt condition, participants show initially a large error that decays over time and a significant aftereffect. B, During the random condition, participants experience large errors (shown here as absolute error rather than signed error) but no aftereffects. C, The CBI ratio (conditioned MEP/unconditioned MEP) is plotted before, during, and after learning. The ratio increases (representing less inhibition from the cerebellum over M1) early in learning for the abrupt condition but not in the random perturbation condition. Asterisks indicate significance of Bonferroni's-corrected post hoc t tests, with ** indicating a significant difference in a two-tailed test and * indicating a significant difference with a one-tailed test.

In the random condition (Fig. 3B), we observed no trend for the errors to decrease over time. The absolute error was initially 40.5 ± 5.4° (mean ± SD), and, by the end of the learning, blocks had actually increased slightly to 47.7 ± 9.7° (mean ± SD). There was likely some trial-to-trial learning that did not accumulate over time (Thoroughman and Shadmehr, 2000; Thoroughman et al., 2007), which may have contributed to the increase in error by the end of the block because the perturbation was changed on every trial. There was no aftereffect when the perturbation was removed (−1.85 ± 2.6°, mean ± SD).

Movement time was controlled by our task, with feedback provided (high- and low-pitched tones) for fast and slow movements. As such, we did not statistically evaluate any increases or decreases in movement time across blocks, although no changes were observed overall (Table 1).

Table 1.

Movement time across blocks

	Baseline	Early learning	Late learning	Washout
Experiment 1
Abrupt	250 ± 50	236 ± 46	235 ± 40	235 ± 41
Random	252 ± 51	251 ± 66	247 ± 56	244 ± 40
Experiment 2
Gradual	245 ± 53	228 ± 30	228 ± 29	228 ± 33
Veridical	253 ± 76	229 ± 34	233 ± 31	230 ± 26

We present mean ± SD movement time (ms), defined as the time participants left the target to the time they reached the target distance, was controlled during the task by the presentation of audible tones. Thus, we did not perform any statistical analysis. Notably, there was very little systematic change across blocks.

Cerebellar–M1 connectivity

We measured cerebellar–M1 connectivity using TMS between blocks of the behavioral conditions. We assessed CBI before initiating movement to ensure that we could measure CBI in these individuals and ensure that there were no systematic differences within individuals across conditions. We did not expect to observe any meaningful differences between premovement and baseline TMS measurements. Furthermore, this comparison would not be relevant to understand the effects of learning on cerebellar–M1 connectivity. Thus, we excluded the premovement measurement from analysis to improve the specificity of our statistical analysis. Before participants performed the abrupt condition, the average ± SD premovement CBI ratio was 0.65 ± 0.25. Before performing the random condition, the average ± SD premovement CBI ratio was 0.63 ± 0.22. These ratios were not statistically different from each other (paired t₍₁₃₎ = 0.25, p = 0.81), nor were they significantly different from the assessment of CBI after the baseline behavioral block (abrupt, t₍₁₃₎ = 1.66, p = 0.12; random, t₍₁₃₎ = 0.49, p = 0.63). The amplitude of the MEP generated by the unconditioned TS did not change meaningfully with time or condition (Table 2). This was not surprising, because the stimulator intensity was explicitly adjusted to prevent this. Nevertheless, we observed no interaction between task or block, which could contaminate our CBI results (F_(2,26) = 0.24, p = 0.78), or any significant main effects (all p > 0.1).

Table 2.

Measures of M1 excitability

	Premovement**	Baseline	Early learning	Late learning
Experiment 1
CBI (unconditioned TS)
Abrupt	1.11 ± 0.53	1.17 ± 0.42	1.19 ± 0.50	1.15 ± 0.42
Random	0.99 ± 0.23	1.08 ± 0.26	1.02 ± 0.25	1.04 ± 0.41
MEP (SI1mV)
Abrupt*	1.08 ± 0.26	0.73 ± 0.24	1.00 ± 0.37	0.84 ± 0.43
Random*	1.07 ± 0.31	0.64 ± 0.29	1.01 ± 0.53	0.70 ± 0.27
SICI ratio
Abrupt*	0.45 ± 0.44	0.35 ± 0.22		0.36 ± 0.22
Random*	0.30 ± 0.20	0.40 ± 0.28		0.42 ± 0.34
Experiment 2
CBI (unconditioned TS)
Gradual	1.05 ± 0.31	0.92 ± 0.22	1.18 ± 0.28	1.14 ± 0.32
Veridical	1.11 ± 0.22	1.02 ± 0.35	1.22 ± 0.39	0.99 ± 0.21
MEP (SI1mV)
Gradual	1.11 ± 0.32	0.99 ± 0.48	1.18 ± 0.39	0.96 ± 0.39
Veridical	1.11 ± 0.28	0.92 ± 0.52	1.17 ± 0.64	1.18 ± 0.64
SICI ratio
Gradual	0.49 ± 0.22	0.41 ± 0.24		0.43 ± 0.24
Veridical	0.43 ± 0.21	0.46 ± 0.34		0.53 ± 0.43

Shown are mean ± SD amplitudes of MEPs (in mV). First, we present the amplitude of the unconditioned MEP (in mV) during CBI measurement. We adjusted the intensity to attempt to keep this pulse consistent and close to 1 mV throughout the experiment. We did not observe strong systematic changes across blocks that we could attribute to learning. Next, we show amplitudes of MEPs (in mV) with the stimulator intensity fixed (SI1mV is stimulator intensity to elicit 1 mV MEP at pre-baseline).

*indicates that only a subset of participants (6 of 14) received these stimulation techniques.

**indicate that this column was excluded from statistical analysis to improve specificity of our learning analysis. We observed a slight trend of increased excitability over time on the veridical condition but no changes that were otherwise associated with learning. Finally, we assessed SICI (expressed as a unitless ratio) to explore intrinsic inhibition within M1. No meaningful variations were observed.

To assess the impact of visuomotor learning on CBI (Fig. 3C), we used a 3 × 2 repeated-measures ANOVA, with factors block (baseline, early learning, late learning) and condition (abrupt, random). We observed a significant interaction of these factors (F_(2,26) = 3.49, p < 0.05). Additionally, there was a significant main effect of block (F_(2,26) = 5.59, p < 0.01) but not of condition (F_(1,26) = 0.50, p = 0.49). CBI showed a selective increase (i.e., the cerebellum is less inhibitory) during the abrupt condition between the baseline and early learning measurements, changing from an average ± SD of 0.54 ± 0.17 after baseline to an average ± SD of 0.75 ± 0.22 after the early learning block. CBI then decreases to an average ± SD of 0.68 ± 0.25 after the late learning block. During random, no modulation is observed, with measured CBI values of 0.61 ± 0.23 (mean ± SD) after baseline, 0.64 ± 0.27 after early learning, and 0.65 ± 0.28 after late learning. We performed nine post hoc t tests to confirm this assessment statistically, using a Bonferroni's correction to determine significance, which required adjusting our α from 0.05 to 0.0056. Cerebellar inhibition after early learning in the abrupt condition is significantly decreased (ratio closer to 1) when compared with baseline (t₍₁₃₎ = 3.753, p = 0.002) and moreover is nearly significantly decreased compared with early learning in the random condition (t₍₁₃₎ = 3.216, p = 0.007; note that this passes our adjusted α in a one-tailed test). No other comparisons revealed significant differences in this analysis. Of note, the comparison between baseline and late learning was not significant when we corrected for multiple comparisons (t₍₁₃₎ = 2.13, p = 0.049; note that this does not pass our adjusted α).

Relationship between cerebellar–M1 connectivity and adaptation

Previous investigation showed that the change in CBI was correlated with the amount of locomotor adaptation that occurred (Jayaram et al., 2011). We tested whether a similar effect held for visuomotor reach adaptation during the abrupt condition. However, no significant correlations were observed. We found no correlation between the change in CBI after the early learning block and the amount learned during the previous block (r = −0.03, p = 0.93), the total amount learned (r = 0.06, p = 0.84), or the size of the aftereffect (r = −0.13, p = 0.66). The change in CBI between the baseline and late learning blocks was similarly uncorrelated with the total amount learned (r = 0.05, p = 0.86) and the aftereffect (r = 0.22, p = 0.45), and the amount of CBI assessed at baseline was not predictive of the total amount learned (r = 0.26, p = 0.37) or the aftereffect (r = 0.24, p = 0.42).

M1 excitability

In a subset of participants (6 of 14), we also conducted more explicit tests for M1 excitability (Table 2). We tested MEP amplitude at fixed stimulator output, at an intensity previously set to achieve an MEP near 1 mV during the premovement test. We detected lower M1 excitability after the baseline and late learning blocks, which involved many reaching trials. After the early learning block (which was short), M1 excitability was higher. In an ANOVA, this resulted in a significant main effect of block (F_(2,10) = 6.4, p < 0.025). Importantly, we observed no meaningful interaction between condition and time (F_(2,10) = 0.22, p = 0.8), suggesting that any modulation of cortical excitability was independent of learning. SICI (tested at 2 ms) did not appear to be affected by our task (all p > 0.4). Furthermore, these measurements did not correlate with behavioral performance.

Experiment 2

Behavior

When the gradual rotation was applied (Fig. 4A), as expected by the nature of the perturbation, errors took much longer to build up. By the final epoch of the late learning block, the average error was 3.75 ± 3.35° (mean ± SD), slightly less than that observed at the same time point in the abrupt perturbation condition in experiment 1 (although not significantly so: t₍₂₄₎ = 0.32, p = 0.75). After removal of the perturbation, there was an aftereffect of −12.0 ± 2.8° (mean ± SD). This was significantly smaller than the aftereffect observed after the abrupt perturbation (t₍₂₂₎ = −2.9, p < 0.01). During the no rotation condition (Fig. 4B), errors remained constant and nearly zero. This suggests that assessing brain physiology using TMS between blocks did not cause a substantial drift in performance. We explored the trial-by-trial variance in errors during the learning phase and observed very little difference between the two sessions. After removing any linear trends, the variance during the gradual condition was 16.4 ± 8.5° (mean ± SD), and the variance during the veridical condition was 16.6 ± 9.3° (mean ± SD). These were not statistically distinguishable (paired t₍₁₁₎ = −0.13, p = 0.9) and were in fact highly correlated (r = 0.87, p < 0.001). This suggests that the errors available to the motor system were indistinguishable for these two tasks.

Figure 4.

Results from experiment 2. A, Participants in the gradual condition do not experience large errors during learning but show an aftereffect. B, During the veridical condition, participants maintain their performance across the entire experiment. C, The CBI ratio (conditioned MEP/unconditioned MEP) is plotted before, during, and after learning. The ratio remains unchanged in the gradual as well as the veridical conditions.

Cerebellar–M1 connectivity

Before participating in the gradual condition, the average ± SD premovement CBI ratio was 0.62 ± 0.23, and before the no rotation condition the average ± SD premovement CBI ratio was 0.59 ± 0.30. These premovement values did not differ (paired t₍₁₁₎ = 0.58, p = 0.57). Furthermore, the average premovement CBI did not differ between the abrupt group in experiment 1 and the gradual group (independent t₍₂₄₎ = 0.25, p = 0.81). As in experiment 1, movements during baseline reaches did not affect the CBI ratio (paired t₍₁₁₎ = 0.24, p = 0.82). The average ± SD CBI ratio after the baseline block was 0.65 ± 0.25.

We analyzed CBI data from the gradual and veridical blocks using a 3 × 2 repeated-measures ANOVA, exploring the effects of block and condition (Fig. 4C). We observed no significant main effects (block, F_(2,22) = 0.07, p = 0.93; condition, F_(1,11) = 0.01, p = 0.91) or interaction (F_(2,22) = 0.26, p = 0.77). Examining the amplitude of MEPs generated by the unconditioned TS during CBI measurements (Table 2) with the same 3 × 2 repeated-measures ANOVA, we observed a weak but significant effect of block (F_(2,22) = 4.788, p < 0.025) but no effect of learning condition (F_(1,11) < 0.01, p = 0.98) or interaction (F_(2,22) = 1.86, p = 0.18). The block effect was similar to the change in M1 excitability that we observed (see below), with slightly larger MEPs found after short blocks. This change was consistent despite adjustments to maintain unconditioned MEPs near 1 mV.

Relationship between cerebellar–M1 connectivity and adaptation

To assess any relationships between CBI and the amount of learning observed during the gradual condition, we explored correlations between the aftereffect and CBI changes. No significant correlations were observed between the aftereffect and CBI changes after the early learning block (r = 0.44, p = 0.15) or after the late learning block (r = 0.48, p = 0.11). Furthermore, baseline CBI was not predictive of the aftereffect (r = −0.39, p = 0.21).

M1 excitability

We performed tests of motor cortical excitability in all 12 subjects in the gradual and veridical conditions (Table 2). Exploring the amplitude of MEPs to pulses of fixed stimulator intensity, we observed a slight effect of block (F_(2,22) = 3.5, p < 0.05) but no effect of condition (F_(1,11) = 0.16, p = 0.69) or interaction (F_(2,22) = 1.4, p = 0.26). This suggests that our task may have changed M1 excitability in a nonspecific manner but learning per se did not. Furthermore, during washout of the gradual condition, there was a slight increase in MEP amplitude (1.19 mV from 0.99 mV at the end of learning). SICI was not affected by our task in any meaningful way (all p > 0.1).

Discussion

The main finding of this study is that cerebellar–M1 connectivity changes early in the process of adapting to a visuomotor rotation. This change occurs early when adapting to an abrupt perturbation, when errors are large. Importantly, this change is an overall decrease in the level of cerebellar inhibition. Later in adaptation, when errors are small and performance has reached a plateau, cerebellar inhibition increases toward baseline levels. No modulation of the level of cerebellar inhibition was observed when participants were provided with a random or gradual perturbation, nor was there a change during unperturbed reaching movements.

Previous work has shown that cerebellar excitability changes during locomotor adaptation on the split-belt treadmill (Jayaram et al., 2011), testing CBI at two time points (before and after learning). The visuomotor adaptation studied here is a faster process than locomotor adaptation; therefore, we also evaluated CBI during learning. Interestingly, we only observed a measurable change in CBI at the early stages of adaptation to an abrupt perturbation. This suggests that a sufficiently large and consistent perturbation is required to observe the effects of reach adaptation on CBI and that CBI returns to equilibrium values when errors are less prevalent. However, a large error alone is not sufficient to drive cerebellar–M1 connectivity to a new level, because we did not see similar neurophysiological changes in the random condition. Although here people are likely to learn something from one trial to the next (Thoroughman and Shadmehr, 2000; Donchin et al., 2003; Thoroughman et al., 2007), performance changes do not accumulate during this task. This may mean that there is also no accumulation of neurophysiological changes during the random task. In line with this prediction, we observed no modulation of cerebellar inhibition during the random condition, suggesting that the increased error magnitude was not by itself sufficient to produce measurable changes in cerebellar neurophysiology. This is not to say that the cerebellum is uninvolved in this task, however. We believe that failure to detect changes in the random condition may reflect a sensitivity limit of TMS, namely that cerebellar stimulation might be insensitive to small, transient changes that occur with trial-by-trial adaptation.

Why did we see a decrease in CBI in early adaptation? Within the cerebellar cortex, there are several forms of plasticity, with at least two that could be important here. The first, predicted by early models of cerebellar function, such as those promoted by Marr and Albus (Marr, 1969; Albus, 1971), is a decrease in efficiency at the parallel fiber/Purkinje cell synapses triggered by simultaneous activation of climbing fibers, a process called long-term depression (LTD; Ito, 1972, 2002). The second is long-term potentiation (LTP) at the mossy fiber–granule cell synapse, in which mossy fibers that are activated repeatedly begin to more strongly activate parallel fibers, potentially affecting a larger portion of the cerebellar cortex (D'Angelo et al., 2005). LTP has also been observed between parallel fibers and inhibitory interneurons in the cerebellar cortex, which has the same net effect as LTD at the parallel fiber/Purkinje cell synapse (Jörntell et al., 2010). Thus, the observed changes in cerebellar–M1 inhibition observed in the current study make some predictions about the type of plasticity that may underlie the cerebellar contribution to reach adaptation. Because errors are much more prevalent early in learning and errors are believed to be conveyed by climbing fibers (Marr, 1969; Albus, 1971; Ito, 1972, 2002), one would expect that adaptation results in decreased efficacy of parallel fiber/Purkinje cell synapses. This in turn should result in these neurons firing less robustly after TMS, which will reduce the amount of CBI elicited. A decrease in CBI is exactly what we observe. Importantly, a similar decrease in CBI is also observed in locomotor adaptation (Jayaram et al., 2011). Thus, although we did not directly induce plasticity in the cerebellum through techniques such as theta burst stimulation (Koch et al., 2008), we think the current results suggest that a mechanism similar to LTD underlies the cerebellar contribution to reach adaptation. Later in learning, CBI increases again, which could result from LTP-like mechanisms working to restore an equilibrium level of efficacy of Purkinje cell synapses (at least at a broad scale) once the error signals are reduced.

Motor adaptation has been classically defined as a cumulative process of recalibrating an action using error feedback (Martin et al., 1996b). The cerebellum has long been considered to be an error-based learning machine (Marr, 1969; Albus, 1971; Ito, 1972, 2001), with experimental evidence suggesting that it contributes strongly to adaptation tasks (Martin et al., 1996a; Smith and Shadmehr, 2005; Morton and Bastian, 2006; Tseng et al., 2007; Xu-Wilson et al., 2009). However, more recent work suggests that, in traditional adaptation paradigms, there is a balance between error-based learning and other forms of learning, such as use-dependent plasticity or reinforcement learning (Diedrichsen et al., 2010; Huang et al., 2011). This balance is likely to be sensitive to the type and/or magnitude of the perturbation delivered, with abrupt perturbations requiring more error-based learning and gradual rotations requiring less, with behaviorally and neurologically dissociable consequences (Kagerer et al., 1997; Criscimagna-Hemminger et al., 2010; Orban de Xivry et al., 2011).

However, the balance of learning processes should be sensitive to more than simply the external perturbation and may change over time as performance itself changes. When considering the abrupt perturbation, for example, we would propose that cerebellar-dependent error-based learning is likely to be active when the perturbation has been introduced recently and errors are still large. Once performance has improved, sensory prediction errors become less prevalent, and different mechanisms (for example, reinforcement learning and/or use-dependent plasticity) likely play a larger role in stabilizing performance. These refinement and storage stages of learning probably occur in extracerebellar regions, possibly M1 (Hadipour-Niktarash et al., 2007). The current TMS results are consistent with this framework, because they suggest that the cerebellum is most involved early in adaptation, when errors are prevalent and decreasing. This framework is consistent with recent work with transcranial direct current stimulation, which suggests that cerebellar excitation increases the rate of adaptation measured early in learning but does not affect the total amount learned (Galea et al., 2011; Jayaram et al., 2012). This also agrees with results suggesting that the cerebellum rapidly learns to compensate for oculomotor perturbations (Xu-Wilson et al., 2009), acting as the fast learning mechanism in multi-rate learning models (Smith et al., 2006; Kording et al., 2007).

We observed no relationship between the observed change in cerebellar excitability and the amount of learning that occurred. Previous work did observe a relationship between the change in cerebellar excitability and final performance in locomotor adaptation (Jayaram et al., 2011). Importantly, the time course of locomotor adaptation is long compared with visuomotor reach adaptation. This leaves open alternative interpretations. First, it may be that the visuomotor rotation used in the present study is not a strong enough perturbation to overcome variability between subjects. Similarly, it may be the case that, because errors experienced while walking (i.e., falls) are very costly, the gain on error-based learning mechanisms is much higher for locomotor adaptation and is therefore reflected in a correlation between cerebellar inhibition and behavior.

We observed no CBI modulation during adaptation in the gradual condition. Why was this the case? First, adapting to a gradual perturbation occurs in the absence of large errors (Kagerer et al., 1997) and can take place in response to a binary reward signal (Izawa and Shadmehr, 2011). This suggests that error-based learning mechanisms play a reduced role in this type of adaptation. Second, previous evidence suggests that individuals with cerebellar disease adapt to gradually introduced perturbations (Criscimagna-Hemminger et al., 2010). Perhaps these patients are able to use a different learning mechanism (e.g., reinforcement learning) in place of cerebellar mechanisms. Collectively, these observations together with our results suggest that gradual adaptation does not require substantial cerebellar input.

We expected that M1 would exhibit a change to store the new motor pattern. We conducted probes of M1 excitability and observed no changes with learning. The lack of effect within M1 was unexpected, because interference with M1 has been observed to change the aftereffect after motor adaptation (Hadipour-Niktarash et al., 2007). However, that work only looked at TMS-mediated interference and not M1 excitability. Our findings are consistent with a previous study in which M1 excitability did not change in association with learning (Jayaram et al., 2011). It may be that these tests are not sensitive enough or that changes within M1 during adaptation result in no net change in excitability. However, it should be emphasized that we conducted only a small subset of tests to assess M1 function, because this was of secondary interest in this study.

In conclusion, TMS can demonstrate changes in cerebellar neurophysiology during visuomotor adaptation of arm movements. These changes occur early in learning, when error-based learning is most active. These changes are not simply attributable to error processing but likely reflect the accumulation of new neural and behavioral patterns.