Multispecies model of cell lineages and feedback control in solid tumors

Abstract

We develop a multispecies continuum model to simulate the spatiotemporal dynamics of cell lineages in solid tumors. The model accounts for protein signaling factors produced by cells in lineages, and nutrients supplied by the microenvironment. Together, these regulate the rates of proliferation, self-renewal and differentiation of cells within the lineages, and control cell population sizes and distributions. Terminally differentiated cells release proteins (e.g., from the TGFβ superfamily) that feedback upon less differentiated cells in the lineage both to promote differentiation and decrease rates of proliferation (and self-renewal). Stem cells release a short-range factor that promotes self-renewal (e.g., representative of Wnt signaling factors), as well as a long-range inhibitor of this factor (e.g., representative of Wnt inhibitors such as Dkk and SFRPs). We find that the progression of the tumors and their response to treatment is controlled by the spatiotemporal dynamics of the signaling processes. The model predicts the development of spatiotemporal heterogeneous distributions of the feedback factors (Wnt, Dkk and TGFβ) and tumor cell populations with clusters of stem cells appearing at the tumor boundary, consistent with recent experiments. The nonlinear coupling between the heterogeneous expressions of growth factors and the heterogeneous distributions of cell populations at different lineage stages tends to create asymmetry in tumor shape that may sufficiently alter otherwise homeostatic feedback so as to favor escape from growth control. This occurs in a setting of invasive fingering, and enhanced aggressiveness after standard therapeutic interventions. We find, however, that combination therapy involving differentiation promoters and radiotherapy is very effective in eradicating such a tumor.

1. Introduction

Tumors arise when the carefully regulated balance of cell proliferation and programmed cell death (apoptosis) that ordinarily exists in normal homeostatic tissues breaks down. In the traditional view, cancer cells are assumed to acquire, through genetic or epigenetic changes, a common set of traits (Hanahan and Weinberg 2000): (i) self-sufficiency in growth signals, (ii) insensitivity to growth inhibitory signals, (iii) ability to evade apoptosis, (iv) limitless replicative potential, (v) ability to sustain angiogenesis, (vi) invasiveness and metastatic capability. There is an increasing body of evidence, however, that not all proliferating cells in a tumor matter equally (e.g., Visvader and Lindeman 2008, Charafe-Jauffret et al. 2009; Alison et al. 2011).

As with cells in normal tissues, tumor cells appear to progress through lineage stages, in which the capacity for unlimited self-renewal is, at some point, lost. The existence of a small population of cells capable of initiating cancer, known as cancer initiating cells or cancer stem cells (CSCs), was first demonstrated in leukemia (Furth and Kahn, 1937; Lapidot et al., 1994; Bonnet and Dick, 1997) by showing that the transplantation of only certain types of leukemic cells consistently result in leukemia in the animal. Implantation of even one of these cancer stem cells into a mouse can cause leukemia. Later, studies have identified such cancer stem cells in solid tumors including breast (Al-Hajj et al. 2003), brain (Hemmati et al. 2003; Singh et al. 2004), prostate (Collins et al. 2005), melanoma (Fang et al 2005; Monzani et al. 2007), ovarian (Bapat et al., 2005), colon (O’Brien et al. 2007; Ricci-Vitiani et al. 2007), liver (Ma et al., 2007; Yin et al. 2007), lung (Ho et al., 2007), pancreas (Hermann et al. 2007; Li et al. 2007; Olempska et al. 2007), and gastric cancer (Fukuda et al. 2009; Takaishi et al. 2009). These studies have given further credence to the cancer stem cell hypothesis, which states that cancer diagnostic, prognostic and therapeutic efforts need to be focused on that population of cells—often a small minority—that undergoes long-term self-renewal. While this hypothesis acknowledges the existence of lineage progression in cancers, it does not address the role that lineages normally play in cancer biology.

A lineage is a set of progenitor-progeny relationships within which progressive changes in cell character occur. Typically, lineages are traced back to a self-perpetuating stem cell, and end with a terminally differentiated cell that is either postmitotic or divides slowly compared with its normal lifespan. In between stem and terminal cells are a number of “committed” progenitor cell stages. There is increasing evidence, however, that stem and committed progenitor cells are not necessarily cell types per se, but rather patterns of cell behavior that emerge when cells at different lineage stages find themselves in specific environments (e.g., Loeffler and Roeder 2002; Zipori 2004; Jones et al. 2007; Clayton et al. 2007; Chang et al. 2008; Lander et al. 2009). Thus, within a lineage, which cell stages behave as stem cells and which as committed progenitor cells may be more a matter of context than pre-determination, may change over time, and may vary with spatial location.

Every population of dividing cells at a given lineage stage can be characterized by a parameter P, that is the fraction of daughter cells resulting from cell division that remains at the same lineage stage (i.e., 1−P is the fraction of the daughter cells that progress to the next stage). When P=0.5, we are usually inclined to call this population stem cells, because they maintain constant numbers while producing differentiated progeny. When P<0.5, we tend to call this population committed progenitor cells, or transit amplifying cells, because their lineages self-extinguish after several rounds of division (the lower the P, the sooner the extinction). Note that this characterization makes no reference to cell division symmetry. From the population standpoint it does not matter whether a value of P=0.5 is achieved by having all cells divide asymmetrically or having some divide symmetrically to generate two of themselves and an equal number divide symmetrically to generate two cells of the next stage.

It has long been argued that tissue growth must be controlled by feedback (e.g., Bullough 1965). Tissue-specific signals affect the behaviors of stem, committed progenitor and also possibly terminally differentiated cells. For instance, McPherron et al. (1997) showed that when growth and differentiation factor 8 (GDF-8)/myostatin, a protein belonging to the transforming growth factor-beta (TGFβ) superfamily, is genetically eliminated in mice, this results in the production of an excessive number of terminally differentiated cells (myocytes) and increase in muscle mass. Wu et al. (2003) and Gokoffski et al. (2011) showed that other closely related members of the TGFβ superfamily, activin B and GDF11, control the number of stem and committed progenitor cells in the mouse olfactory epithelium. Control of cell numbers through the regulation of self-renewal also occurs during hematopoiesis (e.g., Kirouac et al. 2009; Marciniak-Czochra et al. 2009). In all cases, control of cell populations involves negative feedback loops that reduce not only mitosis rates, but also the self-renewal fractions, i.e. P.

Other TGFβ superfamily members have been found to decrease self-renewal and differentiation rates of stem cells both in normal tissues and in cancer (e.g., Watabe 2009; Anido et al. 2010; Meulmeester and ten Dijke 2011). Some members of the TGFβ family may also increase tumor invasiveness in the later stages of tumor progression. Many other factors, such as Wnts, Notch, Sonic Hedgehog (Shh), and Fibroblast Growth Factor (FGF) have been found to upregulate stem and committed progenitor cell renewal and proliferation rates in normal tissues and cancer (e.g., Dontu et al. 2004; Lie et al. 2005; Katoh and Katoh 2007; Bailey et al. 2007; Klaus and Birchmeier 2008; Kalani et al. 2008; Bisson and Prowse 2009; Pannuti et al. 2010; Turner and Grose 2010). A number of these signaling factors, together with their inhibitors such as Dickkopf (Dkk) and secreted frizzled proteins (SFRPs) which inhibit Wnt singaling, are also found to promote the development of invasive cancer (e.g., González-Sancho 2005; Guo et al. 2007; Klaus et al. 2008; Bovolenta et al. 2008; Takahashi et al. 2010; Li et al. 2011; Meulmeester and ten Dijke 2011). Further, experiments reveal considerable spatial heterogeneity in signaling factors and in the distributions of stem and non-stem cells; see for example Figs. 3 and 4 and the accompanying description in Sec. 4.1 below.

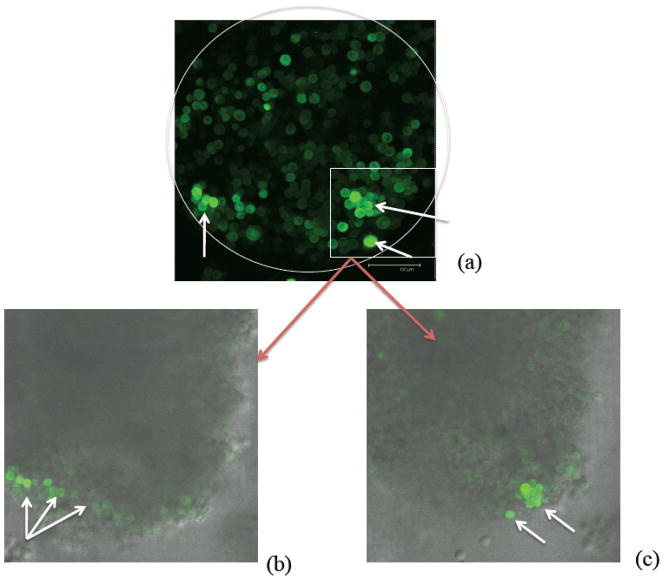
Figure 3.

Visualization of U87MG-derived in vitro tumor spheroids showing cancer stem cells at the spheroid boundary. The green color (online) denotes the accumulation of ZsGreen-ODC and marks the location of what are believed to be cancer stem cells (Vlashi et al. 2009) highlighted by the arrows (white). (a) shows an image from three dimensional confocal microscopy (projected into the plane). The white circle provides a rough outline of the boundary of the tumor spheroid. The scale bar corresponds to 100μm. In Figs. (b) and (c), an overlay of fluorescence and phase contrast images is shown at different vertical slices of the tumor spheroid. The figures are courtesy of C. Lagadec and F. Pajonk.

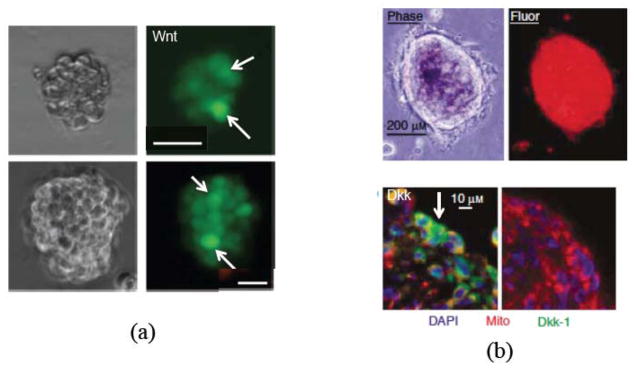
Figure 4.

Heterogeneous spatial patterning of Wnt signaling activity (a) and the Wnt-inhibitor Dkk (b) in in vitro tumor spheroids. In (a), two single-cell-cloned colon cancer spheroids (scale bars are 20 μm) are shown using phase contrast (left), fluorescence microscopy (right). The green color (online; TOP-GFP) denotes Wnt signaling activity highlighted by white arrows. (a) is adapted from Fig. 1b in Vermeulen et al. (2010), with kind permission. In (b), tumor spheroids of MG63 osteosarcoma cells are shown using phase contrast (upper left), fluorescence (mitochondrially localized red fluorescent protein, upper right), a section of the spheroid (red; color online) immunostained for Dkk1 (green; color online), highlighted by a white arrow, and nuclei (blue; color online; DAPI), with scale bars 200μm (top) and 10μm (bottom). (b) is adapted from Figs. 3(c) and 3(d) in Lee et al. (2007), with kind permission.

Using a mathematical model, Lander et al. (2009) and Lo et al. (2009) demonstrated that feedback regulation of the P-values of the cell stages by more differentiated cells in the lineage forms the basis of a powerful integral control strategy that can explain many features of homeostasis, such as insensitivity of tissue size to stochastic fluctuations (e.g., in proliferation, renewal and differentiation rates) and the rapid regeneration of tissues in response to injury. Such feedback can also drive the spatial stratification of epithelia (Chou et al. 2010). Moreover, such studies show that in multistage lineages, the relative strengths of the different feedback loops determine which cell stage adopts stem or committed progenitor cell behaviors and suggest that feedback is the reason why stem and committed progenitor cell behaviors emerge in tissues.

The fact that lineages are also apparently present in cancer, suggests therefore that feedback regulation is operating in tumors although not necessarily normally. As evidence for this hypothesis we note that recent research shows that there may be several types of stem and committed progenitor cell subpopulations in solid breast tumors (e.g., Hwang-Verslues et al. 2009). Further, by implanting BRCA1/p53 breast tumor cells in mice, Shafee et al. (2008) demonstrated that the fraction of cells displaying normal mammary stem cell markers in the fully developed tumors varies little from tumor to tumor (roughly 3%–8% of all cells) regardless of the stem cell fraction initially implanted. Yet perturbations of the tumor and its microenvironment can dramatically change the stem cell fractions. For example, repeated treatment by cisplatin can cause the stem cell fraction in the BRCA1/p53 breast tumors to dramatically increase, which can lead to chemoresistance and enhanced invasiveness (Shafee et al. 2008). Analogously, stem cell fractions may increase during fractionated radiotherapy, which can result in an accelerated repopulation of the tumor and increased invasiveness (e.g., Kim and Tannock 2005; Pajonk et al. 2010). Hypoxia in the microenvironment, however, can act as a radiosensitizer and protects cells from radiation damage (e.g., Pajonk et al. 2010). In addition, hypoxia may also increase stem cell fractions and invasiveness by promoting reprogramming cells to a cancer stem cell phenotype (e.g., Heddleston et al. 2009). In general, feedback processes in tumors may create new ways for tumor progression and invasion to occur.

There have been many mathematical models of tumor growth developed in recent years. See, for example, the recent reviews by Roose et al. (2007), Harpold et al (2007), Anderson and Quaranta (2008), Tracqui (2009), Attolini and Michor (2009), Preziosi and Tosin (2009), Lowengrub et al. (2010), Byrne et al (2010), Edelman et al. (2010), Rejniak and Anderson (2011), and Frieboes et al. (2011). Increasingly, mathematical models incorporating stem cell dynamics have been developed. Much of this work has dealt with hematopoietic cancers such as leukemia and their treatment. See, for example, the review by Michor (2008) and the references therein. In solid tumors, much work has focused on studies of colorectal cancer including stochastic and deterministic models of intestinal crypts that incorporated limited feedback loops among the cell types as well as extracellular sources of signaling factors such as Wnt (e.g., D’Onofrio and Tomlinson 2007; Johnston et al. 2007a, 2007b and 2010; van Leeuwen et al. 2006, and 2009). General stochastic spatiotemporal discrete models have been recently developed to simulate the dynamics of stem and differentiated cells in tumor clusters that were not specific to a particular type of cancer (e.g., Galle et al. 2009; Enderling et al. 2009a, 2009b, 2009c, 2010; Sottoriva et al. 2010a, 2010b). A general ODE-based cell compartment model was developed earlier (Ganguly and Puri 2006). None of these models, however, explicitly accounted for spatiotemporally varying cell signaling and feedback among tumor cells at the different lineage stages.

In this paper, we present a general model that accounts for spatiotemporally heterogeneous signaling factors produced by cells in the lineages and nutrients supplied by the microenvironment. Together, these regulate the rates of proliferation, self-renewal and differentiation of the cells within the lineages and control the cell population sizes and distributions. In particular, terminally differentiated cells release proteins (e.g., from the TGFβ superfamily) that feedback upon less differentiated cells in the lineage and promote differentiation and decrease rates of proliferation (and self-renewal). Stem cells release a short-range feedback factor that promotes self-renewal (e.g., representative of Wnt signaling factors), as well as a long-range inhibitor of this factor (e.g., representative of Wnt inhibitors such as Dickkopf (Dkk) and secreted frizzled proteins (SFRPs)). Generally speaking, the results of modeling such feedback are generic—i.e. they do not depend on the type of molecule that implements feedback—and therefore should also be relevant to processes such as Notch, BMP, Shh, FGF mediated signaling, “contact inhibition”, mechanical forces, or even indirect feedback through depletion of nutrients, growth factors or spatial limitations.

The outline of the paper is as follows. In Sec. 2, we present the mathematical model. In Sec. 3, we nondimensionalize and simplify the equations. In Sec. 4, results are presented where we investigate tumor progression and the response to treatment under various feedback and treatment scenarios. In Sec. 5, we present conclusions, comparisons with previous work and discussions of future work. In the Appendix, we present a nondimensionalization of the model. Additional details are provided in the Supplementary Material.

2. Mathematical model

2.1 Multispecies tumor model

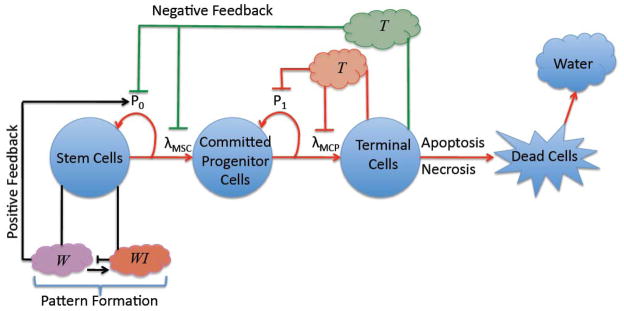
We develop a spatial model for lineage dynamics by adapting the multispecies tumor mixture model from Wise et al. (2008) and Frieboes et al. (2010) to account for cell lineages. In Fig. 1, a schematic is shown of a cell lineage, which is composed of cancer stem cells (CSC), committed progenitor cells (CP), terminal cells (TC) and dead cells (DC). Differentiation and feedback processes, described below, link the cells in the lineage through the self-renewal fractions and mitosis rates of the CSC and CP populations (Lander et al., 2009). The dependent variables in the model are the local volume fractions of the cell species, host (H) and water (W): φ_CSC, φ_CP,φ_TC, φ_DC, φ_H, φ_W. Assuming that there are no voids, the sum of the volume fractions equals 1. Following Wise et al. (2008), we further assume that the total solid volume fraction (tumor and host cells) and the water volume fraction are constant. This enables the water to be determined solely by the dynamics of the solid components (Wise et al. 2008). For more general multispecies tumor models, see the review by Lowengrub et al. (2010), the book by Cristini and Lowengrub (2010) and the references therein.

Figure 1.

A schematic of a cell lineage with positive and negative feedback factors affecting the self-renewal and mitosis rates of cancer stem cells and committed progenitor cells. Terminally differentiated cells produce soluble factors T that reduce the self-renewal fraction and mitosis rates of less differentiated cells (e.g. members of TGFβ family). Note that the T factors that act on the committed progenitor and stem cells may be different (e.g., Wu et al. 2003; Gokoffski et al. (2011)). Additional feedback factors W produced by cancer stem cells (e.g. Wnt) promote self-renewal and increase mitosis rates of cancer stem cells. The self-renewing promoters may also be inhibited by other factors WI (e.g. Dkk, SFRPs), which can lead to pattern formation and spatiotemporally heterogeneous cell distributions.

For each cell type, a conservation equation of the form

$$\frac{\partial \phi }{\partial t}=\stackrel{\text{Generalized}\text{Diffusion}}{\overbrace{-\nabla ·\mathbf{J}}}+\stackrel{\text{source}/\text{mass}-\text{exchange}}{\overbrace{\mathit{Src}}}-\stackrel{\text{convection}}{\overbrace{\nabla ·({\mathbf{u}}_{\text{s}}\phi )}}$$ (1)

is posed, where φ denotes the volume fraction of the cell type, J is a generalized diffusion, Src denotes the source or mass-exchange terms and u_s is the mass-averaged velocity of the solid components. Although each cell type could move with its own velocity, here we assume that cells move with the mass-averaged velocity, which is equivalent to assuming that the cells are closely packed (Wise et al. 2008). Using a variational argument, the flux is derived from an adhesion energy that accounts for interactions among the cells. We assume for simplicity that tumor cells prefer to adhere to one another rather than the host and thus we write the adhesion energy as (Wise et al 2008)

$$E=\frac{\gamma }{\epsilon }\underset{\mathrm{\Omega }}{\int }F({\phi }_T)+{\epsilon }^2{\mid \nabla {\phi }_T\mid }^{2}dx,$$ (2)

where Ω is a domain that contains the tumor and its host microenvironment, φ_T = φ_CSC +φ_CP +φ_TC +φ_DC denotes the solid tumor volume fraction, γ is a measure of cell-cell adhesion and effectively controls the stiffness of the tumor/host interface like a surface tension. The parameter ε models longer-range interactions among the components and introduces a finite thickness (proportional to ε) of the tumor-host interface. Scaling the volume fractions by the total solid volume fraction, we get φ_T + φ_H = 1. Thus, the tumor and host domains and the tumor-host interface may be written as Ω_T (t) = {x|φ_T (x, t) > 1/2}, Ω_H (t) = {x|φ_T (x, t ) < 1/2} and Σ_T(t) = {x|φ_T (x, t) = 1/2}, respectively. We may then take $F({\phi }_T)=\frac{1}{4}{\phi }_T^2{(1-{\phi }_T)}^2$ to be a double-well potential, which is minimized when φ_T = 1 (tumor) or φ_T = 0 (host).

The fluxes for the tumor components can be given by (Wise et al. 2008)

$$\mathbf{J}=-M\phi \nabla \mu ,\mu =\frac{\delta E}{\delta {\phi }_T}=\frac{\gamma }{\epsilon }\left(\frac{dF}{d{\phi }_T}({\phi }_T)-{\epsilon }^2{\nabla }^2{\phi }_T\right),$$ (3)

where M is a mobility, μ is the chemical potential which is equal to the variational derivative of the adhesion energy $\frac{\delta E}{\delta {\phi }_T}$. This choice makes Eq. (1) a fourth order nonlinear advection-diffusion of Cahn-Hilliard type (Cahn and Hilliard, 1958). The flux for the host component is (Wise et al. 2008)

$${\mathbf{J}}_H=M{\phi }_T\nabla \mu .$$

The cell velocity is assumed to satisfy a generalized Darcy’s law (Wise et al. 2008)

$${\mathbf{u}}_{\text{s}}=-\kappa ({\phi }_{\mathit{CSC}},{\phi }_{CP},{\phi }_{TC},{\phi }_{DC})(\nabla p-\mu \nabla {\phi }_T),$$ (4)

where κ is the cell-motility which contains the combined effects of cell-cell and cell-matrix adhesion, p is the solid, or oncotic, pressure generated by cell proliferation and the remaining term is the contribution from cell-cell adhesion forces. This constitutive law assumes that the tumor can be treated as a viscous, inertialess fluid and also models flow through a porous media. Again, other constitutive laws may be found in Lowengrub et al. (2010) and Cristini and Lowengrub (2010). Note that cell-cell adhesion arises in the model from two sources—the fluxes in the conservation equation (3) and the extra forces in the velocity equation (4). Overall, these equations guarantee that in the absence of mass sources, the adhesion energy is non-increasing in time as the fields evolve (thermodynamic consistency). Further, because of the double well potential F in the adhesion energy, 0 and 1 are energetically favored states of the volume fraction of the total tumor φ_T. This is true even when mass is added or removed via the source terms, and when the cells move rapidly (either passively or actively), provided the mobility is large enough to enable the cells to redistribute and approach the energetically favored states (e.g., Wise et al. 2008). Note that the water component can be determined once the solid components are found (Wise et al. 2008) and thus we do not present the equations governing the water fraction here.

Assuming that the source term for host tissue is zero (e.g., homeostasis, Src_H = 0 ), the conservation equations may be summed to yield the following equation for the velocity:

$$\nabla ·{\mathbf{u}}_S={\mathit{Src}}_{\mathit{CSC}}+{\mathit{Src}}_{CP}+{\mathit{Src}}_{TC}+{\mathit{Src}}_{DC},$$ (5)

which together with Eq. (4) can be used to solve for the pressure p. To close the system, it remains to specify the source/mass-exchange terms. We assume that the fractions of CSCs and CPs that self-renew are P₀ and P₁ and that the CSC, CP and TC mitosis rates are linearly proportional to the level of oxygen, glucose and other growth and survival promoting factors, which are modeled using a single concentration field C_O. Following Lander et al. (2009), we do not distinguish between symmetric and asymmetric division, but rather just consider the fraction of proliferating cells that self-renew (P₀ or P₁) and differentiate (1−P₀ or 1−P₁). Death may occur by either apoptosis or necrosis due to nutrient levels that are insufficient to support cell viability. Accordingly, the source terms, which appear in Eq. (1), are given as

$${\mathit{Src}}_{\mathit{CSC}}=\stackrel{\text{Self}-\text{renewal}\text{of}\text{stem}\text{cells}}{\overbrace{{\lambda }_{\mathit{MSC}}(2P_0-1){\varphi }_{\mathit{CSC}}{C}_{O}G({\varphi }_{\mathit{CSC}})}}-\stackrel{\text{Apoptoasis}}{\overbrace{{\lambda }_{\mathit{ASC}}{\varphi }_{\mathit{CSC}}}}-\stackrel{\text{Necrosis}}{\overbrace{{\lambda }_{\mathit{HSC}}\mathit{Hvn}({\overline{C}}_O-C_O){\varphi }_{\mathit{CSC}}}},$$ (6)

$${\mathit{Src}}_{CP}=\stackrel{\text{Differentiation}\text{of}\text{stem}\text{cells}}{\overbrace{2{\lambda }_{\mathit{MSC}}(1-P_0){\varphi }_{\mathit{CSC}}{C}_{O}G({\varphi }_{\mathit{CSC}})}}+\stackrel{\text{Self}-\text{renewal}\text{of}\text{committed}\text{progenitor}\text{cells}}{\overbrace{{\lambda }_{\mathit{MCP}}(2P_1-1){\varphi }_{CP}{C}_{O}G({\varphi }_{CP})}}-\stackrel{\text{Apoptosis}}{\overbrace{{\lambda }_{\mathit{ACP}}{\varphi }_{CP}}}-\stackrel{\text{Necrosis}}{\overbrace{{\lambda }_{\mathit{HCP}}\mathit{Hvn}({\overline{C}}_O-C_O){\varphi }_{CP}}},$$ (7)

$${\mathit{Src}}_{TC}=\stackrel{\text{Differentiation}\text{of}\text{committed}\text{progenitor}\text{cells}}{\overbrace{2{\lambda }_{\mathit{MSP}}(1-P_1){\varphi }_{CP}{C}_{O}G({\varphi }_{CP})}}+\stackrel{\text{Mitosis}\text{of}\text{terminally}\text{differentiated}\text{cells}}{\overbrace{{\lambda }_{\mathit{MTC}}{\varphi }_{TC}{C}_{O}G({\varphi }_{TC})}}-\stackrel{\text{Apoptosis}}{\overbrace{{\lambda }_{\mathit{ACC}}{\varphi }_{TC}}}-\stackrel{\text{Necrosis}}{\overbrace{{\lambda }_{\mathit{HTC}}\mathit{Hvn}({\overline{C}}_O-C_O){\varphi }_{TC}}},$$ (8)

where the λ_M., λ_A., λ_H. parameters denote the mitosis, apoptosis and necrosis rates. The function G(.) cuts off proliferation if the volume fraction is sufficiently low (see Sec. 4 and Wise et al. 2008) and the function Hvn(x) denotes the Heaviside function which is equal to 1 when x>0 and is 0 otherwise. The parameter C̄_O denotes the minimum level of oxygen, glucose and growth promoting factors required for cell viability. The DC population increases as a result of the death of the viable cell species and decreases due to cell lysis, which provides a source of water:

$${\mathit{Src}}_{DC}=\stackrel{\text{Apopotosis}\text{of}\text{live}\text{cells}}{\overbrace{{\lambda }_{\mathit{ASC}}{\varphi }_{\mathit{CSC}}+{\lambda }_{\mathit{ACP}}{\varphi }_{CP}+{\lambda }_{\mathit{ATC}}{\varphi }_{TC}}}+\stackrel{\text{Necrosis}\text{of}\text{CSC}}{\overbrace{{\lambda }_{\mathit{HSC}}\mathit{Hvn}({\overline{C}}_O-C_O){\varphi }_{\mathit{CSC}}}}+\stackrel{\text{Necrosis}\text{of}\text{CP}}{\overbrace{{\lambda }_{\mathit{HCP}}\mathit{Hvn}({\overline{C}}_O-C_O){\varphi }_{\mathit{CSC}}}}+\stackrel{\text{Necrosis}\text{of}\text{TC}}{\overbrace{{\lambda }_{\mathit{HTC}}\mathit{Hvn}({\overline{C}}_O-C_O){\varphi }_{CP}}}-\stackrel{\text{Lysis}\text{of}\text{DC}}{\overbrace{{\lambda }_L{\varphi }_{DC}}},$$ (9)

where λ_L is the lysis rate. Note that water is taken up by cells during the cell cycle. We do not present the water equation here, see Wise et al. (2008). Summing the mass exchange terms for tumor species yields the source term for the tumor volume fraction:

$${\mathit{Src}}_T=\stackrel{\text{Mitosis}\text{of}\text{stem}\text{cells}}{\overbrace{{\lambda }_{\mathit{MSC}}{\varphi }_{\mathit{CSC}}{C}_{O}G({\varphi }_{\mathit{CSC}})}}+\stackrel{\text{Mitosis}\text{of}\text{committed}\text{progenitor}\text{cells}}{\overbrace{{\lambda }_{\mathit{MCP}}{\varphi }_{CP}{C}_{O}G({\varphi }_{CP})}}+\stackrel{\text{Mitosis}\text{of}\text{terminal}\text{cells}}{\overbrace{{\lambda }_{\mathit{MTC}}{\varphi }_{TC}{C}_{O}G({\varphi }_{TC})}}-\stackrel{\text{Lysis}\text{of}\text{dead}\text{exlls}}{\overbrace{{\lambda }_L{\varphi }_{DC}}}$$ (10)

Eqs. (1), (3) and (4)–(10) are posed in the domain Ω with boundary Σ_∞. At Σ_∞, homogeneous Neumann boundary conditions are imposed for the tumor species 0 = ω_∞·∇φ_T = ω_∞·∇φ_CSC = ω_∞·∇φ_CP = ω_∞·∇φ_TC = ω_∞·∇φ_DC, where ω_∞ is the outward-pointing normal vector on the far-field boundary Σ_∞. Dirichlet conditions are imposed for the chemical potential and pressure μ = p = 0 on Σ_∞, which allow the tumor to move freely out of the computational domain (Wise et al. 2008).

2.2 Oxygen, glucose and growth promoting factors

Oxygen, glucose and other growth promoting factors are assumed to diffuse through the tumor microenvironment and are supplied by an underlying microvasculature. Since we model only their combined effect, we refer to these factors generically as “O” hereafter. Following previous work (e.g., Cristini et al. 2003; Wise et al. 2008; Frieboes et al. 2010), the uptake of O is assumed to be negligible in the host domain compared to the level of uptake by the viable tumor cell species, which typically exceeds the supply of O diffused to the tumor cells. Compared to the cell cycle for tumor cells, in which proliferation occurs on the order of a day, O diffusion is rapid and occurs on the order of minutes (e.g., estimated from the diffusion coefficients of oxygen and glucose). Therefore, the concentration C_O can be described using a quasi-steady equation (Wise et al. 2008, Frieboes et al. 2010):

$$0=\nabla ·(D_O\nabla C_O)-({\nu }_{\mathit{UOSC}}{\phi }_{\mathit{CSC}}+{\nu }_{\mathit{UOCP}}{\phi }_{CP}+{\nu }_{\mathit{UOTC}}{\phi }_{TC})C_O+{\nu }_{PO}({\overline{C}}_{AO}-C_O)Q({\phi }_T)$$ (11)

where D_O is the diffusion coefficient, ν_UOSC, ν_UOCP and ν_UOTC are the uptake rates by CSCs, CPs and TCs respectively. The parameter ν_PO models the rate at which O is supplied to the microenvironment. The parameter C̄_AO is the concentration of O in the blood (in vivo) or in the medium (in vitro) far from the tumor. In addition, we take the Dirichlet boundary condition C_O = C̄_AO on Σ_∞. The function Q(φ_T) ≈1−φ_T approximates the characteristic function of the host domain and thus models the source of O as being external to the tumor (i.e., the tumor is avascular).

2.3 The self-renewal fraction and feedback from self-renewal and differentiation promoters

Following Lander et al. (2009), we assume that the proliferation and differentiation of the tumor cells in lineages are regulated by factors in the tumor microenvironment that feedback on self-renewal fractions and mitosis rates. In particular, we assume that the TCs produce soluble differentiation promoters, referred to hereafter as “T”, that reduce the self-renewal fractions and mitosis rates of the CSC and CPs. Candidates for T include TGFβ superfamily members. We do not model the potential effects of T on cell motility that could enhance tumor invasiveness even though some TGFβ superfamily members do enhance tumor invasiveness (e.g., Meulmeester and ten Dijke 2011). This is currently under study.

We also account for a self-renewal promoter, hereafter referred to as “W”, which increases the self-renewal fraction of CSCs and an inhibitor of W, hereafter referred to as “WI”. Candidate self-renewal promoters include Wnts, BMP, Shh, and Notch (see, for example, Bailey et al. 2007; Pannuti et al. 2010) and their inhibitors such as Dkk and SFRPs in the case of Wnt.

We then define the CSC self-renewal fraction to be

$$P_0=P_{\mathit{Min}}+(P_{\mathit{Max}}-P_{\mathit{Min}})(\frac{\xi C_W}{1+\xi X_W})(\frac{1}{1+\mathrm{\Psi }{C}_T}),$$ (12)

where P_Min and P_Max are the minimal and maximal levels of self-renewal. The functions C_W and C_T are the concentrations of the self-renewal promoter W and the differentiation promoter T, respectively. The parameters ξ and Ψ quantify the feedback response of the CSCs to the regulating proteins. The self-renewal rate of the CPs and the mitosis rates λ_MSC and λ_MCP may also depend on the self-renewal and differentiation promoters using a relation analogous to Eq. (12), although the CPs may respond to different promoters than that CSCs, e.g. see Wu et al. (2003), and Gokoffski et al. (2011).

As in the case of O, we assume that T is more diffusive than either W or WI, which are assumed to have smaller effective diffusivities. Therefore, on the time scale of cell proliferation (λM⁻¹) the diffusion of T and O occurs rapidly and the time derivatives and advection terms can be neglected. This is motivated by the observation that some TGF-β superfamily members, such as Activin, diffuse over long ranges (e.g. Jones et al. 1996). We note that relaxing this assumption to include time derivatives and advection terms for T does not qualitatively change the results presented below (data not shown). Therefore, the concentration C_T can be described using the quasi-steady reaction-diffusion equation:

$$0=\nabla ·(D_T\nabla C_T)-({\nu }_{UT}{\phi }_{\mathit{CSC}}+{\nu }_{DT})C_T+{\nu }_{PT}{\phi }_{TC},$$ (13)

where D_T is the diffusion coefficient, ν_UT, ν_DT, and ν_PT are the uptake rate by the CSCs, the rate of natural decay and rate of production by the TCs, respectively. Note that if T is also taken up by CPs, then Eq. (13) is modified accordingly. We take the absorbing Dirichlet boundary condition C_T = 0 on Σ_∞. This mimics the intravasation of C_T into the underlying vascular network or the use of a large in vitro container.

To model the self-renewal promoter W and its inhibitor WI, we use a generalized Gierer-Meinhard-Turing system of reaction-diffusion equations (Turing 1953; Gierer and Meinhard 1972). We assume that W is the activator and WI is the inhibitor. The nonlinear reaction terms in the Gierer-Meinhard model are suggested by the diversity of Wnt signaling, and its inhibition, through canonical and non-canonical pathways where the production of Wnts and their signaling may be self-promoting (e.g., Amerongen and Nusse 2009; Cha et al. 2009; Nadji et al. 2011). Because Wnt and Wnt-producing cells tend to be co-localized in space (e.g., Vermeulen et al. 2010), we assume that W diffuses only over a short range while WI is assumed to diffuse over a longer range. Because Wnt and Dkk are produced by CSCs (e.g., see Gregory et al., 2003; Byun et al. 2005; Niehrs 2006; Lee et al. 2007; Qiao et al. 2008; Salazar et al., 2009; Vermeulen et al., 2010), we assume that this is also the case for W and WI and that their production rates depend on the levels of oxygen, glucose and growth promoting factors O available. An interesting experiment would be to increase the oxygen tension in the tumor microenvironment, which can be done in vitro (e.g., Pennacchietti et al. 2003), and measure Wnt and Dkk expressions to assess this hypothesis. While we recognize that hypoxia may also have the potential to upregulate the stem cell phenotype (e.g., Heddleston et al. 2009) and that hypoxia and Wnt pathways converge (e.g., Mazumdar et al. 2010; Choi et al. 2010), we do not model these effects here. Further, we do not model upregulation of Wnt signaling by stromal cells (e.g., Vermeuelen et al. 2010). These effects are currently under investigation. We therefore take:

$$\frac{\partial C_W}{\partial t}+\nabla ·({\mathbf{u}}_s{C}_W)=\nabla ·(D_W\nabla C_W)+f(C_W,C_{WI}),$$ (14)

$$\frac{\partial C_{WI}}{\partial t}+\nabla ·({\mathbf{u}}_s{C}_{WI})=\nabla ·(D_{WI}\nabla C_{WI})+g(C_W,C_{WI}),$$ (15)

where C_WI is the concentration of WI and

$$f(C_W,C_{WI})={\nu }_{PW}\frac{C_W^2}{C_{WI}}{C}_O{\phi }_{\mathit{CSC}}-{\nu }_{DW}{C}_W+u_0{C}_O({\phi }_{\mathit{CSC}}+{\phi }_{CP}+{\phi }_{TC}),$$ (16)

$$g(C_W,C_{WI})={\nu }_{\mathit{PWI}}{C}_W^2{C}_O{\phi }_{\mathit{CSC}}-{\nu }_{\mathit{DWI}}{C}_{WI}.$$ (17)

The parameters D_W and D_WI are the diffusion coefficients, ν_PW, ν_DW and ν_PWI, ν_DWI are the production and decay rates of W and WI. The parameter u₀represents a low-level source of W from all the viable tumor cells. The assumption is that W is produced mainly by CSCs, but the CPs and TCs may also produce a small quantity of this factor. Note that similar systems have been used in the context of hair follicles as well as other systems such as hydra regeneration and lung branching (e.g., Sick et al. 2006, Kondo and Kura 2010).

We use homogeneous Neumann boundary conditions ω_∞·∇C_W = ω_∞·∇C_WI = 0 on Σ_∞. This choice has little effect on the results while the tumor is sufficiently far from the domain boundary.

Finally, the model does not depend on the particular choice of self-renewal promoter and inhibitor. However, if Notch signaling is studied, then the effects should be highly localized. In addition, model equations other than the Gierer-Meinhard system given above could also be used, but the equations should be capable of forming patterns.

3. Model simplification and nondimensional equations

We next simplify the model and consider only two types of viable tumor cells: TCs and non-TCs. In particular, the non-TC population contains the CSCs and CPs. For simplicity, we refer to the non-TC population as CSCs in the remainder of the paper, although we expect that the CPs dominate the population of the non-TC compartment. Consequently, the proliferation rate for the combined population is taken to be that for the CPs (e.g., on the order of 1 day). Preliminary results (not shown) from the more general model tracking the evolution of CSCs, CPs and TCs separately, where CSCs slowly divide and the CPs divide rapidly, are consistent with the results presented here using the simplified model. Results from the more general model will be presented in a future work.

To further simplify the problem, we neglect the effects of necrosis due to insufficient nutrients and we ignore changes in the mitosis rate of CSCs due to the feedback factors. Both these effects will also be considered in a future investigation. We further assume that there is no apoptosis of CSCs as the apoptosis rate should be very small over the time scales we consider here. We assume that TCs may undergo apoptosis.

Following Cristini et al. (2003), Frieboes et al. (2006) and Wise et al. (2008), we nondimensionalize the equations using the O diffusion length scale $l=\sqrt{D_O/{\nu }_{\mathit{UOSC}}}$ and the mitosis time scale τ = (λ_MSCC̄_AO)⁻¹. Following Frieboes et al. (2006), these can be estimated as l ≈200 μm, using characteristic rates of oxygen diffusion and uptake, and τ ≈1day. The details of the nondimensionalization are given in the Appendix, where the nondimensional parameters are introduced. Here, we summarize the nondimensional system of equations. Although the parameters are nondimensional, we use the same notation as in Sec. 2.

The nondimensional system of equations for the CSC, TC and DC volume fractions is given by

$$\frac{\partial {\phi }_{\mathit{CSC}}}{\partial t}=M\nabla ·({\phi }_{\mathit{CSC}}\nabla \mu )+{\mathit{Src}}_{\mathit{CSC}}-\nabla ·(u_s{\phi }_{\mathit{CSC}}),$$ (18)

$$\frac{\partial {\phi }_{TC}}{\partial t}=M\nabla ·({\phi }_{TC}\nabla \mu )+{\mathit{Src}}_{TC}-\nabla ·({\mathbf{u}}_s{\phi }_{TC}),$$ (19)

$$\frac{\partial {\phi }_{DC}}{\partial t}=M\nabla ·({\phi }_{DC}\nabla \mu )+{\mathit{Src}}_{DC}-\nabla ·({\mathbf{u}}_s{\phi }_{DC}),$$ (20)

The nondimensional velocity is

$${\mathbf{u}}_s=-\kappa \left(\nabla p-\frac{\gamma }{\epsilon }\mu \nabla {\phi }_T\right),$$ (21)

and the nondimensional chemical potential is $\mu =\frac{\partial F}{\partial {\phi }_T}({\phi }_T)-{\epsilon }^2{\nabla }^2{\phi }_T$. The velocity further satisfies the equation:

$$\nabla ·{\mathbf{u}}_s={\phi }_{\mathit{CSC}}{C}_{O}G({\phi }_{\mathit{CSC}})+{\lambda }_{\mathit{MTC}}{\phi }_{TC}{C}_{O}G({\phi }_{TC})-{\lambda }_L{\phi }_{DC},$$ (22)

which is used to solve for the pressure. Note that we do not have to solve for the host species φ_H since it is determined by the tumor species, e.g., φ_H = 1−φ_T = 1−(φ_CSC + φ_TC +φ_DC).

Neglecting necrosis and the apoptosis of CSCs, the nondimensional source terms are

$${\mathit{Src}}_{\mathit{CSC}}=(2P_0-1){\phi }_{\mathit{CSC}}{C}_{O}G({\phi }_{\mathit{CSC}}),$$ (23)

$${\mathit{Src}}_{TC}=2(1-P_0){\phi }_{\mathit{CSC}}{C}_{O}G({\phi }_{\mathit{CSC}})+{\lambda }_{\mathit{MTC}}{\phi }_{TC}{C}_{O}G({\phi }_{TC})-{\lambda }_{\mathit{ATC}}{\phi }_{TC},$$ (24)

$${\mathit{Src}}_{DC}={\lambda }_{\mathit{ATC}}{\phi }_{TC}-{\phi }_L{\phi }_{DC},$$ (25)

where $P_0=P_{\mathit{Min}}+(P_{\mathit{Max}}-P_{\mathit{Min}})\left(\frac{\xi C_W}{1+\xi C_W}\right)\left(\frac{1}{1+\mathrm{\Psi }{C}_T}\right)$ is the self-renewal fraction. The nondimensional equation for O is

$$0={\nabla }^2{C}_O-C_O({\phi }_{\mathit{CSC}}+{\nu }_{\mathit{UOTC}}{\phi }_{TC})+{\nu }_{PO}(1-C_O)Q({\phi }_T),$$ (26)

and the nondimensional equation for T is

$$0={\nabla }^2{C}_T-({\nu }_{UT}{\phi }_{\mathit{CSC}}+{\nu }_{DT})C_T+{\nu }_{PT}{\phi }_{TC}.$$ (27)

The nondimensional equations for W and WI are

$$\frac{\partial C_W}{\partial t}+\nabla ·({\mathbf{u}}_s{C}_W)=D_W{\nabla }^2{C}_W+Rf(C_W,C_{WI}),$$ (28)

$$\frac{\partial C_{WI}}{\partial t}+\nabla ·({\mathbf{u}}_s{C}_{WI})=D_{WI}{\nabla }^2{C}_{WI}+Rg(C_W,C_{WI}),$$ (29)

where

$$f(C_W,C_{WI})=\frac{C_W^2}{C_{WI}}{C}_O{\phi }_{\mathit{CSC}}-C_W+u_0{C}_O({\phi }_{\mathit{CSC}}+{\phi }_{TC}),$$ (30)

$$g(C_W,C_{WI})=C_W^2{C}_O{\phi }_{\mathit{CSC}}-{\nu }_{\mathit{DWI}}{C}_{WI},$$ (31)

The nondimensional parameters are summarized in Tables 1–6. Because the knowledge of many model parameters is not currently available from existing experimental data, the choices of the nondimensional parameters reflect the results of experimentation and parameter studies, in addition to data available in the literature. The baseline nondimensional parameters for self-renewal and feedback response and for the T and the W and WI systems (Tables 1, 3 and 4) are obtained from numerical experimentation by requiring that the fractions of CSCs in the tumors are small, and that W and WI form co-localized patterns.

Table 1.

Nondimensional parameters for self-renewal and feedback response

Minimum probability of self renewal of stem cells	PMin = 0.2
Maximum probability of self renewal of stem cells	PMax = 1.0
Negative feedback response	Ψ = 0.5
Positive feedback response	ξ = 1.0

Table 6.

Other nondimensional model parameters

Diffuse interface thickness	ε = 0.05
Adhesion	γ = −0.1
Mobility	M = 10.0

Table 3.

Nondimensional parameters for T

Uptake rate of stem cells	νUT = 0.05
Decay rate	νDT = 0.0
Production rate	νPT = 0.1

Table 4.

Nondimensional parameters for W and WI

W source term	u0 = 0.2
Reaction rate	R = 50
WI decay rate	νDWI = 1.0
Diffusivity of WI	DWI = 25.0
Diffusivity of W	DW = 1.0

We note that for certain parameter ranges, the space-independent version of the Gierer-Meinhard model (28)–(31) with uniform coefficients does have a limit cycle which may or may not be stable according to additional parameter constraints (e.g., Granero-Porati and Porati 1984). With the values of the nondimensional parameters given in Table 4, and assuming that C_O ≈ 1 and φ_CSC +φ_TC ≈ 1, which is consistent with the simulation results near the tumor boundary where the spatial patterns form (see Sec. 4), we find that there is a limit cycle, but it is unstable. Consistent with this, we do not observe oscillations in W and WI in our numerical simulations.

Because the TCs are either postmitotic or proliferate slowly, we assume that their proliferation rate is 10 times smaller than that of the combined CSC/CP population and that their apoptosis rate is equal to their mitosis rate. Since the effective mitosis rate depends on the availability of oxygen, glucose and other growth-promoting factors, this would effectively lead to a diminishing TC population in the absence of CSC/CP differentiation. Other parameters such as the lysis and O production rates, adhesion and motility were chosen to be consistent with those values used by Wise et al. (2008).

4. Results

In this section, we present numerical results in 2D and 3D for tumor progression with varying degrees of response to feedback signaling, shape perturbations and therapy application. To solve the governing equations efficiently, an adaptive finite difference-nonlinear multigrid method is developed following previous work by Wise et al. (2008, 2011). The details of the method and numerical implementation are briefly described in the Supplementary Material (Sec. S1).

Unless otherwise specified, we investigate the progression of solid tumors starting from an initially circular distribution of CSCs. At time t = 0, there are no TCs or DCs. We have tested other initial configurations and found results similar to those presented here. The initial conditions for the tumor species are given by

$${\phi }_T(x,0)={\phi }_{\mathit{CSC}}(x,0)=\frac{1}{2}\left(1-tanh\left(\frac{\sqrt{\left(\frac{x^2}{a}+\frac{y^2}{b}\right)}-1}{2\sqrt{2}\epsilon }\right)\right),{\phi }_{TC}(x,0)={\phi }_{DC}(x,0)=0,$$ (32)

where a=b=3. This initial condition provides the diffuse interface representation of the circle with radius $\sqrt{3}$ centered at the origin. For the self-renewal promoter W, the initial condition is a small perturbation from the homogeneous steady state. The inhibitor concentration is taken to be the steady-state value. In particular, the steady state values for the concentrations of W and WI are obtained by setting f and g to zero in Eqs. (30) and (31) and setting C_O = 1 and φ_CSC = 1 in those equations. We confine the initial concentrations to be in the tumor domain by multiplying by φ_T and therefore take as initial conditions

$$C_W(x,0)=(1.2+0.1(\mathit{rand}-0.5)){\phi }_T$$ (33)

$$C_{WI}(x,0)=1.44{\phi }_T,$$ (34)

for the values of the parameters listed in Table 4. Here, rand is a small random number that differs at each point in the computational mesh and is uniformly distributed in the unit interval [0,1]. The same initial seed for the random number generator is used for all simulations, which allows the comparison of simulations using different model parameters with the same initial tumor morphology. We have tested other initial configurations for W and WI and the results are also qualitatively similar to those presented here. Finally, we neglect advective transport of W and WI here as simulations indicate that advection does not change the qualitative behavior of the system (see the Supplementary Material, Sec. S6).

The cut-off function and interpolation functions introduced in Sec. 2 are taken to be (Wise, 2008)

$$G({\phi }_i)=\{\begin{array}{lll}\hfill 1& if\hfill & {\phi }_i>\frac{3}{2}\epsilon \hfill \\ \hfill {\phi }_i-\frac{1}{2}\epsilon & if\hfill & \frac{1}{2}\epsilon <{\phi }_i<\frac{3}{2}\epsilon \hfill \\ \hfill 0& if\hfill & {\phi }_i<\frac{1}{2}\epsilon \hfill \end{array},Q({\phi }_T)=\{\begin{array}{lll}1\hfill & if\hfill & 1-{\phi }_T>1\hfill \\ 0\hfill & if\hfill & 1-{\phi }_T<0\hfill \\ 1-{\phi }_T\hfill & \hfill & \mathit{else}\hfill \end{array}.$$ (35)

Note that G only provides a cutoff when φ_i is small. When φ_i >3ε/2, there is no cutoff and G=1. In the results presented below, we take ε = 0.05 (see Table 6). As we will demonstrate below, the results for other choices of G, including G = 1 (no cut-off) are similar. In particular we present results both for G given as Eq. (35) and G=1.

Finally, note that because C_T and C_O satisfy quasi-steady diffusion equations, no initial condition is required for these fields. Because there are no TCs initially, the initial concentration of the differentiation promoter isC_T (x,0) = 0.

4.1 The progression of a tumor in 2D

We next consider the progression of a 2D tumor where the specific feedback response parameters to the self-renewal and differentiation promoters are taken to be ξ = 1 and Ψ=0.5, respectively. All other non-dimensional parameters for this case are given in Tables 1–6. Note that the cell-cell adhesion parameter γ= −2ε (=−0.1). As discussed earlier in Sec. 2, γ models cell-cell adhesion and controls the stiffness of the tumor boundary with larger values of γ corresponding to stiffer interfaces. Here, the small negative value of γ is chosen to offset the additional interface stiffness introduced by the Cahn-Hilliard-like equation for the volume fraction φ_T for finite interface thickness ε. This makes the tumor interface highly susceptible to instability and thus is used to highlight the shape changes possible during tumor progression. The effect of γ on tumor progression is shown in the Supplementary Material (Sec. S3) and discussed further below. For simplicity, we have neglected the contribution of the advection terms in W and WI (this is the case for all simulations presented below). In the Supplementary Documents, we show that including the advective terms does not change the results qualitatively (see Fig. S6).

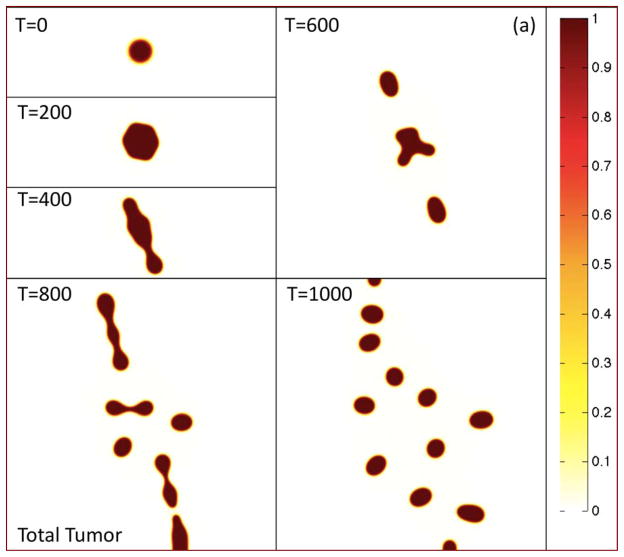
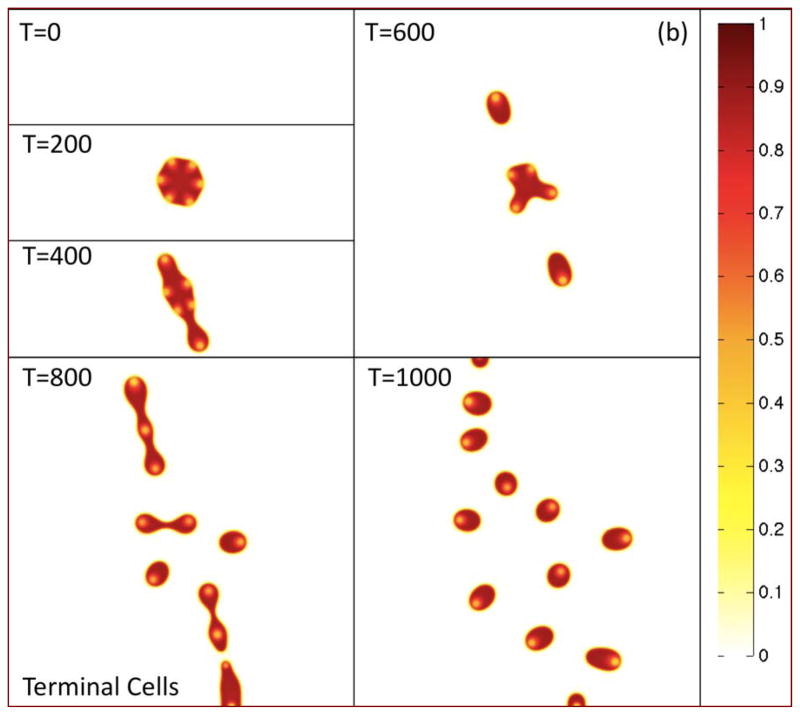
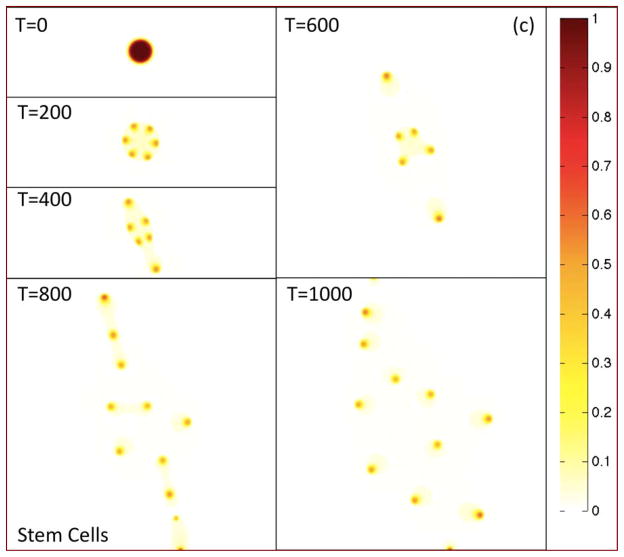
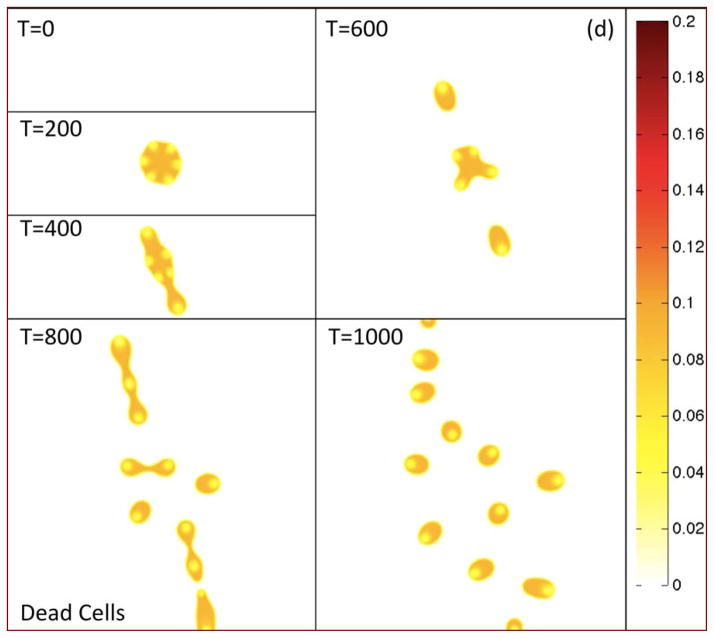
In Fig. 2(a), the morphologies of the growing tumor are shown at the indicated times by plotting the contours of the tumor volume fraction φ_T. The initially circular tumor develops a morphological instability as it grows, leading to the development of two dominant invasive fingers and an elongated tumor. The tumor then breaks apart yielding numerous fragments some of which leave the computational domain. In Figs. 2(b)–(d), the contours of the TC, CSC and DC local volume fractions φ_TC, φ_CSC and φ_DC are plotted, respectively, at the corresponding times.

Figure 2.

The progression of a tumor in 2D under the effects of spatiotemporally varying feedback signaling. (a) Contours of the total tumor volume fraction φ_T are shown at the times indicated. (b)–(j). see following pages. Colors online.

Figure 2(b). Contours of the terminal cell volume fraction φ_TC are shown at the times indicated. Colors online.

Figure 2(c). Contours of the cancer stem cell volume fraction φ_CSC are shown at the times indicated. Colors online.

Figure 2(d). Contours of the dead cell volume fraction φ_DC are shown at the times indicated. Colors online.

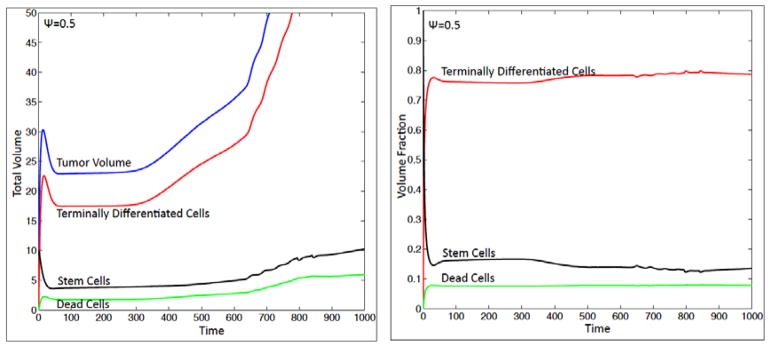
Figure 2(e). Time evolution of the volumes (left) and total volume fractions (right) of the tumor components. Colors online.

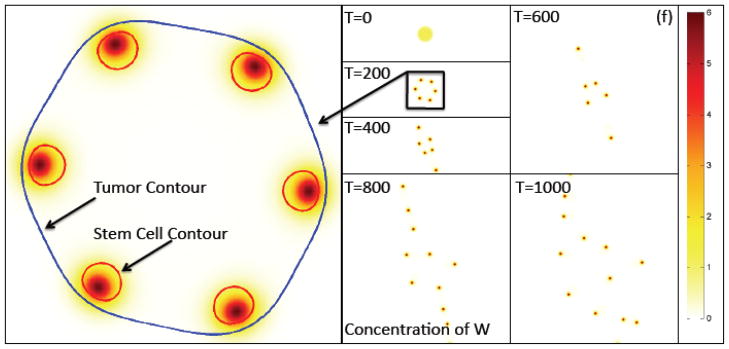
Figure 2(f). The contours of the concentration of W (e.g., representative of Wnt signaling factors) at the times indicated together with a close-up showing the φ_T=0.5 and φ_CSC=0.4 contours. The latter shows the tumor boundary and boundaries of the stem cell clusters, respectively. The peak W concentration is offset from the center of the stem cell cluster, which leads to instability. Colors online.

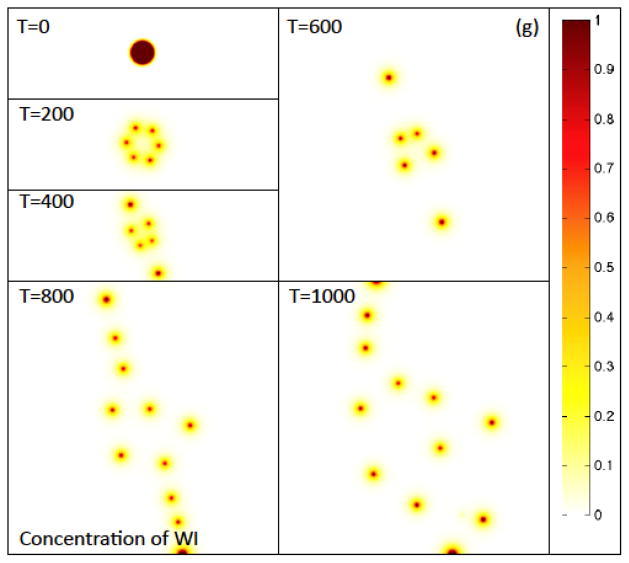
Figure 2(g) The contours of the concentration of WI, the inhibitor of W (e.g., representative of Wnt inhibitors such as Dkk and SFRPs). Colors online.

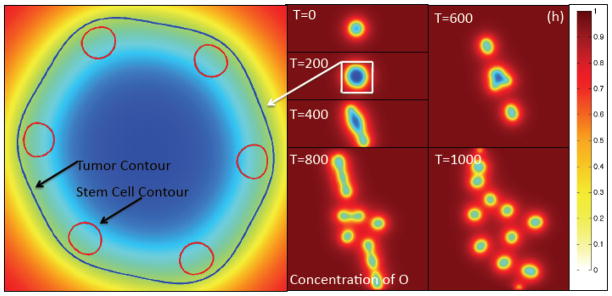
Figure 2(h). The contours of the O concentration at the times indicated together with a close-up showing the φ_T = 0.5 and φ_CSC = 0.4 contours indicating the tumor boundary and boundaries of the stem cell clusters, respectively. Colors online.

Figure 2(i). The contours of the cancer stem cell self-renewal fraction P₀ at the times indicated together with a close-up showing the φ_T = 0.5 and φ_CSC = 0.4 contours. The latter shows the tumor boundary and boundaries of the cancer stem cell clusters, respectively. Note that the peak self-renewal fraction is offset from the center of the stem cell cluster, which leads to instability. Colors online.

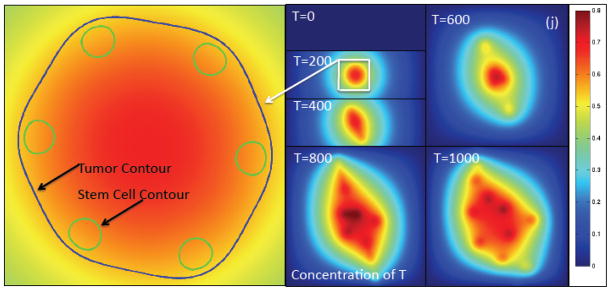
Figure 2(j). The contours of the concentration of T (e.g., TGFβ superfamily member) at the times indicated together with a close-up showing the φ_T=0.5 and φ_CSC=0.4 contours. The latter shows the tumor boundary and boundaries of the cancer stem cell clusters, respectively. Note that the concentration of T is nearly uniform across the stem cell clusters. Colors online.

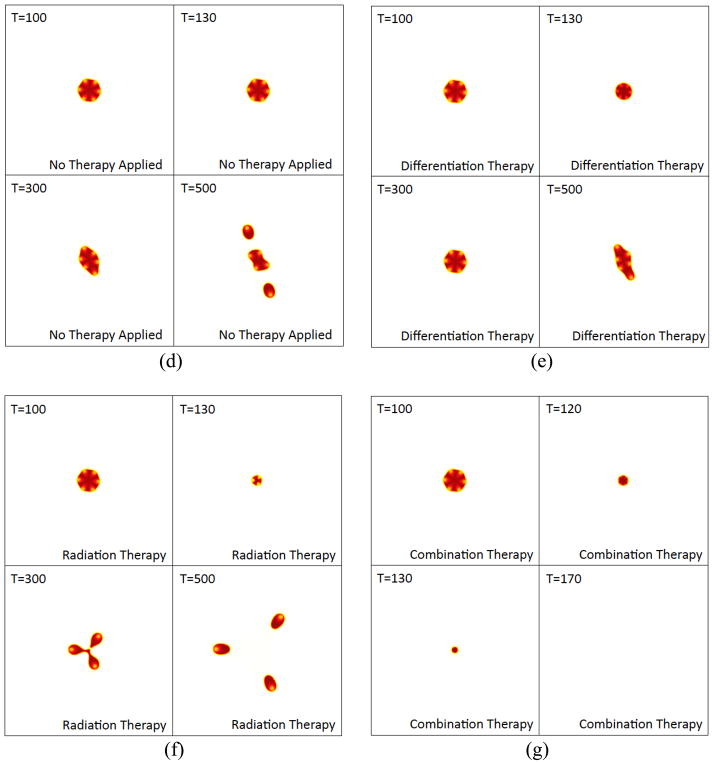
At early times, patterning develops and the CSC population becomes localized in discrete clusters near the tumor boundary, resulting in a heterogeneous distribution of cells. Interestingly, the Pajonk group at UCLA recently confirmed this predicted arrangement of CSCs in sufficiently large U87MG-derived in vitro tumor spheroids. This is shown in Fig. 3 where a U87MG tumor spheroid with a radius of approximately 250 μm is shown; the green color marks the locations of what are believed to be CSCs (Vlashi et al. 2009) and the white curve marks the approximate location of the spheroid boundary. In small spheroids, CSCs tend to be located more uniformly throughout the spheroid (Vlashi et al. 2009)—a result also consistent with our model (results not shown).

Since the CSCs do not experience death, the DC and TC populations are co-localized. The regions of locally small TC volume fractions correspond to regions where the CSC fractions are highest. The tumor morphology and heterogeneous distribution of the cellular components are both apparent from the contours of φ_TC.

The CSC, TC and DC volumes and total volume fractions are plotted in Fig. 2(e). The total volumes are obtained by integrating φ_TC, φ_CSC and φ_DC over the computational domain. At early times, there is a rapid increase in the TC population as the CSC cells begin to differentiate and pattern. This drives an increase in the tumor volume. There is a concomitant increase of DCs as the TCs begin to die. Before feedback drives the CSC population to decrease due to differentiation to TCs, the CSC population actually increases slightly at very early times since the CSC cells initially start to self-renew (not shown). After an initial transient, the total volume fractions settle down to nearly constant values with TCs, CSCs and DCs consisting of about 77%, 15% and 8% of the tumor respectively.

The heterogeneous distribution of CSCs and TCs is driven by the Gierer-Meinhard-Turing equations (28)–(31) characterizing the W and WI system, which leads to pattern formation. In Figs. 2(f) and 2(g), the concentrations C_W and C_WI are plotted at the corresponding times, respectively. As expected from a linear stability analysis, the system forms patterns consisting of isolated regions of high concentrations of C_W and C_WI, which are also co-localized. These regions form near the tumor boundary because the production of W and WI depends on the concentration of O, which is largest at the tumor boundary as seen in Fig. 2(h). This is consistent with recent experiments where heterogeneous Wnt and Dkk patterning has been observed in in vitro tumors that is strikingly similar to that obtained here. For example, in Fig. 4 heterogeneous spatial patterns of Wnt signaling activity (a) from colon cancer (Vermeulen et al. 2010) and the Wnt inhibitor Dkk (b) from osteosarcoma (Lee et al. 2007), are shown for in vitro tumor spheroids. In Fig. 4(a) the green color denotes Wnt signaling activity. Note that high levels of Wnt activity are observed near the tumor boundary. In Fig. 4(b), immunostaining of osteosarcoma shows that Dkk (green) tends also to be located at the tumor boundary. Heterogeneous Wnt and Dkk patterning is also observed in in vivo tumors (e.g., Vermeulen et al. 2010; Lee et al. 2007). However, we are unaware of studies in which Wnt and Dkk signaling are observed simultaneously. Direct measurements of this signaling, as well as that of other inhibitors of Wnts such as SFRPs, would be useful to test the hypothesis of the model that the short-range activator, W, and long-range inhibitor, WI, are co-localized.

As can be seen in the close-up in Fig. 2(f), the peak W distribution is slightly offset from the center of the CSC cluster and is shifted towards the tumor boundary due to the gradient of O in the tumor interior. Gradients in O develop near the tumor and in its interior because of O uptake by the viable tumor cells. The concentration of O far from the tumor remains nearly uniform. As we show in the Supplementary Material (Sec. S5), removing the O dependence of the source terms in the W and WI system tends to remove the shift between the CSC populations and W concentrations and make them much more co-localized.

In the regions where the concentration of W is large (C_W ≈ 6), the self-renewal fraction P₀ of CSCs also becomes large, as seen in Fig. 2(i). In the close-up (left), P₀ is plotted together with the boundary (φ_T=0.5) of the tumor and the φ_CSC=0.4 contour of the CSC volume fraction. Observe that there is a gradient of P₀ in the CSC clusters with the larger values being located close to the tumor boundary. The gradient of P₀ is maintained primarily by the gradient of C_W and to a lesser extent by that of T (as discussed below in Fig. 2(j)) across the CSC cluster. Thus, near the tumor boundary the self-renewal fraction of CSCs is higher. This, together with the larger effective mitosis rates of cells near the tumor boundary because of increased O concentrations, produces more CSCs at the tumor boundary. This is the mechanism that drives the fingering instability and the tumor fragmentation.

The negative feedback regulated by the TCs through T also affects the CSC clusters. However, because there is only a small variation in C_T across the CSC cluster, as seen in Fig. 2(j), the reduction in P₀ due to T is nearly uniform across the cluster. The highest levels of T are still on the side of the CSC clusters farthest from the tumor boundary. This reinforces the gradient in P₀ across the CSC cluster due to C_W. The magnitude of the gradient of T depends of course on its diffusivity, uptake and natural decay. For example, we find that decreasing the diffusivity, or increasing uptake or decay, enhances instability by increasing the gradient in P₀ across the stem cell cluster (results not shown).

The CSC-driven instability mechanism occurs repeatedly. In addition, new CSC clusters form in areas previously dominated by TCs. This occurs because all tumor cells (CSCs, TCs) are assumed to produce W at relatively low levels (recall Eq. (16)) and as the tumor changes morphology, the distributions of W and WI reorganize to create new regions of locally large concentrations. The newly created regions of large W concentrations then induce the small population of CSCs that reside in between the original clusters to proliferate and self-renew, creating the new clusters. The parameter u₀ primarily controls the number of new CSC clusters that may form during the evolution. Note that in a discrete model, the local CSC population away from the original clusters may be identically zero, which would prevent the emergence of new CSC clusters under this mechanism.

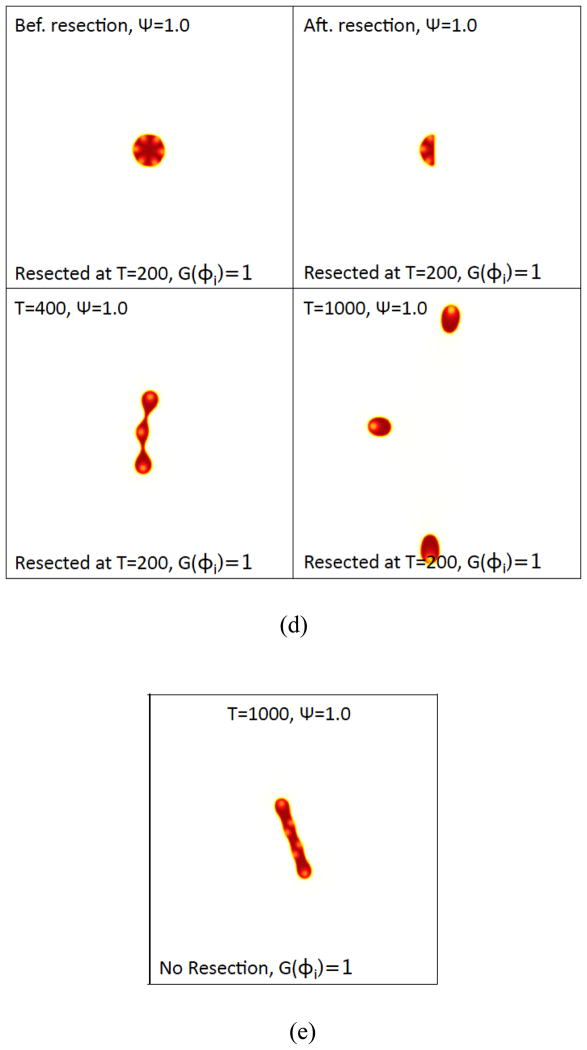
Some of the new CSC clusters form in the interior of the tumor fragments. As the tumor fragments grow in size it can be seen that the clusters of CSCs tend to move toward the fragment boundary, just as is observed for the original tumor. As we show later (see Fig. 7(d)), the cut-off function G can influence this behavior. When G is given by Eq. (35), mitosis is prevented at small volume fractions, which effectively prevents differentiation of CSCs since CSCs need to divide in order to differentiate. This results in increased W production and decreased T production compared to the case in which G=1 and can change the number of new CSC clusters that form.

Figure 7.

Radiation, differentiation and combination therapies. See text for details. (a) Evolution of the tumor volume for treated and untreated tumors as marked. (b) Volume fraction of cancer stem cells. (c) Volume fraction of terminal cells. (d)–(g) See next page.

Figure 7. (d)–(g) The corresponding tumor morphologies (φ_TC contours), as labeled. Colors online.

The nonuniform distribution of the CSC self-renewal fraction P₀ also induces an apparent migration of the tumor fragments. The tumor fragments move in a direction specified by the locations of the CSC clusters at their boundaries. In this case, the migration is due to cells proliferating primarily at the outer edge of the CSC cluster and other cells (TCs) dying and undergoing lysis in other parts of the tumor fragment.

Because of the random initial condition for C_W, the accuracy of the simulation presented in Fig. 2 cannot be tested easily using mesh refinement. However, fixing the spatial resolution (and the random initial condition) and refining the time step shows convergence of the results with those presented here being virtually indistinguishable with those obtained using smaller time steps (data not shown). Refining the spatial mesh changes the initial condition and thus the evolution. Nevertheless, using deterministic initial data, our algorithm converges as the spatial mesh is refined and the features observed here are characteristic of all the results we obtained.

4.2 Variations in feedback response

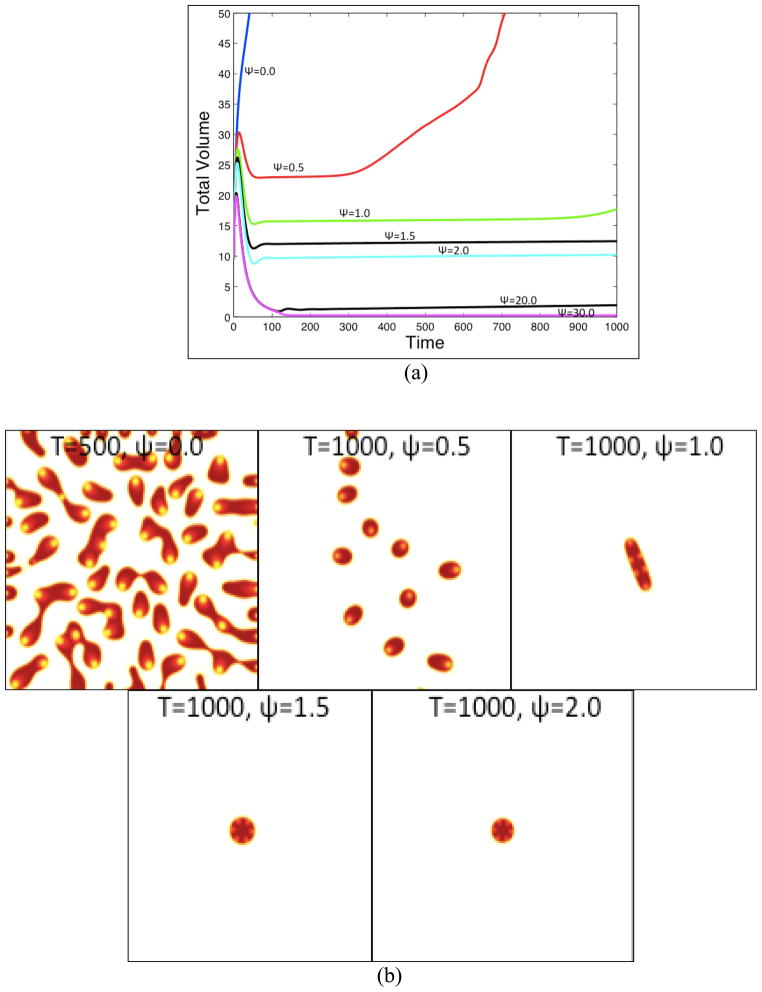
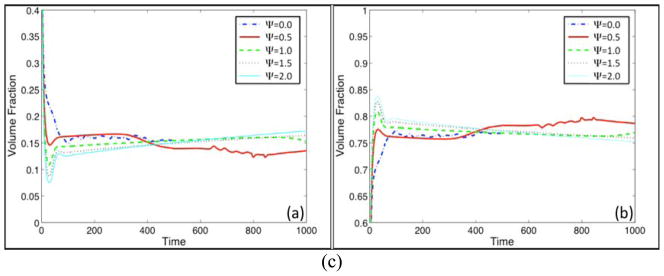
We next vary the strength of feedback response to T by varying the parameter Ψ and investigate the consequences on tumor progression. The initial conditions and all other parameters are the same as in Fig. 2. The results are presented in Fig. 5. In Fig. 5(a), the tumor volumes are plotted as a function of time for different values of Ψ as labeled while in Fig. 5(b) the corresponding tumor morphologies (contours of φ_TC) are shown at a late time as indicated. The colorscale is the same as in Fig. 2(b); all subsequent contour plots of φ_TC use this colorscale. In Fig. 5(c) the time evolutions of the total volume fractions of CSCs (left) and TCs (right) are shown.

Figure 5.

The effect of tumor response to negative feedback regulation of the cancer stem cell self-renewal fraction by T. (a) Evolution of tumor volume for the feedback strengths Ψ as indicated. (b) The corresponding tumor morphologies (contours of φ_TC) at the times indicated. (c) See next page. Colors online.

Fig. 5(c) The corresponding total volume fractions of cancer stem cells (left) and terminal cells (right). Colors online.

When Ψ=0, so that the CSCs are insensitive to negative regulation by T, the tumor grows very rapidly, forms invasive fingers and fragments thereby acquiring a very complex morphology consisting of fragments whose size is controlled by O diffusion and uptake as well as the self-renewal promoter W. As Ψ is increased, the tumor grows more slowly and has a more compact shape. Note that at early times, there is a sharp increase in the tumor size due to the proliferation and differentiation of CSCs into TCs. Then there is a sharp decrease in tumor size due to the death of TCs. Interestingly, the evolution consists of long plateaus of nearly constant tumor volume with perturbations arising at later times according to increasing levels of feedback response Ψ. These perturbations are driven by the CSC instability mechanism described above. As Ψ increases, the gradient in the self-renewal factor P₀ decreases, which results in progressively longer time intervals over which the instability develops. When Ψ=30, after a short interval of rapid growth, the feedback is sufficiently strong to drive the tumor volume fractions below the proliferation cut-off level ε/2 by strongly favoring the differentiation of CSCs to TCs which subsequently die. As a result, the tumor volume does not tend exactly to zero but remains unchanged after the cut-off is reached. When the proliferation is not cut-off (e.g, G =1), the evolution is similar although the volume continues to change.

These examples show that the negative feedback regulation of CSCs by the TCs, which release the differentiation promoter T, significantly influences both the kinetics and morphologies of the growing tumor. Although some of the cases (e.g., Ψ=1.5 or 2) appear to be steady, they are actually growing very slowly and numerical evidence suggests they become unstable at later times and grow in size. Numerical evidence (not shown) suggests that the plateau length may be an exponentially increasing function of feedback response Ψ. These results suggest that there may be a metastable steady state; this is currently under study. As shown in the Supplementary Material (Sec. S3), increasing the cell-cell adhesion parameter γ also leads to longer plateaus of nearly unchanging tumor volume after which morphological instability occurs and the volume increases concomitantly. We have not yet found evidence of the existence of stable steady states. It may be that additional features need to be included in the model to achieve stable steady states. However, it is worthwhile to note that states do not need to be truly stable to be effectively stable on an organism’s time scale.

As can be seen in Fig. 5(c), the volume fractions are somewhat insensitive to the levels of feedback response, with the volume fraction of CSCs and TCs being about 15% and 75% respectively. The remaining volume of the tumor is composed of dead cells. Observe that when Ψ = 0.5, and to a lesser extent when Ψ =1.0, there is a decrease in the volume fraction of CSCs and an increase in the volume fraction of TCs at late times due to the development of shape instability.

4.3 Perturbations of the tumor morphology

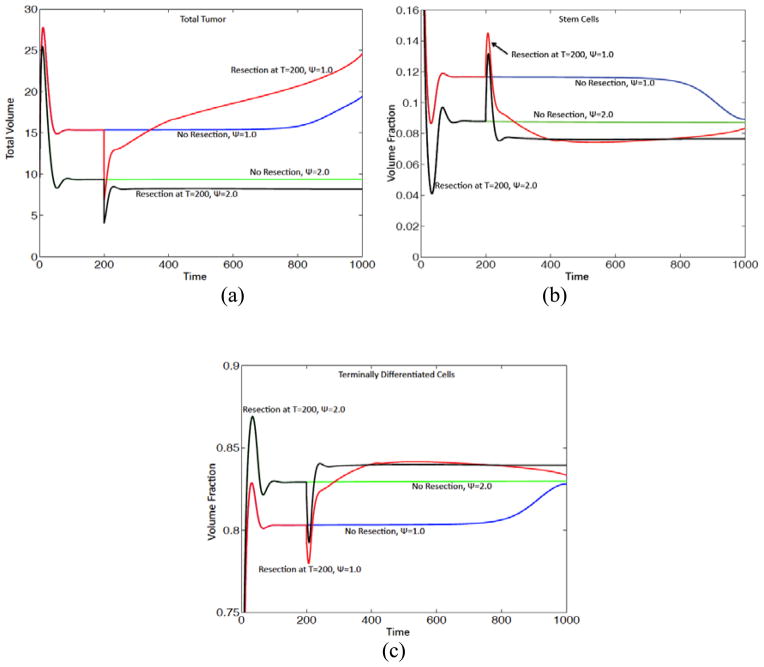
To illustrate the effect of spatial perturbations on feedback regulation of tumor progression, we study the consequences of resecting the tumor by removing one half of the tumor during the stable phase of the tumor’s progression. We note that the initial shape also has an influence on tumor progression, as shown in the Supplementary Material (Sec. S2).

We consider two levels of feedback response Ψ= 1.0 and Ψ= 2.0. Here, however, we take G =1 so that there is no cut-off in the mitosis rates. At time t =200, one half of the tumor is removed thereby disrupting the feedback processes. The evolution is continued until t =1000 and the results are shown in Fig. 6. When Ψ= 1.0, the resected tumor rapidly develops a morphological instability leading to invasive fingering and fragmentation (Fig. 6(d)). The resected tumor grows rapidly with its volume exceeding that of the unresected tumor after a relatively short time (Fig. 6(a)), indicating that the feedback regulation has been severely compromised.

Figure 6.

Progression of tumors after resection. One half of the tumors with Ψ=1 and Ψ=2 from Fig. 5 are removed at time t = 200. (a) Total volume of the resected and unresected tumors as indicated; (b) Volume fraction of cancer stem cells. (c) Volume fraction of terminal cells. (d) and (e) See next page.

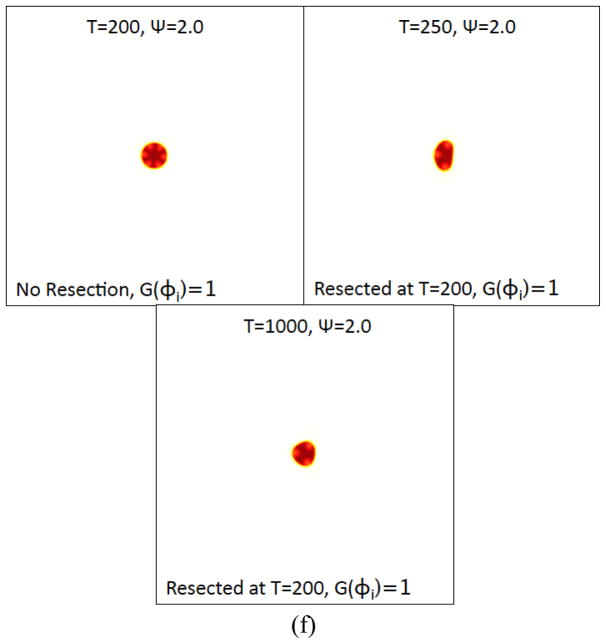
Figure 6(d) The tumor morphologies (φ_TC contours) with Ψ=1. The unresected tumor (with Ψ=1) at t=1000 is shown in (e), for comparison. (f). See next page. Colors online.

Figure 6(f). The tumor morphologies (φ_TC contours) with Ψ=2 are shown just before resection (t = 200) and after resection (t = 250 and t =1000). Colors online.

Immediately after resection, the CSC fraction of the tumor increases abruptly (Fig. 6(b)), in part due to the resection itself as more TCs are removed than CSCs due to asymmetry of stem cell clusters with respect to the resection line and in part due to the disruption of the feedback holding the CSC population in check by the removal of TCs. Correspondingly, the TC fraction decreases rapidly (Fig. 6(c)). Subsequently, as the feedback processes try to establish a new equilibrium, the CSC and TC fractions reach a maximum and minimum, respectively, shortly after t=200 and the trends reverse. The CSC fraction decreases to a level below that for the unresected tumor while the TC fraction increases to a level above that for the unresected tumor. When Ψ= 1.0, the CSC and TC fractions at long times tend toward their values for the unresected tumor. Note that due to the shape instability, the volume fraction of the CSCs in the unresected tumor deceases while that of the TCs increases, as observed earlier (e.g., Fig. 5(d)).

Interestingly, when the feedback response is stronger ( Ψ= 2.0 ), the feedback processes rapidly re-establish a new, stably progressing tumor with a different number of stem cell clusters (3) than the unresected tumor (6). The total tumor volume, and the volume fraction of CSCs, are smaller than that in the unresected tumor. These results suggest that morphological changes also have the potential to enhance feedback regulation.

Further, it would be interesting to develop and perform experiments to test the predicted correlation between signaling, growth and tumor morphology.

4.4 Therapy

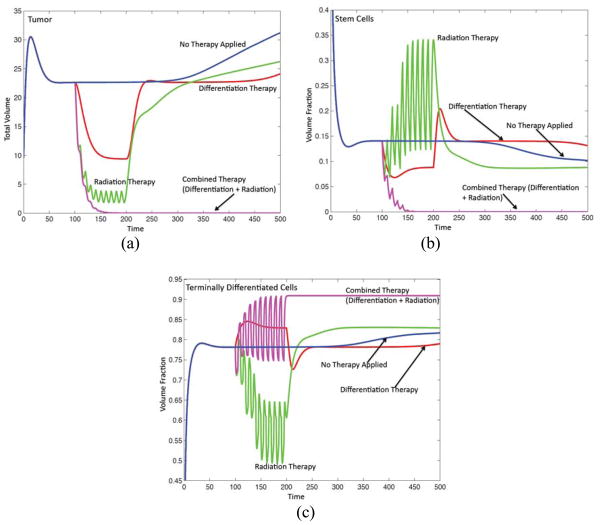
We next test the effectiveness of different therapeutic intervention methods on tumor progression. We set the cut-off function G=1 and take the feedback parameter Ψ = 0.5. All other parameters are as in Tables 1–6. Using these parameters as a base case, we then investigate the effectiveness of differentiation therapy by increasing the concentration of T, radiotherapy by cyclically increasing cell death, and a combination therapy where differentiation therapy and radiotherapy are applied together. The results are presented in Fig. 7, which shows the tumor volumes, the total volume fractions of the components and the tumor morphologies (contours of φ_TC).

At early times, the evolution of the untreated tumor is very similar to that shown in Fig. 2 where G is given by Eq. (35). At later times, the tumor with G =1 does not form new CSC clusters for this set of parameters, unlike the tumor in Fig. 2. As mentioned earlier, this is due to a lower production of W and higher production of T when G =1 since CSCs continually proliferate and differentiate even at low volume fractions. In the Supplementary Material (Sec. S4), we show that if the production of W is increased, then new CSC clusters form during the evolution even with G = 1.

To model differentiation therapy, we introduce an external source of T by changing the far-field boundary condition from the absorbing boundary condition C_T = 0 to C_T = 1. Then, T diffuses into the tumor microenvironment. To simulate radiotherapy, we use a very simple model. Namely, we introduce an additional mechanism of cell death in both the CSC and TC equations. To account for radiation-induced death due to irreparable DNA damage detected at cell cycle checkpoints, we assume that the radiation-induced death rate depends on the overall mitosis rate of the cells. Accordingly, we obtain new source terms in the CSC and TC equations:

$${\mathit{Src}}_{\mathit{CSC}}=\stackrel{\text{Self}-\text{renewal}\text{of}\text{stem}\text{cells}}{\overbrace{(2P_0-1){\varphi }_{\mathit{CSC}}{C}_O}}-\stackrel{\text{Radiation}\text{induced}\text{death}\text{during}\text{self}-\text{renewal}}{\overbrace{2P_0{C}_O{\lambda }_{\mathit{ASCT}}{\varphi }_{\mathit{CSC}}}},$$ (36)

$$\begin{array}{l}{\mathit{Src}}_{TC}=\stackrel{\text{Differentiation}\text{of}\text{stem}\text{cells}}{\overbrace{2(1-P_0){\varphi }_{\mathit{CSC}}{C}_O}}+\stackrel{\text{Mitosis}\text{of}\text{terminally}\text{differentiated}\text{cells}}{\overbrace{{\lambda }_{\mathit{MTC}}{\varphi }_{TC}{C}_O}}-\stackrel{\text{Apoptosis}}{\overbrace{{\lambda }_{\mathit{ATC}}{\varphi }_{TC}}}\\ -\stackrel{\text{Radiation}\text{induced}\text{death}\text{during}\text{differentiation}}{\overbrace{2{\lambda }_{\mathit{ATCT}}(1-P_0){\varphi }_{\mathit{CSC}}{C}_O}}-\stackrel{\text{Radiation}\text{induced}\text{death}\text{during}\text{division}\text{of}\text{TCs}}{\overbrace{2{\lambda }_{\mathit{ATCT}}{\lambda }_{\mathit{MTC}}{\varphi }_{TC}{C}_O}}.\end{array}$$ (37)

The source terms for the DCs and the volume fraction of the total tumor are also modified:

$$\begin{array}{l}{\mathit{Src}}_{DC}=\stackrel{\text{Radiation}\text{death}\text{due}\text{to}\text{self}-\text{renewal}\text{of}\text{SCs}}{\overbrace{2{\lambda }_{\mathit{ASCT}}{P}_0{C}_O{\varphi }_{\mathit{CSC}}}}+\stackrel{\text{Radiation}\text{induced}\text{death}\text{due}\text{to}\text{differentiation}\text{of}\text{SCs}}{\overbrace{2{\lambda }_{\mathit{ATCT}}(1-P_0)C_O{\varphi }_{\mathit{CSC}}}}\\ +\stackrel{\text{Radaition}\text{induced}\text{death}\text{during}\text{mitosis}\text{of}\text{TCs}}{\overbrace{2{\lambda }_{\mathit{ATCT}}{\lambda }_{\mathit{MTC}}{C}_O{\varphi }_{TC}}}+\stackrel{\text{Apoptosis}\text{of}\text{live}\text{cells}}{\overbrace{{\lambda }_{\mathit{ATC}}{\varphi }_{TC}}}-\stackrel{\text{Lysis}\text{of}\text{Dead}\text{Cells}}{\overbrace{{\lambda }_L{\varphi }_{DC}}},\end{array}$$ (38)

$${\mathit{Src}}_T=\stackrel{\text{Mitosis}\text{of}\text{stem}\text{cells}}{\overbrace{{\varphi }_{\mathit{CSC}}{C}_O}}+\stackrel{\text{Mitosis}\text{of}\text{terminal}\text{cells}}{\overbrace{{\lambda }_{\mathit{MTC}}{\varphi }_{TC}{C}_O}}-\stackrel{\text{Lysis}\text{of}\text{dead}\text{cells}}{\overbrace{{\lambda }_L{\varphi }_{DC}}}.$$ (39)

In the above equations, λ_ASCT and λ_ATCT are the radiation-induced death rates of the CSCs and TCs. Note that since the overall rates of death due to radiation damage depend on C_O, our model also accounts for the radiosensitizing role of oxygen in a simple way by reducing death rates in regions of hypoxia (e.g., Pajonk et al. 2010).

The duration of each therapy application and corresponding response is taken to be 5 time units (e.g., days) and λ_ASCT and λ_ATCT are taken to be 0.6 and 0.9, respectively (see Table 2), which models the greater sensitivity of TCs to radiation damage (e.g., Pajonk et al. 2010). After each application, λ_ASCT and λ_ATCT are reset to zero until the next application of radiotherapy is performed. The time interval between each therapy application is also taken to be 5 time units. Although clinically, radiation is applied in fractionated doses over short time intervals (e.g., ranging from a few minutes up to an hour), the damage caused by radiation may not kill the cells instantly but instead may kill cells gradually over time as DNA damage is detected at cell cycle checkpoints. Our implementation is thus a simple model of this temporally delayed response. Even though cells continue to proliferate throughout the therapy applications, regrowth is most apparent during the intervals between therapy applications. We note that other, more sophisticated models of radiotherapy, such as the linear-quadratic (LQ) model (e.g., Douglas and Fowler 1975; Dale 1985; Brenner et al. 1998; Powathil et al. 2007; Rockne et al. 2010; Enderling et al. 2009b, 2010; Schnieder et al. 2011) have been previously used and fitted to specific experimental data. In future work, we will consider versions of the LQ model appropriate for cell lineages. We expect that the results will be qualitatively similar to those presented here.

Table 2.

Nondimensional mitosis, apoptosis, necrosis, and lysis rates

Mitosis rate of terminally differentiated cells	λMTC= 0.1
Apoptosis rate of terminally differentiated cells	λATC= 0.1
Lysis rate of dead cells	λL= 1.0
Apoptosis rate of stem cells during radiotherapy	λASCT= 0.6
Apoptosis rate of terminally differentiated cells during radiotherapy	λATCT = 0.9

In our model, at time t =100, the differentiation therapy, radiotherapy and combined therapies are started. In particular, the tumor is treated by performing ten applications of radiotherapy. Differentiation therapy is applied continuously. The therapies are stopped at t = 200. That is, at time t = 200, λ_ASCT and λ_ATCT are reset to 0 and the T boundary condition is reset to C_T = 0.

In Fig. 7(a), the corresponding tumor volumes are shown as a function of time. Results are shown for the untreated tumor (blue curve; color online), a tumor treated using only radiotherapy (green curve; color online), only differentiation therapy (red curve; color online) and the tumor treated using the combination therapy (purple curve; color online). Observe that the treatment solely using radiotherapy or differentiation therapy is ineffective for this set of parameters. In particular, when radiotherapy is applied, the feedback mechanisms are disrupted and the tumor fragments and grows back more aggressively than that treated using differentiation promoters solely. The simulation results show that after each session of therapy, the tumor volume is reduced by about 50%. At the end of all the radiotherapy cycles, the tumor volume is reduced from its pretreatment value by about 80%. These data lie within biological range reported from clinical studies (e.g., Pajonk et al. 2010). Note that oscillations are present in the tumor volume as cells repopulate the tumor cyclically during the intervals between radiotherapy applications. When differentiation therapy is applied solely, the tumor quickly regresses. The tumor volume decreases and reaches a short plateau (around t =150) where the volume changes slowly as the system tries to equilibrate. Once the differentiation therapy is discontinued, the tumor rapidly grows back to its pretreatment levels and the subsequent progression is similar to the untreated tumor, but shifted in time roughly by the therapy duration.

On the other hand, when the radiation and differentiation therapies are applied together, the tumor rapidly dies out as the differentiation therapy drives the CSCs to differentiate and the radiotherapy rapidly kills the newly formed TCs. In particular, at t = 200 after the last therapy application, the CSC volume is approximately 10⁻¹⁰, while the TCs and DCs have volumes 10⁻³ and 10⁻⁴ respectively. Because the volume of CSCs is so low, the production of W and hence the self-renewal fraction P₀ are correspondingly low as well. This indicates that the CSC niche environment has been severely disrupted. As a result, the remaining CSCs differentiate into TCs and without any additional treatment, the CSC volume at t = 1000 reaches 0, while the volumes of the TCs and DCs are 10⁻⁴ and 10⁻⁵ respectively.

The volume fractions of the CSCs and TCs are shown in Figs. 7(b) and (c). Consistent with experimental and clinical data (e.g., Pajonk et al. 2010), the radiotherapy cycles result in a cyclical increase in the maximum CSC fraction. This is due in part to the fact that the CSCs are more resistant to radiation than the TCs and in part due to the fact that as TCs are killed, the levels of T are lowered and thus there is less feedback control on the self-renewal of CSCs further enabling their numbers to increase.

Differentiation therapy, on the other hand, causes the CSC fraction to decrease initially and then rebound to a nearly steady value (around 0.075) until the therapy is discontinued. Once the differentiation therapy is stopped, there is a spike in the CSC fraction as the CSCs rapidly self-renew in response to the ensuing deregulation. Shortly thereafter, the CSC fraction returns to its pre-treatment value as the feedback regulation between TC-produced T and CSCs is re-established. As noted earlier, the decrease in CSC fraction at later times is associated with the development of tumor morphological instability. In contrast, under combination therapy, the CSC fraction decreases very rapidly in an oscillatory manner, eventually becoming zero.

The TC volume fractions under the differentiation and combination therapies tend to increase during treatment, reflecting the increased tendency of CSCs to differentiate into TCs. In contrast, when radiotherapy is applied solely, the TC fraction tends to decrease reflecting the increased sensitivity of TCs to radiation while the CSC fraction increases. When the separate radiation and differentiation therapies are discontinued, the CSC and TC fractions tend to behave oppositely of one another: one population rapidly increases and the other decreases as the system tries to equilibrate under feedback regulation. When the combination therapy is applied, the CSC fraction tends to zero while the TC fraction tends to a constant, which reflects a balance between the proliferation and death of TCs and the lysing of dead cells.

The corresponding tumor morphologies (contours of φ_TC ) are shown in Figs. 7(d)–(g). While all the tumors receiving therapy shrink as the therapies are applied, observe that when radiotherapy is applied solely (Fig. 7(f)), the number of CSC clusters changes due to spatiotemporal variations in the production of W and WI induced by the changing tumor domain and the increasing fraction of CSCs. This results in a fingering instability once radiotherapy is discontinued, which is clearly driven by the CSC clusters. In contrast, the number of CSC clusters in the tumors undergoing treatment with the differentiation and combination therapies remains unchanged (Figs. 7(e) and (g)) while those therapies are applied. In the case of differentiation therapy, the CSC-driven instability that occurs after the therapy is discontinued is milder than that which occurs after radiotherapy and follows that of the untreated tumors (shifted in time). In the case of the combination therapy, the tumor simply shrinks to a vanishingly small size roughly as a circle.

To summarize, these results suggest that it is possible to combine two ineffective therapy protocols involving radiation treatment and differentiation therapy, which act on cells in different lineage stages, to obtain a highly effective therapeutic strategy to eradicate the tumor. It would be particularly useful to design an experiment to test these model predictions.

4.5 The progression of a 3D tumor

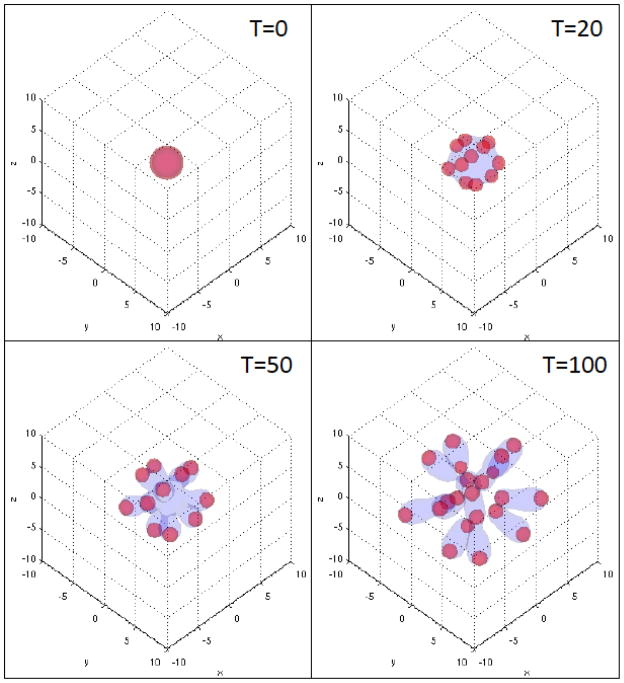
The model, and numerical method, extend straightforwardly to three dimensions, and here we study the progression of a 3D tumor with feedback parameter Ψ=0.5. All other parameters for this case are given in Tables 1–6, and G is given by Eq. (35). The initial condition is a sphere of radius $\sqrt{3}$, constructed using a straightforward extension of Eq. (32) to three dimensions. The initial sphere consists entirely of CSCs.

The resulting tumor morphologies are shown in Fig. 8. In that figure, the φ_T=0.5 isosurface (grey; color online) is shown together with the φ_CSC= 0.3 isosurface (red; color online). The evolution is qualitatively similar to that observed in two dimensions. CSC clusters form and are localized at the tumor boundary and in particular at the tips of the invading fingers. As in 2D, there is a gradient in the self-renewal fraction P₀ that drives a fingering instability and new CSC clusters form in response to the spatiotemporal reorganization of W and WI, which creates new regions of large P₀. Work is ongoing to determine the sensitivity of the progression and instability to the feedback strength Ψ with all indications suggesting that the behavior is qualitatively similar to that presented earlier in two dimensions.

Figure 8.

The development of cancer stem cell-driven invasive fingers in a 3D tumor under the effects of feedback signaling at the times indicated. The φ_T=0.5 (grey; color online) and φ_CSC=0.3 (red; color online) isosurfaces are shown at the indicated times.

5. Summary

In this paper we have developed and simulated a multispecies continuum model of the dynamics of cell lineages in solid tumors. We have also suggested a number of experiments that could be performed to test the model predictions. The model accounted for spatiotemporally varying cell proliferation and death mediated by the heterogeneous distribution of oxygen and factors with varying solubilities that regulated the self-renewal and differentiation of the different cells within the lineages. Terminally differentiated cells produced feedback factors T (e.g., from the TGFβ superfamily) that promoted differentiation of stem cells and provided negative feedback regulation of self-renewal fractions. In addition, stem cells produced a short-range positive feedback factor W (e.g., representative of Wnt signaling factors) that promoted self-renewal, as well as a long-range inhibitor of this factor WI (e.g., representative of Wnt inhibitors such as Dkk and SFRPs). The model is applicable to in vitro tumors and to avascular in vivo tumors in a quiescent host environment. The model predicts the development of spatiotemporal heterogeneous feedback signaling and tumor cell distributions where clusters of stem cells appeared at the boundary of sufficiently large tumor spheroids—a finding that was confirmed by recent experiments.

We found that the progression of the tumors and their response to treatment was controlled by the spatiotemporal dynamics of the signaling processes. In particular, the tumor dynamics were observed to develop long plateaus over which the tumor volumes and shapes showed little variation. The plateaus were then followed by rapid tumor growth driven by morphological instability and invasive fingering. This is suggestive that a metastable steady state may exist.

Feedback processes were found to play a critical role in tumor progression, plateau length, and the development of morphological instability and invasive fingers. Increasing the feedback response to T decreases tumor growth rates and enhances morphological stability. Perturbing the shape of a stable tumor was found to upset the balance of feedback factors and could lead to unstable and much more aggressive growth than if the tumor was unperturbed. Alternatively, perturbations in the presence of strong feedback response can also lead to tumor shrinkage.

Qualitatively, these results are similar to those obtained by Enderling et al. (2009a, 2009b, 2009c, 2010) and Sottoriva et al. (2010a, 2010b), who observed instability in cellular automaton models of tumor clusters with stem and non-stem cells. In the cellular automaton models, negative feedback on cell proliferation and movement occurs through the competition for space and other resources. In these models, increasing non-stem cell death rates, or stem cell motilities, effectively reduces the negative feedback (see also Hillen et al. 2011) and results in increased tumor instability and invasiveness. This is consistent with what we observed here where in our case the negative feedback influences the self-renewal fractions and comes from T. Together, these suggest that the results of modeling such feedback are generic—i.e. they do not depend on the type of molecule or mechanism that implements feedback, which is particularly important since signaling processes and feedback mechanisms are typically tissue-dependent and arise from the different performance objectives of the tissues. Thus, the type of modeling described here should also be relevant to feedback processes in many tissues and tumor types through, for example, Notch, BMP, Shh, FGF mediated signaling, stress response signaling, mechanotransduction, and contact inhibition. In many cases, however, the signaling and feedback processes are not known and more detailed experiments are needed to elucidate signaling and control mechanisms. Here, the model can help identify signaling and feedback control pathways by predicting characteristic outcomes. This will be further investigated in future work.

The distributions of the cell populations obtained from the cellular automata models of Enderling et al. and Sottoriva et al. and our multispecies model are different, however. In the cellular automaton models, the CSCs tend to be located either at the center of small tumor clusters or are distributed relatively uniformly throughout the viable rim of cells. Some CSCs may migrate past the tumor boundary and generate new tumor clusters that may join the primary cluster, helping to create an irregular boundary, or may simply grow on their own. In our work, we observe that the CSCs tend to be located at the boundary of sufficiently large tumor spheroids, consistent with recent experiments. For smaller spheroids, the CSCs may be more uniformly distributed throughout the region of viable cells. This is due to the cell signaling model implemented here, where self-renewal fractions are regulated by feedback factors produced by the different cells in the lineage.

We note that using an agent-based model, Galle et al. (2009) also found that cells with the highest degree of stemness tended to reside at the tumor/host interface, however in their model, Galle et al. assumed that the stroma provides a stem cell niche and thus nearness to the stroma is assumed to enable cells to acquire stem cell properties, which is different from the signaling model implemented here.

1. We found that the development of morphological instability during tumor progression was driven by an asymmetry between the spatiotemporally varying W, the self-renewal fraction P₀ and the CSC clusters. In particular, the maxima in W and P₀ were located off the center of the CSC clusters leading to larger self-renewal fraction on one side of the cluster (closest to the tumor boundary) than the other. This led to the development of invasive fingers. While this was shown to be a consequence of O-dependent production of W and WI, other mechanisms are also capable of generating asymmetry and morphological instabilities during growth. For example, asymmetry can be generated by varying the decay/uptake rate of WI such that the decay/uptake rate is larger inside the tumor than outside (not shown). This models the case in which the viable tumor cells uptake significant amounts of WI. Alternatively, asymmetry and instability may also be introduced by decreasing the diffusion coefficient of T, or by increasing its uptake/decay rates, such that the effect of T is more localized. Asymmetries can also be generated by stochastic effects, which we will investigate in a future work. Interestingly, this asymmetric self-renewal mechanism provides a new pathway for tumor invasion that is complementary to stem cell motility-driven instabilities and diffusional instabilities that arise from limited nutrient supply (e.g., Cristini et al. 2003).

Therapeutic intervention by increasing the amount of T in the system may arrest the growth of the tumor. If the amount of T is sufficient to reduce the self-renewal fraction P₀ to become less than one-half then, after a sufficient period of time, the tumor will extinguish itself. However, the time and amount of T needed for this is tumor-dependent and generally not known a priori. Here, we demonstrated that a single application of differentiation therapy of insufficient duration and strength leads to rapid repopulation of the tumor, led by the remaining CSCs that self-renew at a high rate as soon as the therapy is stopped and feedback control can be re-established.

Radiotherapy, which was stopped before all the CSCs were eradicated, was also seen to result in a rapid repopulation of the tumor and a dramatic increase of aggressiveness compared to an untreated tumor—a result also found by Enderling et al. (2009b) and observed in experiments (Pajonk et al. 2010).

We found that a more effective strategy for therapy combines differentiation therapy that targets CSCs (and CPs) with a traditional therapy, such as radiotherapy, that more selectively targets TCs. In particular, by targeting cells in different lineage stages, we find that combining these therapies is particularly effective in eradicating the tumor.

Implementing differentiation therapy via T may have some drawbacks, however, since it is known that some TGFβ members may also promote tumor invasiveness under certain circumstances (e.g., Watabe 2009; Meulmeester and ten Dijke 2011). Other approaches could be used to induce CSC differentiation that should have a similar effect as observed here. These include disrupting Wnt or other signaling pathways such as Notch, Shh, and BMP.

Table 5.

Nondimensional parameters for O

Uptake rate by terminal cells	νUOTC = 1.0
Production rate	νPO = 0.5

Highlights.

• A model of spatiotemporal dynamics of cell lineages in solid tumors is developed.

• Soluble factors regulate cell proliferation, self-renewal and differentiation.

• Spatiotemporal heterogeneous distributions of cells and factors develop.

• Clusters of stem cells appear at the tumor boundary, consistent with experiments.

• Combining differentiation and radiation therapies is a very effective strategy.

Appendix. Nondimensionalization

Following Cristini et al. (2003), we nondimensionalize the equations using the oxygen diffusion length scale $l=\sqrt{D_O/{\nu }_{\mathit{UOSC}}}$ and the mitosis time scale τ = (λ_MSC C̄_AO)⁻¹. The O concentration is measured against that in the blood, or medium for in vitro tumors, and is thus nondimensionalized as $C_O^{\prime }=C_O/{\overline{C}}_{AO}$. The velocity and pressure are nondimensionalized as ${\mathbf{u}}_s^{\prime }={\mathbf{u}}_s/(l/\tau )$ and p′ = p/(l₂/(τκ̄)), where κ̄ is a characteristic value of the cell motility. Further, we nondimensionalize the feedback factors as $C_T^{\prime }=C_T/{\overline{C}}_T$ where C̄_T is a characteristic concentration of T (note that we alternatively could have used ν_PT to nondimensionalize C_T), $C_W^{\prime }=C_W/{\overline{C}}_W$ and $C_{WI}^{\prime }=C_{WI}/{\overline{C}}_{WI}$, with C̄_W = ν_PW/ν_PWI and ${\overline{C}}_{WI}={\nu }_{PW}^2{\overline{C}}_{AO}/({\nu }_{\mathit{PWI}}{\nu }_{DW})$ being intrinsic W and WI concentrations.

Accordingly, the nondimensional system of equations is given by

$$\frac{\partial {\phi }_{\mathit{CSC}}}{\partial t^{\prime }}=M^{\prime }{\nabla }^{\prime }·({\phi }_{\mathit{CSC}}{\nabla }^{\prime }{\mu }^{\prime })+{\mathit{Src}}_{\mathit{CSC}}^{\prime }-{\nabla }^{\prime }·({\mathbf{u}}_s^{\prime }{\phi }_{\mathit{CSC}}),$$ (A1)

$$\frac{\partial {\phi }_{TC}}{\partial t^{\prime }}=M^{\prime }{\nabla }^{\prime }·({\phi }_{TC}{\nabla }^{\prime }{\mu }^{\prime })+{\mathit{Src}}_{TC}^{\prime }-{\nabla }^{\prime }·({\mathbf{u}}_s^{\prime }{\phi }_{TC}),$$ (A2)

$$\frac{\partial {\phi }_{DC}}{\partial t^{\prime }}=M^{\prime }{\nabla }^{\prime }·({\phi }_{DC}{\nabla }^{\prime }{\mu }^{\prime })+{\mathit{Src}}_{DC}^{\prime }-{\nabla }^{\prime }·({\mathbf{u}}_s^{\prime }{\phi }_{DC}),$$ (A3)

where M′= τ/τ_M, and τ_M = l²ε/(Mγ) is the time scale associated with the mobility. The nondimensional velocity is

$${\mathbf{u}}_s^{\prime }=-{\kappa }^{\prime }\left({\nabla }^{\prime }{p}^{\prime }-\frac{{\gamma }^{\prime }}{{\epsilon }^{\prime }}{\mu }^{\prime }{\nabla }^{\prime }{\phi }_T\right),$$ (A4)

where κ′ = κ/κ̄, ε′ = ε/l and γ′ = τ/τ_R with τ_R = l³ (γκ̄) the relaxation time scale associated with the combined effects of cell-cell, cell-ECM adhesion. The nondimensional chemical potential is ${\mu }^{\prime }=\frac{\partial F}{\partial {\phi }_T}({\phi }_T)-{{\epsilon }^{\prime }}^2{{\nabla }^{\prime }}^2{\phi }_T$. The velocity further satisfies the equation:

$${\nabla }^{\prime }·{\mathbf{u}}_s^{\prime }={\phi }_{\mathit{CSC}}{C}_O^{\prime }G({\phi }_{\mathit{CSC}})+{\lambda }_{\mathit{MTC}}^{\prime }{\phi }_{TC}{C}_O^{\prime }G({\phi }_{TC})-{\lambda }_L^{\prime }{\phi }_{DC},$$ (A5)

which is used to solve for the pressure.

Neglecting necrosis and the apoptosis of CSCs, the nondimensional source terms are

$${\mathit{Src}}_{\mathit{CSC}}^{\prime }=(2P_0^{\prime }-1){\phi }_{\mathit{CSC}}{C}_O^{\prime }G({\phi }_{\mathit{CSC}}),$$ (A6)

$${\mathit{Src}}_{TC}^{\prime }=2(1-P_0^{\prime }){\phi }_{\mathit{CSC}}{C}_O^{\prime }G({\phi }_{\mathit{CSC}})+{\lambda }_{\mathit{MTC}}^{\prime }{\phi }_{TC}{C}_O^{\prime }G({\phi }_{TC})-{\lambda }_{\mathit{ATC}}^{\prime }{\phi }_{TC},$$ (A7)

$${\mathit{Src}}_{DC}^{\prime }={\lambda }_{\mathit{ATC}}^{\prime }{\phi }_{TC}-{\lambda }_L^{\prime }{\phi }_{DC},$$ (A8)

where $P_0^{\prime }=P_{\mathit{Min}}+(P_{\mathit{Max}}-P_{\mathit{Min}})\left(\frac{{\xi }^{\prime }{C}_W^{\prime }}{1+{\xi }^{\prime }{C}_W^{\prime }}\right)\left(\frac{1}{1+{\mathrm{\Psi }}^{\prime }{C}_T^{\prime }}\right)$, ξ′ = ξ C̄_W and Ψ′ = ΨC̄_T. The nondimensional rates of mitosis and apoptosis of TCs are ${\lambda }_{\mathit{MTC}}^{\prime }=\tau /{\tau }_{\mathit{MTC}}$, and ${\lambda }_{\mathit{ATC}}^{\prime }=\tau /{\tau }_{\mathit{ATC}}$ where τ_MTC = 1/(λ_MTC C̄_AO) and τ_ATC = 1/λ_ATC are the characteristic time scales for mitosis and apoptosis of TCs respectively. The nondimensional lysis rate is ${\lambda }_L^{\prime }=\tau ·{\lambda }_L$, which is the ratio of the mitosis and lysis time scales.

The nondimensional equation for O is

$$0={{\nabla }^{\prime }}^2{C}_O^{\prime }-C_O^{\prime }({\phi }_{\mathit{CSC}}+{\nu }_{\mathit{UOTC}}^{\prime }{\phi }_{TC})+{\nu }_{PO}^{\prime }(1-C_O^{\prime })Q({\phi }_T),$$ (A9)

where the nondimensional uptake and transfer rates are ${\nu }_{\mathit{UOTC}}^{\prime }={\nu }_{\mathit{UOTC}}/{\nu }_{\mathit{UOSC}}$ and ${\nu }_{PO}^{\prime }={\nu }_{PO}/{\nu }_{\mathit{UOSC}}$. The nondimensional equation for T is

$$0={{\nabla }^{\prime }}^2{C}_T^{\prime }-({\nu }_{UT}^{\prime }{\phi }_{\mathit{CSC}}+{\nu }_{DT}^{\prime })C_T^{\prime }+{\nu }_{PT}^{\prime }{\phi }_{TC},$$ (A10)

where ${\nu }_{UT}^{\prime }={\tau }_T·{\nu }_{UT},{\nu }_{DT}^{\prime }={\tau }_T·{\nu }_{DT},{\nu }_{PT}^{\prime }={\tau }_T·{\nu }_{PT}$ and τ_T= l²/D_T is the time scale associated with diffusion of T.

The nondimensional equations for W and WI are

$$\frac{\partial C_W^{\prime }}{\partial t^{\prime }}+\nabla ·({\mathbf{u}}_s^{\prime }{C}_W)=D_W^{\prime }{{\nabla }^{\prime }}^2{C}_W+R\stackrel{\sim }{f}(C_W^{\prime },C_{WI}^{\prime }),$$ (A11)

$$\frac{\partial C_{WI}^{\prime }}{\partial t^{\prime }}+\nabla ·({\mathbf{u}}_s^{\prime }{C}_{WI})=D_{WI}^{\prime }{{\nabla }^{\prime }}^2{C}_{WI}^{\prime }+R\stackrel{\sim }{g}(C_W^{\prime },C_{WI}^{\prime }),$$ (A12)

where $D_W^{\prime }=\tau /{\tau }_W,D_{WI}^{\prime }=\tau /{\tau }_{WI}$ and τ_W= l²/D_W, τ_WI= l²/D_WI are the time scales associated with diffusion of the self-renewal promoter and its inhibitor. Further, R = τ · ν_DW is the ratio of the mitosis time scale and the time scale for the natural decay of W. Finally,

$$\stackrel{\sim }{f}(C_W^{\prime },C_{WI}^{\prime })=\frac{C_W^{\prime 2}}{C_{WI}^{\prime }}{C}_O^{\prime }{\phi }_{\mathit{CSC}}-C_W^{\prime }+u_0^{\prime }{C}_O^{\prime }({\phi }_T-{\phi }_{DC}),$$ (A13)

$$\stackrel{\sim }{g}(C_W^{\prime },C_{WI}^{\prime })=C_W^{\prime 2}{C}_O^{\prime }{\phi }_{\mathit{CSC}}-{\nu }_{\mathit{DWI}}^{\prime }{C}_{WI},$$ (A32)

where $u_0^{\prime }=u_0{\overline{C}}_{AO}/({\overline{C}}_W{\nu }_{DW})$ and ${\nu }_{\mathit{DWI}}^{\prime }={\nu }_{\mathit{DWI}}/{\nu }_{DW}$. Dropping the prime (and tilde) notation yields the equations given in Sec. 3.