Traveling Waves on the Organ of Corti of the Chinchilla Cochlea: Spatial Trajectories of Inner Hair Cell Depolarization Inferred from Responses of Auditory-Nerve Fibers

Abstract

Spatial magnitude and phase profiles for inner hair cell (IHC) depolarization throughout the chinchilla cochlea were inferred from responses of auditory-nerve fibers (ANFs) to threshold- and moderate-level tones and tone complexes. Firing-rate profiles for frequencies ≤2 kHz are bimodal, with the major peak at the characteristic place and a secondary peak at 3–5 mm from the extreme base. Response-phase trajectories are synchronous with peak outward stapes displacement at the extreme cochlear base and accumulate 1.5 period lags at the characteristic places. High-frequency phase trajectories are very similar to the trajectories of basilar-membrane peak velocity toward scala tympani. Low-frequency phase trajectories undergo a polarity flip in a region, 6.5–9 mm from the cochlear base, where traveling-wave phase velocity attains a local minimum and a local maximum and where the onset latencies of near-threshold impulse responses computed from responses to near-threshold white noise exhibit a local minimum. That region is the same where frequency-threshold tuning curves of ANFs undergo a shape transition. Since depolarization of IHCs presumably indicates the mechanical stimulus to their stereocilia, the present results suggest that distinct low-frequency forward waves of organ of Corti vibration are launched simultaneously at the extreme base of the cochlea and at the 6.5–9 mm transition region, from where antiphasic reflections arise.

Introduction

Hearing in mammals begins when vibrations of the middle-ear ossicles or the skull introduce acoustic waves into the fluids of the cochlea, which in turn generate displacement waves that travel on the basilar membrane (BM), the organ of Corti, and the tectorial membrane (TM). Those waves deflect the stereocilia of IHCs, depolarizing them and causing excitation of ANFs (Robles and Ruggero, 2001). Cochlear waves are thought to travel from base to apex with decreasing speed and initially increasing amplitudes, reaching amplitude maxima and stopping nearby at sites laid out tonotopically, with high- and low-frequency waves peaking, respectively, near the base and apex (von Békésy, 1947; Lighthill, 1981). The increasing phase lag of vibrations as a function of distance, the key feature of traveling waves, has been directly observed in short stretches of the BM or TM in a few species (von Békésy, 1947; Rhode, 1971; Cooper and Rhode, 1996; Russell and Nilsen, 1997; Rhode and Recio, 2000; Ren, 2002). Vibrations of the organ of Corti, arguably of even greater interest than those of the BM because they are the mechanical input for transduction in IHC stereocilia, have been recorded at isolated spots of the cochlea (Chen et al., 2011; Ren and He, 2011) but seldom directly observed as a function of distance (Cooper and Rhode, 1996). Here we describe the spatial trajectories of IHC-depolarization phases, normalized to middle-ear motion and calibrated against BM vibrations at the base of the cochlea, inferred from large populations of ANF responses to tones and to tone complexes recorded in many chinchillas. Since depolarization of IHCs indicates the mechanical stimulus to their stereocilia, the present results suggest that, contrary to the classical description of cochlear traveling waves, distinct forward mechanical waves are launched simultaneously at the extreme base of the cochlea and at the 6.5–9 mm transition region, from where antiphasic reflections arise.

Materials and Methods

ANF recordings were obtained in deeply anesthetized male chinchillas, using conventional methods fully described previously (Temchin et al., 2008; Temchin and Ruggero, 2010) and approved by the Animal Use and Care Committee of Northwestern University. Phase-frequency curves for ANF responses to tones presented at 70 dB sound pressure level (SPL) were measured from 434 ANFs in 63 chinchillas. Average rates (see Fig. 5) were computed from the same population within 1/6-oct characteristic frequency (CF) bands and then smoothed using three-point averaging. Average phase trajectories (see Figs. 2, 5) were drawn according to the following procedure. First, phase means were computed. If the SD from the mean was <0.25 period, the mean phase was considered unambiguous (see Fig. 2, thick red traces; Fig. 5B–D, open black symbols). In the case of SDs ≥0.25 period, phases with values higher and lower than the overall mean were averaged separately and two traces were drawn (see Fig. 2, thin red lines; Fig. 5B–D, black lines without symbols). Phase-frequency curves for frequencies >2 kHz were measured from 65 ANFs in 17 chinchillas by anchoring the phases of responses to tone complexes (“zwuis stimuli”) (van der Heijden and Joris, 2003), which do not yield absolute phases, with the phase of responses to tones with frequency <2 kHz (van der Heijden and Joris, 2005; Cai et al., 2009). The computation of second-order Wiener kernels from ANF responses to white noise (303 ANFs from 40 chinchillas) has also been fully described (Recio-Spinoso et al., 2005; Temchin et al., 2005). Latencies (see Fig. 4) are those of the (2D) first-rank vectors obtained by singular value decomposition of the second-order kernels, which are 3D objects (Recio-Spinoso et al., 2005). IHC phases were derived from ANF responses by subtracting at each frequency a phase equivalent to 0.96 ms, the estimated sum of CF-independent neural and synaptic delays (Ruggero and Rich, 1987). Local phase velocities of BM or IHC stereociliar vibration were computed from phase-frequency curves for two flanking cochlear sites. At any given frequency the phase delay (expressed in periods) divided by the distance between the two sites (expressed in millimeters) yields the wave number (with units of mm⁻¹). Frequency (in kilohertz) divided by the wave number yields a local phase velocity (meters per second) (Lighthill, 1981) corresponding to a position with CF equal to the geometric mean of the CFs of the flanking sites. The dotted traces of Figure 3, local phase velocities for single frequencies, were computed using wave numbers obtained by computing the negative slopes of the phase versus distance curves of Figure 2. Distances were determined from the CFs using the chinchilla cochlear map of (Müller et al., 2010).

Figure 5.

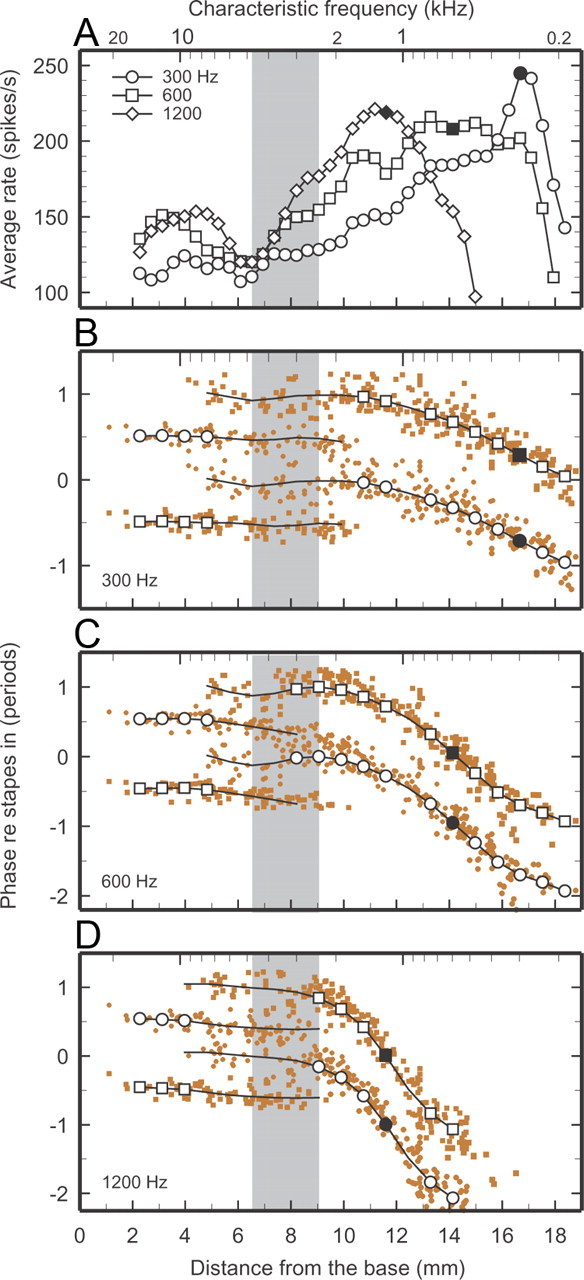
Spatial profiles of average rates and phases of ANF responses to tones. Color symbols in B–D indicate depolarization phases of individual IHCs inferred from ANF responses to tones presented at 70 dB SPL. Symbols for 300-, 600-, and 1200-Hz tones represent responses to 369, 394, and 318 ANFs, respectively, recorded from 54, 47, and 44 chinchillas. A, Connected black symbols indicate average rates computed over nonoverlapping sixth-octave CF bands and subjected to three-point smoothing. B, Black traces indicate average phase trajectories; open black symbols identify third-octave CF bands in which trajectories are unambiguous. (See Materials and Methods for the criterion used to define phase ambiguity and for the computation of single or double trajectories.) Filled black symbols indicate rates (A) and phases (B) at the characteristic places. Data from the same population of ANFs represented in Figures 1 and 2. Gray bands mark the region where ANF tuning curves change their shape (Fig. 1), IHC responses change their polarity (Fig. 2), traveling wave velocities attain a local maximum (Fig. 3), and latencies of near-threshold IHC impulse responses exhibit a local minimum (Fig. 4).

Figure 2.

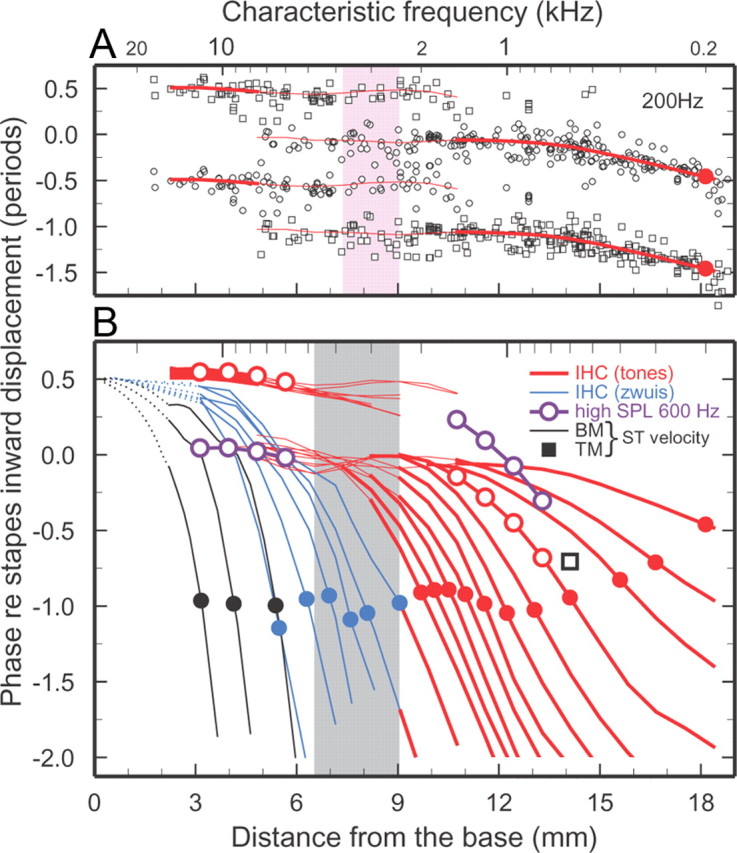
Phase-place curves for BM and TM vibrations and IHC depolarization in the chinchilla cochlea. A, Open symbols indicate average phases of IHC depolarization, inferred from responses of 346 ANFs, for stimulation with 200-Hz tones presented at 70 dB SPL. Each data point is plotted twice as a circle and a square separated by one period. The traces indicate central trends, computed over 1/3-octave bands, which are also plotted in B. The thick traces indicate regions in which response phases are clustered unambiguously around a single trajectory. Thin traces indicate regions in which phases are clustered around parallel tracks with dual polarities. (See Materials and Methods for the procedure followed in determining phase ambiguity and for computing single or double trajectories.) The solid red circles indicate phase at the 200-Hz characteristic place. The area shaded in pink corresponds to the region where responses to 200-Hz tones presented at threshold flip their polarity [Ruggero and Rich (1987), their Fig. 4]. B, Each curve represents the variation of phase with distance for a single frequency, relative to peak inward displacement of the stapes. BM peak velocity toward scala tympani: black traces. IHC-depolarization phases were inferred from ANF responses to tones presented at 70 dB SPL (red; 200, 300, and 400–2000 Hz, every 200 Hz), 600-Hz tones (violet) presented at 90–100 and 100–110 dB SPL at apical and basal regions, respectively [Ruggero et al. (1996), their Figs. 3, 7], and from near-threshold tone complexes (blue). IHC phases were determined by correcting ANF phases for 0.96 ms neural/synaptic delays. For responses to tones, averages were computed for nonoverlapping 1/3-octave CF bands. To avoid clutter, the corresponding phases are represented solely as red traces except for two ranges where open red circles indicate responses to tones presented at 70 dB SPL and open violet circles indicate responses to tones presented at 90–100 and 100–110 dB SPL. Solid circles indicate phases at the characteristic places. Black square: average phase of peak velocity toward scala tympani for TM responses to 600-Hz tones at sites with corresponding CFs in two cochleae (Rhode and Cooper, 1996). Cochlear distance corresponds to the map of Müller et al. (2010). Gray band marks the region where ANF tuning curves change their shape [Temchin et al. (2008), their Fig. 7B]. IHC phase data derived from the same ANF populations represented in Figure 1.

Figure 4.

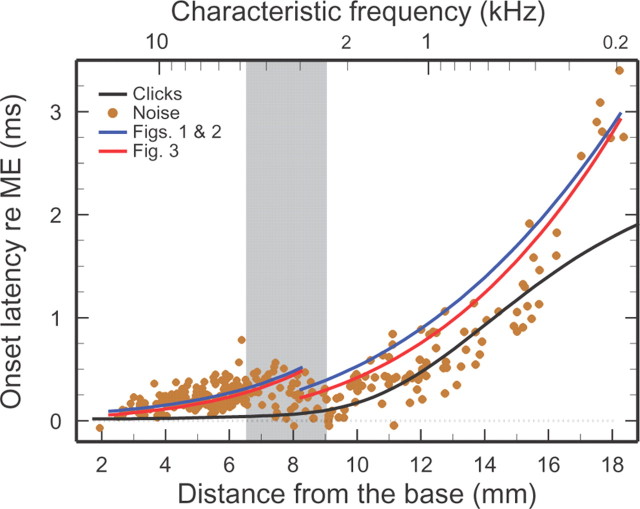
Onset latencies of IHC impulse responses plotted against cochlear place. Onset latencies of IHC depolarization (filled color symbols) were estimated from the time-domain onsets of Wiener kernels for ANF responses to low-level white noise, which resemble impulse responses but are dominated by frequencies near CF. The black trace indicates the signal-front delay, i.e., the onset latency of BM responses to intense clicks [Temchin et al. (2005), their Fig. 13A]. The Wiener-kernel latencies are longer than signal-front delays because the latter include spectral components that travel at higher speeds than near-CF frequencies (“frequency dispersion”). Onset latencies of IHC depolarization were also estimated from the CF phases of Figures 1 and 2 (blue traces) and by spatial integration of the velocity curves of Figure 3 between 0 mm and the characteristic places (red traces). In the basal region, the latencies measured by the two procedures fully coincided. Therefore, for the sake of display clarity, the red trace was displaced downward by 25 μs. All latencies have been corrected for neural/synaptic (0.96 ms) and middle-ear delays. Gray band marks the region where ANF tuning curves change their shape, IHC responses change their polarity (Fig. 2), and traveling wave velocities attain a local maximum (Fig. 3). Wiener-kernel data recorded from 303 ANFs in 40 chinchillas.

Figure 3.

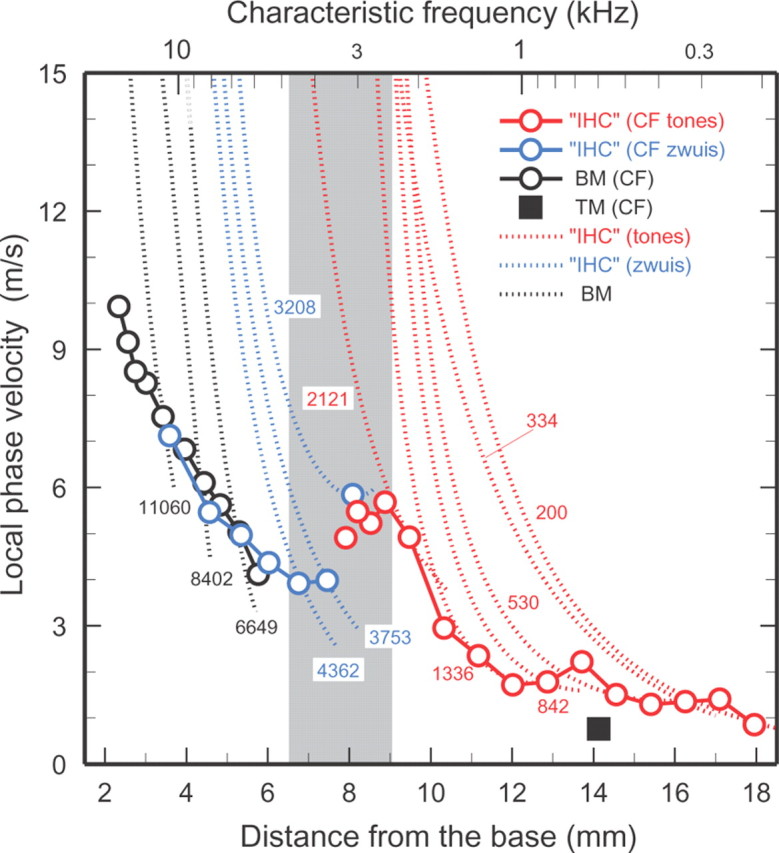
Local phase velocities of IHC depolarization and of BM and TM vibrations in the chinchilla cochlea. Dotted traces: local traveling-wave phase velocities for the indicated frequencies (200–11060 Hz), computed from the phase-place curves of Figure 2. Black traces: BM vibrations. IHC velocities were inferred from ANF responses to tones (red) and tone complexes (blue). Open symbols: velocities at the characteristic places, computed from Figure 1. Apical TM vibration velocity at CF (black square) is from Cooper and Rhode (1996). Gray band marks the region where ANF tuning curves change their shape [Temchin et al. (2008), Fig. 7B] and where IHC responses change their polarity (Fig. 2). IHC phase velocities derived from the same ANF populations represented in Figures 1 and 2.

Results

Phase-frequency curves for IHC depolarization inferred from responses of ANFs

Figure 1 shows averages of phase-frequency curves of chinchilla IHC depolarization, inferred from phase-locked ANF responses to tones presented at 70 dB SPL (red traces) or to near-threshold tone complexes (blue traces), which permit extracting relative phases for frequencies at which ANFs do not phase lock (van der Heijden and Joris, 2003, 2005). To obtain absolute phases, the responses to tone complexes (frequencies >2 kHz) have been anchored to the responses to tones (frequencies <2 kHz). For responses to tones, each average trace (except those for the two highest CFs) represents 10–38 ANFs with CFs within a 1/3-octave band and center CF indicted by a red circle for CFs ≤3 kHz or text labels. Each trace for responses to tone complexes represents responses of 4–10 ANFs with individual CFs flanking the indicated center CF (blue circle). For CFs >2 kHz, the IHC phase-frequency curves include two segments: one, shallow, for low frequencies and another, steeper, around CF (Temchin and Ruggero, 2010). For the lowest CFs (<600 Hz), the curves have slight but opposite curvature, with steeper slopes around CF than at higher frequencies. For mid-CFs, the curves transition between the two forms of curvature and are (very roughly) straight. At the lowest frequencies (<500 Hz), phase-frequency curves for apical and basal regions of the cochlea are nearly antiphasic (Ruggero and Rich, 1983, 1987). However, the CF phases are nearly the same, ∼1 period in reference to inward stapes displacement, for both apical and basal sites with CFs 0.6–12 kHz. The red dotted traces in Figure 1A indicate average phases for sites within or near the 6.5–9 mm region (Fig. 1B, gray band), where phases are highly variable (Temchin and Ruggero, 2010) as a result of a polarity transition in ANF responses to low-frequency tones (Ruggero and Rich, 1983, 1987).

Figure 1.

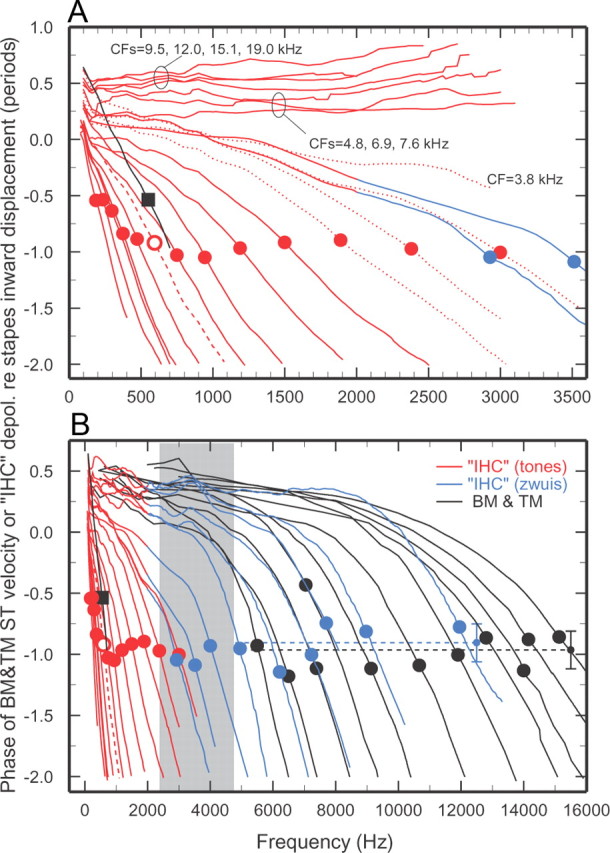
Phase-frequency curves for IHC depolarization and BM and TM vibrations. A, Presents the data of B (CFs ≤3 kHz) using an expanded frequency scale. Phases are referred to inward displacement of the middle-ear ossicles [for IHCs, see Ruggero et al. (1990), their Fig. 11]. Red traces: IHC phase-frequency curves derived from averages of responses to tones of many ANFs with CFs (red circles) within nonoverlapping 1/3-octave bands [Temchin and Ruggero (2010), their Fig. 10]. Dotted red traces in A indicate data for CFs in the transition region (gray band), which have exceptionally large SDs for low stimulus frequencies. Blue traces: IHC phase-frequency curves derived from averages of responses to tone complexes (“zwuis” stimuli) (van der Heijden and Joris, 2003), anchored to the phases of responses to tones (van der Heijden and Joris, 2005; Cai et al., 2009). The blue traces for central CFs of 2.9, 3.5, 4, 4.9, 6.2, 7.2, 7.7, 9, and 12 kHz (blue circles) represent, respectively, 5, 6, 10, 7, 8, 7, 7, 4, and 5 ANFs. B, The overall mean phase (−0.91 period) is indicated by the blue dashed trace and small symbol, with ±SD (0.15 period) indicated by the vertical blue bracket. BM and TM curves (black traces) indicate peak velocity toward scala tympani. The BM curves (CFs, filled circles) represent all available measurements in chinchilla ears in which middle-ear vibrations were also recorded [Rhode and Recio (2000), their Figs. 5B, 6B; Recio and Rhode (2000), their Fig. 6A,B; Narayan and Ruggero (2000), their Fig. 2; Ruggero et al. (1997), their Fig. 15]; and unpublished data of A. Recio-Spinoso and W.S. Rhode. Most of the BM curves are averages of measurements at two or three sites. The overall BM mean phase (−0.97 period) is indicated by the black dashed trace and small symbol, with ±SD (0.21 period) indicated by the vertical black bracket. The TM curve (average CF = 600 Hz; filled square) represents measurements in six chinchillas [Rhode and Cooper (1996), their Fig. 5B]. Gray band: CF range where ANF tuning curves change their shape [Temchin et al. (2008), their Fig. 7B]. IHC phases inferred from responses to tones of 434 ANFs in 63 chinchillas and tones complexes (selected from a total of 65 ANFs in 17 chinchillas).

For comparison with the IHC data inferred from ANF responses, Figure 1, A and B, also present phase-frequency curves (black traces) for chinchilla BM and TM vibrations, specifically for peak velocity toward scala tympani. These curves, several of their averages encompassing different cochleae, summarize the entire literature on BM/TM responses in chinchilla ears from which middle-ear vibrations were also measured. Apical TM and basal BM phase-frequency curves converge at the lowest frequencies and nearly coincide with stapes outward displacement. On average, peak velocity toward scala tympani at CF lags peak inward stapes displacement by 0.97 period for BM basal recordings (Fig. 1B, black circles) and 0.54 period for TM recordings near the 600-Hz characteristic place (Fig. 1A,B, black squares). The shapes of phase-frequency curves for IHCs closely resemble those of their BM or TM counterparts at both basal and apical sites (Fig. 1A,B, respectively), demonstrating that the two types of ANF phase-frequency curves are counterparts of corresponding BM/TM vibrations and undergo a transition in a limited region of the cochlea with CFs of ∼2.4–4.8 kHz (gray band). This is the same CF region where tuning-curve shapes transition between a “V” shape at apical sites and “tip-and-tail” at basal sites (Temchin et al., 2008).

At basal sites, IHC phase curves are approximately synchronous with phase curves for peak BM velocity toward scala tympani (Fig. 1B, compare black and blue curves). This IHC velocity sensitivity is consistent with the proportionality of ANF thresholds and BM velocity magnitudes at a basal site of the chinchilla cochlea (Narayan et al., 1998; Ruggero et al., 2000; Temchin et al., 2008). Since, as shown in Figure 1A, the polarities of IHC responses to low-frequency tones (red traces) are nearly opposite at basal and apical sites (Ruggero and Rich, 1983, 1987; Ruggero et al., 1996, 2000), it is likely that IHC depolarization at apical sites coincides with BM/TM velocity toward scala vestibuli.

Traveling waves of ANF excitation and IHC depolarization

Chinchilla ANF responses to near-threshold low-frequency tones undergo 180° phase shifts in the cochlear region between 6.5 and 9 mm from the extreme base, depending on frequency (Ruggero and Rich, 1983, 1987). For 200-Hz tones presented at near-threshold levels, the phase flip of ANF excitation, which follows IHC depolarization, occurs within a narrow region, 7.3–9 mm (Figure 2A, shaded pink area) [Ruggero and Rich (1987), their Fig. 11)]. Figure 2A also shows that both polarities coexist over a wider region in the case of responses to 200-Hz tones presented at 70 dB SPL (open circles). In the basal-most 5 mm, phases are clustered around a single locus (thick red trace at base), synchronous with peak outward stapes displacement. In the region of the cochlea spanning 5–11 mm, ANF responses tend to fire in synchrony with either of two different phases, ∼180° apart. One phase trajectory is a continuation of the basal-most locus and nearly vanishes at ∼11 mm, i.e., several millimeters basal to the characteristic place (18 mm). The other trajectory (thick red trace at apical sites), initially synchronous with peak inward stapes displacement, remains flat up to about the 14 mm site, where it starts to systematically accumulate phase lags. At the characteristic place, the accumulated lag for the 200-Hz wave amounts to 0.5 period (filled red circle). Except for quantitative details, the spatial distributions of response phases for tones with frequencies ≤2 kHz presented at 70 dB SPL are similar to those shown in Figure 2A in that they exhibit antiphasic trajectories at basal and apical sites, which overlap in the central cochlear region. More examples of the depolarization phases of individual IHCs as a function of cochlear place, for 300-, 600-, and 1200-Hz tones, are shown in Fig. 5B–D.

Figure 2B presents the data of Figure 1 as a collection of single-frequency phase-place curves for peak BM velocity toward scala tympani (black traces) and for IHC depolarization, derived from ANF responses to tones presented at 70 dB SPL (red) and near-threshold tone complexes (blue). For responses to tones (200–2000 Hz), red traces indicate the modes of the two phase loci. Thick traces indicate segments dominated by a single response phase, e.g., 2–5 mm and <10 mm for 200 Hz. Regardless of frequency, all phase curves (for both BM vibrations and for IHC depolarization derived from ANF responses to 70 dB tones or near-threshold tone complexes) exhibit the classical signatures of cochlear traveling waves. First, at sites basal to their characteristic places, all curves asymptotically approach flat loci, which indicate fast wave propagation. Second, at sites closer to the characteristic place, curves exhibit monotonically increasing phase-lag accumulation, as waves slow down. The trajectories of high-frequency waves fan out from sites near the extreme base of the cochlea, where they are synchronous with peak outward stapes displacement. In the basal-most 5 mm, low-frequency IHC waves also have flat trajectories synchronous with the same asymptotes as high-frequency waves, synchronous with peak outward stapes displacement. However, these initial low-frequency trajectories vanish before reaching the characteristic places. The trajectories of phase accumulation that do reach low-frequency characteristic places originate in asymptotes synchronous with peak stapes inward displacement. IHC waves then accumulate phase lags of one period at the characteristic places for frequencies >600 Hz but somewhat less for the lowest frequencies. Thus, Figure 2 demonstrates that, differing from the classical description of BM traveling waves, high- and low-frequency IHC-depolarization waves (and, hence, the mechanical waves that provide stimulus) have antiphasic trajectories over a large segment of the cochlea.

For high-frequency stimuli, the spatial trajectories for IHC depolarization and BM velocity toward scala tympani (Fig. 2B, blue and black traces, respectively) are similar, as exemplified by the near overlap between the traces for frequencies ∼5.5 kHz, with characteristic places near 5 mm. Both IHC and BM curves nearly coincide with outward stapes displacement at the extreme basal end of the cochlea and then increasingly and continuously lag as a function of distance, reaching approximately the same phase value, −1 period in reference to inward stapes displacement, at the characteristic places. In other words, IHC-depolarization phases at basal sites are synchronous with peak vibration velocity toward scala tympani throughout their trajectories. IHC-depolarization responses to tones with frequency 600–2000 Hz presented at 70 dB SPL (red traces) also lag stapes inward displacement by ∼1 period at the characteristic places. Taking into account the opposite polarities of the two asymptotes, and the fact that basal IHC trajectories are synchronous with peak BM velocity toward scala tympani, apical IHC trajectories should be synchronous with peak BM or TM velocity toward scala vestibuli.

The IHC-depolarization phase at the 600-Hz characteristic place (red circle in Fig. 2B) can be directly compared with existing TM data (black square in Fig. 2B) for the same site (Rhode and Cooper, 1996). This comparison, which suggests that IHC depolarization at the 600 Hz site actually leads TM peak velocity toward scala vestibuli by 90°, should be viewed with greater caution than the BM/IHC comparisons for basal sites. One source of uncertainty is that the phases of apical TM vibrations were recorded in a single study and solely in cochleae impaired by surgical penetration of Reissner's membrane. Another is that precise estimation of CF is difficult at apical sites, due to broad tuning; even a 100-Hz error in CF could result in a large phase error.

As the level of tone stimuli is increased beyond 85–90 dB SPL, ANF responses throughout the chinchilla cochlea undergo abrupt phase shifts approaching 180°, usually accompanied by bimodality of period histograms and, sometimes, by sharply decreased rates of discharge (Ruggero and Rich, 1983; Ruggero et al., 1996). Comparable phase shifts do not exist for BM vibrations at basal sites (Ruggero et al., 2000). Figure 2B illustrates stimulus level-dependent dual spatial trajectories, nearly antiphasic, for IHC depolarization inferred from ANF responses to 600-Hz tones: compare the open red circles, for responses to tones presented at 70 dB SPL, and the open violet circles, which indicate basal (CFs 6–12 kHz) and apical (CFs 0.75–1.5 kHz) IHC responses to tones presented, respectively, at 90–100 and 100–110 dB SPL.

Local phase velocities of IHC depolarization

Pairs of phase-frequency functions for known locations, such as those of Figure 1, can be used to compute local phase velocities (Lighthill, 1981). This has been done previously only for short segments of the BM or TM in chinchilla (Cooper and Rhode, 1996; Narayan and Ruggero, 2000) and a few other species (Rhode, 1971; Lighthill, 1981; Russell and Nilsen, 1997; Ren, 2002). It is now possible to compute local phase velocities throughout most of the chinchilla cochlea (Fig. 3) on the basis of the BM and IHC phase data available for this species as functions of both frequency (Fig. 1) and place (Fig. 2). Each dotted trend line in Figure 3 shows the spatial velocity profile of the traveling wave for a single stimulus frequency. Wave velocities for BM vibrations (6.6–11.1 kHz) are indicated by the black traces. Wave velocities for IHC depolarization were derived from ANF responses to tones (200–2121 Hz; red traces) and tone complexes (3.2–4.4 kHz; blue traces). Regardless of frequency, BM and IHC wave velocities are high basal to the characteristic places but decelerate rapidly. At sites basal to the 8-mm place, deceleration continues at high rates even beyond the characteristic places (open circles). In contrast, at sites apical to the 6.5–9 mm transition region (gray band) deceleration decreases substantially basal to the characteristic places and reach velocity minima nearby.

The spatial profile of velocities at the characteristic places (Fig 3, open symbols) is markedly non-monotonic, exhibiting a minimum around the 7-mm site and a maximum around the 8–9 mm site, both within the transition region. At sites basal to the transition region, both BM and IHC velocities at CF decrease steeply with distance, from >10 m/s near the extreme base to ∼4 m/s around the 7-mm site. At sites apical to the transition region, IHC-depolarization velocities (red symbols) also decrease monotonically, but at lower rates, from ∼6 m/s around the 8- to 9-mm place to ∼1 m/s near the apex. At 14 mm, the 600 Hz place, TM velocity is also ∼1 m/s.

It is worth noting that the local velocities at the characteristic places depicted in Figure 3, although based on the data of Figure 1, provide information largely independent of the phase trajectories of Figure 2, also derived from Figure 1. This is because velocities are computed from the differences between pairs of phase-frequency traces with CFs corresponding to characteristic places bracketing narrow cochlear spans. Thus, the crucial result of Figure 3, namely that CF velocity is maximal at the site 8–9 mm from the base, nonredundantly complements the salient finding of Figure 2, namely that antiphasic spatial trajectories exist for responses to low-frequency tones in a region of the cochlea with much higher CFs.

Onset latencies of IHC impulse responses

The existence of a local velocity minimum and a local velocity maximum at sites of the transition region near its basal and apical edges (Fig. 3) suggests that travel time should exhibit a local maximum and a local minimum at those sites. This is confirmed in Figure 4, which presents onset latencies of IHC impulse responses (filled color symbols) inferred from time-domain Wiener kernels for ANF responses to near-threshold noise (Recio-Spinoso et al., 2005; Temchin et al., 2005). Also shown in Figure 4 are BM signal-front delays (black trace) inferred from the latencies of ANF and BM responses to intense rarefaction clicks [Temchin et al. (2005), their Fig. 13A]. Both the time-domain Wiener kernels for noise stimuli presented near threshold and the responses to intense clicks are approximations to impulse responses but, whereas the latter are relatively wide band, the former are largely determined by near-CF spectral components. Therefore, due to cochlear frequency dispersion (i.e., different frequencies travel at different velocities), the latencies of time-domain Wiener-kernels obtained with near-threshold stimuli and signal-front delays generally are different. At basal sites (<8 mm), signal-front delays are shorter because the earliest BM responses are determined by frequencies lower than CF (Recio et al., 1998). At apical sites (>16 mm), signal-front latencies are also shorter because the earliest BM responses are determined by frequencies higher than CF (Temchin et al., 2005). In the 8–16 mm region, the latencies of near-threshold impulse responses and signal-front delays are similar because dispersion is minimal in that region (Temchin et al., 2005, 2011). Near-threshold impulse-response latencies reach a local maximum at, ∼400 μs, near the mid-point of the transition region but are almost nil both near the base and around the 9 mm location. Such a latency profile is consistent with dual traveling waves launched simultaneously at the extreme base of the cochlea and in the transition region, but it contradicts the classical view of traveling waves that decelerate monotonically as they progress from base to apex.

Figure 4 also demonstrates that the main features of the spatial profile of near-threshold impulse-response latencies are consistent with the phase-frequency trajectories of Figure 1, the phase-place trajectories of Figure 2, and the velocity-place trajectories of Figure 3. The blue trend lines of Figure 4 are phase delays at CF computed from Figures 1 and 2. The CF phase-lag accumulations were measured from the time of peak outward displacement for basal sites and from the time of peak inward displacement for apical sites. Therefore, for example, phase delays are 150 μs for the 10-kHz site (i.e., 1.5 periods/CF) and 1 ms for the 1-kHz site (i.e., 1 period/CF). The good match between the blue trend lines thus computed and the near-threshold impulse-response latencies supports the interpretation of Figure 2 as illustrating dual waves launched simultaneously at the extreme base and at the transition region. The red trend lines correspond to delays computed by spatial integration of the velocity curves of Figure 3 between the extreme base and the characteristic places. The delays computed from Figures 1–3 are similar and match the near-CF impulse-response latencies excellently at basal (<8 mm) and apical (>15 mm) sites, where dispersion is large, but less well at intermediate sites, where dispersion is small.

Bimodal spatial profiles of ANF response rates

ANF and IHC-depolarization responses to low-frequency tones presented at 70 dB SPL are in-phase and antiphase with outward stapes displacement, respectively, in the segments of the cochlea basal and apical to the transition region (Figs. 2, 5B). In the transition region and in the regions immediately flanking it, individual ANFs lock to either stimulus phase. Thus, locking to a particular stimulus phase appears to be determined by the summation of two antiphasic waves, leading to the prediction that when both waves have identical magnitudes, cancellation should occur and response rate should be sharply reduced. This prediction is consistent with spatial profiles of average rates of ANF responses to low-frequency tones (<2 kHz), examples of which are shown in Figure 5A for 300, 600, and 1200 Hz. In the apical region of the cochlea, the spatial profiles of average rate respond to the classical description of traveling waves: increasing magnitudes as a function of increasing distance from the base culminating in absolute maxima around the characteristic places, and sharper apical slopes than basal slopes. In the basal region, however, the spatial rate profiles also include local maxima at 3–5 mm, as well as minima ∼6 mm. The local rate minima nearly coincide with the basal edge of the transition region (gray band), where antiphasic waves coexist. The local maxima at 3–5 mm correspond to responses dominated by waves that asymptote in synchrony with stapes outward displacement, whereas those at the characteristic places correspond to responses dominated by waves that asymptote in synchrony with stapes inward displacement (Fig. 5A, compare B–D).

Summary of results

We have presented fairly complete descriptions of the phases of IHC depolarization as functions of both frequency and place (Figs. 1, 2, 5B–D), and of local phase velocities throughout most of the chinchilla cochlea (Fig. 3). These descriptions are unique among all species. For frequencies ≤2–3 kHz phase accumulation starts from an asymptote synchronous with stapes inward displacement. For frequencies ≥3–4 kHz phase accumulation starts from a baseline synchronous with stapes outward displacement. Accumulated phase lags at the characteristic places are approximately the same, 1 period in reference to inward stapes displacement, throughout the cochlea except the extreme apex, where it is less. Near-threshold impulse responses exhibit a latency minimum (Fig. 4), phase velocities at CF attain a local minimum and a local maximum (Fig. 3), and the phases of IHC depolarization flip (Fig. 2) in the same region, 6.5–9 mm from the extreme base, where ANF frequency-threshold tuning curves transition in shape. Rate-place profiles for ANF responses to low-frequency tones are bimodal, including peaks near the characteristic place and the 3- to 5-mm region (Fig. 5A).

Discussion

Interpretation of results

Sound-induced vibrations of the stapes or the skull generate (fast) acoustic waves that reach everywhere in the cochlea within a few microseconds. In the classical view, (slow) differential pressure waves between scala vestibuli and scala tympani (Olson, 1998) generate (slow) vibration traveling waves of the BM, the organ of Corti, and the TM, which begin to accumulate phase lags immediately adjacent to the stapes. In contrast, the spatial profiles of IHC-depolarization phase (Fig. 2), phase velocity (Fig. 3), and latencies (Fig. 4) imply that the mechanical stimuli that deflect IHC stereocilia start accumulating phase lags simultaneously at two sites: one immediately adjacent to the stapes, which dominates IHC-depolarization responses to high-frequency stimuli at the base of the cochlea, and the other at the transition region, which dominates IHC-depolarization responses to low-frequency stimuli in the apical half of the cochlea. In addition, the basal IHC-depolarization responses synchronous with outward stapes displacement suggest that low-frequency IHC-depolarization waves are also reflected at the transition region. Specifically, the minimum near 6 mm in the ANF rate profiles for low-frequency stimulation (Fig. 5A) is consistent with destructive interference between a forward wave launched at the extreme base and an antiphasic backward wave arising in the transition region. Overall, the spatial profiles of phase, phase velocity, latencies, and rate, as well as the shapes of ANF tuning curves, suggest that the cochlea consists of two largely independent basal and apical segments that meet at the transition region.

Connection between spatial phase profiles and active processes

The changeover in shape of IHC phase-frequency functions (Fig. 1) [Temchin and Ruggero (2010), their Fig. 17], which underlies the non-monotonic spatial profiles of velocities and onset latencies (Figs. 3, 4), occurs in the same region where ANF frequency-threshold tuning curves change their shape (Temchin et al., 2008), V-like in apical regions but including low-frequency tails in basal regions (Figs. 2–4, gray shading) [Temchin et al. (2008), their Figs. 2, 5, 7]. It is probable that the spatial transitions in frequency-threshold tuning curves and phase-frequency curves are intimately linked since, when measured in the same ANFs, they exhibit inflections at the same frequencies [Temchin and Ruggero (2010), their Figs. 13, 14]. The relation between magnitude and phase spectra is so strict that it permits computing the main features of the phase-frequency curves and their changes at the 6.5- to 9-mm transition region from the tuning curves (Temchin et al., 2011).

The transition region also coincides with spatial changeovers in the effects of furosemide on ANF tuning curves (Sewell, 1984), which closely parallel the effects on BM tuning at basal sites (Ruggero and Rich, 1991), and of the relation between the rate-level functions of ANF responses to CF and low-frequency tones (Cooper and Yates, 1994). Since those effects are linked to the active processes that boost BM vibrations, their changeovers in the transition region suggests that the polarity flip and the non-monotonic features of traveling waves are also linked to active processes. Furthermore, given that the TM profoundly affects BM vibrations (Legan et al., 2000; Russell et al., 2007), TM/organ of Corti interactions might influence outer hair cells and hence, via feedback, BM vibrations. In other words, the response polarity flip in the central region of the cochlea might also be present in BM or TM vibrations. The spatial correlation between active processes, frequency-threshold tuning curves, and the phases of IHC responses suggests that the anatomical relations and functional interactions between the organ of Corti and the TM differ at sites basal and apical to the transition region of the chinchilla cochlea.

Generality across mammalian species of findings in chinchilla

Bimodal distributions of the phases of IHC depolarization, such as shown in Figures 2A, 5B–D, and, especially, 2B (compare violet and dashed red traces for 600 Hz curves) in chinchilla (Ruggero and Rich, 1983; Ruggero et al., 1996), were first adumbrated by the level-dependent “peak splitting” in period histograms first discovered in cat ANF responses to tones (Liberman and Kiang, 1984; Kiang et al., 1986). Similarly, the existence of distinct apical and basal cochlear segments, joined by a central transition region, is unlikely to be a peculiarity of the chinchilla species. In cat, the shape of phase-frequency curves change with CF (Pfeiffer and Molnar, 1970; van der Heijden and Joris, 2003) much as they do in chinchilla. In both cat and gerbil, ANF frequency-threshold tuning curves undergo changes in shape (Liberman, 1978; Schmiedt, 1989; Ohlemiller and Echteler, 1990) at CFs similar to those in chinchilla. The most direct antecedents of the present investigation in chinchilla are studies that presented spatial phase-place and/or rate-place plots for cat ANF responses to tones (Kim et al., 1980; van der Heijden and Joris, 2006). One of the phase-plots [Kim et al. (1980), their Fig. 5] includes a jog reminiscent of the phase transition in chinchilla (Figs. 2, 5B). Another cat study presented bimodal rate-place plots (Kim and Molnar, 1979) strongly resembling the bimodal rate profiles in chinchilla (Fig. 5A).

However, no evidence for a transition in response polarity was found in another study in cat (van der Heijden and Joris, 2006). That study suggested that the accumulated ANF phase lags at CF increased monotonically from 1 period at the 200-Hz place to 2.5 periods at the 4-kHz place (van der Heijden and Joris, 2006), contrasting with our finding of ∼1 period over most of the chinchilla cochlea excepting the extreme apex (Fig. 2B). It is difficult to evaluate the discrepancies between results for chinchilla with those of the cat study by van der Heijden and Joris (2006). They may involve species differences, the fact that IHC responses were normalized to middle-ear motion in chinchilla but not in cat and, perhaps most importantly, the fact that the convergence of spatial phase trajectories at the extreme base of the cat cochlea was an assumption not ascertained by measurements.

Forward and reflected traveling waves

The possibility of dual cochlear traveling waves, first postulated on theoretical grounds (Hubbard, 1993), has received empirical support (Ghaffari et al., 2007; Chen et al., 2011). One interpretation of the transition region in chinchilla is that it is the boundary between cochlear regions, apical and basal, where distinct waves dominate. Another interpretation, not necessarily contradictory, is that the transition region contains a mechanical impedance irregularity. In transmission lines, which often serve as models of cochlear mechanics, impedance irregularities interrupt forward waves and cause reflections. For example, in a tube open at one end and closed at the other, standing acoustic waves are generated by the interaction between forward waves and antiphasic backward waves reflected from the closed end. In the cochlea, low-frequency waves may bounce off the transition region. Such reflections might give rise to otoacoustic emissions, which emanate from the inner ears in many tetrapod species, including humans (Kemp, 1978). The path of propagation of the antecedents of otoacoustic emissions in mammalian cochleae is a controversial subject, with some experiments supporting “slow” BM backward traveling waves (Dong and Olson, 2008) and others “fast” acoustic waves in the cochlear fluids (Ren, 2004; Siegel et al., 2005; Ren et al., 2006). Whether or not the transition region is confined to the organ of Corti or also involves BM vibration, it could well play a role in the generation of otoacoustic emissions, since these exist even in amphibians, whose hearing organs lack BMs (Palmer and Wilson, 1982; van Dijk et al., 1996). Interestingly, stimulus-frequency otoacoustic emissions in chinchillas exhibit frequency dependencies consistent with the existence of basal and apical segments of the cochlea, which transition in the 6.5–9 mm region. Their average magnitudes exhibit a conspicuous minimum at ∼3 kHz (Siegel et al., 2005), whose characteristic place lies in the transition region, and their suppression tuning curves differ drastically for probe frequencies 4 and 12 kHz, which closely resemble ANF tuning curves, versus 1-kHz probes, which have high-frequency arms that are nearly flat over a two-octave range, as might be expected from basal emission sources due to reflections at the transition region (Charaziak and Siegel, 2012).

Tentative conclusions

(1) In contrast with high-frequency IHC and BM forward waves, which start their travel from an extreme-base asymptote synchronous with stapes outward displacement, low-frequency forward waves of IHC depolarization are launched at the transition region from a baseline synchronous with stapes inward displacement. (2) Antiphasic “backward” low-frequency IHC-depolarization waves also arise at the transition region; coexist with the dominant forward waves in the central region of the cochlea, depending on stimulus frequency and level; and are dominant in the basal-most 5 mm of the cochlea, where forward low-frequency waves are weak. (3) If the polarity of IHC stimulation in reference to BM vibration is the same throughout the cochlea, then points 1 and 2 also apply to BM vibrations: distinct and antiphasic BM traveling waves exist in the apical and basal segments of the chinchilla cochlea. Alternatively, the polarity of IHC stimulation in reference to BM flips in the transition region, as previously suggested (Ruggero and Rich, 1987).