Digital optical phase conjugation of fluorescence in turbid tissue

Abstract

We demonstrate a method for phase conjugating fluorescence. Our method, called reference free digital optical phase conjugation, can conjugate extremely weak, incoherent optical signals. It was used to phase conjugate fluorescent light originating from a bead covered with 0.5 mm of light-scattering tissue. The phase conjugated beam refocuses onto the bead and causes a local increase of over two orders of magnitude in the light intensity. Potential applications are in imaging, optical trapping, and targeted photochemical activation inside turbid tissue.

Most biological tissues are turbid: they scatter and diffuse light. Turbidity is the main limitation for the penetration depth of microscopes and methods such as optical coherence tomography and photodynamic therapy. In the last couple of years, a tremendous effort has been made to suppress the effects of turbidity. Light was focused through strongly turbid materials,^{1, 2} and subsequently used for optical trapping of particles³ and microscopic imaging.^{4, 5}

Ultimately, one wants to use turbidity suppression to focus or deliver light inside turbid living tissue, where it can be used for imaging or optical activation of drugs,⁶ genes,⁷ or neuronal activity.⁸ In a recent experiment,⁹ light was delivered into a scattering tissue by combining optical phase conjugation and ultrasound tagging. The ultrasound was used to define a target area, and a gated phase conjugating mirror (PCM)—sensitive only to the ultrasound-tagged light—was used to construct a back-propagating field that returned to the targeted area.

In this letter, we demonstrate an alternative approach: phase conjugation of fluorescence. In our approach, the area is labeled with a fluorescent marker. Our apparatus collects the scattered fluorescence and generates an amplified, phase conjugated beam that refocuses at the target (see Fig. 1). The main advantage of using fluorescent labeling is that fluorophores can be designed to have chemical, biological, or genetical¹⁰ selectivity. This makes it possible to selectively refocus light only onto areas of (biological) interest. Moreover, the resolution of fluorescent tagging is limited only by the optical wavelength, not by that of the ultrasound.

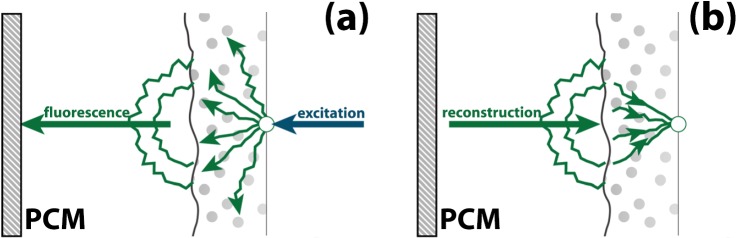
Figure 1.

Principle of phase conjugation of fluorescence. (a) A fluorescent particle is excited and the scattered fluorescence is collected by a PCM. (b) The PCM conjugates the phase of the light and reverses its direction. Thanks to the reciprocity of light propagation, the light refocuses at the position of the particle. Note that the conjugated light matches the wavelength of the emitted light (not that of the excitation light).

So far, it has not been possible to phase conjugate fluorescence. This is because phase conjugation methods are either not sensitive enough or rely on interfering the scattered light with a reference beam.¹¹ The latter will not work since fluorescent light is temporally incoherent.

We present a reference-free digital optical phase conjugation (DOPC) method that is sensitive enough to detect very weak fluorescent signals, and works for light that is both spatially and temporally incoherent. We used our method to refocus light onto a fluorescent marker through 0.5 mm of chicken breast tissue, thereby demonstrating that fluorescent light can be phase conjugated.

The two main elements of a DOPC apparatus¹² are a wavefront sensor and a wavefront generator (see Fig. 2). The sensor and the generator are placed in the mirror conjugate planes of a beam splitter (BS). First, the wavefront sensor records the wavefront of the scattered light that is leaving the sample. Then, the wavefront generator sends back the phase conjugated wave into the sample, where the wave refocuses onto the fluorescent marker.

Figure 2.

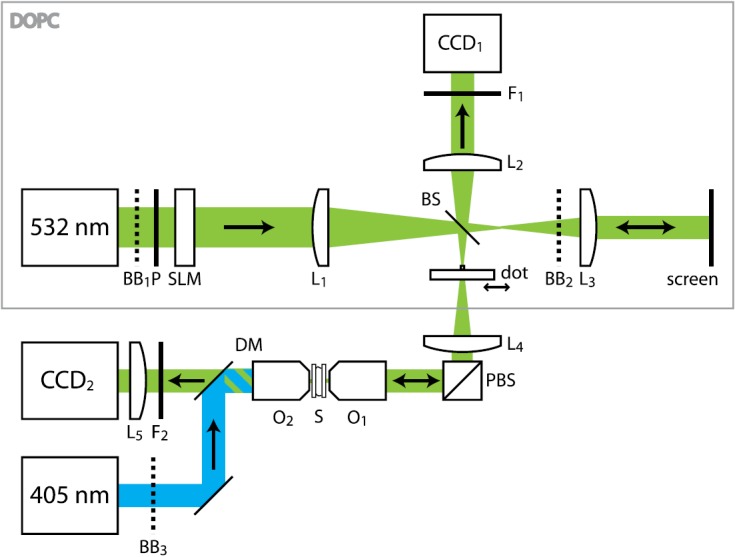
Simplified schematic of the experiment. The DOPC apparatus is marked with a gray rectangle. Beam expanders and folding mirrors are not shown. ${\text{BB}}_{1-3}$, removable beam blocks; ${\mathrm{L}}_{1-5}$, lenses, focal lengths 1000, 200, 1000, 400, 100 mm, respectively; ${\mathrm{F}}_{1-2}$, emission filters; DM, dichroic mirror; P, polarizer; PBS, polarizing beam splitter; S, sample; O₁₋₂, 40X microscope objectives; BS, 8% beam sampler; SLM, light modulator; 405 nm, excitation laser; 532 nm, reconstruction laser; and ${\text{CCD}}_{1-2}$, cameras.

We chose to use binary phase modulation where the elements of the conjugated beam have a phase of either 0 or π. With binary phase modulation, the intensity of the reconstructed focus is slightly lower than with full $0-2\pi$ phase modulation^{13, 22} at the benefit of greatly reducing the system’s complexity.

Regular DOPC uses interference with a reference beam to measure the phase of the scattered light. Since a reference beam is not available for fluorescent light, we have developed a reference-free method for measuring the phase. This method combines an ordinary CCD camera (Allied Vision Technologies Stingray F-145) with a gold/chromium mask in the shape of a single 0.2 mm diameter disk. Initially, the disk is positioned exactly in the focus of lens $L_2$, so that it blocks the k = 0 Fourier component of the fluorescence coming from the sample. This component corresponds to a plane wave on the CCD surface. The mask can be translated so that the dot is moved out of the light path. We measure the intensity at the CCD without the dot and then again with the dot in place. The difference between these two measurements is given by

$$\Delta I(x,y)=2\left|E_0\right||E(x,y)|\cos (\varphi (x,y))-|E_0{|}^2,$$ (1)

where E(x,y) is the optical field and $E_0$ is the spatial average of E(x,y) (i.e., the k = 0 Fourier component of the light). ϕ is the phase difference between E(x, y) and $E_0$. In a speckle pattern, ϕ is uniformly distributed¹⁴ between 0 and $2\pi$, so on average $\Delta I=|E_0{|}^2$. For binary phase detection, we can simply use

$${\varphi }_{\text{binary}}(x,y)=\{\begin{array}{cc}0\hfill & \text{if}\Delta I(x,y)>\langle \Delta I\rangle ,\hfill \\ \pi \hfill & \text{if}\Delta I(x,y)\le \langle \Delta I\rangle ,\hfill \end{array}$$ (2)

where the angle brackets denote averaging over the CCD image. Unlike phase contrast methods or Shack-Hartmann type sensors, our method for measuring the phase of the light works for arbitrarily complex wavefronts.

An extra complication is the limited temporal coherence of the fluorescent light. As a rule of thumb, the minimum coherence length that is needed equals the width of the optical path length distribution function. To increase the coherence length of the signal beam, we placed a laser line filter (Semrock LL01-532-25, center wavelength 532 nm, FWHM 2 nm) in front of the CCD camera. The filter bandwidth of 2 nm gives a coherence length of 0.14 mm. Because scattering in biological tissue is mainly directed forwards, this relatively short coherence length was still sufficient to phase conjugate the light through a piece of scattering tissue of 0.5 mm thick.

A Holoeye LC-2002 transmissive spatial light modulator (SLM) is used for generating the reconstruction beam. The modulator, and polarizers P and PBS are set up for binary amplitude modulation (E = 0 or E = 1). In order to achieve binary phase modulation instead, we use the mask to block $E_0^r$, the 0th order of the reconstruction beam. Since the “0” and “1” states are equally likely, $E_0^r=1/2$ and the filtered reconstruction beam has binary phase modulation (E = −1/2 or E = 1/2).

For the DOPC to work, the correspondence between camera pixels and SLM pixels must be near perfect, which makes alignment far from trivial.¹² The first step in the one-time alignment process is to optimize the collimation of the laser beam at the position of the SLM. Then, a paper screen is placed exactly in the image plane of the SLM pattern (see Fig. 2). A dot-grid pattern is displayed on the SLM. This grid defines the “screen coordinates.” The position and angle of the camera are finely adjusted until all of the dots are in focus in the CCD image. The SLM and the CCD are now in exact mirror conjugate planes of beam sampler BS.

Subsequently, the exact position of each dot in the camera image is determined. These positions define the “texture coordinates” corresponding to the screen coordinates. For each position, we define a vertex¹⁵ holding both the screen coordinates and the texture coordinates. To map the camera image onto the SLM, the camera image is loaded into the graphics processing hardware of the computer as a Direct3D texture. This texture is then mapped onto the mesh grid defined by the vertices. Using this remapping technique (also see Ref. 12), all image distortions are compensated for, and the CCD pixels are mapped to SLM pixels with an error of less than 2 pixel widths.

Our sample consists of a 0.5 mm thick slice of chicken breast, sandwiched between two microscope cover glasses. From ballistic transmission measurements, a scattering mean free path of 0.04 mm was found. For this sample thickness, the absorption loss is negligible. We deposited fluorescent marker beads on the inner side of the back cover glass by evaporating a dilute (2.5 μl/ml) suspension of Invitrogen 505/515 0.2 μm diameter amino-modified FluoSpheres. The beads are well separated and in the experiment we illuminate a single bead.

We excited the bead with 405 nm light from the back of the sample (right side in Fig. 1, left side in Fig. 2) and used our DOPC apparatus at the front side of the sample (left side in Fig. 1) to record the wavefront of the fluorescent light that has passed through the scattering tissue. During this measurement, beam blocks ${\text{BB}}_1$ and ${\text{BB}}_2$ are in place. After the measurement, we place beam block ${\text{BB}}_3$ and remove ${\text{BB}}_1$. The SLM is programmed with the phase conjugated wavefront and illuminated by a 1 mW, 19 mm diameter beam from a 532 nm diode pumped solid state laser (OEM) to generate the reconstruction beam.

The experimental results are shown in Fig. 3. Figure 3a shows the intensity of the reconstructed light at the back surface of the sample. The DOPC reconstruction beam has traveled through the scattering chicken tissue and converged to an intense focus at the position of the fluorescent bead. The intensity of the reconstructed focus is a factor of $2.7\times {10}^2$ higher than that of the original fluorescent signal.

Figure 3.

Experimental results. (a) Intensity of the phase conjugated beam at the back surface of the sample. The reconstruction beam refocuses back onto fluorescent bead. (b) Intensity of the same phase conjugated beam, after translating the sample over approximately 10 μm (same color scale as in a). The focus has disappeared because the microscopic scattering properties of the sample are different at this position. (c) Measured binary phase of the wavefront (at ${\text{CCD}}_1$). The raw data were filtered with a 1-pixel radius Gaussian filter to reduce measurement noise and then processed using Eq. 2. Scale bars are 10 μm (a and b) and 1 mm (c).

The focal spot in Fig. 3a has a full width at half maximum of 0.8 μm. Note that this resolution is not related to the resolution of the SLM or the numerical aperture of the microscope objective ($O_1$). In effect, it is the scattering medium itself that focuses the light. Therefore, the resolution is given by the effective numerical aperture of the medium.¹⁶

Of all possible incident wavefronts, the phase conjugated wave is the unique optimal one that maximizes the intensity at the fluorescent bead.¹⁷ One might argue that ballistic (unscattered) light transmission through the sample is responsible for creating the focus.¹⁸ However, this theory can be disproven in the following way: first, in cases were ballistic light transmission is significant, the optimal wavefront will have a distinct bullseye pattern to compensate for the defocus. Such patterns were seen only for extremely thin samples (a single layer of 3 M Scotch tape). For the chicken tissue, the optimal wavefront is a disordered speckle pattern (see Fig. 3c). Second, when the focus is formed by ballistic light, the focus will remain intact when the sample is translated. We observed that the focus disappears completely when the sample is translated even slightly (see Fig. 3b). These two observations are clear indications that it is scattered light, rather than ballistic transmission that is responsible for creating the focus.

It is worthwhile to compare this experiment with a known iterative method for focusing light on fluorescent beads embedded in a scattering material.¹⁹ Since our method is essentially a single-shot technique, it is potentially much faster than any iterative method. The complete DOPC process needs to take place faster than the persistence time of the medium (the time over which the speckle pattern remains stable), so speed is of the essence. The current experiment took about 90 s to complete. Even though our experiment was not optimized for speed, this is already over a factor of 10 faster than the result described in Ref. 19. We estimate that a further speed increase of about a factor of 100 is readily available by more efficient use of fluorophores or quantum dots, using a special low-light sensitive camera, and increasing the pump power. This brings down the required time to less than a second, which is already sufficient for phase conjugation in some living tissues.²⁰ A further speedup can be achieved using digital mirror device SLMs, which were recently shown to be able to focus light through semifluid phantoms.²¹

In this experiment, the fluorescent bead was positioned at the back surface of the sample so that it was possible to show that the phase conjugated light forms a focus (Fig. 3a). Placing the bead at the surface had the extra advantage of being able to efficiently excite the fluorescence. Of course, the most useful applications of our method are for focusing light onto targets that are embedded inside scattering tissue. In such an experiment, the depth would most likely be limited by the power of the pump laser, since scattering limits the amount of pump light that reaches the bead.

The maximum depth that can be reached with DOPC is further related to the resolution of the CCD/SLM combination. When the target is embedded deeper in the tissue, the scattered light will spread out over a larger area. This area will increase quadratically with the depth. Therefore, to effectively phase conjugate the emitted light, the CCD/SLM should be larger or have a higher density. From Fig. 3c, it was estimated that there are currently on the order of 100 independent “segments” in the wavefront. With the use of high resolution light modulators, a total of over ${10}^5$ independent segments could be addressed,¹² which indicates that the depth penetration could be increased to 5 mm at the expense of having a lower signal per pixel and being more sensitive to misalignment.

In conclusion, we have demonstrated phase conjugation of scattered fluorescent light. Conjugation of the weak, incoherent fluorescence signal was made possible with our digital phase conjugation method, which has a sensitivity that is orders of magnitude higher than conventional phase conjugation methods.¹¹ Like with regular DOPC, the reconstruction beam can have an arbitrarily high intensity and the hologram can be kept and used as long as needed without fading, even after the signal beam is gone.

Our results pave the road for applications where the reconstructed focus is used for optical or thermal manipulation of gene expression or other chemical processes. The next step will be to combine our phase conjugation method with existing methods for scattered light microscopy,^{4, 5} which will make it possible to perform high resolution microscopy deep inside turbid tissue.