Four-dimensional cone beam CT reconstruction and enhancement using a temporal nonlocal means method

Abstract

Purpose: Four-dimensional cone beam computed tomography (4D-CBCT) has been developed to provide respiratory phase-resolved volumetric imaging in image guided radiation therapy. Conventionally, it is reconstructed by first sorting the x-ray projections into multiple respiratory phase bins according to a breathing signal extracted either from the projection images or some external surrogates, and then reconstructing a 3D CBCT image in each phase bin independently using FDK algorithm. This method requires adequate number of projections for each phase, which can be achieved using a low gantry rotation or multiple gantry rotations. Inadequate number of projections in each phase bin results in low quality 4D-CBCT images with obvious streaking artifacts. 4D-CBCT images at different breathing phases share a lot of redundant information, because they represent the same anatomy captured at slightly different temporal points. Taking this redundancy along the temporal dimension into account can in principle facilitate the reconstruction in the situation of inadequate number of projection images. In this work, the authors propose two novel 4D-CBCT algorithms: an iterative reconstruction algorithm and an enhancement algorithm, utilizing a temporal nonlocal means (TNLM) method.

Methods: The authors define a TNLM energy term for a given set of 4D-CBCT images. Minimization of this term favors those 4D-CBCT images such that any anatomical features at one spatial point at one phase can be found in a nearby spatial point at neighboring phases. 4D-CBCT reconstruction is achieved by minimizing a total energy containing a data fidelity term and the TNLM energy term. As for the image enhancement, 4D-CBCT images generated by the FDK algorithm are enhanced by minimizing the TNLM function while keeping the enhanced images close to the FDK results. A forward–backward splitting algorithm and a Gauss–Jacobi iteration method are employed to solve the problems. The algorithms implementation on GPU is designed to avoid redundant and uncoalesced memory access, in order to ensure a high computational efficiency. Our algorithms have been tested on a digital NURBS-based cardiac-torso phantom and a clinical patient case.

Results: The reconstruction algorithm and the enhancement algorithm generate visually similar 4D-CBCT images, both better than the FDK results. Quantitative evaluations indicate that, compared with the FDK results, our reconstruction method improves contrast-to-noise-ratio (CNR) by a factor of 2.56–3.13 and our enhancement method increases the CNR by 2.75–3.33 times. The enhancement method also removes over 80% of the streak artifacts from the FDK results. The total computation time is 509–683 s for the reconstruction algorithm and 524–540 s for the enhancement algorithm on an NVIDIA Tesla C1060 GPU card.

Conclusions: By innovatively taking the temporal redundancy among 4D-CBCT images into consideration, the proposed algorithms can produce high quality 4D-CBCT images with much less streak artifacts than the FDK results, in the situation of inadequate number of projections.

INTRODUCTION

When cone beam computed tomography (CBCT) is applied to thorax or upper abdomen regions, the image quality can be heavily degraded due to patient respiratory motion. Serious motion-induced artifacts compromise the efficacy of CBCT in image guided radiation therapy (IGRT). To overcome this problem, four-dimensional CBCT (4D-CBCT), or respiratory correlated CBCT,^{1, 2, 3, 4, 5} has been developed to provide respiratory phase-resolved volumetric images. In such an imaging modality, all the x-ray projections are first retrospectively grouped into different respiratory phase bins according to a breathing signal tagged on every projection image. A CBCT image for each breathing phase is then reconstructed independently, yielding an image with much less motion-induced artifacts. More importantly, this approach provides us a set of phase-resolved volumetric images that are of particular use when treating tumors inside organs with appreciable motion, such as lung.

Although 4D-CBCT is capable of reducing the motion artifacts, it poses another challenge for reconstruction. In fact, the phase binning approach leads to insufficient number of x-ray projections in each respiratory phase bin and thus causes severe streaking artifacts, when a standard 3D-CBCT scanning protocol and reconstruction algorithm is applied. In the past, many attempts have been made towards removing or relieving this problem. For example, scanning protocols of multiple gantry rotations and slow gantry rotations^{3, 5, 6} have been proposed to considerably increase the projection number per phase. Nonetheless, the reduced mAs levels to avoid amplified imaging dose to a patient decrease signal-to-noise ratio and hence degrade image quality. Advanced reconstruction techniques have also been invented. Among them, PICCS-based algorithm reconstructs each image by regularizing the total variation of the image and its difference from a prior image obtained by using all projections.⁷ Motion estimation and correction have been incorporated into the reconstructions.⁸ It has also been proposed to split the reconstruction region according to volume of interest and treat the reconstructions separately.⁹ Meanwhile, a number of research efforts have been made on postprocessing of the 4D-CBCT images. For instance, a prior image-based approach¹⁰ has been developed by first reconstructing a blurred CBCT images with all projections and then using it to estimate and remove the streaking artifacts. It has also been investigated to enhance the CBCT image by first deforming images at all phases into a single one and superimposing them together.^{11, 12} The efficacy of these approaches, however, largely depends on the accuracy of the algorithms involved, such as deformable image registration algorithms.

Recently, nonlocal means (NLM) operators have become an effective tool for solving image restoration problems.^{13, 14, 15} The underlying assumption is that the image to be restored contains repetitive features that can be utilized to constructively enhance each other. This assumption naturally holds for 4D-CT and 4D-CBCT problems, if the temporal dimension is included, as the same image feature can always be found at different spatial/temporal locations. Inspired by this idea, we have previously investigated a 4D-CT reconstruction problem by proposing a generalized nonlocal means method, termed temporal nonlocal means (TNLM) (Refs. ¹⁶ and ¹⁷) via simulation studies. It was observed that such an approach is able to greatly increase the 4D-CT quality by suppressing noise, as well as streaking artifacts to a certain extent.

As for extending the TNLM approach to 4D-CBCT problems, although the generalization is conceptually straightforward, a series of further investigations are necessary, especially on algorithmic efficacy and computational efficiency. First of all, the TNLM-based 4D-CT reconstruction was conducted preliminarily on a digital phantom, where many realistic issues were neglected, such as data truncation. A further validation with real patient cases is necessary. Second, the success of the TNLM method relies on the robustness of identifying similar structures by comparing different patches. In contrast to 4D-CT, streaking artifacts are much more severe in 4D-CBCT images. Considering that the presence of streaks impedes the identifications of similar structures, it remains unclear whether this TNLM method is still applicable. Third, in a 4D-CBCT problem, a patch $p_{f_i}\left(x\right)$ associated with a given voxel x in phase i is compared to many other patches $p_{f_j}\left(y\right)$ in the 3D space in phase j. Those patches similar to $p_{f_i}\left(x\right)$ are identified and are used to enhance the voxel at x. As such, a weight $w_{f_i,f_j}(x,y)$ is assigned to each pair of patches with a normalization condition ${\Sigma }_{y,j}{w}_{f_i,f_j}(x,y)=1$. For a given patch $p_{f_i}\left(x\right)$, since the number of candidate patches in 4D-CBCT is much more than that in 4D-CT due to the additional spatial dimension, the efficacies of patches similar to $p_{f_i}\left(x\right)$ are effectively reduced due to the normalization, which may degrade the algorithm effectiveness. Even for image processing problems using the original NLM approaches, the robustness in 3D problems has not been fully established. Last, 4D-CBCT is much more computationally demanding than 4D-CT due to the simultaneous processing of a whole 3D volume as opposed to a 2D slice. Recently, the rapid development of GPU technology for scientific computing has offered a promising prospect to speed up computationally heavy tasks in radiotherapy.^{18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31} Although GPU has been utilized in the TNLM-based 4D-CT reconstruction study, the implementation was not optimal. A new implementation of the algorithm in the 4D-CBCT context is necessary to fully explore the GPU's computational power.

Aiming at these particular aspects, in this paper, we will present our work on solving a 4D-CBCT reconstruction problem using the TNLM method in both a simulation case and a patient case. A novel implementation of the TNLM algorithm that is particularly suitable for the GPU's parallel processing scheme will also be presented. We will also propose a TNLM-based 4D-CBCT enhancement algorithm, where 4D-CBCT images are first reconstructed by the conventional FDK algorithm³² and postprocessed by utilizing a TNLM approach. This enhancement model is, in particular, effective to remove the streaking artifacts caused by the FDK algorithm when reconstructing a 4D-CBCT image with insufficient projections at each phase.

METHODS

4D-CBCT reconstruction model

Let us divide a respiratory cycle into N_p phases labeled by i = 1, 2, …, N_p. The 4D-CBCT image of phase i is denoted by a vector f_i. P_i is the projection matrix of phase i that maps the image f_i into a set of projections corresponding to various projection angles. The measured projections for this phase are denoted by a vector y_i. We attempt to reconstruct the 4D-CBCT images by solving the following optimization problem:

$$\begin{array}{ccc}\hfill \left\{f_i\left(x\right)\right\}& =& {\mathrm{argmin}}_{\left\{f_i\right\}}\sum _{i=1}^{N_p}\{\frac{\mu }{2}\Vert P_i{f}_i-y_i{\Vert }_2^2\hfill \\ & & +\frac{1}{2}J\left[f_i,f_{i+1}\right]\},\hfill \end{array}$$ (1)

where the first term in the summation is a data fidelity term, ensuring that the projections of the reconstructed 4D-CBCT images at each phase match the corresponding observations. ‖·‖₂ stands for the standard l₂ norm of a vector. The second term, J[·, ·] is the regularization term imposed on neighboring phases as a temporal regularization to explore the interphase redundancy. A constant μ > 0 in Eq. 1 adjusts the relative weight between the data fidelity and regularization terms. A periodic boundary condition along the temporal direction is assumed, i.e., $f_{N_p+1}=f_1$. Note that, in this approach, we are reconstructing the images at all phases {f_i} altogether instead of reconstructing each of them independently.

As for the regularization term, we use a recently proposed TNLM function^{16, 17} to impose regularizations along the temporal direction between 4D-CBCT images at successive respiratory phases. As such, for two volumetric images f_i and f_j, J[f_i, f_j] is defined as

$$J[f_i,f_j]=\int \int \mathrm{d}x\mathrm{d}y{\left[f_i\left(x\right)-f_j\left(y\right)\right]}^2{w}_{f_i^{*},f_j^{*}}(x,y),$$ (2)

where x and y are coordinates on the image i and j, respectively. Suppose we know the ground truth images $f_i^{*}\left(x\right)$ and $f_j^{*}\left(x\right)$, the weighting factors $w_{f_i^{*},f_j^{*}}(x,y)$ are defined based on them and are independent of f_i(x) and f_j(x). Specifically,

$$w_{f_i^{*},f_j^{*}}(x,y)=\frac{1}{z}\exp \left[-\frac{1}{2h^2}\Vert p_{f_i^{*}}\left(x\right)-p_{f_j^{*}}\left(y\right){\Vert }_2^2\right],$$ (3)

where $p_{f_i^{*}}\left(x\right)$ denotes a small cubic volume in the image $f_i^{*}$ centering at the coordinate x. Z is a normalization factor such that ${\Sigma }_j\int \mathrm{d}y{w}_{f_i^{*},f_j^{*}}(x,y)=1$ for any voxel x in f_j. Yet, since we would never know the solution before performing the reconstruction, we will estimate the weighting factors during the reconstruction process using the latest available solutions, as will be described in Sec. 2C. This TNLM regularization term compares every pair of voxels, namely, x in image f_i and y in image f_j. If they are considered similar, a relatively high weighting factor will be assigned to this pair. The similarity is quantified by computing the l₂ distance between the two cubic volumes centered at those two voxels. The underlying reason why such a TNLM term will impose interphase similarity will be discussed in Sec. 2C.

4D-CBCT enhancement model

In this paper, we also propose an image enhancement model to directly improve the image quality of those 4D-CBCT images reconstructed from available algorithms, such as the conventional FDK-type algorithms,³² using the phase binned x-ray projections. Let us consider a set of 4D-CBCT images ${\left\{g_i\left(x\right)\right\}}_{i=1}^{N_p}$. Due to the insufficient number of projections in each phase bin, serious streaking artifacts are expected in {g_i(x)}. It is the objective of this enhancement model to directly remove these streaks and produce a new set of 4D-CBCT images ${\left\{f_i\left(x\right)\right\}}_{i=1}^{N_p}$ by exploiting the temporal redundancy between images at successive phases. This goal can be achieved by solving the following optimization problem:

$$\begin{array}{c}\hfill \left\{f_i\left(x\right)\right\}={\mathrm{argmin}}_{\left\{f_i\right\}}\left\{\frac{\mu }{2}{\Sigma }_i\Vert f_i-g_i{\Vert }_2^2+\frac{1}{2}J[f_i,f_{i+1}]\right\}.\end{array}$$ (4)

The first term ensures that the enhanced images do not largely deviate from the input low quality images, while the second term imposes the temporal regularization conditions on the solution.

It is worth mentioning that in both models, we exclude the nonlocal regularization terms [f_i, f_i] from the energy function, namely, those terms comparing cubic volumes within a single phase image, for the following two considerations. First, the efficacy of TNLM approaches relies on the fact that similar features at different spatial-temporal locations can be utilized to constructively enhance each other. It is expected that similar features can exist at spatially different locations in two neighboring phases due to the smooth respiratory motion. Yet, similar structures are hardly found in a CBCT image at a given phase. Second, it is our main goal to remove streaking artifacts caused by the insufficient number of projections in each breathing phase. If the regularization term J[f_i, f_i] were used, the streaking artifacts would be in fact strengthened rather than suppressed, since this term tends to locate those straight lines in a single image and consider them to be similar to each other. On the other hand, since the x-ray projections are usually along different directions at two different breathing phases, the streaking artifacts do not repeat themselves at different phases and thus will be suppressed by the TNLM term proposed in this paper.

Algorithms

We utilize a forward–backward splitting algorithm^{33, 34} to solve the reconstruction problem posed by Eq. 1, which allows us to obtain the solution by iteratively solving the following two subproblems:

$$\begin{array}{ccc}\hfill {\displaystyle \left(\mathrm{P}1\right):\left\{g_i^{\left(k\right)}\right\}}& =& {\mathrm{argmin}}_{\left\{g_i\right\}}\sum _{i=1}^{N_p}\Vert P_i{g}_i-y_i{\Vert }_2^2,\hfill \\ \hfill {\displaystyle \left(\mathrm{P}2\right):\left\{f_i^{\left(k\right)}\right\}}& =& {\mathrm{argmin}}_{\left\{f_i\right\}}\sum _{i=1}^{N_p}\{\frac{\mu }{2}\Vert f_i-g_i^{\left(k\right)}{\Vert }_2^2\hfill \\ & & +\frac{1}{2}J[f_i,f_{i+1}]\},\hfill \end{array}$$ (5)

where k is the index for iteration steps. The energy function in the subproblem (P1) is of a simple quadratic form, which can, therefore, be easily solved using a conjugate gradient least square (CGLS) method.³⁵ Since the images at different phases are uncoupled, this minimization problem can actually be solved in a phase-by-phase manner. Due to the underdetermined nature of this subproblem, its solution depends on the initial value. In practice, this initial value at iteration k is taken to be $\left\{f_i^{(k-1)}\right\}$.

Note that the intermediate variables $g_i^{\left(k\right)}$ are obtained purely based on the data fidelity condition, it can be interpreted as 4D-CBCT images that are contaminated by serious artifacts such as streaks. The purpose of the subsequent subproblem (P2) is to remove those artifacts while preserving the true anatomy using the interphase similarity. The subproblem (P2) of Eq. 5 can be obtained by a Gauss–Jacobi-type iterative scheme³⁶ as

$$\begin{array}{ccc}\hfill f_i^{l+1}\left(x\right)& =& \frac{\mu }{2+\mu }{g}_i\left(x\right)+\frac{1}{2+\mu }[\int \mathrm{d}y{f}_{i+1}^{\left(l\right)}\left(y\right)w_{f_i^{*},f_{i+1}^{*}}(x,y)\hfill \\ & & +\int \mathrm{d}y{f}_{i-1}^{\left(l\right)}\left(y\right)w_{f_i^{*},f_{i-1}^{*}}(x,y)],\hfill \end{array}$$ (6)

where l is the iteration index for this subproblem. For the derivation of this algorithm and the mathematical aspects, readers can refer the publications in Refs. ¹⁵ and ³⁶. Note that our reconstruction algorithm iteratively solves the two subproblems (P1) and (P2) and this iterative scheme in Eq. 6 is invoked a number of times during the entire reconstruction process. For the purpose of increasing efficiency, we only perform Eq. 6 once, each time when (P2) is solved.

The meaning of Eq. 6 is straightforward. At each iteration step, the algorithm updates the solution to $f_i^{(l+1)}$ via a weighted average over the image g_i and the images at neighboring phases $f_{i+1}^l$ and $f_{i-1}^l$. In particular, as in the square bracket in Eq. 6, this update incorporates information from images at neighboring phases in a nonlocal fashion. As such, any features that repetitively appear in successive phases, such as true anatomical structures, are preserved during the iteration. In contrast, those features that do not repeat, such as streaking artifacts, are suppressed.

Moreover, since the weighting factors $w_{f_i^{*},f_j^{*}}(x,y)$ are defined according to the ground truth images $f_i^{*}\left(x\right)$ and $f_j^{*}\left(y\right)$ that are not known beforehand, we estimate these weights during the iteration according to the latest available images $g_i^{\left(k\right)}\left(x\right)$ and $g_j^{\left(k\right)}\left(y\right)$ as

$$w_{f_i^{*},f_j^{*}}(x,y)\approx \frac{1}{z}\exp \left[-\frac{1}{2h^2}\Vert p_{g_i^{\left(k\right)}}\left(x\right)-p_{g_j^{\left(k\right)}}\left(y\right){\Vert }_2^2\right].$$ (7)

Since a reconstructed 4D-CBCT image physically represents the x-ray attenuation coefficient at a spatial point, its positiveness has to be ensured during the reconstruction in order to obtain a physically meaningful solution. For this purpose, we perform a correction step on the reconstructed images at each iteration by setting any voxels with negative values to be zero. In practice, we also initialize the reconstruction process by estimating $f_i^{\left(0\right)}$ using the FDK algorithm. In summary, the algorithm solving the 4D-CBCT image reconstruction problem is as follows:

TNLM Reconstruction (TNLM-R) Algorithm:

Initialize: $f_i^{\left(0\right)}$ for i = 1, …, Np.
For k = 0, 1, …, do the following steps until convergence:
1.	Solve (P1) using CGLS with initial value $\left\{f_i^{(k-1)}\right\}$ to obtain $\left\{g_i^{\left(k\right)}\right\}$;
2.	Update weights $w_{f_i^{*},f_j^{*}}$ according to Eq. 7 using the image$\left\{g_i^{\left(k\right)}\right\}$;
3.	Compute images $\left\{f_i^{\left(k\right)}\right\}$ according to Eq. 6;
4.	Ensure image positiveness: $f_i^{\left(k\right)}=0,\mathrm{if}{f}_i^{\left(k\right)}<0.$

We also note that the enhancement model in Eq. 4 is identical to the second subproblem, (P2) in Eq. 5, in the reconstruction model. Both of them attempt to generate a new image set based on the input g_i by solving the minimization problem. In the enhancement model g_i is the input 4D-CBCT images obtained using another reconstruction algorithm, while in the reconstruction model g_i is an intermediate variable produced by the first subproblem (P1). As such, the algorithm for the enhancement model is only part of the one for the reconstruction. The only difference is that the weighting factors are estimated using the latest available images $f_i^{\left(l\right)}\left(\mathit{x}\right)$ and $f_j^{\left(l\right)}\left(\mathit{y}\right)$.

TNLM Enhancement (TNLM-E) Algorithm:

Initialize: $f_i^{\left(0\right)}=g_i$ for i = 1, …, Np.
For k = 0, 1, …, do the following steps until convergence:
1.	Update weight $w_{f_i^{*},f_j^{*}}$ according to Eq. 7 using the image $\left\{f_i^{\left(k\right)}\right\}$;
2.	Compute images $\left\{f_i^{\left(k+1\right)}\right\}$ according to Eq. 6.

Implementation

One drawback of the TNLM-based reconstruction and enhancement algorithms is high computational burden. During the implementation, a cubic volume $p_{f_i^{\left(k\right)}}\left(\mathit{x}\right)$ centering at the voxel x on the image f_i is compared with cubic volumes centered at all other voxels y on the image f_j to compute the weighting factors $w_{f_i^{*},f_j^{*}}(\mathit{x},\mathit{y})$. If this cube has (2d + 1) voxels in each dimension, the complexity of such an algorithm is in the order of O(N³N³(2d + 1)³), where N is the dimension of the 4D-CBCT images. However, this approach is neither computational efficient nor necessary. In fact, the voxels that are similar to x will locate in its vicinity in the neighboring phases due to the finite motion amplitudes. Therefore, it is adequate to search for the similar voxels only within a search window centering at the voxel x as opposed to searching over the entire image domain. In practice, we set this search window to be a cubic volume with (2M + 1) voxels in each dimension to reduce the algorithmic complexity to O(N³(2M + 1)³(2d + 1)³). Moreover, since $w_{f_i^{*},f_j^{*}}(\mathit{x},\mathit{y})$ is a mutual weight factor shared by the voxel x and the voxel y, apart from the different normalization factors, the nonlocal update step in Eq. 6 can be implemented in such a way that both the image at phase i and the one at phase j are updated simultaneously using the common weighting factor. This strategy can almost save half of the computation time for the nonlocal update step.

To speed up the computation, we implement our algorithms on NVIDIA CUDA programing environment using an NVIDIA Tesla C1060 card. This GPU card has a total number of 240 processor cores (grouped into 30 multiprocessors with 8 cores each), each with a clock speed of 1.3 GHz. It is also equipped with 4 GB DDR3 memory, shared by all processor cores. In the remaining of this subsection, we will describe carefully the implementations of our algorithms on a GPU platform to fully explore the GPU's parallel processing capability for our problems.

CGLS algorithm

The subproblem (P1) in the reconstruction algorithm is a simple quadratic model for CBCT reconstruction. We utilize a CGLS method³⁵ to efficiently solve this problem, which involves a series of matrix-vector, scalar-vector, and vector–vector operations. In terms of GPU implementation, those vector–vector and scalar-vector operations are handled by CUBLAS library.³⁷ As for the matrix-vector operations, specifically the multiplications of a projection matrix P_i or its transpose $P_i^T$ with a vector are performed in such a way that these matrices are not stored due to the limited GPU memory space. In particular, the multiplication with P_i can be interpreted as a forward x-ray projection calculation and is conducted by a ray-tracing algorithm on GPU. The multiplication with $P_i^T$ is achieved by a numerical algorithm developed previously,²¹ which avoids the GPU memory writing conflict issue. We note that these complicated implementations are quite different from those in our previous 4D-CT reconstruction work, where the projection matrices P_i can be stored in GPU in a sparse matrix format and the multiplications can be simply conducted by calling sparse-matrix operation functions.

TNLM update

The implementation of the TNLM update part, namely, Eq. 6, could be in principle very similar to what has been used in the TNLM-based 4D-CT reconstruction work,¹⁵ due to the similarity of these problems in terms of mathematical structures. However, compared to the 4D-CT problem, the additional spatial dimension in 4D-CBCT problem increases the algorithm complexity from O(N²(2M + 1)²(2d + 1)²) to O(N³(2M + 1)³(2d + 1)³). For a problem of a typical size, this implies a dramatically reduction of computational efficiency, if the same implementation strategy is used. We have actually implemented this part in the same way as described in the TNLM-based 4D-CT reconstruction work, where each GPU thread updates a voxel value and the computational efficiency was found to be hardly acceptable.

The disadvantages of this straightforward implementation are twofold. (1) When a GPU thread computes the expression in Eq. 7 for a particular voxel x, it accesses a lot of voxel values around x. As there are a lot of threads computing this expression for many voxels nearby at the same time, there exist considerably redundant accesses to the slow GPU memory. (2) Only when GPU threads visit the memory in a coalesced fashion, namely, consecutive threads visit consecutive memory addresses simultaneously, can a high GPU performance be achieved. When evaluating Eq. 7, each thread visit voxels around its assigned voxel without considering synchronization with others, causing uncoalesced memory access and low efficiency.

Aiming at removing or relieving these problems, we developed a whole new implementation regarding the computations of Eqs. 6, 7. First, we rewrite Eq. 6 as

$$\begin{array}{ccc}\hfill f_i^{\left(l+1\right)}\left(\mathit{x}\right)& =& \frac{\mu }{2+\mu }{g}_i\left(\mathit{x}\right)+\frac{1}{2+\mu }\int \mathrm{d}\mathit{\delta }\hfill \\ & & \times [f_{i+1}^{\left(l\right)}\left(\mathit{x}+\mathit{\delta }\right)w_{f_i^{*},f_{i+1}^{*}}\left(\mathit{x},\mathit{x}+\mathit{\delta }\right)\hfill \\ & & +f_{i-1}^{\left(l\right)}\left(\mathit{x}+\mathit{\delta }\right)w_{f_i^{*},f_{i-1}^{*}}\left(\mathit{x},\mathit{x}+\mathit{\delta }\right)],\hfill \end{array}$$ (8)

where δ = (δ₁, δ₂, δ₃) is a vector indexing the relative shift of voxel y with respect to x in the search window. The integral is numerically achieved by looping over all δ's and accumulating the summation. For each δ in this loop, the computations of the weighing factors according to Eq. 7, for instance $w_{f_i^{*},f_{i+1}^{*}}\left(\mathit{x},\mathit{x}+\mathit{\delta }\right)$, are conducted in the following three steps. To simplify notation, we denote $g_i^{\left(k\right)}\left(x\right)$ by g_i(x). (1) Compute the shifted difference square at all voxels t(x) = [g_i(x) − g_j(x + δ)]². Note this step involves a coalesced memory access, if results at all voxels are computed simultaneously by a number of GPU threads, each for a voxel. (2) We note that the squared norm term in Eq. 7 can be rewritten into

$$\begin{array}{ccc}\hfill \Vert p_{g_i}\left(\mathit{x}\right)-p_{g_j}\left(\mathit{y}\right){\Vert }_2^2& =& \sum _s{[g_i\left(\mathit{x}+\mathit{s}\right)-g_j\left(\mathit{x}+\mathit{\delta }+\mathit{s}\right)]}^2\hfill \\ & =& \sum _{s}t(\mathit{x}+\mathit{s}),\hfill \end{array}$$ (9)

where s = (s₁, s₂, s₃) is a vector labeling the location of a voxel relative to the voxel x in a cube. Once the intermediate result t(x) is available from the previous step, evaluating Eq. 9 is equivalent to a convolution operation, namely, $p_{g_i}\left(\mathit{x}\right)-p_{g_j}{\left(\mathit{y}\right)}_2^2=t\left(\mathit{x}\right)\otimes h\left(\mathit{s}\right)$, where h(s) = 1 is a 3D kernel of the same size as the cube. Furthermore, the convolution kernel can be viewed as a product of three functions of s₁, s₂, and s₃ as h(s) = h₁(s₁)h₂(s₂)h₃(s₃), where h_i(s_i) = 1 for i = 1, …, 3. This implies that the 3D convolution with h(s) can be conducted by sequentially performing three 1D convolutions with h_i(s_i), respectively. This reduces the complexity of the convolution from O((2d + 1)³) to O(3(2d + 1)). (3) Finally, we compute the weighting factors $w_{f_i^{*},f_{i+1}^{*}}\left(\mathit{x},\mathit{x}+\mathit{\delta }\right)$ in Eq. 7 using the results $p_{g_i}\left(\mathit{x}\right)-p_{g_j}{\left(\mathit{y}\right)}_2^2$. In retrospect, the above three steps effectively eliminate the redundant memory access by using a convolution step. They also visit GPU memories in a coalesced manner.

Experiments and metrics

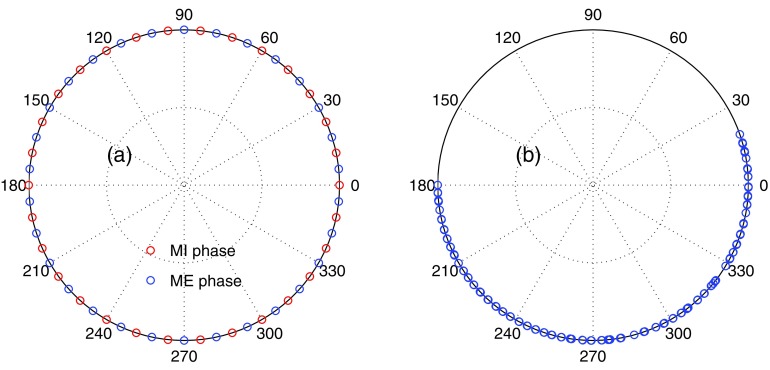
To evaluate the performance of our algorithms, we have conducted studies on a digital NURBS-based cardiac-torso (NCAT) phantom³⁸ and one real clinical case. All of the 4D-CBCT images are of a resolution 128³ voxels and the voxel size is 0.2 cm along all three spatial dimensions. For the NCAT phantom, it is generated at thorax region with a high level of anatomical realism such as detailed bronchial trees. The virtual patient has a regular respiratory pattern of a period 4 s and the respiratory cycle is divided into ten phases. A 2 min 4D-CBCT scan is simulated, within which a total number of 300 x-ray projections equally spaced in a 360° gantry rotation are taken. The source-to-isocenter distance and the source-to-detector distance are 100 cm and 153.6 cm, respectively. The x-ray detector size is 40.96 × 40.96 cm² with a resolution 512 × 512 pixel². All of these parameters mimic a realistic configuration in Elekta XVI system (Elekta AB, Stockholm, Sweden). The virtual patient is purposely off-center positioned such that the isocenter is on a tumorlike structure inside the lung and the phantom outside the reconstructed region is truncated. For each projection image, we first identify the associated gantry angle and the breathing phase. The x-ray projection is then numerically generated using Siddon's ray-tracing algorithm.³⁹ These projection images are grouped according to their breathing phases, so that each phase is associated with 30 projections equally spaced in a full 360° gantry rotation. The projection angles for the maximum inhale (MI) and the maximum exhale (ME) phases are illustrated in Fig. 1a.

Figure 1.

Illustration of the x-ray projection angles for (a) the NCAT phantom and (b) the patient case. Each small circle represents one x-ray projection. The inset in (b) shows a zoom in view of the projections around 0° to demonstrate the projection clustering issue.

The real patient is scanned using an Elekta XVI system. A total number of 1169 x-ray projections are acquired in a 200° gantry rotation in 4 min. The patient is positioned such that the isocenter is inside the tumor in the left lung. The respiratory motion signal is obtained by using Amsterdam Shroud algorithm^{40, 41} and the acquired x-ray projections are binned into ten respiratory phases according to it. Though on average there are 116.9 x-ray projections per phase, this number is only nominal. In fact, the patient breathing cycle is about 4 s long and only about 60 cycles are covered during the scan. For a given phase at a given breathing cycle, the high x-ray imaging rate leads very similar projection images due to their very close projection angle. Those duplicated projections do not provide substantially different x-ray projection information useful for the 4D-CBCT reconstruction. As a consequence, there are only about 50–60 distinguishable and useful projections in each phase bin. This effect is illustrated in Fig. 1b.

We remark that the scanning protocols are different between the simulation and the patient cases. For the NCAT phantom, it is a relatively simpler case because of the absence of noise and data truncation (discussed in Sec. 4A). Therefore, we reduce the scan time to 2 min to increase the difficulty and hence test the capability of our algorithm. The 360° projection angle range is selected for simplicity. It is expected that the different projection angular range in the patient case, namely, a short scan covering about 200°, has little impacts on the image quality, as both the full-scan and the short-scan covers enough angular range for reconstruction. In particular, for iterative reconstruction, the CBCT image is adjusted by numerical algorithms to match all projections. As long as the projections cover a large enough angular range to determine the solution, the solution quality is barely affected by the projection angular range.

Apart from visual inspections, quantitative metrics are necessary to assess the reconstructed 4D-CBCT image quality. In our studies, the first metrics we utilized is contrast-to-noise ratio (CNR). For a given region of interest (ROI), CNR is calculated as CNR = 2|S − −S_b|/(σ + σ_b), where S and S_b are the mean pixel values in the ROI and in a nearby region considered as the background, respectively. σ and σ_b are the standard deviation of the pixel values inside the ROI and in the background.

The main advantage of our TNLM-based 4D-CBCT enhancement algorithm is its capability of removing streak artifacts from input images. To quantify this effect, we define streak-reduction ratio (SRR) to quantitatively measure how much streaks in the input images, namely, the FDK results, are removed by the TNLM enhancement algorithm. For a given phase, the SRR is defined as

$$\mathrm{SRR}=\frac{\mathrm{TV}\left(f_{\mathrm{FDK}}-f^{*}\right)-\mathrm{TV}(f_{\mathrm{TNLME}}-f^{*})}{\mathrm{TV}(f_{\mathrm{FDK}}-f^{*})},$$ (10)

where f* stands for the ground truth images for the corresponding phase. f_FDK and f_TNLME represent the images reconstructed by the FDK algorithm and our TNLM-E algorithm, respectively. The difference term, such as (f_FDK − f*), is expected to mainly contain the streak artifacts, if there are any. Therefore, by taking a total variation seminorm defined as $\mathrm{TV}\left(h\right)=\int \mathrm{d}\mathit{x}\left|\nabla h\left(\mathit{x}\right)\right|$, we are able to use a single number to quantify the amount of streaks in the reconstruction results. Note that this TV term contains spatial image gradient, its value is dominated by the region where the intensity largely fluctuates. As such, TV(f_FDK − f*) − TV(f_TNLME − f*) represents an estimation regarding the absolute amount of streaks that the TNLM-E algorithm removes from the FDK results and hence the SRR defined in Eq. 10 reports this effect in a relative manner. Though the calculation of SRR is straightforward for the NCAT phantom case, one practical difficulty for the patient case is the lack of the ground truth 4D-CBCT images. In practices, we choose f* to be the CBCT image reconstructed via the FDK algorithm using all the projections at all phases. This is also the image obtained by averaging the ten phases of the FDK results, since FDK reconstruction is a linear operation. The CBCT image chosen as such is free of streaking artifacts due to the large number of projections. However, some anatomical structures in f* are blurred due to the patient respiratory motion. Though f* is not the ground truth image any more, it can be considered to be the ground truth image blurred by the motion artifacts. It is expected that using such a f* can still give us a reasonable estimation regarding the amount of streaks in the reconstructed images. This is because the TV term is only sensitive to the high image gradient parts, and the blurring in f* will only lead to slowly varying components in the difference images and hence not considerably impacts on the value of the TV term. Note that we do not compute SRR for the reconstruction cases, as this metric is designed to quantify the amount of streaks reduced from the original input 4D-CBCT images. The TNLM-R algorithm reconstructs the 4D-CBCT images from scratch and does not require input images. Hence, the SRR metric does not apply.

EXPERIMENTAL RESULTS

Visualization of the results

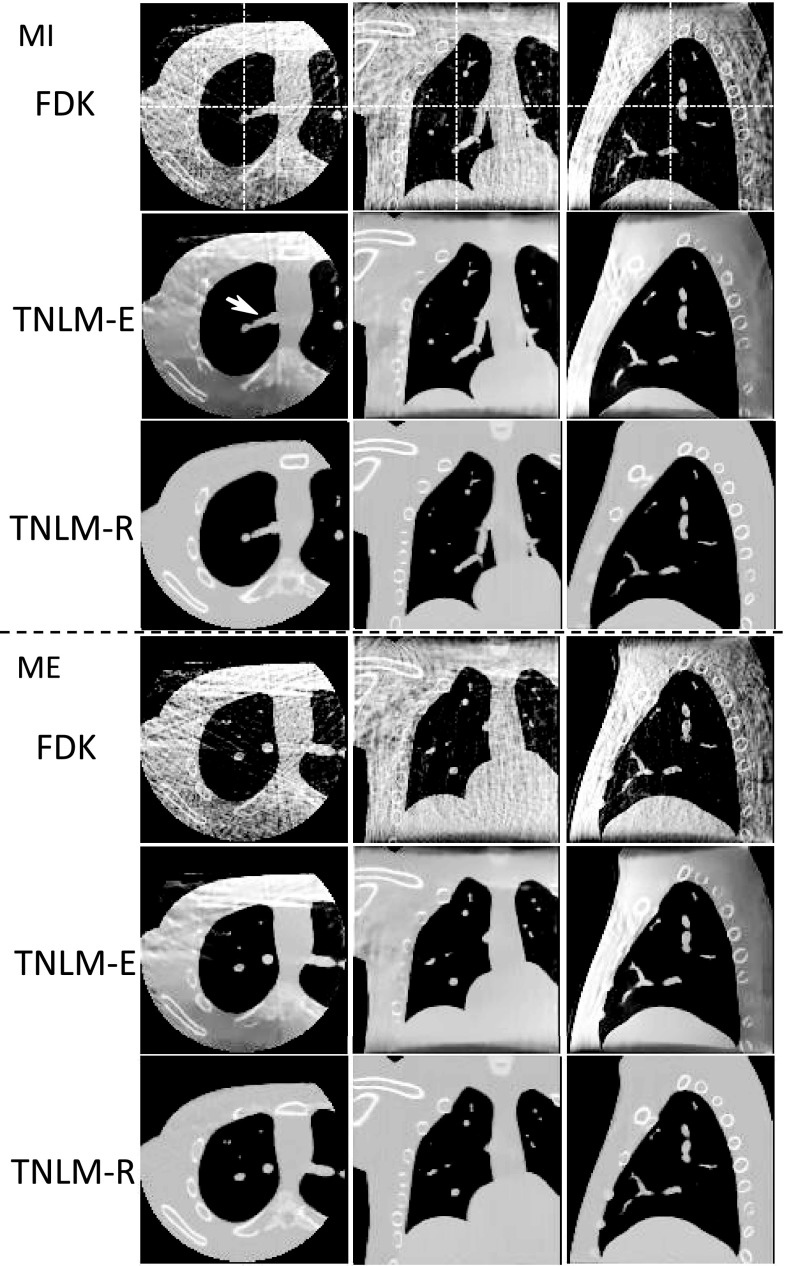
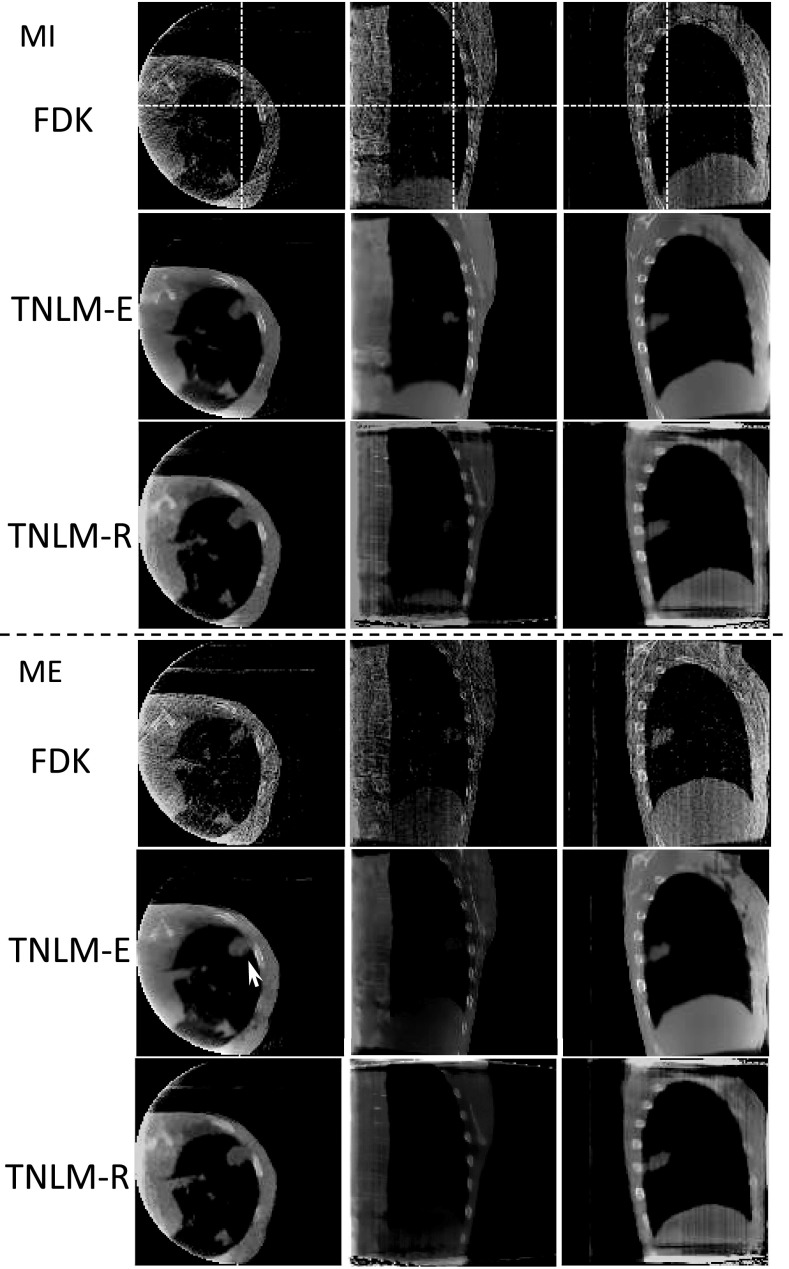
We first present the reconstructed and the enhanced 4D-CBCT images for the visualization purpose in Figs. 23 for the NCAT case and the patient case, respectively. In both figures, the top group shows the set of 4D-CBCT images at the MI phase, while the bottom group is for the ME phase. Within each group, three rows correspond to the FDK results, the results from the TNLM enhancement algorithm (TNLM-E) using the FDK results as the input, and the TNLM reconstruction (TNLM-R) results, respectively. Due to insufficient number of x-ray projections in each phase, obvious streak artifacts are observed in the 4D-CBCT images reconstructed from the FDK algorithm. On the other hand, the images produced by the other two methods undoubtedly demonstrate the efficacy of our algorithms, as those streaking artifacts are effectively suppressed, while the true anatomical structures are well preserved. As FDK gives the right structural location information despite the obvious streaks, comparing the structure locations in our methods with those in the FDK results can be used to justify the fidelity of our algorithms in terms of preserving true structures. The results demonstrate this point. Take the tumor pointed out by the arrow in the patient case as an example. The locations relative to the nearest rib are unchanged among all three methods.

Figure 2.

4D-CBCT images of the NCAT phantom at the MI phase (top) and the ME phase (bottom). In each group, the three rows are the FDK results, the FDK results enhanced by the TNLM-E algorithm, and the TNLM-R results. The white arrows indicate the tumorlike structure used to compute CNR and crosshairs show the locations of different views.

Figure 3.

4D-CBCT images of a patient at the MI phase (top) and the ME phase (bottom). In each group, the three rows are the FDK results, the FDK results enhanced by the TNLM-E algorithm, and the TNLM-R results. The white arrows indicate the tumorlike structure used to compute CNR and crosshairs show the locations of different views.

Quantitative analysis

In the two cases we studied, the ROIs for CNR measurements are chosen to be the tumor or a tumorlike structure close to the isocenter in three-dimensional space, as indicated by the arrows in Figs. 23, as these structures are usually of interest in the 4D-CBCT images. We measure the CNRs in both cases at each respiratory phase for the results obtained by all the three algorithms, namely, FDK, TNLM-R, and TNLM-E algorithms. We use the averaged CNRs over all ten phases to represent on average the CNR level for each algorithm for a comparison. The results are shown in Table 1. Due to the insufficient projection numbers in each breathing phase, large streaks lead to high levels of fluctuation of image intensity in the FDK results, causing relatively low CNRs for the FDK algorithm. In contrast, both the two TNLM-based algorithms can considerably increase the CNRs. These numbers undoubtedly demonstrate that our TNLM-based algorithms outperform the conventional FDK algorithm in terms of CNR ratio.

Table 1.

CNRs and SRRs for the 4D-CBCT images of the NCAT phantom and the patient case obtained using various algorithms.

	Algorithm	NCAT	Patient
CNR	FDK	6.8149	3.6959
	TNLM-R	21.3043	9.4593
	TNLM-E	22.7081	10.1515
SRR (%)	TNLM-E	85.09	88.27

To report the effects of reducing streak artifacts for the FDK-reconstructed 4D-CBCT set by the TNLM-E algorithm, we have also computed the SRR for each phase and reported the average over ten phases. As seen in Table 1, 85% and 88% of the streaks in the FDK results are removed by the TNLM-E algorithm, which clearly demonstrates its efficacy.

Computational efficiency

Our TNLM-based 4D-CBCT reconstruction and enhancement algorithms are implemented on NVIDIA CUDA programing environment using a NVIDIA Tesla C1060 card. The total computation time as well as the time per iteration are listed in Table 2, where the total computation time is for seven iterations for the TNLM-R algorithm and ten iterations for the TNLM-E algorithm, corresponding to the results shown in Figs. 23. The time per iteration for TNLM-R algorithm is longer than that in the TNLM-E algorithm. Since the enhancement algorithm is the same as the subproblem in the reconstruction algorithm in terms of computational complexity, this difference in computation time comes from the CGLS algorithm used in the subproblem (P1) in Eq. 5. Moreover, this difference is larger in the patient case than in the NCAT phantom case due to more x-ray projections in the former.

Table 2.

Total computation time t_tot and time per iteration t_iter of our TNLM-based algorithms using a NVIDIA Tesla C1060 GPU card.

	NCAT (s)		Patient (s)
	ttot	titer	ttot	titer
TNLM-R	509.8	72.8	683.4	97.6
TNLM-E	524.3	52.4	540.9	54.1

DISCUSSIONS

Dependence on FDK algorithm

Since the TNLM-E algorithm takes the FDK results as inputs, the resulting image quality highly depends on the input images, specifically, on whether those true anatomical structures can be observed in the FDK results. For the NCAT phantom, due to the limited number of projections in each phase bin, i.e., 30, some structures are hardly resolved by the FDK algorithm. For instance, the vertebral body and the sternum are seriously contaminated by the streaks. In this context, the TNLM-E algorithm is not able to find similar structures between breathing phases, resulting in regions with low image quality. See the area close to the sternum in the TNLM-E results in Fig. 2. While for those areas where clear structures can already be observed in the FDK results, such as inside the lung region of the NCAT phantom, TNLM-E algorithm can distinguish between these structures and the streaks and is able to suppress the latter to a satisfactory extent. This is also the case for the patient case, where a relatively large number of projections are available in each phase and relatively clear patient anatomy can be seen on the FDK results.

In contrast, FDK results are only used to initialize the iteration process in the TNLM-R algorithm. Its performance is not largely related to the corresponding FDK results. For the NCAT phantom, with high quality projections the TNLM-R algorithm is capable of reconstructing images of high quality, demonstrating its advantages over the TNLM-E algorithm. Especially, the vertebral body and the sternum can be clearly observed and overall there are less streak artifacts in the entire images than in the TNLM-E results. When it comes to the patient case, it is found that the results of TNLM-R are not obviously superior to those of TNLM-E, possibly owing to the following two reasons. First, the FDK algorithm performs very well in this case by itself due to the sufficient number of projections and hence provides good input images for the TNLM-E algorithm. Second, TNLM-R algorithm encounters a well-known data truncation issue in this case. In an iterative CBCT reconstruction problem, when the reconstructed region is smaller than the whole patient body, it is impossible to satisfy the projection condition Pf = y in the reduced reconstruction region, leading to artifacts around the image boundary where the intensity tends to blow up. See, for example, the artifacts around the superior and inferior regions of the TNLM-R results in Fig. 2. On the other hand the FDK algorithm is a direct algorithm and does not have severe truncation issues at the top and the bottom regions. The enhancement model, therefore, does not encounter this problem. Since the main objective here is to study the use of TNLM method in 4D-CBCT, for the NCAT phantom we deliberately truncate the phantom before generating projections and hence the truncation problem does not appear in the TNLM-R algorithm in this phantom case.

Computation time

Although the computation time for these cases are long and cannot compete with the FDK reconstruction algorithm, the efficiency we have achieved is already a considerable improvement over the CPU implementation. In our work, we did not implement our algorithms on CPU due to the unacceptably long computation time. Since there is no work on the TNLM algorithm reported previously to our knowledge, we estimate its CPU computation time based on the NLM algorithm due to the similar computation complexity. In fact, even for the NLM algorithm, its application is mainly limited to 2D images because of its computational complexity. For those 3D image-processing problems with the NLM method, the NLM filter is usually used, in the sense that the image is enhanced by using a scheme akin to Eq. 6 but for only one iteration step. For instance, it has been reported that it takes 21 790 s to perform a NLM operation on a 3D MRI image for an image denoising purpose⁴² using a typical CPU. Considering the image size difference (181 × 217 × 181 for this MRI case and 128³ for our problem) and the fact that there are ten phases in our problem, it can be estimated that the computation time for one step TNLM update is about 18 h on CPU for the cases studied in this paper. Comparing this number with those listed in Table 2, we have achieved a considerable speed up using the GPU card over a typical CPU with our careful implementation.

Another note regarding the computation time is the necessity of the complex implementation described in Sec. 2D1 regarding the TNLM update. We have also implemented this step using a simple approach previously employed in the 4D-CT reconstruction work,¹⁵ where each thread updates a voxel value. Because of the disadvantages of unnecessary and unsynchronized memory access mentioned in Sec. 2D1, the computational efficiency is so low that it takes about 460 s to compute the TNLM update in Eq. 6. Compared with the numbers reported in Table 2, an eightfold speedup has been achieved in our GPU-friendly implementation. We remark that this implementation will be also of practical meanings to the conventional NLM method used in the context of image denoising, for instance, for the purpose of kV CBCT noise removal.⁴³

Parameter selection

Parameter selection is another important issue to iterative reconstruction algorithms of this type. The parameter μ in Eqs. 1, 4 controls the relative weights between the data fidelity term and the TNLM term. From Eq. 6, it is also seen that this parameter governs how much information is borrowed from the two neighboring phases to enhance the current one so as to smear out streaks and enhance structures. When conducting experiments, we have manually adjusted this parameter, so that the best image quality to observer eyes is achieved. It is found that the reconstruction results are not sensitive to the exact μ value, as long as μ ∼ 1, and hence μ = 1 is used throughout this paper. This implies that, in each TNLM update, the output image contains ∼1/3 information from the current phase, and ∼2/3 from its previous and subsequent phases.

Another group of parameters is d and M relating to the cube size and the search window size. Small values for these two parameters are preferred for the consideration of efficiency. The parameter d defines a cube centering at each voxel, which allows the algorithms to justify similarity between two cubes by comparing the image features within them, e.g., edges. Therefore, the parameter d should be selected such that there exist identifiable structures in the cube. Throughout this paper, d = 1 is used, which corresponds to a cube size of 3 × 3 × 3 voxels. This seems to be a good choice to identify structure similarities at a relatively low computational expense. This parameter is also consistent between the phantom case and the patient case, and perhaps for more practical cases, because the main features in a CBCT image, namely, edges, can be seen reasonably well inside this cube. Further study regarding the robustness of this parameter will be our future work.

As for the parameter M, its introduction is for reducing the search region. Therefore, M should be large enough to allow the similar cubes to be found inside this search region. In both cases, we used M = 4, corresponding to a search region of 9 × 9 × 9 voxels or equivalently a region with a side length of 1.8 cm. For a typical patient motion, we believe this is large enough for any structures to move between successive phases, except for some extreme cases, such as cough, which may lead to a sudden change of structure locations.

Finally, the sharpness of the resulting images is impacted by the parameter h in the weighting factors defined in Eq. 3. The merit of the TNLM approaches lies in Eq. 6, where voxels are averaged to remove artifacts and reinforce signals. In this process, the weights between voxels are automatically determined by comparing the cubes centering at them. The choice of h governs the strictness and correctness when justifying the similarity. For instance, for a given voxel, a large h value makes this weighting factor insensitive to the difference between cubes and tends to give high weights to more voxels. Hence, when the weighted average step of Eq. 6 is performed, voxel values at many places are mixed together, which smoothens the resulting images. On the other hand, a too small value of h leads to a strict criterion that cannot detect similar cubes successfully, causing observable artifacts. In practice, we manually select the h value for each case to yield visually the best results.

Algorithm convergence

Regarding the convergence of the TNLM algorithm, we remark that the algorithm converges for a fixed set of weights $w_{f_i^{*},f_j^{*}}$ due to the convergence properties established for the forward–backward splitting algorithm^{33, 34} and the Gauss–Jacobi iteration.³⁶ However, in practice, the weighting factors are not known before solving the problem. The strategy of estimating the weights using the latest available images does not warrant convergence anymore. In principle, the generated sequences of images $f_i^{\left(k\right)}\left(x\right)$ may oscillate during the iteration due to this adaptive weight estimation. Yet, this potential violation of convergence is not found to be a problem in our studies and many other similar NLM approaches.^{13, 14, 15} But one should be cautious when using this adaptive weight estimation strategy. The related mathematical problems will be future research topic.

CONCLUSION

In this paper, we have developed a novel iterative 4D-CBCT reconstruction algorithm and an enhancement algorithm via temporal regularization. The 4D-CBCT images of different phases are reconstructed or enhanced simultaneously by minimizing a whole energy function consisting of a data fidelity term of all the respiratory phases and a temporal regularization between every two neighboring phases, in which a TNLM method is employed to take the temporal redundancy of the 4D-CBCT images into account. The only difference between the reconstruction algorithm and enhancement algorithm is that, in our reconstruction algorithm the data fidelity term is to enforce the consistency between the reconstructed image and the measured projections, while in the other the data fidelity term ensures that the enhanced images do not deviate from the input images largely. The energy functions in these two algorithms are minimized utilizing a forward–backward splitting algorithm and a Gauss–Jacobi update scheme. These algorithms are implemented on a GPU platform with a carefully designed scheme to ensure the computational efficiency.

We have tested our algorithms on a digital NCAT phantom and a clinical patient case. The experimental results indicate that both the reconstruction and the enhancement algorithms lead to better image quality than the conventional FDK algorithm. In particular, quantitative evaluations indicate that, compared with the FDK results, our TNLM-R method improves CNR by a factor of 2.56–3.13 and our TNLM-E method increases the CNR by 2.75–3.33 times. The TNLM-E method also removes over ∼80% of the streak artifacts from the FDK reconstruction results. The total computation time is 509–683 s for the reconstruction algorithm and 524–540 s for the enhancement algorithm on a NVIDIA Tesla C1060 GPU card.

Comparing the TNLM-R and TNLM-E algorithms, it is found that the two algorithms attain their own advantages as well as disadvantages. TNLM-E is comparable to or slightly better than the TNLM-R algorithm in terms of computation time. Yet, the resulting image quality is limited by the input 4D-CBCT images obtained by other algorithms such as FDK. Especially when there are insufficieny number of projections, 4D-CBCT image quality may not be satisfactory. On the other hand, the TNLM-R algorithm reconstructs images from the x-ray projections directly. In the absence of other problems such as data truncation, the resulting image quality is higher than that from TNLM-E, as evidenced by the NCAT phantom case. The computation time may be, however, prolonged due to one more subproblem to solve. At present, users may choose one of the two algorithms for an overall consideration of image quality and performance. Our future work will focus on the further improvement of computational efficiency by algorithmic optimization and using hardware with higher performance, as well as to develop better algorithms to improve image quality.