Trading Stages: Life Expectancies in Structured Populations

Abstract

Interest in stage-and age structured models has recently increased because they can describe quantitative traits such as size that are left out of age-only demography. Available methods for the analysis of effects of vital rates on lifespan in stage-structured models have not been widely applied because they are hard to use and interpret, and tools for age and stage structured populations are missing. We present easily interpretable expressions for the sensitivities and elasticities of life expectancy to vital rates in age-stage models, and illustrate their application with two biological examples. Much of our approach relies on trading of time and mortality risk in one stage for time and risk in others. Our approach contributes to the new framework of the study of age- and stage-structured biodemography.

1 Introduction

Biologists and demographers have a long standing interest in describing and understanding the evolutionary forces behind age-specific survival patterns (Hamilton, 1966), and studies of senescence and aging now span and bring together social and natural science (Carey and Tuljapurkar, 2003; Vaupel et al., 1998; Ricklefs, 2010; Monaghan et al., 2008). In recent years, increasing attention is given to stages, individual characteristics that determine population dynamics and evolution (Pfister, 1998; Tuljapurkar et al., 2009). Stages are characteristics other than age that influence vital rates (e.g., growth, survival, reproduction), may be discrete (e.g., developmental stages) or continuous (e.g., size) and can comprise many attributes: biomarkers, health states, development, morphology, behavior, physiology, or location (Caswell, 2001). The changing stages experienced by an individual follow a trajectory over the course of life. In a population, mortality, survivorship, and life expectancy become functions of such trajectories of phenotypic stages, and of the variation among trajectories. Age alone cannot describe stage changes and therefore standard age-based demography has been extended to stage-and-age structured demography. Examples include (a) models of plant populations that track developmental stage and size (Cochran and Ellner, 1992; Caswell, 2001; Tuljapurkar and Horvitz, 2006; Horvitz and Tuljapurkar, 2008; Caswell, 2006, 2009; Silvertown et al., 2001); (b) size-and-age structured models for mammals including Soay sheep, red deer, and marmots (Coulson and Tuljapurkar, 2008; Ozgul et al., 2009, 2010); (c) human aging and epidemiology, in which biomarkers and health status have been shown to affect mortality and longevity (Crimmins et al., 2005; Yashin et al., 2006, 2009); and (d) in many species of birds, and other animals, reproductive stages switch frequently over time, and multi-stage models are needed to describe this pattern (Fujiwara and H., 2002; Lebreton, 1996; Tuljapurkar et al., 2009; Steiner et al., 2010; Orzack et al., 2011). Such multi-stage models are of course versions of multi-state branching processes and some of their properties may be deduced from results in that subject (Bartlett, 1978; Caswell, 2001).

Stage-structured models yield new insights into mortality change and longevity. In many species of birds, stage-age dynamics generate substantial heterogeneity among individuals that in turn produces large variation in age at death (Tuljapurkar et al., 2009; Steiner et al., 2010; Orzack et al., 2011). Other examples include: plants, in which expected lifespan varies with birth stage, and the dynamics of stage-structure determines mortality change and old-age mortality plateaus (Horvitz and Tuljapurkar, 2008; Roach and Gampe, 2004); some mammalian populations, in which growth and size-dependent survival change dramatically with climate (Ozgul et al., 2009), and humans, who display great variation in physiological stage trajectories that determine variation in mortality and longevity (Yashin et al., 2009). Stage dynamics are even of great interest in populations of supposedly simple individuals such as bacteria (Leibler and Kussell, 2010; Lindner et al., 2008).

Here we show how stage-age dynamics shape survivorship and life expectancy, developing general tools that extend the recent literature on these topics (Caswell, 2009, 2011). The mathematics used here draws on and rests on known results about classical absorbing Markov chains (Chung, 1967; Iosifescu, 1980; Kemeny and Snell, 1960) and perturbations of such chains (Schweitzer, 1968). Our results allow us to explore key biological features of stage-and-age structured demography that cannot be described in age-only demography. First, an individual’s stage at birth affects its subsequent stage and so determines cohort survivorship and life expectancy: e.g., in plants where an individual may be born as a seed or in a newly produced clonal (vegetative) stage; and in a mammalian population where an individual’s birth size determines subsequent growth and survival. Differences in birth stage may be caused by genetics, environments, or by maternal effects (e.g., differences in offspring within a clutch or litter). Second, when survival rates depend on both age and stage, increased survival of, say, large young individuals has different effects than increased survival of smaller young, or of larger, older individuals. Third, stage dynamics depend on switching probabilities, the probabilities that an individual changes its stage over time. These switching probabilities determine the partition of life into times spent in distinct stages. Thus, a change in the survival rate of a given stage at a young age can change the fractions of time spent in different stages in all later years. More strikingly, a change in stage switching probabilities with no change in survival results in the trading of time and mortality risk in one stage for time and risk in others, thereby changing subsequent survival and longevity.

We provide general yet interpretable equations for the sensitivity and elasticity of survivorship and lifespan. For stage-structured models without age, Caswell (2006, 2008) has derived general formulas that are eminently computable but use a matrix vec-calculus that makes them quite opaque for qualitative interpretation and broad understanding. For stage-and-age structure, we provide the first general expressions for the sensitivity and elasticity of survivorship and life expectancy. Our formulas generalize familiar results from age-only demography, are explicit and straightforward to interpret and compute, and illuminate the differences between age-only and stage-and-age demography.

We begin by reminding readers of the age-only results and then present our general results on stage-and-age structure. We illustrate these using a model for the Mute swan (Cygnus olor) (McCleery et al., 2002), a model with stage and age and only one newborn stage(Tuljapurkar et al., 2009). Then we apply our results to a stage-only model with newborns produced in one of two distinct stages (seedlings and suckers), the treelet Myrsine guianensis (Hoffmann, 1999).

2 Background: Age-only Demography

We use discrete time and ages, a with values 0, 1, …, A (past the final age A all individuals have died). We briefly summarize familiar results of age-only demography.

Survival rates p(a) depend only on age a. Survivorship l(a), the probability of living to at least age a, is given by l(0) = 1, l(1) = p(0) l(0), …, l(a + 1) = p(a) l(a). Life expectancy is e(0) at birth, and e(a) at age. For indices see also Table 1.

Table 1.

Parameter index

a	age
A	final age all individuals have died
k, l, i, j	stage
K, M	last stage
p(a)	survival rate at age a
p(a, j)	survival rate at age a in stage j
l(a)	Survivorship, the probability of living to at least age a
e(a)	life expectancy at age a
Q(a) q(a, i, j)	Switching probability at age a, from stage j to stage, i conditional on survival
T(a)	Transition probability matrix at age a
t(a, i, j)	Transition probability of an age a individual in stage j to transition to stage i
I	Identity matrix
Ł(a) L(a, i, j)	Survivorship, probability of an indvidual being born into stage j to be alive in stage i at age a.
N(a) N(a, i, j)	Note this survivorship is the probability of being alive in stage i at age a and hence can rise and fall during the life course stage duration, an individual in stage j at age a is expected to spent the amount of time in stage i before it dies
D(a)	matrix of change in transition probabilities at age a
d(a, i, j)	change in transition probability of an stage j indvidual at age a to transition to stage i
θ	parameter describing a function for instance between survival and a quantitative trait such as size
z	distribution of changes in the switching probabilities
§	sensitivity matrix
S(i, j|a, z, l)	Sensitivity of the i, j element given that perturbation at age a with a distribution of change following z, out of stage l
E(i, j|stasisa, l)	Elasiticity of element (i, j) given a perturbation for stasis at stage l at age a
η(a, j)	remaining life expectancy for individuals in stage j at age a

Suppose we increase survival rate at age a by a small amount d(a) to p(a)+d(a). In response, life expectancy at birth changes by the product of the probability of reaching a, the change d(a), and the expected remaining life,

$$\mathrm{\Delta }e(0)=e(a+1)d(a)l(a).$$ (1)

This is the classical result (for a proof see the Appendix) that we generalize below. (Note that as written here we mus respect constraints when specifying d(a), e.g., we must have 0 ≤ (p(a) + d(a)) ≤ 1. We could avoid such issues by working instead with infinitesimal perturbations and rates of change; we note this fact at appropriate places below.)

If we change p(a) by a small proportion ε then Δe(0) = εe(a + 1) l(a + 1). If we now change survival rates by the same proportion at every age, life expectancy at birth changes by

$$\mathrm{\Delta }e(0)=\epsilon \sum _a{\mathrm{\Delta }}_{a}e(0)=\epsilon \sum _{a}e(a+1)l(a+1)=\epsilon \sum _a(e(a)-1)l(a),$$ (2)

Proofs are given in the Appendix.

3 Stage-and-Age Demography

There are K stages, labelled i or j. These may be developmental stages, sizes, locations, physiological stages, behaviors, or other attributes. At age a, stage j has a survival rate p(a, j). An individual in stage j at age a who survives to age a + 1 can switch to a different stage i with a switching probability q(a, i, j) or stay in stage j with (stasis) probability q(a, j, j). The probabilities of switching add to 1, Σ_i q(a, i, j) = 1, because living individuals have to be in some stage. The transition rate at which individuals of age a move from stage j in one period to stage i in the next period is q(a, i, j) p(a, j) = t(a, i, j) and form a matrix T(a). Hence, switching probabilities are conditional on survival whereas transition probabilities include survival. The elements of the stage-transition matrix T(a) are computed from data using direct counts or estimation using capture-mark-recapture and multi-stage models (Fujiwara and H., 2002; Lebreton et al., 1992). We use such estimates in the examples below.

An individual begins life in a specific stage, and its subsequent life is distributed over the stages that it occupies over time. We first explain how survivorship and life expectancy are generalized from their age-only analogs, slightly extending Lebreton (1996).

3.1 Stage Durations

For an individual born into stage j, we define survivorship L(a, i, j) as the probability of being alive in stage i at age a (see also Table 1). The age-stage-specific survivorships are elements of a matrix L(a). At birth L(0) = I, the identity matrix. Then L(1) = T(0), L(2) = T(1) L(1), · · · L(A) = T(A − 1) L(A − 1).

For an individual born into stage j the expected amount of time spent alive in stage i before death is here called the stage duration N(0, i, j), and is the i, j element of what we call the stage duration matrix

$$\mathbf{N}(0)=\mathbf{I}+\mathbf{T}(0)+\mathbf{T}(1)\mathbf{T}(0)+\cdots +\mathbf{T}(A)\mathbf{T}(A-1)\cdots \mathbf{T}(1)\mathbf{T}(0).$$ (3)

Life expectancy at birth into stage j is a sum over stage durations (see Appendix).

An individual alive at age a in stage j survives to age a + x in stage i with probability given by the (i, j) element of a conditional survivorship matrix L(a + x|a), and

$$\mathbf{L}(a\mid a)=\mathbf{I},\mathbf{L}(a+1\mid a)=\mathbf{T}(a),\mathbf{L}(a+x\mid a)=\mathbf{T}(a+x-1)\cdots \mathbf{T}(a+1)\mathbf{T}(a),$$ (4)

and subsequent stage durations N(a, i, j) are given by

$$\mathbf{N}(a)=\mathbf{I}+\mathbf{T}(a)+\mathbf{T}(a+1)\mathbf{T}(a)+\cdots +\mathbf{T}(a+x-1)\cdots \mathbf{T}(a+1)\mathbf{T}(a).$$ (5)

It follows that

$$\mathbf{N}(a)=\mathbf{I}+\mathbf{N}(a+1)\mathbf{T}(a).$$ (6)

As shown in the Appendix, we can use this result to rapidly compute all of the N(a).

3.1.1 Example I: Age-stage demography with one type of offspring

A bird, the Mute swan (Cygnus olor), makes transitions among five stages: immature and four reproductively mature stages, non-breeding (after having reproduced at least once in a previous year), low clutch size (1–4 eggs), medium clutch size(5–6 eggs), or high clutch size(7–12 eggs). The original data has been collected from the population at Abbotsbury, UK (for details, see e.g. McCleery et al. (2002)). We have analysed this data using a multistage Capture-mark-recapture model (Tuljapurkar et al., 2009). Individuals stay immature at ages 0, and 1, start to move into a breeding stage (3, 4, or 5) from age two onwards, and by age eight most individuals have recruited into the breeding population. When recruited they switch among mature stages 2 – 5. Stage-specific switching probabilities are constant from age three onwards. Stage-specific survial is age independent for the immature stage (perfect survival; only indviduals that recruit are included in the study), and the non-breeding stage (survival rate 0.675), while for the successfull breeding stages survival rates decrease with increasing age. Additional details including matrices are in our online Appendix. Individuals exhibit dynamic heterogeneity, meaning that they frequently switch between reproductive stages throughout their lives (Tuljapurkar et al., 2009).

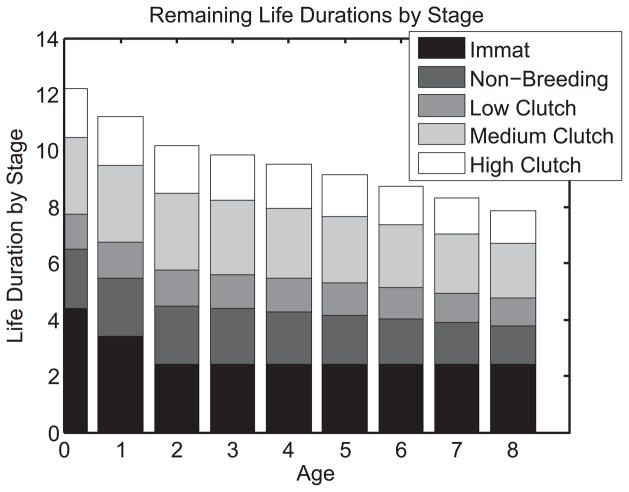
Figure 1 displays values N(a, k, 1) of subsequent stage duration in stage k for individuals who are in immature stage 1 at age a. At birth (age 0) in stage 1, the leftmost vertical bar in Figure 1 shows that 36% (4.41 years) of remaining life is in stage 1 (given by N(1, 1, 1)), however, individuals that do not recruit into the breeding population are excluded. Therefore the 36% of remaining life spent as immatures is underestimated and the 4.41 years is overestimated. Another 17% (2.08 years) of life is spent as a non-breeder (N(1, 2, 1)) and 47% (5.71 years) in one of the three successful breeding stages (i.e., N(1, 3, 1) + N(1, 4, 1) + N(1, 5, 1)). With increasing age, the absolute remaining life duration decreases for each stage, but the distribution of remaining stage duration shifts among stages. Even in the non-breeding stage, with constant survival and transition probabilities across ages ≥3, remaining stage duration decreases because of the transition dynamics with breeding stages that show senescence in survival.

Figure 1.

Average remaining life duration N(a, k, l) (in years) in stage k of individual Swans that are in immature stage 1 at age a. The five stages are 1 = immature, 2 = non-breeding, 3 = low clutch (1–4 eggs), 4 = medium clutch (5–6 eggs), 5 = high clutch (7–12 eggs). The leftmost column gives the life expectancy of newborn individuals, because all individuals are born into the immature stage.

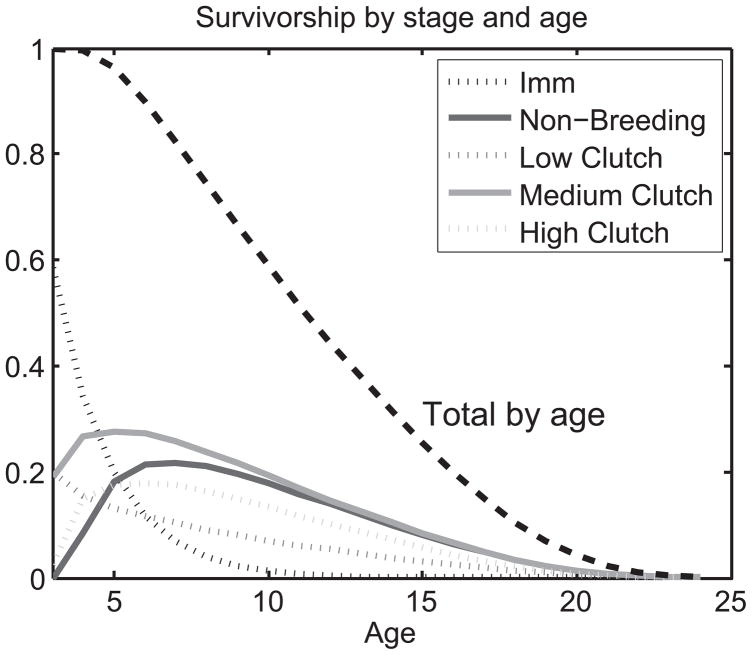
Figure 2 displays survivorship L(a, i, 1) for newborns to reach stage i at age a. Survivorship in the immature stage (L(a, 1, 1)) falls sharply with increasing age ≥ 3 because of maturation. Survivorship to a breeding stage rises as individuals mature and begin to switch among breeding stages. There is a peak in survivorship for most of the stages 2 through 5, as individuals begin to arrive at those stages, and then fall as individuals begin to switch stages. The exception is for low clutch size stage, the stage that shows a constant decrease in survivorship, and the earliest decline in survival probabilities (see Appendix). Survivorship varies strongly with stage at each age; for example, individuals who attain age 10 are most likely to be non-breeders or lay a medium clutch in that year, with successively smaller odds of laying a high clutch size, a low clutch size, or being the odd individual that has not yet recruited to the breeding population. The figure also shows the total survival at each age; this total sums across stages and so reveals nothing about the distribution of stages by age, or of subsequent survival given present stage. The full stage-age analysis reveals important new biological information that can be used, e.g., to determine how duration in immature or breeding stages changes with age.

Figure 2.

Survivorship L(a, i, 1) for newborn Swans to reach stage i at age a. For details of stages see also Fig. 1, Appendix, and main text. The total survival at each age a is shown by the dashed line.

3.2 General Equations

In the age-only case, life expectancy depends only on age-specific survival. With stage-and-age, stage durations (N(0)) depend on both: (i) survival rates p(a, i) of every stage i at every age a, [e.g., at age 5, p(a = 5, i = 5) is the survival rate of Swans having a high clutch size (stage 5)], and (ii) the switching probabilities q(a, i, j) [e.g., also at age 5, q(a = 5, i = 5, j = 5), the probability that Swans with a high clutch (stage 5) remain as successful the next year].

Changes in these quantities at age a will change one or more elements of the stage-transition matrix T(a). Suppose that T(a) changes by a small amount to [T(a)+ D(a)], so that the i, j transition rate changes from t(a, i, j) to [t(a, i, j) + d(a, i, j)]. The resulting change in N(0) is given (see online Appendix) by the simple expression

$$\mathrm{\Delta }\mathbf{N}(0)=\mathbf{N}(a+1)\mathbf{D}(a)\mathbf{L}(a).$$ (7)

We have here the product of the probability L(a) of reaching a, the change D(a), and the expected remaining life N(a + 1). This generalizes equation (1) in a sensible way.

For the same change as above, survivorship will change for later ages a + x. To find the change, call it ΔL, multiply the odds of reaching age a, the change at age a, and subsequent survivorship,

$$\mathrm{\Delta }\mathbf{L}(a+x)=\mathbf{L}(a+x\mid a)\mathbf{D}(a)\mathbf{L}(a).$$ (8)

We can now find the sensitivities and elasticities we seek.

3.3 Sensitivity and Elasticity to Survival Rates

We seek the sensitivity and elasticity of stage duration N(0, i, j), i.e., time spent alive in stage i given you start life in stage j. If we change the survival rate of stage l at age a by a small amount, the entries in column l of T(a) will change. Using equation (7) yields (see Appendix) a matrix of sensitivities (∂N(0)/∂p(a, l)) whose entries are

$$\frac{\partial N(0,i,j)}{\partial p(a,l)}=\left[\sum _{k}N(a+1,i,k)q(a,k,l)\right]L(a,l,j).$$ (9)

This is an intuitively sensible product of (i) the probability L(a, l, j) of living to stage l at age a, (ii) an average over the subsequent stage duration. From here we can write expressions for the sensitivity of total life expectancy, and for elasticities (see Appendix for details). Note there is an entire matrix of sensitivities for each survival rate: that’s a lot of numbers. To make sense of these we return to our example.

3.3.1 Example I continued

Swans are born in stage 1, so life expectancy at birth means the stage durations N(0) = {N(a, i, 1)}. Here we examine elasticities of life expectancy to the survival rates p(a, j), j = 2, 3, 4, 5 of the mature stages. Once a bird reaches one of these four stages, it never returns to immature stage 1. So the elasticity of life expectancy to any one survival rate will consist of four numbers, the percentage responses of N(a, 2), N(a, 3), N(a, 4), N(a, 5).

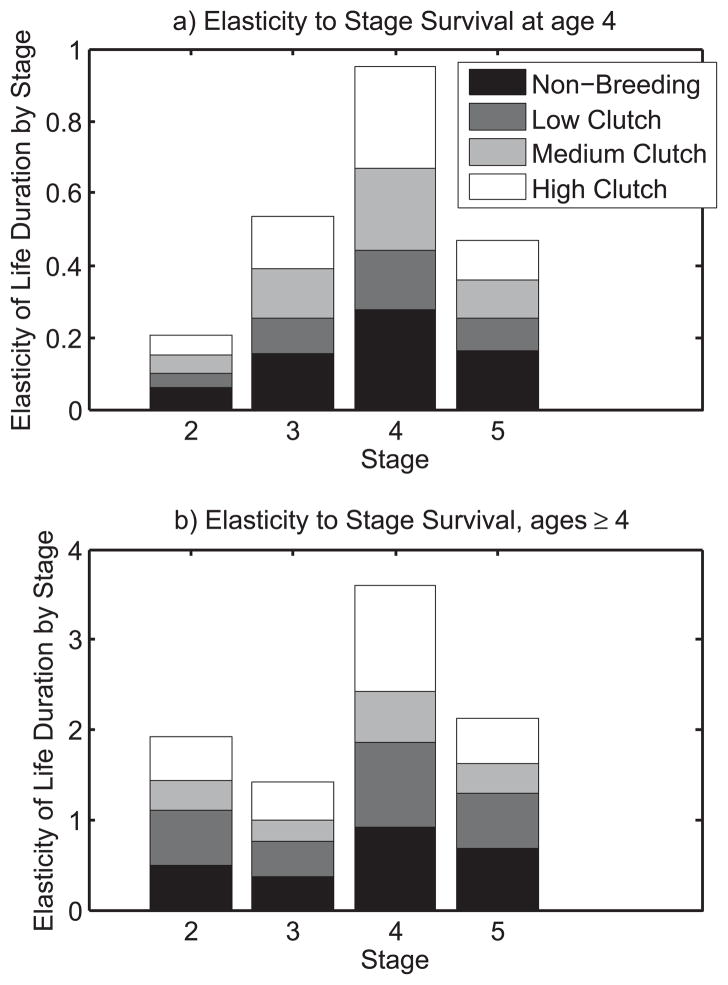
We first ask, what is the elasticity of N(0) to changing survival rates of mature birds only at age 4? From equation (9) (see Appendix for details), the elasticities of N(a, i, 1) to p(a, j) are proportional to the survivorships L(a, j, 1). Recall from Figure 2 that these survivorships are all much less than 1 at age 4, so we expect the elasticities to be small; also birds who are alive at age 4 are most likely to be in stage 4, followed by stages 3, 5, and 2. Figure 3a shows that the elasticities follow this pattern. Stage 2 survival has the smallest effect, since few birds are in stage 2 at age 4 (birds need to have bred at least once before they can transition to stage 2). The largest elasticities are to the survival rate of the most occupied stage 4, and the largest percent changes occurs in stage durations of stage 2 (non-breeding) and 3 (low clutch)(distribution within the column stage 4). These results show how stage-specific survival rates shape expected lifetime reproductive success, by influencing the durations of stages with differing reproductive success.

Figure 3.

Elasticities of life duration for newborn Swans when stage j survival is perturbed at a) age 4 p(4,j) or b) all ages ≥ 4 p(a,j). For details of stages see also Fig. 1, Appendix, and main text.

What is the effect on stage durations at birth of a permanent 1% increase in these survival rates (i.e., at all ages ≥ 4)? The answer is found by summing the elasticity at age a, given above, over all ages ≥ 4, and is shown in Figure 3b. The difference between changing survival at just one age versus all ages: (i) much larger elasticities, as is reasonable; (ii) smaller (relative) differences among stages as the single-age effects, because survivorship differences decline with age (as in Figure 2); (iii) large increases in the durations spent in stages 3 (low clutch) shown by shifts in distribution towards this stage within the columns.

These age-stage elasticities provide new and useful tool to predict the consequences of changing stage-specific survival, e.g, by interventions used in population management. Our results show that raising the survival of swans laying medium clutches (stage 4) has largest potential payoff in adding to the expected length of life, and perhaps as important, in increasing duration in the upper clutch size stages. We can also compare the effects of interventions aimed at the survival of specific stages at different ages. None of this information is available in age-only demography.

3.3.2 Parametric Sensitivity and Elasticity

In many cases, e.g., size-structured models or integral population models (Coulson et al., 2010; Ellner and Rees, 2006), the survival rates and switching probabilities are determined using parametric models. E.g., survival is estimated as a function p(a, θ, z) of size z. This function determines survival for discrete stages j as p(a, θ, j) as discussed in the references above. To find sensitivity with respect to the parameter θ, just use the chain rule, for example,

$$\frac{\partial N(0,i,j)}{\partial \theta }=\sum _l\left(\frac{\partial N(0,i,j)}{\partial p(a,\theta ,l)}\right)\left(\frac{\partial p(a,\theta ,l)}{\partial \theta }\right).$$

3.4 Sensitivity and Elasticity to Switching Probabilities

An individual in a stage l at age a may stay there or switch to another stage k. Say we change the switching probabilities q(a, k, l) at age a from stage l into other stages. For any individual, this change means that some stages will be more frequently occupied and others less. In words, the result of the change is that we are trading stages in individual lives.

At age a, stage l, let us change the q(a, k, l) to [q(a, k, l) + z(k, l)]; because the qs add to 1 the distribution of changes z must Σ_k z(k, l) = 0. For small z, the rate of change of N(0) will be given by a sensitivity matrix that we call S. For clarity, write the (i, j) element of this sensitivity as S as S(i, j|a, z, l): this is the sensitivity of N(0, i, j) to changes in the switching probabilities q(a, k, l) as described by the z. As shown in the Appendix,

$$S(i,j\mid a,z,l)=\left\{\sum _{k}N(a+1,i,k)z(k,l)\right\}[p(a,l)L(a,l,j)].$$ (10)

Technically, S is a matrix of directional derivatives of the elements of N(0) in the direction of the vector z; our notation is a (surely imperfect) effort to make clear what S depends on. Here the factor in curly brackets, the sensitivity factor, captures the effect of trading stages. It describes whether we gain or lose life by changing the odds of switching to different stages. Consider for example the probabilities of switching at age a = 5. Say we increase stasis in stage 3 (i.e., increase q(5, 3, 3)) by reducing the probability of switching to stage 4, leaving all other transitions unchanged. Then z(3, 3) = +1 and z(4, 3) = −1 and the sensitivity factor is

$$\left\{\sum _{k}N(a+1,i,k)z(k,l)\right\}=N(a+1,i,3)-N(a+1,i,4).$$

This is just the difference between the stage duration we gain by staying in stage 3 versus moving to stage 4, and can be read off from columns 3 and 4 of the known matrix N(a + 1). The square-bracketed term in (10) shapes the age-dependence of sensitivity.

Elasticities result from proportional changes and we must specify the proportional (rather than actual) changes in the switching probabilities. Thus, to examine elasticity to stasis in stage 3 while reducing switching to stage 4, we change q(3, 3) by a proportion z(3, 3) = +1 and reduce q(4, 3) by a proportion z(4, 3) = −[q(5, 3, 3)/q(5, 4, 3)]. Using these z in (10), we find (see Appendix for details) that the elasticities to stasis in stage 3 are

$$E(i,j\mid \text{stasis}a,l)=q(a,l,l)S(i,j\mid a,l,z)/N(0,i,j).$$ (11)

3.4.1 Example I continued

Again, we examine change in the stage durations at birth, N(0) = {N(a, k, 1)}. What happens if we increase the persistence of high clutch sizes. We do this by increasing q(a, 5, 5) for ages a ≥ 4 and reducing transitions from stage 5 to all other stages by equal amounts (i.e. z(5, 5) = +1, z(2, 5) = −1/3, z(3, 5) = −1/3, z(4, 5) = −1/3). To quickly assess the effect take the sensitivity factor in equation (10): we set a = 4 and compute

$$N(a+1,i,5)-(1/3)\ast \{N(a+1,i,2)+N(a+1,i,3)+N(a+1,i,4).$$

The result, Figure 4a, shows that stage durations will decrease in stages 3 and 4, remains almost the same in stage 2, and increase in stage 5. The time spent in lower cluch stages 3 and 4 decreases about the same than time gained in the high clutch stage 5, so the net change increases average clutch size and overall lifespan (such effects on lifespan do not need to be close to adding up to 0 as in this example). The survivorship factor (L(a, l, j)) in (10) peaks if we change switching at ages a near 5 or 6 (cf. Figure 2) and then declines if we change switching at later ages. Figure 4b shows the computed elasticity to increasing persistence in stage 5 at all ages ≥ 4. These effects are lower in size than those of changing survival (Fig. 3b right column), mainly because the changes in the high clutch stage (z(5, 5)) are traded against multiple changes of lower value in the other stages (z(2, 5), z(3, 5), z(4, 5)).

Figure 4.

Swan a) sensitivity factors for increased stasis at stage 5 (q(a, 5, 5)) compensated by reduced transitions out of stage 5 (q(a, 2, 5), q(a, 3, 5), q(a, 4, 5)) at age a = 4; and b) elasticities for change in stasis and reduced transitions out of stage 5 as in panel a) but for all ages ≥ 4. Elasticities (and sensitivity factors) are signed because such changes in stasis lead to increased life duration in stage 5 but reduced life duration in stages 3 and 4. c) sensitivity factors for decreased stasis at stage 2 (q(a, 2, 2)) compensated by increased transitions out of stage 2 (q(a, 3, 2), q(a, 4, 2), q(a, 5, 2)) at age a = 4; and d) elasticities for change in stasis and increased transitions out of stage 2 as in panel c) but for all ages ≥ 4. For details of stages see also Fig. 1, Appendix, and main text.

A different way of increasing reproductive success would be to reduce non-breeding, by reducing the probability q(a, 2, 2) of staying in an unsuccessful stage, and boosting the switching rate from 2 to the other stages. Figure 4c shows the sensitivity factor for this case and we see that mid and high clutch stages 4 and 5 gain the most duration. Figure 4d shows the elasticities, larger than those in Figure 4b because stage 2 has low survival among mature stages. Age only demography hides such details about trading stages, intrinsic trade-offs, and sensitivities.

3.5 Multiple Birth Stages

We have pointed out that newborns can arrive in different stages. Such differences commonly arise in, for example, size at birth. More fundamental are differences between sexual offspring such as seeds and vegetative or clonal offspring (e.g. suckers). Age-only demography averages across such differences at birth. To show how offspring stage shapes subsequent stage durations, we consider the tropical treelet Myrsine guianensis that produces seeds and suckers. The model we use for this treelet (Hoffmann, 1999) has transition rates varying by stage but not age, so we can also show how our general results simplify for stage-only models. Our results are more directly applicable to such models than earlier work on Markov chain perturbations (Schweitzer, 1968).

3.5.1 Example II: Stage-only, Two Newborn Stages

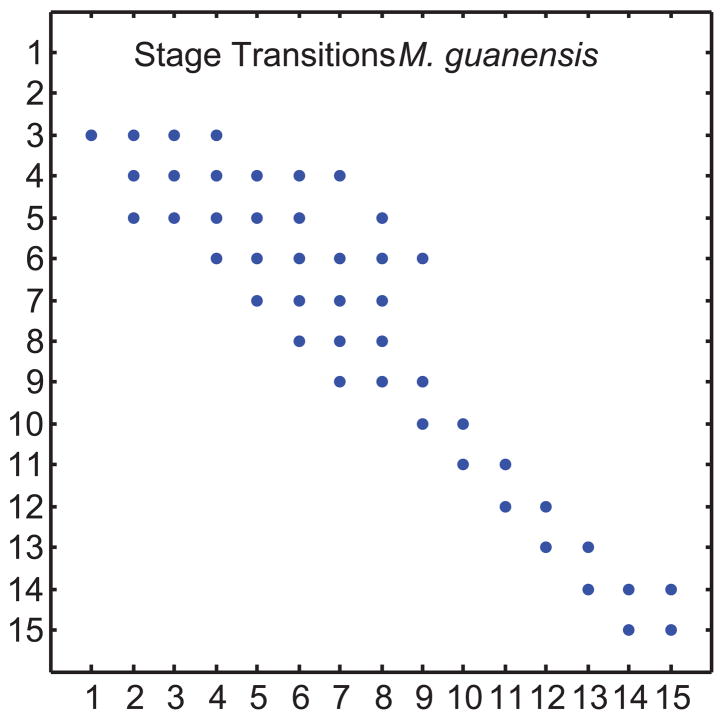
A stage-only model for M. guianensis (unburned habitat, see online Appendix and (Hoffmann, 1999)) has 15 stages: seedlings (stage 1), suckers (stage 2), and then 13 size classes (0–2 mm, 2 mm classes to size 10 mm, 5 mm classes to size 20 mm, 10 mm classes to size 70 mm, then 70–99 mm, and 100+ mm). All treelets produce suckers but only treelets with stem diameters >10mm (stages 8–15) produce seeds. Figure 5 shows the many stage transitions that can occur, with a tendency for growth and stasis rather than regression. Stages 3 to 15 all display stasis; stages 3 to 8 can switch into two or more different stages. This is a stage-only model, so the transition rates T are constant and equal for all ages, and stage duration N(a) does not change with attained age a. Hence we need only compute one set of stage durations N = (I − T)⁻¹ (this stage-only matrix is also called the fundamental matrix (Caswell, 2001); our terminology is more biologically meaningful).

Figure 5.

Stage transition probabilities t(i, j) for the treelet Myrsine guianensis. Stage 1= seedlings, stage 2= suckers, stage 3–15 = size classes. Stasis is given by the t(i, i) elements, transitions above the diagonal describe regression, transitions below describe growth. For more details of stages see the Appendix.

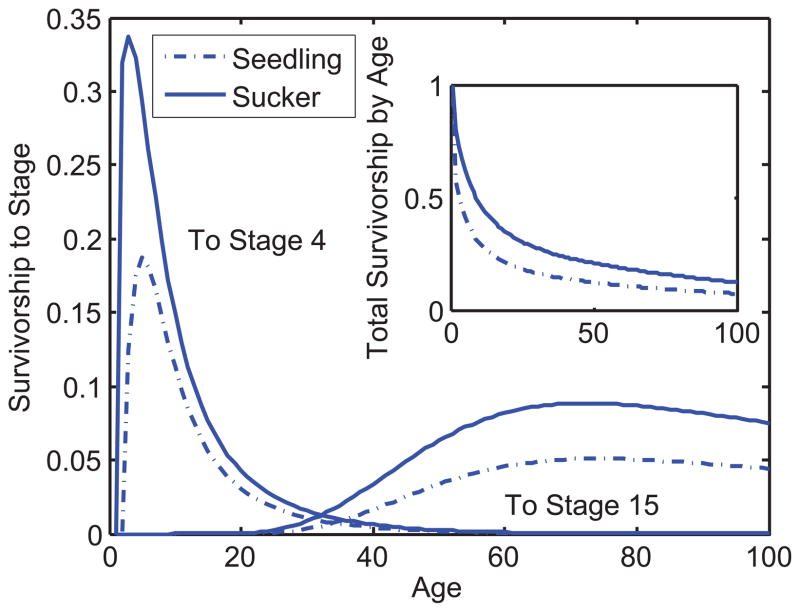
Figure 6 displays stage durations in each stage for seedlings and suckers. Note the obvious but important fact that seedlings never become suckers so N(1, 1) = N(2, 2) = 1 while N(2, 1) = N(1, 2) = 0. After the birth year seedlings or suckers move to stage 3 or higher, their subsequent transition rates are the same. Suckers spend nearly twice as much time as do seedlings in stages ≥ 4, in part because seedlings have a lower survival rate than suckers, and in part because year-old seedlings are always in stage 3 whereas year-old suckers can jump to stages 4 or 5. Thus, seedling life expectancy η(1) = 23.52 is much lower than of suckers η(2) = 38.31 years. Once seedlings or suckers reach stage 3, their subsequent transition rates are identical. So we find, as shown in the inset in Figure 6, that the ratio of stage durations for seedlings and suckers becomes constant as we move to higher stages.

Figure 6.

Treelet stage duration for newborn seedlings (solid bars) and suckers (open bars) in each of the 15 stages. The inlet shows the ratio between suckers and seedlings at stage 3 to 15. For more details of stages see Fig. 6 and the Appendix.

In this stage-only case, survivorship to age a is just Ł(a) = T^a but of course differs between birth stages: seedlings survive to stage i at age a with probability L(a, i, 1) whereas this probability is L(a, i, 2) for suckers. Figure 7 compares these survivorships to stages 4 and 15 with increasing age. As with the previous example (cf. Figure 2) survivorship to a stage rises as individuals grow into that stage, then falls as individuals move on in their life cycles. The peaks for the suckers are slightly earlier than those for seedlings because of their larger sizes in their initial year. The peaks at stages 4 and 15 are separated by more than 60 years! If we sum over all living stages we get the total age-dependent survivorships shown in the inset of Figure 7. Suckers enjoy higher early survival and maintain that initial advantage throughout life. Once individuals reach stage 10 (>20 mm), they experience only stasis or growth until stage 13. Stages 14 and 15 (>70mm) are terminal stages, meaning that treelets never leave these stages once they arrive (except when they die). In fact treelets spend the largest part of their lives in these two stages (Fig. 6). Even though transition rates do not change with age, these treelets will exhibit a senescence plateau, meaning that the curves in Figure 7 will eventually decline with same exponential rate. The terminal survival rate is a weighted average of the survival rate of stages 14 and 15 (Horvitz and Tuljapurkar, 2008).

Figure 7.

Treelet survivorship to stage i at age a of seedlings, L(i, a, 1) (dotted lines), and suckers L(i, a, 2) (solid lines). The left two curves is survivorship to stage i = 4 (2–4 mm), the right two curves show surviorship to stage i = 15 (≥ 100mm) for increasing ages. The inset shows the surviorships summed over all stages, not only the two stage specific example surviorships that are given in the main Figure.

3.5.2 Sensitivity and Elasticity in Stage-only Demography

In this stage-only setting any change in survival or switching applies at every age. To use equation (7), let us change the stage-transition matrix T to [T + D]. Sum over all ages in (7) to find the stage-only result

$$\mathrm{\Delta }\mathbf{N}=\mathbf{N}\mathbf{D}\mathbf{N}.$$ (12)

Sensitivity to survival rate simplifies to

$$\frac{\partial N(0,i,j)}{\partial p(l)}=\left[\sum _{k}N(i,k)q(k,l)\right]N(l,j).$$ (13)

and sensitivity to switching rate, defined as in (10), simplifies to

$$S(i,j\mid z,l)=\left\{\sum _{k}N(i,k)z(k,l)\right\}[p(l)N(l,j)].$$ (14)

Elasticities are derived from these as shown earlier for stage-age models.

3.5.3 Example II Continued

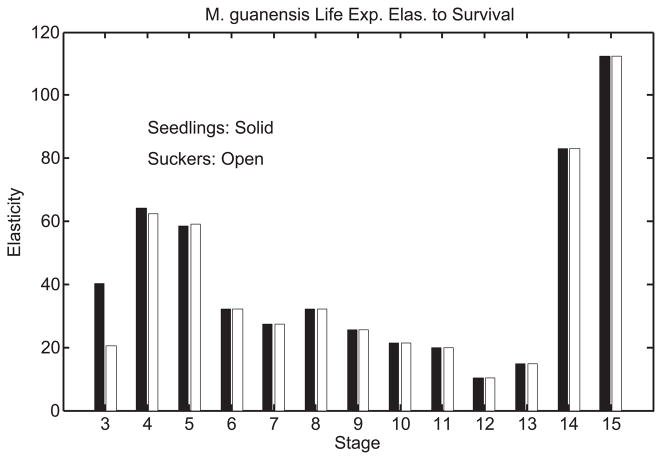
Consider individuals born in stage j = 1 or 2 and the sensitivity of any stage duration to the survival rate of stage l. From (13), high sensitivities should be found for transitions out of those stages l in which individuals spend a lot of time, i.e., stages with large values of N(l, j). For seedlings and suckers these are stages 3, 4, 5, 14 and 15 (see online Appendix for the matrix N). Sensitivities to survival are also going to be relatively large for stages from which individuals make transitions into stages of long duration. These factors determine the pattern in Figure 8 of elasticity to survival rate in each of stages 3 through 15.

Figure 8.

Treelet elasticity of total life expectancy to survival rate p(l) of stage l for seedlings (solid bars) and suckers (open bars).

There are many stage transitions possible, but every stage except 1 and 2 displays stasis. So we examine the sensitivity of stage durations to stasis; individuals never return to their birth stages so there is no change in the durations of those stages. To find sensitivities, we increase stasis in a given stage, offset by compensating reductions in switching probabilities to other stages. Stasis in a given stage affects durations in all stages that are (directly or indirectly) reached from that stage. For example, consider stage 3, from which an individual can switch to stages 4 or 5, or stay put in stage 3. We increase stasis (i.e., q(3, 3)) by z(3, 3) = 1, and reduce transitions to stage 4, 5 respectively by −0.5. Equation (14) shows that the sensitivities of the durations N(i, 1) and N(i, 2) are both proportional to

$$N(i,3)z(3,3)+N(i,4)z(4,3)+N(i,5)z(5,3),$$

and we can determine these values from the elements of matrix N. Figure 9 shows the resulting sensitivities to stasis in stages 3, 9 and 12. Sensitivities decrease in their absolute values with increasing stage of change in stasis, because a change in stasis of a lower stage (small individuals) will affect more individuals than a change at higher stages (large individuals) [compare the three panels of Fig. 9]. Seedlings are more sensitive compared to suckers to a change in stasis only at stage 3, because some suckers jump that stage (Fig. 6); change in stasis of higher stages affects more individuals that originated from suckers and therefore suckers respond more sensitive. Increased stasis at stage 3 (top panel) decreases duration in all subsequent stages (4–15) even though stages 6–15 can not be reached directly from stage 3. The duration gained in stage 3 is smaller than the duration lost in higher stages leading to a decreased total life expectancy. Increased stasis at stage 9 (mid panel) reduces duration at lower stages (4–8, i.e. less regression) and increases durations in stages 9 and higher (9–15), with substantial increases in duration at the highest stages (14, 15). Increased stasis at stage 12 (bottom panel) exactly trades duration gained in stage 12 against duration lost at higher stages (13–15), because all stages 12–15 have identical survival rates; increased stasis at stage 12 does not affect duration in lower stages because there is no shrinking once that stage has been reached. Time and risk in one stage is traded against time and risk in others and this trading can lead to no change (stasis 12), increased (stasis 9), or decreased (stasis 3) total life expectancy. Such trading of duration describe life history trade-offs, but here trade-offs include dynamics among stages and not only sensitivities (evolutionary forces) of single parameters.

Figure 9.

Treelet sensitivity of stage duration to stasis of stage 3 (upper panel), stage 9 (mid panel), and stage 12 (bottom panel). Seedling sensitivities are shown as solid bars and sucker sensitivities as open bars.

4 Discussion

Our results provide straightforward quantitative and qualitative insights into survivor-ship, stage duration, and life span in a stage-and-age structured population. Our approach is based on an understanding of trading time and mortality risk in one stage for time and risk in others, which provides intuitive insights into how vital parameters influence longevity. Our results simplify known stage-only results (Caswell, 2006, 2009) and extend them to general age-stage models; they have easily recognizable roots in the theory of absorbing Markov chains (Chung, 1967; Iosifescu, 1980; Kemeny and Snell, 1960; Schweitzer, 1968), as noted in our introduction. Because we use only matrix algebra our equations are easy to apply and to interpret biologically, features that are useful for empiricists. We note that it should be possible to develop similar results using multistate lifetables that use continuous ages (Schoen, 1988). The stages in our analyses include categorical traits and binned continuous traits and our results are given for matrix models. But our results apply directly to the dicrete version of integral population models (IPMs) (Ellner and Rees, 2006) that are used in any application.

Age-stage-structured models track quantitative characters that are essential when populations cannot be accurately described by age alone (Lefkovitch, 1965; Caswell, 2001). Plants are often better characterized by size rather than age; stages must be tracked when they are ontogenetically distinct, e.g, insects with resting or instar stages, or seeds and seedlings in plants. More generally, many life-historical, ecological, and evolutionary processes depend on variation in individual characteristics including development, reproduction, morphology, physiology, biomarkers, behavior, or location. Age-only models average across such traits (i.e. stages) and are not accurate if the trait influences survival or fecundity (see empirical example above). Age-stage-structured models also focus on duration in distinct stages which may differ in survival (affecting life expectancy and reproduction and thereby population growth rate). Movement among stages along the life course is typical in a large range of species, and has been quantified in terms of dynamic heterogeneity (Tuljapurkar et al., 2009) measured as the entropy of the transition matrix, or individual stochasticity as termed by Caswell (2009).

Our analyses highlight time as a currency: an individual’s current stage (or birth stage) affects how subsequent life is partitioned among different stages. We show how sensitivities describe changes in the duration of life spent in different stages in response to changes in stage dynamics (trait dynamics). For example, life expectancy in the treelet is most strongly influenced by transitions to and from the largest stage, because these are the stages where they spend most of their lives in. This simple intuition seems obvious in retrospect, but only follows from the results we give here.

A change in one transition rate always needs to be accompanied by a change in at least one other transition rate, something that does not apply to age-only demography and therefore is often neglected. Our analysis of such changes shows how time and mortality risk in one stage is traded for time and risk in another, corresponding to a class of potential life-history trade-offs. Changes in vital rates can directly or indirectly change duration in stages and so change life-histories in complex and surprising ways. For example, with no change in survival rates, increased stasis in the treelets can increase life expectancy inspite of slower growth of the treelets. In contrast, any life-history change in an age-only model only deals with changes in the levels of survival and fertility.

Age-stage models satisfy essential mathematical conditions, e.g., switching probabilities out of a stage need add to 1 because any individual has to transition to some stage (including the death stage). In applications to a specific biological system there will likely be other conditions on the survival rates or switching probabilities due to evolutionary history or biological constraints. Our results are only the first step towards understanding selection on life histories, especially for understanding evolutionary forces acting on the dynamics of changing traits throughout the life of individuals. In subsequent work, we hope to extend out methods to an analysis of reproduction and population growth rate.

Table 2.

Swan: transition rates t(a, i, j) of individuals moving from stage j to stage i at age a, and N(a), the expected numbers of years to live in stage i when in stage j at age a.

	T(1)					N(0)
	Imm	Non-breed	Low	Medium	High	Imm	Non-breed	Low	Medium	High
Immature	1	0	0	0	0	4.4096	0	0	0	0
Non-breeding	0	0.6752	0	0	0	2.0825	2.8451	2.2503	2.3149	2.4051
Low clutch	0	0	0.993	0	0	1.2526	0.3003	3.8368	0.8501	0.8062
Medium clutch	0	0	0	0.9995	0	2.7415	0.8025	2.5529	5.5022	2.1525
High clutch	0	0	0	0	0.9991	1.7115	0.5098	1.7451	1.9397	4.3645
	T(2)					N(1)
Immature	1	0	0	0	0	3.4096	0	0	0	0
Non-breeding	0	0.6752	0	0	0	2.0825	2.7325	2.2661	2.316	2.4072
Low clutch	0	0	0.9906	0	0	1.2526	0.4447	2.8567	0.8505	0.807
Medium clutch	0	0	0	0.9993	0	2.7415	1.1884	2.5708	4.5044	2.1544
High clutch	0	0	0	0	0.9988	1.7115	0.755	1.7574	1.9406	3.3675
	T(≥ 3)					N(2)
Immature	0.585	0	0	0	0	2.4096	0	0	0	0
Non-breeding	0	0.1938	0.2093	0.1448	0.636	2.0825	2.5657	2.2876	2.3177	2.4101
Low clutch	0.198	0.1391	0.1086	0.0729	0.1038	1.2526	0.6586	1.8743	0.8511	0.8079
Medium clutch	0.191	0.2762	0.4285	0.3376	0.2067	2.7415	1.7599	2.5951	3.5068	2.157
High clutch	0.026	0.0662	0.2409	0.4435	0.0519	1.7115	1.1182	1.774	1.942	2.3703
	T(≥ 3)					N(3)
Immature	0.585	0	0	0	0	2.4096	0	0	0	0
Non-breeding	0	0.1938	0.2084	0.1448	0.6357	1.9806	2.512	2.1997	2.2379	2.3399
Low clutch	0.198	0.1391	0.1081	0.0729	0.1038	1.2149	0.6388	1.8417	0.8216	0.782
Medium clutch	0.191	0.2762	0.4267	0.3375	0.2066	2.631	1.7018	2.4996	3.4207	2.0812
High clutch	0.026	0.0662	0.2399	0.4433	0.0519	1.6318	1.0762	1.7055	1.8797	2.3157
	T(≥ 3)					N(4)
Immature	0.585	0	0	0	0	2.4096	0	0	0	0
Non-breeding	0	0.1938	0.2072	0.1447	0.6353	1.8708	2.4536	2.103	2.1513	2.2637
Low clutch	0.198	0.1391	0.1075	0.0728	0.1037	1.1742	0.6172	1.8058	0.7896	0.7539
Medium clutch	0.191	0.2762	0.4242	0.3372	0.2064	2.5119	1.6387	2.3944	3.3271	1.9991
High clutch	0.026	0.0662	0.2385	0.4429	0.0519	1.5457	1.0306	1.63	1.812	2.2564
	T(≥ 3)					N(5)
Immature	0.585	0	0	0	0	2.4096	0	0	0	0
Non-breeding	0	0.1938	0.2056	0.1445	0.6347	1.7533	2.3907	1.997	2.0574	2.1814
Low clutch	0.198	0.1391	0.1067	0.0727	0.1036	1.1307	0.5939	1.7664	0.755	0.7235
Medium clutch	0.191	0.2762	0.4209	0.3368	0.2063	2.3843	1.5706	2.2789	3.2259	1.9104
High clutch	0.026	0.0662	0.2366	0.4424	0.0518	1.4536	0.9813	1.5471	1.7385	2.1924

Table 3.

Myrsine: a) the transition rates t(i, j) of individuals moving from stage j to stage i, b) the expected numbers of years lived in stage i when born in stage j (depending if an indvidual starts life as a seedling or as sucker we need to consider column 1 or 2).

	a) Transition Matrix T with transition rates t(i, j)
	seedling	sucker	0–2mm	2–4mm	4–6mm	6–8mm	8–10mm	10–15mm	15–20mm	20–29mm	30–39mm	40–49mm	50–69mm	70–99mm	100+mm
seedling	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
sucker	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1–2mm	0.574	0.439	0.66	0.022	0	0	0	0	0	0	0	0	0	0	0
2–4mm	0	0.32	0.216	0.749	0.07	0.022	0.018	0	0	0	0	0	0	0	0
4–6mm	0	0.041	0.01	0.15	0.688	0.146	0	0.026	0	0	0	0	0	0	0
6–8mm	0	0	0	0.018	0.188	0.506	0.071	0.013	0.0153	0	0	0	0	0	0
8–10mm	0	0	0	0	0.031	0.247	0.553	0.0391	0	0	0	0	0	0	0
10–15mm	0	0	0	0	0	0.034	0.321	0.688	0	0	0	0	0	0	0
15–20mm	0	0	0	0	0	0	0.018	0.221	0.7233	0	0	0	0	0	0
20–29mm	0	0	0	0	0	0	0	0	0.2513	0.7306	0	0	0	0	0
30–39mm	0	0	0	0	0	0	0	0	0	0.2594	0.7613	0	0	0	0
40–49mm	0	0	0	0	0	0	0	0	0	0	0.2287	0.6484	0	0	0
50–69mm	0	0	0	0	0	0	0	0	0	0	0	0.3415	0.8098	0	0
70–99mm	0	0	0	0	0	0	0	0	0	0	0	0	0.1802	0.9039	0.0525
100+mm	0	0	0	0	0	0	0	0	0	0	0	0	0	0.0861	0.9375
	Matrix N with N(i, j ), expected years lived in stage i when born in stage j
	seedling	sucker	0–2mm	2–4mm	4–6mm	6–8mm	8–10mm	10–15mm	15–20mm	20–29mm	30–39mm	40–49mm	50–69mm	70–99mm	100+mm
seedling	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0
sucker	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0
1–2mm	1.8233	1.5165	3.1765	0.3641	0.1339	0.0794	0.044	0.0231	0.0044	0	0	0	0	0	0
2–4mm	2.0871	3.482	3.6361	5.6277	2.0698	1.2273	0.6808	0.3571	0.068	0	0	0	0	0	0
4–6mm	1.4717	2.5648	2.5639	3.7744	5.6449	2.4573	1.1301	0.8109	0.1362	0	0	0	0	0	0
6–8mm	0.7551	1.3094	1.3155	1.948	2.6482	3.4881	1.1005	0.6409	0.1934	0	0	0	0	0	0
8–10mm	0.5786	1.0043	1.0079	1.4909	2.066	2.3418	3.2243	0.7658	0.1298	0	0	0	0	0	0
10–15mm	0.6775	1.176	1.1804	1.7462	2.4141	2.7895	3.4372	4.0628	0.1546	0	0	0	0	0	0
15–20mm	0.5788	1.0047	1.0084	1.4918	2.0628	2.3806	2.9554	3.2951	3.7464	0	0	0	0	0	0
20–29mm	0.5401	0.9374	0.9409	1.3919	1.9246	2.2211	2.7574	3.0744	3.4954	3.7122	0	0	0	0	0
30–39mm	0.5869	1.0186	1.0224	1.5126	2.0914	2.4136	2.9964	3.3409	3.7984	4.034	4.1895	0	0	0	0
40–49mm	0.3818	0.6626	0.6651	0.9839	1.3605	1.5701	1.9492	2.1733	2.4709	2.6242	2.7254	2.8445	0	0	0
50–69mm	0.6856	1.19	1.1945	1.7671	2.4434	2.8198	3.5006	3.9031	4.4376	4.7129	4.8946	5.1086	5.2582	0	0
70–99mm	5.1934	9.014	9.0478	13.3851	18.5077	21.3587	26.5159	29.5644	33.613	35.6982	37.0744	38.6956	39.8285	42.039	35.3096
100+mm	7.1604	12.428	12.4746	18.4546	25.5173	29.4482	36.5586	40.7617	46.3436	49.2185	51.1161	53.3512	54.9133	57.961	64.6904

Myrsine.

The Myrsine is a common, mostly South American, evergreen treelet species (Hoffmann, 1999). It grows in a variety of habitats and reproduces sexually by seeds and vegetatively by root suckers. The study population is located in south-central Brasil, in a tropical savanna (Cerrado), with dry winters and moist summers. Frequent fires increase treelet mortality mainly of small individuals, and resprouting is vigorous after a fire. Sexual reproduction is unsuccessful in years that burning occurs. The data comprising 5102 samples was collected over a four year period between 1992 and 1995, and originates from six 10 ha study plots that were unburned during the study and have been unburned for at least seven years prior to the start of the study. Individual treelets were marked, and at each annual cencus the stem diameter was recorded in 15 classes. These classes included the two reproductive types, seedlings and suckers. More detail on the population and the estimation of the transition matrix is given in Hoffmann (1999). The original publication assumes perfect survival for some of the larger treelets, here we assume that the maximum survival rate for any size class is 0.99. The transition matrix T with transition rates t(i, j) and the stage duration matrix N is given in the table below.