Social dilemmas among supergenes: intragenomic sexual conflict and a selfing solution in Oenothera

Abstract

Recombination is a powerful policing mechanism to control intragenomic cheats. The ‘parliament of the genes’ can often rapidly block driving genes from cheating during meiosis. But what if the genome parliament is reduced to only two members, or supergenes? Using a series of simple game-theoretic models inspired by the peculiar genetics of Oenothera sp. we illustrate that a 2 supergene genome (α and β) can produce a number of surprising evolutionary dynamics, including increases in lineage longevity following a transition from sexuality (outcrossing) to asexuality (clonal self-fertilization). We end by interpreting the model in the broader context of the evolution of mutualism, which highlights that greater α, β cooperation in the self-fertilizing model can be viewed as an example of partner fidelity driving multi-lineage cooperation.

Introduction

In some plant species the genome has congealed into two supergenes which always are present in the heterozygous condition (Levin, 2000). Such is the case in the genus Oenothera, where one finds 50 species that are permanent translocation heterozygotes (PTH) involving all 14 chromosomes (Raven, 1979; Wagner, et al., 2007). Permanent chromosomal heterozygosity has arisen approximately 20 times from lineages with traditional chromosomal systems, and the majority of these lineages occur within the section Oenothera (Wagner et al, 2007; Johnson et al., 2010). The PTH in Oenothera section Oenothera are more successful than their bivalent-forming relatives in colonizing environments following glaciation in the New World (Johnson et al., 2010)

In species with PTH, alternate disjunction during meiotic anaphase I allows all chromosomes from the paternal (pollen) parent to segregate as a unit, and all maternal chromosomes to segregate as another unit. Accordingly, half of the pollen and half of the eggs have one chromosome set (complex or supergene) and half have the other. Crossing over is in the telomeric regions, and therefore will not generate genetic diversity (Ranganath, 2008; Rauwolf et al., 2008).

Permanent translocation heterozygosity is accomplished by three different mechanisms, two of which involve a system of balanced lethals (Harte, 1994). Most often lethality is expressed in pollen and eggs, such that only one chromosome complex, referred to as α, is transmitted through pollen, and only one complex (β) is transmitted through the egg. Lethality also may be expressed in zygotes, such that only those with one α and one β complex survive. In the absence of balanced lethals, chromosomal heterozygosity is insured by selective fertilization. An allele in the α chromosome complex causes pollen to fertilize only eggs carrying the complementary allele associated with the β complex. Similarly, pollen carrying the β complex fertilizes only eggs with the α complex.

Nearly all Oenothera chromosomal heterozygotes are predominantly selfers, but occasional outcrossing does occur (Holsinger and Ellstrand, 1984). Outcrossing may bring together new combinations of α and β complexes, and thereby generate a modicum of genetic diversity within local populations. Selfing will yield progeny genetically identical to the parent and identical to each other. In essence, selfing in PTH organisms allows clones to be produced through a sexual process, which we refer to as clonal selfing. This clonal selfing allows the fixing of beneficial heterozygous genotypes (Charlesworth 1979) and can be viewed as a form of functional asexuality, with genetic associations both within and between chromosomal complexes remaining unaltered.

Given the permanent suppression of recombination and the formation of two distinct chromosome complexes (‘supergenes’), a conflict between these chromosome complexes is likely to ensue (Ubeda & Haig 2005). Conflict occurs when sub-units within a genome undermine the cooperative construction of a functioning organism, to further the representation of the sub-unit in future generations (Burt & Trivers 2006). More broadly, intra-genomic conflict can be seen as an example of social conflict (Sachs et al 2004, West et al. 2007). In Oenothera obligate heterozygotes, the α supergene gains no reward from egg functioning, and the β supergene gains no reward from pollen functioning. Accordingly, the former is liable to usurp resources to increase egg production, and the latter supergene is liable to usurp resources to increase pollen production. Neither complex is rewarded for promoting the opposite sex function. This situation is in contrast to one where meiosis is normal (substantial recombination), wherein genes within genomes are rewarded for their cooperative functioning (Leigh 1971, Haig & Grafen 1991, Frank 2003, Ubeda & Haig 2005).

We develop and analyse a sequence of game-theoretic models capturing key dilemmas between α and β complexes at a series of hypothesised intermediate points in their evolutionary development. We assume that the progenitors of permanent translocation heterozygotes were outcrossers, as were the early PTH. These assumptions are consistent with the evolutionary trend in Oenothera (Wagner et al., 2007, Johnson et al., 2010). We consider the evolutionary conflict among sexualised α complexes (only transmitted via pollen) and β complexes (only transmitted via eggs), and the potential extinction risk or ‘evolutionary suicide’ that ensues from a loss of reproductive functioning. We demonstrate that any mutation in α that has the net effect of increasing pollen production from an α β individual will be favoured when outcrossing occurs, irrespective of its impact on egg production, as eggs are a dead-end for α. Conversely, any mutation in β that has the net effect of increasing egg production from an outcrossing α β individual will be favoured, irrespective of any costs to pollen production. Finally we consider how the evolution of selfing presents a potential evolutionary escape from population reproductive failure and extinction, accessible both via individual and lineage selection.

Model and results

Conflict among sex supergenes

The association of the α and β supergenes with distinct gametic routes to future generations (pollen and eggs, respectively) presents a particular risk of intragenomic conflict over resource allocation to reproductive functions. Conceptually it is possible that maximisation of both egg and pollen production can occur without conflict – it is not in the interest of either party to directly reduce the output of its partner. However in practice, basic principles of resource allocation suggest that in outcrossing species increasing pollen production will come at the expense of egg production, and vice-versa when the energy allocated to reproduction is fixed (Charlesworth and Charlesworth, 1981; Goldman and Willson, 1986; Mazer et al., 2007; Lankinen and Larsson, 2009). To pick a simple extreme case, a mutation on the α supergene that completely suppresses egg production is likely, via basic resource allocation mechanisms, to enhance pollen production, and so be selected for among α supergene variants in an outcrossing population.

We can now characterise the potential resource allocation conflict in terms of a basic two-player game-theoretic social dilemma. Here we can view the ancestral α and β supergenes as cooperative, in the sense that the α supergene carries a fair complement of genes that contribute to female functioning (and vice versa for β). Now we can characterise a mutant α that suppresses female function (in order to boost pollen production) as a defector. Specifically, we assume that the mutant defector α (α_D) will increase plant pollen investment from 1 to 1+b units when paired with a cooperator β supergene (β_C), and the cooperator supergene partner will in turn suffer reduced egg investment of 1-c units (where the unit is the reference investment in pollen or sperm production in an ancestral outcrossing cooperator-cooperator plant). We furthermore assume that total gamete investment remains constant (or is partially diminished) in α_D-β_C and α_C-β_D plants, implying that c ≥ b. Finally, we assume that defector-defector supergene pairings produce plants that are deficient in both egg and pollen production, producing 1-c pollen and 1-c eggs. Together, these assumptions lead to the payoff matrix summarised in Table 1.

Table 1.

Fitness of α and β supergenes (presented as α / β ) as a function of their combined strategies (cooperate C or defect D). Fitnesses w are normalised to mutual cooperation w(C,C) = 1/1. b is the benefit to a manipulative ‘defector’ allele combined with a cooperator partner. c is the cost to a cooperator paired with a defector. Furthermore we assume that c ≥ b (manipulation can yield a net cost to plant individual fitness).

		β strategy
		C	D
α strategy	C	1 / 1	1-c / 1+b
	D	1+b / 1-c	1-c / 1-c

To understand the dynamics of this system, we construct replicator equations (Hofbauer & Sigmund 1998, appendix) based on the payoffs in Table 1 to describe changes in time of the proportions of cooperative α and β supergenes in the population (the proportion of α_C among male supergenes α is labelled p_α, while the proportion β_C among all β is labelled p_β),

$$\begin{array}{cc}\hfill & d{p}_{\alpha }∕dt=-p_{\alpha }(1-p_{\alpha })p_{\beta }b\hfill \\ \hfill & d{p}_{\beta }∕dt=-p_{\beta }(1-p_{\beta })p_{\alpha }b.\hfill \end{array}$$ 1

Given that b > 0, we find that mutual cooperation is unstable, selection will drive the population towards increasing levels of mutual defection. Note however that the strength of selection against cooperation within one supergene population is dependent on the frequency of cooperators p in the partner population. The result of this dependency can be seen as a race to total defection; as soon as one population of supergenes achieves total defection, selection for defection in the partner population is totally relaxed, and intermediate cooperation in the partner population can persist (figure 1). Figure 1 illustrates that this race will be won by the supergene that defects first, or that defects the most aggressively (ie, allowing for the values of b and/or c to differ for each supergene, see appendix for complete model). Thus while mutual defection is not here an ESS (so we do not have a strict Prisoner’s dilemma, Hofbauer & Sigmund 1998), both mutual and unilateral total defection are Nash equilibria (rare cooperators do no better than defectors when facing a population of pure defectors). Table 1 and equations 1 focus on the relative success of cooperator and defector variants in producing gametes, without explicitly tracking the ultimate success of these gametes in forming offspring plants. In the case of pure outcrossing, any population-scale costs of the spread of defector alleles (for instance, declining population size) will be felt equally by cooperator and defector alleles entering the mating market and therefore will not modify the relative payoffs and replicator dynamics in equation 1.

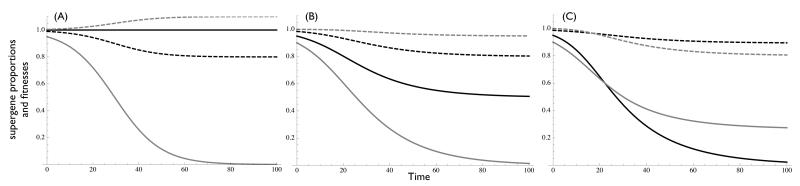
Figure 1. Outbreeding generates a race to defection.

Solid lines represent proportions of cooperative α (black) and β (gray) supergenes. Dashed lines represent mean fitnesses of α (black) and β (gray) supergenes. A) invasion of a defector supergene (here, β defector) reduces fitness of partner supergene, and when c > b, reduces mean supergene fitness. B) Invasion of defection in the partner supergene can follow, so long as first supergene has not yet fixed for defection. C) The partner supergene can overtake the initial defector supergene, if it has a sufficiently high reward b for defection. Simulations based on models 1. Parameters c = 0.2, b = 0.1 (except C, where b_α = 0.15, b_β = 0.1). Initial conditions (A) p_α = 1, p_β = 0.95. (B, C) p_α= 0.95, p_β = 0.9. Model 1 is equivalent to the complete model 4 with i = 0.

Conflict resolution via selfing

The partial preservation of cooperative alleles in one of the two supergene populations offers some possibility of cooperation being rescued at a later stage by a reversion in selective pressures, and selfing offers one route to a reversion in selection.

If a plant lineage were to preferentially self, then its α supergenes would have to depend on their β supergene partners to provide a productive context for their pollen, and vice versa, they are no longer able to to exploit the population mating market equally. We first assume that selfing has some intrinsic cost x (0<x<1), so that the fitness of cooperator-cooperator supergene pairings will be reduced to 1-x. As in model 1, a mutant defector α will increase plant pollen production if coupled with a cooperator β, however this increased pollen can only fertilise the diminished supply of eggs provided by its partner supergene, thus their fitness is limited to (1-x)(1-c). Similarly, a defector β supegene will receive the penalty of its actions by suffering a limited supply of pollen, yielding the payoffs in Table 2. Together, these assumptions ensure that given complete self-fertilization, pure mutual cooperation is an ESS whenever c > 0 (for both α and β supergenes, switching from C to D imposes a cost c) for any cost of selfing x. Later, we relax the assumption that pollen limitation is costly during self-fertilisation. System dynamics can be again described by coupled replicator equations (appendix), which for the pure selfing model (table 2) become

$$\begin{array}{cc}\hfill & d{p}_{\alpha }∕dt=p_{\alpha }(1-p_{\alpha })p_{\beta }c(1-x)\hfill \\ \hfill & d{p}_{\beta }∕dt=p_{\beta }(1-p_{\beta })p_{\alpha }c(1-x)\hfill \end{array}$$ 2

Table 2.

Fitness of α and β supergenes (presented as α / β ) as a function of their combined strategies (cooperate C or defect D), given complete self-fertilization. x is cost of selfing. c is the cost of being paired with a defector.

		β strategy
		C	D
α strategy	C	1-x / 1-x	(1-x)(1-c) / (1-x)(1-c)
	D	(1-x)(1-c) / (1-x)(1-c)	(1-x)(1-c) / (1-x)(1-c)

From these equations we can see that if c > 0 there is always positive selection for cooperation in a focal supergene, given there is non-zero cooperation among the partner supergene population. This effect is illustrated in figure 2, where we track the dynamics of cooperative α and β, given rare α and for differing initial frequencies of β (potentially reflecting different stasis points following rounds of mutual defection in an outbred population, figure 1). Increasing the initial density of β accelerates the rate of recovery of cooperation.

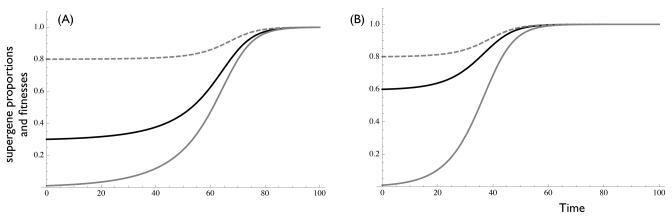
Figure 2. Complete inbreeding can restore selection for mutual cooperation, and increase plant fitness.

Solid lines represent proportions of cooperative α (black) and β (gray) supergenes. Dashed lines represent mean fitnesses of α and β supergenes (here, overlaid). Given perfect inbreeding (model 2), cooperation is restored in both supergenes, which experience identical mean fitness due to their shared reproductive outlet. A) 30% prevalence of cooperation among alpha supergenes. B) 60% prevalence of cooperation among alpha supergenes. Increasing prevalence of cooperation in the partner supergene reduces time to cooperator fixation in both supergenes. Simulations based on models 2. Parameters c = 0.2, b = 0.1. Initial conditions (A) p_α = 0.3, p_β = 0.01. (B) p_α = 0.6, p_β = 0.01. Model 2 is equivalent to the complete model 4 with i = 1, x = 0 and d = -c.

Next, we relax the assumption that intragenomic conflict is costly to both supergene partners in a selfing individual. In particular, we explore the idea that a modest switch in gametic investment from pollen to ovules (induced by a defector β supergene, transmitted via ovules) may increase total reproduction in a selfing plant. Selfing lines are known to increase seed-set by reducing pollen:ovule ratios, due to greater proximity of anthers and stigmas, and thus more efficient pollen transport. The energy conserved by reducing pollen production may be used to produce more flowers with the unexpended energy as in Trillium (Tominatsu and Ohara, 2006), or make larger seeds as in Oenothera and Calylophus (Johnson et al., 2010). Thus an α_C - β_D plant may have more eggs and still have sufficient pollen, so potentially both gametes have higher success, determined by an increased output of fertilized eggs. Under pure selfing, the payoffs are illustrated in Table 3. System dynamics can be again described by coupled replicator equations (appendix), which for the pure selfing model (table 3) become

$$\begin{array}{cc}\hfill & d{p}_{\alpha }∕dt=p_{\alpha }(1-p_{\alpha })(c+d(1-p_{\beta }\left)\right)(1-x)\hfill \\ \hfill & d{p}_{\beta }∕dt=-p_{\beta }(1-p_{\beta })p_{\alpha }d(1-x)\hfill \end{array}$$ 3

Table 3.

Fitness of α and β supergenes (presented as α / β ) as a function of their combined strategies (cooperate C or defect D), given complete self-fertilization. x is cost of selfing. c is the cost of α-induced reductions in egg production (shared by both supergenes) and d is the net effect of β-induced increases in egg production (shared by both supergenes).

		β strategy
		C	D
α strategy	C	1-x / 1-x	(1-x)(1+d) / (1-x)(1+d)
	D	(1-x)(1-c) / (1-x)(1-c)	(1-x)(1-c) / (1-x)(1-c)

Note when d = b, we have perfect recovery of benefits of excess egg production (for both parties). When d = -c, we have the previous model (shortage of pollen trumps excess of eggs, eg when pollen is totally aborted). A stability analysis of model 3 illustrates that pure mutual cooperation is an ESS if d < 0 < c (figure 2), whereas pure male cooperation and female defection is an ESS if - c < d (figure 3). When –c < d < 0 both inequalities hold, implying that both ESSs are locally stable with the observed outcome (cooperation-cooperation or cooperation-defection) dependent on initial conditions.

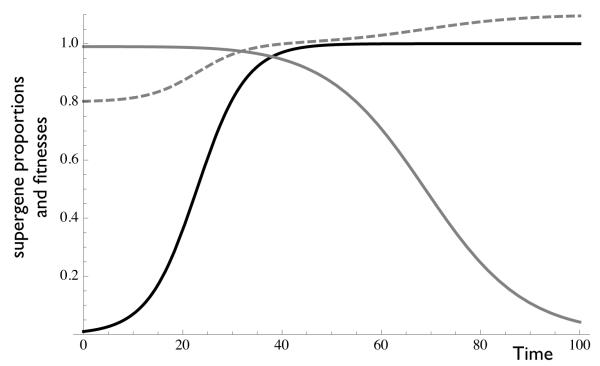
Figure 3. Complete inbreeding can restore male supergene cooperation alone, if reduced pollen production is not limiting.

Solid lines represent proportions of cooperative α (black) and β (gray) supergenes. Dashed lines represent mean fitnesses of α and β supergenes (here, overlaid). Given perfect inbreeding and non-limiting pollen production (model 3), the global ESS is pure male α cooperation and β defection, resulting in identical mean fitness due to their shared reproductive outlet. Simulations based on model 3. Parameters c = 0.2, b = 0.1, d = 0.1. Initial conditions p_α = 0.01, p_β = 0.99. Model 3 is equivalent to the complete model 4 with i = 1 and x = 0.

Note in figure 3 we see two distinct rounds of (joint) fitness improvement, first due to the spread of α-cooperation then due to the spread of β-defection.

We can now ask whether lineages that undergo selfing will outperform lineages that outcross, despite our assumption of an inherent cost to selfing (x > 0), due to the ability of selfing lineages to preserve more cooperative and productive genomes (contrast figure 1 with figures 2 and 3). The mean supergene fitness in model 1 is 1-c + p (b+c)/2, where p is the proportion of cooperators in the partially-cooperative supergene population. Whenever c>b (whenever one-way manipulation imposes a net productivity cost to the plant), we see that mean supergene fitness is diminished below 1, and approaches 1-c as p tends to zero (and is potentially diminished further due to reduced mating success in a declining population). In contrast, the mean supergene fitness at the ESS for model 2 is 1-x, and (1-x)(1+d) in model 3. Contrasting these selfing outcomes with the average fitness in an outcrossing lineage, we see selfing lineages will dominate when c > x + p (b+c)/2. When selfing is relatively costless and if c > b, we see that this inequality is always true, even in absence of any additional mating costs for outcrossing gametes in a defector-ridden population. The value of selfing is simply that it allows the avoidance of destructive intragenomic conflict. The peculiar implication of these results is that if c > x + p (b+c)/2, lineage selection favours asexual (clonal selfing) over sexual (outcrossing) lineages, in contrast to the broadly observed pattern of deeper sexual clades (Maynard Smith 1978, Lynch 1990; but see Judson & Normark 1996).

Intermediate selfing

We can now generalise the selfing model to a variable amount or investment in inbreeding, i. Here we assume that with probability i, an individual plant will self-fertilise, and with probability (1-i) the individual will out-cross with a random member of the plant population. To conservatively assess the conditions favouring selfing, we again make the assumption that outcrossing gametes are not penalised by a lack of mating opportunities as the population prevalence of defector supergenes rises. Combining the selfing parameter i with the assumptions in models 1 and 3 (outcrossing and selfing limit cases, respectively), we can describe the full system dynamics via the following replicator equations (derived in the appendix)

$$\begin{array}{cc}\hfill & d{p}_{\alpha }∕dt=p_{\alpha }(1-p_{\alpha })\left(ci\right(1-x)-b{p}_{\beta }(1-i)+di(1-p_{\beta }\left)\right(1-x\left)\right)\hfill \\ \hfill & d{p}_{\beta }∕dt=p_{\beta }(1-p_{\beta })p_{\alpha }(-id(1-x)-b(1-i\left)\right)\hfill \end{array}$$ 4

Note that when d=-c, we recover equations [1] with i = 0 (pure outcrossing), and equations [2] with i = 1 (pure selfing). Equations [3] can be recovered from [4] when i = 1. A stability analysis of the full model (equations 4) illustrates that mutual cooperation (p_α = p_β = 1, fig 2) is a candidate ESS even for intermediate levels of selfing i, being stable whenever $i>\frac{b}{b+c(1-x)}$, given pollen damage is sufficiently limiting to plant fitness $\left(d<\frac{-b(1-i)}{i(1-x)}\right)$. Conversely, if we allow for pollen reduction to increase fitness of a selfing plant (d > 0) then a mix of cooperation and defection (p_α = 1, p_β = 0) can be an ESS for non-zero i (illustrated for the case of i = 1 in fig. 3), specifically when d > -c and $d>\frac{-b(1-i)}{i(1-x)}$.

Finally, consider a strategic choice between selfing and outbreeding. Consider that one supergene alone (e.g. α) has control over the inbreeding phenotype of the plant, by exerting control over selfing behaviours (and note that the following argument is symmetrical for both supergenes), then cooperative α in a CC (perfectly cooperative) plant will be selected to switch to selfing whenever the selfing payoff exceeds the expected outbreeding payoff. The expected payoff to an outbreeding α cooperator can be calculated from table 1 to be no more than F_α,C = p_α + (1-p_β)(1-c). Therefore, selfing is favoured whenever 1-x > F_α,C, which can be re-arranged as a condition dependent on the supply of cooperative partners, ie selfing controlled by the α supergene is favoured whenever p_β < (c-x)/c. Note that when selfing is cost-free (x = 0), this analysis suggests that any amount of defection among the population of partner supergenes will select for inbreeding in the focal supergene.

Discussion

Self-fertilization in PTH (in Oenothera and in six other genera) heretofore has been considered to be a mechanism that evolved because it guarantees the identity of offspring and parents while conferring reproductive assurance (cf. Holsinger and Ellstrand, 1984). The retention of offspring-parent identity maintains advantageous gene combinations and relatively high levels of heterozygosity, while preventing the union of the same deleterious alleles. In contrast to the aforementioned theory, we present a model which shows that self-fertilization in PTH may have evolved as a solution to intragenomic sexual conflict. Indeed almost all PTHs are predominantly selfers (Holsinger and Ellstrand, 1984), and in general selfing clades are associated with a reduced load of selfish genetic elements (Wright et al. 2008).

Our models assumed that PTH is engineered via balanced gametic lethality, assuring that α supergenes are transmitted purely via pollen and β supergenes purely via eggs. This gamete-specific mode of transmission is not the case in PTH lineages displaying zygotic lethality (α-α and β-β zygotes are aborted), viable zygotes can be generated under this mechanism from α pollen plus β eggs or α eggs plus β pollen (Harte, 1994). Given the mixed gametic routes of transmission available to either supergene, biasing plant sexual investment is unlikely to be a successful supergene strategy no matter the degree of outcrossing: an α defector that hits eggs would be of no value as half the eggs carry α. However, more direct forms of driving (directly killing the rival supergene, whether in eggs or pollen) may still be favoured in an outcrossing population. Importantly, the common thread of obligate heterozygosity ensures that selfing still gives protection against defector supergenes: an α gamete (whether in eggs or pollen) would need to mate with a β gamete produced from the same plant (and vice-versa), exposing defectors and rewarding cooperator supergenes. Thus even with zygotic lethality, α and β supergenes in a selfing plant must still form an enduring ‘marriage’ and are therefore selected for greater cooperation. Conistent with this logic, PTH shaped by zygotic lethals are also typically selfers (Dietrich 1977; Raven 1979). The importance of selfing in reducing intra-genomic conflict has also been investigated in the context of cyto-nuclear gene combinations (Wade & Goodnight 2006).

While the empirical focus of our work has been based on the unusual genetic system in some species of Oenothera , the resulting theoretical model describes a generic strategic tussle between two distinct lineages (α and β), which could just as well be distinct species α and β engaged in some interspecific social interaction. For the specific case of intragenomic conflict in Oenothera, the social interaction consists of the construction of a shared organism, however the payoffs in Tables 1-3 are more generic. How does our general model relate to existing theoretical treatments of interspecific cooperation, or mutualism?

Whereas cooperation among individuals within a species can be understood as being favoured due to ‘nepotism’, or the carriage of shared genes (Hamilton 1964), the maintenance of costly cooperation among unrelated individuals can only be achieved through some form of reciprocation, assuring a direct fitness return to the focal actor (for reviews, see Sachs et al 2004, West et al. 2007, Lehmann & Keller 2006). Two principal mechanisms of reciprocation have been proposed, partner choice and partner fidelity feedback (Bull & Rice 1991, Sachs et al. 2004). Partner choice allows individuals to modify their behaviour in response to the actions of their partner(s), so to punish non-cooperation and reward cooperation. In contrast, partner fidelity feedback simply requires a coupling of fitnesses among interacting individuals, for instance due to repeated interactions. Given sufficient coupling, defection by a focal organism will be ultimately self-defeating, as the partner organism will be increasingly unable to return any reward to the focal player (Harcombe & Bull 2010).

While these mechanisms of reciprocity can readily coexist (most famously, both are present in the ‘iterated prisoners’ dilemma’; Trivers 1971, Axelrod & Hamilton 1981, Sachs et al. 2004), it is partner fidelity feedback that allows the evolution of cooperation in our model. In figure 1 (outcrossing; or more generally, low partner fidelity / high mixing), we see that mutual cooperation cannot be maintained, as there is is no reciprocity. For example, a defector α can exploit and undermine a cooperative β, and the resulting super-abundance of α-carrying pollen can fertilise a representative sample of β eggs from the across the global population. In contrast, in figure 2 (selfing; or more generally, high partner fidelity / low mixing) cooperative supergenes are maintained. A defector α facing a cooperative β within a selfing plant would now be punished as the super-abundant α-pollen would only be able to fertilise the population of reduced β-eggs that the α ‘individual’ had itself attacked.

Whereas figure 2 (mutual cooperation) supports the established result that partner fidelity will favour mutually cooperative outcomes (Sachs 2004, Sachs & Bull 2005, Harcombe & Bull 2010), figure 3 suggests that fidelity can also lead to asynchronous outcomes, here showing an evolutionary stable partnership between a cooperator (α) and a defector (β). The reason for the asynchronous outcome in figure 3 is the underlying asynchrony between the costs and benefits of cooperation to the two partners. For a selfing plant, we assume (in model 3) that plant fitness is sharply increasing with egg production, and less so with pollen production. Given that one party is strongly rate-limiting on the productivity of the pairing (here, β productivity is rate limiting), it can pay for the α partner to continue to cooperate in the face of defection, as the α_C-β_D pairing has greater overall productivity (plant seed set), which is then equally shared among the two partners. The resulting bias in gametic investment (towards female β) in selfing populations can be viewed as an intragenomic example of local mate competition theory (Hamilton 1967); Under outcrossing the gametic sex ratio tends towards 1:1, but investment becomes female-biassed (due to driving β alleles) under local mating, to maximise descendents (seed set). It is important to note that the asynchronous interaction driven by high partner fidelity in figure 3 can still be described as mutually cooperative. The β behaviour remains defective in a mechanistic sense (being deficient in its support for male functioning) but still enhances the fitness (seed set) of its α partner. Thus a mechanistically defective β allele can be functionally either a cooperator or a cheat with respect to its α partner, dependent on social context (shaped by partner fidelity).

We have argued that the establishment of selfing in PTH lineages offers a route out of a debilitating intragenomic conflict: driving supergenes lose in selfing plants as they must seek to mate with the decimated ranks of their victims. The advantages of clonal selfing for cooperative supergenes must then be weighed against the potential costs. Given the protection afforded to favourable heterozygous states by PTH (Charlesworth 1979), inbreeding depression is expected to be minimal in PTH lineages. Even if PTH lineages are robust against inbreeding depression, additional costs of selfing may emerge due to Muller’s ratchet causing a growing erosion in the functioning of any specific α (or β) supergene, implying the selfing cost x increases with time since the shift to selfing. Muller’s ratchet may therefore generate time-dependent costs of selfing where old partner supergenes become selective liabilities and are replaced by new ones via limited outcrossing. While specific supergenes may then go extinct (due to their genetic load) their younger partner can then persist via periodically favourable outcrossing. If supergenes deteriorate over time, it follows that there must be a source of new supergenes, that is a close bivalent-forming relative, if PTH are to persist for very long spans of time. Although initially rare, a new supergene complex may increase in frequency if its intrinsic genetic makeup is superior to resident supergenes and if it can combine (interact) favourably with new partner supergenes during occasional oucrossing. The more successful marriages that a supergene has, the longer it is likely to persist. If a new supergene was successful when coupled with only one partner complex, its fate would be tied to the fate of is partner, which may be mature and may have accumulated a substantial genetic load.

The focus on our study has been on how evolution might proceed following the establishment of a perturbation (permanent translocation heterozygosity) to normal sexual genome functioning, highlighting the possibility of intragenomic conflict, and how selfing presents a route out of conflict. It is useful at this point to discuss how genome harmony is typically maintained in outcrossing lineages. Outcrossing lineages assure ‘partner feedback fidelity’ through fair meiosis, which again couples the interests of a specific gene with the interests of the entire organism (fair meiosis has also been interpreted as a policing mechanism (Leigh 1977, Frank 2003), which can in turn be viewed as a form of partner fidelity (Sachs et al. 2004)). In our case, policing has broken down, as β has no chance of progress via pollen and vice versa for α in eggs, opening the possibility of strategies of defection. Selfing then emerges as an emergency mechanism for restoring ‘fidelity’ across the entire genome (all genes are equally rewarded by the reproductive fate of the entire organism).

Appendix.

We label the proportion of cooperative male supergenes as p_α and the proportion of cooperative female supergenes as p_β. The dynamics of the two cooperative populations can now be described by the replicator equations dp_x /dt = p_x (1-p_x)(F_xC - F_xD), where F_xC is the expected payoff for the cooperative variant and F_xD is the expected payoff for the defector variant of supergene type x. For background and derivation of replicator equations, see Hoffbauer & Sigmund 1998, Nowak 2006.

Combining the inbreeding parameter i with the assumptions in models 1 and 3 (outcrossing and selfing limit cases, respectively), the expected fitnesses of cooperator and defector supergenes can be calculated as follows. For completeness, we allow each of the cost/benefit parameters described in the main text (c, b, d) to vary between the two supergenes (distinguished by α and β superscripts)

$$\begin{array}{cc}\hfill & F_{\alpha C}=i(1-x)(p_{\beta }+(1-p_{\beta }\left)\right(1+d_{\alpha }\left)\right)+(1-i)(p_{\beta }+(1-p_{\beta }\left)\right(1-c_{\alpha }\left)\right)\hfill \\ \hfill & F_{\alpha D}=i(1-x)(1-c_{\alpha })+(1-i)\left(p_{\beta }\right(1+b_{\alpha })+(1-p_{\beta }\left)\right(1-c_a\left)\right)\hfill \\ \hfill & F_{\beta C}=i(1-x)(p_{\alpha }+(1-p_{\alpha }\left)\right(1-c_{\beta }\left)\right)+(1-i)(p_{\alpha }+(1-p_{\alpha }\left)\right(1-c_{\beta }\left)\right)\hfill \\ \hfill & F_{\beta D}=i(1-x)\left(p_{\alpha }\right(1+d_{\beta })+(1-p_{\alpha }\left)\right(1-c_{\beta }\left)\right)+(1-i)\left(p_{\alpha }\right(1+b_{\beta })+(1-p_{\alpha }\left)\right(1-c_{\beta }\left)\right).\hfill \end{array}$$ A1

Substituting these expected fitness values [A1] into replicator equations, we find the system dynamics to be described by

$$\begin{array}{cc}\hfill & d{p}_{\alpha }∕dt=p_{\alpha }(1-p_{\alpha })\left(i{c}_{\alpha }\right(1-x)-b_{\alpha }{p}_{\beta }(1-i)+i{d}_{\alpha }(1-p_{\beta }\left)\right(1-x\left)\right)\hfill \\ \hfill & d{p}_{\beta }∕dt=p_{\beta }(1-p_{\beta })p_{\alpha }(-i{d}_{\beta }(1-x)-b_{\beta }(1-i\left)\right).\hfill \end{array}$$ A2

Model [4] can be recovered from [A2] when c_α = c_β = c, b_α = b_β = b and d_α = d_β = d. A stability analysis of [A2] using standard techniques (Otto & Day 2007) reveals two candidate ESSs, first mutual cooperation (p_α = p_β = 1; Fig 2) and second male cooperation and female defection (p_α = 1, p_β = 0; Fig 3). The former is locally stable when ($i>\frac{b_{\alpha }}{b_{\alpha }+c_{\alpha }(1-x)}$ and $d_{\beta }<\frac{-b_{\beta }(1-i)}{i(1-x)}$) and the latter when (d_α > -c_α and $d_{\beta }>\frac{-b_{\beta }(1-i)}{i(1-x)}$). In addition, when neither ESS is locally stable (for low i, d_α and d_β), unilateral or mutual defection (fig 1) is a Nash equilibrium.