SUMMARY
Karyopherinβ2 (Kapβ2) or transportin imports numerous RNA binding proteins into the nucleus. Kapβ2 binds substrates in the cytoplasm and targets them through the nuclear pore complex, where RanGTP dissociates them in the nucleus. Here we report the 3.0Å crystal structure of unliganded Kapβ2, which consists of a superhelix of 20 HEAT repeats. Together with previously reported structures of NLS and Ran complexes, this structure provides understanding of conformational heterogeneity that accompanies ligand binding. The Kapβ2 superhelix is divided into three major segments. Two of them (HEAT repeats 9–13 and 14–18), which constitute the substrate binding site, are rigid elements that rotate relative to each other about a flexible hinge. The third (HEAT repeats 1–8), which constitutes the Ran binding site, exhibits conformational changes throughout its length. An analogous segmental architecture is also observed in Importinβ, suggesting that it is functionally significant and may be conserved in other import karyopherins.
INTRODUCTION
Karyopherinβ proteins (Kapβs; importins/exportins) mediate transport of macromolecules between the nucleus and the cytoplasm. At least 19 members of this protein family have been identified in human cells, and most of them have been reported to function in nuclear import, export, or bidirectional transport (reviewed in Chook and Blobel, 2001; Conti and Izaurralde, 2001; Gorlich and Kutay, 1999; Weis, 2003). All known Kapβs consist of 19 or 20 contiguous HEAT repeats (Huntington, Elongation factor 3, A subunit of protein phosphatase 2A and Tor1 kinase, proteins where these types of helical repeats were first found; Andrade and Bork, 1995) that pack to form a spiral-shaped or superhelical molecule (Chook and Blobel, 2001; Conti et al., 2006; Cook et al., 2007). Each Kapβ recognizes multiple ligands, including numerous transport substrates, nucleoporins, and the Ran GTPase. Kapβs bind specific sets of substrates through nuclear localization or nuclear export signals (NLSs or NESs). The number of substrates for a Kapβ ranges from one to hundreds. For example, Kapα is the only known substrate for export-Kapβ Cas/Cse1p, whereas Importinβ (Impβ or Kapβ1) and Crm1 bind hundreds of substrates each (Matsuyama et al., 2006; Mosammaparast and Pemberton, 2004). Kapβs also bind FG repeats in nucleoporins to translocate substrates through the nuclear pore complex (NPC). Finally, the Ran GTPase regulates Kapβ-substrate interactions and transport directionality through its nucleotide cycle and the asymmetric distribution of its nucleotide states across the NPC. Thus, it is critical that this family of transporters maintains an architecture that facilitates binding and exchange of many diverse ligands.
Multiple crystal structures of four different full-length Kapβs and small-angle X-ray scattering (SAXS) models of six different Kapβs have been reported. Previously solved crystal structures are: (1) complexes of human Impβ with substrates Kapα IBB domain and SREBP2 (Cingolani et al., 1999; Lee et al., 2003); (2) complexes of yeast homolog Kap95p with RanGTP and a Nup1p fragment (Lee et al., 2005; Liu and Stewart, 2005); (3) human Kapβ2 or transportin complexed with RanGppNHp, substrates hnRNP A1-NLS and hnRNP M-NLS, respectively (Cansizoglu et al., 2007; Chook and Blobel, 1999; Lee et al., 2006); and (4) unliganded and substrate-bound Cse1p (Cook et al., 2005; Matsuura and Stewart, 2004). SAXS models are available for multiple states of Impβ, Kapβ2, Crm1, Cse1p, and Xpo-t and its yeast homolog Los1p, and comparisons within each karyopherin series show substantial protein flexibility (Fukuhara et al., 2004). However, low-resolution SAXS models limit characterization of flexibility to large-scale changes in radius of gyration and descriptions of extended versus compact conformations (Fukuhara et al., 2004). Crystal structures of Cse1p (Cook et al., 2005; Matsuura and Stewart, 2004) and full-length Impβ complexes (Cingolani et al., 1999; Lee et al., 2003, 2005; Liu and Stewart, 2005) show that both karyopherins undergo large conformational changes upon ligand binding, also showing that Kapβs are quite flexible. However, despite the large number of crystal structures, there are relatively few studies of Kapβ conformational flexibility (Cingolani et al., 1999; Conti et al., 2006; Cook et al., 2005; Lee et al., 2003, 2005). With the exception of a recent review on Kapβ flexibility (Conti et al., 2006), most studies involve qualitative descriptions of differences in superhelical pitches and regions of structural changes. Analysis of conformational flexibility may be complicated by the unusual nonglobular and nonmodular architecture of these proteins and the limited number of structures within each Kapβ series (Impβ, Kap95p, Kapβ2, and Cse1p).
We have solved the 3.0Å structure of unliganded Kapβ2 to extend the structural map of this import pathway that transports numerous RNA binding proteins into the nucleus. A suite of Kapβ2 structures (unliganded, hnRNP A1-NLS, hnRNP M-NLS, and Ran complexes) is now available to explain conformational changes that accompany substrate recognition, Ran binding, and substrate release (Cansizoglu et al., 2007; Chook and Blobel, 1999; Lee et al., 2006). Most importantly, through three independent methods of domain motion analysis, rotation vector clustering (Hayward and Berendsen, 1998), B factor grouping (Painter and Merritt, 2006), and structural superpositions, we have identified three major segments of the Kapβ2 superhelix that show intrinsic flexibility and also respond to binding of different ligands. We also observe segmental architecture in Impβ, suggesting generality across nuclear import factors.
RESULTS AND DISCUSSION
Structure Determination and the Overall Structure of Unliganded Kapβ2
Kapβ2 has 20 HEAT repeats, each consisting of two anti-parallel helices, A and B. The A helix of HEAT repeat 1 (H1) is abbreviated as H1A. All helices are connected by short loops or small helices except for H8A and H8B, which are connected by a 62 residue acidic loop called the H8 loop (Lee et al., 2006). The Kapβ2 superhelix can be divided into two arches. The N-terminal arch is composed of H1–H13, and the C-terminal arch is composed of H9–H20. Ran binds in the N-terminal arch and substrates have been observed so far to bind in the C-terminal arch.
We have solved the 3.0Å crystal structure of unliganded Kapβ2 using a combination of single-wavelength anomalous dispersion (SAD) and molecular replacement (MR). Full-length native and selenomethionine Kapβ2s (residues 1–890) were crystallized. The native crystals (space group P21, a = 129.9Å, b = 169.3Å, c = 141.1Å, and β = 93.1°, four molecules in the asymmetric unit; Table 1) diffracted to 3.0Å. MR using the Kapβ2-Ran structure was unsuccessful (McCoy et al., 2005), suggesting significant conformational differences between the unliganded and Ran states.
Table 1.
Data Collection and Refinement Statistics for Crystals of Full-Length Native and Selenomethionine Derivatives of Unliganded Kapβ2
| Data Collection | Native | Selenomethionine |
|---|---|---|
| Space group | P21 | P21 |
| Unit cell parameters | ||
| a, b, c (Å) | 129.9, 169.3, 141.1 | 108.5, 294.0, 108.3 |
| α, β, γ (°) | 90.0, 93.1, 90.0 | 90.00, 92.1, 90.00 |
| Resolution (Å) | 50–3.0 (3.1–3.0) | 50–3.6 (3.4–3.6) |
| Rsyma | 0.099 (0.45) | 0.126 (0.88) |
| I/σI | 24 (4.8) | 22 (2.7) |
| Completeness (%) | 100 (99.8) | 99.9 (100) |
| Redundancy | 5.0 (4.9) | 4.2 (4.1) |
| Refinement | ||
| Number of unique reflections | 114,642 | |
| Rfree/R factorb | 0.286/0.261 | |
| Rmsd from ideal bond lengths (Å) | 1.144 | |
| Rmsd from ideal bond angles (°) | 0.008 | |
| Ramachandran plot | ||
| Most favored regions (%) | 90.64 | |
| Generously allowed regions (%) | 0.9 | |
| Additional allowed regions (%) | 8.7 | |
| Disallowed regions (%) | 0.0 | |
| Model | Average B factor (Å2) | |
| Chain A (residues 6–319, 370–890) | 70.0 | |
| Chain B (residues 30–158, 167–319, 372–890) | 73.7 | |
| Chain C (residues 5–21, 30–158, 164–319, 369–890) | 81.5 | |
| Chain D (residues 7–319, 369–890) | 67.4 |
Values in parentheses are calculated for data in the highest-resolution shell.
Rsym = ΣhΣi(Ii(h) – < I(h) >)|/ΣhΣiIi(h); Ii(h) is the ith measurement of reflection h and < I(h) > is the weighted mean of all measurements of h.
R factor = Σh||Fobs (h)| – |Fcalc(h)||/Σh|Fobs (h)|. Rfree is calculated with 5% of the data.
Selenomethionine Kapβ2 crystals (space group P21, a = 108.5Å, b = 294.0Å, c = 108.5Å, and β = 92.0°, four molecules in the asymmetric unit) were pseudo-merohedrally twinned, but a 1:1 molar mixture of native and selenomethionine proteins resulted in a single crystal (space group P21, a = 108.5Å, b = 294.0Å, c = 108.3Å, and β = 92.0°) from which 3.6Å SAD data were obtained. Even though MR using Kapβ2 residues 396–864 from the Kapβ2-Ran structure was successful (McCoy et al., 2005), we calculated experimental SAD phases to avoid model bias. To facilitate determination of the 104 selenium sites in the asymmetric unit (26 methionines/Kapβ2), 72 selenium sites were extracted from the partial MR model followed by determination of the next 28 by iterative phase refinement and difference Fourier methods (Brunger et al., 1998). Phase refinement with 100 selenium sites followed by density modification with solvent flipping resulted in an electron density map where three of the four Kapβ2s in the asymmetric unit could be traced. This incomplete and low-resolution SAD model was not refined, but instead used for MR with the higher-resolution native data. Residues 88–656 gave an MR solution, resulting in an interpretable electron density map. Differences between the SAD and native models are discussed in Experimental Procedures. Given the four molecules in the asymmetric unit and the unusual helical repeat structure of Kapβ2, the final 3.0Å model of residues 6–890 for chains A, C, and D and residues 31–890 for chain B was refined using many combinations of noncrystallographic symmetry (NCS) constraints (described in Experimental Procedures; see Tables S1 and S2 in the Supplemental Data available with this article online). Statistics of a refinement using NCS to constrain chain A to D and chain B to C, both in three segments, are reported in Table 1 (Rfree = 28.6% and R factor = 26.1%) and Tables S1 and S2 (CCP4, 1994).
All four copies of Kapβ2s are arranged with their superhelical axes parallel to the crystallographic y axis, and two pairs (chains A and B, and C and D) are related to each other by a pseudo-translation of approximately a half-unit cell along the crystallographic z axis. Approximately 4700Å2, or 12% of each molecule's total surface area, is buried in crystal contacts. The low percentage of surface area involved in crystal contact compared to other protein crystals is consistent with the low resolution and high solvent content (>70%) of the Kapβ2 crystal (Carugo and Argos, 1997). All NCS-related Kapβ2s have similar crystal contacts and similar overall structure.
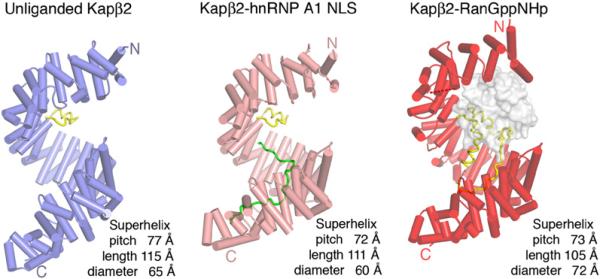
The unliganded Kapβ2 molecule is a rather symmetrical superhelix with a 77 Å pitch, 115 Å length, and 65 Å diameter (Figure 1). Its overall structure is similar to those of Kapβ2-substrate complexes. Both unliganded and substrate-bound karyopherins are more elongated along their superhelical axes compared to the Ran-bound molecule, consistent with previous SAXS studies of Kapβ2 (Fukuhara et al., 2004).
Figure 1. Ribbon Diagrams of Unliganded and Substrate- and Ran-Bound Kapβ2s.
β helices are represented as cylinders and structurally disordered loops as dashed lines. Unliganded Kapβ2 is in blue, Kapβ2 bound to substrate is in pink, Kapβ2 bound to Ran is in red, and H8 loops in all three structures are in yellow. Substrate hnRNP A1-NLS is in green and Ran is drawn as a surface representation in gray.
Conformational Flexibility of Unliganded Kapβ2
The four unliganded Kapβ2s in the asymmetric unit show obvious conformational heterogeneity. We used three independent methods to analyze conformational heterogeneity. The first involves several different pairwise superpositions (CCP4, 1994): (1) we scanned the length of Kapβ2 chains superimposing groups of 1–20 HEAT repeats, (2) we superimposed A helices of each repeat and examined B helices for changes within HEAT repeats, and (3) we superimposed B helices and examined A helices of the next repeat for changes between HEAT repeats. The second method of analysis involves clustering rotation vectors using the program DynDom (Hayward and Berendsen, 1998). The third method involves analysis of the spatial distribution of individual atomic B factors in a single protein chain using the program TLSMD (translation/libration/screw motion determination; Painter and Merritt, 2006). The first two methods compare pairs of structures, whereas the third analyzes single protein chains.
When the structure was refined without using any NCS constraints (Table S1, refinement 1), unliganded Kapβ2 chains A and D are similar (Cα root-mean-square deviation [rmsd] 1.2Å) and chains B and C are also similar (Cα rmsd 1.0Å). In contrast, other pairwise comparisons give a Cα rmsd of 2.6—3.2Å. Given the similarity of the AD and BC pairs, the two pairs were constrained by NCS in the final structure reported in Table 1. Structural comparisons below are therefore limited to chains A and C.
Unliganded Kapβ2s are similar in their central regions. Exclusion of terminal repeats H1–H4 and H19-H20 decreased Cα rmsd from 2.9Å for all residues to 1.8Å (Table 2). Moreover, when superimposed at H8–H13 (Cα rmsd < 1.0Å), their termini deviate up to 11 Å (Figure 2A). HEAT repeats at the N and C termini also have higher B factors despite ~2200 Å2 of surface area buried by crystal contacts in these regions. For example, average B factors for H1–H4, H5–H18, and H19-H20 in chain B are 112, 65, and 84 Å2, respectively (electron density maps for the N and C termini are shown in Figures S1A and S1B).
Table 2.
Summary of Cα Rms Deviations for Kapβ2 Superpositions
| HEAT Repeats (Residues) | Unliganded Kapβ2 Chains A and C (Å) | Unliganded Kapβ2, Kapβ2-Substrate (Å) | Unliganded Kapβ2, Kapβ2-RanGppNHp (Å) | Kapβ2-Substrate, Kapβ2-RanGppNHp (Å) |
|---|---|---|---|---|
| 1–20 | 2.9 | 4.2 | 7.7 | 6.1 |
| 1–13 | 2.3 | 2.2 | 6.8 | 6.0 |
| 1–7 | 2.4 | 2.5 | 6.6 | 5.5 |
| 1–4 | 1.1 | 3.0 | 6.3 | 5.4 |
| 5–20 | 2.6 | 4.1 | 5.8 | 4.1 |
| 5–18 | 1.8 | 3.3 | 5.1 | 4.1 |
| 5–13 | 1.3 | 1.3 | 4.1 | 4.0 |
| 8–20 | 2.3 | 3.6 | 4.5 | 2.4 |
| 8–13 | 0.8 | 1.2 | 2.0 | 1.7 |
| 14–20 | 2.5 | 0.9 | 1.7 | 2.2 |
| 14–18 | 0.5 | 0.6 | 1.0 | 1.3 |
| 19–20 | 2.2 | 0.5 | 1.7 | 1.9 |
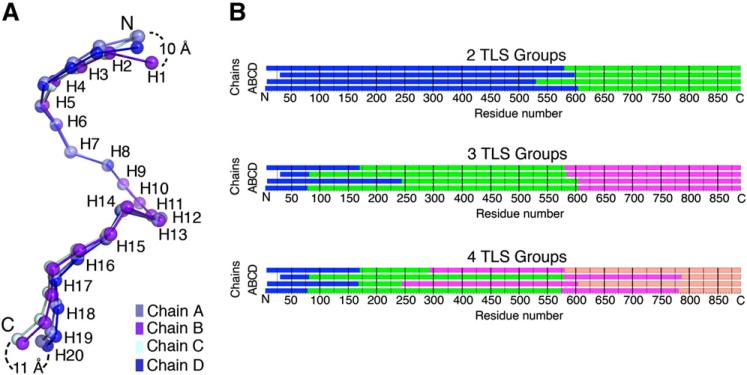
Figure 2. The Four Molecules of Unliganded Kapβ2 in the Asymmetric Unit Show Conformational Heterogeneity.
(A) Four NCS-related Kapβ2s (chains A–D) are superimposed at H8–H13. The chains (each in a different shade of blue) are drawn as spheres at the geometric center of each HEAT repeat. Maximum deviations between geometric centers at the termini are shown. (B) Results of TLSMD analysis for partitioning of the four Kapβ2 chains into two to four TLS groups (each in a different color).
Repeats H5–H13 of all four unliganded Kapβ2s are virtually identical, but their superhelical paths deviate at H14 (Figure 2A). To characterize conformational flexibility in the C-terminal arch, we analyzed each unliganded chain using the program TLSMD (Painter and Merritt, 2006). The molecule is partitioned through analysis of the spatial distribution of individual atomic B factors into 1–20 contiguous pseudo-rigid segments termed TLS groups. We used these multigroup TLS models as a starting point for analysis of large-scale motion in unliganded Kapβ2. The junction for the two-group TLS model mapped to residues 560–610 (H13-H14; Figure 2B). As partitioning progressed, this H13-H14 junction persisted, and additional TLS groups include the two flexible N and C termini segments (H1–H4 and H18–H20) discussed above.
Analyses of full-length unliganded Kapβ2 molecules using DynDom (Hayward and Berendsen, 1998) identified a hinge in H18, which is consistent with the flexible C-terminal segment (H19-H20). Removal of terminal H1–H4 and H19-H20 segments revealed a second hinge at H13-H14 which corresponds to the prominent TLS junction discussed above. A 9° rotation of rigid H5–H13 and H14–H18 segments relative to each other about this hinge axis explains the small conformational difference in C-terminal arches of chains A and C (Table 2; Cα rmsd H5–H13 is 1.3Å, H14–H18 is 0.5Å, and H5–H18 is 1.8Å).
Based on structural superpositions and two independent methods of identifying pseudo-rigid bodies in a molecule, the intrinsically flexible unliganded Kapβ2 can be divided into four moving segments. Two small segments, H1–H4 and H19-H20, are found at the termini. Two larger central segments, H5–H13 and H14–H18, are somewhat rigid elements that rotate relative to each other about a flexible hinge. Interestingly, results of structure refinements using NCS restraints are also consistent with the division of unliganded Kapβ2 into the four segments (Tables S1 and S2).
NLS Recognition: A Hinge in the Kapβ2 C-Terminal Arch
Kapβ2 binds RNA binding proteins through recognition of PY-NLS, a 20–30 residue long signal in the substrates (Lee et al., 2006). PY-NLSs are sequentially diverse, but share three common characteristics: structural disorder, overall basic character, and a set of a weakly conserved hydrophobic or basic N-terminal motif and a C-terminal R/K/Hx2–5PY motif. Crystal structures of Kapβ2 bound to two diverse PY-NLSs from splicing factors hnRNP A1 and M (Cansizoglu et al., 2007; Lee et al., 2006) show that the two NLSs bind a common interface (B helices of H8–H18) on the structurally invariant Kapβ2 C-terminal arch (H2–H20 Cα rmsd is 0.8 Å). Because the karyopherins in both substrate complexes are virtually identical, we use the hnRNP A1-NLS complex to represent the substrate-bound state, and chain A in the unliganded Kapβ2 crystal represents the unliganded state.
Although overall structures of unliganded and substrate-bound Kapβ2s appear similar, a 4.2 Å Cα rmsd suggests substantial conformational differences (Table 2). With the exception of the first four HEAT repeats, most of their N-terminal arches are similar (H5–H13 Cα rmsd is 1.3 Å). Thus, conformational differences mostly map to the C-terminal arch. Like unliganded Kapβ2, analysis using DynDom (Hayward and Berendsen, 1998) to compare unliganded and substrate states also identified a flexible hinge at H13-H14. Subdomains on both sides of the hinge, H5–H13 and H14–H20, behave like rigid segments (Cα rmsd for H5–H13, H14–H20, and H5–H20 are 1.3, 0.9, and 4.1 Å, respectively; Table 2), and NLS binding rotates one segment relative to the other ~16° about the hinge axis (Figure 3). This movement originates from the cumulative effect of small rotations between helices H12B, H13A, H13B, H14A, and H14B within the flexible H13-H14 hinge.
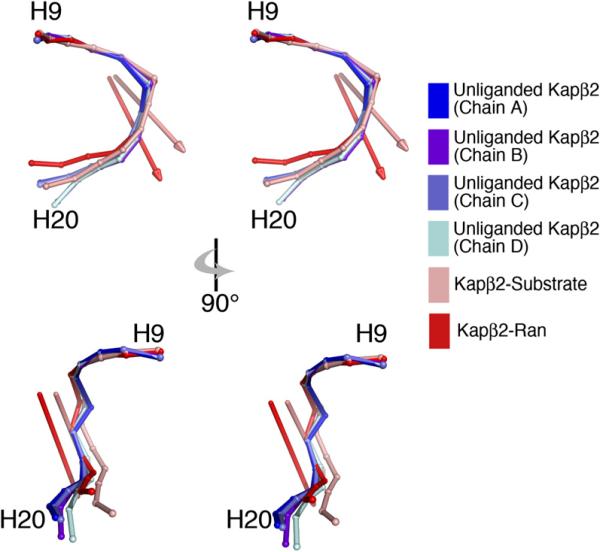
Figure 3. Hinge Motion in the C-Terminal Arch of Kapβ2.
Stereo diagrams of the C-terminal arch (H9–H20) of chains A–D of unliganded Kapβ2 and substrate- and Ran-bound Kapβ2s superimposed at H9–H13 and drawn as spheres at the geometric center of each HEAT repeat. The hinge axes that rotate unliganded Kapβ2 with respect to substrate- and Ran-bound Kapβ2s are in pink and red, respectively.
Interestingly, even though RanGTP binding results in large conformational changes in the Kapβ2 N-terminal arch, the C-terminal arch in Ran- and substrate-bound states are quite similar (H9–H18 Cα rmsd is 1.4 Å; Lee et al., 2006). Furthermore, comparison of H8–H20 (N-terminal arches removed as a result of large conformational changes) in the unliganded and Ran states again identified a flexible hinge in H13-H14 that rotates rigid segments H9–H13 and H14–H18 ~18° relative to each other (Cα rmsd for H9–H13, H14–H18, and H9–H18 are 1.5, 1.0, and 3.2 Å, respectively). The hinge axes that relate unliganded Kapβ2 to substrate- and to Ran-bound conformations are also somewhat similar (Figure 3). The C-terminal arches in Ran and substrate states are probably similar because in the former, Kapβ2's long H8 acidic loop occupies that arch and much of the loop overlaps spatially with bound NLSs (Cansizoglu et al., 2007; Chook and Blobel, 1999; Lee et al., 2006). Thus, conformational similarity in the C-terminal arch in the two ligand states supports the idea that the H8 loop is a pseudo-NLS (Lee et al., 2006).
The same rigid segments, H9–H13 and H14–H18, rotate relative to each other in the different unliganded Kapβ2 chains and between unliganded, substrate-, and Ran-bound Kapβ2s. Intrinsic segmental flexibility observed in the unliganded chains suggests varying degrees of rotation about the hinge. Paradoxically, similarity of the C-terminal arches in the NLS- and pseudo-NLS/Ran-bound Kapβ2s suggests a discrete energetically favorable arch conformation that binds ligands. What is the range of motion about this hinge? Does a range of rotation about the hinge allow fine-tuning of the substrate binding site to accommodate diverse PY-NLSs that vary significantly in length and composition? Or accommodate entirely new classes of undiscovered NLSs? Or accommodate interactions with nucleoporins? Crystal structures of Kapβ2 in complex with longer and more diverse PY-NLSs such as those in HuR and TAP (Fan and Steitz, 1998; Lee et al., 2006; Truant et al., 1999) and structures of Kapβ2-nucleoporin complexes will shed light on these questions.
Kapβ2-Ran Interaction: The Flexible N-Terminal Arch and H8 Acidic Loop
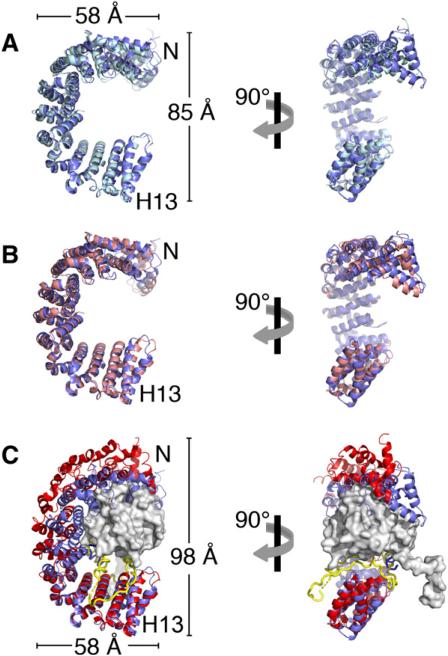
Ran binds in the N-terminal arch of Kapβ2, contacting B helices of H1–H4, H7-H8, and the H8 acidic loop (Chook and Blobel, 1999). Dimensions of the Kapβ2 N-terminal arch change upon Ran binding (Figure 4C). The arch opens as the width of its base increases by 13 Å compared to unliganded and substrate-bound structures, enabling Ran to fit between the interfaces with H1–H4 and the H8 loop (Figures 4A and 4B). The C-terminal third of the N-terminal arch (H9–H13) does not contact Ran, and is similar between unliganded and Ran states (Cα rmsd 1.5 Å; Figure 4C). However, large changes in helical orientations occur within and between each HEAT repeat from H1 to H8. These large helical reorientations occur as helical content of the A, B, and connector helices changes, particular at helix termini, and connector loops also change in conformation. HEAT repeats move both laterally toward the dome of the arch and along the superhelix toward the N terminus to form a larger N-terminal arch.
Figure 4. Conformational Change in the Kapβ2 N-Terminal Arch.
(A) Ribbon diagram of the N-terminal arches of chains A (blue) and C (light blue) of unliganded Kapβ2, superimposed at H9–H13.
(B) Same as (A), except that chain A of unliganded Kapβ2 is superimposed on substrate-bound Kapβ2 (pink).
(C) Same as (A), except that chain A of Kapβ2 is superimposed on Ran-bound Kapβ2 (red). Ran is shown as a surface representation in gray and the H8 loop of the Ran complex is in yellow.
A second obvious conformational difference between unliganded and Ran-bound Kapβ2s is found at the H8 loop. Proteolysis studies have suggested that the loop is exposed in unliganded and substrate-bound Kapβ2s (Chook et al., 2002). This was confirmed by both the Kapβ2-substrate structures (Cansizoglu et al., 2007; Lee et al., 2006) and is now also confirmed in the unliganded Kapβ2 structure. The H8 loop in the unliganded Kapβ2 crystals is biochemically intact, but only 13 of its 62 residues are observed, indicating that most of the loop is indeed mobile and disordered. Electron density is present only for residues 312–319 and 370–375 (Figure 5). Ordered loop residues 312–319 emerge from helix H8A and residues 370–374 precede helix H8B (Figure S2), and these have similar structures in unliganded and substrate-bound Kapβ2s. Residues 312–319 are in similar positions in all Kapβ2 structures, but residues 370–374 have shifted to direct the loop away from the arch in the unliganded and substrate-bound structures (Figure 1) (Lee et al., 2006). In contrast, in the Ran complex, H8 loop residues 332–340 and 363–373 form a platform that interacts with the basic patch of Ran while the rest of the loop resides in the C-terminal arch (Chook and Blobel, 1999). In summary, the concave surface of the unliganded C-terminal arch is free to bind substrate. The structure of unliganded Kapβ2 provides additional evidence that the H8 loop is flexible and does not reside in the C-terminal arch until Ran is present. Interactions with Ran changes the conformation of the loop, converting it into a pseudo-NLS to displace substrate from the C-terminal arch.
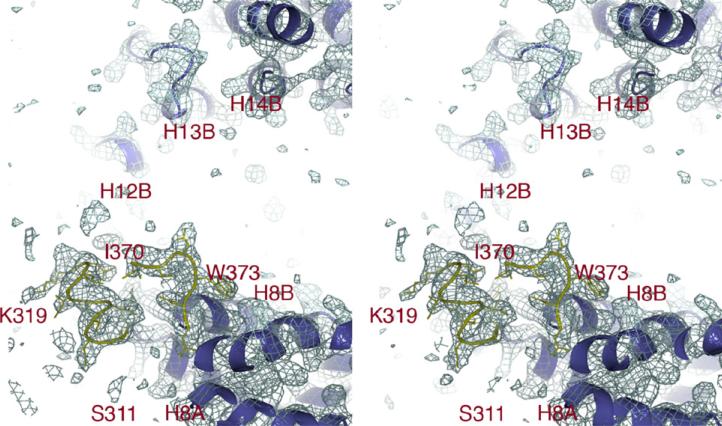
Figure 5. The H8 Loop of Kapβ2 Is Mostly Disordered.
The 2Fo – Fc map (stereo diagram, 1.0σ, blue mesh) of unliganded Kapβ2 at the H8 loop (yellow) and C-terminal arch (blue) shows that most of the loop is disordered and not bound in the C-terminal arch. H8 loop (yellow) residues 311–319 are shown connecting to H8A and residues 370–375 to H8B. No continuous density is observed beyond residue K319 until residue I370, indicating that the rest of the H8 loop is structurally disordered and no additional density is observed bound to the concave surface of the C-terminal arch. A zoomed-in view of the ordered portions of the H8 loop is shown in Figure S5.
When Ran is absent, the N-terminal arches have almost identical dimensions (85 Å height and 58 Å width in its base) that are too small to accommodate Ran. Segments H5–H13 have similar conformations (Cα rmsd ~1.1 Å), but segments H1–H4 show conformational heterogeneity (Table 2; Figures 4A and 4B). H1–H4 is intrinsically flexible, with high B factors (>100 Å2), weak electron density, and a different conformation in every structure (Figure S3; Cansizoglu et al., 2007; Chook and Blobel, 1999; Lee et al., 2006). Structural differences here are of a continuous nature, with changes in helical orientations within and between HEAT repeats. Because the disordered H8 loop and the H1–H4 segment appear to be most flexible in the N-terminal arch, we speculate that either or both regions may serve as capture sites for initial interactions to “reel” in Ran. This is then followed by helical rearrangements in H5–H8 to optimally position the GTPase in the N-terminal arch and the rest of the H8 loop in the C-terminal arch. Kinetic studies of Ran binding and substrate dissociation will be necessary to investigate this model.
The stretched or expanded Ran-bound N-terminal arch is likely in a strained or higher-energy conformation. Transition to this high-energy conformation is balanced by large binding energy from Ran interactions, and subsequent removal of the GTPase relaxes it to a lower energy state. Karyopherin flexibility enables this allosteric phenomenon and was proposed for energy storage in Kap95 and Cse1 (Conti et al., 2006; Lee et al., 2005; Matsuura and Stewart, 2004). The ability of the N-terminal arch to change conformation along most of its length may also facilitate binding of additional ligands. Impβ binds substrate PTHrP in its N-terminal arch (Cingolani et al., 2002). Conformational flexibility of Kapβ2's N-terminal arch may also enable binding of undiscovered substrates in that region. Finally, N-terminal arch flexibility is also likely to be important for nucleoporin interactions.
In summary, conformational heterogeneity in Kapβ2 can be organized into three major segments. The N-terminal H1–H8 segment shows large changes along its entire length upon Ran binding. Segments H9–H13 and H14–H18 in the C-terminal arch are rigid bodies that rotate about a flexible hinge to bind NLSs and the H8 loop. Three additional small flexible segments are also observed. The flexible C-terminal H19-H20 segment is detected in most structural comparisons (Figure S4). The N-terminal H1–H8 segment can be further divided: intrinsically flexible H1–H4 is different in every structure, whereas H5–H8 changes conformation only when bound to Ran.
Segmental Architecture in Impβ and Kap95p
Impβ and its Saccharomyces cerevisiae homolog Kap95p are the best-studied Kapβs. Many structures of Impβ have been determined, but most are of the N-terminal half of the molecule (Bayliss et al., 2000, 2002; Cingolani et al., 2002; Lee et al., 2000; Vetter et al., 1999), and thus unsuitable for analysis of conformational flexibility along the superhelix. Three crystal structures of full-length Impβ are available: two crystal forms of Impβ bound to the IBB domain of Kapα and a SREBP2 complex (Cingolani et al., 1999; Lee et al., 2003). Two crystal structures are also available for full-length Kap95p, which is 33% identical to Impβ. These are Kap95p bound to RanGTP and Kap95p bound to a Nup1p fragment (Lee et al., 2005; Liu and Stewart, 2005). We performed domain motion and TLS group analyses on both pairs of structures to examine potential segmental architecture analogous to those in Kapβ2.
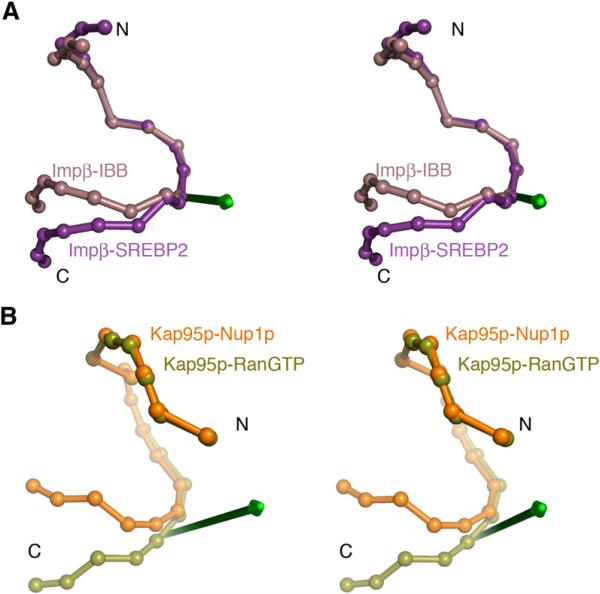
Hinges in Impβ were previously reported to rotate H1–H11 by 10° with respect to H12–H17, and to rotate the latter by 10° with respect to H18-H19 in different Impβ-IBB crystal forms (Cingolani et al., 1999). Hinge analysis of the IBB and SREBP complexes located a flexible hinge in H13 (Figure 6A). The N-terminal H1–H13 segment (Cα rmsd is 1.9 Å) swings 22° about the hinge axis with respect to the C-terminal H14–H19 segment (Cα rmsd is 1.1 Å), changing the superhelical pitch by 18 Å to bind conformationally diverse substrates. The N-terminal segment appears not to be rigid, with small changes in helical orientations along its length.
Figure 6. Hinge Motion in Impβ and Kap95p Structures.
(A) IBB-bound Impβ (brown) and SREBP2-bound Impβ (purple) are superimposed at HEAT repeats 5–10, and shown as spheres at the geometric center of each HEAT repeat. The hinge axis that rotates H1–H12 with respect to H14–H19 is shown in green.
(B) RanGTP-bound Kap95p (light green) and Nup1p-bound Kap95p (orange) are superimposed at HEAT repeats 6–13, and shown as spheres at the geometric centers of their HEAT repeats. The hinge axis that rotates H1–H14 with respect to H15–H19 is shown in green.
Similar analyses of the Kap95p structures located a flexible hinge at H14-H15. In this case, subdomains on either side of the hinge are H6–H14 (Cα rmsd is 1.5 Å) and H15–H19 (Cα rmsd is 1.2 Å). These segments rotate 38° relative to each other, resulting in a superhelical pitch difference of 10 Å. TLS group analysis maps a junction between TLS groups to H14 (residues 598–600) consistent with the position of the flexible hinge. Finally, examination of the Kap95p N-terminal arch alone (H1–H14) identified another hinge at H5, where segment H1–H4 (Cα rmsd is 0.7 Å) rotates 11° relative to segment H6–H14 (Cα rmsd is 1.5 Å).
In summary, like Kapβ2, conformational heterogeneity in Impβ and Kap95p is also segmental. Impβ can be divided into three segments that rotate about two flexible hinges in H12-H13 and H18 (Cingolani et al., 1999), and Kap95p can also be divided into three segments, with flexible hinges at H5 and H14-H15. Structures of full-length unliganded Impβ and Kap95p are not available, but a SAXS model of unliganded Impβ shows this state to be significantly more extended than the Ran or substrate states (Fukuhara et al., 2004). Crystal structures of full-length unliganded Impβ/Kap95 and additional structures of full-length ligand-bound proteins will be necessary for more comprehensive analysis of conformational heterogeneity in this nuclear import pathway.
Conclusions
The crystal structure of unliganded Kapβ2 has an overall superhelical structure similar to those of Ran, hnRNP A1-NLS, and hnRNP M-NLS complexes, confirming previous SAXS studies that the different Kapβ2 states adopt extended S-shaped structures. More importantly, the four Kapβ2 chains in the asymmetric unit show conformational heterogeneity, allowing characterization of intrinsic flexibility. Comparison with substrate- and Ran-bound Kapβ2s also showed significant conformational differences. Conformational flexibility analysis using three independent methods of structural superpositions, clustering of rotation vectors, and B factor analysis revealed the moving parts. Kapβ2 can be divided into three major segments. Rigid segments H9–H13 and H14–H18 in the C-terminal substrate-binding arch rotate relative to each other about a flexible hinge in H13-H14. H1–H8 in the N-terminal arch shows continuous changes along its length upon Ran binding. Using the same approaches, Impβ and its yeast homolog Kap95p can also be divided into three major segments that rotate about flexible hinges, suggesting that conformational heterogeneity in import-Kapβs may be generally segmental.
EXPERIMENTAL PROCEDURES
Expression and Purification of Kapβ2
Full-length human Kapβ2 (residues 1–890; GenBank accession number: AAB58254) was in a pGEX-Tev vector (modified from pGEX-4T-3) expressed as a GST fusion protein and was purified as previously described (Lee et al., 2006). Selenomethionine Kapβ2 was expressed in BL21 (DE3) cells using M9 minimal media as previously described (Lee et al., 2006), and its purification is similar to that for native Kapβ2. The purified native and selenomethionine proteins were concentrated to 20 mg/ml and 35 mg/ml, respectively, for crystallization.
Crystallization, Data Collection, and Structure Determination
Native Kapβ2 was crystallized by vapor diffusion in hanging drops using 3.2 M potassium formate, 0.1 M HEPES (pH 7.5), and 10% glycerol in the reservoir solution. The crystals were flash-frozen in liquid propane. Data (3.0 Å) from these crystals (space group P21, a = 129.9, b = 169.3, c = 141.1, and β = 93.1° with four molecules in the asymmetric unit) were collected at X-ray wavelength 0.97933 Å at 100K at beamline 19ID of the Advanced Photon Source, Argonne National Laboratory. Data were processed using HKL2000 (Otwinowski and Minor, 1997). MR using Kapβ2 fragments from the Kapβ2-Ran structure (Protein Data Bank [PDB] ID code: 1QBK) as search models failed, indicating significant conformational differences in both N- and C-terminal arches between the two states. The Kapβ2-Ran structure was the only Kapβ2 structure available at the time of structure determination.
Selenomethionine Kapβ2 was crystallized by vapor diffusion in hanging drops using 2.7 M potassium formate and 20% glycerol in the reservoir solution. Unfortunately, these crystals (space group P21, a = c = 108.5, b = 294.0, and β = 92° with four molecules in the asymmetric unit) were pseudo-merohedrally twinned. In an effort to obtain single selenomethionine Kapβ2 crystals, mixtures of selenomethionine and native proteins were crystallized. A 1:1 molar mixture of the two proteins gave single crystals (space group P21, a = 108.5, b = 294.0, c = 108.3, and β = 92.1°), and a 3.6 Å SAD data set (λpeak = 0.97903 Å) was collected at beamline 19ID, Argonne National Laboratory.
We performed MR using the program Phaser (McCoy et al., 2005) and multiple search models, each comprising a different Kapβ2 segment from the Kapβ2-Ran structure. Only a search model of Kapβ2 residues 396–864 (H9–H19 or C-terminal arch) resulted in a successful molecular replacement solution. This result suggests that the C-terminal arch of selenomethionine unliganded Kapβ2 is more similar to that of the Ran complex than the native unliganded Kapβ2, but the N-terminal arches of both unliganded Kapβ2s are significantly different from the Ran state. However, to avoid model bias, 72 selenium sites (of the total 104) were extracted from the partial MR model and iterative refinement of these heavy-atom sites allowed the heavy-atom model to be extended to 100 selenium sites. The last four seleniums belonging to N-terminal methionines were not located. Phase refinement followed by density modification with solvent flipping, both using the program CNS (Brunger et al., 1998), resulted in an electron density map where three of the four Kapβ2s in the asymmetric unit could be modeled using O (Jones et al., 1991) and Coot (Emsley and Cowtan, 2004). Density for the fourth and untraceable chain was weak, with density absent for many side chains. This incomplete and low-resolution model was not refined.
Instead, the unrefined selenomethionine Kapβ2 model was used as an MR search model for the 3.0 Å resolution native Kapβ2 data. Using the program Phaser (McCoy et al., 2005), the Kapβ2 segment corresponding to residues 88–656 (H3–H14 or N-terminal arch) gave a successful molecular replacement solution for all four molecules in the asymmetric unit, suggesting similarities in the N- but not the C-terminal arches between the selenomethionine and native Kapβ2s. Overall superhelical structures of the native unliganded Kapβ2 (refined), the selenomethionine unliganded Kapβ2 (unrefined), and the Kapβ2-Ran complex are compared in Figure S5. The resulting electron density map for the native Kapβ2 crystal was interpretable for all four molecules in the asymmetric unit.
MR was not successful with native unliganded Kapβ2 using Kapβ2-Ran as a search model because the two states show large conformational differences in both the N- and C-terminal arches (Figure 4C; Figure S5). However, we found an MR solution for selenomethionine Kapβ2 that corresponds to the C-terminal arch of Kapβ2 in the Ran state. Figure S5 shows conformational differences between selenomethionine, native unliganded, and Ran-bound Kapβ2s. The C-terminal arch of selenomethionine Kapβ2 is somewhat intermediate in conformation between native unliganded and Ran-bound Kapβ2s, but is similar enough to the latter for MR. This partial MR model allowed us to locate most of the 104 selenium sites without determining them de novo using SHELX (Sheldrick et al., 1993). Unfortunately, structure determination of the selenomethionine protein was hampered by low resolution, pseudo-translation, and weak SAD phases (phasing: Rcullis 0.76, phasing power 1.06, Se site B factors 41–85 Å2 when occupancies were set to 1). Fortunately, the N-terminal arch of selenomethio-nine Kapβ2 was similar to the native protein (Figure S5), and we could use this segment of the unrefined selenomethionine model to bootstrap our way to an MR solution for the higher-resolution native data set. Interestingly, when comparing the selenomethionine and native Kapβ2s, a hinge was also located at H13-H14 that rotates rigid segments H9–H13 and H14–H18 relative to each other.
Structure Refinement
There are four unliganded Kapβ2 chains in the asymmetric unit and the protein has an unusual nonglobular helical repeat architecture. Therefore, NCS restraints may be used in many different ways when refining the structure. Refinement of the model (residues 6–890 for Kapβ2 chains A, C, and D and residues 31–890 for chain B) was done with 50–3.0 Å data, using the program REFMAC5 (Murshudov et al., 1997) from the CCP4 package (CCP4, 1994). Results of 16 different refinement protocols are listed in Tables S1 and S2. Without NCS restraints (Table S1, refinement 1), Rfree is 28.4% and R factor is 24.6%. However, without the use of NCS, refinement is not efficient, as the ratio of observables to unknowns is low at 3.0 Å resolution and with a large asymmetric unit. Tight NCS restraints of all four chains resulted in very high R factors (Rfree = 42.6% and R factor = 40.5%; Table S2, refinement 7), suggesting significant conformational heterogeneity among the four chains and that NCS restraints should be relaxed.
Analysis of the structure that was refined without NCS restraints (Table S1, refinement 1) suggested that chain A is very similar to D, and chain B is very similar to C. When entire chains AD and BC are refined with tight NCS restraints, Rfree dropped by ~11% (Table S1). However, R factors are still significantly higher than without NCS restraints, suggesting that the chains may need to be divided into multiple NCS groups. Structural comparison of chains A and C from refinement 1 suggested that Kapβ2 could be divided according to conformational heterogeneity into four segments: H1–H4, H5–H13, H14–H18, and H19-H20. Segment junctions H13 and H18 show clear conformational differences. This information guided our division of the molecule into NCS groups. We experimented with dividing each chain into four NCS groups (H1–H4, H5–H12, H14–H17, and H19-H20) and using tight NCS restraints in REFMAC5 (Murshudov et al., 1997) to constrain respective groups within the AD and BC pairs (refinement 3). The 3% drop in Rfree indicated that relaxation of NCS constraints is warranted and that there is conformational heterogeneity of segmental nature even within the two similar pairs of Kapβ2. When contiguous segments are combined to generate trisegmented Kapβ2 (refinements 4–6), R factors increased except when the last two segments are combined. We chose that structure from refinement 6 (Rfree = 28.6% and R factor = 26.1%; Table 1) for analysis. Comparison of this structure with refinement 1 shows that they are virtually identical, with Cα rmsd 0.3 Å.
We also experimented with NCS restraints on all four chains (Table S2). Dividing Kapβ2 into four segments (H1–H4, H5–H12, H14–H17, and H19-H20) for refinement of all groups with tight NCS restraints decreased Rfree by 10%, again consistent with segmental conformational heterogeneity within the four chains. Relaxing NCS restraints of the H5–H12 and H19-H20 groups decreased Rfree further by about 4%, suggesting conformational differences within these among the four unliganded Kapβ2 chains. Interestingly, superposition of H5–H13 of chains A and C gives Cα rmsd of 1.3 Å, suggesting that differences may occur in side chains or in the H8 loop (always omitted when superimposing structures) rather than in helical arrangements. Superposition of H19-H20 of chains A and C (Cα rmsd 2.2 Å) suggests that this C-terminal segment is indeed conformationally heterogeneous in all four chains. Comparison of structures from refinements 1 and 16 shows that they are virtually identical, with Cα rmsd 0.2 Å. We also experimented with dividing Kapβ2 into NCS groups other than H1–H4, H5–H12, H14–H17, and H19-H20. These include four 5-HEAT repeat groups and combining two of our contiguous segments at a time to make three groups. In all cases, Rfree was to ~36% (data not shown).
TLS refinement (Painter and Merritt, 2006) with 12 TLS groups (three groups for each molecule) resulted in Rfree = 27.0% and R factor = 23.3%. However, because there was no improvement in the electron density map and the structure is similar to that in refinement 6, we did not deposit this TLS-refined structure in the Protein Data Bank. Finally, the weakest density occurs at the N-terminal region of Kapβ2 molecules, which is also part of the MR search model. To reduce model bias, we calculated simulated annealing omit maps (Brunger et al., 1998) to omit each of the first four HEAT repeats of Kapβ2.
Analysis of Conformational Heterogeneity
We used three independent/orthogonal methods to analyze flexibility. The first method involved pairwise superpositions of HEAT repeats. We performed comprehensive superpositions: (1) scanned the length of Kapβ2 chains for groups of 1–19 HEAT repeats, (2) superimposed A helices of individual repeats and examined the B helices for reorientations within each HEAT repeat, and (3) superimposed B helices and examined A helices for changes between HEAT repeats. The Superpose program from the CCP4 package (CCP4, 1994) was used to determine Cα-Cα distance rms deviations. The Helix Packing Pair program was used to determine angles between helices (Dalton et al., 2003).
The second method to analyze conformational flexibility involved domain motion analysis by clustering rotation vectors (that relates two protein chains) using the program DynDom (Hayward and Berendsen, 1998). Domain motion analysis to locate hinged motions was performed using coordinates for unliganded Kapβ2 (chains A–D) and Kapβ2s in the Ran, hnRNP A1-NLS (chains A and B; PDB ID code: 2H4M), and hnRNP M-NLS (chains A and B; PDB ID code: 2OT8). The nine Kapβ2 molecules extracted from four coordinate files were subject to pairwise analysis for the presence of hinged conformational differences using the program DynDom (Hayward and Berendsen, 1998). The window length for these analyses was set at five residues and the minimum ratio for interdomain to intradomain displacement was set to 1.0.
The final method involved analysis of the spatial distribution of individual atomic B factors in a single protein chain using the program in TLSMD for TLS group analysis (Painter and Merritt, 2006). Individual structures with refined B factors were used. This procedure identifies the portions of the protein with similar atomic displacement/thermal factor characteristics and determines the optimal TLS segments that behave like a pseudo-rigid body. For each protein chain, this analysis partitions the molecule into TLS groups and further analyzes the pseudo-rigid body translational and rotational motion of each group and how well these parameters fit the refined atomic thermal parameters in the crystal structure.
Methods 1 and 2 locate conformational differences by comparing pairs of structures, whereas method 3 locates pseudo-rigid segments using a single protein chain. Finally, all figures were prepared using the program PyMOL (DeLano, 2002).
Supplementary Material
ACKNOWLEDGMENTS
We thank Mischa Machius and Shae Padrick for critical discussions, and Diana Tomchick and Chad Brautigam for expert assistance with data collection. The U.S. Department of Energy, Offices of Science and Basic Energy Sciences (contract W-31-109-ENG-38) supported the Advanced Photon Source use. Y.M.C. is funded by National Institutes of Health grant R01-GM069909, Welch Foundation grant I-1532, and the University of Texas Southwestern Endowed Scholars Program.
Footnotes
Supplemental Data
Supplemental Data include five figures and two tables and can be found with this article online at http://www.structure.org/cgi/content/full/15/11/1431/DC1/.
Accession Numbers
Coordinates and structure factors of unliganded Kapβ2 have been deposited in the Protein Data Bank under ID code 2QMR.
REFERENCES
- Andrade MA, Bork P. HEAT repeats in the Huntington's disease protein. Nat. Genet. 1995;11:115–116. doi: 10.1038/ng1095-115. [DOI] [PubMed] [Google Scholar]
- Bayliss R, Littlewood T, Stewart M. Structural basis for the interaction between FxFG nucleoporin repeats and importin-β in nuclear trafficking. Cell. 2000;102:99–108. doi: 10.1016/s0092-8674(00)00014-3. [DOI] [PubMed] [Google Scholar]
- Bayliss R, Littlewood T, Strawn LA, Wente SR, Stewart M. GLFG and FxFG nucleoporins bind to overlapping sites on importin-β. J. Biol. Chem. 2002;277:50597–50606. doi: 10.1074/jbc.M209037200. [DOI] [PubMed] [Google Scholar]
- Brunger AT, Adams PD, Clore GM, DeLano WL, Gros P, Grosse-Kunstleve RW, Jiang JS, Kuszewski J, Nilges M, Pannu NS, et al. Crystallography & NMR System: a new software suite for macromolecular structure determination. Acta Crystallogr. D Biol. Crystallogr. 1998;54:905–921. doi: 10.1107/s0907444998003254. [DOI] [PubMed] [Google Scholar]
- Cansizoglu AE, Lee BJ, Zhang ZC, Fontoura BM, Chook YM. Structure-based design of a pathway-specific nuclear import inhibitor. Nat. Struct. Mol. Biol. 2007;14:452–454. doi: 10.1038/nsmb1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carugo O, Argos P. Protein-protein crystal-packing contacts. Protein Sci. 1997;6:2261–2263. doi: 10.1002/pro.5560061021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CCP4 (Collaborative Computational Project, Number 4) The CCP4 suite: programs for X-ray crystallography. Acta Crystallogr. D Biol. Crystallogr. 1994;50:760–763. doi: 10.1107/S0907444994003112. [DOI] [PubMed] [Google Scholar]
- Chook YM, Blobel G. Structure of the nuclear transport complex karyopherin-β2–Ran-GppNHp. Nature. 1999;399:230–237. doi: 10.1038/20375. [DOI] [PubMed] [Google Scholar]
- Chook YM, Blobel G. Karyopherins and nuclear import. Curr. Opin. Struct. Biol. 2001;11:703–715. doi: 10.1016/s0959-440x(01)00264-0. [DOI] [PubMed] [Google Scholar]
- Chook YM, Jung A, Rosen MK, Blobel G. Uncoupling Kapβ2 substrate dissociation and Ran binding. Biochemistry. 2002;41:6955–6966. doi: 10.1021/bi012122p. [DOI] [PubMed] [Google Scholar]
- Cingolani G, Petosa C, Weis K, Muller CW. Structure of importin-β bound to the IBB domain of importin-α. Nature. 1999;399:221–229. doi: 10.1038/20367. [DOI] [PubMed] [Google Scholar]
- Cingolani G, Bednenko J, Gillespie MT, Gerace L. Molecular basis for the recognition of a nonclassical nuclear localization signal by importin β. Mol. Cell. 2002;10:1345–1353. doi: 10.1016/s1097-2765(02)00727-x. [DOI] [PubMed] [Google Scholar]
- Conti E, Izaurralde E. Nucleocytoplasmic transport enters the atomic age. Curr. Opin. Cell Biol. 2001;13:310–319. doi: 10.1016/s0955-0674(00)00213-1. [DOI] [PubMed] [Google Scholar]
- Conti E, Muller CW, Stewart M. Karyopherin flexibility in nucleocytoplasmic transport. Curr. Opin. Struct. Biol. 2006;16:237–244. doi: 10.1016/j.sbi.2006.03.010. [DOI] [PubMed] [Google Scholar]
- Cook A, Fernandez E, Lindner D, Ebert J, Schlenstedt G, Conti E. The structure of the nuclear export receptor Cse1 in its cytosolic state reveals a closed conformation incompatible with cargo binding. Mol. Cell. 2005;18:355–367. doi: 10.1016/j.molcel.2005.03.021. [DOI] [PubMed] [Google Scholar]
- Cook A, Bono F, Jinek M, Conti E. Structural biology of nucleocytoplasmic transport. Annu. Rev. Biochem. 2007;76:647–671. doi: 10.1146/annurev.biochem.76.052705.161529. [DOI] [PubMed] [Google Scholar]
- Dalton JA, Michalopoulos I, Westhead DR. Calculation of helix packing angles in protein structures. Bioinformatics. 2003;19:1298–1299. doi: 10.1093/bioinformatics/btg141. [DOI] [PubMed] [Google Scholar]
- DeLano WL. The PyMOL Molecular Graphics System. DeLano Scientific; Palo Alto, CA: 2002. [Google Scholar]
- Emsley P, Cowtan K. Coot: model-building tools for molecular graphics. Acta Crystallogr. D Biol. Crystallogr. 2004;60:2126–2132. doi: 10.1107/S0907444904019158. [DOI] [PubMed] [Google Scholar]
- Fan XC, Steitz JA. HNS, a nuclear-cytoplasmic shuttling sequence in HuR. Proc. Natl. Acad. Sci. USA. 1998;95:15293–15298. doi: 10.1073/pnas.95.26.15293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuhara N, Fernandez E, Ebert J, Conti E, Svergun D. Conformational variability of nucleo-cytoplasmic transport factors. J. Biol. Chem. 2004;279:176–181. doi: 10.1074/jbc.M309112200. [DOI] [PubMed] [Google Scholar]
- Gorlich D, Kutay U. Transport between the cell nucleus and the cytoplasm. Annu. Rev. Cell Dev. Biol. 1999;15:607–660. doi: 10.1146/annurev.cellbio.15.1.607. [DOI] [PubMed] [Google Scholar]
- Hayward S, Berendsen HJ. Systematic analysis of domain motions in proteins from conformational change: new results on citrate synthase and T4 lysozyme. Proteins. 1998;30:144–154. [PubMed] [Google Scholar]
- Jones TA, Zou JY, Cowan SW, Kjeldgaard M. Improved methods for building protein models in electron density maps and the location of errors in these models. Acta Crystallogr. A. 1991;47:110–119. doi: 10.1107/s0108767390010224. [DOI] [PubMed] [Google Scholar]
- Lee SJ, Imamoto N, Sakai H, Nakagawa A, Kose S, Koike M, Yamamoto M, Kumasaka T, Yoneda Y, Tsukihara T. The adoption of a twisted structure of importin-β is essential for the protein-protein interaction required for nuclear transport. J. Mol. Biol. 2000;302:251–264. doi: 10.1006/jmbi.2000.4055. [DOI] [PubMed] [Google Scholar]
- Lee SJ, Sekimoto T, Yamashita E, Nagoshi E, Nakagawa A, Imamoto N, Yoshimura M, Sakai H, Chong KT, Tsukihara T, et al. The structure of importin-β bound to SREBP-2: nuclear import of a transcription factor. Science. 2003;302:1571–1575. doi: 10.1126/science.1088372. [DOI] [PubMed] [Google Scholar]
- Lee SJ, Matsuura Y, Liu SM, Stewart M. Structural basis for nuclear import complex dissociation by RanGTP. Nature. 2005;435:693–696. doi: 10.1038/nature03578. [DOI] [PubMed] [Google Scholar]
- Lee BJ, Cansizoglu AE, Suel KE, Louis TH, Zhang Z, Chook YM. Rules for nuclear localization sequence recognition by karyopherin β 2. Cell. 2006;126:543–558. doi: 10.1016/j.cell.2006.05.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu SM, Stewart M. Structural basis for the high-affinity binding of nucleoporin Nup1p to the Saccharomyces cerevisiae importin-β homologue, Kap95p. J. Mol. Biol. 2005;349:515–525. doi: 10.1016/j.jmb.2005.04.003. [DOI] [PubMed] [Google Scholar]
- Matsuura Y, Stewart M. Structural basis for the assembly of a nuclear export complex. Nature. 2004;432:872–877. doi: 10.1038/nature03144. [DOI] [PubMed] [Google Scholar]
- Matsuyama A, Arai R, Yashiroda Y, Shirai A, Kamata A, Sekido S, Kobayashi Y, Hashimoto A, Hamamoto M, Hiraoka Y, et al. ORFeome cloning and global analysis of protein localization in the fission yeast Schizosaccharomyces pombe. Nat. Biotechnol. 2006;24:841–847. doi: 10.1038/nbt1222. [DOI] [PubMed] [Google Scholar]
- McCoy AJ, Grosse-Kunstleve RW, Storoni LC, Read RJ. Likelihood-enhanced fast translation functions. Acta Crystallogr. D Biol. Crystallogr. 2005;61:458–464. doi: 10.1107/S0907444905001617. [DOI] [PubMed] [Google Scholar]
- Mosammaparast N, Pemberton LF. Karyopherins: from nuclear-transport mediators to nuclear-function regulators. Trends Cell Biol. 2004;14:547–556. doi: 10.1016/j.tcb.2004.09.004. [DOI] [PubMed] [Google Scholar]
- Murshudov GN, Vagin AA, Dodson EJ. Refinement of macromolecular structures by the maximum-likelihood method. Acta Crystallogr. D Biol. Crystallogr. 1997;53:240–255. doi: 10.1107/S0907444996012255. [DOI] [PubMed] [Google Scholar]
- Otwinowski Z, Minor W. Processing of X-ray diffraction data collected in oscillation mode. Methods Enzymol. 1997;276:307–326. doi: 10.1016/S0076-6879(97)76066-X. [DOI] [PubMed] [Google Scholar]
- Painter J, Merritt EA. Optimal description of a protein structure in terms of multiple groups undergoing TLS motion. Acta Crystallogr. D Biol. Crystallogr. 2006;62:439–450. doi: 10.1107/S0907444906005270. [DOI] [PubMed] [Google Scholar]
- Sheldrick GM, Dauter Z, Wilson KS, Hope H, Sieker LC. The application of direct methods and Patterson interpretation to high-resolution native protein data. Acta Crystallogr. D Biol. Crystallogr. 1993;49:18–23. doi: 10.1107/S0907444992007364. [DOI] [PubMed] [Google Scholar]
- Truant R, Kang Y, Cullen BR. The human tap nuclear RNA export factor contains a novel transportin-dependent nuclear localization signal that lacks nuclear export signal function. J. Biol. Chem. 1999;274:32167–32171. doi: 10.1074/jbc.274.45.32167. [DOI] [PubMed] [Google Scholar]
- Vetter IR, Arndt A, Kutay U, Gorlich D, Wittinghofer A. Structural view of the Ran-Importin b interaction at 2.3 Å resolution. Cell. 1999;97:635–646. doi: 10.1016/s0092-8674(00)80774-6. [DOI] [PubMed] [Google Scholar]
- Weis K. Regulating access to the genome: nucleocytoplasmic transport throughout the cell cycle. Cell. 2003;112:441–451. doi: 10.1016/s0092-8674(03)00082-5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.