Electric fields yield chaos in microflows

Abstract

We present an investigation of chaotic dynamics of a low Reynolds number electrokinetic flow. Electrokinetic flows arise due to couplings of electric fields and electric double layers. In these flows, applied (steady) electric fields can couple with ionic conductivity gradients outside electric double layers to produce flow instabilities. The threshold of these instabilities is controlled by an electric Rayleigh number, Ra_e. As Ra_e increases monotonically, we show here flow dynamics can transition from steady state to a time-dependent periodic state and then to an aperiodic, chaotic state. Interestingly, further monotonic increase of Ra_e shows a transition back to a well-ordered state, followed by a second transition to a chaotic state. Temporal power spectra and time-delay phase maps of low dimensional attractors graphically depict the sequence between periodic and chaotic states. To our knowledge, this is a unique report of a low Reynolds number flow with such a sequence of periodic-to-aperiodic transitions. Also unique is a report of strange attractors triggered and sustained through electric fluid body forces.

Chaos in scalar fields driven by deterministic, low Reynolds number (Re) flows was first described by H. Aref in the early 1980s (1); and chaotic advection was first leveraged to achieve fast mixing in microchannel flows by Liu et al. (2). Indeed, deterministic chaos has been studied in a wide variety of experimental systems including turbulent flows (3), chemical reactions (4), biological systems (4), and atomic force microscopy (5). Here, we report evidence demonstrating the existence of dynamic transitions from periodicity to aperiodicity and chaos in low Re electrokinetic micron-scale flows. Microfluidic devices often use liquid-phase electrokinetic phenomena to transport, concentrate, and separate samples (6). Electrokinetics is the branch of electrohydrodynamics that describes the coupling of ion transport, liquid flow, and electric fields, and it is characterized by the importance of electric double layers (7).

Typical electrokinetic flows, in order of 10 micron channels, have low Reynolds numbers and are often stable as inertial forces are strongly damped by viscous forces. However, applied electric fields can couple with heterogeneous electric properties, in particular gradients of ionic conductivity, to generate electric body forces in the bulk liquid (outside electric double layers). These body forces can drive instability of bulk liquid flow fields. This phenomena was first reported by Oddy et al. and termed electrokinetic instabilities (EKIs, see ref. 8). These electrokinetic flow instabilities are driven by electric body forces, ρ_eE (where ρ_e is the net free charge density and E is the electric field vector), in these heterogeneous regions (8, 9). These body forces can be distributed over relatively large flow regions and can exist outside of electric double layers (10, 11).

In this paper, we present compelling evidence that an unstable, low Reynolds number electrokinetic flow can become chaotic in regimes characterized by the relative importance of electrical and viscous forces. Temporal power spectra and time-delay phase-maps distinguish between periodic and chaotic regimes. We believe this is the first demonstration of a strange attractor triggered and sustained through electric fluid body forces in a low Reynolds number flow. We show that the flow exhibits at least two periodic-to-aperiodic (chaotic) transitions as the electric Rayleigh number control parameter is monotonically increased. Although such transitions are well known in the nonlinear dynamics field (12–15) and occur in Taylor-Couette flows (16) (where fluid inertia is important), we know of no reported microflow system with such a sequence of transitions.

Results and Discussion

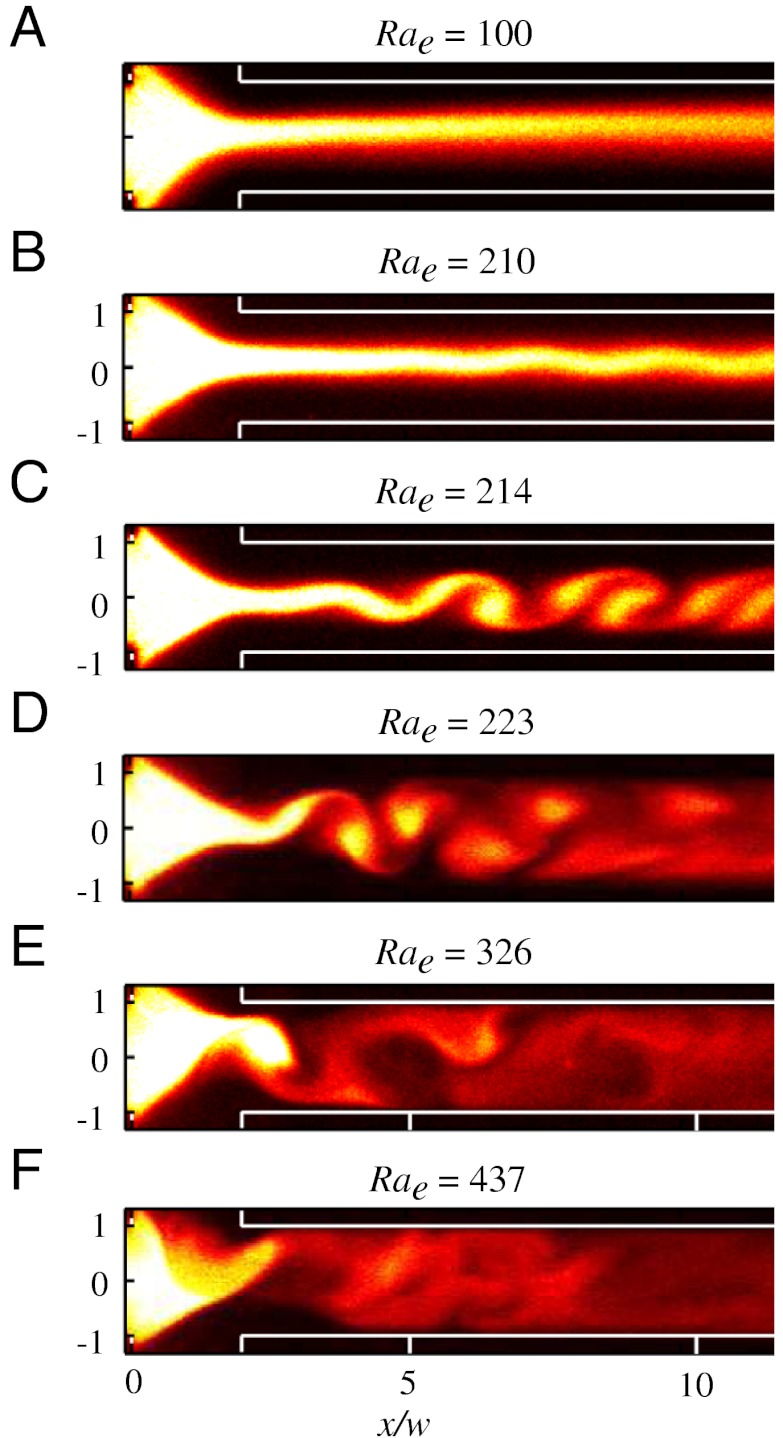
Fig. 1 shows experimental scalar imaging of our electrokinetic flow at various (constant) values of electric field. The Reynolds numbers of these flows range from about 0.01 to 0.1 (based on hydraulic channel diameter and electroosmotic velocity). Fig. 1A shows a representative measured scalar concentration field of the stable base state flow in a cross shaped microchannel. Electroosmotic flow drives high-conductivity electrolyte dyed with an electrically neutral fluorescent molecule from the west (left) channel and lower conductivity background electrolyte from the north (top) and south (bottom) channels toward a common outlet in the east (right) channel. The north and south sheath streams focus the center, dyed stream into a wedge-shaped “head” structure. Downstream of the intersection (x/w > 1), the sheath and center streams form two diffuse conductivity interfaces, which develop within the east channel. Posner and Santiago (17) proposed that the relative strength of electric and viscous forces are described by a local electric Rayleigh number, Ra_e, of the form,

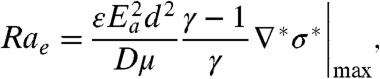[1]

where ε is the fluid permittivity, E_a is the nominally applied and constant electric field (voltage difference between south and east channels per axial length of south and east channels), d is the channel depth, D is the effective diffusivity of the ions, and μ is the fluid viscosity. ∇^∗σ^∗|_max is a nondimensional maximum transverse conductivity gradient in the flow (see ref. 17). For our flows, a critical electric Rayleigh number of about 200 results in an easily observable EK flow instability (17).

Fig. 1.

Representative instantaneous scalar concentration fields of unstable electrokinetic flows, each subject to constant electric field. The center-to-sheath conductivity ratio γ is 100 and the electric Rayleigh number Ra_e is indicated above each image. For our parameters, the conversion between electric field and Rayleigh number is E = 1.78Ra_e for electric field in V/cm.

Below a critical Rayleigh number of about 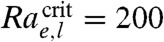, the flow is stable (c.f. Fig. 1A). For Ra_e > 205, a sinuous dye pattern develops and disperses as it advects downstream, as shown in Fig. 1B. A further increase of the Rayleigh number of less than 2% results in disturbances that grow (briefly) exponentially in space and roll up in alternating sequences, qualitatively similar in appearance to Bénard-von Kàrmàn vortex street (18, 19 and see Fig. 1 C and D). At Ra_e values of 326 and 437, the scalar fields are highly asymmetric about the channel axial centerline, as shown in Fig. 1 E and F. In these highly unstable conditions, the wedge-shaped head aperiodically oscillates strongly along the spanwise direction. This strongly unstable flow results in highly disordered scalar patterns and a well-mixed fluid a few channel widths downstream.

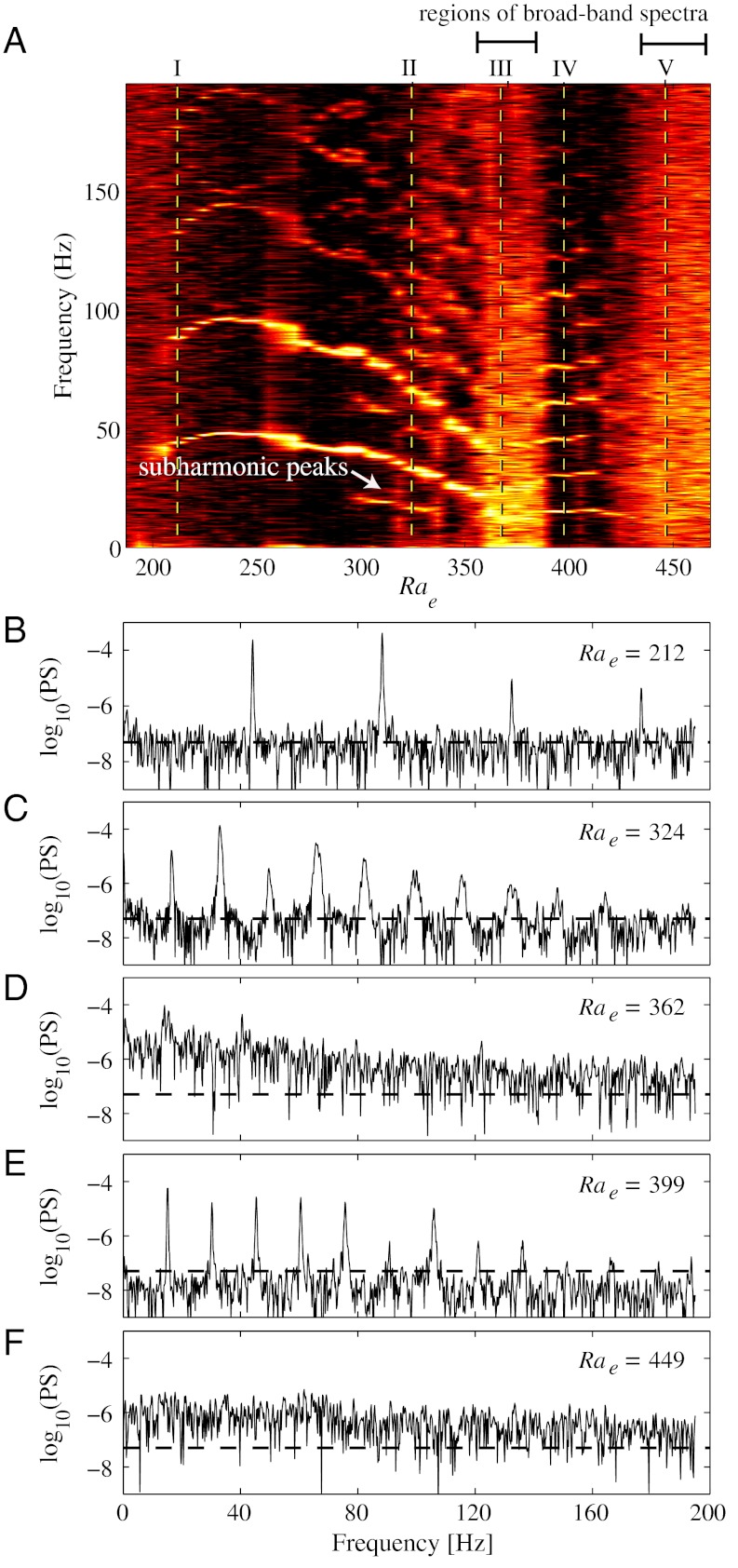
Fig. 2A shows a map of the temporal spectral intensity as a function of the electric Rayleigh number (abscissa) and temporal frequency (ordinate). Spectral density was calculated using a normalized fluorescence intensity of the form,

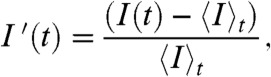[2]

where I^′(t) is the fluorescence intensity taken at a point on the channel centerline and x/w = 2 and the angle brackets and subscript t denote a temporal average. For Ra_e less than about 200, the flow is stable and the power spectrum only shows power near DC and low-amplitude image noise. Starting near Ra_e = 205, we observe periodic motion with at fundamental frequency of f₁ = 42 Hz (at Ra_e = 205) and weak harmonics at 2f₁ and 3f₁, consistent with the periodic dye pattern of Fig. 1B. In the range 230 < Ra_e < 325, the frequency of the fundamental and harmonic peaks slowly decrease, which coincides with an increase in the disturbance wavelength, perhaps due to increasing electroosmotic flow (17). Subharmonic intensity peaks associated with period doubling bifurcations are evident in the region near Ra_e = 290–350 (20). As an example, we labeled the subharmonic peak at f₁/2, but we also observe peaks at 3f₁/4 and 5f₁/6. As we discuss below, further increases in Ra_e result in a transition to fully chaotic, aperiodic behavior. Such transitions from steady state to time-dependent solutions, then period doubling, and eventually fully chaotic behavior are well known in fluid flows. However, it is most common for complexity in these flows to increase monotonically with an increase of the controlling parameter. For example, increasing Rayleigh number, Ra, in Rayleigh-Bernard flows (13) results in transitions from steady flow to time-dependent flow and, eventually, to fully chaotic, aperiodic behavior.

Fig. 2.

(A) Temporal power spectrum of I^′(t) (in log ₁₀) as a function of electric Rayleigh number and temporal frequency, f. Black and white colors represent low and high spectral intensity, respectively. For Ra_e < 200, the flow is stable (energy concentrated near f = 0). Spectrum contains a fundamental frequency and harmonics for 205 < Ra_e < 325. Subharmonic peaks appear at Ra_e = 290–350. Aperiodic regimes are observed for Ra_e ranges of 350–390 and 415–490 (labeled with horizontal bands above figure). Aperiodic regimes are defined here as those exhibiting a broadband power spectrum that is at least one order of magnitude above instrument noise. The individual power spectra at five representative Ra_e are shown in (B–F) and denoted with a roman numeral and vertical dashed line in (A). (B) Power spectrum (in semilog coordinates) for Ra_e = 212 shows flow instability with a single-fundamental frequency at f = 42 Hz and harmonics 2f and 3f. (C) Spectrum for Ra_e = 324 shows subharmonic peaks. (D) Aperiodicity with broadband spectrum above instrumental noise (dashed line). (E) Second time-periodic state with at least 11 observable harmonics. (F) Final chaotic state.

The most interesting aspect of the current flow is the fact that, unlike classic low-Reynolds fluid flows, the relation between the controlling parameter, Ra_e, and dynamic complexity of the system is not monotonic. As we increase Ra_e we observe steady behavior (Ra_e <  ∼ 200) and this is followed by time-periodic dynamics including a series of four harmonics (Ra_e = 200 to 290), evidence of period doubling (Ra_e = 290 to 350), transition to a chaotic state (350 to 390), a second time-periodic state with at least 11 observable harmonics (390 to 415), and then a second, final chaotic state (Ra_e > 415 to 490). That is to say, surprisingly, the flow transitions sequentially in and out of chaos as Ra_e increases so that, as the electric Rayleigh number is increased from 200 to 490, we observe two sequential aperiodic regimes, each of which is preceded by time-periodic regimes.

The two aperiodic regimes are labeled as solid horizontal bands above Fig. 2A. The regimes at Ra_e ∼ 350–390 and Ra_e > 415 are strongly aperiodic as evidenced by well-distributed spectral content (greater than 1 order of magnitude above noise, as shown in Fig. 2 B–F). Other regions show some evidence of aperiodicity, such as the region near Ra_e ∼ 320–340, which has some broadband spectral content, but not as strongly as the latter two regimes. Note that although the distinction between periodic and aperiodic dynamics is typically made based on the existence of broadband spectra, the minimum strength of broadband spectra that warrants identification as aperiodicity is arbitrary. Broadband spectra values significantly above 1 order of magnitude above instrument noise leaves us reasonably confident that aperiodic dynamics exist. This definition is supported by the phase maps presented below. The first and second aperiodic regimes are also separated by a periodic region (Ra_e ∼ 390–415) with a fundamental of f₂ = 15.8 Hz and harmonics at 2f₂,3f₂…11f₂ (see dashed line IV at Ra_e = 399 in Fig. 2A). Periodic windows sandwiched between aperiodic regimes have been observed experimentally in, for example, the Belousov-Zabotinsky reaction (21) and in moderately high Reynolds number Taylor-Couette flow (3, 16, 22). They are also well known as in mathematical models with one-dimensional mappings such as the Rössler attractor (4). To our knowledge, the current paper is the first reported instance of a sequence of alternating periodic-chaotic dynamical states in a low-Reynolds number flow system. In this microflow, monotonic increase of the Ra_e controlling parameter (proportional to electric field) drives the flow sequentially into and out of chaos.

Example power spectra of the periodic and aperiodic regimes are shown in Fig. 2 B–F for Ra_e = 212, 324, 362, 399, and 449, respectively. These Ra_e values are highlighted in Fig. 2A using vertical dashed lines labeled I to V. At Ra_e = 212, we see distinct sharp peaks in the power spectra at the fundamental frequency f₁ = 42 Hz and at harmonics 2f₁, and 3f₁. At Ra_e = 324, we observe clear evidence of period doubling and a broadening of peaks as frequency increases. In the first chaotic region, at Ra_e = 362, we observe broadband spectral content tapering off at higher frequencies and well above background noise. At Ra_e = 399, we observe the second periodic region, including a series of over 11 harmonics. Lastly, at Ra_e = 449, we observe the second chaotic regime, which persists until the high-field limitations of our experimental setup.

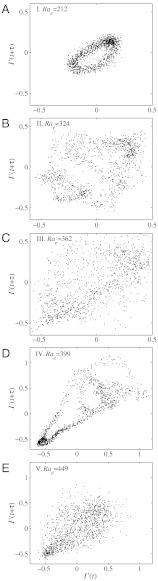
We constructed multidimensional phase-maps from time series of normalized fluorescent intensity values, I^′(t_k) (k = 1…2,000), taken at x/w = 2 and y/w = 0 using the method of time delays (23, 24). Here, time delay τ is used to construct a sequence of m-dimensional points [I^′(t_k),I^′(t_k + τ),…I^′(t_k + τ(m - 1)] resulting in an m-dimensional phase-space trajectory. We employed the method of Fraser and Swinney to obtain an optimum τ defined by the first minimum of the mutual information function (25). Fig. 3 shows I^′(t + τ) versus I^′(τ) phase-maps for Ra_e = (a)212, (b) 324, (c) 362, (d) 399, and (e) 449 for τ = 2.6 ms. The sequence of attractors illustrates the sequence of periodic to aperiodic dynamics transitions observed in the range of Ra_e of 150–490 with each map showing between 50–120 orbits. For Ra_e = 212 (Fig. 3A) the attractor shows an elliptical geometry (with a curve thickness, which we attribute to experimental image noise) characteristic of periodic dynamics. Well into the first periodic regime and in the period doubling region, at Ra_e = 324, the attractor is multidimensional, as shown in Fig. 3C. Here, more complex temporal evolution is characterized by weaving of smaller orbits within larger ones. At Ra_e = 362, we are within the aperiodic power spectrum of the first chaotic regime (see Fig. 2 A and D), and the respective attractor (cf. Fig. 3C) shows a dramatic change including significant spreading of the orbits throughout the phase map. Spreading of attractor orbits of chaotic flow has been observed experimentally in the multiple periodic-to-chaotic regime transitions in Taylor-Couette flows (3, 22). The phenomenon is also evident in classical dynamical systems attractors such as the Rössler attractor and the differential-delay equation (Mackey-Glass (4). Fig. 3D (Ra_e = 399) shows the transition back to a more ordered, periodic state as Ra_e is increased, and the attractor shows a much tighter set of orbits. Fig. 3E shows the dynamical structure for Ra_e = 449 within the second aperiodic regime. Here, the geometric structure found in previous attractors is lost, suggesting higher attractor dimensionality and dynamics reminiscent of turbulence, but occurring here at Reynolds numbers less than about 0.1.

Fig. 3.

Phase-maps (I^′(τ),I^′(t + τ)) for Ra_e = (A)212, (B) 324, (C) 362, (D) 399, and (E) 449. Together they illustrate the alternating sequence of periodic-chaotic dynamical behavior that occurs as Ra_e is swept from 190 to 490. The axis limits for D and E are expanded for clarity. The power spectra contours (in the Ra_e vs. frequency plane) for each Ra_e number case shown here is labeled with a roman numeral in Fig. 2A.

The power spectra and phase-maps collectively are strong evidence that the regions of aperiodicity are chaotic. Our data show compellingly that that low Reynolds number EKI flows exhibit alternating regimes of periodic motion and low dimensional chaos. The transitions between periodic and aperiodic dynamics occur twice (within Ra_e ranges of 350–390 and Ra_e > 415) as the electric Rayleigh number is monotonically varied from 190 to 490. To our knowledge, this is the first report of such a sequence of order-chaos transitions in low Reynolds number flows.

Materials and Methods

The experiments reported here were performed at the Stanford Microfluidics Laboratory in Stanford University. We performed experiments in glass, cross-shaped microchannels isotropically etched (D-shape) to w = 50 μm wide and 20 μm deep (Micralyne, Alberta, Canada). Direct current (DC) electrical potentials and current were applied by submerging platinum wire electrodes in the electrolyte solutions at end-channel reservoirs. We obtained instantaneous concentration fields of rhodamine B dye using epifluorescence microscopy, high speed CCD camera imaging (Roper Scientific, Tucson, Arizona). This dye is electrically net neutral (26) with a molecular weight of 479 g/mol; so our images are those of a passive, diffuse scalar and motion perpendicular to material lines is due to advection of the bulk solvent (water) and not a drift velocity due to the electric field. Potentials and CCD image acquisitions were synchronized using a high voltage sequencer (LabSmith, Livermore, CA, USA). Flows were imaged with a microscope (Nikon, Japan) equipped with a 20X, NA = 0.45 ELWD objective (Nikon, Japan). More details of the experimental setup and conditions are given by Posner and Santiago (17) additional details on the image acquisition and data analysis can be found in the SI Text.