Weak temporal signals can synchronize and accelerate the transition dynamics of biopolymers under tension

Abstract

In addition to thermal noise, which is essential to promote conformational transitions in biopolymers, the cellular environment is replete with a spectrum of athermal fluctuations that are produced from a plethora of active processes. To understand the effect of athermal noise on biological processes, we studied how a small oscillatory force affects the thermally induced folding and unfolding transition of an RNA hairpin, whose response to constant tension had been investigated extensively in both theory and experiments. Strikingly, our molecular simulations performed under overdamped condition show that even at a high (low) tension that renders the hairpin (un)folding improbable, a weak external oscillatory force at a certain frequency can synchronously enhance the transition dynamics of RNA hairpin and increase the mean transition rate. Furthermore, the RNA dynamics can still discriminate a signal with resonance frequency even when the signal is mixed among other signals with nonresonant frequencies. In fact, our computational demonstration of thermally induced resonance in RNA hairpin dynamics is a direct realization of the phenomena called stochastic resonance and resonant activation. Our study, amenable to experimental tests using optical tweezers, is of great significance to the folding of biopolymers in vivo that are subject to the broad spectrum of cellular noises.

The cell is a highly crowded and dynamic place with millions of biomolecules and their interactions (1). Only recently the notion that the self-assembly and function of biomolecules in vivo could be very different from those in isolation has been highlighted in terms of macromolecular crowding and confinement (2–4). However, the implication from dynamics in vivo should not necessarily be limited to the confinement or crowding effect. Besides the thermal noise, which is essential for activated internal motions and folding dynamics of biomolecules, of particular note are the nonequilibrium athermal signals produced from a plethora of active processes and collective actions among cellular constituents. For example, ribosome translocate along mRNA strand less than every 0.1 s per codon (5); Molecular motor, kinesin, takes a step along the microtubule approximately every 10 ms (6); Collective beating of cilia occurs approximately every 1 min (7). How these nonequilibrium signals or noises affect fundamental processes in biology, particularly the folding dynamics of biopolymers (8, 9), is the main concern of this paper. To address this issue, we study the effect of a weak oscillatory force on the transition dynamics of stretched RNA hairpins as a test case.

In recent years a combination of experiments, theoretical arguments, and simulations have been used to extensively study the conformational dynamics of biopolymers under mechanical control (10–20). Among others, paramount precision of optical tweezers, which can both exert piconewton force to molecules and probe structural changes in nanometer scale, not only allowed us to quantify thermodynamic and kinetic properties of the molecule at single molecule level (11, 13) but also provided unprecedented chances to manipulate the process of life (6, 21–24). To emulate nonequilibrium athermal noise in vivo and study its effect on the conformational dynamics of biopolymers, high precision force instruments seem to hold good promise; yet, no experiment to date has explored this issue.

Given that the dynamics of proteins and nucleic acids occur at overdamped fluctuating media, it may be surprising to learn that conformational transitions of biopolymers could become enhanced or synchronized to an externally exerted weak oscillatory signal. However, according to the notion of stochastic resonance (SR), sensitivity of a system to external signal can be improved under thermal fluctuation so that the system can discriminate the weak information carrying signals (25). Theoretically, it has been shown for a single Brownian particle in a bistable potential that synchronization of barrier crossing events to an externally driven oscillation occurs not only at an optimal noise strength but also at resonance frequency (25, 26). Furthermore, at another oscillation frequency that differs from the frequency of synchronization, the mean first passage time over the barrier is minimized, which is called the resonant activation (RA) (27). Hence, it is possible to demonstrate the SR and RA in the conformational transition dynamics of biopolymers like RNA hairpins, whose folding landscape is bistable near transition midforce, by properly tuning the frequency of additive oscillatory force.

Since the pioneering work of Benzi et al. (28), there have been efforts to extend the idea of SR to a vast range of physical and biological phenomena (25, 29, 30). However, SR often mentioned in terms of macroscopic systems such as recurrence of the ice age cycle and sensory systems for higher order organisms, especially the latter of which is wired with complex biochemical networks, is always a subject of debate because the inherent complexity of a system consisting of a formidable number of variables often makes the origin of such resonance-like phenomena inconclusive. Although phenomenological modeling of system dynamics using SR is still possible, there seems to be little convincing proof that the biological systems actually use SR in the cellular level (31). In this aspect, recent theoretical demonstrations of SR and RA of a polymer chain in a confined space has more direct relevance to the biology (32, 33). Here we show that SR and RA can indeed be manifested in a self-organization process of biopolymers by using molecular simulation. Although careful investigation is further required to confirm whether the SR and RA are actively utilized in the cell for its biological functions, it should be straightforward to demonstrate SR in the folding and unfolding dynamics of biopolymers by using single molecule force experiments. We provide a simple experimental protocol for the demonstration.

Results and Discussion

Bistable Transition of P5GA Hairpin Under Constant Tension.

To study the dynamics of biopolymers under tension, we used the self-organized polymer (SOP) model, a new class of versatile coarse-grained model that has been proven powerful in describing diverse problems in biomolecular dynamics at single molecule level, which includes proteins, RNA, and molecular motors (18–20, 34–36). Among the molecules studied using SOP model, the 22-nucleotide P5GA RNA hairpin is the simplest one, whose dynamics was studied under various mechanical conditions such as force clamp and force ramp (see Materials and Methods), providing microscopic insights into RNA hairpins in single molecule force experiments (18–20). Here, we performed Brownian dynamics simulation of the RNA hairpin under varying tensions (see Materials and Methods). As shown previously (18–20), the time trajectories that describe the dynamics of molecular extension (z) show that the RNA hairpin undergoes thermally induced hopping transitions when the molecule is held around the transition midforce f_m. The force-dependent free energy profile F(z; f) = -k_BT log P(z; f) with T = 300 K, calculated from the distribution of molecular extension P(z; f), becomes bistable at f = f_m(F(z; f_m) = F_m(z)) by forming the native basin of attraction (NBA) and unfolded basin of attraction (UBA) at z_F ≈ 2 nm and z_U ≈ 8 nm, respectively (Fig. 1A). The tension greater (or smaller) than f_m, f > f_m (or f < f_m) tilts the free energy profile towards the UBA (or NBA). The force-dependent probability of being in the UBA P_U(f) is calculated using 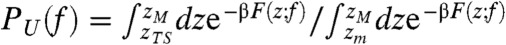, where β = (k_BT)^-1, z_TS is the extension corresponding to the barrier top (transition state), z_m and z_M (see Fig. 1A) are the minimum and maximum extensions, respectively. P_U(f), fitted to a two state model, 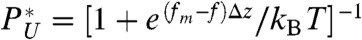(11), gives f_m = 14.7 pN and Δz ≈ 6 nm (Fig. 1B). From the time trajectories, the f-dependent mean folding [τ_F(f)] and unfolding time [τ_U(f)] are also calculated and found to “approximately” obey the Bell-like relation (37) (Fig. 1C). It is of note that the deviation from linearity on a log folding time scale is due to moving transition state resulting from the underlying folding landscape that deforms under mechanical force (38–40).

Fig. 1.

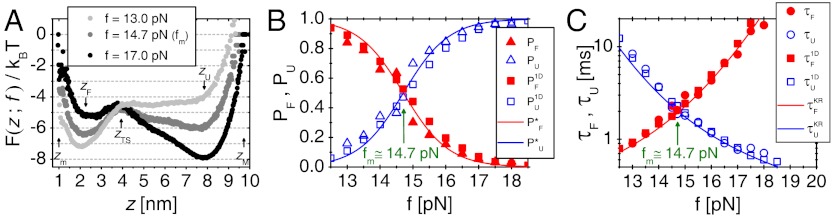
Thermodynamics and kinetics of P5GA hairpin under tension. (A) Free energy profile as a function of molecular extension z under tension f, obtained from the molecular simulation using SOP model. Shown are the three free energy profiles at f = 13.0, 14.7, and 17.0 pN. At f = f_m = 14.7 pN, the probability of being in UBA and NBA are equal. The profile is tilted towards UBA (or NBA) when f = 17.0 > f_m (or f = 13.0 < f_m). (B) Unfolding and folding probability P_U(f) and P_F(f)[ = 1 - P_U(f)] of P5GA against tension f. Results from the SOP model [P_F(f) and P_U(f)] and two state model (solid curves) are in good agreement. 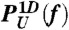[or 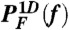] calculated from the tilted 1D free energy profile interpolated from results of the SOP model displays a good agreement with other results. (C) Mean folding time [τ_F(f)] and unfolding time [τ_U(f)] at varying tensions, obtained from the SOP simulation (circles), 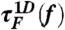and 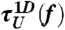obtained from the 1D simulation on the tilted free energy profile (squares), and mean first passage times (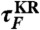, 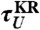calculated using the tilted free energy profile (solidcurves) are in a good agreement. The transition midforce determined at the intersection between τ_F(f) and τ_U(f) and is f_m = 14.7 pN.

Oscillation-Induced Coherent Transition of the P5GA Hairpin.

According to theories, the nonlinear and bistable characteristics of the folding landscape of RNA hairpin guarantee the manifestation of SR and RA if an oscillatory driving is externally applied to the molecule just like the SR discussed in the context of Brownian particle on a bistable potential. However, given that there are many degrees of freedom whose dynamics experiences continuous dissipation over time, it is not obvious whether a small oscillatory force added to the RNA can indeed be sensed along the backbone of biopolymer and renders the folding transition synchronous to the oscillatory force. For proteins and RNAs where entropy play dominant role in shaping the underlying free energy landscape, the thermal noise strength (temperature), kept at a physiological condition, is not a good variable to vary. Instead, it would be more appropriate to vary the frequency of oscillatory force. To this end, we performed the many-body simulations using the SOP model by applying a small oscillatory force δf sin(Ωt) with δf = 1.4 pN to the 5′-end of P5GA hairpin at f = 17 pN and monitored the change in folding–unfolding dynamics, for various driving frequencies Ω = 2π/T_Ω.

Our many-body simulations using the SOP model of RNA hairpin show that although the probability of being in the NBA at f = 17 pN is only ≈5% so that the folding is improbable, folding transitions occur more frequently and in coherence to a small oscillatory force at the period of T_Ω = T^SR ≃ 10.2 ms (Fig. 2C). Here, it is noteworthy that T^SR for our RNA hairpin at f = 17 pN is similar to the sum of the two transition times in the absence of oscillatory driving, τ_F(f) + τ_U(f) ≈ 10.8 ms (see Fig. 1C at f = 17 pN), a theoretically well-known SR condition for symmetric bistable potential (25).

Fig. 2.

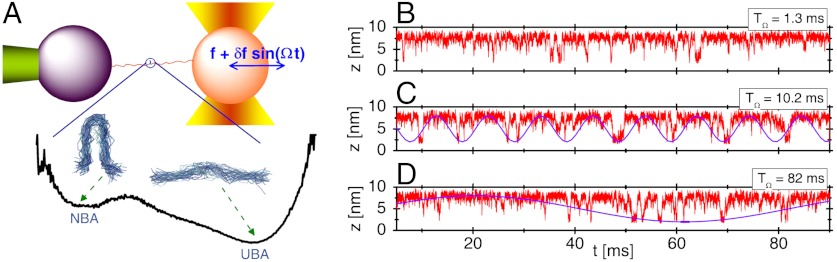
Demonstration of SR using simulation of P5GA hairpin under an oscillating force. (A) Structural ensemble of P5GA hairpin at NBA and UBA shown on the free energy profile F(z; f = 17 pN). Time trajectories of molecular extension z(t) at constant tension f = 17 pN are shown from the simulation of SOP model when a small time dependent oscillatory force δf sin(2πt/T_Ω) (δf = 1.4 pN) is added with (B) T_Ω( = 2π/Ω) = 1.3 ms, (C) 10.2 ms, and (D) 82 ms. Coherent hopping transition between folding and unfolding is found with T_Ω = T^SR ≈ 10.2 ms, which clearly shows the SR. The oscillatory forces with T_Ω = 10.2 ms and 82 ms are overlaid on the time trajectory in C and D, respectively, to emphasize the effect of synchronization. See Fig. S1 for the SR of P5GA hairpin in the presence of handles.

Mapping P5GA Dynamics onto One-Dimensional Free Energy Profile.

To explore the details of SR and RA in the dynamics of RNA hairpin more extensively, we simplified our many-body simulation using the SOP model into 1D simulation by showing that the dynamics of molecular extension z(t) from many-body dynamics can effectively be projected onto the dynamics of a quasi-particle under the 1D free energy profile F(z; f). By using f-dependent free energy profile F(z; f) = F_m(z) - (f - f_m)z where the F_m(z) is directly interpolated from the energy profile at f_m = 14.7 pN obtained by the SOP simulation (Fig. 1), we modeled an associated Langevin dynamics of the quasi-particle with a position z(t) as follows: 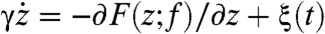. Here, γ is the effective friction coefficient and ξ(t) is the random force that satisfies the fluctuation–dissipation theorem 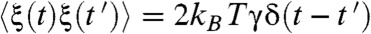with 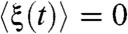. Folding and unfolding times, determined from time trajectories z(t) on F(z; f), 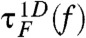and 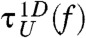are in excellent agreement with those from the SOP model [τ_F(f) and τ_U(f)] (Fig. 1C). In addition, by imposing reflecting boundary condition at z_m ≈ 1.01 nm and z_M ≈ 9.7 nm,which are the minimum and maximum molecular extension, we analytically calculated the mean first passage (Kramers) times 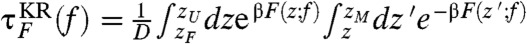for the folding and 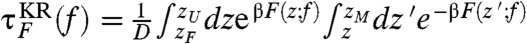for the unfolding.We set the effective diffusion constant D = k_BT/γ ≈ 13.7 μm²/s to match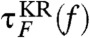 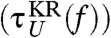(solid curves in Fig. 1C) to τ_F(f) [τ_U(f)] at f = f_m from the simulation results using the SOP model (circles in Fig. 1C).

The excellent agreement among differently calculated mean transition times 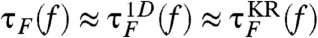justifies mapping the many-body dynamics of P5GA hairpin under varying f onto the dynamics on 1D free energy profile described with molecular extension, z. In fact, previous studies showed that z is a good reaction coordinate on which both thermodynamics and kinetics of P5GA hairpin are faithfully described as long as f does not greatly differ from f_m(19, 20). This enables us to explore SR and RA of the RNA folding–unfolding dynamics in a simpler way without compromising the goal of our study. To take into account the effect of external oscillatory force, we simply added a term δf sin (Ωt);thus,the stochastic equation describing the dynamics of z(t) in the presence of external oscillatory signal reads as follows:

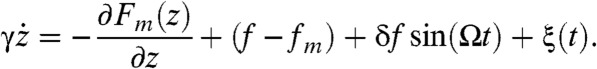[1]

Resonant Activation in the Folding and Unfolding Transitions of RNA Hairpins.

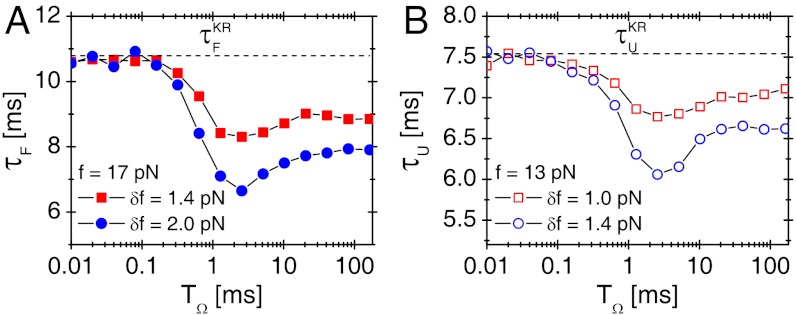
To investigate the effect of oscillatory driving on transition kinetics, we calculated the average folding time τ_F as a function of T_Ω for time trajectories generated using Eq. 1 at f = 17 pN for δf = 1.4, 2.0 pN or unfolding time τ_U at f = 13 pN for δf = 1.0, 1.4 pN (Fig. 3). We found that the external oscillatory signal accelerates both folding and unfolding dynamics and maximizes the transition rates (defined by 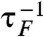, 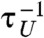) at T_Ω = T^RA ≈ 2.56 ms by about 60% and 30% for both folding and unfolding, compared with those in the absence of the oscillatory driving. The enhancement of folding (unfolding) rate could still be called RA, following the theoretical studies on symmetric bistable potential (27).

Fig. 3.

Resonant activation (RA) in folding and unfolding transitions of P5GA. (A) Mean folding time τ_F of P5GA under f = 17 pN as a function of T_Ω with δf = 1.4 pN (filled squares) and δf = 2.0 pN (filled circles). The transition times are minimized at T_Ω = T^RA ≃ 2.56 ms. (B) Mean unfolding time τ_U of P5GA under f = 13 pN as a function of T_Ω with δf = 1.0 pN (empty squares) and δf = 1.4 pN (empty circles). The transition times are minimized at T_Ω = T^RA ≃ 2.56 ms.

The presence of optimal condition of T_Ω = T^RA that minimizes the transition time indicates that there should be a matching condition for two frequencies between conformational fluctuation in folding landscape, which is induced by thermal noise, and the oscillation of input signal. For T_Ω ≪ T^RA ≲ τ, net driving force provided by the fast oscillating force is essentially zero; 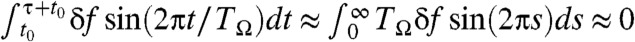. In contrast, when T^RA ≪ T_Ω ≲ τ, the molecule experiences external tension that slowly varies between f - δf and f + δf during the transition time τ depending on the time interval t₀ < t < t₀ + τ. As a result, for T_Ω ≈ 100 ms, τ_F at f = 17 pN and δf = 1.4 pN varies between 2 ms and 30 ms (Fig. 1C), and the corresponding mean folding time becomes 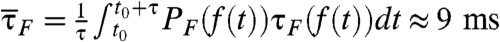as shown in Fig. 3A, which is greater than the τ_F ≈ 8 ms at T_Ω = T^RA (41).

The extent of RA varies with the amplitude of oscillatory force (δf) (compare circles and squares in Fig. 3). It is conceivable that 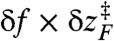where 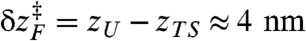at f = 17 pN (Fig. 1) provides extra work to rectify the random fluctuation of molecule in UBA. Therefore, the ratio of 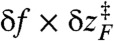to free energy barrier ΔF^‡ from the UBA to NBA, i.e., 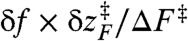should determine the enhancement of folding rate at the RA condition.

Stochastic Resonance in the Refolding Dynamics of RNA.

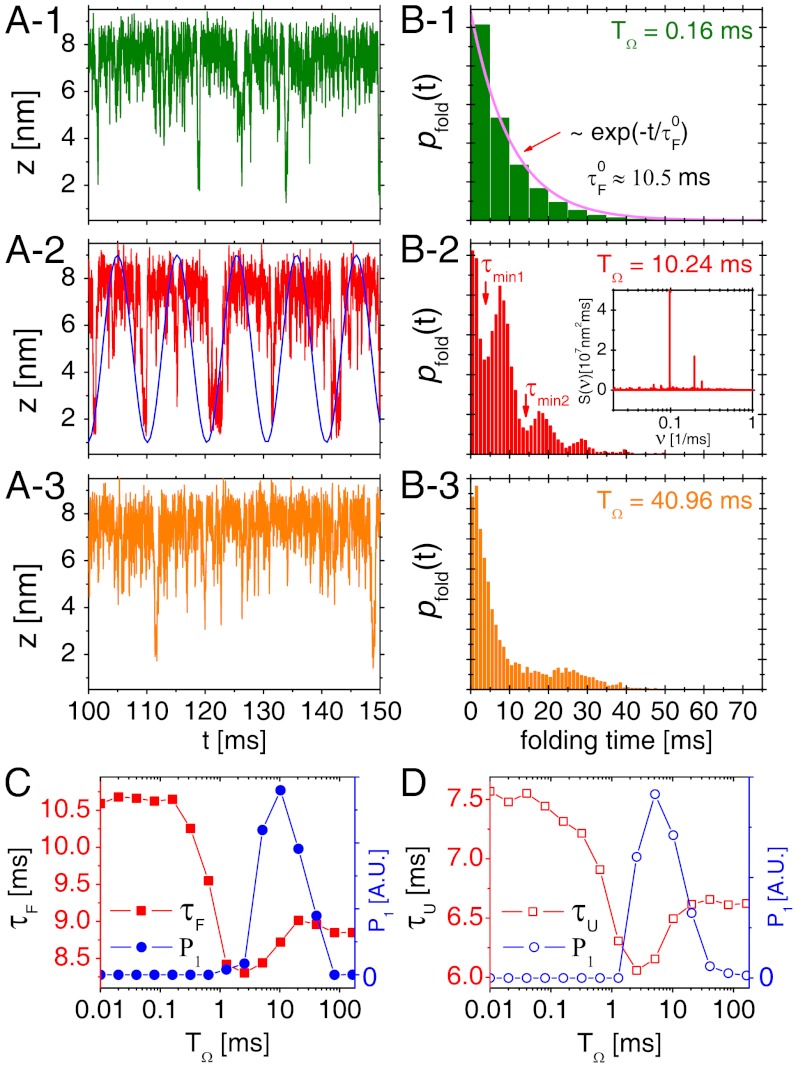
Folding time distributions p_fold(t) (Fig. 4B) calculated from time trajectories (Fig. 4A) are useful measure for characterizing SR. At fast driving T_Ω = 0.16 ms (Fig. 4B- 1), p_fold(t) decays exponentially with a decay time 10.5 ms, which is consistent with the folding time in the absence of driving, 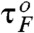(see Fig. 1C). But at T_Ω = 10.24 ms near the resonant condition, p_fold(t) displays multiple peaks whose periodicity corresponds to the driving period of input signal, which is approximately equal to 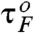(Fig. 4B- 2). The multiple peaks are superimposed on the above-mentioned exponentially decaying contribution (Fig. 4B- 1) (25). At a slow driving T_Ω = 40.96 ms (Fig. 4B- 3), the p_fold(t) has a broad and small peak around 25 ms and shows only a weak signature of coherence.

Fig. 4.

SR in the folding and unfolding transitions of P5GA under time dependent tension f + δf sin(Ωt). (A) Time trajectories and (B) folding time distributions p_fold(t) with f = 17 pN and δf = 1.4 pN at T_Ω = 0.16 ms, 10.24 ms, and 40.96 ms are shown. The synchronization (SR condition) occurs around 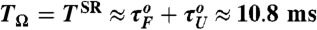, as shown in (A- 2). The inset in (B- 2) depicts the power spectrum S(ν), showing the sharpest peak at ν = 1/T^SR ≈ 0.1 ms^-1. (C) Mean folding time τ_F and measure of coherence P₁ as a function of T_Ω. (D) Mean unfolding time τ_U and measure of coherence P₁ as a function of T_Ω with f = 13 pN and δf = 1.4 pN. Note that the SR and RA conditions are made at different T_Ωs in C and D.

The degree of synchronization is quantified by calculating the P₁ value corresponding to the area under the first peak of p_fold(t), which is defined as 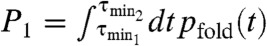where the integration is done over a time interval between τ_min 1 and τ_min 2 that defines the first peak in the p_fold(t) (25, 26, 42). For example, for T_Ω = 0.16 ms, the p_fold(t) exponentially decreases with no peak, thus P₁ = 0. In contrast, p_fold(t)s with T_Ω = 10.24 ms and 40.96 ms (Fig. 4B- 2 and Fig. 4B- 3) have the first peaks around 7 ms and 25 ms, respectively, leading to nonzero P₁. P₁(T_Ω) calculated for the data p_fold(t) of our 1D simulation for P5GA hairpin (filled circles in Fig. 4C) is nonmonotonic with T_Ω and is maximized around 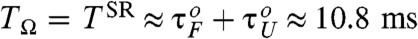. Notably, P₁(T_Ω) rise sharply for T_Ω ≳ T^RA ≃ 2.56 ms (Fig. 4C) and the T^SR that maximizes P₁ differs from the T^RA that minimizes τ_F. The P₁ for the unfolding with f = 13 pN and δf = 1.4 pN, by calculating unfolding time distribution p_unfold(t), are also depicted with empty circles in Fig. 4D. We find that the unfolding is also synchronized with an optimal driving period around 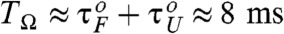(see Fig. 1C). Thus, RNA folding (unfolding) becomes maximally coherent at 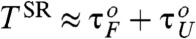. Due to asymmetric shape of potential leading to τ_F≫τ_U, the SR condition for folding becomes 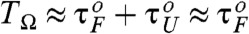, which is worth comparing with the conventional SR condition 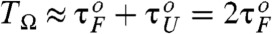for symmetric bistable systems.

There are many alternative measures to demonstrate the manifestation of SR. One measure, directly amenable to experiment, is the power spectrum 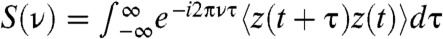where denotes ensemble and long time averages for the trajectory z(t) (25). The S(ν) shows a narrow sharp peak with the frequency ν = 1/T_Ω ≈ 1/10 ms^-1 (see the Inset of Fig. 4B- 2). In addition, spectral behavior of dynamic susceptibility defined 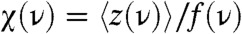, which also becomes optimal at ν ≈ 1/10 ms^-1, can be used to quantify the response of system to an external driving force.

Biopolymers Can Filter the Resonance Frequency from the Spectrum of an External Signal.

Due to the multitude of cellular processes nonequilibrium noise in the cell is decomposed into various frequencies. To check if our model can discriminate the resonant frequency using SR, we performed the 1D simulation for RNA hopping transitions under f = 17 pN by adding oscillatory forces consisting of different angular frequencies 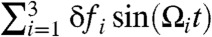where Ω₁ = 2π/0.1 ms^-1, Ω₂ = 2π/10 ms^-1 and Ω₃ = 2π/100 ms^-1; here, the optimal folding period for the SR, T_SR ≈ 10 ms, is included in the i = 2. The p_fold(t) for uniform amplitudes of the additive forces with δf₁ = δf₂ = δf₃ = 1.4 pN (Fig. 5) displays an oscillatory pattern with multiple peaks, suggesting that the folding is synchronous with the oscillatory force with the period T^SR. Even for the case of nonuniform amplitudes, in which δf₁ and δf₃ have greater values than δf₂, the signature of synchronization to the oscillatory driving with T^SR is retained (Fig. 5). Furthermore, even when we choose δf randomly from the values distributed between 0 and 2 pN at every time step, we still found the p_fold(t) with multiple peaks, which suggests that the P5GA system is capable of filtering the signal with frequency of 2π/T^SR out of the nonequilibrium noise.

Fig. 5.

Filtering of SR condition. Shown are the p_fold(t) of P5GA under 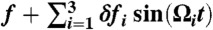at varying combinations of δf_i with Ω₁ = 2π/0.1 ms^-1, Ω₂ = 2π/10 ms^-1, Ω₃ = 2π/100 ms^-1, and f = 17 pN. For filled symbols, we fix δf₂ = 1.4 pN, corresponding to the amplitude for the optimal frequency Ω₂ for SR, and vary the other amplitudes to be δf₁ = δf₃ = 1.4 pN (filled squares), 1.7 pN (filled circles), and 2.0 pN (filled triangles), respectively. The starred symbols represent the cases where δf₁, δf₂ and δf₃ are taken randomly between 0 and 2 pN every time step to make a nonequilibrium noise δf(t). Notably, the folding transition filters the optimal driving period despite other drivings with larger or transient amplitudes.

Experimental Demonstration of SR in Biomolecular Dynamics.

Although the results discussed above are based on the numerical simulation that applies mechanical force directly acting to the ends of RNA hairpin without mediating polymer handle as in actual optical tweezers experiment, our findings on SR and RA conditions for folding transition should not change qualitatively. As quantitatively discussed by Hyeon et al. (19) as well as recognized by others (11), the presence of handle polymers simply slows down the transition kinetics by pinning the motion of the two end points of biopolymers connected to the handles. Furthermore, in all practical situations, the conformational transition time of biopolymers is much slower than the tension propagation time (43). Therefore, even in the presence of handles SR is still realized at the optimal frequency, corresponding to the sum of the folding and unfolding transition times that are measured in the presence of handles. Many-body simulation using the SOP model of RNA hairpin in the presence of 20 nm handles attached to the two ends of the hairpin confirms the realization of SR in the presence of handles (see SI Text and Fig. S1). For the purpose of experimental demonstration of SR using biopolymers, it is recommended that the experiment is conducted at the transition midforce (f_m), at which the folding and unfolding transitions are the most frequently observed (11, 13) (Fig. S2). In this case, SR condition is expected to be formed around twice the mean hopping transition time (≈2τ_F(f = f_m)).

Concluding Remarks

Originally, the SR refers to the phenomenological observation that a system under an optimal thermal noise can amplify a weak external signal if the system is nonlinear. This paper restates the SR and RA condition by focusing more on the transition dynamics of biopolymers rather than the amplification of signal. Furthermore, unlike the many studies that consider the SR using noise strength, i.e., temperature, as a variable, the present study focuses on the “bona-fide SR” with respect to the driving frequency. For a biologically relevant environment, whose temperature range should be narrowly defined, it is more appropriate to consider the effect of driving frequency on SR. Folding and unfolding transitions of biopolymers enhanced under and synchronized to external periodic signals, which is clearly demonstrated in our simulations, suggest that as long as the SR condition is met, conformational sampling of biopolymers in vivo occurs more frequently than in vitro, in response to the spectrum of athermal noise in the cell.

True manifestation of SR and RA in the context of biopolymer dynamics in vivo should hinge on existence of the actual periodic frequency that is in resonance to the transition dynamics of biopolymer. It would be of great interest to investigate the power spectra of cellular noise and how biological dynamics, for instance, conformational transitions of riboswitch, are modulated in the presence of athermal signals from other dynamic components such as motion of ribosome translocation and associated gene regulation (14).

Materials and Methods

Model.

We used the SOP model to simulate the dynamics of P5GA RNA hairpin under tension. In the SOP model, the effective Hamiltonian is defined as follows (18, 19):

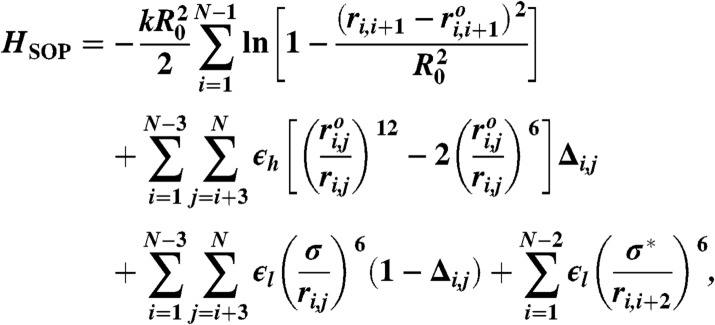[2]

where we modeled each nucleotide as an interaction center; thus N = 22. The first term restrains the bond length between the neighboring beads by using the finite extensible nonlinear elastic potential with k = 20 kcal/(mol × Å²) and R₀ = 0.2 nm. Here, r_i,i+1 is the distance between neighboring interaction centers i and i + 1, and 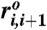is the distance in the native structure. Lennard–Jones potential was employed to stabilize the base pair present in the native structure in the second term with ϵ_h = 0.7 kcal/mol, but make the nonnative base pair repulsive in the third term, so that the model can easily reach the native topology without being trapped into nonnative conformations. If i and j are in contact in the native state Δ_ij = 1; otherwise Δ_ij = 0. 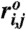is the distance between i and j interaction centers that satisfy |i - j| > 2 and Δ_ij = 1. For nonnative pairs, the strength and range of interaction were set by ϵ_l = 1 kcal/mol and σ = 0.7 nm. The last term involving the repulsion with σ^∗ = 0.35 nm maintains a certain angle between i and i + 2 interaction centers.

Simulation.

We performed Brownian dynamics simulation by numerically integrating the discretized equation of motion:

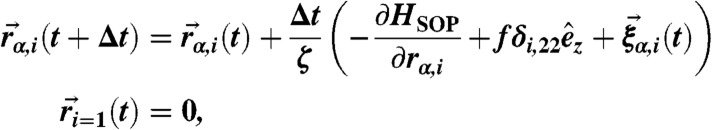[3]

where α = x,y,z and the random force 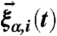satisfies 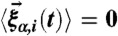and it is assumed that the probability distribution of the noise in the random force is Gaussian, i.e., 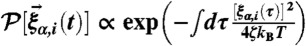and 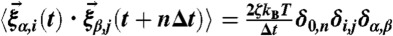with n = 0,1,2,…. We probed the folding–unfolding dynamics of RNA hairpin by applying tension f to the 3′-end of the hairpin while fixing the position of 5′-end at temperature T = 300 K. Also, we chose the friction coefficient ζ = 100 m/τ_L with τ_L = (ma²/ϵ_h)^1/2 ≈ 3–5 ps corresponding to the value that a nucleotide whose size a ≈ 0.5 nm feels in water environment whose viscosity is approximately 1 cP (18). We applied the tension f between 13 ≤ f ≤ 18 pN (Fig. 1) to the molecule and added small sinusoidal forces of δf sin(Ωt) with varying Ω values (Fig. 2). We set the simulation time step Δt = 4.7 × 10^-5 μs and recorded data at every 10⁵ time steps (4.7 μs). After equilibrating the RNA in native state for ∼47 μs, we applied tension f or f + δf sin(Ωt) and recorded the z(t) of each trajectory for t > 10² ms.