Cooperation and assortativity with dynamic partner updating

Abstract

The natural tendency for humans to make and break relationships is thought to facilitate the emergence of cooperation. In particular, allowing conditional cooperators to choose with whom they interact is believed to reinforce the rewards accruing to mutual cooperation while simultaneously excluding defectors. Here we report on a series of human subjects experiments in which groups of 24 participants played an iterated prisoner’s dilemma game where, critically, they were also allowed to propose and delete links to players of their own choosing at some variable rate. Over a wide variety of parameter settings and initial conditions, we found that dynamic partner updating significantly increased the level of cooperation, the average payoffs to players, and the assortativity between cooperators. Even relatively slow update rates were sufficient to produce large effects, while subsequent increases to the update rate had progressively smaller, but still positive, effects. For standard prisoner’s dilemma payoffs, we also found that assortativity resulted predominantly from cooperators avoiding defectors, not by severing ties with defecting partners, and that cooperation correspondingly suffered. Finally, by modifying the payoffs to satisfy two novel conditions, we found that cooperators did punish defectors by severing ties, leading to higher levels of cooperation that persisted for longer.

Why, and under what circumstances, presumptively selfish individuals cooperate is a question of longstanding interest to social science (1, 2) and one that has been studied extensively in laboratory experiments, often as some variant of a public goods game (also called a voluntary contribution mechanism) or a prisoner’s dilemma (see refs. 2 and 3 for surveys). One broadly replicated result from this literature is that in unmodified, finitely repeated games cooperation levels typically start around 50–60% and steadily decline to around 10% in the final few rounds (2). The explanation for this decline is that when conditional cooperators, who are thought to constitute as much as 50% of the population (4), are forced to interact with a heterogeneous mix of other types, in particular free riders, the conditional cooperators tend to reduce their contributions over time (3).

Previous work has shown that explicit enforcement mechanisms such as punishment (5) and reward (6) can alleviate the observed decline in cooperation in fixed groups. Here we investigate a related but distinct mechanism that exploits a well-known feature of human social interactions—namely that they change over time, as individuals form new relationships or sever existing ones (7). By allowing participants engaged in a repeated game of cooperation to update their interaction partners dynamically, cooperation levels might be enhanced in two ways. First, conditional cooperators could implicitly punish defectors by denying them a partner, thereby encouraging potential defectors to cooperate. Second, conditional cooperators could benefit from assortative mixing (1) by avoiding defectors and seeking cooperators, thus sustaining their own cooperative tendencies.

Two recent studies have argued that dynamic partner updating is capable of promoting cooperation (8, 9); however, the studies, in fact, reached somewhat different conclusions. In particular, whereas one study (8) found that allowing individuals to update one partner every round led to a significant increase in cooperation, the other study (9) found no significant increase at that rate. The latter result has been interpreted as supporting prior theoretical claims that dynamic partner updating enhances cooperation only when it exceeds a critical threshold rate (10). Because the former study considered only one rate, however, and the latter study considered only two rates, and because in both cases the effect sizes were small, the existence or otherwise of a threshold rate remains ambiguous. Moreover, both studies used an “active linking” (10) design in which players were offered opportunities to make and break links with randomly chosen partners, but were not allowed to choose with whom they wished to make and break links; moreover, players were unable to refuse new links proposed by others. Although appealingly simple, active linking is somewhat unrealistic. In real-world social networks individuals can generally select among a multiplicity of potential partners (11) and hence can choose new partners selectively. Moreover, social networks are typified by high levels of reciprocity (12–15), implying that mutual acceptance of new links is the social norm.

Our study builds upon this work in three ways. First, our design is fully endogenous, allowing individuals to decide with whom they will make and break ties. As we explain below, the resulting effect sizes are much larger than in previous studies of dynamic networks (8, 9), reaching close to 100% cooperation in some cases. Second, we consider an extremely wide range of update rates, affording us a much clearer understanding of the importance of varying rates. We find no evidence of the hypothesized threshold effect (9, 10), instead finding significant and positive increases in cooperation at rates well below those previously reported. Finally, and in contrast to both previous studies that considered only one set of payoffs, we manipulate the payoff structure itself, effectively varying the attractiveness of the “outside option” (16), meaning roughly the payoff associated with choosing not to interact with a potential partner. We find that only in the presence of an attractive outside option do conditional cooperators punish defectors (by proactively deleting ties with them). By contrast, when the outside option is less attractive, we find that cooperators tolerate defecting partners, eventually leading them to defect themselves.

Our work is also related more generally to a number of recent experiments that have investigated various aspects of the relationship between cooperation and partner selection, such as unilateral vs. bilateral choice (17, 18), the effect of introducing an outside option of varying attractiveness (16), and the attributes of the individuals (age, sex, race, etc.) as predictors of selection and cooperation (19, 20). Although our treatment of the outside option is consistent with previous work (16), it is distinct in that it extends it to the case of a dynamic network. Finally, other related work (21, 22) has examined how individuals select groups or are excluded by them. Although at a high level these papers clearly resemble both the partner selection literature and dynamic updating studies such as ours, they differ substantially from both literatures in that the object of selection (21) or the actor (22) is the group, not the individual.

Experimental Setup

We conducted a series of online human subjects experiments in which groups of 24 participants played an iterated prisoner’s dilemma (PD) game, where in addition to choosing their action each round—cooperate or defect—they also were given the opportunity to update their interaction partners at some specified rate, which was varied across experimental conditions. (See SI Appendix, Figs. S1 and S2 for details of the experimental platform and recruiting.) All games comprised 12 “strategy update” rounds during which players could update their strategy: cooperate (C) or defect (D). Consistent with standard PD conditions, a cooperator received four points when interacting with another cooperator, but lost one point when interacting with a defector. A defector received seven points when interacting with a cooperator and one point when interacting with another defector (see SI Appendix for details).

In addition, after every r strategy update rounds, players entered a “partner updating” turn in which they were permitted to make up to k partner updates. By adjusting r and k we were therefore able to explore an extremely wide range of relative updating rates, from one opportunity every several strategy update rounds to several opportunities every round. A single partner update comprised either severing a link with an existing partner or proposing a link to a new partner, where, importantly, players could choose the partner in question. Also of importance, our design specified that severing a link was a unilateral action, requiring no consent from the corresponding partner; however, proposing a link was a bilateral action that required acceptance for the edge to be formed. These requirements in turn necessitated that each partner-updating turn consist of two phases: a proposal phase, during which players submitted their link proposals and link deletions, and an approval phase during which they were required to accept or reject any outstanding link proposals. If a proposal was rejected, the proposing player could not reuse that action, and hence players had an incentive to make proposals they thought would be accepted. After each partner-updating turn was completed, the network of partners was updated to reflect severed and accepted links, and a new strategy update round commenced.

Players were shown the identities (anonymous player IDs) and strategy choices for up to the previous five rounds for all players. Players were also shown who they were and were not connected to, their current cumulative payoff, their payoff from the previous round, and the time remaining in the current round. Consistent with previous work (23, 24), players were not given explicit information about the structure of the network beyond their immediate network neighbors (see SI Appendix, Figs. S3–S5 for screenshots). Nevertheless, to test for the possibility that initial conditions could affect outcomes, players were randomly assigned to positions in one of two initial network topologies: “cliques” composed of four cliques of six players each; and “random” comprising a random regular graph, where in both initial graphs, each player had exactly five neighbors (i.e., partners). These topologies were chosen because they are as different as possible in terms of standard network metrics such as path length and clustering coefficient (25, 26) while still maintaining the same number of ties per person.

Results

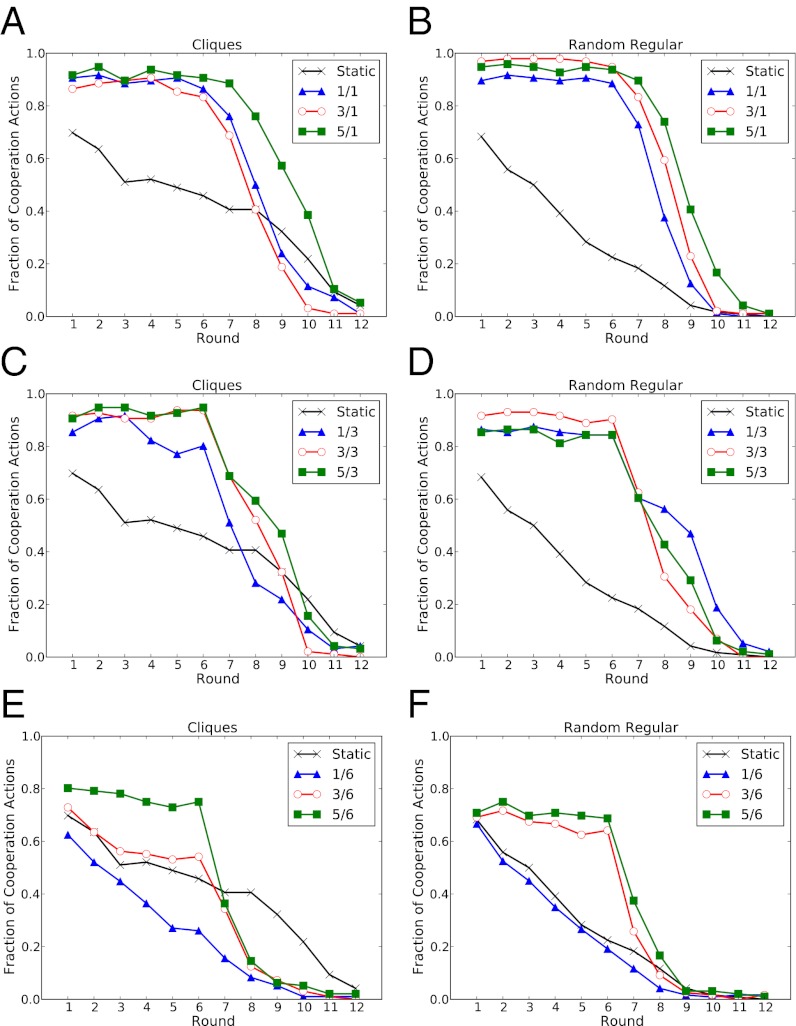
Fig. 1 shows the average fraction of cooperators by round for k = 1, 3, 5 and r = 1, 3, 6 (Top, Middle, and Bottom rows, respectively) and for the cliques (Left column) and random (Right column) initial conditions, respectively. For r = 1 and r = 3, we observe three striking features of networks with dynamic partner updating: first, cooperation levels start significantly higher than in fixed networks; second, cooperation levels remain between 80% and 100% in the presence of updates even as they decline in fixed networks; and third, cooperation declines rapidly as the game nears its end, finishing as low as in the absence of partner updates. Taken as a whole this behavior is far from the Nash prediction of all players defecting on all turns (see SI Appendix for the theorems and proofs). We note, however, that for r = 6, the initial increase is largely absent, and the persistence effect is present only for the higher values of k = 3, 5. This lack of effect for the r = 6 case can be understood by noting that the players experienced only one partner-updating opportunity (because round 12 was the final round of the game); thus for the r = 6, k = 1 case, players were permitted to update just one partnership in the entire game. Because this treatment is only slightly different from the static case, it is unsurprising that its effect, if any, was small.

Fig. 1.

Fraction of cooperation by round for the cliques (A, C, and E) and random (B, D, and F) initial conditions. (Top row) r = 1; (Middle row) r = 3; (Bottom row) r = 6. Symbols indicate different values of k (solid triangles, k = 1; open circles, k = 3; solid squares, k = 5).

Next, Fig. 2A summarizes these findings for all values of r and k, showing the average rate of cooperation as a function of the total number of updates u per player over the course of a game [i.e., u = k*(12/r − 1)]. Consistent with Fig. 1, Fig. 2A shows that increases in cooperation rates were relatively small for the very lowest (r = 6) rates of updating (i.e., compared with the variation between the two static cases). However, when r = 1, 3 the average cooperation rate was substantially higher than the static (i.e., no partner updating) case. Correspondingly, average payoffs also increased severalfold over the static case (see SI Appendix, Fig. S6A for details). To account for subject- and game-level variations, the treatment effects in Fig. 2A were estimated using a nonnested, multilevel model (27) with error terms for treatment, subject, and game as well as the experience level of a given subject in a given game (see Materials and Methods for more details). To test for significance, Fig. 2B shows the estimated difference in average cooperation levels between the various treatments and the corresponding static case, where error bars represent 95% confidence intervals. For the cliques initial condition all r = 1 and r = 3 treatments yield positive effects that are significant at the 5% level, and for the random regular initial condition the r = 6, k = 3, 5 conditions are also positive and significant. In general, regardless of initial condition, allowing as few as one update every three rounds was sufficient to significantly increase cooperation (see SI Appendix, Fig. S6B for a similar analysis of average payoff levels), a rate that is well below the previously reported threshold for a positive effect (9).

Fig. 2.

Average fraction of cooperation as a function of partner update rate (A) and estimated difference in fraction of cooperation from the corresponding static cases as a function of k (B) for cliques (dashed lines) and random (solid lines) initial conditions, for r = 1, 3, 6 and k = 0, 1, 3, 5. Symbols indicate different values of k (triangles, k = 1; circles, k = 3; squares, k = 5). Error bars are 95% confidence intervals (see Materials and Methods for details).

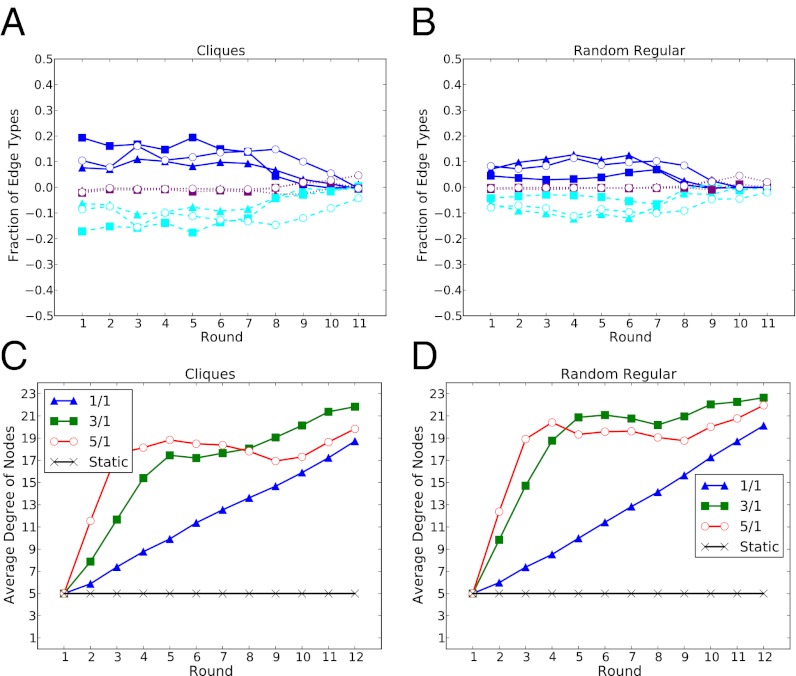
Next, Fig. 3 shows the relationship between assortativity and cooperation for r = 1 (see SI Appendix, Figs. S7 and S8 for equivalent r = 3, 6 results). To quantify assortativity, we first label each link in the network as CC, CD, or DD according to the states of the players who share the link. Then we define CC, CD, and DD assortativity as the difference between the observed fraction of CC, CD, and DD links and the corresponding fraction that would be expected under a random permutation of the player IDs. The difference is necessary to account for “baseline assortativity” (also called baseline homophily) (28), which varies dramatically over the course of the game as the overall fraction of cooperators changes. Fig. 3 A and B show that for both cliques and random initial conditions CC assortativity is positive for most of the game and CD assortativity is negative, whereas DD assortativity is essentially absent. In other words cooperators displayed a tendency to avoid defectors and gravitate to other cooperators, whereas defectors were neutral with respect to other defectors.

Fig. 3.

Assortativity by round for cliques (A) and random (B) initial conditions for r = 1. The differences between observed and baseline homophily for CC, CD, and DD links are shown by dark blue, light blue, and magenta lines, respectively. k = 1, 3, 5 is shown by triangles, circles, and squares, respectively. Average degree by round for cliques (C) and random (D) initial conditions: r = 1 and k = 0, 1, 3, 5.

Finally, Fig. 3 C and D show that players continued to add links throughout the game (see also SI Appendix, Figs. S7 and S8 for r = 3, 6). Although the addition of links is superficially consistent with the Nash prediction (see SI Appendix for details), the equilibrium analysis also predicts that all players defect on all turns; hence players form links with each other on the grounds that the payoff to (D, D) exceeds their outside option (16) (a payoff of zero for having no links). In reality, however, it is not only defectors who accept and maintain ties with other defectors. For the r = 1 case, for example, cooperators also accepted proposals from defectors roughly 40% of the time and rarely deleted them, even though such ties were costly. Overall, deletions accounted only for 10% of updates (see SI Appendix, Table S1 and Figs. S9–S11 for more details). Moreover, defectors were also more than twice as likely to propose links to other defectors than to cooperators (0.24 for D → D vs. 0.1 for D → C). Together, these results suggest that observed assortativity derived less from cooperators “punishing” defectors by deleting ties and more from two related mechanisms: (i) cooperators avoiding defectors and (ii) defectors failing to propose links to cooperators in the first place. A striking illustration of the lack of punitive deletion can be seen in the cases of r = 1 and k = 3, 5 in Fig. 3 C and D. By round 4 the graph was close to, and in some trials precisely, a clique. Because in these cases there were almost no edges available to be added, deleting edges exerted no opportunity cost. Nevertheless when exposed to a small number of defectors in later rounds, cooperators chose to defect rather than cut ties to the defectors, resulting in a defection cascade (see SI Appendix, Fig. S12 for an illustrative example).

Although surprising in light of simulation and theoretical models that assume punitive partner deletion (10, 29–33), its relative rarity can be understood in terms of two related conditions of the payoff matrix. First, because the benefit to a cooperator forming an additional tie with another cooperator (four points) outweighed the loss of maintaining a tie with a defector (minus one point), when a cooperator was faced with a choice to sever a tie with a defector or add new tie to a cooperator, players rationally chose the latter. Second, because defectors gained a positive amount from all interactions (i.e., seven points when interacting with cooperators and one point when interacting with defectors), defecting players rationally preferred to maintain all their ties, even with other defecting players.

The upshot of these two conditions of the payoff matrix was that early on in the game, when most players were cooperating, all players wished to add links as fast as possible, even if that required tolerating occasional defectors. Defectors, therefore, were not punished for their actions, thereby persisting and encouraging cooperators to switch. Finally, as the end game neared, and the availability of other cooperators diminished, all players preferred to defect rather than cooperate and cut ties with defectors. One can conclude that dynamic partner updating combined with these payoffs resulted in cooperation being promoted, but not sustained.

To quantify the effect of these conditions on cooperation and assortativity, we conducted a new set of experiments with modified payoffs such that cooperators were penalized five points when interacting with defectors instead of just one point, and defectors lost one point each when interacting with each other, rather than gaining one point each. These payoffs still fulfilled the usual requirements of the PD, but had two additional properties: (i) maintaining a tie with a defector was more costly for a cooperator than creating a new tie with another cooperator; and (ii) defectors could no longer profit by interacting with other defectors. In addition, because the results from the k = 3 condition were not substantively different from k = 1, 5, we replaced this condition with k = (N − 1) = 23 to explore more of the parameter space (as before, a static condition was also included for comparison). By permitting every player to propose or delete an edge with every other player each round, the k = 23 condition effectively removed any budget constraint on deleting links, hence further increasing the likelihood of deleting links to defectors. Also, because it was previously established that initial conditions did not have a qualitative impact on cooperation levels, only the cliques initial condition was studied for the modified payoffs.

For these new payoffs, equilibrium analysis again predicts that all players will defect on all rounds; however, in contrast to the initial payoffs, the analysis predicts that players will delete as many links as possible, leading to an empty graph for the parameters we tested (see SI Appendix for details). Clearly, we did not expect all players to defect on all rounds; hence the equilibrium prediction regarding the network is again best viewed as a baseline for comparison rather than a hypothesis. We emphasize, however, that although the new payoffs were designed to make interacting with defectors less attractive, it is not obvious that they would lead either to higher levels of cooperation or to longer persistence. The reason is that the punishment for a cooperator interacting with a defector was also greater than in the original payoffs and could easily have increased the prevalence of strategic defections (i.e., in anticipation of others defecting or to exploit cooperators), especially for low rewiring rates.

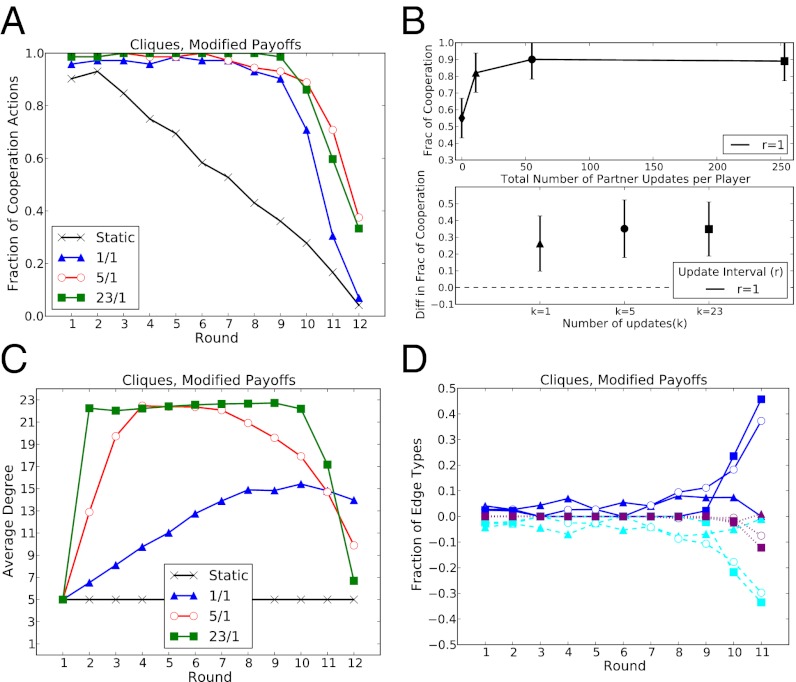
It is therefore striking that, as Fig. 4A shows, the modified payoffs led to significantly higher rates of cooperation and longer persistence of cooperation for all rewiring rates. Cooperation levels approached and in many treatments reached 100% and were sustained at that level until close to the end of the game. In fact, in seven of the nine trials performed with the modified payoffs, cooperation levels were over 90% in 9 of the 12 rounds. Fig. 4B, Upper summarizes the effects, showing that a small amount of dynamic partner updating, r = 1, k = 1, resulted in large increases in cooperation levels over the static case. As before, further increases in update rate resulted in smaller increases in cooperation levels, where, interestingly, the highest rate of rewiring, k = 23 did not lead to appreciably more cooperation or higher average payoffs than were obtained in the k = 5 condition, consistent with our hypothesis that the earlier payoff structure, not the constraints on partner updating imposed by the update rate, was responsible for the previous absence of punitive deletions. Fig. 4B, Lower, meanwhile, shows that the differences between the average cooperation levels of the r = 1, k = 1, 5, 23 and the static case were significant at the 5% level (see Materials and Methods for more details and SI Appendix, Fig. S13 for the corresponding analysis of player earnings).

Fig. 4.

Results for modified payoffs, r = 1 and k = 0, 1, 5, 23, cliques initial condition. (A) Fraction of cooperation by round. (B) Aggregate fraction of cooperation as a function of total number of partner updates (Upper) and estimated difference in fraction of cooperation from the static case as a function of k (Lower). (C) Average degree by round. (D) CC (dark blue), CD (light blue), and (DD) (magenta) assortativity by round, where k = 1, 5, 23 is shown by triangles, circles and squares, respectively. In B the error bars are 95% confidence intervals (Materials and Methods).

Fig. 4 C and D also shows interesting similarities with and differences from the original payoffs: In early rounds, players added edges much as they did previously, leading in fact to even denser networks; however, unlike in the previous case, they deleted edges as rapidly as possible toward the end of the game as defection began to spread. In fact, in the modified payoffs 22% of the partner update actions were deletions, compared with only 10% in the original payoffs (see SI Appendix, Table S2 and Fig. S14 for more details). The increased amount of deletions suggests that the amount of exploitation of cooperators by defectors was mitigated as a result of these new payoffs. CC and CD assortativity, meanwhile, had the same signs as before, but much lower magnitudes in the early rounds for the simple reason that cooperation levels were close to 100%, and hence baseline CC assortativity was also close to 100%. As the end of the game approached, however, the assortativity measure increased dramatically as cooperators attempted to segregate themselves from defectors, and defectors also began cutting ties with other defectors—an effect that is illustrated graphically in SI Appendix, Fig. S15. Thus, in the modified payoffs cooperators and conditional cooperators were able to separate themselves from defectors, further helping cooperation to be promoted and sustained.

Discussion

At a high level, our results are consistent with prior work (8–10, 30–35), in that allowing players to form new ties and sever existing ones generates assortative mixing between cooperators along with increased cooperation. However, our results advance upon previous work in three key respects.

First, in spanning a wide range of update rates, Fig. 2 goes beyond the qualitative claim that updating should aid cooperation, revealing the functional form of the relationship. Interestingly, for both cooperation and payoffs the effect of updating is strongly concave, meaning that small increases in the update rate near zero correspond to much larger effects than subsequent increases (i.e., the marginal return to increasing update rate is strongly decreasing). This finding therefore helps clarify previous theoretical and experimental work, which has made conflicting claims regarding the importance of the update rate. In some cases (31, 32) cooperation has been claimed to increase smoothly with update rate, whereas in others (9, 10, 34, 35) partner updating has been claimed to impact cooperation only when the rate exceeds a critical threshold. We found that both cooperation and payoffs were sensitive to the update rate across the entire range and that the effects became very large and significant at much lower rates than had been found previously. Thus, high rates of updating are not required to realize measurable improvements.

Second, our results revealed that the effect of dynamic partner selection on cooperation levels depends on a novel condition of the PD payoffs. Unlike in static games, where only the relative payoffs matter, in games with partner updating the absolute payoff that a tie yields becomes highly relevant. The rationale behind this result is obvious—when faced with a choice between adding a profitable link and severing a costly one, players rationally chose the action that yielded the higher aggregate payoff. Cooperators did not sever ties to defectors when the result of cutting a tie to a defector yielded less than the gain of a link to another cooperator. But the resulting failure to punish defectors also had a less obvious consequence: Network density increased even as defectors proliferated, thereby further increasing the temptation to defect, leading ultimately to a sudden and irreversible collapse in cooperation. Because cooperators could not segregate themselves from defectors, cooperation was promoted early but not sustained. Only when the cost of interacting with defectors outweighed the benefits to cooperators of forming new ties with each other did we see punitive deletion of links with defectors. This increased willingness to sever links with defectors in turn isolated from cooperators, leading ultimately to higher levels of cooperation that were sustained until almost the end of the game.

Third, we attribute the much greater sensitivity and effectiveness of the update rate, relative to previous results (8, 9), to two features of our design that capture important elements of real-world social networks: first, that players could choose which others they wish to make or break ties with (as opposed to having those choices imposed exogenously); and, second, that new partnerships required the consent of both partners, whereas existing partnerships could be terminated unilaterally. Allowing participants to choose their partners allowed cooperators to separate themselves from defectors more effectively than with random partner choices. As a result, cooperation levels approached and in some cases were sustained at nearly 100%, a rate far higher than prior work which showed only a slight increase in cooperation over the baseline (9).

In closing, we note that our focus on dynamic partner updating complements previous experimental work that has explored related mechanisms for increasing cooperation, such as punishment (36), reward (6), assortative group formation (21), and ostracism (22, 37). Although clearly analogous in some respects, dynamic partner updating is distinct in others. First, in contrast to explicit punishment and reward mechanisms, fully endogenous partner updating of the kind we have studied effectively uses implicit punishment, by link deletion, and implicit reward, by proposing or maintaining links. Clearly it is not always feasible for individuals to choose with whom they interact, in which case explicit mechanisms may be required; however, our results suggest that when they are free to choose, other, more explicit, forms of punishment and reward may be unnecessary. Second, in contrast to assortative group formation and ostracism, both of which require coordination among a group of individuals, partner updating can be accomplished in an entirely distributed manner, via the natural process of individuals making and breaking ties with their choice of others. For both these reasons, along with the frequently large size of the effects we observe, dynamic partner updating deserves to be considered among the most promising levers for eliciting cooperation between humans, especially in informal settings. Nevertheless, the specific conditions under which different forms of feedback—punishment, reward, ostracism, or dynamic partner selection—are most realistic and/or effective in practice remain an important question for future work.

Materials and Methods

This research was reviewed and approved by Yahoo! Labs' Human Subjects Research process. Correspondingly, informed consent was obtained from all participants (see SI Appendix for informed consent statement). All experiments were conducted online using Amazon’s Mechanical Turk, a crowd-sourcing platform that is increasingly used to conduct experimental behavioral research (9, 23, 38–41). Over the course of 4 wk, a total of 108 unique subjects participated in a total of 94 experiments (82 for the initial payoffs and 12 for the modified payoffs), where each experiment required 24 subjects to participate simultaneously (see SI Appendix text and SI Appendix, Figs. S1 and S2 for details of recruiting). One consequence of this recruiting strategy was that some individuals played many games, whereas others played only once; hence the possibility arises that overrepresented individuals will bias our results, either because they are systematically different from those who play rarely or because they learn to play differently with experience. In addition, it is well known that cooperation levels in iterated games of cooperation exhibit temporal dependencies, in the sense that random differences in initial cooperation levels persist over many rounds. To mitigate potential interactions between treatment and other (e.g., learning, time of day) effects, the order in which the various treatments were applied was randomized. In our analysis, moreover, we accounted for the various forms of nonindependence across observations (repeated observations of individual subjects, game effects, and learning effects), by fitting the data to the following nonnested, multilevel model (27):

where y_i is the expected cooperation level for the ith observation (i = 1, … n_obs, and t[i], s[i], g[i], and h[i] are all index variables that map the ith observation to a particular treatment, subject, game, and experience level, respectively. Each observation refers to the average contribution of a particular player in a single game; hence for the initial payoffs, we have n_obs = 82 × 24 = 1,968, and for the modified payoffs, n_obs = 12 × 24 = 288). Moreover, is a dummy variable for treatment, where t[i] = 1, … , 20 for the initial payoffs (we have two initial conditions, a static case for each, and r = 1, 3, 6 and k = 1, 3, 5; hence 2 × 3 × 3 + 2 = 20 treatments), and for the modified payoffs t[i] = 1, … , 4 (we have one initial condition, a single static case, and r = 1 and k = 1, 5, 23, and hence 4 treatments); 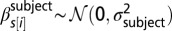is a group-level predictor for subjects; 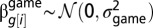is a group-level predictor for games; and is a group-level predictor for the number of games played by player s[i] at the time of the g[i]th game. Note that unlike for subject, game, and history effects, we do not model the treatment effects, preferring the simpler and more conservative approach of using a dummy variable for each treatment and hence avoiding the need to worry about potentially erroneous distributional assumptions (27). To test for significance, we computed 95% confidence intervals for the difference between each treatment and its corresponding static case; hence if zero is not contained in the interval, then the null hypothesis that they are the same can be rejected at the 5% level. As described in the main text, for the initial payoffs the null hypothesis can be rejected for all treatments except for r = 6 and k = 1, 3, 5 for the cliques initial conditions and r = 6 and k = 1 for the random initial condition. For the modified payoffs, all treatments had a significant and positive effect.