Evidence for discrete-state processing in recognition memory

Abstract

We provide evidence that recognition memory is mediated by a detect-or-guess mental-state model without recourse to concepts of latent-strength or multiple-memory systems. We assess performance in a two-alternative forced-choice recognition memory task with confidence ratings. The key manipulation is that sometimes participants are asked which of two new items is old, and the resulting confidence distribution is unambiguously interpreted as arising from a guessing state. The confidence ratings for other conditions are seemingly the resultant of mixing this stable guessing state with an additional stable detect state. Formal model comparison supports this observation, and an analysis of associated response times reveals a mixture signature as well.

Recognition memory refers to the ability to differentiate previously encountered stimuli from novel ones. Understanding this ability remains timely and topical, and underlies more complex theories of human memory and associated pathology. One popular conceptualization, called dual-process accounts, is that memoranda are mediated by two distinct processes: an unconscious process based on familiarity, and an effortful, conscious one based on recollection (1). An alternative conceptualization is that memoranda are mediated by a single latent-strength process. Items have a baseline strength before study, and studying items increases this strength. Latent-strength theories are at the core of a large set of computational memory models, including trace-based memory models (2–5) and neural network models (6, 7). In this paper, we propose an account that is simpler than either the dual-process recognition memory or latent-strength accounts. In our alternative, items are either remembered or not, and there are no intermediate states. We posit that stimulus factors, such as the number of times an item is studied, only affects the probability of entering the remember state. Once a participant enters this state, however, the performance is the same regardless of stimulus factors. This property forms a key signature or invariance of discrete-state models. We propose a experiment for testing this invariance, and find that it holds to reasonable precision.

Discrete-State Models

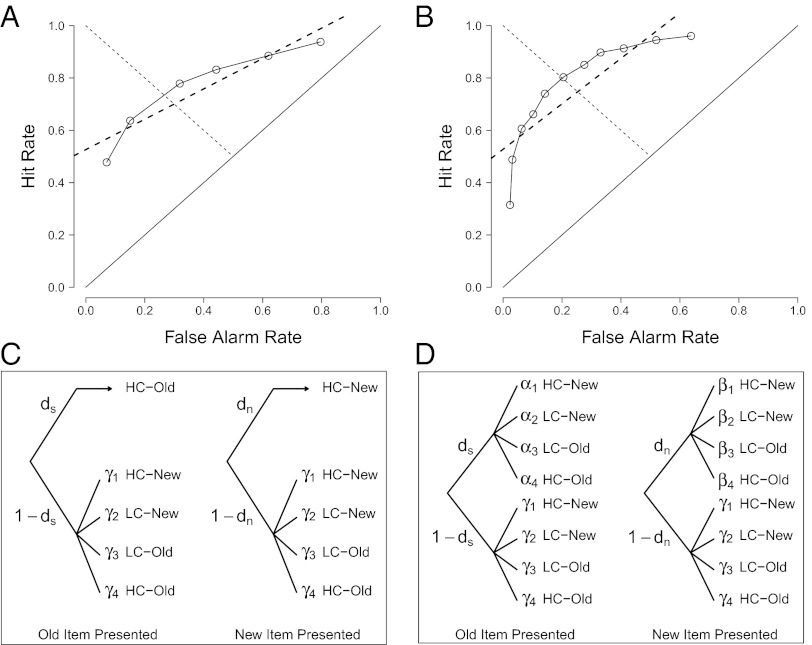
Discrete-state models remain unpopular because some authors mistakenly consider them to be incompatible with extant receiver operator characteristic (ROC) data (8–10). The points in Fig. 1 A and B are ROC functions from previous recognition memory experiments, and these are constructed by having participants rate their confidence and choice on a unidimensional scale (11). As can be seen, the points are best fit with a curved function. Fig. 1C shows the conventional high-threshold discrete-state model for a four-choice confidence scale (the generalization to any number of choices is straightforward). When a tested item was previously studied (Fig. 1C, Left), the participant enters either a detect state with probability d_s or a guessing state with probability 1 − d_s. When in the detect state, the participant responds with highest confidence that the item was old. When entering the guessing state, the participant distributes her or his responses with a fixed distribution (denoted γ₁ … γ_K, where K is the number of response options). Likewise, when the tested item is new, the participant enters a detect state with probability d_n or a guessing state with probability 1 − d_n. When in this detect state, the participant responds with the highest confidence response that the item is new. A critical assumption in this model is that participants use highest confidence responses when in detect states. This assumption is termed the certainty assumption. The discrete-state model with the certainty assumption yields straight-line ROC predictions that are incompatible with the plotted data in Fig. 1 A and B (dashed lines represent predictions).

Fig. 1.

ROCs in extant confidence-ratings recognition memory tasks show curvature. (A) Points are data from Slotnick and Dodson (9), where the task was yes/no memory recognition. Dashed and solid lines show the best fit of a discrete-state model with and without the certainty assumption, respectively. (B) Points are data from Qin et al. (27), where the task was 2AFC source-memory recognition. Dashed and solid lines show the best fit of a discrete-state model with and without the certainty assumption, respectively. (C) A discrete-threshold model with the certainty assumption. The figure shows the case for four response options: sure new, maybe new, maybe old, and sure old, and detection leads to highest-confidence responses (the certainty assumption). Parameters d_s and d_n denote the probability of detection for old and new items, respectively. Parameters γ₁, … , γ₄ denote the probability of making a response conditional on guessing. (D) A more general discrete-state model without the certainty assumption. Parameters α₁, … , α₄ and β₁, … , β₄ denote the probability of making a response conditional on detecting an old or new item, respectively.

Luce (12) argued that the certainty assumption may be unrealistic. Participants may enter states without any control or volition, and occasionally enter them in error. To meet response-demand characteristics, participants may shape how they respond when in a state. To compensate for the possibility of entering a state incorrectly, participants may occasionally produce low-confidence responses even in detect states. The plausibility of low-confidence responses in detect states is enhanced when considering that participants are often asked to distribute their responses. Even if this instruction is withheld, there may be an implicit demand to distribute responses from the presentation of several response options. Hence, the certainty assumption is tenuous and, as shown next, greatly affects model predictions.

Fig. 1D shows how the assumption may be relaxed, and in this case, participants may produce even low-confidence responses from the detect state. ROC predictions from discrete-state models without the certainty assumption are more flexible than those with it. The constraint is that points must be connected by line segments, but the slopes of these segments may vary (12–15). The predicted ROCs for the data examples in Fig. 1 A and B are shown as solid lines. These predictions account for the shown data perfectly. Contrary to popular assertions, the extant ROC plots do not rule out discrete-state models per se; they rule out only discrete-state models with the certainty assumption.

Predictions of Discrete-State and Latent-Strength Models

It may appear that discrete-state models are too unconstrained to be useful. Indeed, as might be surmised from Fig. 1 A and B, the general discrete-state model does account for a single ROC curve from any single experimental condition. Fortunately, most experiments involve several conditions; for example, items may be studied one time or several times before test. In this case, there are separate ROC curves for those items studied once and those items studied several times. As shown next, the discrete-state model is highly constrained when accounting for data from multiple conditions.

The key property of these models is that the distribution of responses from a mental state is not dependent on the experimental condition. For instance, participants may enter the detect state for either the several-repetition or the single-repetition condition, and they are more likely to do so for the former than latter. Nonetheless, once a participant enters this detect state, the distribution of responses is the same. Restated, conditional on a detection state, the distribution across responses is invariant across conditions. We term this property “conditional independence.” The conditional independence property represents the core of discrete-state models and it may be tested without recourse to the certainty assumption.

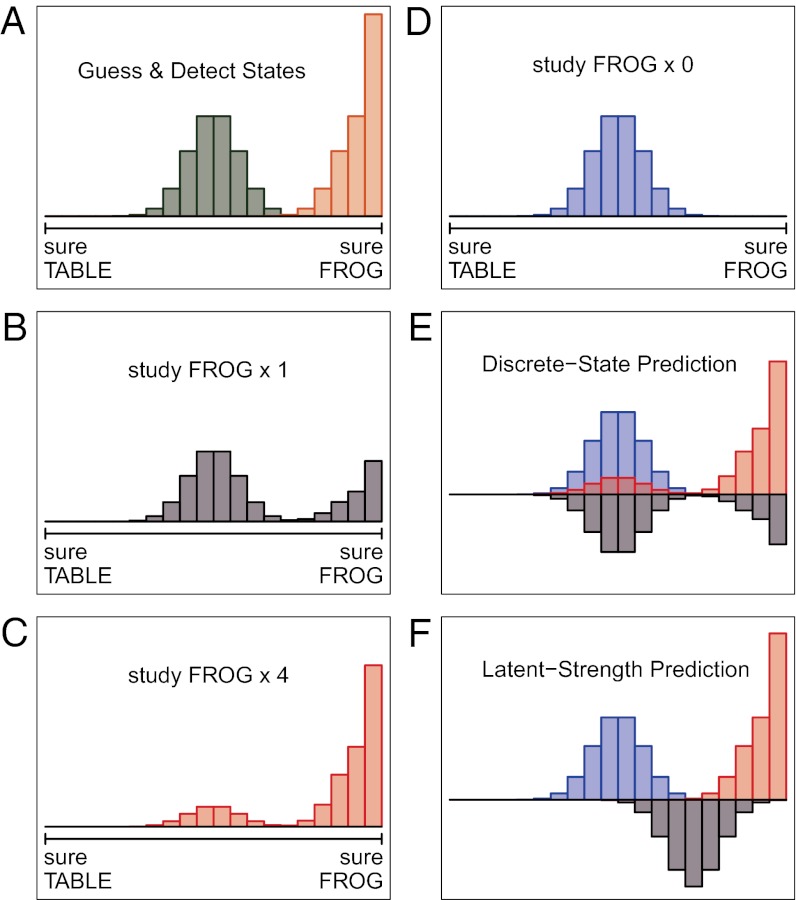
Conditional independence is most easily seen by plotting distributions of confidence ratings themselves rather than ROCs. Fig. 2 shows an example from a two-alternative forced-choice (2AFC) paradigm where the word “frog” was studied. At test, the participant is shown the target “frog” and distracter, in this case “table.” The participant then rates his or her confidence on a scale from “sure table” to “sure frog.” Fig. 2A shows the distribution of confidence for the guess state (green) and the detect state (orange). We have drawn the ratings for guessing as centered, indicating no particular bias. Detection, in contrast, yields responses for the frog end of the scale, because frog was indeed studied. The predictions for the observed confidence ratings are shown in Fig. 2B, and these are a mixture of the confidence ratings in the two states. In the reported experiments, participants may study frog once or four times. Fig. 2B shows the case for once, and there is an equal amount of detection and guessing. Fig. 2C shows the case that frog was studied four times, and here it is far more likely that the participant enters the detect state. Note that when the participants guess, they follow the same distribution as in Fig. 2B, the difference is simply that they enter the guessing state less often. The same is true for the detect state: repetition affects the probability of entering states, not the distribution of responses within a state. We also include a condition in which neither frog nor table was studied; because neither alternative was studied, the participant must guess, as shown in Fig. 2C. We refer to this condition as the zero-repetition condition because frog the target, was studied no times. The utility of this condition is that it allows for direct assessment of the distribution during guessing, should discrete states exist.

Fig. 2.

Model predictions on the distribution of confidence ratings. (A) Distributions of confidence ratings conditional on guessing (green) and detection (orange). (B–D) Discrete-state predictions for the distribution of confidence ratings for the one-, four-, and zero-repetition condition, respectively. (E) A discrete-state model predicts that confidence ratings are a mixture of ratings from detect states and guess states. Increases in study repetition increase the probability that a judgment is from the detect-state distribution. (F) A latent-strength model predicts that as the stimulus is repeated more often, the distribution of confidence ratings shifts toward high-confidence correct responses. Ratings for the zero-repetition and four-repetition condition are shown upright; ratings for the one-repetition condition are facing downward to reduce clutter.

In this report, we present data from all conditions in one panel as shown in Fig. 2E rather than in separate panels, as in Fig. 2 B–D. In Fig. 2E, the color of the histogram indicates the condition (blue for no repetitions, purple for one or two repetitions, and red for four repetitions). For the no-repetition and four-repetition conditions, the histograms are oriented upward. The histograms for the one- and two-repetition conditions are oriented downward to reduce clutter. Also, the data are plotted as if the studied item was always on the right-hand side (i.e., if the studied item was on the left, the confidence ratings are reversed). Fig. 2E shows the predictions for a discrete-state model, and it is simply the combined predictions from Fig. 2 B–D. The key structure is evident in the geometry: the modes of the histogram for the one-repetition condition mirror the modes for the zero- and four-repetition conditions. Fig. 2F shows a latent-strength competitor. Here, the histograms of confidence shift with the number of repetitions. A comparison of Fig. 2 E and F shows the distributional differences between discrete-state and latent-strength models.

Three 2AFC recognition-memory experiments were ran to test the differential predictions in Fig. 2 E and F. These experiments vary in minor procedural differences, as discussed in Methods.

Results

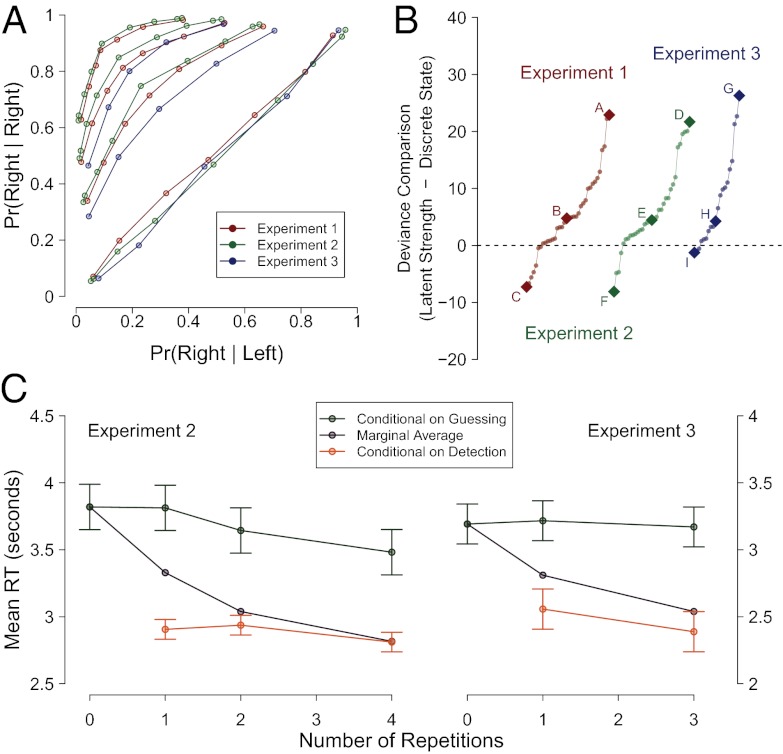
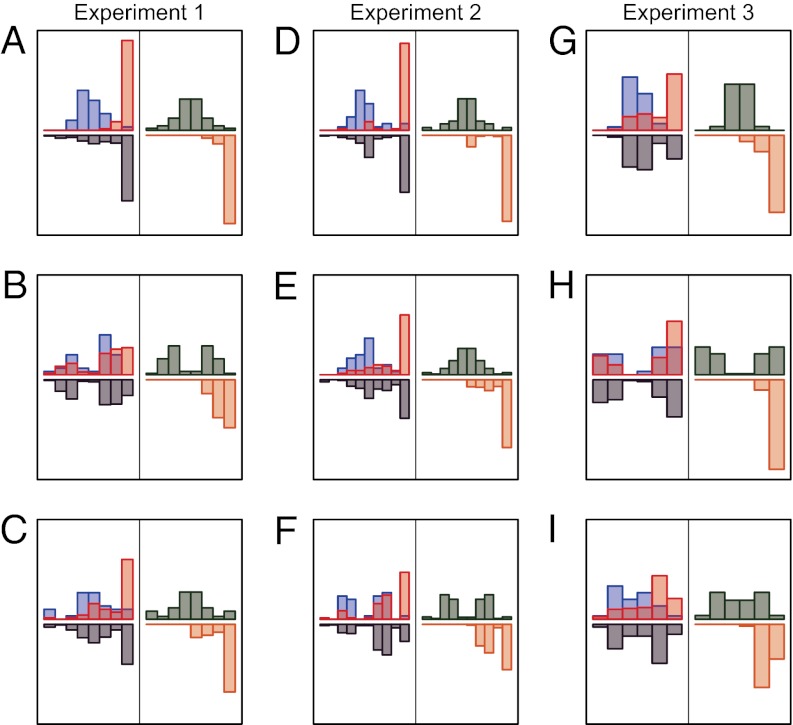
Fig. 3A shows the ROCs for the three experiments across the repetition conditions. As can be seen, these ROCs are orderly and fairly typical for 2AFC paradigms. Fig. 4 shows histograms for nine selected participants (labeled A–I) in the three experiments, and we discuss how we selected these participants subsequently. For each participant, there are two sets of histograms. The left of each histogram shows of confidence ratings for the zero-repetition condition (blue), combined one- and two-repetition conditions (purple), and the four-repetition condition (red). For the zero-repetition condition, the true pattern must be symmetric because the participant has no knowledge which new item is considered the studied one. Hence, deviations from symmetry are necessarily noise and provide a rough guide to range of variation. The right side of each histogram shows discrete-state model estimates of the distributions of confidence for a state (green for guessing, orange for detection). If the discrete-state model holds, the observed confidence distributions for the conditions should be a mixture of these state distributions. By inspection, it seems plausible that the observed distributions in blue, purple, and red are mixtures of the bases in green and orange.

Fig. 3.

(A) Average ROC plots from each repetition condition across each experiment. The curvature and symmetry about the negative diagonal is typical for a 2AFC recognition memory task. (B) Deviance difference values for all subjects. Positive values indicate lower penalized deviance (better fit) for the discrete-state model than the latent-strength model. The plot shows that for a majority of the subjects, the comparison favors the discrete-state model. (C) Mean response time as a function of repetition for experiments 2 and 3. Observed marginal RTs, RTs conditional on detection, and RTs conditional on guessing are shown in purple, orange, and green, respectively. Error bars denote 95% within-subject confidence intervals.

Fig. 4.

Histograms of confidence ratings across repetition conditions for selected participants. (A–C) Best, median, and worst discrete-state fits for experiment 1. (D–F) Best, median, and worst discrete-state fits for experiment 2. (G–I) Best, median, and worst discrete-state fits for experiment 3.

To more formally assess the plausibility of the discrete-state model, we fit it to each participant’s histograms individually (see Methods for full specification of the discrete-state model) and calculated the log-likelihood ratio test statistic G². If the discrete-state model holds, these G² values should be distributed as a χ² distribution with 39, 51, and 18 df for experiments 1, 2 and 3, respectively. The number of participants for which the discrete-state model could be rejected at α = 0.05 is 2 of 36, 1 of 33, and 5 of 20 for experiments 1, 2, and 3, respectively. The total number is 8 of 89, or ∼0.08, which is reasonably close to the expected type I error under the null that the discrete-state model holds.

We competitively fit the discrete-state model against latent-strength alternatives. In fact, we fit several discrete-state and latent-strength models and found that both classes of models did reasonably well. Model-selection outcomes were largely a function of the simplicity of the compared models. Simple discrete-state models outperformed complex latent-strength models and vice versa. Consequently, we kept our focus on discrete-state and latent-strength models that shared the same number of parameters for a given experiment (see Methods for full model specifications). In these cases, we found overall advantages for the discrete-state model. Fig. 3B shows the case for a simple discrete-state and a simple latent-strength competitor with 10, 12, and 7 parameters each for experiments 1–3, respectively. Plotted is the difference in deviance (−2 log L, where L is the maximum likelihood). Positive values indicate that the discrete-state model fits better, and negative values indicate that the latent-strength model fits better. These results show an advantage for simple discrete-state model compared with a simple normal latent-strength model. The results may not necessarily generalize to other classes of latent-strength models, although after extensive experimentation we have yet to find a latent-strength model that outperforms a discrete-state model with the same number of parameters.

There are nine lettered points in the deviance plots corresponding to the nine selected participants whose data are displayed in Fig. 4. These nine participants were chosen as follows: three had data patterns best described by the discrete-state model (A, D, G); three had data patterns best described by the latent-strength model (C, F, I); and three were in between (B, E, H). Hence, the selected participants in Fig. 4 reflect a fair sample for assessing discrete-state and latent-strength predictions.

The above analyses show that the discrete-state model provides not only a good account of the data, but a better account than the latent-strength model. It is worthwhile to consider whether the discrete-state is improved by adding in a latent-strength familiarity component (i.e., a dual-process account). To this end, we compared the discrete-state model to a popular dual-process alternative (16). In the alternative, participants recollect the studied item and respond with highest confidence (the certainty assumption) or, if recollection fails, use familiarity, which is modeled as an equal-variance, normally distributed latent-strength process. We compared the two models by the Akaike information criterion (AIC) (17) and the Bayesian information criterion (BIC) (18) because there was no way to equate the number of parameters (the dual-process alternative is more richly parameterized than the discrete-state model). Across all three experiments, the discrete-state model was selected over the dual-process alternative for 73 and 87 of the 89 participants by AIC and BIC, respectively.

We also constructed a dual-process signal detection (DPSD) model without the certainty assumption. In this version, recollection may lead to a range of responses. The model is a proper generalization of the discrete-state model. What was a guessing component in the discrete-state model is now a familiarity component that is free to vary with repetition. Because this model is a proper generalization of the discrete-state model, the two may be compared with a log-likelihood ratio test statistic G² with 3 df. We found that the restricted discrete-state model could not be rejected for 73 of the 89 participants (80%). Therefore, there is no need to postulate a familiarity mechanism for the vast majority of our participants. Whereas these tests occur on a per-participant basis, it is reasonable to consider the power of them. We performed a small Monte Carlo simulation in which the familiarity of studied items was 0.5 (in d′ units) for the one-, two-, and four-repetition conditions. Recollection was set to match overall accuracy, and the other parameters were set to approximate trends in the data. We found that the discrete-state model without familiarity could be rejected for 439 of 1,000 simulation runs, indicating that the above test has modest power on a per-participant basis. Nonetheless, we observed far less than 44% rejections. We can safely conclude that if there is any familiarity component, it must be less than 0.5 in value.

The discrete-state model also makes a constrained prediction about the time to make a response (RT). Accordingly, RT conditional on a mental state does not depend on stimulus parameters (conditional independence). Hence, conditional mean RT should not vary with the number of repetitions. To assess this prediction, we assigned each response to a mental state by computing the model-based probability that a given response was in the detect state or guess state from the confidence-ratings data. If this probability was greater than 0.5, the response was considered from the detect state; otherwise it was considered from the guess state. Fig. 3C shows the mean RT as a function of repetition for experiments 2 and 3. The points in purple are the observed or marginal RTs plotted as a function of repetition. For both experiments, RT decreases substantially with repetition (decreasing ∼0.9 and 0.6 s in experiments 2 and 3, respectively). The critical sequences are the RTs conditional on a mental state (green for guessing; orange for detection). If the discrete states from the confidence ratings data capture no variance, then these state-conditional RTs should be the same as the marginal RTs. Conversely, if the discrete-state model holds and the state membership is perfectly estimated for each observation, then these state-conditional RTs should be constant across repetition conditions. As can be seen, although there is a slight decrease in state-conditional mean RT with repetition in some cases, the degree of decrease is much less than in the marginal RTs. In experiment 2, marginal RT fell at a rate of 0.238 s per repetition, whereas the conditional RT fell at an average of 0.043 s per repetition, or at ∼18.1% of the marginal rate. Likewise, in experiment 3, marginal and conditional RT fell at 0.206 and 0.032 s per repetition, for a ratio of 15.5%. To assess the statistical significance of the slopes of the conditional RTs, we constructed a one-sample t test. The decrease was not significant [for experiment 2, t(32) = 1.62; for experiment 3, t(19) = 0.92]. A modern approach to assessing these t statistics is to compute the Bayes factor between a model with zero slope and one with nonzero slope (19). These Bayes factors favor the no-slope model by values of 2.2 and 3.92 for experiments 2 and 3, respectively. These findings are impressive because state membership was estimated solely from the confidence ratings without consideration of the response times.

The response time data from experiment 1 is omitted because there is no dependency of RT on repetition. In this case, consideration of RT has no diagnostic value. (We suspect the lack of a repetition effect reflects an idiosyncrasy in the procedure where participants could and did overshoot the “absolutely sure” anchors. When this happened, participants had to move the cursor back to the valid range before depressing the mouse button to indicate their response. In experiment 2, in contrast, the cursor could not be moved outside the valid range of responses.)

Discussion

The vast majority of models in recognition memory are, or contain, continuously valued latent-strength components. We show here that previous rejections of discrete-state models were premature because they were made with recourse to the tenuous certainty assumption. The current experiments test the key property of discrete-state models: conditional independence. The observe data increase the plausibility of conditional independence as follows: (i) mixtures seem apparent by inspection (Fig. 4); (ii) a formal version of the discrete-state model fits acceptably well by a likelihood-ratio test; (iii) this discrete-state model outperforms a latent-strength competitor with the same number of parameters (Fig. 3B) and outperforms a more richly parameterized, popular dual-process alternative; and (iv) mean response times also display the conditional independence property (Fig. 3C). Hence, discrete-state models may serve as as parsimonious descriptions of the structure of recognition-memory responses.

The discrete-state interpretation is not necessarily incompatible with the existence of continuously valued mnemonic signals. However, these signals seemingly affect performance inasmuch as they affect the probability of entering a detect state or guess state. Consequently, an alternative description of recognition memory may focus on factors and mechanisms that affect the probabilities of entering various discrete mental states.

Methods

Experiments 1–3 were approved by the University of Missouri-Columbia Campus Institutional Review Board (IRB), and all participants provided written informed consent. The three experiments were highly similar. The differences across them were in the procedure for collecting confidence ratings. In experiment 1, participants used a mouse to position a cursor on one of 200 points on a scale with anchors of 100% positive. For example, if the words table and frog were presented on the left and right, the left and right anchors were 100% positive table and 100% positive frog, respectively. In experiment 1, three additional intermediary positions were labeled on each side of the scale (“pretty sure,” “believe,” and “guess”) to help calibrate the confidence ratings. In experiment 2, we removed these intermediary positions, and, instead, rewarded participants with points; they risked more points per trial with more extreme confidence ratings. Experiment 3 was a replication of experiment 1, except that confidence was rated with six options (e.g., “sure table,” “likely table,” “guess table,” “guess frog,” “likely frog,” and “sure frog”). Instead of moving a mouse on a continuous scale, participants depressed one of six corresponding keys on a keyboard.

Participants.

Participants were groups of 36, 33, and 20 University of Missouri students who participated for course credit in experiments 1, 2, and 3, respectively.

Design.

The main independent variables were side of presentation of the old item (old item on left/right) and the number of repetitions of the old item at study. These variables were crossed in a within-subject factorial design.

Stimuli.

For experiments 1 and 2, 480 nouns from the MRC Psycholinguistic Database (20). Word length varied between four and nine characters, and Kucera–Francis frequency varied between 1 and 200 occurrences per million (21). For each participant, a subset of 240 items was chosen at random to serve as the studied items, and these items were randomly crossed with experimental factors. For experiment 3, 250 nouns obtained from the University of South Florida Free Association Norms Database (22) served as study items. At test, the distracter for each studied item was a highly associated noun (e.g., if “alligator” was studied, “crocodile” served as a distracter).

Procedure.

The experiments were conducted on Mac OSX computers under the Psychophysical Toolbox (23) in Octave. During study, words were visually displayed, one at a time, at a fixation of 2 s each. At test, participants were shown a studied and new word to the left and right of fixation.

In experiment 2, participants earned and lost points as follows: Let x be the rating for a given trial, −1 ≤ x ≤ 1, where x = −1 and x = 1 correspond to 100% positive responses for the left and right test items, respectively. Let z be an indicator that denotes whether the response was correct (z = 1) or incorrect (z = 0). The total points earned on a trial is z(100|x|) − (1 − z)(100|x| + 400|x|⁵). This expression favors more intermediary responses because the losses for high-confidence responses are disproportionately larger than the gains. Trial-by-trial feedback consisted of presenting participants with the points they had won or lost.

Model Analysis.

We developed and fit a number of discrete-state and latent-strength models. We fit models to each individual separately, and the following development is at the level of a single participant. For experiments 1 and 2, the ratings were continuous; for the purposes of modeling, these are treated here as binned or discrete. Let Y = 1, …, K denote the binned rating, where K is the total number of bins (for experiments 1, 2, and 3, K = 8, K = 10, and K = 6, respectively, and these different values reflect the specifics of the ratings procedure for the experiment). Rating Y_ijs is the rating for the ith replicate in the jth repetition condition for target words presented on side s (s = 0 and 1 for presentations on the left and right, respectively).

Vacuous model.

The most general model that can account for any pattern of data are the multinomial model where there is a separate probability parameter per cell. Let p_jsk be the probability that the person produces the kth rating in the (j, s) combination of conditions, subject to the constraint that probabilities across the K responses sum to 1. In fitting this model, we also constrained the probabilities in the no-repetition condition to be independent to the side of the target. The number of free parameters for this model is (K − 1)(2J − 1), which evaluates to 49, 63, and 25 parameters for the three experiments.

Discrete-state model.

In discrete-state models, the probability of a response is conditional on a mental state. Let d_0k and d_1k denote the probability of the kth response for detecting that the target is on the left and right, respectively; and let g_k denote the same for guessing. Let π_js denote the probability of entering the appropriate detect state for the (j, s) combination of conditions. For the zero-repetition condition, π_js = 0, and it increases with repetition. The discrete-state model is a restriction on the vacuous model, where

We fit a number of different versions of this model with different symmetry constraints. The most parsimonious models (by both AIC and BIC) had the following reasonable symmetry constraints: (i) Detection did not depend on the side of presentation, e.g., π_j0 = π_j1 = π_j. (ii) The response upon entering a detection state was symmetric; i.e., the probability of saying “sure left” for the target on the left is the same as saying “sure right” for the target on the right. Formally, d_0k = d_{1(K −k + 1)} for all k options. (iii) Guessing obeyed a conditionally symmetric structure. There was one parameter, termed “bias,” that was the probability of guessing toward the left or right test item. Conditional on a side, however, the level of confidence was symmetrically distributed. With these three constraints, the number of free parameters is J + K − 2, which evaluates to 10, 12, and 7 for the three experiments. Model parameters were estimated by maximizing likelihood in R with both simplex and conjugate-gradient decent algorithms (24, 25).

Latent-strength model.

In latent-strength models, the participant observes a latent strength, denoted X_ijs on each trial. This strength is compared with K − 1 free criteria to produce responses. We have implemented a number of different parametric forms for latent strength, including the normal, logistic, and gamma. It matters little which is chosen because there is much flexibility in the model with free criteria. We describe here the case for the normal, with variance and mean as free parameters. For the normal, the most parsimonious model contained the following symmetry constraints: (i) The variance of the latent distributions was constant across side and repetition condition—that is, the equal variance model held. (ii) For each repetition condition, the locations of the latent-strength distributions for items presented on the left and right were symmetric about zero. For example, if the mean of the latent-strength distribution for items on the right was 1.5, then the mean for items presented on the left was −1.5 for the same repetition condition. Model parameters were estimated by maximizing likelihood in R with both simplex and conjugate-gradient decent algorithms (24, 25).

Likelihood-ratio test.

The vacuous model is a proper generalization of both the discrete-state and latent-strength model, and is used to test each through a likelihood-ratio test (26). If the nested model holds, either discrete state or latent strength, the corresponding G² statistic is asymptotically distributed as a χ² with 39, 51, and 18 df for the three experiments.

Deviance.

Because the discrete-state and latent-strength models contained the same number of free parameters, the deviance is a suitable statistic for comparing the two. Model comparison results by deviance in this case are the same as by either AIC or BIC. Larger deviance values indicate a poorer fit for a model.