Modeling the dynamics of virus shedding into the saliva of Epstein-Barr virus positive individuals

Abstract

Epstein-Barr virus (EBV) can infect both B cells and epithelial cells. Infection of B cells enables the virus to persist within a host while infection of epithelial cells is suggested to amplify viral output. Data from a recent study have shown that the virus shedding in EBV positive individuals is relatively stable over short periods of time but varies significantly over long periods. The mechanisms underlying the regulation of virus shedding within a host are not fully understood. In this paper, we construct a model of ordinary differential equations to study the dynamics of virus shedding into the saliva of infected hosts. Infection of epithelial cells is further separated into infection by virus released from B cells and virus released from epithelial cells. We use the model to investigate whether the long-term variation and short-term stability of virus shedding can be generated by three possible factors: stochastic variations in the number of epithelial cells susceptible to virus released from infected B cells, to virus released from infected epithelial cells, or random variation in the probability that CD8⁺ T cells encounter and successfully kill infected cells. The results support all three factors to explain the long-term variation but only the first and third factors to explain the short-term stability of virus shedding into saliva. Our analysis also shows that clearance of virus shedding is possible only when there is no virus reactivation from B cells.

1. Introduction

Epstein-Barr virus (EBV) is a human herpesvirus, infecting over 90% of humans worldwide (Rickinson and Kieff, 2001). EBV is transmitted by intimate contact, mainly through saliva (Andiman, 2006). Most people infected with EBV are asymptomatic (i.e. healthy carriers), especially if infected in early childhood (Cohen, 2005). However, EBV can persist inside memory B cells for the lifetime of an infected person. Persistent infection with EBV has been associated with many types of cancers including Burkitt’s lymphoma, Hodgkin’s disease, and nasopharyngeal carcinoma (NPC) (Kieff et al., 2010).

Within a host, EBV can infect both B cells and epithelial cells. Infection of B cells helps the virus to persist within a host (Robertson, 2005). Infection of epithelial cells helps EBV to amplify its population of shedding into the saliva (Hutt-Fletcher, 2005). It has been usually believed that the majority of infected people shed virus into the saliva intermittently, which possibly results from viral suppression by the immune response, and that individuals can be classified into different groups of high, intermediate, or low shedder (Niederman et al., 1976; Yao et al., 1985).

The dynamics of virus shedding in EBV positive individuals are poorly understood, partially due to the lack of a sensitive biological assay to quantify the virus population. Recently, Hadinoto et al. (Hadinoto et al., 2009) have shown that high levels of virus shedding have been constantly detected in the saliva of 8 healthy carriers using sensitive and quantitative assays. They found that the level of virus shedding was quite stable over short periods (days) but varied significantly over longer periods (months/years). They also observed that the levels of latently infected memory B cells were low and remained stable in all subjects. This posed a challenge to an early view that the level of virus shedding is positively correlated with the level of latently infected memory B cells and that individuals could be classified into groups of high, intermediate, or low shedders (Niederman et al., 1976; Yao et al., 1985). A natural question is what regulates the level of virus shedding? Hadinoto et al. proposed a biological mechanism to explain the virus shedding into the saliva. Latently infected memory B cells can differentiate into infected plasma-like B cells within which virions replicate and burst out (lytic infection). Virus released from plasma B cells can infect epithelial cells of the tonsil epithelium. Virus released from infected epithelial cells go through more rounds of epithelial cell infections before being shed into saliva. The amount of virus that is lost due to swallowing can be replenished quickly by virus released from infected epithelial cells (Hadinoto et al., 2009).

Despite the success in modeling HIV, hepatitis B and C, and influenza virus dynamics with/without treatments, very few models have been developed to study EBV dynamics. Mathematical models have been used to study the dynamics of other herpesvirus infection like cytomegalovirus (CMV) (Emery and Griffths, 2000; Wodarz et al., 2007), HHV-6 (Wang et al., 2003) and HSV-2 (Schiffer et al., 2009). In these studies, both deterministic and stochastic approaches have been used to model reactivation of herpesviruses. The dynamics of EBV infection of B cells have been studied using agent-based models (Castiglione et al., 2007; Shapiro et al., 2008). A mathematical model using ordinary differential equations has been developed by Davenport et al. (Davenport et al., 2002) to describe the within-host dynamics of EBV infection. This model was used to study the T cell responses to persistent virus infection. Infection of epithelial cells, which was shown to play an important role in virus shedding, has not been included in these models. In our previous work, we developed mathematical models of within-host dynamics to study EBV long-term infection, the effect of switching infection between B cells and epithelial cells, the evolution of infection, and the age dependence of EBV associated infectious mononucleosis (Huynh and Adler, 2011a,b).

In this paper, we develop a mathematical model to study the dynamics of virus shedding in EBV positive individuals. The model is constructed based on the biological mechanism proposed by Hadinoto et al. that involves reactivation of virus from B cells, infection of epithelial cells and virus shedding into saliva (Hadinoto et al., 2009). We focus the model on the epithelium of the tonsils where virus is replicated and shed into saliva of an infected host. Human tonsil epithelium is heterogenous and contains different cell lines (Perry, 1994). It has been observed that different epithelial-cell lines can have differential susceptibility to EBV in vitro (Imai et al., 1998; Pegtel et al., 2004). Moreover, the structure of the tonsil epithelium is complex and the degree of infiltrated lymphocytes like T cells and B cells varies (Perry, 1994). We thus hypothesize that the number of epithelial cells susceptible to EBV may vary locally depending on the site of the tonsil where the reactivation of lytic infection in B cells occurs. We further discriminate the infection of epithelial cells by virus released from B cells (B-cell virus) from that released from epithelial cells (epithelial cell virus) in our model since epithelial cells can have different susceptibility to EBV of divergent cellular origin (Borza et al., 2004). We also include the control of virus shedding by the immune response in the model. By comparing modeling predictions with the data published in the Hadinoto study, we investigate which factor(s) can explain both the long-term variation and short-term stability of virus shedding into the saliva of EBV positive individuals.

2. Description of data

The experimental data on the levels of virus shedding that we used to compare with our model predictions were published in (Hadinoto et al., 2009). In their study, saliva and blood samples were obtained from 8 EBV positive subjects over months/years. These 8 subjects are healthy volunteers. To study virus shedding in the short term, saliva samples were collected hourly and daily from two subjects, 1 and 2. Saliva samples were collected by mouth rinse with 5 ml of water. Viral DNA was detected using the real time Tagman DNA PCR assay that can detect a single virion in 0.1 ml of saliva. This PCR assay was also used to measure the frequency of latently infected memory B cells from the blood samples.

High levels of virus shedding were consistently detected in the saliva of the 8 EBV positive healthy carriers. Only on a minority of measurements (8 out of 173) was no virus detected in the saliva of these subjects. Subjects 1 and 2 were asked for 8 sequential mouth rinses every 2 minutes (approximately equal to the time it takes for people to swallow). The shedding of virus into the saliva was replenished at a very fast rate such that the level of shedding remained stable even after these subjects had repeated mouth rinses (Hadinoto et al., 2009). Calculations in the study (Hadinoto et al., 2009) showed that the number of productively infected B cells in the tonsil, which were reactivated from latent infection, was too small to account for the high level of virus shedding observed in the saliva. Data from the studied subjects also showed that the level of virus shedding within an individual was relatively stable (variation < 1 log) over short periods (hourly, and daily for 5 days) but varied significantly (up to 5.5 logs) over long periods (months/years). A more detailed description of the data can be found in (Hadinoto et al., 2009). We compare our models to the published virus shedding data of subjects 1, 2 and 3.

3. Model

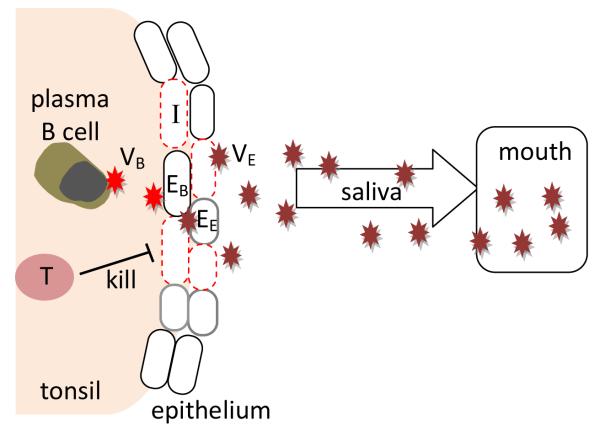
Our model of the dynamics of EBV shedding (Figure 1) tracks the number of infected epithelial cells in the tonsil epithelium (I), the number of cytotoxic T cells (T) responding to EBV infection, and the level of virus shedding (V_E). Viruses produced in the tonsil are shed into saliva. In this model, we only track the virus shedding from epithelial cells since it has been shown that most of virus shedding found in the saliva has the characteristics of being produced by infected epithelial cells (Jiang et al., 2006). The model consists of 3 differential equations

$$\begin{array}{cc}\hfill \frac{dI}{dt}& =I_B+I_E-kIT-\delta I\hfill \\ \hfill \frac{dT}{dt}& =\theta \frac{I}{K+I}T-dT\hfill \\ \hfill \frac{d{V}_E}{dt}& =pI-c{V}_E.\hfill \end{array}$$ (3.1)

Figure 1.

A model of virus shedding into the saliva. Reactivation of latently infected B cells gives rise to plasma B cells that initiate virus production (V_B). B-cell virus can infect cells in the tonsil epithelium to amplify the population of virus shedding into the saliva. Infected epithelial cells (red dashed) can be killed by effector T cells.

Epithelial cells can be infected by both the virus released from B cells (B-cell virus) and the virus released from epithelial cells (epithelial-cell virus) (Hadinoto et al., 2009). I_B represents the infection of epithelial cells by virus released from the lytic activation of memory B cells and is assumed to take on the following form

$$I_B=f\propto E_B{V}_B.$$ (3.2)

We assume that B-cell virus, V_B, infects cells of the tonsil epithelium at the reactivation site, E_B, at a rate α. We fix V_B because the level of latently infected memory B cells remains stable over time within a host and there is no correlation between the level of these B cells and the level of virus shedding (Hadinoto et al., 2009). The function f determines the time when latently infected memory B cells differentiate into plasma cells and activate the lytic infection to replicate and release viruses. This activation function is assumed to take on two values in our simulation, either 0 when there is no lytic activation or 1 when there is an activation. We note that f may not be binary but rather continuous, accounting for partial activation of latently infected B cells at any time. I_B is built in as a parameter in our model and how the variation in this number affects the dynamics of viral shedding is investigated in the next section.

Infection of epithelial cells by virus released from epithelial cells is described by the term I_E, which takes on the following form

$$I_E=\beta E_E{V}_E.$$ (3.3)

Epithelial-cell virus, V_E, can infect epithelial cells at a rate β. We assume that epithelial cells that are susceptible to B-cell virus and epithelial-cell virus, E_B and E_E, are different since different cell lines may have different susceptibility to EBV of divergent cellular origin and the two types of virus express different levels of glycoproteins which can affect the virus effciency in infecting epithelial cells (Borza and Hutt-Fletcher, 2002; Borza et al., 2004).

Infected epithelial cells have the life span of 1/δ and are killed by CD8⁺ T cells, T, at a rate k. A large number of CD8⁺ T cells have been shown to exist in the tonsil of EBV positive patients (Hislop et al., 2005). We assume that infected epithelial cells can stimulate the proliferation of CD8⁺ T cells in the tonsils. Proliferation of CD8⁺ T cells saturates as a function of the available infected cells, where K is the number of infected cells at which proliferation is half maximal. CD8⁺ T cells die at a rate d. Free virus is produced by infected epithelial cells at a rate p and cleared at a rate c. A summary of parameter definitions and values can be found in Table 1.

Table 1.

Parameters used in model (Equation 3.1) and simulations. Initial conditions used in all simulations: I₀ = 100, T₀ = 1 × 10⁶ for all 3 subjects and V₀ = 3:5 × 10², 1 × 10⁴, and 8 × 10³ for subjects 1, 2 and 3, respectively

Parameter	Definition	Value	Units
f(t)	Activation function	see text	no unit
α	Infection rate per B-cell virus	fitted	day−1 virion−1
EB	Number of epithelial cells susceptible to−1B-cell virus	see text	cells
Vb	Number of virus released by B cells	7.3 × 104 (Hadinoto et al., 2009)	virions
β	Infection rate per epithelial-cell virus	fitted	ml day−1 virion−1
EE	Number of epithelial cells susceptible to epithelial-cell virus	fitted	cells
k	Rate of infected cells killed by effector T cells	fitted, see text	cell−1 day−1
δ	Death rate of infected cells	0.24 (Huynh and Adler, 2011a)	day−1
θ	Rate of effector T cell proliferation stimulated by infected cells	fitted	day−1
K	Number of infected cells when T cell proliferation is half maximal	1000 (Huynh and Adler, 2011a)	cells
d	Death rate of effector T cells	0.0095 (Hadinoto et al., 2008)	day−1
P	Virus production rate by infected epithelial cells	173 (Hadinoto et al., 2009)	virions ml−1 day−1 cell−1
c	Death rate of virus	2 (Shapiro et al., 2008)	day-1

4. Results

4.1. Clearance of virus shedding is possible only when there is no virus reactivation from B cells

Analyzing the system of Equations (3.1) shows that the free-shedding equilibrium, where all three state variables equal zero (I* = 0, T* = 0, and V* = 0), exists if and only if there is no epithelial cell infection by virus released from B cells (I_B = 0). This equilibrium is stable when

$$\frac{\beta E_{Ep}}{c\delta }<1.$$

Existence of the free-shedding equilibrium is possible only when there is no virus reactivation from latently infected memory B cells (fV_B = 0) or when the tonsil epithelium is not susceptible to infection by B-cell virus (αE_B = 0). Assuming that EBV positive individuals always have some cells susceptible to B-cell virus in the tonsil epithelium, clearance of virus shedding into the saliva is only possible when there is no virus reactivation from B cell infection. The condition for stability of the shedding-free steady state implies that when virus reactivation from B cells is off (f = 0 and hence I_B = 0), the rates at which the infected epithelial cells and virus are cleared need to be greater than the rate at which the virus is spreading through infection of epithelial cells in order for no virus to be shed into the saliva.

4.2. Regulation of virus shedding within a host

The structure of the tonsil epithelium is complex and includes different types of epithelial cells. The number of epithelial cells that are susceptible to EBV infection may vary randomly depending on the sites of the tonsil epithelium where virus reactivation from B cells occurs (Hadinoto et al., 2009). Infected cells in the tonsil can be killed by CD8⁺ T cells responding to the infection. How effcient T cells control the spread of infection may depend on the probability that these effector CD8⁺ T cells encounter infected cells. We use our model to investigate if these two random effects, the availability of epithelial cells and CD8⁺ T-cell killing, can explain the variation in the level of virus shedding into saliva that has been observed within EBV positive individuals.

Spacial variation in the degree of infiltrated lymphocytes like T cells and B cells and also in the different epithelial cell lines can lead to local variation in the number of susceptible epithelial cells over time at the site of the tonsil where the reactivation of lytic infection in B cells occurs. We thus further break the first random effect down into two cases where random variation can occur either in the number of epithelial cells susceptible to B-cell virus (E_B) or in the number of cells susceptible to epithelialcell virus (E_E) at the sites of occurring lytic infection in B cells. These two cases are studied independently to determine which one better describes the observed dynamics of virus shedding from the data.

4.2.1. Variation in the number of epithelial cells susceptible to virus released from B cells

Depending on the site of the tonsils where virus reactivation from latently infected B cells occurs, the number of epithelial cells that can be infected by B-cell virus may vary. We first assume that there is virus reactivation from B cells at any time and hence the activation function, f (Equation 3.2), takes on the value 1. The number of epithelial cells susceptible to B-cell virus, E_B, is assumed to vary randomly due to the random site of activation while keeping the number of epithelial cells susceptible to epithelial-cell virus, E_E, fixed. We fix the values of a few parameters in Table 1 from the literature. Using Berkeley-Madonna (http://www.berkeleymadonna.com), we estimate the parameters α, βE_E, k, θ, and the random values of E_B by fitting our model to the viral shedding data from three EBV positive subjects published in Hadinoto et al. (Hadinoto et al., 2009).

For each subject, we estimate n – 5 values of E_B, where n is the number of data points. At any time, reactivation of virus replication from B cells may occur at random sites of the tonsil where E_B may vary. We assume that there is a change in the value of E_B whenever there is a change of direction (from increase/decrease to decrease/increase) in the kinetics of virus shedding from the data, unless the decrease or increase is small (< .7 log). For example, we assume that E_B = E_B1 when t < 15 and E_B = E_B2 when 15 ≤ t < 63 for subject 1. Hence, we estimate 12 values of E_B for subject 1, 9 values for subject 2, and 10 values for subject 3. The best-fit parameter values for each patient are listed in Table 2.

Table 2.

Best-fit parameter values obtained from comparing our model (Equation 3.1) including variation in the number of epithelial cells susceptible to B-cell viruses with the viral shedding kinetic data from three EBV positive subjects. The value of root mean square (RMS) for each fit is listed in the last row.

Parameter	Units	Subject 1	Subject 2	Subject 3
α	ml day−1 virion−1	6.73 × 10−5	8.80 × 10−4	2.3 × 10−4
βEE	ml cell day−1 virion−1	1.47 × 10−4	1.58 × 10−4	2.20 × 10−4
k	cell−1 day−1	2.39 × 10−6	2.53 × 10−5	3.34 × 10−5
θ	day−1	2.06 × 10−2	3.25 × 10−2	8.79 × 10−3
E B1	cells	244	1491	15
E B2	cells	106	100852	1941
E B3	cells	2917	98104	156
E B4	cells	79	9264	38
E B5	cells	1488	953	252
E B6	cells	81527	654535	29
E B7	cells	1017	432	3
E B8	cells	69669	134410	344
E B9	cells	81337	7311	18
E B10	cells	11		2741
E B11	cells	66
E B12	cells	5914
RMS		0.30	0.40	0.18

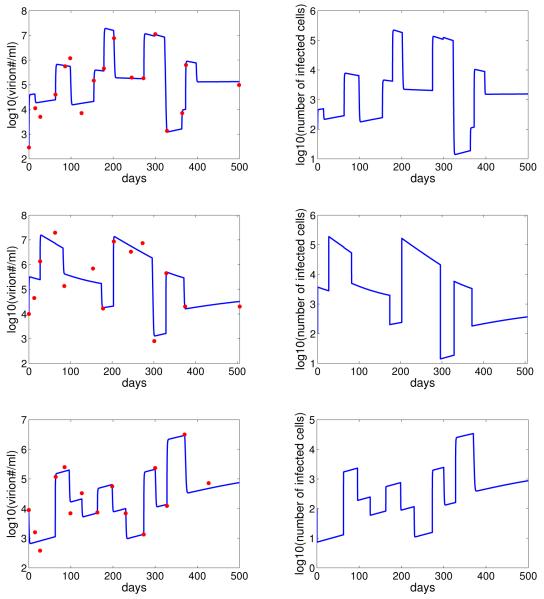
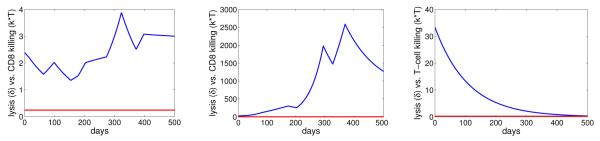
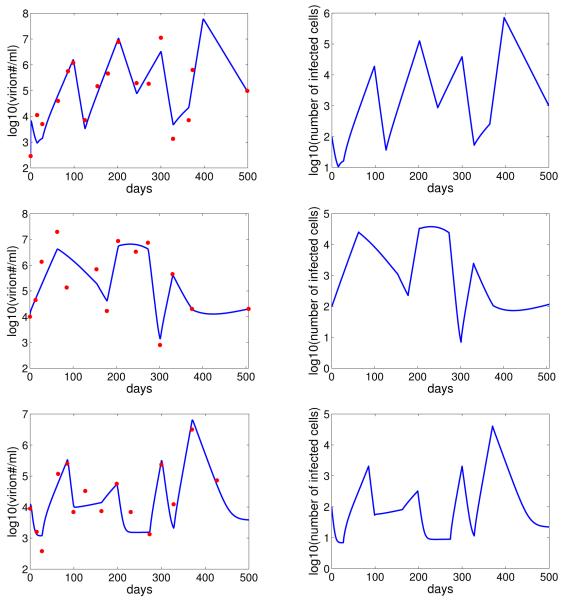
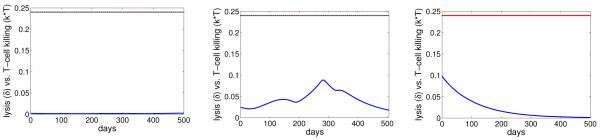
Our model provides good fits to the viral shedding kinetic data (Figure 2). A change in the number of epithelial cells susceptible to B-cell virus, E_B, leads to a rapid change in the level of infected epithelial cells and virus shedding. When E_B stays the same, the levels of infected cells and virus shedding are relatively stable. This short-term stability of virus shedding is due to a balance between the spread of infection and the regulation by the immune response. In fact, infected cell death is dominated by CD8⁺ T-cell killing in this case, i.e. kT > δ (Figure 3).

Figure 2.

Comparison between the model (with random variation in the value of E_B) and the virus shedding kinetic data (red) for three EBV positive subjects. The corresponding level of infected epithelial cells is showed in the right column.

Figure 3.

The rates of infected cell death by lysis, δ (red), versus CD8 T-cell killing, kT (blue), for 3 subjects in the case of random variation in E_B.

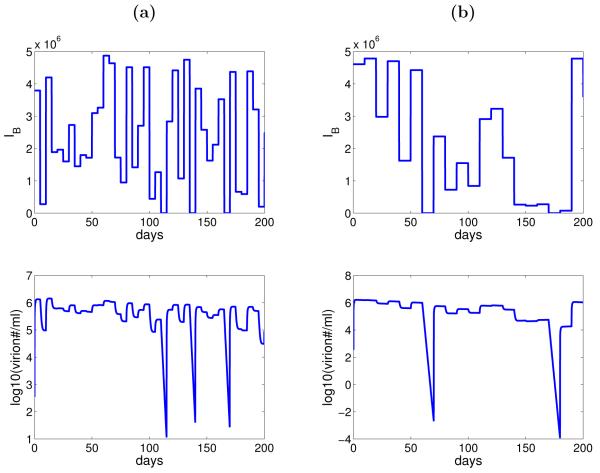
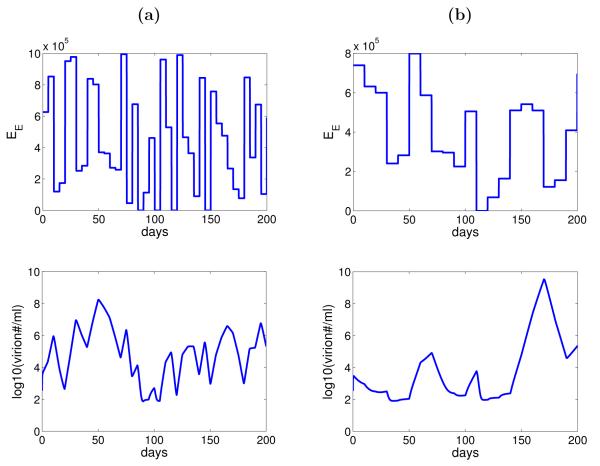
Without estimating the different levels of E_B needed for viral changes, we also explore the effect of random variation in the number of epithelial cells infected by B-cell virus, I_B, on the dynamics of viral shedding through numerical simulation. We assume that the activation function, f, takes on the value 0 (lytic activation from B cells is “off”) with the probability of 8/173 and 1 (lytic activation is “on”) with the probability 1 – 8/173 using the result that no virus shedding was detected in 8 out of 173 measurements from the study (Hadinoto et al., 2009). Whenever f = 1, the parameter E_B is assumed to take on a value from a uniform distribution between 0 and 10⁶, which is approximately the number of epithelial cells in the tonsil epithelium that may be lytically infected (Hadinoto et al., 2009). Stochastic simulation of the model (Equation 3.1) shows that variation in the number of epithelial cells infected by B-cell virus can generate the random variation in the level of virus shedding within a host showed in the data (Figure 4). The values for f and E_B are redrawn every 5 days (Figure 4(a)) and 10 days (Figure 4(b)). When the period of no lytic activation from B cells is short, for example t = 5 days, infection of epithelial cells by epithelial-cell virus is enough to sustain the virus shedding in the saliva. A longer period of no lytic activation from B cells, for example t = 10 days, is required for no virus to be detected.

Figure 4.

Numerical simulation of the model (Equation 3.1) with random variation in the number of epithelial cells susceptible to B-cell virus. (a) The values of f and E_B (I_B = f_αE_BV_B) are redrawn every 5 days. (b) The values of f and E_B are redrawn every 10 days. Other parameters are listed in Table 1 and 2 (subject 1).

4.2.2. Variation in the number of epithelial cells susceptible to virus released from epithelial cells

In this case, we fix the number of epithelial cells infected by B-cell virus, I_B, and assume random variation in E_E, the number of epithelial cells susceptible to epithelial-cell virus. Using Berkeley-Madonna, we estimate the parameters I_B, β, k, θ, and various values of E_E by fitting our model to the viral shedding data from the three positive EBV subjects.

Similar to the case of E_B, we assume that there is a change in the value of E_E when there is a change of direction (from increase/decrease to decrease/increase) in the kinetics of virus shedding from the data, unless the decrease or increase is small (< .7 log). We estimate 12 values of E_E for subject 1, 9 values for subject 2, and 10 values for subject 3. The best-fit parameter values for each patient are listed in Table 3. In this case, the estimated values of I_B are small for all three subjects. This implies B-cell virus is responsible for only a small number of infected epithelial cells. Most of virus shedding into the saliva comes from the spreading of infection between epithelial cells. This result is in agreement with the hypothesis proposed by Hadinoto et al. (Hadinoto et al., 2009). However for most of the time, the short-term stability is not observed (Figure 5). This is because the death of infected cells is dominated by natural lysis rather than killing by CD8⁺ T cells, i.e. δ > kT (Figure 6).

Table 3.

Best-fit parameter values using the model with variation in the number of epithelial cells susceptible to epithelial-cell viruses. The value of root mean square (RMS) for each fit is listed in the last row.

Parameter	Units	Subject 1	Subject 2	Subject 3
IB	cells day−1	1.68	1.35	2.20
β	ml day−1 virion−1	5.06 × 10−8	3.32 × 10−8	1.81 × 10−8
k	cell−1 day−1	1.80 × 10−9	2.45 × 10−8	3.22 × 10−6
θ	day−1	1.74 × 10−2	2.10 × 10−2	1.50 × 10−3
E B1	cells	3135	66309	0
E B2	cells	35955	40733	1273
E B3	cells	79021	34485	23
E B4	cells	374	96825	781
E B5	cells	82234	51301	944
E B6	cells	26290	0	6
E B7	cells	72956	100660	1584
E B8	cells	140	37039	11
E B9	cells	63038	44766	1601
E B10	cells	123027		450
E B11	cells	39336
E B12	cells	34213
RMS		0.44	0.50	0.35

Figure 5.

Comparison between the model (with random variation in the values of E_E) and the virus shedding kinetic data for three EBV positive subjects. The corresponding level of infected epithelial cells are showed in the right column.

Figure 6.

The rates of infected cell death by lysis, δ (red), versus CD8 T-cell killing, kT (blue), for 3 subjects in the case of random variation in E_E.

Similarly, we explore the effect of random variation in the number of epithelial cells susceptible to epithelial-cell virus, E_E, on the dynamics of virus shedding using stochastic simulation of the model (Equation 3.1). The parameter E_E is assumed to take on a value from a uniform distribution between 0 and 10⁶, with the probability of 8/173 taking on the value of 0. The results (Figure 7) show that random variation in E_E can generate the variation in the level of virus shedding. However, it is more diffcult to obtain the short term stability in comparison to the case of E_B, especially for short periods between redrawn values of E_E (Figure 7, column (a)). When there are no epithelial cells susceptible to epithelial-cell virus (E_E = 0 and hence I_E = 0), the virus shedding can still be detected (Figure 7 (a) and (b)). This result confirms our analysis in the previous section that clearance of virus shedding is possible only if there is no infection of epithelial cells by B-cell virus (I_B = 0).

Figure 7.

Numerical simulation of the model (Equation 3.1) with random variation in the number of epithelial cells susceptible to epithelial-cell virus. (a) The value of E_E is redrawn every 5 days. (b) The value of E_E is redrawn every 10 days. Other parameters are listed in Table 1 and 3 (subject 1).

4.2.3. The role of CD8⁺ T cell response

Random variation in the level of virus shedding may also be induced by the random probability that CD8⁺ T cells encounter and kill infected cells in the tonsil epithelium (Hadinoto et al., 2009). To investigate this hypothesis, we assume that I_B and I_E are constant rates and only apply random variation to the parameter k, which includes the probability at which CD8⁺ T cells encounter and kill infected cells. Assuming k obeys to the gamma distribution, the probability distribution function for k has the form

$$f\left(k\right)=k^{p-1}\frac{e(-k∕\lambda )}{\Gamma \left(p\right){\lambda }^p},$$ (4.1)

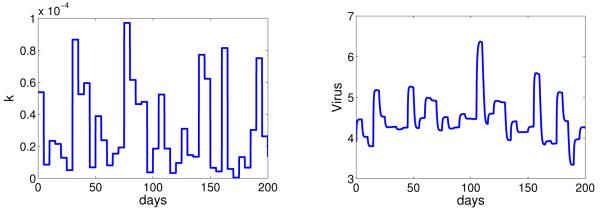
where p is the shape parameter and λ is the scale parameter. We let the mean of k (E(k) = pλ) be the estimated value from subject 1 (Table 2). We draw the values of k from the gamma distribution (Equation 4.1) every 5 days and examine its effect on the dynamics of virus shedding (Figure 8).

Figure 8.

Numerical simulation of the model (Equation 3.1) with random variation in the rate at which CD8⁺ T cells encounter and kill infected cells. We let the mean value of k be the estimated value for subject 1, E(k) = pλ = 8.33 × 10⁻⁴, with p = 1.5. Other parameters are listed in Table 1 and 2 (subject 1).

A decrease or increase in the value of k quickly leads to an increase or decrease in the level of virus shedding, respectively. When there is no change in the value of k, the level of virus shedding remains relatively stable. This stochastic simulation shows that random variation in k could also generate the pattern of virus shedding that was observed in the EBV positive subjects.

5. Discussion

We have developed a mathematical model to study the dynamics of virus shedding in EBV positive individuals. The model focuses on the tonsil epithelium, and tracks infected epithelial cells, CD8⁺ T-cell response and virus shedding. EBV positive individuals shed high level of virus into saliva. In consistence with Hadinoto et al. (Hadinoto et al., 2009), our result shows that infection of epithelial cells can account for the high level of shedding detected in saliva of infected hosts. Despite the high level of virus shedding, the level of infected epithelial cells remains low (Figure 2) compared to the number of epithelial cells (~ 10¹⁰) in the tonsil epithelium (Hadinoto et al., 2009). This low level of infected epithelial cells may explain why it remains diffcult to detect infected epithelial cells within infected individuals. Moreover, our analysis shows that viruses produced by reactivated B cells are enough to sustain epithelial cell infection and hence the virus shedding. Clearance of virus shedding (negative detection) can happen only when there is no virus reactivation from B cells. This result highlights the importance of EBV latent infection in B cells.

The level of virus shedding is relatively stable over short periods (hours/days) but varies significantly over long periods (months/years) within an individual (Hadinoto et al., 2009). Using our model we investigate if variations in the number of infected epithelial cells or in the probability at which CD8⁺ T cells encounter and kill infected cells can generate this pattern of shedding within a host. Because different epithelial cell lines may have differential susceptibility to EBV of different cell origins (Imai et al., 1998; Pegtel et al., 2004), we further explore the effects of epithelial cell infection by B-cell virus and epithelial-cell virus independently through studying the effects of random variations in the number of epithelial cells susceptible to B-cell virus (E_B) and to epithelial-cell virus (E_E) at the sites of occurring lytic infection in B cells. We compare the effects of these two factors through fitting the models to virus shedding data from three EBV healthy carriers, and also through stochastic simulation. Both of them can describe the long-term variations in the level of virus shedding. The model with random variation in E_B, however, can capture the stability of virus shedding over the short periods better. Since the two models have the same number of estimated parameters for each subject, we compare the fits through the root mean square (RMS) values. In comparison to the model with variation in E_E, the RMS values of the model with variation in E_B are smaller. However, the differences are not significant to conclude which one fits the data better from a statistical viewpoint.

In the case of random variation in E_B, the terms I_B and I_E can be numerically compared at any time using the estimated parameters in Table 1 and 2. We found the term I_B dominates the term I_E throughout the time and drives viral production. This implies that the high level of virus shedding detected in saliva is mainly induced by the infection of epithelial cells by B-cell virus. This result is supported by experimental studies showing that B-cell virus is more effcient at infecting epithelial cells than epithelial-cell virus (Borza and Hutt-Fletcher, 2002; Borza et al., 2004). For the case of random variation in E_E, the term I_E dominates the term I_B, which implies B-cell virus infects only a small number of infected epithelial cells. Most of virus shedding into the saliva comes from the spreading of infection between epithelial cells. This result is in agreement with the hypothesis proposed by Hadinoto et al. (Hadinoto et al., 2009). We obtained big differences in the estimated values of E_B and E_E for both cases (Tables 2 and 3). Whether differences in the susceptibility of epithelial cell lines to EBV can be this big in vivo requires further experimental studies. We also note that the assumption of two distinct types of susceptible epithelial cells to EBV may be oversimplifying since there could be a gradient of susceptibility to EBV within the population of epithelial cells depending on the HLA presentation (Borza et al., 2004). The variation in E_B or E_E may be due to different spatial access of virus to epithelial cells. The dataset that we used to fit the models is rather limited in size with only three subjects and 14 to 17 data points for each subject over a period of 500 days. The objective of our data fit is to test different possible mechanisms for regulating virus shedding rather than provide an accurate estimate of the number of epithelial cells. More subjects and data points are needed to achieve better analysis and fits of the models, especially when analyzing the short-term stability of virus shedding.

Beside the important role of epithelial cells, we have shown that CD8⁺ T-cell response can also contribute to the regulation of virus shedding. When the estimated values of k are large in the case of variation in E_B (Table 2), infected cell death is dominated by CD8⁺ T-cell killing and the short-term stability is achieved (Figure 2). When the estimated values of k are small in the case of variation in E_E (Table 3), CD8⁺ T-cell induced killing is a minor factor contributing to cell death. Thus, the short-term stability is diffcult to achieve in this case (Figure 5).

Random variation in the probability at which CD8⁺ T cells encounter and kill infected cells is shown to be able to capture both the long-term variation and the short-term stability of virus shedding. Our model has assumed that CD8⁺ T cells exist in the tonsil epithelium, can proliferate and recruit more CD8⁺ T cells upon stimulation by infected cells. There are other approaches to model T-cell response. Even though a large number of CD8⁺ T cells have been shown to exist in the tonsils of EBV positive patients (Hislop et al., 2005), little is know regarding the kinetics of these cells. CD8⁺ T cell data are needed to verify model predictions.

In our model, we examined the effect of one of the three factors on the dynamics of virus shedding while keeping the other two fixed. For example, when we applied the random variation to the number of epithelial cells susceptibility to B-cell virus, we assumed that the number of epithelial cells that are susceptible to epithelial-cell virus and the rate at which CD8⁺ T cells encounter, recognize, and kill an infected cell are fixed. However, in reality random variations in more than one factors should contribute simultaneously to the variability in virus shedding. This is not surprising because V_B and E_B are included in the same term I_B in our model. Variation in V_B or E_B would have similar effects on virus shedding.

We only consider the three listed factors in this study but there are other competing hypotheses that can also be considered. We have assumed that the level of B-cell virus, V_B, is fixed since the level of latently infected B cells is quite stable over time within each subject. Further, there is no correlation between the level of virus shedding and the level of latently infected B cells. The level of reactivated B cells from latent infection, however, may be low and prone to stochasticity. This may lead to variation in the level of V_B which can subsequently account for variability in the level of virus shedding. In Supplementary Materials, tested a model that assumes a fixed level of susceptible epithelial cells and stochastic variation in the level of B-cell virus. We showed that variation in V_B can also generate the long-term variation and short-term stability of virus shedding.

Differences in the susceptibility of epithelial cells to EBV infection or in the effectiveness of CD8⁺ T-cell killing may affect not only the level of virus shedding within individuals but also the risk of individuals to develop EBV associated diseases. Indeed, different studies have linked people with specific types of HLA-I and HLA-II alleles, which affect CD8⁺ T cell response and individual susceptibility to EBV infection respectively, to infectious mononucleosis and EBV associated cancers including Hodgkin’s disease and nasopharyngeal carcinoma (Alexander et al., 2001; Hildesheim et al., 2002). Further experimental studies to understand the susceptibility of different epithelial cell lines to EBV infection and the kinetics of CD8⁺ T-cell responses to EBV in the tonsil epithelium would help understand the risk of developing the virus associated diseases within an EBV positive individual.