Transmission of Force in the Lumbosacral Spine During Backward Falls

Abstract

Study Design

Mathematical model, combined with and verified using human subject data.

Objective

(1) To develop and verify a lumped-parameter mathematical model for prediction of spine forces during backward falls; (2) to use this model to evaluate the effect of floor stiffness on spine forces during falls; and (3) to compare predicted impact forces with forces previously measured to fracture the spine.

Summary of Background Data

Vertebral fractures are the most common osteoporotic fractures and commonly result from falls from standing height. Compliant flooring reduces the force at the ground during a backward fall from standing; however, the effect on spine forces is unknown.

Methods

A 6-df model of the body was developed and verified using data from 10 human subjects falling from standing onto 3 types of compliant floors (soft: 59 kN/m, medium: 67 kN/m, and firm: 95 kN/m). The simulated ground forces were compared with those measured experimentally. The model was also used to assess the effect of floor stiffness on spine forces at various intervertebral levels.

Results

There was less than 14% difference between model predictions and experimentally measured peak ground reaction forces, when averaged over all floor conditions. When compared with the rigid floor, average peak spine force attenuations of 46%, 43%, and 41% were achieved with the soft, medium, and firm floors, respectively (3.7, 3.9, 4.1 kN vs. 6.9 kN at L4/L5). Spine forces were lower than those at the ground and decreased cranially (4.9, 3.9, 3.7, 3.5 kN at the ground, L5/S1, L4/L5, and L3/L4, respectively, for the soft floor).

Conclusion

Lowering the floor stiffness (from 400 to 59 kN/m) can attenuate peak lumbosacral spine forces in a backward fall onto the buttocks from standing by 46% (average peak from 6.9 to 3.7 kN at L4/L5) to values closer to the average tolerance of the spine to fracture (3.4 kN).

Vertebral body fractures are the most common type of osteoporotic fractures.^1,2 These fractures represent a growing public health concern because the incidence is projected to increase as the population ages.³ Vertebral fractures are associated with substantial increases in back pain, functional limitation, disability, and mortality.^4,5 Falls are a major contributing factor to the occurrence of osteoporotic fractures^6; 41% of vertebral fractures in older men are associated with falls from standing height or lower.⁷ The most common vertebral fracture site for older men is the lumbosacral spine, which represents 56% of all cases.⁷ Falls from standing height or lower also account for between 8% and 26% of spinal cord injuries,^7,8 and more than two-thirds of these injuries occur in older adults.⁸

The risk of vertebral fracture in a backward fall depends, by definition, on a “factor of safety.” This factor of safety is defined as the ratio of the force that will typically result in failure under a loading configuration similar to that applied in the fall (i.e., tolerance) divided by the peak-applied force. Previous studies have measured the force applied to the buttocks in subinjurious backward falls in human subjects.⁹ The compressive force required to cause fracture of lumbar vertebrae has been determined by testing isolated cadaver spine segments.^10–17 However, the peak forces occurring at the lumbosacral spine during a backward fall are not known, and this is a barrier to the development of injury prevention strategies.

An intervention that has been suggested to reduce the incidence of fall-related fractures is the use of compliant or low-stiffness flooring.^9,18,19 In a previous experimental study conducted by a subset of this study’s authors, human subjects fell from standing onto floors of various stiffnesses.⁹ Impact forces at the buttocks decreased with decreases in floor stiffness; however, the effect on spine forces was not addressed. To determine the effect of floor stiffness on spine forces experimentally, direct measurement of spinal component loads would be necessary; however, these are difficult to measure even during benign activities in vivo.^10,11 Numerical models have been used to study the loads generated in the human spine during various activities,^12–15 and this method has also been used to study spinal forces during trauma.^16–18

Some of the previous models have been complex, have simulated multiple degrees of freedom at each joint, and have incorporated anatomic details such as the rib cage, lumbar muscles, viscera, facet joints, and intervertebral discs.^12,14–16 Axial spine forces are related to fracture risk^19–23; therefore, they are of primary interest in this study. It was our objective to develop an appropriate model to allow examination of the effect of floor stiffness on axial loading at various levels of the spine during a fall. We had access to a unique set of data to incorporate into our model. These human subject-specific data from our previous experimental study provided a level of verification for the present computational model.⁹ No previous mathematical modelling or experimental studies have examined spine forces resulting from a backward fall onto the buttocks.

Accordingly, the specific objectives in this study were (1) to develop and verify a lumped-parameter model to predict intervertebral forces at several levels of the lumbosacral spine during backward falls from standing, (2) to evaluate the effect of floor stiffness on these forces, and (3) to examine how these compare with the axial force associated with fracture of the spine.

MATERIALS AND METHODS

Overview

To simulate a backward fall onto the buttocks, a dynamic, 1-dimensional, 6-df lumped-parameter model of the upper body and pelvis was created. The model was verified by comparing it with experimental data from 10 human subjects in our previous experimental study who fell onto their buttocks.⁹ The model was further verified by simulating a fall from a height of 3 m, which can result in lumbar spine fractures,²⁴ and ensuring that the predicted forces were consistent with the lumbar spine tolerance. Finally, we used the verified model to examine the effect of floor stiffness on peak spine forces by simulating a fall from standing onto the buttocks.

Model

We implemented our lumped-parameter model of the upper body and the pelvis in Matlab (Matlab version 7.0; Math-works, Natick, MA). It included 6 rigid bodies representing the upper body, L4, L5, sacrum, pelvis, and the skin overlying the ischial tuberosities (Figure 1). Reference masses of the rigid bodies (Table 1) were based on values used in previous lumped-parameter models,^16,27 on scaled anatomic drawings,²⁵ and on segmented cadaver measurements.^26,28 Those at the lumbosacral spine represent the body’s entire transverse cross section at the corresponding spinal level. We scaled these masses to those for the 10 subjects using the ratio of the total body mass of each subject (Table 2) and that of the 50th percentile male.^34,53 The joints between these rigid bodies were defined as the L3/L4, L4/L5, L5/S1, sacroiliac joints, and the soft tissue overlying the ischial tuberosities (i.e., buttocks) at the inferior portion of the model (Figure 1). Each joint was assumed to act as a linear spring and linear damper acting in parallel (i.e., Voigt viscoelastic model³⁵). The stiffness and damping coefficients for L3/L4, L4/L5, L5/S1, and the sacroiliac joints were assigned values on the basis of previously published experiments that measured the experimental response of cadaveric spine material (Table 1).

Figure 1.

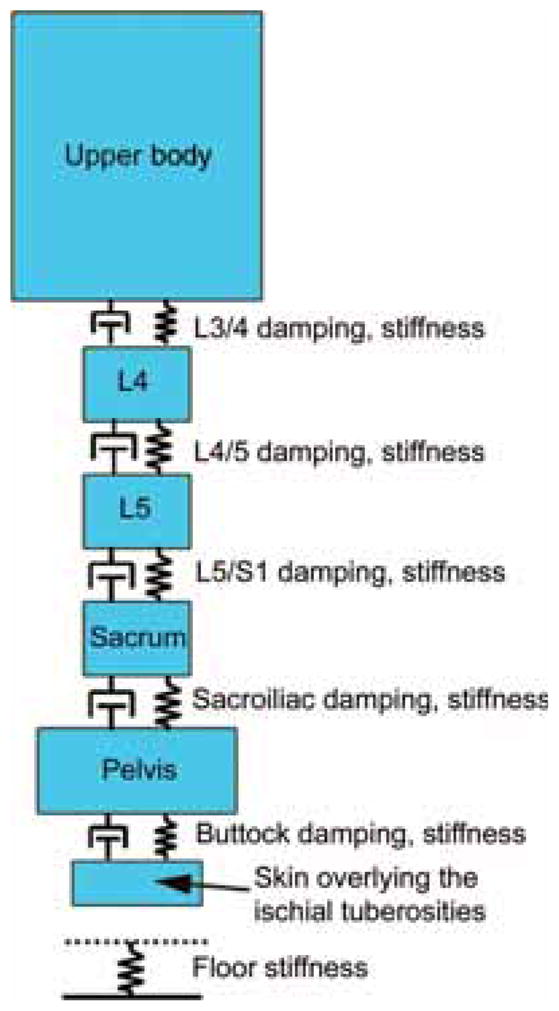
Schematic of the lumped-parameter model used to calculate spine forces during a backward fall onto the buttocks. The upper body, L4, L5, sacrum, pelvis, and skin overlying the ischial tuberosities were modeled as masses separated by linear springs and dampers, which represented the L3/L4, L4/L5, L5/S1, sacroiliac joints, and the soft tissue overlying the ischial tuberosities (buttocks). The floor was represented as a linear spring.

TABLE 1.

Summary of Model Parameter Values

Parameter		Value	References
Mass	Pelvis	16 kg	16, 25, 26
	L4	2.5 kg	25, 27, 28
	L5	1.8 kg
	Sacrum	0.7 kg
	Upper body	33 kg
	Skin overlying the ischial tuberosities	0.01 kg	Estimate
Stiffness	L3/L4	2749 kN/m	54
	L4/L5	2399 kN/m
	L5/S1	3503 kN/m
	Sacroiliac	1050 kN/m	55
	Floor	59 kN/m (soft)	9
		67 kN/m (medium)
		95 kN/m (firm)
		400 kN/m (rigid)	31
Damping	L3/L4, L4/L5, L5/S1, sacroiliac	237 Ns/m	56

Mass values at the lumbosacral spine represent masses of transverse cross sections at each axial level. Model parameter values were scaled using each subject’s body mass and that of the 50th percentile male.⁵³ Floor stiffnesses for the soft, medium, and firm floors were measured experimentally⁹ and the stiffness of the “rigid” floor was set to a value equivalent to that of a gymnasium floor.³¹

TABLE 2.

Summary of the Subject-Specific Parameters Used in the Model

Subject	Height (cm)	Mass (kg)	Buttock Stiffness (kN/m)		Buttock Damping (kNs/m)
			Average	SD	Average	SD
1	171.5	77.3	175.0	35.4	3.07	0.55
2	182	80.9	305.0	98.0	5.25	1.11
3	183	92.3	*	*	*	*
4	187	117.3	189.0	10.2	3.24	0.23
5	179	75.0	*	*	*	*
6	168.5	68.2	181.0	18.9	2.99	0.30
7	185	91.4	128.0	12.2	1.82	0.16
8	177	71.4	152.0	26.9	3.01	0.68
9	164.3	62.3	85.2	15.3	1.75	0.30
10	175	71.4	229.0	80.4	3.92	1.27
Across-subject average	177.2	80.7	180.5		3.13
Across-subject SD	7.4	16.0	17.2		0.25

Stiffness and damping of the soft tissue overlying the ischial tuberosities (buttocks) were calculated using equations 1 to 4 and the experimental force-time response of subjects falling onto the firm floor (stiffness of 95 kN/m).

^*Buttock stiffness and damping could not be calculated for subjects 3 and 5. Mean values were used.

We calculated subject-specific stiffness and damping coefficients for the buttocks of each participant using vibration analysis³⁶ in an approach similar to that described previously for determining the effective stiffness and damping of the soft tissues overlying the hip in falls to the side.³⁷ In these calculations, we assumed that the body behaves as a single rigid mass (Figure 2), and we used the experimental force-time records of each participant falling onto the firm floor (95 kN/m, the most stiff floor that was examined experimentally). The effective mass at the buttocks was assumed to equal the total body mass and the effective stiffness and damping was assumed to be dominated by the spring and damper of the buttocks. Briefly, we used the time between the first 2 peaks in the force response (Figure 2) to characterize the damped natural frequency of the system (ω_d)

Figure 2.

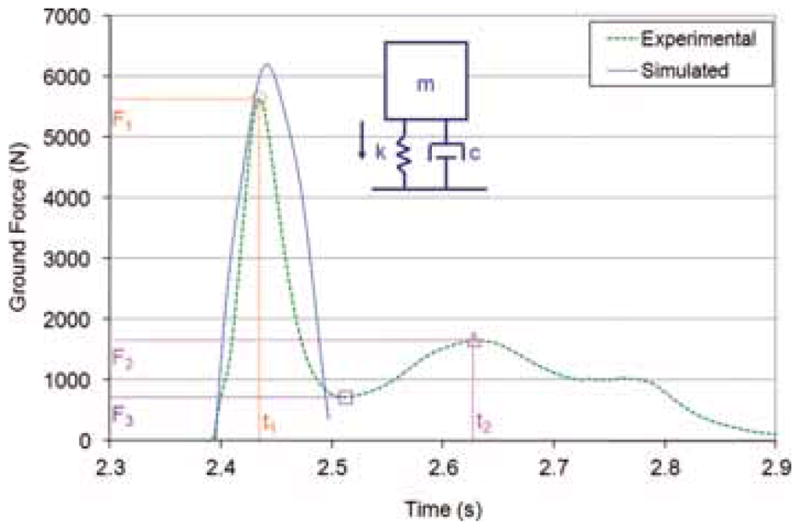
Sample graph of the experimental ground force versus time for a typical trial (subject 4 falling onto the firm floor, stiffness of 95 kN/m, trial 2) showing key points for buttock stiffness and damping co-efficient calculations (first peak, second peak, and the valley between the first 2 peaks are shown with a circle, triangle, and square, respectively). The inset diagram shows the model used to determine buttock stiffness and damping (m: body mass, k: buttock stiffness coefficient, c: buttock damping coefficient). The simulated ground force for this trial is also shown (only the first peak in ground force was simulated, which was created with the 6-df model shown in Figure 1, not the single df model shown in the inset diagram).

$${\omega }_d=\frac{2\pi }{t_2-t_1}.$$ (1)

We then calculated the logarithmic decrement (δ) as follows:

$$\delta =ln\left(\frac{F_1-\frac{F_2+F_3}{2}}{F_2-\frac{F_2+F_3}{2}}\right).$$ (2)

Where F₁ and F₂ are the first 2 peaks in the force (Figure 2) and F₃ is the valley between the 2 peaks. We then calculated buttock stiffness (k) and damping (C) as

$$k=\left(\frac{{\omega }_d^2}{1-\frac{\delta }{2\pi }}\right)m$$ (3)

and

$$C=\frac{\delta }{\pi }\sqrt{km}$$ (4)

where m is the total body mass of the subject (Table 2). These parameters were calculated for all successful trials of each subject (between n = 4 and n = 10 trials per subject), and the average values were used in the lumped-parameter model.

We modeled the floors with linear springs because they were found experimentally to exhibit negligible damping.³⁸ We assigned values to the spring constants on the basis of previous indentation tests with a servohydraulic materials testing machine for the soft, medium, and firm floors.³⁸

Verification

For model verification, the falls of 10 human subjects who participated in our previous experimental study were simulated.⁹ In that previous study, subjects fell backward after being suddenly released (by means of a tether and electromagnet) from a lean angle of 15° from the vertical. The subjects landed on a floor covered with various thicknesses of ethylene vinyl acetate foam rubber mats. Three different thicknesses of ethylene vinyl acetate mats (4.5, 7.5, or 10.5 cm) were modeled with corresponding stiffnesses of 95, 67, and 59 kN/m, respectively. To verify the model, we compared model predictions of peak ground reaction forces and rise times of these forces with experimental results. Four falls for each of the 3 foam floors were simulated for each subject. We determined the impact fall velocity of each fall from the vertical velocity of a skin surface marker on the spinous process of L3 at the initiation of the ground reaction force.⁹ These data were previously collected using an 8-camera, 240-Hz motion measurement system (Eagle system and EVaRT 4.6 software Motion Analysis Corp., Santa Rosa, CA). The average impact velocity was 3.5 (SD 0.32) m/s.

As a further verification of the model results, we compared the spine forces predicted from our model for falls from 3 m (and corresponding to a 7.8 m/s impact velocity) with the forces that have been shown to cause fracture experimentally. In these simulations, the floor stiffness was set to 400 kN/m, which is representative of that of the basic unpadded surface of a gymnasium floor.³¹ These conditions have been reported in a study of accident reconstructions as the falling height necessary to exceed the strength of the lumbar spine (3.3 ± 1.2 kN and 4.2 ± 1.7 kN for compression velocities of 3 vertebra segments of the lumbar spine of 0.01 and 2.5 m/s, respectively³⁹) when falling onto the buttocks on a rigid floor.²⁴ Simulated peak joint compression velocities of 3 vertebra segments of the spine were calculated for each subject, and corresponding tolerance values were interpolated between those reported for loading rates of 0.1 and 2.5 m/s³⁹ to incorporate the increasing tolerance of the spine with loading rate due to the viscoelastic nature of bone tissue.⁴⁰

Effect of Floor Stiffness on Vertebral Forces

We examined the effect of floor stiffness on forces at the buttocks and at various spinal levels by simulating each of the 10 participants falling (in this case, with the same velocity of 3.5 m/s) onto floors of 4 different stiffnesses. We included 3 floor stiffnesses used in our experimental study (59, 67, and 95 kN/m) and a “rigid” floor with a stiffness of 400 kN/m.³¹

Comparison of Vertebral Forces With Tolerance Values

Vertebral forces for the falls onto floors of different stiffnesses were compared with the rate-dependant tolerance of the lumbosacral spine to loading. Simulated peak joint compression velocities of 3 vertebra segments of the spine were calculated for each subject and floor stiffness and corresponding tolerance values were interpolated between those reported for loading rates of 0.1 and 2.5 m/s.³⁹ “Factors of safety” for each floor type were calculated as the ratio of the spine tolerance force to the average peak spine force.

RESULTS

Model

The average buttock stiffness and damping were 180.5 (SD 17.2) kN/m and 3.13 (SD 0.25) kNs/m, respectively (Table 2). Within-subject standard deviations during the repeated trials for each subject were between 5% and 35% of mean values for stiffness and between 7% and 32% of mean values for damping. Stiffness and damping coefficients were not calculated for subject 3, because a second peak in the force-time response was not observed, and for subject 5, who exhibited a very small second peak in force 80 ms after the initial peak, whereas other subjects exhibited approximately 200 ms between these peaks. Average stiffness and damping coefficients of the remaining 8 participants were used in the model for these 2 subjects.

Verification

In our simulations of subject-specific falls from standing, the average error in peak ground force was −11% (SD 13) (Figure 2); the model more often overpredicted than under-predicted the peak ground forces, but both situations were observed. The average absolute error in peak ground force was 13% (SD = 11). The average error in time to peak ground force was 13% (SD = 7); the model more often underpredicted than overpredicted time to peak ground force, but again both situations were observed.

In our simulation of subjects falling from 3 m and impacting the ground with a velocity of 7.8 m/s, the average peak spine forces at L3/L4, L4/L5, and L5/S1 were 13.6, 14.5, and 15.0 kN, respectively. The average peak intervertebral compression velocities at L3/L4, L4/L5, and L5/S1 were 0.49 ± 0.05, 0.60 ± 0.07, and 0.43 ± 0.05 m/s, respectively. As the most relevant tolerance data we identified are for 3 vertebra, 2 intervertebral disc segments³⁹, the comparable compression velocity is equal to 2 times the intervertebral compression velocity—approximately 1.0 m/s. The tolerance of the spine at this compression velocity is estimated at 3.6 ± 1.4 kN (interpolated assuming a linear relationship between previously reported values of 3.3 ± 1.2 kN at 0.01 m/s and 4.2 ± 1.7 kN at 2.5 m/s³⁹). Therefore, the simulated peak spine forces were higher than the spine forces that have been reported to cause fractures in axial impact experiments.

Effect of Floor Stiffness

For the 3.5 m/s impact velocity, peak ground and spine forces increased with an increase in floor stiffness (Figures 3 and 4). Decreasing floor stiffness had a more pronounced effect on decreasing peak forces at the spine than at the skin surface. Average peak ground forces were reduced by 26%, 35%, and 37% for the firm, medium, and soft floors, respectively, compared with the rigid floor (5.8 ± 0.7 kN, 5.1 ± 0.6 kN, 4.9 ± 0.6 kN vs. 7.8 ± 1.0 kN) (Figure 4). Average peak forces at L5/S1 were reduced by 40%, 44%, and 46% for the firm, medium, and soft floors, respectively, compared with the rigid floor (4.3 ± 0.5 kN, 4.0 ± 0.5 kN, 3.9 ± 0.5 kN vs. 7.2 ± 1.1 kN). Average peak forces at L4/L5 were reduced by 41%, 43%, and 46% for the firm, medium, and soft floors, respectively, compared with the rigid floor (4.1 ± 0.5 kN, 3.9 ± 0.5 kN, and 3.7 ± 0.5 kN vs. 6.9 ± 1.0 kN).

Figure 3.

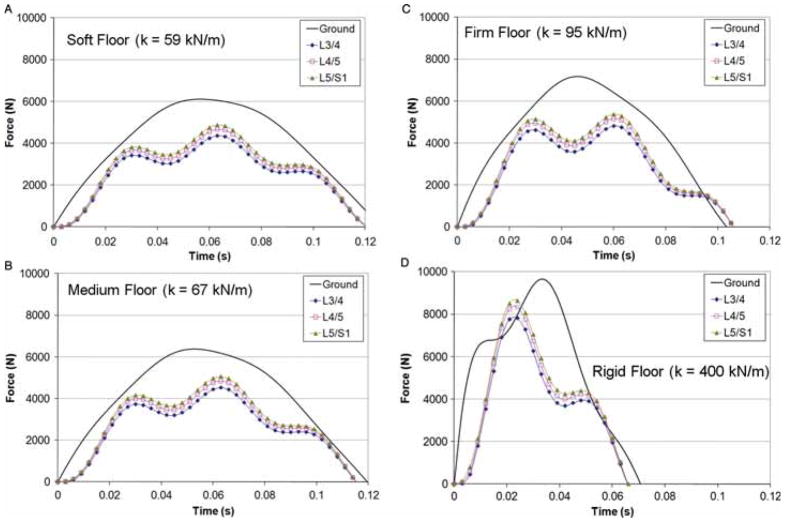
Sample-simulated ground reaction and spine forces for a subject (number 4) falling with a velocity of 3.5 m/s onto floors with stiffnesses of 59 kN/m (soft) A, 67 kN/m (medium) B, 95 kN/m (firm) C, and 400 kN/m (rigid) D.

Figure 4.

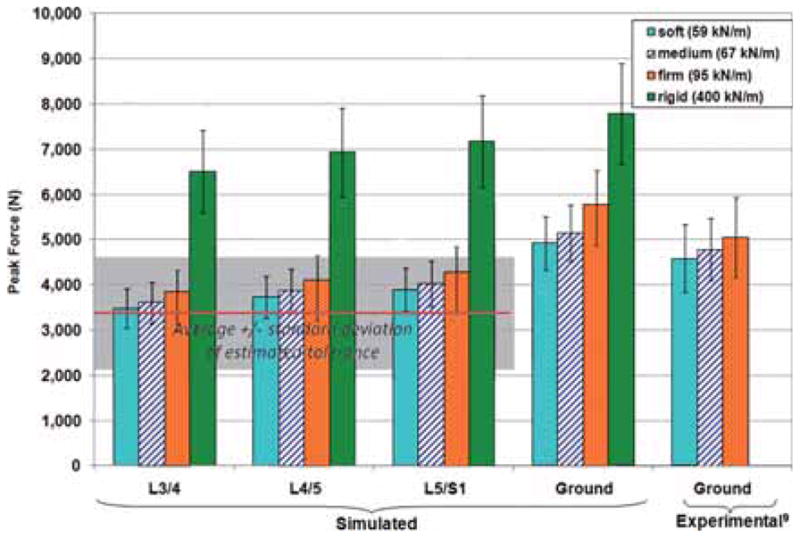
Average peak simulated ground and spine forces for 10 subjects falling at 3.5 m/s onto floors of 4 different stiffnesses. Standard deviations are shown with error bars. Experimentally measured average peak ground forces are also shown,⁹ which correspond to impact velocities between 2.5 and 4.1 m/s. The average tolerance (+/− 1 SD, shown with the shaded area) of the lumbosacral spine for a compression velocity of 0.2 m/s is also shown, which was extrapolated between tolerance values for compression velocities between 0.01 and 2.5 m/s.³⁹

Average peak spine forces were lower than the average peak ground forces (Figure 4), with the lowest force at the most cranial intervertebral level modelled (L3/L4). For the soft floor, average peak spine forces at L3/L4, L4/L5, and L5/S1 were 3.5, 3.7, and 3.9 kN, respectively, and the average peak ground force was 4.9 kN (Figure 4). On average, L5/S1 forces were 21%, 22%, 26%, and 8% lower than ground forces for the soft, medium, firm, and rigid floors, respectively; L4/L5 forces were 3% to 4% lower than L5/S1 forces; and L3/L4 forces were 6% to 7% lower than L4/L5 forces.

Comparison With Spine Tolerance

The average peak intervertebral compression velocities at L3/L4, L4/L5, and L5/S1 were 0.08 ± 0.01, 0.09 ± 0.01, and 0.06 ± 0.01 m/s, respectively, for falls onto the compliant floors and 0.19 ± 0.02, 0.23 ± 0.03, and 0.16 ± 0.02 m/s, respectively, for falls onto the rigid floor. For comparison with tolerance data, which used 3 vertebra, 2 intervertebral disc segments of the spine, comparable compression velocities are equal to 2 times the intervertebral compression velocities—approximately 0.2 m/s and 0.4 m/s for compliant and rigid floors, respectively. The tolerance of the spine at these compression velocities is estimated at 3.4 ± 1.2 kN (interpolated between previously reported values of 3.3 ± 1.2 kN at 0.01 m/s and 4.2 ± 1.7 kN at 2.5 m/s³⁹). Average peak spine forces for the rigid floor are greater than the average estimated tolerance of the spine, whereas those for the compliant floors are greater than but closer to the tolerance of the spine (Figure 4). The average spine force “factor of safety” for falls onto the rigid floor is 0.5, whereas those for falls onto the firm, medium, and soft floors are 0.8, 0.9, and 0.9, respectively.

DISCUSSION

Accurate models of impact loading are required to understand vertebral fracture risk in backward falls, and they should likely play a key role in developing injury prevention devices, such as compliant flooring. Although compliant flooring has been shown to reduce ground forces resulting from a backward fall, it was not clear how such reductions would influence spine forces and the risk of vertebral fracture in the osteoporotic population. If significant reductions in fracture risk are feasible with changes in floor compliance that do not concurrently encumber balance and mobility, it may be feasible to cover floors in high-risk environments, such as senior’s centers and hospital wards, with compliant flooring⁹ or to implement the use of padded underwear for high-risk individuals, similar to hip protectors.⁴¹ Although previous dynamic lumped-parameter and finite element models have examined spine forces in response to whole-body vibrations^12–15 and pilot ejections,^16–18 this is the first time that any model has been used to examine spine forces resulting from a backward fall onto the buttocks.

The compression tolerance of the spine varies with loading rate⁴⁰ and with bone properties, such as bone mineral density.^42–46 Experimental studies of isolated vertebral bodies (fresh and fixed in formalin)^42,45 and of functional spinal units with and without posterior elements (fixed in formalin)^43,44,46 have demonstrated significant relationships between the compressive tolerance of the spine and bone mineral density. However, it is known that formalin fixation alters the mechanical properties of the spine.³³ The magnitude of this correlation for fresh functional spinal units with posterior elements, which most closely simulates the in vivo loading environment, is unclear. In this study, the estimated compression tolerance for the lumbosacral spine (3.4 ± 1.2 kN) is based on experimental data from fresh specimens from the thoracolumbar spine (with posterior elements) with bone mineral density measurements of 0.683 ± 0.091 g/cm².³⁹ Using the World Health Organization criteria for diagnosis of osteoporosis,²⁹ the average specimen in this study is osteoporotic. Using this tolerance, average peak spine forces in this study correspond to “factors of safety” of 0.9, 0.9, and 0.8 for the compliant floors (soft, medium, and firm, respectively) and a factor of 0.5 for the rigid floor. These factors of safety would increase for subjects with healthy bone, and they would decrease for subjects with extreme cases of osteoporosis. This study has shown that although a backward fall from standing height onto a rigid floor (stiffness of 400 kN/m, similar to that of a gymnasium floor) could cause a lumbar spine fracture, floors with reduced stiffness (between 59 and 95 kN/m) are more likely to prevent lumbar spine fractures from occurring.

On average, peak spine forces decreased cranially by 3% to 4% from L5/S1 to L4/L5 and by 6% to 7% from L4/L5 to L3/L4. Decreasing spine forces for more cranial levels is consistent with previously reported computational models^15,17 and our intuitive expectation that more intervening discs would remove more energy and force. Clinically, compressive vertebral injuries in the osteoporotic population and those associated with falls are most frequently observed in the mid-thoracic area and in the transition from the thoracic to the lumbar areas (i.e., at L1).^30,32 However, it is likely that the vertebra that fails does so due to the maximum stress being exceeded rather than due to the maximum force. The vertebral dimensions decrease moving cranially, so the effective stress (force normalized by area) may be increasing as one moves cranially. Furthermore, the facet joints of the lumbar spine are oriented vertically, whereas those in the thoracic spine are angled anteriorly by 30°.⁴⁷ This transition at T12/L1 may also result in higher susceptibility of fracture at L1 as the axial forces transmitted through the vertebral body and facet joints of T12 are passed primarily through the vertebral body of L1 while the forces are shared with the facet joints cranially, resulting in increased stress at this level. The present model is highly simplified but brings several key factors related to compliant flooring into focus. To perform detailed study of the effects of the change in load sharing at the thoracolumbar junction of the spine, a detailed finite element model would be required.

Average calculated stiffness and damping coefficients for the buttocks in the present model (180 kN/m and 3.13 kN·s/m, respectively) are in the range of those previously reported using a computational model of whole-body vibration that incorporated rotation of the pelvis and spine (153 kN/m and 3.15 kN·s/m).¹³ To compare the present stiffness with values from experimental literature, Young’s modulus was calculated using values for buttock contact area^48,49 and length from the skin surface to the ischial tuberosities⁵⁰ from the literature. Using this method, the present buttock stiffness corresponds to Young’s modulus of 628 kPa. This is greater than a previously reported range of Young’s moduli for human in vivo buttock tissue (47.5–64.8 kPa)⁵⁰; however, the previous study loaded tissues quasistatically whereas this study involved dynamic tissue loading. As biological tissues are viscoelastic, stiffness is known to be rate dependent. The present buttocks Young’s modulus is within the range of moduli that were reported for porcine in vitro gluteus maximus tissue tested at frequencies between 5 and 30 Hz (146–5961 kPa)⁵¹; however, this study applied very small peak strains (0.1% vs. 22% in this study), and the tissue properties and boundary conditions applied in this study may be less representative of the human in vivo condition. The porcine in vitro study also reported damping coefficients for cylindrical samples of tissue between 40 and 556 N·s/m. To account for the geometric differences between these studies, the damping coefficients were converted to damping ratios (by dividing them by the critical damping). By assuming a mass of the buttock tissue in this study (according to geometric assumptions listed earlier), a damping ratio of 1.99 was calculated and this was within the range of those for porcine gluteus maximus tissue (1.42–3.09).

Although this model is a 1-dimensional simplification—its inertial, stiffness, and damping characteristics were based on values from the published literature—it simulated the response of the body in the primary direction of interest for the current research question (vertical), and it was verified using human subject data. This simple model allowed us to examine the effect of floor stiffness on spine forces during a passive backward fall from standing in a straightforward manner. The present model produced errors in peak force and time to peak force that were below 14%, which was reasonable for the experimental and numerical context. Some of the assumptions that may have contributed to this error include the lack of rotational degrees of freedom in the model and the assumption that the mass of the viscera moves as part of the rigid bodies of the spine. Because the model lacked rotational degrees of freedom, the effects of posture at impact could not be evaluated. It is expected that addition of sagittal plane posture and spine lordosis and kyphosis would reduce peak axial compression forces and increase peak shear forces, particularly in the lower lumbar spine as the L5/S1 joint in the upright neutral posture is 19° more forward than the L4/L5 joint whereas the L1/L2 joint is only 3° more forward than the T12/L1 joint.⁵² However, osteoporotic vertebral fractures are compressive or wedge-type fractures,³⁰ which are primarily caused by axial forces, not shear forces.²³ Although the assumptions inherent to this model may have altered the absolute values of spine forces, the reductions in spine force at each level resulting from decreased floor stiffness is expected to remain unchanged for a constant orientation of the lumbar spine. Also, the absolute values of spine forces were compared with the values of spine tolerance for falls onto rigid flooring at a higher speed that have been shown to result in spine fractures (7.8 m/s). Although the simulated spine forces were higher than experimental spine tolerances (15.0 vs. 3.6 kN), this model represents a worst-case scenario of the axial forces in the spine during a fall onto the buttocks. Therefore, the present simple, straightforward model provides a general quantitative measure of the expected reductions in spine forces with the use of compliant flooring. Further research is required to determine the effect of posture and vertebral orientation on forces in the spine.

In conclusion, a dynamic lumped-parameter model for prediction of intervertebral forces in the lumbosacral spine during a backward fall from standing was developed and verified against experimental data from human subjects with errors less than 14%. Using this model, we showed that lowering the floor stiffness by amounts that are consistent with currently available floors (from 400 to 59 kN/m) can attenuate peak lumbosacral spine forces in a backward fall from standing by 46% (average peak from 6.9 to 3.7 kN at L4/L5) to values closer to the estimated tolerance of the spine to fracture (3.4 kN).³⁹ Decreasing floor stiffness had a more pronounced effect on decreasing peak forces at the spine than at the skin surface; for the soft floor, average peak ground and spine (L4/L5) forces were reduced by 37% and 46%, respectively, compared with the rigid floor (4.9 ± 0.6 kN vs. 7.8 ± 1.0 kN and 3.7 ± 0.5 kN vs. 6.9 ±1.0 kN, respectively). Average peak forces at L5/S1 were 8% lower than the ground forces for the rigid floor and 21% to 26% lower than the ground forces for the compliant floors. On average, peak forces at L4/L5 were 3% to 4% less than those at L5/S1 and peak forces at L3/L4 were 6% to 7% less than those at L4/L5. Further research is required to identify flooring types and characteristics that are likely to prevent vertebral body fractures due to backward falls without impeding balance and mobility.

Key Points.

• A dynamic lumped-parameter model for prediction of intervertebral forces in the lumbosacral spine during a backward fall from standing was developed and verified against experimental data from human subjects with errors less than 14%.

• Lowering the floor stiffness (from 400 to 59 kN/m) attenuated peak lumbosacral (L4/L5) spine forces by 46%, on average from 6.9 ± 1.0 kN to 3.7 ± 0.5 kN, to values closer to the average dynamic tolerance of the spine to fracture (3.4 kN).

• Decreasing floor stiffness had a more pronounced effect on decreasing peak forces at the spine than at the skin surface. Average peak ground forces were reduced by 26%, 35%, and 37% for the firm (95 kN/m), medium (67 kN/m), and soft (59 kN/m) floors compared with the rigid (400 kN/m) floor (5.8 ± 0.7 kN, 5.1 ± 0.6 kN, 4.9 ± 0.6 kN vs. 7.8 ± 1.0 kN). Average peak forces at L5/S1 were reduced by 40%, 44%, and 46% for the firm, medium, and soft floors compared with the rigid floor (4.3 ± 0.5 kN, 4.0 ± 0.5 kN, 3.9 ± 0.5 kN vs. 7.2 ± 1.1 kN).

• Peak forces were lower at the more cranial than caudal spine units, averaging 3% to 4% lower at L4/L5 than at L5/S1 (3.7 ± 0.5 kN compared with 3.9 ± 0.5 kN for the soft floor) and 6% to 7% lower at L3/L4 than at L4/L5 (3.5 ± 0.4 kN for the soft floor).