Towards a unified model of pavlovian conditioning: short review of trace conditioning models

Abstract

There are three basic paradigms of classical conditioning: delay, trace and context conditioning where presentation of a conditioned stimulus (CS) or a context typically predicts an unconditioned stimulus (US). In delay conditioning CS and US normally coterminate, whereas in trace conditioning an interval of time exists between CS termination and US onset. The modeling of trace conditioning is a rather difficult computational problem and is a challenge to the behavior and connectionist approaches mainly due to a time gap between CS and US. To account for trace conditioning, Pavlov (Conditioned reflexes: an investigation of the physiological activity of the cerebral cortex, Oxford University Press, London, 1927) postulated the existence of a stimulus “trace” in the nervous system. Meanwhile, there exist many other options for solving this association problem. There are several excellent reviews of computational models of classical conditioning but none has thus far been devoted to trace conditioning. Eight representative models of trace conditioning aimed at building a prospective model are being reviewed below in a brief form. As a result, one of them, comprising the most important features of its predecessors, can be suggested as a real candidate for a unified model of trace conditioning.

Variety of the computation mechanisms of trace conditioning

Theoretical preview

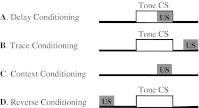
There are four basic paradigms of the classical conditioning (see Fig. 1) where presentation of a conditioned stimulus (CS) or context typically predicts an aversive outcome such as a shock. A conditioned response (CR) to a CS alone is taken as evidence that association between the CS and the unconditioned stimulus (US) has been learned. Delay and trace procedures differ in the temporal relationship between CS and US. In delay conditioning CS and US normally coterminate, whereas in trace conditioning some time passes between a CS termination and an US onset. The delay conditioning is usually not hippocampus-dependent, while trace and context conditioning typically result in a weaker response than delay conditioning does and require an intact hippocampus. The magnitude of trace conditioning is inversely related to the duration of the trace interval.

Fig. 1.

Four basic paradigms of classical conditioning

Modeling of trace conditioning is a rather difficult computational problem mainly due to a time gap between CS and US. To account for trace conditioning, Pavlov (1927) postulated the existence of a stimulus “trace” in the nervous system which did not disappear with the physical stimulus, but persisted long enough to allow associations between this trace and a subsequent US even in the case of a time gap between CS and US presentations. Meanwhile, there exist many other ways to solve the association problem. For example, some researchers suggested restoring the contiguity between CS and US by means of a tapped delay-line (Desmond and Moore 1991; Zipser 1986) or by stochastic sustained neural activity (Yamazaki and Tanaka 2005; Rodriguez and Levy 2001), or by using an STM to fill the time gap (Larrauri and Schmajuk 2008). These approaches allowed explanation of many new data and put restrictions on a possible neuronal mechanism of trace conditioning. It will be useful to have a closer look at such approaches which may provide components for a unified model of trace conditioning.

According to Marchand et al. (2004), there are basically three classes of theoretical descriptions of trace conditioning: timing models, multiple-time-scale models and conditioning of secondary cues. Each is briefly described as follows. According to the timing models, any association is indicative of the of time interval between the events, wherefore trace conditioning is not different in nature from simple delay conditioning. A trace interval does not prevent establishment of an association, because it is the time that is encoded rather than the residual trace of a particular stimulus. According to the multiple-time-scale models, any sensory event elicits multiple parallel basis functions in the central nervous system, each function having its particular time course. Basis functions may be triggered by the CS onset or offset, but will not necessarily be maintained during the CS. Thus, the time elapsed since the event is uniquely represented by a pattern of active basis functions, and this pattern can become associated with the US. The third way to account for trace conditioning is to assume that CS somehow becomes associated with other stimuli that call up secondary cues which can bridge the temporal gap between CS and US. According to this theory, each stimulus, context including, is composed of a set of elements which become associated together as long as they are simultaneously presented. Trace fear conditioning should first generate CRs to both the context and the CS trace. Contextual conditioning is often parallel to long-trace fear conditioning, it is sensitive to hippocampal lesions and can bridge the time gap. One can also include in this list the traditional, and recently updated, attentional theory of trace conditioning. According to the present-day attentional theory, increases and decreases in attention can influence the stimulus processing response in such a way that the time gap between CS and US will be bridged by additional attentional resources governed by novelty (Larrauri and Schmajuk 2008).

Besides the timing problem, the main question is what function of the hippocampus is necessary during trace and contextual conditioning, but is not needed in delay conditioning. There have been proposed several theories regarding the specific role of the hippocampus during trace conditioning. For example, the hippocampus may be needed to overcome stimulus discontiguity (Wallenstein et al. 1998), to time CRs accurately (e.g. Balsam et al. 2002) or to distinguish between the intertrial interval and the trace interval (Bolles et al. 1978). Another possibility is that the hippocampus is more active during complicated and difficult forms of classical conditioning (Beylin et al. 2001; Quinn et al. 2008; Shors 2004). Trace conditioning, according to Clark et al. (2001), is fundamentally different from delay conditioning. It resembles delay conditioning in that it also depends on the cerebellum (Takehara et al. 2003; Clark and Squire 2004) but it is additionally dependent on the hippocampus and the neocortex (for a review see Clark et al. 2002). Another theory is that it is trace but not delay conditioning that is an associative learning task dependent on awareness which requires hippocampus activity (Clark and Squire 1998, 2004; Cheng et al. 2008; Shors 2004).

There are several excellent reviews of computational models of classical conditioning (e.g. Vogel et al. 2004; Schmajuk 2008; Moustafa et al. 2009) that have provided mathematical and/or simulation explanation and described of various effects of delay conditioning in the last 40 years. Below, we shall briefly review some representative models of trace conditioning with the aim of establishing a prospective unified model. For each model we follow the same outline: the class of the model, the main task of the model, the model architecture, the learning rule, the main predictions, possible specific contributions to the unified model, as well as its limitations.

The tapped delay-lines model (Desmond and Moore 1991)

This model belongs to the multiple-time-scale class of models. It was developed from earlier neuronal network models of trace conditioning proposed at first to associate noncontiguous stimuli by means of a delay line to a delay CS until a US comes. It allows simulating the following complex timing characteristics of CRs: (1) in trials presenting a CS alone, the CR would reach its maximum at the time a US would be expected; (2) CR onset tends to be delayed for a period corresponding to the expected time of the US; (3) the length of the delay of the CR depends upon the CS–US interstimulus interval (ISI), but the CR timing is also adaptive in that a change in the ISI produces a corresponding change in the time of the peak; (4) double peaks are also observed if the ISI alternates between two different values.

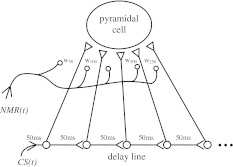
The original idea (due to Zipser 1986) of using the tapped delay-line to compensate the variable trace interval in the nictitating membrane response (NMR) is illustrated in Fig. 2. If the output from all these taps is used as the CS input to the hippocampus, then pulses of the CS-derived signal will overlap all phases of the undelayed NMR. It is only those synapses emanating from the taps at the appropriate delays that will be strengthened, because they will be the only ones where CS and NMR activities are coincident in time. Thus, this network describes in principle the ability to learn both the ISI and the time–amplitude profile of the NMR. The full network architecture is illustrated in Fig. 3. Basically, each CS is committed to activate two tapped delay-lines: one at the onset of the CS and the other at the offset. Each tap forms Hebb-like modifiable connections1 with two units, labelled V and E.

Fig. 2.

Basic structure of the hippocampal delay line model of adaptive timing as proposed by Zipser (1986). Each synapse introduces a delay; the total delay from activation of the first element in the delay-line to the last element is a direct function of the number of sequential synapses. Taps from the delay-line units send timing information to higher-order processing units. NMR(t) is the nictitating membrane response produced by US, which acts as teaching signal. unmodified, 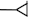modified synapse. CS input initiates sequential propagation of signal through a delay-line

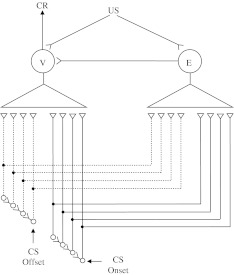
Fig. 3.

Diagram of the tapped delay-line network (from Desmond and Moore 1991). CS onset and CS offset are assumed to activate separate tapped delay-line stimulus traces. The taps form modifiable connections—denoted by closed synaptic terminals—with the V and E units. CR is generated when V-unit connections that have positive weights are activated

The function of the E-unit is to learn the time of US occurrence relative to the onset and offset of all CSs, which corresponds to the tap with the strongest connection. With repeated CS–US presentations, the E-unit starts sending a signal to the V-unit indicating the time when a US is expected. This signal permits the V-unit connection strengths to be modified. The network’s output (the simulated CR) is derived from the V-unit. As each tap is activated, its connection weight contributes to the magnitude of the CR, affecting it in either an excitatory (positive weight) or inhibitory (negative weight) manner, thus simulating the above CR complex. This model makes a prediction that an increase of the CS duration will produce double-peaked CRs. Indeed, CR peaks were often observed at two different points at a time when the duration of a trace-conditioned CS was lengthened.

While some investigators observed that the arrangement of parallel fibers in the cerebellar cortex resembled a delay-line, Moore et al. (1989) suggested that the timing functions were performed by the cerebellum, and according to Zipser (1986), the tapped delay-line input to hippocampal neurons could account for the response firing properties of those neurons during rabbit NMR conditioning. Whether the tapped delay-line stimulus processing is a neurobiologically plausible mechanism, especially with long delays (tens of seconds) or is simply an analogy for the timing processes that underlie conditioning, is an open question. The timing mechanism assumed in this model is speculative. Although the tapped delay-line structure is capable of providing the timing functions necessary for CR appearance, it cannot account for the ISI function, which is the conditioning strength plotted as a function of the CS–US interval, which tends to have an inverted-U shape.

Nevertheless, the use of the delay-line in stimulus processing is supported by single-neuron studies of the limbic system (Vinogradova 2001; McEchron et al. 2003; Gilmartin and McEchron 2005) although the role of CS offset is relatively insignificant (Burman and Gewirtz 2004). The tapped delay-line is probably an indispensible part of the mechanism of trace conditioning and should be utilized in the unified mechanism of trace conditioning, if it is physiologically supported.

The temporal basis functions model (Ludvig et al. 2008)

This model also belongs to the multiple-time-scale class of models of trace conditioning and is designed to solve more complicated problems. It is a reinforcement-learning connectionist model describing the role of the hippocampus in classical conditioning, focusing on the difference between the trace and delay conditioning. It is a modern variety of the so-called spectral models that perform Fourier-like stimulus representation. In particular, all stimuli are represented both as an intact whole and as a series of temporal elements with varying delays. These two stimulus representations interact, producing different patterns of learning in the trace and delay conditioning.

The model consists of three separate modules: the stimulus representation, the learning algorithm, and the response rule. The stimuli are represented as a series of basic elements or internal microstimuli, which are gradually broadening elements of Gaussians. The model learns through a well-known Sutton-Barto algorithm (Sutton and Barto 1998), which can be explained as follows. At each time step, the US prediction is determined by the linear weighted combination of the above basis functions. This US prediction is compared to the reward received in the comparator to generate a time difference error which is then used to update the weight vector. Finally, these US predictions are used as a driving into responses through a simple, threshold leaky-integrator response rule.

The model suggests that hippocampal lesions eliminate the long-latency temporal elements, but preserve the short-latency ones. In accord with the empirical data, simulated hippocampal damage impairs trace conditioning, but does not delay conditioning at medium-length intervals. With the longer intervals, learning is impaired in both procedures, with shorter intervals in neither. As it is mentioned in the Theoretical preview, there are several theories for the role of the hippocampus in trace conditioning, including modulation of timing, establishment of contiguity, and overcoming of task difficulty. This model is designed to provide a computational mechanism that could unite these three proposed theories.

Although a simple Gaussian basis function approach suffices for the datasets considered in the connectionist approach, other related mathematical functions are certainly possible. For example, replacing the temporal microstimuli in this model with the spectral traces as in Grossberg and Schmajuk (1989) produces results that are similar to this model. However, there is one important characteristic of the microstimulus series in both cases which shows that the individual elements should not decay too quickly. Another key challenge for the future modeling is reconciling the abstract account of the hippocampal function in trace conditioning of this model with the approaches that consider some greater physiological details (e.g. Rodriguez and Levy 2001; Yamazaki and Tanaka 2005, see later). At the same time, the principle of comparator and the feedback learning by extracting the time difference error is essential for the unified model of trace conditioning.

Inherent dynamics model (Rivest et al. 2009)

The representation gained by this model can be viewed as learning one of the temporal basis functions and associating it with a relevant stimulus, while the previous two models need to be given a whole set of fixed basis functions, covering the necessary temporal space for every possible stimulus. Delay-line representations require multiple predefined lines with specific parameters to accommodate all the possible timing information for all possible stimuli of a given task, similar to having axons of various lengths or diameters or a set of polysynaptic connections. This seems physiologically unrealistic for delays in the order of seconds. The proposed model involves a representation of the environment dynamics in an adaptive biologically plausible framework, and predicts a US without a recourse to delay lines or other special-purpose timing circuits. The model predicts that the task-dependent representation of time is learned by experience, is encoded in ramp-like changes in a single-neuron cortical activity distributed across small neural networks, and points out a temporal integration mechanism resulting from the inherent dynamics of recurrent connections within the network. The model also reproduces the known finding that trace conditioning is more difficult than delay conditioning.

The major weakness of this model at the moment is the considerable extent of training it requires using a method similar to back propagation. In the best cases, some networks learned the task in about 4,000 trials. The model clearly cannot accommodate the rapid acquisition of timing found in animals (e.g. Balsam et al. 2002). Animals are probably helped by an episodic memory system such as the hippocampus, while a lack of episodic memory in this model could also be a crucial factor contributing to a slow learning rate and a limited insight in this model. Acquisition of an eye-blink trace conditioning without the hippocampus is very difficult, sometimes almost impossible even with 1- or 2-s delays, although with shorter delays it may well take place within the neocortex-cerebellum network. This model can direct trace modeling to neocortical columns as a possible place of long STM traces in trace conditioning (cf. Larrauri and Schmajuk 2008) if the extension to long delays is possible, e.g. by slowing down cortical column intrinsic dynamics near the point of phase transitions, as described in the following model.

Phase transition model (Rodriguez and Levy 2001; Levy et al. 2005a, b)

This model, like the previous one, stresses the importance of the inherent dynamics of neuronal activity not in the neocortex but in the hippocampus which is able to effectively bridge the time gap by means of activity that emerges upon an increase of synaptic connection strengths as a result of learning and subsequent phase transition. The model hypothesizes the hippocampus functions as a time-indexed encoding device for the CS, rather than as a CS storage buffer. Specifically, the CS initiates a sequence of neural activity during the trace interval which is but indirectly representative of the CS. This sequence of CS-initiated firing patterns is stable enough across training so that neurons that are consistently active at the end of the interval become associated with the US. But initially, the CS-initiated activity is low and only after some training does it become self-sustained to the point of bridging the time gap between CS and US. This basic result is robust to variations in input size, length, and adjustments to parameters.

The model may be outlined as follows: neurons are McCulloch-Pitts-type threshold elements; input is a weighted sum; output is a binary threshold of this sum with no memory of the past. Recurrent excitatory connections are sparse and randomly distributed. Inhibitory neurons control activity in a broad manner. Most connections are excitatory, have a time-spanning, and can be modified associatively based on a local Hebbian-type rule.

The model allows making two predictions: Some cells will increase their activity only during the trace interval, and some US-coding cells will shift in time and fire before US onset. That is, some US-related neurons will be activated earlier in time, during a trial before the initial increase in CRs. These neurons are responsible for predictive US encoding in the hippocampus which provides information for timing an anticipatory CR.

The model presents the hippocampus as the critical site of US prediction in the brain mainly due to the state of phase transition in the CA3 field. The boundary line of its phase diagram shows the upper boundary of the reliably learnable trace interval. During this transition, three behaviorally distinguishable modes of eye-blink conditioning can occur: failure to blink; blinking too soon; and occasionally, appropriate predictive blinking.

The authors believe these simulations to provide currently the best explanation of how the hippocampus can predict a US across a learnable trace interval by using dentate gyrus with CA3 as a recoder and CA1-subiculum with deep layers of entorhinal cortex as a decoder. However, the network of formal neurons used in the model does not necessarily predict the phase transition in more realistic neuronal nets due to the exponential decay of membrane potential and stochastic spike activity (Kryukov 2008). Besides, stochastic activity in the hippocampus alone cannot explain the complex timing characteristics of CRs, as described by the tapped delay-lines model. Therefore, some important operations for US prediction must be performed beyond the hippocampus as can be seen in the models described below.

The strength of this model lies in the fact that trace conditioning is considered not as attributed to the single neuron activity, but as an emergent phase transition property in the stochastic net activity of the whole hippocampus. Contrary to an almost universally held view, the hippocampus here is not a memory store, but performs a rather simple operation of the US timing prediction. These ideas are yet to be further developed in the unified model of trace conditioning.

Septo-hippocampal model (Yamazaki and Tanaka 2005)

This model suggests using the septo-hippocampal loop to stop sustained hippocampal activity during trace conditioning that is needed to bridge the CS–US time gap and to start a new learning cycle. For that purpose the CA3 network is modeled as having both a recurrent all-to-all excitatory and random inhibitory connections and an output neuron corresponding to a neuron in CA1 which is connected to all excitatory neurons in the model, with synaptic weights representing Schaffer collaterals. The study of the dynamics of a neural network that has both recurrent excitatory and random inhibitory connections shows that neurons start to become active when a relatively weak transient excitatory signal is presented, and that this activity is sustained due to the recurrent excitatory connections. The sustained activity stops when a strong transient signal is presented or when neurons are disinhibited through the CA1-septum pathway.

It is assumed in this model that the output neuron will only receive a US directly through another pathway corresponding to the perforant path and the CA3 neurons will only receive a CS. Activation of neurons in the perforant path to CA1 does not evoke neuronal activity in CA1 unless neurons in CA3 are activated. That is, the CA1 field serves as an AND-gate for CA3 field inputs. The CA1 neurons excite inhibitory neurons in the septum, and these, in turn, inhibit the inhibitory neurons in CA3. As a result, CA3 neurons cease to be active only after the stimulation.

The output neuron learns to associate the US onset with the CS onset, which are separated by an off-stimulus interval and can be associated due to sustained CA3 activity. The synaptic modification corresponds to long-term potentiation (LTP) at Shaffer collaterals induced by the conjunctive stimulation of the output neuron by the US and by the signals from CA3 neurons.

The model hypothesizes that increasing activity is developed in two stages. At the first stage, a time code is generated, and at the second stage increasing activity is develops. Therefore, the model consists of two circuits: the first circuit corresponding to CA3 generates a time passage signal and at the second circuit representing CA1 shows increasing activity during the delay period.

Despite some deviations from experiments (e.g. inhibitory reset is gradually habituating during presentations of a stimulus according to Vinogradova et al. 1998) the model implies close interaction of the hippocampus with other brain structures. The model can explain to some extent the temporal evolution of the total hippocampal activity during trace conditioning but does not present any specific predictions apart from the modulatory role of the septum. The reason for this lies in the fact that the hippocampus and the septum, while playing the central role in trace conditioning, alone are not sufficient to explain timing in trace conditioning. Timing can only be accounted for by the interaction of many brain structures as demonstrated by the following model.

Pacemaker-accumulator model (Buhusi and Meck 2005)

This model implies that trace conditioning is not a matter of forming associations between stimuli and responses but involves estimations as to when an emitted response will be rewarded, and this is mainly the timing problem. From this perspective, the time gap issue or the difference between trace and delay conditioning is a comparatively minor problem.

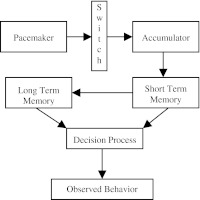
Briefly, the pacemaker-accumulator model (PAM) suggests the processing of temporal information by four synchronized modular information processing systems: the clock, accumulator, memory, and decision (see Fig. 4). The clock system consists of a pacemaker that regularly generates or emits neural ticks or pulses that are transferred (via a gaiting switch) to the accumulator, which accumulates ticks/pulses (neural counts) that correspond to a specific CS–US time interval. The raw representation of the stimulus duration in the accumulator is then transferred to the short-term memory, a component of the PAM memory system. The contents of the short-term memory are then compared with a standard in the long-term (reference) memory, the second component of the PAM memory system. Finally, the decision level of the PAM is conceptualized to include a comparator that determines an appropriate response based on a decision rule involving a comparison between the interval duration present in the short-term memory and the corresponding duration in the reference memory.

Fig. 4.

Outline of the pacemaker-accumulator model. The upper level shows the pacemaker-accumulator clock, the middle level the long-term reference memory and the short-term working memory, and the lowest level the decision mechanism

The model predicts that conditioned responses follow a normal distribution over the ISI duration and, more importantly, that the width of this response distribution is proportional to the length of that interval duration. The way in which the mean and standard deviation of the response distribution covary implies a constant coefficient of variation, which is usually referred to as the scalar property, and resembles Weber’s law, which is reflected in most sensory dimensions.

The first challenge is to connect PAM with more conventional cognitive psychology, in particular where it deals with context, memory and attention. Numerous studies have shown that attention, picking out a stimulus from its context, plays a critical role in timing behavior. Another major challenge is to understand the physiological processes underlying timing. Some researchers (e.g. Matell and Meck 2000) have criticized PAM and its derivatives on physiological grounds. The biggest drawback of PAM, however, is according to Meeter et al. (2005) that it is entirely functional, with few guidelines as to how it might be implemented in the brain. Perhaps, when it is made biologically more plausible, e.g. involving attention, and becomes closer to associative models, then both classes of models will converge to form a unified model.

Attentional-associative model (Schmajuk et al. 1996; Larrauri and Schmajuk 2008)

This is a behavior model of classical conditioning that incorporates and extends the properties of several association models to include the effects of attention, extinction and trace conditioning. Therefore, it is reasonable to consider it as a behavioral version of the unified model of trace conditioning. The model incorporates: (a) a mechanism capable of establishing associations between CS and US and between two CSs, (b) a real-time attentional variable regulated by the novelty of the US, the CSs, and the context (CX), and (c) a competitive rule that describes CS–US, CS–CS and CS–CX associations.

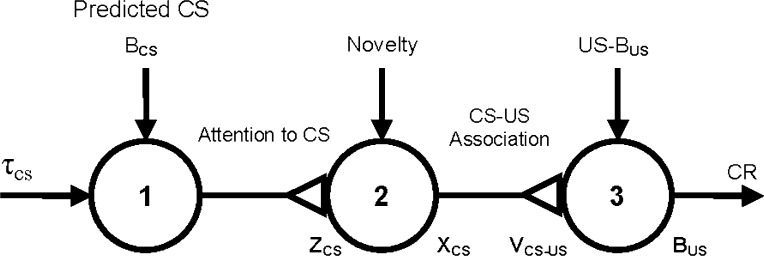
The model works as follows. To allow for a CS to establish associations with other CSs or a US, even when separated by a temporal gap in trace conditioning, the model suggests that the CS activates a short-term memory trace, τ_CS (see Fig. 5), which gradually increases over time from zero to a maximum when the CS is present and then decays back to zero when the CS is absent. It is assumed in this model that animals respond to novelty by increasing attention to environmental stimuli. The synaptic weight (represented by a triangle) connecting Node 1 to Node 2 reflects the value of attention z_CS, which can vary between 1 and −1. When novelty is greater than a certain value, z_CS gradually increases; when novelty is smaller than another value, z_CS decreases. The novelty of a CS, CX, or US is computed as the absolute value of the difference between the average observed value of the CS, CX, or US, and the average of the sum of all predictions for the CS, CX, or US and all active CSs and CXs. The total novelty, Novelty, is the sum of the novelties of all stimuli present or predicted at a given time, normalized between 0 and 1. Attentional control of learning (memory storage) and performance (retrieval) is the most important feature of the model.

Fig. 5.

A simplified diagram of the attentional-associative model (from Larrauri and Schmajuk 2008). Triangles represent variable connections between nodes. Arrows represent fixed connections between nodes. τ_cs—trace of the CS; z_cs—attention to the CS; X_cs—internal representation of the CS; V_cs–us—CS–US association; B_cs—predicted CS; B_us—predicted US; CR—conditioned response

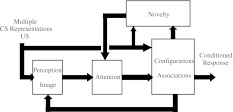
Figure 6 is a block diagram of the same model which is able to describe many of the properties of classical conditioning, and incorporates the above mechanisms with explicit interconnections. The error correction feedback from output to input is especially important since the appearance of Rescorla and Wagner’s (1972) model, and is applied here for trace conditioning to slow the CS decay in STM.

Fig. 6.

A model that incorporates many of the mechanisms required to describe the multiple properties of classical conditioning (from Schmajuk et al. 1996). Novelty is the sum of the absolute values of the differences between perceived and expected (through associations with other CSs) CSs and USs. The configuration refers to internal representation of combined simple CS representations. This configural representation has the highest activity when some CSs are present and others are absent. Associations refer to the connections established between the representations of CSs and USs which allows simple and configural CSs to predict other CSs and USs

Common to Pavlov’s theory (1927) and this model is the notion that during extinction attention to the CS decreases and this is because Novelty decreases as the prediction of the US increases. Also common to both approaches is the idea that extinction shares some properties with both habituation and latent inhibition.2 In this model, both habituation and latent inhibition occur because novelty and attention to a stimulus are supposed to decrease with its repeated presentations.

As in the Rescorla–Wagner model, changes in associations are also proportional to the difference between predicted and real values of the US (US–B_US). This allows explaining almost all classical effects (such as blocking, latent inhibition, etc.) as well as those requiring attention, e.g. extinction and its numerous properties. However, the model is admittedly unable to explain the important effect that extinction does not erase the original excitatory learning (e.g. Brooks and Bowker 2001), nor some other effects such as saving and overtraining (Schmajuk and Larrauri 2006).

Among many predictions of this model the most important is the rate of reacquisition, decreased by extended extinction, which should increase with presentation of a novel CS preceding each US presentation. According to this model, the novel CS will increase Novelty, increase attention to the target CS, and speed up reacquisition. The question is: what does novelty mean in biological terms, where is it located and how is it detected in the neural system3? A more general problem of this model is that it is entirely behavior-functional and far from biological reality. No wonder that the model simulation reveals discrepancies with the relevant literature when describing the hippocampal lesion effects on trace conditioning with shock US under short and long ISIs, and trace conditioning with an air-puff US under long ISIs. Nevertheless, this model’s ability to explain many classical results when updated attentional mechanisms are incorporated is remarkable. Attention and memory should be the central aspect of the unified model of trace conditioning.

Theta-regulated attention model (Vinogradova 2001; Kryukov 2008)

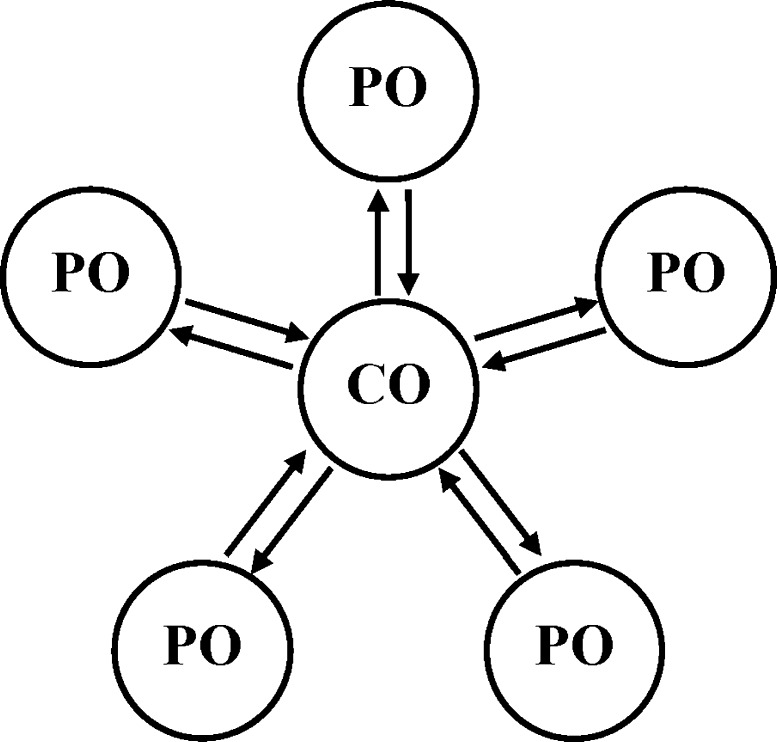
This model belongs to the class of physiologically motivated attentional models, and therefore can in principle explain all of the abovementioned attentional effects as well as many new ones. Despite the fact that the model was originally proposed for solving of long-term memory problems, it can be easily adapted to trace conditioning as a particular case model of attention and hippocampus-dependent memory (Kryukov 2008). Indeed, here again attention is the key to all effects. It is closely connected with theta/gamma partial synchronization of basic brain structures with the specific function of binding oscillatory representations of CS, US and action, so that the CR is possible without US as a result of learning and partial synchronization. Such synchronization is most easily realized by introduction of the central oscillator with variable frequency acting as a global pacemaker. The simplified star-like architecture with a central oscillator (CO) and peripheral oscillators (POs) is given in Fig. 7. Some POs represent a CS, some a US, and some others a final reaction. The association of CS and US through synchronization in trace conditioning is usually difficult because oscillatory CS representation decays during a trace interval. But repeated presentation of CS, recruiting new POs through phase resetting by CS and recirculating activity between CO and POs, leads to a stronger CS representation until synchronization of CS and US becomes possible despite the time gap. The flexible control and adaptivity are attributed to the forward–backward connections of POs with CO that can change the current frequency of ensemble synchronization, involving cortical, cerebellar, and amygdalar POs with different natural frequencies in various multimodal ensembles. Accordingly, attention is switched (automatically as well as voluntarily) from one group of oscillators to another through this changing of the frequency of the CO, thus realizing different configural and contextual acquisition, retrieval and extinction. Detailed descriptions of this model, its structure, working principles, and predictions are given elsewhere (Kryukov 2005, 2008; Kryukov et al. 1990). In this review, we shortly restate some details needed for understanding of the trace conditioning model.

Fig. 7.

Simplified architecture with central oscillator CO, and peripheral oscillators POs

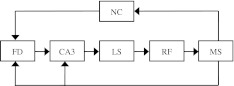
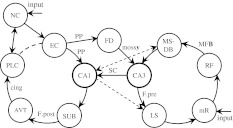
The model works like a PLL4 system, well known in communication engineering. It comprises five standard modules: receiver, voltage-controlled oscillator, phase detector, low-pass filter, and summator. Its neural representation is sketched in Fig. 8, based on the well-established functions of various parts of the limbic system (Vinogradova 2001): the medial septum (MS) is the central pacemaker and voltage-controlled oscillator; the CA3 field of the hippocampus is a comparator or a phase detector; the hippocampal fascia dentata (FD) is an input mixer and receiver of specific inputs; the lateral septum (LS) is an output mixer and summator of individual lamellas of the CA3 field, i.e. as concurrently operating sections of the hippocampal formation, almost independent from each other structurally and functionally (Witter et al. 2000). The similar lamellar structure of the CA1 field and the corresponding parallel pathways of the limbic system are a morphological basis for parallel delay-lines. All these structures, according to Vinogradova (2001) are interconnected and form two closed loops, as shown in Fig. 9. The first loop deals with information and includes the hippocampal field CA1, anterior thalamus, neocortex, and other structures which retain, even if partially, their signal-specific sensitivity. This loop is active during initial information memory formation in the neocortex, as well as during online information treatment, causing, for example, long delays in the recycling of signals for the working memory and trace conditioning. The second CA3-based loop acting as a regulator is responsible for non-specific brain activation (arousal) and control of the activating reticular formation. At the same time, the second loop serves as a negative feedback for regulation of the septal oscillator theta frequency, with CA3 being a phase detector or comparator. As a result, the whole ensemble of POs will be synchronized by phase resetting from CO at the frequency of the system theta rhythm which is defined by the overall activity of all POs, with the relative salience of corresponding stimuli taken into account.

Fig. 8.

Schematic diagram of the theta-regulated attention model. Abbreviations as in Fig. 9

Fig. 9.

Simplified scheme of two limbic circuits: regulatory and informational (adopted from Vinogradova 2001). Only principal connections are shown. AVT—antero-ventral nucleus of thalamus; CA1 and CA3—hippocampal fields; cing—cingulum; FD—fascia dentate; F.pre—fornix precomissuralis; F.post—fornix postcomissuralis; EC—entorhinal cortex; LS—lateral septal nucleus; MFB—medial forebrain bundle; mossy—mossy fibre; MS-DB—medial septal nucleus and nucleus of diagonal band; NC—neocortex; PLC—posterior limbic cortex; PP—perforant path; RF—reticular formation; mR—median raphe nucleus; SC—schaffer collaterals; SUB—subiculum. New powerful reciprocal connections of CA1 with MS added (see dashed lines) according to Takács et al. (2008), as well as well known projections from CA1 to LS according to Risold and Swanson (1996)

The learning rule is non-Hebbian, being based on the following Isolability Assumption: when the number of POs locked in an ensemble reaches a critical value, their physiological labilities5 tend to be equalized, i.e. the oscillators that are gradually brought to a common rhythm in an ensemble will change their natural frequencies towards a common one through synthesis of new proteins, thus implementing isolability coding of information, which is a form of configural coding. Such learning initially may be very rapid, (potentially one-shot), while post-learning fixing of new natural frequencies is rather slow (taking hours or even days due to consolidation and reconsolidation) and starts after the initial signal retention and some rest or sleep. The next important assumption is that the hippocampus functions as a dual comparator system in which CA3 is the comparator of neocortical and septal inputs while CA1 is the time comparator of enthorinal (ECIII) and septal inputs working under inhibition control from the CA3 field. The outputs of both comparators are summed in a lateral septum and jointly regulate the theta frequency of the medial septum: the former for binding of CS and US representations and the latter for compensation of long delays between them.

According to this model, conditioning is a system process with many brain structures interacting through theta synchronization, the septo-hippocampal system being a global coordinator of various centers. Its operation resets not only the sustained CA3 activity, like in the model of Yamazaki and Tanaka (2005) but the whole cortico-septo-hippocampal system (Kitchigina 2010). The time gap between CS and US is bridged by means of two mechanisms. The first, in the case of small trace intervals, involves inherent STM dynamics of cortical columns, much like the way it appears in the models of Rivest et al. (2009) and Larrauri and Schmajuk (2008). The second mechanism, in the case of long trace intervals, uses the delay line for CS in the CA1-based informational circle, like the tapped delay line of Desmond and Moore (1991). By the same token, the model could also account for a more complex CR, like in the model of Ludvig et al. (2008) and Desmond and Moore (1991). The role of phase transition (arousal acting as the physical temperature parameter) in this model, like in the model of Rodriguez and Levy (2001), is bridging the time gap in the CA1-based circle. But in contrast to it, the phase transition also provides long controlled delays, by slowing down the dynamics of cortical columns and theta synchronization of all interacting subsystems. Finally, due to similarity of all basic modules with corresponding modules of PAM (pacemaker, accumulator, comparator, and memory), this model can be considered as neuronal implementation of PAM (Buhusi and Meck 2005) that can meet all of its challenges.

The main predictions that can be derived from the model are as follows. The neocortical columns may act as a permanent repository of traces in trace conditioning. The medial septum may serve as a global pacemaker and (jointly with septo-hippocampal system) as a ‘core timer’ of variable speed. The hippocampus functioning as a phase comparator (CA3), or as a delay time comparator (CA1), or both, could affect the common septal theta pacemaker to change its frequency in an adaptive way. The CA1-based information circuit can provide the controlled long delays through reverberating the trace of the CS in the limbic system. Due to a circular, or spiral, mode of neural reverberation, the multipeak responses in trace conditioning are possible, most probably, with equidistant intervals between the peaks. Many other behavioral and physiological effects can also be explained with this model; some of them (e.g. habituation, extinction, novelty) were described in the original “Neurolocator” model of LTM and attention (Kryukov 2008). However, it is not quite clear whether the model is able to strictly generate the scalar property predicted by PAM. Besides, there are some key empirical findings that may be problematic for this model to explain.6

1. Several studies have shown that hippocampal lesions made after training can eliminate trace conditioning. The model’s prediction of an acquisition deficit is clear, but not so is its effect on retrieval or consolidation.

2. The hippocampus is not related to ISI in trace conditioning in a linear fashion: while in eyeblink conditioning hippocampal involvement emerges at about 500 ms, in fear conditioning it does not occurs until 15 or 20 s into the process, which is too long an interval to support even delay conditioning in eyeblink (Moyer et al. 1990; Chowdhury et al. 2005). For example, at 500 ms there is substantial involvement of the hippocampus in eyeblink but not in trace conditioning. At 3 s no sort of eyeblink conditioning will be obtained but the hippocampus will not be required for fear trace conditioning at this interval.

3. There are even data to cast doubt that the hippocampus has any bridging function in trace conditioning as similar effects of hippocampal lesions are obtained when backward trace intervals are used (Quinn et al. 2002). Indeed, it is hard to see that backwards trace conditioning has anything to do with CR timing. Such findings are not necessarily fatal problems for this model. But can they be incorporated in the “unified” model or do they remain to be serious hurdles?

4. The model is described as non-Hebbian. This may strike readers as questionable, as NMDA receptors, which are known to mediate Hebbian plasticity, have been shown to be critical to trace conditioning (Huerta et al. 2000; Misane et al. 2005; Quinn et al. 2005).

5. Trace conditioning of eyeblink and fear depend on different neural substrates downstream from the hippocampus (cerebellum and amygdala, respectively). Sometimes the transition between these in the proposed model is a bit confusing considering that both trace and delay conditioning depend on the cerebellum, which is not true of fear, though. This point as well as the above problems needs to be addressed in greater detail.

Mathematical analysis of the proposed unified model

Nonlinear differential equation of trace conditioning

To answer the above questions we present a short mathematical description of the proposed unified model as a particular case of the attention and LTM model “Neurolocator” which was previously been described by the following system of stochastic integro-differential equations (Kryukov et al. 1990, Eq. (9.7)).

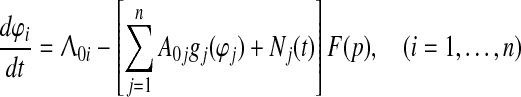1

where φ_i—mean phase difference of the septal and ith groups of cortical oscillators; Λ_0i—frequency detuning between the cortical and septal oscillators; A_0ig_i(φ_i)—non-linear sigmoid output function of the CA3-field phase comparator in the ith lamella of the hippocampus representing the cross-correlation of its two major inputs; N_i(t)—random walk process of the ith lamella; n—total number of lamellas; F(p)—transfer function of the low-pass mRF filter, which stabilizes the PLL system in case of e.g. lapse of attention. Operator multiplication by F(p) on the right-hand side of (1) means convolution with function f(t), for which F(p) is Laplace transform.

In the case of trace conditioning, we first reduce n-dimensional system (1) to two equations corresponding to CS and US representation with intensities A₀₁ and A₀₂ respectively, but with the same discriminative function g₃(φ) of the CA3-based comparator. Then we take into account that, by the Isolability Assumption and phase reset of POs, Λ₀₁ tends to Λ₀₂, and hence φ₁ stochastically tends to φ₂, which is also clear from the numerical simulation of system (1) (Kazanovich et al. 1991, Fig. 5); hence the system (1) with i = 1, 2 can be further reduced to the following single equation:

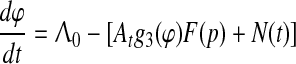2

This is a nonlinear integro-differential equation of trace conditioning sufficient to answer the above questions. Here N(t) is random walk process with Poissonian jumps and exponential drift between jumps; its drift rate is equal to 1/T, if F(p) = K/(1 + pT), where K = K_oK_d is the loop gain.7 The time-dependent intensity or arousal A_t in Eq. 2 is given by

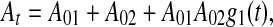3

where the last summand reflects the AND-gate function of the CA1-field comparator (Vinogradova 2001; Ang et al. 2005). This summand can be explained as follows. If we assume that CS(t) = A₀₁1_CS(t), US(t) = A₀₂1_US(t–ISI) and that the CS–US association can be expressed as convolution, then

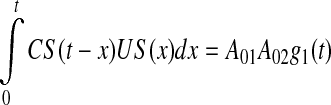4

where g₁(t) is the association function of the CA1-field comparator of CS and US. From (4) we have

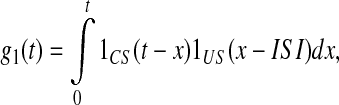5

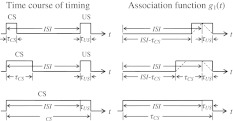
where 1_CS(t) = 1, if CS(t) ≠ 0 and 1_CS(t) = 0, otherwise. The same is true for 1_US(t). Figure 10 shows the structure of function g₁(t) for different duration of the CS stimuli.

Fig. 10.

Association function g₁(t) is formed by time-shifting of CS towards US without overlapping. In fact g₁(t) is not a rectangle but according to Eq. 5 is a triangle for CS and US having equal durations and a trapezium in general case as shown by dashed lines. But since US duration is much less than that of CS, the rectangle is a quite acceptable approximation

Below, Eqs. 2, 3 and 5 will be used for describing five basic properties of the proposed unified model along with the corresponding experimental findings.

Boundary conditions for hippocampal involvement in Pavlovian conditioning

Here, we make some additional assumptions which will help to explain the core mechanism of trace conditioning but will be dismissed later on. We shall consider Eq. 2 in the deterministic case (N(t) = 0), without filter (F(p) = K) and with time-averaged A_t over ISI, i.e.

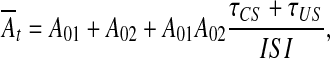6

where τ_CS and τ_US are the durations of CS and US, respectively. Under such conditions, Eq. 2 takes a simple form of

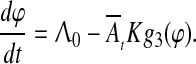7

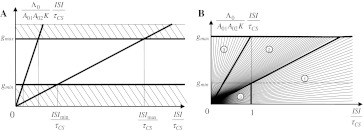
This equation can have a stationary solution only if the following boundary conditions are fulfilled

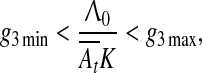8

which together with Eq. 6 implies that the hippocampus is involved in trace conditioning only within some interval of ISI values, in accord with the empirical finding by Misane et al. (2005). This interval depends on particular values of A₀₁A₀₂K/Λ₀: if this value is small it shifts to the lower values of ISI (e.g. in EBC), if high, it shifts to the higher values of ISI (e.g. in fear and appetitive conditioning).

Moreover, our model predicts that sometimes the hippocampus may be involved in delay conditioning, but not involved in trace conditioning. To see that let us suppose that in Eq. 6

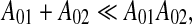9

i.e. nonassociative interaction of CS and US is much weaker than that of associative interaction.8 Then, instead of (8), we have for τ_CS > > τ_US approximately

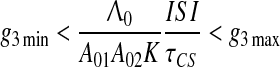10

which explicitly expresses the upper and lower ISI bounds for hippocampal involvement in conditioning (see Fig. 11a). From Inequality (10) it follows that the hippocampus may be needed even for delay conditioning (ISI/τ_CS < 1) if A₀₁A₀₂Kτ_CS is relatively low as found experimentally by Quinn et al. (2008), in case of few training trials or low footshock intensity and Beylin et al. (2001) in case of long delay task. On the contrary, violation of the left side of Inequality (10) means that the hippocampus is not required even in trace conditioning (ISI/τ_CS > 1) if ISI is relatively short and/or A₀₁A₀₂Kτ_CS is relatively high (as found experimentally by Thibaudeau et al. 2007, 2009; Kyd et al. 2008; McGlinchey et al. 2008; Beylin et al. 2001). In general, Eq. 10 provides the boundary lines not only for the hippocampal involvement in conditioning but also the border lines between trace and delay conditioning depending on the task difficulties (see Fig. 11).

Fig. 11.

a The upper and lower ISI-boundaries for the hippocampal involvement in the conditioning according to Inequality (10). b Three parametric regions of Pavlovian conditioning based on Inequality (10): (1)—“Trace but not delay”; (2)—“Both trace and delay”; (3)—“Delay but not trace”

Optimal values of trace conditioning parameters

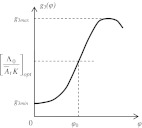
Being a system of automatic control, our model has optimal processing speed. Therefore, there exists an optimal set of parameters of trace conditioning in which learning is fast. It will occur when e.g. K = K₀K_d is maximal (see footnote 7). Since K₀ is constant, K_d = dg₃(φ)/dφ should be maximal, which occurs at the point of inflexion φ₀ = φ, such that d²g₃ (φ₀)/(dφ)² = 0 (see Fig. 12). In general, not only K_d but each parameter involved in equality 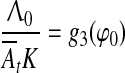can be optimal at fixed values of other parameters. However, the shift of any parameter in conditioning from the optimal value will require some additional learning to reach the optimal regime. This optimality property was repeatedly discovered in many experiments. For example, there exist optimal CS duration τ_CS (Kehoe et al. 2009), optimal US intensity A₀₂ (Oswald et al. 2009), optimal arousal A_t (Berry and Swain 1989; Shors 2001), optimal ISI (Vogel et al. 2004; Kehoe et al. 2010). After the ISI change, additional training proved necessary to allow asymptotic responding at the new ISI (Steinmetz et al. 2011).

Fig. 12.

Non-linear discriminating function of the CA3-field phase comparator

Explanation of timing effects

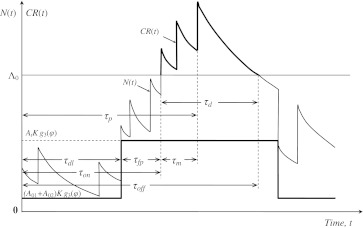
Let us return to the general case, as described by Eq. 2, to make a fundamental assumption relating it to behavior: the conditional response CR(t) can be expressed as a random process that is equal to the positive part of the right hand side of Eq. 2 taken with the opposite sign, i.e.

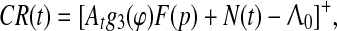11

where [x]⁺=x, if x > 0, and [x]⁺=0, if x < 0. Figure 13 gives a schematic picture of this assumption when F(p) = K. Formation and timing of the CR are as follows:From Eq. 11 it follows that CR(t) = 0 at the initial stage of conditioning when A_t is small due to poor synchronization. Upon repeated stimulation, CS and US representations become synchronized at a common theta frequency so that A_t increases causing the time of threshold Λ₀ being first passed by random process N(t) to be close to the time of US appearance. With further training this tendency increases since function A_t, which was initially evenly distributed over ISI with the mean value given by (6), becomes concentrated near US due to the function g₁(t) as it is shown in Fig. 10. From Fig. 13, it can be seen that acquisition of CR is faster and reaches a higher asymptote with high A_tK, e.g. with more intensive US (in accord with Oswald et al. 2006), or with more intensive CS (in accord with Miller et al. 2008; Weinberger 2003; Fritz et al. 2007; Galvez et al. 2006). Acquisition is complete when A_t reaches the value at which CR habituates, i.e. when 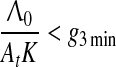, in violation of Inequality (8), and hence the septo-hippocampal system is switched off. However, presentation of CS alone (without US) causes dehabituation9 and CR reappears.

Fig. 13.

Schematic representation of the temporal relationship between all the components of CR(t) as defined by Eq. 11 at F(p) = K. Note that rectangle in the central part is function g₁(t) multiplied by product A₀₁A₀₂Kg₃(φ). It makes most probable crossing of Λ₀ by a random process N(t) near the time at which US occurs. In contrast, the non-associative part of CR(t), connected with earlier portions of the CS is due to crossing of Λ₀ by a process N(t) long before the time at which US appears. It occurs with much lower probability than that of the associative part of CR(t). Pavlov believed that the earlier portion of the CS developed a conditioned inhibition and called it inhibition of delay. Note that the timing of CR(t) is defined by interaction of two major delay sources: the limbic delay time (τ_dl) and the first passage time (τ_fp) of N(t) through threshold Λ₀. The other temporal parameters such as peak time (τ_p). duration (τ_d) and the times of CR onset (τ_on) and offset (τ_off) are only different combinations of these two major delay sources, which allows estimation of variability for each parameter (see Eq. 12) in terms of CVs of these two sources

The above random timing is adaptive in the sense that a change of any parameter e.g. ISI or CS duration, shifts from the optimal value (shown in Fig. 12), which requires additional learning (changing A₀₁A₀₂) to gain the optimal regime. In particular, inhibition of delay as a constraint on the CR to a few seconds prior to US delivery, depends on the ISI duration, such that CR latency decreases when training is conducted with relatively short ISI but increases with relatively long ISI, as found experimentally by Vogel et al. (2003).

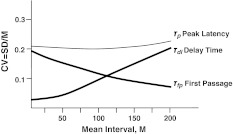
The most difficult problem of timing is explanation of its scalar property in terms of neural activity. It requires a detailed calculation of the mean (M) and the standard deviation (SD) of the first time of N(t) passage over threshold Λ₀. This problem in the context of random walk models of neuron firing was investigated both analytically (Kryukov 1976) and by computer simulation (Stein 1967). In particular, it was found that CV = SD/M varies as inverse root of the neuronal threshold value, while M is proportional to the threshold value itself. Thus, the CV can not be constant and the scalar property can not be explained in terms of the random walk models. Fortunately, the latency of CR in the trace conditioning model includes not only the time of first passage across the threshold Λ₀ but also the delay in the limbic delay line. Simulation shows that the latter has a low CV for short delays but a rising tendency for long delays (see below). Thus, it is possible to explain a constant CV as a combination of rising and declining CVs, at least for not too long delays. To show that, let us calculate the SD of the sum of two independent random delays, one of which has CV with a rising tendency, and the other with a declining tendency.

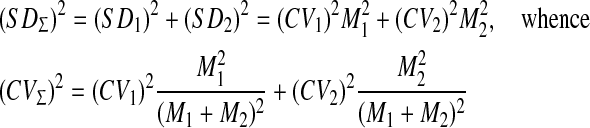12

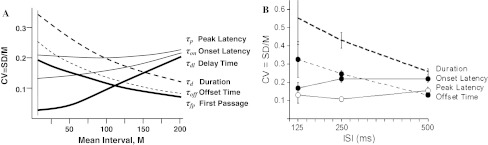
In short, CV of the sum of two independent intervals is an almost linear combination of component CVs. Therefore, we can qualitatively estimate the CVs of all random intervals shown in Fig. 13 taking into account both the rising and declining tendencies weighted by their relative duration (see Fig. 14). Comparison of model predictions and experimental CVs presented in Fig. 15 shows that (a) similar timing characteristics have a similar curvilinear dependence on M ≈ ISI, (b) timing is not strictly scalar across ISI, (c) the only discrepancy is that the model predicts CV_p > CV_on, i.e. the peak latency is more variable than the onset latency, while in experiment CV_p < CV_on. A possible reason for this discrepancy may be that M ≠ ISI, i.e. different abscissas in panels A and B of Fig. 15 are used.

Fig. 14.

Constant CV can be at least partially explained as a result of two opposite tendencies

Fig. 15.

a Model prediction of CVs for each random time interval shown in Fig. 13. The rising CV curve is the same as in the simulation model (see Fig. 16b), the falling CV curve is proportional to 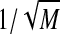, the other curves are plotted according to Eq. 12. b Experimental CV from Kehoe et al. (2010). Note the qualitative agreement of model-predicted curves with experimental ones, except for the unusual upward concavity of the Onset Latency curve, which is probably due to differences in abscissas in a and b graphs

The review of timing literature, in accord with the above analyses, shows that the scalar property may be oversimplification of the real data. Contrary to the constant predicted by Weber’s law, the Weber fraction (CV) is larger at 2 s than at 0.2 s (Lavoie and Grondin 2004). Similarly, Lejeune et al. (2006), showed that the scalar property of variance measured by the CVs of the Gaussian curves would normally hold over a range of durations, but that CVs tended to increase as the interval value became very large. On contrary, Lewis and Miall (2009) found that the CV of human subject timing monotonically decreases. These findings join previous reports in demonstrating a systematic violation of the scalar property in timing data (e.g. Lejeune and Wearden 2006).

Hippocampal lesion effects

In general, the effects of hippocampal lesions in trace conditioning are predicted by the Theta-Regulated Attention Theory (Vinogradova 2001) and the “Neurolocator” model (Kryukov 2008), as in the particular case of hippocampus-dependent memory. But the above specific role of the CA1 and CA3 field as time comparator and phase comparator, respectively, allows predicting the following specific effects.

Pretraining lesions of CA1 or CA3 or both fields attenuate the acquisition of trace memories. Experimental support for this point can be found in Hunsaker et al. (2009), Kishimoto et al. (2006), Quinn et al. (2005), Burman et al. (2006), Wanisch et al. (2005), Seo et al. (2008), Yoon and Otto (2007).

Posttraining lesions of the hippocampus result in more complex effects since the hippocampus is not a place where the LTM of trace conditioning is stored and there are several ways in addition to the hippocampus for the retrieval of memory when the medial septum is activated. While consolidation, reconsolidation and extinction theoretically require an intact hippocampus (Kryukov 2008, 2011a, b) since performance of these tasks is impossible without phase synchronization, the retrieval/expression is possible through frequency synchronization, i.e. without CA3-based regulatory circuits.10 In such a case, CA1-based informational circle can alone synchronize CS and US representations through the direct path to the medial septum (see dash lines in Fig. 9). Moreover, in the case of both CA1 and CA3 lesions, the synchronization needed for retrieval of already consolidated memories can be provided by the direct path from the mPFC to the medial septum (Gabbott et al. 2005; Nieuwenhuis and Takashima 2011) or through phase resetting of theta by the external stimuli (Sauseng et al. 2008).

The most relevant recent data in support of these predictions are as follows:

• Lesions restricted to the dorsal hippocampus blocked acquisition of trace fear conditioning. Larger lesions were required to impair retrieval of trace fear conditioning (Burman et al. 2006).

• Lesion of CA1 connections with the medial septum impairs consolidation/retrieval of auditory-cued and context fear (Hunsaker et al. 2009).

• APV injected in the dorsal hippocampus impairs acquisition of context memories but does not affect its retrieval or retrieval of trace fear memories (Matus-Amat et al. 2007).

• Retrieval of trace memories is possible without the hippocampus at short ISI (Chowdhury et al. 2005; Moyer et al. 1990).

• Trace conditioning is possible without the hippocampus if CS and US were associated through delay conditioning before hippocampal lesion (Beylin et al. 2001).

• Selective lesions in the medial septum induce a perceptible deficit in acquisition, but not in retrieval of EBC using the trace paradigm (Fontán-Lozano et al. 2005).

The central role of theta-regulated attention

Since Eq. 2 is only a slight modification of the previously known equation, governing the attention and the hippocampus-dependent memory (Kryukov 2008, Eq. 2), all properties of attention are applicable to the case of trace conditioning. For example, the very unusual case of simultaneous learning of both trace and delay conditioning with identical ISIs but dissimilar stimuli (Cheng et al. 2008) is only a particular case of divided attention (Kryukov 2008, p. 150). Another important property of attention, its transient character, is found in experiments with the theta-contingent trace conditioning, when learning is unusually fast during transient computer-defined specific time intervals of high attention and spontaneous theta activity (Griffin et al. 2004).

But the most important role of attention in trace conditioning is its mediation in cortical plasticity. Recently, a new type of memory code was discovered in auditory, visual and somatosensory cortexes during classical conditioning. Receptive field (RF) plasticity develops in the primary auditory cortex A1 when a tone CS becomes associated with an appetitive or aversive US. This association is accompanied by shifts of frequency tuning of neurons toward or to the frequency of the CS. RF plasticity has all of the major characteristics of behavioral associative memory: it is highly specific, discriminative, rapidly induced, consolidating, and can be retained indefinitely (Weinberger 2003; Edeline 2003). A similar new coding have been found within the primary visual cortex V1 (Miller et al. 2008), in the extended visual cortex (Bradley et al. 2003), and in the somatosensory cortex (Galvez et al. 2006). In the latter case, it has also been demonstrated that during trace EBC learning-related expansion of the cortical barrel size occurs when rat whisker stimulation is utilized as a CS and corneal air-puff as a US.

All these data support the general, modality-nonspecific, theta-contingent learning rule stated in our model as the Isolability Assumption. According to this assumption, theta synchronization recruiting new oscillators in common pool changes the natural frequencies of synchronized oscillators towards that of the CS oscillators thus rapidly inducing specific long-term memories. Admittedly, no direct evidence has been found yet to this learning rule. Below, however, we present a series of mutually consistent attention-dependent effects which add up to count in favor of the new learning mechanism referred to as the Isolability Assumption, generalizing the RF cortical plasticity. First, it is trace rather than delay fear conditioning that requires attention in mice (Han et al. 2003) and rabbit EBC (Steele-Russell et al. 2006). Second, attention is the key trigger that initiates dynamic RF changes and attention-triggered plasticity in A1 (Fritz et al. 2007). Third, attention is largely theta-contingent and relies on the hippocampal theta rhythm. Moreover the theta rhythm is not only a correlate of attention but is a most important part of the neuronal mechanism of attention and memory (Vinogradova 2001; Sauseng et al. 2008; Sirota et al. 2008). Fourth, theta-contingent training, if it take place only during computer-defined explicit presence of spontaneous theta activity, has a dramatic facilitatory effect on trace conditioning: the animals given theta-contingent training learned several times faster than those given non-theta-contingent training (Griffin et al. 2004, Darling et al. 2011), with the number of required trials reduced by a factor of up to 4 (Berry and Hoffmann 2011; Griffin et al. 2004).

Phase transitions underlie a stimulus trace of long duration

The most serious problem of modeling trace conditioning is to show how neurons and synapses operating on a millisecond time scale can encode information about time intervals on the order of seconds and minutes. Our model solves this problem by using the physical phenomenon of critical slowdown of neural kinetics near the point of phase transition. The existence of phase transitions in physiologically plausible neural nets of integrate-and-fire neurons has been proved and the lifetimes of long-lived states have been estimated (Kryukov et al. 1990), with simulation results (Kirillov et al. 1989; Kryukov et al. 1990; Borisyuk and Cooke 2007) provided to confirm the theoretical predictions. One of the simulation results, which is particularly relevant to the problem of long-duration traces, is as follows (see Kryukov 2008, Fig. 2). A two-dimensional computer simulation network of 30 × 30 integrate-and-fire neurons with fixed nearest-neighbor synaptic connections of identical strength (Basic Neuronal Model), starts with a spot of units of zero background taken as the initial state, and evolves as follows. The net activity dwindles to the DOWN state if the synaptic strength is small, so that the configuration consisting mainly of zeros gets stabilized. On the contrary, if the synaptic strength is high enough, the spot of units spreads out, to result in the UP state. A network with critical parameter values, however, is capable of remaining for a long time in a state close to the initial one, manifesting itself in spot persistence.

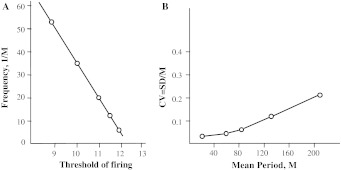
This effect is used in formation of a neuronal oscillator with the unusual property of very slow oscillations with a high period’s stability. It is obtained by introducing into the above Basic Neuronal Model a single inhibitory neuron which receives positive connections of identical strength from all neurons, and sends negative connections of identical strength to all other neurons. As a result, the network becomes capable of producing oscillations of very long periods, with small period’s variance; a wide range of linear frequency regulation is provided by the varying threshold of the excitatory neurons. Such oscillators, locally connected to each other, can hold the spots of activity for a very long time, even after quenching of oscillations, which can explain the long-term memory traces of previous conditioning. The mathematical theory of such persistent states shows (Kryukov et al. 1990, p. 250) that their lifetime depends essentially on the number of elements in the spot, and can be very long in the case of their optimal number, in a way similar to physical metastability phenomena. Figure 16 shows the main characteristics of such a new oscillator: its linearly regulated frequency in a wide range and a comparatively low CV of oscillation periods.

Fig. 16.

Two main properties of the simulated “metastable” oscillator: a wide range of working frequency and b high stability of its period with an upward tendency at long periods

Unfortunately, this CV is not constant but has an upwards tendency over long periods. We supposed that this tendency, at least partly, was due to the small size of the simulated network. In support of this supposition, we have recently reexamined our earlier oscillator simulation results (Kirillov et al. 1989) and have found that the supposition to be correct. The simulation model is as follows. Tree oscillatory submodules A, B, and C are connected consecutively so that submodule A can transmit excitation to submodule B, B to C, and C to A, imitating a relay race-reverberation in the limbic circle (Batuev 1993). The excitation can only be transmitted when the total activity of the module reaches its threshold level, i.e. when the corresponding inhibitory neuron fires. After the inhibitory neuron has fired, the activity of its module is set to be small enough for the module to be inactive with a high probability until excitation from another module comes. Therefore, submodules A, B and C work in succession and the activity of the whole system is nearly periodic. Figure 17a, b display the mean period M and the standard deviation (SD) as a function of the noise amplitude σ, representing an input control signal. The upper curves in Fig. 17 correspond to a square 10 × 10 submodule, the middle ones—to a 9 × 9 submodule and the lower ones—to a 8 × 8 submodule. Using these simulation results, we have lately calculated CV as a function of the mean period M for each σ value. The result is presented in Fig. 17c. It shows that CV still has the upwards tendency, but this tendency is significantly weaker for larger networks. To sum it up, a chain of “metastable” oscillators has a fairly stable oscillation period, its frequency is regulated linearly in a wide range, and it can exhibit arbitrarily long oscillation periods without changing the time constants of its elements. Therefore, it can serve as a neural network model of a limbic delay line with long delays. Thus, the solution to the problem of long time intervals lies not in a single neuron, even less so in its synapses, but in the collective effect similar to the one known in statistical physics.

Fig. 17.

Simulation results of CA1-based circle. Graphs a and b are adopted from Kirillov et al. (1989). Graph c obtained from graphs a and b by computing of SD/M for each fixed σ

As for its neurobiological substrate, the CA1-based information circle with parallel lamellae can operate as a parallel delay line. This function is supported by many studies on the single neuron level (Vinogradova 2001; McEchron et al. 2003; Gilmartin and McEchron 2005), on the neural population level (Chen et al. 2009; Batuev 1993), by the lesion studies (Lee and Kesner 2003; Howland et al. 2008; Risterucci et al. 2003; Huerta et al. 2000; Misane et al. 2005),by research in the brain imaging (Knight et al. 2004), and in the event related potentials (Onoda et al. 2003). In particular, a significant number of neurons at single and population levels reveal upon retrieval maximal firing on CS-alone timed to 10 and 20 s after CS, respectively. These latencies were similar to the duration of the trace interval used in previous trace conditioning (McEchron et al. 2003; Chen et al. 2009), which means that some sort of timing memory should exist in the delay line. As for the longer latencies, the hippocampus and the medial prefrontal cortex (mPFC), as critical structures of the limbic circle, interact with each other to ensure information processing in the time range from 10 s up to 5 min (Lee and Kesner 2003) and even up to 30-min (Floresco et al. 1997). Such long times periods are probably the result of many recurrent NMDAR-dependent transmissions in the mPFC-hippocampus loop (Gilmartin and Helmstetter 2010) with basic recirculation period of 15–30 s (Misane et al. 2005; Huerta et al. 2000).

Discussion

The proposed unified model of trace conditioning is able to answer the major questions that are currently under discussion concerning what the hippocampus does during trace conditioning and how it does it. This model provides not only a computational mechanism that links several existing theories for the role of the hippocampus in trace conditioning, such as gap bridging, overcoming of task difficulty, and temporal processing; it also identifies the neurobiological substrate that enable the hippocampus to perform such a role. For example, the gap bridging is performed by joint action of both CA1 and CA3 fields, the former acting as part of the delay line and AND-gate for restoring CS–US contiguity and the latter as a phase detector to bind the CS and US representations in the theta synchronization process as well as to provide US input to the AND-gate. Such a way of restoring the contiguity is independent of which of the two stimuli comes first, because Eq. 6 is symmetric with respect to the CS and US action, although the time to reach the asymptote depends strongly on their time order, wherefore the backward trace conditioning is much slower to learn than the usual forward one.11

Another important question is how the proposed unified model could explain the key empirical finding that a boundary between trace and delay conditioning has 40-fold difference in the ISI for the fear and eyeblink conditioning (Chowdhury et al. 2005). The proposed unified model give an unexpected answer: there is no clear-cut ISI-defined boundary between the two paradigms, since their respective task difficulties depend not only on the ISI value but also on the whole set of conditioning parameters which for the hippocampus to be involved must meet the strict mathematical limitation expressed, e.g. by Eq. 10. On the contrary, the ISI or trace interval values alone as indicators of the hippocampal involvement may prove misleading unless the CS duration and other parameters are given. For example, Chowdhury et al. (2005) and Burman and Gewirtz (2007) for a similar task using the same (3-s) trace interval, obtained seemingly contradictory results because they used very different CS durations.

But how does the hippocampus “know” which task is difficult enough to be involved in it or what information must be processed and maintained for establishing a hippocampus-dependent trace memory versus that for the delay-type memory (Shors 2004)? The answer is unexpectedly simple: it (hippocampus) does not “know” that and starts the same operations regardless of the paradigm, but an easier delay conditioning task will produce earlier habituation to stimuli and the hippocampus will switch off at very early stages of delay conditioning. This explains why delay conditioning is frequently considered as procedural and hippocampus-independent memory, while trace conditioning is treated as declarative, hippocampus-dependent memory requiring conscious expectance (awareness) for when US is going to occur. In fact, evidence was found for a dissociation of CRs and US expectance occurring regardless of whether there was a delay or trace conditioning (Weidemann et al. 2011). Similarly, adult neurogenesis in hippocampus FD can not be considered longer as required for trace, but not delay, conditioning, since mice, specifically, lacking adult neurogenesis showed proper fear conditioning and many other hippocampus-dependent functions (Jaholkowski et al. 2009).

The learning rule of the proposed unified model is non-Hebbian because according to the Isolability Assumption, a basic element of learning is not a synapse, nor even a whole neuron, but a small oscillatory neural network capable of changing its natural frequency as a result of collective synchronization of isolabile oscillators during learning. The new learning rule can explain many memory effects that are problematic for Hebbian learning, such as reconsolidation, extinction, backward conditioning, etc. A question arises as to how this new learning rule can match the data on the critical role of NMDARs in trace but not delay conditioning (Seo et al. 2008; Gilmartin and Helmstetter 2010; Wanisch et al. 2005). A key to this question can be found in the paper of Claflin et al. (2005) which suggests that trace and delay conditioning have different neural mechanisms for timing but a common neural substrate for memory acquisition. We assume that this different mechanism is NMDARs-dependent transmission in the limbic delay line, which is consistent with the available data (Huerta et al. 2000; Gilmartin and Helmstetter 2010; Sakamoto et al. 2005; Gruart et al. 2006, Misane et al. 2005), while the common neural substrate for trace and delay learning is mainly the sensory cortical theta-dependent plasticity according to the Isolability Assumption. Both the temporal and sensory mechanisms are interdependent in that the delay line needs sensory synchronization of CS and US representations to restore the CS–US contiguity in the CA1 AND-gate, while cortical sensory memory depends on timing of US, in accord with Miller et al. (2008), Galvez et al. (2006, 2007), and Shuler and Bear (2006).

The critical role of NMDARs in trace conditioning does not mean that a trace conditioning model should be based on Hebbian learning for the only reason that NMDARs is also known to mediate the Hebbian LTP. Firstly, trace conditioning is a comparatively slow process requiring a large number of paired CS–US presentations and therefore cannot be directly related to the rapid LTP mechanism (Gruart et al. 2006). Secondly, there exists non-Hebbian LTP (Kato et al. 2009; Engert and Bonhoeffer 1997; Tsukamoto et al. 2003). Thirdly, the Hebbian LTP is computationally insufficient for simulation of many real conditioning features (Krasne et al. 2011). Nevertheless, the memory mechanism in the proposed unified model can be considered as a functional analog or, rather, as generalization of the Hebbial LTP since both mechanisms (a) have the property of associability of weak input with delayed strong stimulus, (b) require synchronous activation of two or more functional units, neurons and neuronal oscillators, respectively, (c) depend upon the synthesis of new proteins, and (d) are most effectively induced by the theta frequency stimulation. However, unlike Hebbian LTP, the learning mechanism in the proposed unified model provides life-long bidirectional association of two (or more) stimuli regardless of the distance between the location of their representations in the brain, and, most importantly, have no problems with the information shifting from the hippocampus to the cortex which arise in the contemporary consolidation theory (Frey and Morris 1997; Lesburguères et al. 2011).

The important question about the functions of different brain structures, such amygdala and cerebellum, in trace conditioning can not be adequately discussed here since Eq. 1, which can describe their role, is reduced here to single Eq. 2. Nevertheless, it is quite clear that the PLL system, being a global synchronization system, makes less than probable the existence of separate specialized memory systems for different paradigms, and even less so for different types of trace conditioning. For example, fear and EBC are universally considered as dependent on different neural substrates downstream from the hippocampus (amygdala and cerebellum, respectively), but according to the model architecture shown in Fig. 7, they both take part in fear and EBC as partner POs. This unusual prediction of our model was recently confirmed by Timmann et al. (2010) who showed that the cerebellum was involved in motor, emotional and cognitive associative learning using classical eyeblink and fear conditioning.

Conclusions

This short review of trace conditioning models shows that there exists a computational potential for building a unified model but simultaneously points to the serious difficulties yet to be overcome. The first point leads to two objectives: (a) to fill the time gap by means of a delay line appended by phase transition to lengthen the delay duration and (b) to use a new model architecture similar to that of PAM but with a global pacemaker automatically regulated by the septo-hippocampal loop to incorporate the attention in conditioning. The second more difficult aspect of modeling may be reduced to three major problems:

1. A way (if any) to be found to relate the unified model to the prevailing memory systems theory which requires different neuronal substrates for declarative, procedural, and emotional memories and a different role of the hippocampus therein.

2. The unified model should explain how neurons and synapses operating on a millisecond time scale can encode information about trace intervals on the order of seconds and tens of seconds.

3. The learning algorithm of the unified model should be able LTM of trace conditioning reconcile to the short living hippocampal LTP.

By combining the desired features of existing models, the proposed unified model of trace conditioning provides a solution to the above three major problems and as a result is capable of explaining most of the experimental effects in the field. Therefore, this model is the best candidate for a unified model of trace conditioning.