Abstract
This paper reports development of an integrated fiber-optic microfluidic device for measuring muscular force of small nematode worms with high sensitivity, high data reliability, and simple device structure. A moving nematode worm squeezed through multiple detection points (DPs) created between a thinned single mode fiber (SMF) cantilever and a sine-wave channel with open troughs. The SMF cantilever was deflected by the normal force imposed by the worm, reducing optical coupling from the SMF to a receiving multimode fiber (MMF). Thus, multiple force data could be obtained for the worm-SMF contacts to verify to each other, improving data reliability. A noise equivalent displacement of the SMF cantilever was 0.28 μm and a noise equivalent force of the device was 143 nN. We demonstrated the workability of the device to detect muscular normal forces of the parasitic nematodes Oesophagotomum dentatum L3 larvae on the SMF cantilever. Also, we used this technique to measure force responses of levamisole-sensitive (SENS) and resistant (LERV) O. dentatum isolates in response to different doses of the anthelmintic drug, levamisole. The results showed that both of the isolates generated a larger muscular normal force when exposed to a higher concentration of levamisole. We also noticed muscular force phenotype differences between the SENS and LERV worms: the SENS muscles were more sensitive to levamisole than the LEVR muscles. The ability to quantify the muscular forces of small nematode worms will provide a new approach for screening mutants at single animal resolution. Also, the ability to resolve small differences in muscular forces in different environmental conditions will facilitate phenotyping different isolates of nematodes. Thus, the present technology can potentially benefit and advance the current whole animal assays.
Introduction
Movement of multicellular organisms, such as the nematode Caenorhabditis elegans, exhibits a sinusoidal pattern induced by alternating dorsal and ventral muscle contraction when swimming/crawling across surfaces.1,2 The waves of the muscle contraction produce local bending in the cuticle and generate lateral thrust or planar force.3 Researchers have showed that the nematodes maintain their motion generation mechanism by producing lateral thrust in either natural or artificially structured surrounding environments.4 There has been considerable attention devoted to organismal biomechanics of important nematode species.5–9 Investigation of correlations between genes, neurons, sensory organs, muscular arms, and motion patterns of these nematodes is critical to understand: a) the coupling between signals in the neuromuscular system, b) the muscle dynamics, and c) the emergent mechanical behaviour of the whole animal.10,11 Applications of organismal biomechanics include ameliorating human health problems (e.g., prosthesis design and movement restoration),12 and developing new therapy for neuromuscular diseases caused by mechanosensory degradation and defects.13 Also, through genetic modification, mutants of C. elegans can be created, which affect the forces of motion and thus the phenotypic locomotive behavior of mutants.14,15 Thus, screening these mutants at the single animal resolution needs a miniature force sensor suitable for detecting the muscular force of these mutants. Furthermore, as we will see later, it is possible to screen drug resistance of parasitic nematodes by directly examining muscular forces of parasitic nematode species under different chemical or drug environmental conditions. This is because drug resistance of parasitic nematodes may be associated with changes in signalling-muscle-contraction pathways.16,17
Many tools have been developed to analyze cellular and molecular mechanics in the past two decades,18 including optical tweezers,19–21 atomic force microscopy,22–24 magnetic twisting cytometry,25,26 micropipette aspiration,27,28 and micro-electromechanical systems (MEMS) sensors and actuators.29,30 These tools have yielded important insights into fundamental biology research.31,32 However, they are not suitable for use in the study of multicellular organismal biomechanics of small nematode worms. The advent of MEMS, microfluidics, and automated imaging techniques have led to a new class of miniature devices and systems to study neurophysiology and behaviour of nematode species via flexible manipulation, imaging and screening of the nematodes.33–46 However, due to a lack of new muscular force sensing tools, the study of the multicellular organismal mechanics currently lags behind that of the cellular and molecular mechanics. Pruitt and co-workers pioneered the use of a piezoresistive cantilever-based indentation system for studying the mechanical properties of C. elegans.3 This system offered advantages such as a wide range of force and displacements matched to different biological materials, and an ability to target a desired dynamic range and a high force resolution of 12 nN; but it was unable to detect the dynamic force of a worm in motion. To detect the dynamic force of moving nematodes, the researchers reported another remarkable nematode force measurement microsystem using an integrated strain gauge force sensor, with a force resolution of the device was 260 nN.47 The device was constructed from multiple layers of SU-8 and metal on quartz substrates, capable of measuring tactile sensitivity and interaction forces exerted during locomotion, but the device structure was relatively complicated. Subsequently, Ghanbari and co-workers developed a simple microfluidic device for measuring force generated by moving nematodes in real-time.4,48 The device used an array of vertical polymeric pillars fabricated in a channel. The force applied by a moving nematode to each pillar was detected via a vision-based approach. This vision-based force sensing system was capable of performing robust force measurements with a 330 nN resolution.4 This technique, however, required a high-resolution microscope with an automated stage, a video camera, and a special algorithm to track worm movement and resolve mechanical deflections of the pillars induced by the nematode-pillar contacts. Also, the deflections of the short pillars were limited by a relatively low manufacturable aspect ratio of the pillars, causing low sensitivity of the device.
Methods and Experimental Section
Device principle and design
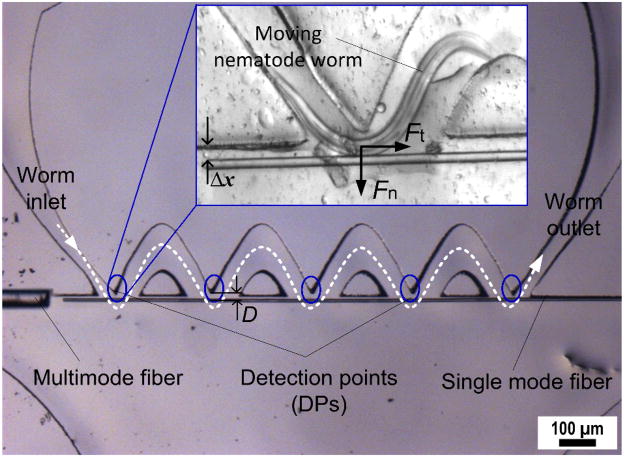
Fig. 1 presents our fiber-optic microfluidic device for detecting muscular forces of small nematode worms. A worm enters a sine-wave channel at a worm inlet without applying any attractants. To minimize body contact between the worm and the sidewalls of the channel, the amplitude and wavelength of the sine-wave channel are designed to be similar to those of the worms under test. Also, the channel is wide enough to neglect constraints from the sidewalls on the worm’s natural movement. The lower part of this sine-wave channel is open, where a silica SMF cantilever is suspended horizontally adjacent to the channel. The SMF cantilever is anchored at one end and free to bend at the other end, accepting an input light at the fixed end (from an external light source). A receiving MMF (unmoveable) is embedded in the channel and aligned with the SMF along central optical axis. As the worm contacts the SMF cantilever and squeezes through the troughs of the sine-wave channel, the SMF cantilever is forced to deflect horizontally away from the channel by the normal force, Fn, of the worm (see inset in Fig. 1, and a video clip in Electronic Supporting Information). This reduces light coupling from the SMF to the MMF and thus the transmitted optical power received by an external photodetector (connecting to the MMF). By this means, Fn of the worm exerted on the SMF cantilever was detected. The horizontal placement of the SMF has the advantage of a high aspect ratio of the SMF, and leads to a more sensitive detection of the responses of the SMF to Fn. As the worm swims through the whole sine-wave channel, the multiple worm-SFM contacts at the different detection points (DPs) generates multiple force data that can be cross-checked and/or averaged, thus improving the reliability of the force data.
Fig. 1.
Optical image of a fabricated fiber-optic microfluidic device for detecting force of a small nematode worm. The white dashed line represents a wave form of a sine-wave channel. The blue circles highlight multiple detection points (DPs) along a thinned single mode fiber (SMF) cantilever. Inset shows a worm (SENS O. dentatum larvae) pushing the cantilever away from the original while squeezing through one of five DPs formed between the SMF cantilever and the lowest edge of the channel’s upper sidewall. Δx is deflection at the free end of the SMF cantilever. Fn and Ft represent the normal force and tangential force, respectively, of a worm applied to the SMF cantilever.
To obtain high mechanical sensitivity while allowing for good light propagation, the SMF cantilever was thinned down to the optical mode field diameter, df, of the fiber. The SMF (here, SMF-28, Corning) was etched to 10 μm in diameter to match the df (9.2 μm) at a light wavelength of 1310 nm and the df (10.4 μm) at 1550 nm of the original fiber. The diameter of the MMF was 65 μm. The sine-wave channel was designed to have an amplitude of 160 μm and a wavelength of 450 μm to match the traveling wave patterns of the SENS and LERV larvae used in this work. The gap between the SMF and the lowest edge of the channel’s upper sidewall, D, was 20 μm (see the denotation of D in Fig. 1; the influence of D on worm force generation will be discussed later). The fiber-to-fiber end distance was 50 μm. To ensure that the SMF cantilever deflection occurs only in planar direction, the central optical axis of the SMF was set to be 12.5 μm, or half the diameter (~25 μm) of the SENS and LERV worms used, above the bottom surface of the channel. The SMF cantilever was 2 mm long spanning over the 5 DPs. As we will see later, the length of the cantilever is limited by its elastic downward deflection in the vertical direction.
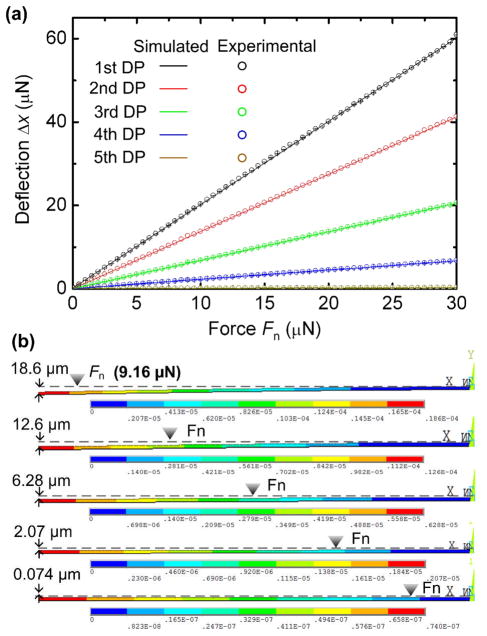
To simulate the deflection responses of the SMF cantilever to Fn applied at different DPs of the cantilever, finite-element analysis (FEA) was performed using the ANSYS software package.49 As shown in Fig. 2a, the deflection at the free end of the cantilever Δx was proportional to magnitude of Fn, following a linear spring force-deflection model given by Fn = kΔx, where k is the stiffness of the cantilever.50 As seen later (Figs. 6d and 7e), the SENS O. dentatum generates the same Fn while deflecting the SMF cantilever at different DPs. We therefore applied Fn = 9.16 μN at the five DPs in this simulation (Fig. 2b). As expected, a larger Δx was obtained as Fn was applied closer to the free end of the cantilever. Specifically, the simulated Δx was 18.6, 12.6, 6.28, 2.07, and 0.074 μm at the five DPs from left to right along the cantilever (Fig. 2b).
Fig. 2.
(a) Finite element analysis (FEA) simulated and nanoindentation determined deflection, Δx, at the end of a SMF silica cantilever, as a function of normal force applied at five DPs along the SMF cantilever. The SMF cantilever used in the FEA simulation was 10 μm diameter and 2 mm long. The SMF cantilever used in the nanoindentation experiment was 10.07 ± 0.11 μm in diameter and 2 mm in length. (b) Deflection profile of the SMF cantilever under a given normal force of 9.16 μN applied at five DPs.
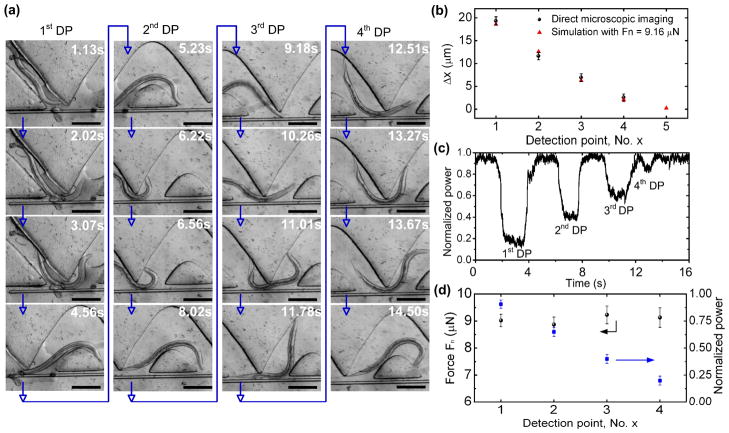
Fig. 6.
(a) Time-lapse images for a SENS O. dentatum worm pushing the SMF cantilever away from the sine-wave channel at different four DPs from left to right shown in Fig. 1. Blue arrows indicate the time-varying sequence of images. Scale bars represent 100 μm. (b) Displacement Δx at the end tip of the SMF cantilever at different DPs. At the 5th DP, only simulation data is shown due to insufficient deflection of the SMF cantilever. Experimental data were obtained via direct microscopic imaging. Calculated data were obtained using ANSYS software. Fn = 9.16 μN was used in the simulation. (c) Normalized optical power measured at the output of the receiving MMF as a function of time. (d) Experimental normal force (left axis) measured when the worm-SMF interactions occurred at the first four DPs. No readable signal was found at the 5th detection point.
Fig. 7.
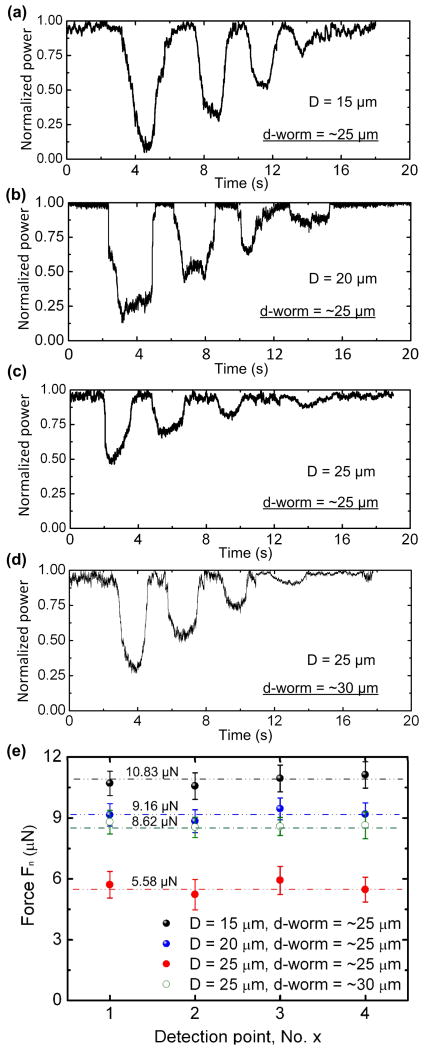
(a–c) Normalized optical power measured at the output of the MMF as function of time when the initial gap distance between the SMF cantilever and the lowest edge of the channel’s upper sidewall D = 15 μm (a), 20 μm (b), and 25 μm (c) with the worm (SENS) diameter d-worm = ~25 μm, and D = 25 μm with d-worm = ~30 μm (d). (e) Normal force of the worms measured at the first four DPs with respect to D and d-worm.
To confirm the accuracy of the model used in the Fn−Δx simulation, we used a nanoindenter (NANO Indenter XP, MTS Systems) to measure the deflections of the fabricated SMF cantilevers (see the fabrication processes in Fig. 5) under various applied forces (Fig. 2a). The SMF cantilevers under test were 10.07 ± 0.11 μm in diameter and 2 mm in length. The force and displacement resolution of the nanoindenter was 50 nN and 0.01 nm, respectively. The controlled forces Fn were applied to each DP (normal to the SMF cantilever). Each measurement was the mean ± standard deviation obtained from 9 data points. As shown in Fig. 2a, the measured displacement at the free end of the cantilever Δx had a good agreement with the simulated result, demonstrating the accuracy of the model used in the FEA simulation. Specifically, when Fn = 9.16 μN, the displacement at the free end of the cantilever Δx was found to be 18.66 ± 0.21, 12.54 ± 0.25, 6.31 ± 0.14, 2.07 ± 0.24, and 0.074 ± 0.14 μm at the five DPs from left to right along the cantilever. Correspondingly, the average changing rate of Δx with respect to Fn was calculated to be 0.50 ± 0.009, 0.75 ± 0.011, 1.48 ± 0.015, 4.49 ± 0.026, and 124.7 ± 0.914 μm/μN at the five DPs from left to right along the SMF cantilever.
Fig. 5.
(a–f) Fabrication processes for the device. (g) Optical images showing the SMF cantilever at five different locations. (f) Optical image showing nine SMFs fabricated in different runs using the same chemical wet etching method. Scale bars in (g) and (h) represent 20 μm.
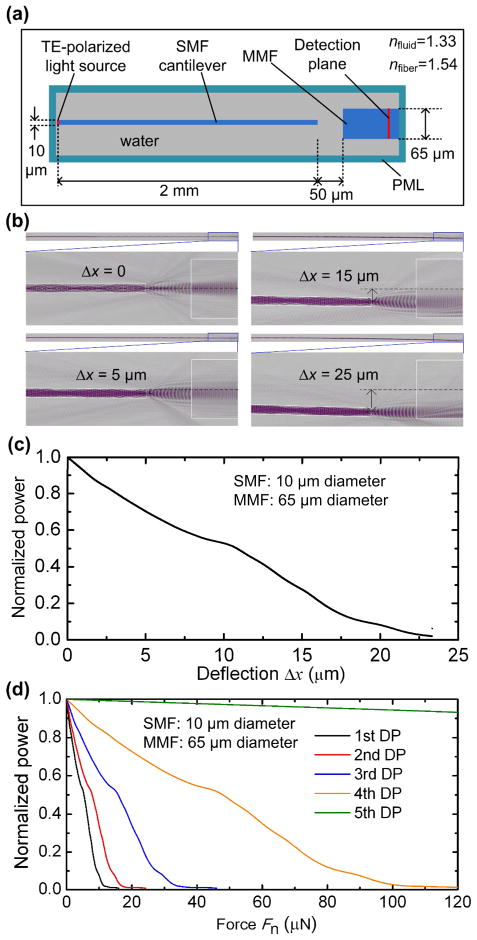
When the SMF cantilever and the fixed MMF were well aligned along their optical axis, the fiber-to-fiber end coupling efficiency reaches a maximum. However, the bending effect of the SMF caused a decrease in the coupling efficiency. Thus, to compute the optical power, P, detected at the output of the MMF as a function of Δx, we employed the three-dimensional finite-difference time-domain (FDTD) method based on the MEEP software package.51 This method allowed us to include the dielectric (or refractive index) properties of all device components (the SMF cantilever, the MMF, and the surrounding environment) into the model. Thus, the simulation inherently took into account the effect of the light refraction at the fiber side–water and fiber end–water interfaces on the final optical readings. The computing region is shown in Fig. 3a. A 10 μm thick perfectly matched layer (PML) was applied at the boundaries of the entire computing region. A transverse electric (TE)-polarized line source was placed at the input of the SMF cantilever. Fig. 3b shows the optical field distributions of the device at different bending conditions. The simulation result includes two factors for determining the level of reduction in the output optical power, including the axial misalignment between the two fibers, and distortion of the SMF’s fundamental mode field (due to small-angle bending). By combining the results shown in Figs. 2a and 3c, we obtained the relationship between the normalized P and applied Fn (Fig. 3d). The result shows that P decreases with increasing Fn applied at each DP.
Fig. 3.
(a) Top-view schematic of the computing region used in the 3D finite-difference time-domain (FDTD) simulation. (b) Optical field distributions in the optical coupling region between the SMF cantilever and MMF under different bending conditions: Δx = 0, 5, 15, and 25 μm. The fields were extracted in the horizontal plane at the optical axis of the two fibers. (c) FDTD simulation result of normalized optical power detected at the output of the receiving MMF, as a function of deflection Δx at the end of the SMF cantilever. (d) Simulation result of normalized optical power as a function of Fn applied to the SMF cantilever at different DPs.
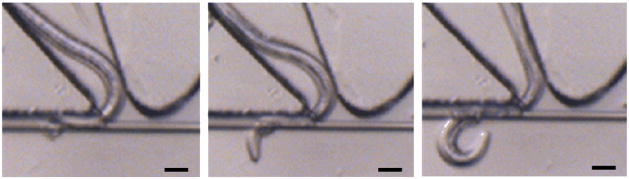
It is desirable to employ longer SMF cantilevers to achieve higher mechanical sensitivity to an applied Fn, but practically, to prevent the worm under test from crossing over the SMF cantilever to the other side of the sine-wave channel, the SMF cantilever needed to be suspended horizontally in the channel. Thus, the length of the cantilever was actually limited by natural elastic deflection of the cantilever in the vertical direction. Our ANSYS simulation result indicates that the 2 mm long SMF cantilever (used in the previous figures) dropped about Δz = 0.75 μm at the free end of the cantilever from the horizontal direction. With this design, 10.66 % of 244 worms were observed to cross over the cantilevers at the 1st DP (see the Handling of Nematodes section). As mentioned in the Introduction section, nematodes generally maintain their motion generation mechanism by producing lateral thrust, We thus believe that there was little vertical force exerted to the 2 mm long SMF cantilever when the central optical axis of the cantilever was designed to be at half the worm diameter above the substrate. Fig. 4 shows a failure of the force test with a 4 mm long SMF cantilever having a relatively large drop of Δz = 2.1 μm at its free end. Since the head part of the worm was a little sharp relative to other parts and could move in more complex ways, the worm had a relatively high chance to first move its head on the upper part of the cantilever, and then, cross over the cantilever from the top of the cantilever via the lateral motion. According to our observation on 55 worms, ~52.7 % of the worms crossed over the 4 mm long SMF cantilever. Thus, the length of the SMF cantilever was chosen to be 2 mm for the present device.
Fig. 4.
Optical images for a SENS O. dentatum larvae crossing over the 4 mm long SMF cantilever from the top of the cantilever at the 1st DP of the device. Scale bars represent 20 μm.
Device fabrication
Figs. 5a–f shows the fabrication processes for the proposed device. First, poly(dimethylsiloxane) (PDMS) microstructures (e.g., the sine-wave channel, and the alignment structures for the fibers) are replica molded using conventional soft lithography techniques (Fig. 5a).52 The silica SMF (SMF-28, Corning) and the MMF (62.5/125-CPC6, Corning) are immersed in 49 wt.% hydrofluoric (HF) acid solution at room temperature for 120 and 60 mins, respectively. This allowed us to pre-thin the SMF from 125 μm down to 25 μm, and the MMF from 125 μm to 65 μm. Then, the two fibers were inserted and positioned in the alignment structures, with the help of a micropositioner (Fig. 5b). To form a 10 μm-diameter SMF cantilever, we protected the MMF from being etched by a buffered HF (BHF, 10 vol./vol. %) solution. Thus, the channel was filled up with a precursor solution consisting of isobornyl acrylate (IBA), tetraethylene glycol dimethacrylate, and 2,2-dimethoxy-2-phenylacetophenone with a weight ratio of 32 : 1.7 : 1.0 (Fig. 5c).53 The precursor solution was then selectively polymerized under ultraviolet light (10 mW/cm2, 24.8 s) with a photomask. This allowed for formation of HF resistant poly-IBA structures around the MMF and fixing one end of the SMF (Fig. 5d). Next, the flexible part of the SMF was etched down to 10 μm diameter in the BHF solution for 75 mins (Fig. 5e). Note that the removal of the fiber cladding did not interfere with light guidance through the silica core, since the original refractive index cladding (n = 1.463) was replaced by water (n = 1.333).54 Lastly, the PDMS structure was bonded to a glass slide by oxygen plasma treatment (Fig. 5f). Thus, the fiber-optic microfluidic device was formed.
It should be pointed out that the final diameter and uniformity of the SMF cantilever would significantly influence the mechanical properties and thus the actual readings of the muscular forces. The use of the low average etching rate of 0.2 μm / min during thinning the SMF from 25 to 10 μm ensured a relatively high uniformity in the final diameter of the SMF cantilever. As shown in Figs. 5h and 5g, the final diameter of the fabricated SMF cantilever was 10.03 ± 0.12 μm (mean ± standard deviation, obtained by averaging the measurement results over nine SMF cantilevers with each cantilever providing 5 data points). Note that these SMF cantilevers were fabricated in different runs by using the same chemical wet etching method, demonstrating the reproducibility of forming the desired thin SMF cantilever (the most important component of the device).
Optical measurement setup
In our optical measurement setup, a fiber pigtailed laser diode of 1310 nm nominal wavelength (LPS-1310, Thorlabs) was used as an external light source and coupled into the SMF cantilever. Real-time output signals from the MMF were detected by an optical power meter (1918-R, Newport) with built-in data acquisition software.
Velocity measurement
While the present force sensing scheme did not require using a microscope or a camera, we used a stereo microscope (MZ205, Leica) and a video camera (QICamera) to show the worm-SMF cantilever interactions and measure the average moving velocity of worms exposed to anthelmintic levamisole with different concentrations (Fig. 8). The worm average velocity was defined as the continuous forward linear distance travelled by a worm’s head with respect to time. The stereo microscope-camera system captured a series of digital images (1392 × 1040 pixels) at a specified time interval of 100 ms. The images were sequenced and compressed into the Audio Video Interleave (.avi) video format. The .avi video was post-processed by a worm tracking program that was able to extract track signatures and locomotion (e.g., number and duration of stops, and cut-off region) of individual and/or worms.45 Briefly, the program analyzed a large number of images to recognize a moving object (here worm) and then, extract motility parameters such as amplitude, wavelength, body postures, and path traversed by the worm.
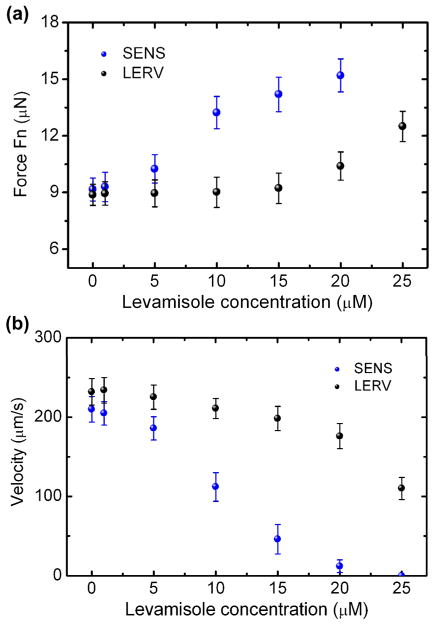
Fig. 8.
Normal force (a) and moving velocity (b) of the SENS and LERV isolates as a function of levamisole concentration. The moving velocity is tested on plate.
Parasitic nematode O. dentatum
Many nematodes are ubiquitous soil-dwelling organisms and are crucial for maintaining soil nutrients and overall symbiotic relationships between plants and other organisms.55 However, many of the more than 10,000 known nematode species are parasitic, infecting plants (e.g. corn, soybean, wheat, and other food grains), animals (e.g. pigs, sheep, goats, and cows) and humans.56 The parasitic nematode used in this research, O. dentatum, is a hog parasite that causes nodule growths in the pig’s gut wall. These nodules repress growth and thereby reduce available pork yield. It is similar to the Oesophagostomum species parasites of humans.
Parasitic nematode larvae SENS (levamisole-sensitive) and LEVR (levamisole-resistant) O. dentatum were originally supplied by the Royal Veterinary and Agricultural School, Frederiksberg, Copenhagen and then reproduced at 6 – 9 month intervals by passage in pigs at the Iowa State University, Ames, Iowa. The L3 larvae isolates were maintained between passages in tap water refrigerated at 11 °C (changed every 2 – 4 months). They were about 6 months old and 400 – 500 μm long and about 25 μm diameter when used for our experiments.
Handling of nematodes
A conventional pipette was used to transfer O. dentatum worms to the sine-wave channel at the worm inlet of the device. No attractant was used to drive worms inside the channel. With the gap D between the SMF and the lowest edge of the channel’s upper sidewall of 20 μm, 183 (75 %) out of 244 worms moved through all five DPs, 26 (10.66 %) crossed over the cantilever at the first DP, and 35 (14.34 %) were stuck at the first DP that could be sucked out by a pipette through the inlet of the device.
Results and Discussion
Fig. 6a shows time-lapse images for a SENS worm interacting with the SMF cantilever at different DPs of the device. Each measurement presented here was the mean ± standard deviation obtained from 22 observations. As the worm squeezed through the 1st, the 2nd, the 3rd and the 4th DP from left to right (Fig. 6a), the maximum deflection at the free end of the SMF cantilever was Δx = 19.3 ± 0.92, 11.6 ± 0.83, 6.9 ± 0.85, and 2.5 ± 0.81 μm (Fig. 6b), respectively. The decreasing tendency of Δx was observed in the microscope and shows good agreement with the simulation result with Fn = 9.16 μN (Fig. 2b). Fig. 6c displays a typical time-varying optical power signal measured at the output of the MMF as the worm travelled through the whole channel. Interestingly, the optical power decreased respectively by 90.4 ± 3.92, 65.2 ± 4.22, 41.2 ± 3.88, and 20.2 ± 4.18 %. This resulted from decreasing the deflection of the cantilever as the worm-SFM contact occurred closer to the fixed end of the cantilever. By extrapolating from the Fn−P curve shown in Fig. 3d, the magnitude of Fn imposed by the worm onto the cantilever at the four DPs (from left to right) was found to be 9.02 ± 0.23, 8.87 ± 0.28, 9.23 ± 0.33, and 9.13 ± 0.36 μN, respectively (Fig. 6d). The force measurement result revealed that the worm generated almost an equal amount of Fn = 9.16 ± 0.32 μN, during squeezing through the multiple DPs (Fig. 6d). Therefore, the closer the DP was to the fixed end of the cantilever, the less the cantilever deflection was, as shown in Fig. 6b. The small standard deviation of Fn might be attributed to individual differences between the worms and/or slight geometric difference between the multiple DPs. We point out that the reduction of optical power due to the worm-SFM contact at the 5th DP was not large enough to be read by the photodetector, which will be discussed later. Nevertheless, by integrating multiple structurally similar DPs to the sine-wave channel along the SMF cantilever, the device provided multiple force data allowing additional validation.
To examine the influence of the gap D between the SMF and the lowest edge of the channel’s upper sidewall on force generation of the worms, we varied D from 5 to 50 μm with steps of 5 μm. The SENS worms were taken from the same batch as those used above, having the body diameter d-worm = ~25 μm. When D = 5 and 10 μm, the worms could hardly squeeze through the 1st DP, while instead they touched the cantilever and then oscillated locally. Thus, with this design, the device was not able to detect force of the worms. As the gap increased becoming comparable to or slightly less than the diameter of the worm, about 75 % of the worms were able to get into the gap and push the cantilever away to pass through the sine-wave channel. Figs. 7a–c show the optical power signals detected at the output of the MMF for the worms with d-worm = ~25 μm when D = 15, 20, and 25 μm, respectively. As D increased, Fn of the worms increased (Fig. 7e). Each data point in Fig. 7e was obtained from measurement of 9 worms. An intuitive explanation is that the worms needed to generate a larger squeezing force to go through a narrower space. When D increased further to be greater than 30 μm, the worms were observed to have relatively random and insufficient contacts with the SFM cantilever, resulting in random optical power signals at the output of the MMF. In addition, we examined the influence of the body diameter of nematodes d-worm on their muscular force generation when the gap D was fixed. Fig. 7d shows the detected optical power signal as a large SENS (d-worm = ~30 μm) went through the DPs with D = 25 μm. Compared to the small worms (d-worm = ~25 μm) with Fn = ~5.58 μN, the large worms (d-worm = ~30 μm; 9 worms tested) generated a larger Fn = ~8.62 μN, which was 54.5 % more than the small ones (Fig. 7e), to pass through the same DPs.
According to the time-varying optical power measurement results shown in Figs. 6c and 7a–d, the mean background noise power level of the detection system, Pns, was approximately 2.5 % of the maximum output optical power, Pmax. Thus, by looking at Figs. 3c and 3d, a noise equivalent displacement (NED) of the cantilever and a noise equivalent force (NEF, at the 1st DP) of the device was found at 0.28 μm and 143 nN, respectively. When the worm-body contact occurred at the last or the 5th DP, the predicted deflection of the cantilever was only Δx = 0.074 μm (Fig. 2b). No obvious optical signal reduction or force data were thus detected at this DP.
As shown in Fig. 3d, the magnitude of the output optical signal was almost saturated at a low level when the SMF deflection goes beyond 23 μm from the central optical axis of the SMF. Thus, we defined the upper boundary of detection range of the device at each DP to be the force at which the saturation starts. It is also noteworthy that the upper limit of the detection range varied with numerical aperture of the MMF, and with the end-to-end distance between the SMF and MMF. Here we define the lower boundary of detection range to be two times the value of NEF at each DP. Table 1 summarizes the NEP and detection range of the device.
Table 1.
Summary of the noise equivalent force and detection range of the device at each DP
| Detection point | Noise equivalent force (μN) | Detection range (μN) |
|---|---|---|
| 1st | 0.143 | 0.28–12.48 |
| 2nd | 0.21 | 0.42–16.65 |
| 3rd | 0.42 | 0.84–34.02 |
| 4th | 1.29 | 2.58–103.17 |
| 5th | 36.02 | 72.04–3094.60 |
Many anthelmintic drugs act on the neuromuscular system of nematodes, causing neuromuscular contraction.16 Drug resistance of parasitic nematodes may be related to effects on the signalling-muscle-contraction pathways by these drugs.16 We conducted an initial pilot experiment to explore the possibility of adapting the present force measurement technique to examine muscular force dose responses of the SENS and LEVR O. dentatum larvae to the anthelmintic levamisole. The levamisole solutions with different concentrations were prepared by dissolving levamisole stock solution with appropriate amounts of M9 buffer solution. The recipe for the M9 buffer (3 g KH2PO4, 6 g Na2HPO4, 5 g NaCl, 1 mL 1 M MgSO4, and H2O to 1 L) was a standard recipe. The devices used here had the same D = 20 μm as those used in the previous experiments. Each data point in Fig. 8 was obtained from measurement of 11 worms.
Fig. 8a shows that as the levamisole dose increased from 1 to 20 μM, Fn of the SENS isolate increased from 9.16 to 15.25 μN. The result is logical as the levamisole depolarized muscle and increased muscle contraction and thus the muscular force of the whole worm. No force data were obtained at 25 μM and higher concentrations because the SENS isolate became paralyzed at those high doses. On the other hand, for the LEVR isolate, there was only a slight increase in Fn as the levamisole concentration increased from 1 to 20 μM. At the higher concentration of 25 μM, an obvious increase of Fn occurred to the LERV isolate. Also, the result in Fig. 8a indicates that in the presence of the same dose of levamisole below 20 μM, the drug effect on the SENS muscles in the normal direction (with respect to the movement) was greater than that on the LEVR muscles. Thus, we have observed the distinct phenotype differences in the muscular force of the SENS and LEVR isolates when exposed to levamisole. The result was consistent with the larval migration studies where SENS was inhibited more than LEVR by levamisole.16 To relate the muscular force phenotype to the locomotive behavior of the worms, we tested the moving velocity of the SENS and LERV isolates on a 1 inch diameter Petri dish. The result in Fig. 8b shows that although the average velocity of both of the isolates decreased with increasing levamisole concentration, the LERV was less sensitive to levamisole than the SENS in terms of the moving velocity. The cause of the velocity reduction may be associated with the increasing muscular force in the direction normal to the worm’s translational movement and thus the resultant spastic paralysis. Thus, the device allowed for clear separation of the muscular force phenotype differences between nematode isolates. The drug response test conducted here not only verified the workability of the present technique further, but also demonstrated the useful capability to bridge the observations on the motility and the muscular force generation of individual worms when exposed to different drug environments.
Conclusions
To summarize, we have developed an integrated fiber-optic microfluidic device capable of measuring the muscular force of nematode worms normal to the translational movement direction. Multiple identical DPs were formed along a thinned SMF cantilever horizontally placed adjacent to a sine-wave channel with multiple open troughs. Physical contacts between a moving worm and the SMF cantilever at the DPs bent the SMF cantilever, reducing light coupling from the SMF to the receiving MMF. Thus, the SMF cantilever transduced the normal force of the worm into optical transmission signals. We have demonstrated the workability of the device to detect normal forces exerted by the O. dentatum L3 larvae onto the SMF cantilever. It was important that the space dimension between the SMF cantilever and the sine-wave was comparable to or slightly less than the diameter of the worm. We have shown that the worm imposes an equal amount of normal force on the SMF cantilever at different DPs. The NEP of the device was 143 nN at the 1st DP. We have measured the force responses of the SENS and LERV O. dentatum larvae to different doses of the anthelmintic levamisole. The result showed that the both of the isolates generate larger muscular (normal) force when exposed to a higher concentration of levamisole, and the SENS muscles were more sensitive to levamisole than the LEVR muscles. We have noticed muscular force differences between the two isolates in the degree of their drug resistance.
The ability of the present device to measure muscular force of multicellular nematodes can benefit and advance the current whole animal assays. For example, conventional nematode motility assays (e.g., larval migration assay57) for detection of drug resistance uses a mesh system, where the worms resistant to a certain anthelmintic can move through the mesh, whereas the sensitive worms are restricted. The output information obtained is thus only a percentage of worms that are inhibited by the applied drug. Recent microfluidic approaches, along with imaging systems and automated algorithm, have made it possible to provide important phenotypic parameters of nematodes such as average velocity and oscillation frequency.58,59 However, these methods are limited by a lack of more direct measures of drug resistance. Since drug resistance of parasitic nematodes may be associated with the many different changes in signalling-muscle-contraction pathways, our technology will have the potential to provide a more direct measure of the effectiveness of drugs, by qualifying the muscular force of parasitic nematode species. Furthermore, this technology can provide a new insight into developing better quantitative models for revealing phenotypic differences in nematodes under various drug concentrations, as well as screening mutants at the single animal resolution.
Supplementary Material
Acknowledgments
This work is supported by the NSF under award no. ECCS-1102354, the McGee-Wagner Research Fund, the NIH grant: R56 AI047194–11 National Institute of Allergy and Infectious Diseases, and the China Scholarship Council. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of Allergy and Infectious Diseases. The authors thank all members in the Laboratory for NEMS and Lab-Chips for helpful discussion.
Footnotes
Electronic Supplementary Information (ESI) available: a video clip showing a typical body contact between a parasitic nematode (levamisole-sensitive O. dentatum larvae) and the thinned single mode optical fiber in the microflluidic channel, and the resultant bending of the fiber. See DOI: 10.1039/b000000x
Notes and references
- 1.Niebur E, Erdos P. Biophys J. 1991;60:1132–1164. doi: 10.1016/S0006-3495(91)82149-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Harris JE, Crofton HD. J Exp Biol. 1957;34:116–130. [Google Scholar]
- 3.Park S, Goodman MB, Pruitt BL. Proc Natl Acad Sci U S A. 2007;104:17376–17381. doi: 10.1073/pnas.0702138104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ghanbari A, Nock V, Blaikie R, Chen XQ, Wang WH. The 6th Annual IEEE International Conference on Automation Science and Engineering; 21–24 Aug. 2010; Toronto, Ontario, Canada. pp. 198–203. [Google Scholar]
- 5.Herndon LA, Schmeissner PJ, Dudaronek JM, Brown PA, Listner KM, Sakano Y, Paupard MC, Hall DH, Driscoll M. Nature. 2002;419:808–814. doi: 10.1038/nature01135. [DOI] [PubMed] [Google Scholar]
- 6.Fang-Yen C, Wyart M, Xie J, Kawai R, Kodger T, Chen S, Wen Q, Samuel ADT. Proc Natl Acad Sci U S A. 2010;107:20323–20328. doi: 10.1073/pnas.1003016107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Korta J, Clark DA, Gabel CV, Mahadevan L, Samuel ADT. J Exp Biol. 2007;210:2383–2389. doi: 10.1242/jeb.004572. [DOI] [PubMed] [Google Scholar]
- 8.Sznitman J, Purohit PK, Krajacic P, Lamitina T, Arratia PE. Biophys J. 2010;98:617–626. doi: 10.1016/j.bpj.2009.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sznitman J, Shen X, Purohit PK, Arratia PE. Exp Mech. 2010;50:1303–1311. [Google Scholar]
- 10.Sivasundar A, Hey J. Genetics. 2003;163:147–157. doi: 10.1093/genetics/163.1.147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dent JA, Smith MM, Vassilatis DK, Avery L. Proc Natl Acad Sci U S A. 2000;97:2674–2679. doi: 10.1073/pnas.97.6.2674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nishikawa K, Biewener A, Aerts P, Ahn AN, Chiel HJ, Daley MA, Daniel TL, Full RJ, Hale ME, Hedrick TL, Lappin AK, Nichols TR, Quinn RD, Satterlie RA, Szymik B. Intergr Comp Biol. 2007;47:16–54. doi: 10.1093/icb/icm024. [DOI] [PubMed] [Google Scholar]
- 13.Dimitriadi M, Sleigh J, Walker A, Chang HC, Sen A, Kalloo G, Harris J, Barsby T, Walsh MB, Satterlee JS, Li C, Vactor DV, Tsakonas SA, Hart AC. PLoS Genet. 2010;6:e1001172. doi: 10.1371/journal.pgen.1001172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Brenner S. Genetics. 1974;77:71–94. doi: 10.1093/genetics/77.1.71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang W, Sun Y, Dixon S, Alexander M, Roy PJ. J Lab Autom. 2004;14:269–276. [Google Scholar]
- 16.Martin RJ, Bai G, Clark CL, Robertson AL. Br J Pharmacol. 2003;140:1068–1076. doi: 10.1038/sj.bjp.0705528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Devaney E, Winter A, Britton C. Trends Parasitol. 2010;26:428–433. doi: 10.1016/j.pt.2010.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bao G, Suresh S. Nat Mater. 2003;2:715–725. doi: 10.1038/nmat1001. [DOI] [PubMed] [Google Scholar]
- 19.Conia J, Edwards B, Voelkel S. J Clin Lab Anal. 1997;11:28–38. doi: 10.1002/(SICI)1098-2825(1997)11:1<28::AID-JCLA6>3.0.CO;2-G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Neuman KC, Block SM. Rev Sci Instrum. 2004;75:2787–2809. doi: 10.1063/1.1785844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Svoboda K, Block SM. Annu Rev Biophys Biomol Struct. 1994;23:247–285. doi: 10.1146/annurev.bb.23.060194.001335. [DOI] [PubMed] [Google Scholar]
- 22.Charras GT, Horton MA. Biophys J. 2002;82:2970–2981. doi: 10.1016/S0006-3495(02)75638-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Langer MG, Koitschev A. Method Cell Biol. 2002;68:141–169. doi: 10.1016/s0091-679x(02)68008-2. [DOI] [PubMed] [Google Scholar]
- 24.Mathur AB, Collinsworth AM, Reichert WM, Kraus WE, Truskey GA. J Biomech. 2001;34:1545–1553. doi: 10.1016/s0021-9290(01)00149-x. [DOI] [PubMed] [Google Scholar]
- 25.Fass JN, Odde DJ. Biophys J. 2003;85:623–636. doi: 10.1016/S0006-3495(03)74506-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chen J, Fabry B, Schiffrin EL, Wang N. Am J Physiol Cell Physiol. 2001;280:C1475–C1484. doi: 10.1152/ajpcell.2001.280.6.C1475. [DOI] [PubMed] [Google Scholar]
- 27.Hochmuth RM. J Biomech. 2000;33:15–22. doi: 10.1016/s0021-9290(99)00175-x. [DOI] [PubMed] [Google Scholar]
- 28.Evans E, Yeung A. Biophys J. 1989;56:151–160. doi: 10.1016/S0006-3495(89)82660-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Galbraith CG, Sheetz MP. Proc Natl Acad Sci U S A. 1997;94:9114–9118. doi: 10.1073/pnas.94.17.9114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kim DH, Wong PK, Park J, Levchenko A, Sun Y. Annu Rev Biomed. 2009;11:203–233. doi: 10.1146/annurev-bioeng-061008-124915. [DOI] [PubMed] [Google Scholar]
- 31.Asbury CL, Fehr AN, Blcok SM. Science. 2003;302:2130–2134. doi: 10.1126/science.1092985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fernandez JM, Li HB. Science. 2004;303:1674–1678. doi: 10.1126/science.1092497. [DOI] [PubMed] [Google Scholar]
- 33.Chronis N. Lab Chip. 2010;10:432–437. doi: 10.1039/b919983g. [DOI] [PubMed] [Google Scholar]
- 34.Weibel DB, DiLuzio WR, Whitesides GM. Nat Rev Microbiol. 2007;5:209–218. doi: 10.1038/nrmicro1616. [DOI] [PubMed] [Google Scholar]
- 35.Miller AC, Thiele TR, Faumont S, Moravec ML, Lockery SR. J Neurosci. 2005;25:3369–3378. doi: 10.1523/JNEUROSCI.5133-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Qin J, Wheeler AR. Lab Chip. 2007;7:186–192. doi: 10.1039/b613414a. [DOI] [PubMed] [Google Scholar]
- 37.Lockery SR, Lawton KJ, Doll JC, Faumont S, Coulthard SM. J Neurophysiol. 2008;99:3136–3143. doi: 10.1152/jn.91327.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Rohde CB, Zeng F, Gonzalez-Rubio R, Angel M, Yanik MF. Proc Natl Acad Sci U S A. 2007;104:13891–13895. doi: 10.1073/pnas.0706513104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Chung K, Crane MM, Lu H. Nat Methods. 2008;5:637–643. doi: 10.1038/nmeth.1227. [DOI] [PubMed] [Google Scholar]
- 40.Heng X, Erickson D, Baugh LR, Yaqoob Z, Sternberg PW, Psaltis D, Yang C. Lab Chip. 2006;6:1274–1276. doi: 10.1039/b604676b. [DOI] [PubMed] [Google Scholar]
- 41.Hulme SE, Shevkoplyas S, McGuigan A, Apfeld J, Fontana W, Whitesides GM. Lab Chip. 2010;10:589–597. doi: 10.1039/b919265d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zhang Y, Lu H, Bargmann CI. Nature. 2005;438:179–184. doi: 10.1038/nature04216. [DOI] [PubMed] [Google Scholar]
- 43.Croll NA. J Zool. 2009;176:159–176. [Google Scholar]
- 44.Cronin CJ, Mendel JE, Mukhtar S, Kim YM, Stirbl RC, Bruck J, Sternberg PW. BMC Genet. 2005;6:5. doi: 10.1186/1471-2156-6-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Carr JA, Parashar A, Gibson R, Robertson AP, Martin RJ, Pandey S. Lab Chip. 2011;11:2385–2396. doi: 10.1039/c1lc20170k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Shi W, Qin J, Ye N, Lin B. Lab Chip. 2008;8:1432–1435. doi: 10.1039/b808753a. [DOI] [PubMed] [Google Scholar]
- 47.Doll JC, Nahid H, Klejwa N, Kwon R, Coulthard SM, Petzold B, Goodman MB, Pruitt BL. Lab Chip. 2009;9:1449–1454. doi: 10.1039/b818622g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ghanbari A, Nock V, Wang W. The 15th International conference on Mechatronics and Machine Vision in Practice; 2–4 Dec. 2008; Auckland, New-Zealand. pp. 680–685. [Google Scholar]
- 49.Kruusing A. Smart Mater Struct. 2000;9:186–196. [Google Scholar]
- 50.Syed Asif SA, Wahl KJ, Colton RJ. Rev Sci Instrum. 1999;70:2408–2413. [Google Scholar]
- 51.Oskooi AF, Roundy D, Ibanescu M, Bermel P, Joannopoulos JD, Johnson SG. Comput Phys Commun. 2010;181:687–702. [Google Scholar]
- 52.Xia Y, Whitesides G. Annu Rev Mater Sci. 1998;28:153–184. [Google Scholar]
- 53.Dong L, Agarwal AK, Beebe DJ, Jiang H. Nature. 2006;442:551–554. doi: 10.1038/nature05024. [DOI] [PubMed] [Google Scholar]
- 54.Lien V, Vollmer F. Lab Chip. 2007;7:1352–1356. doi: 10.1039/b706944h. [DOI] [PubMed] [Google Scholar]
- 55.Albonico M, Wright V, Ramsan M, Haji HJ, Taylor M, Savioli L, Bickle Q. Int J Parasitol. 2005;35:803–811. doi: 10.1016/j.ijpara.2005.02.016. [DOI] [PubMed] [Google Scholar]
- 56.Diawara A, Drake LJ, Suswillo RR, Kihara J, Bundy DA, Scott ME, Halpenny C, Stothard JR, Prichard RK. PLoS Negl Trop Dis. 2009;3:e397. doi: 10.1371/journal.pntd.0000397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Tang HP, Ho C, Lai SS. Rapid Commun Mass Spectrom. 2006;20:2565–2572. doi: 10.1002/rcm.2635. [DOI] [PubMed] [Google Scholar]
- 58.Rezai P, Siddiqui A, Selvaganapathy PR, Gupta BP. Lab Chip. 2010;10:220–226. doi: 10.1039/b917486a. [DOI] [PubMed] [Google Scholar]
- 59.Rezai P, Siddiqui A, Selvaganapathy PR, Gupta BP. Appl Phys Lett. 2010;96:153702. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.