When and why might a Computer Aided Detection (CAD) system interfere with visual search? An eye-tracking study

Abstract

Rational and Objectives

Computer Aided Detection (CAD) systems are intended to improve performance. This study investigates how CAD might actually interfere with a visual search task. This is a laboratory study with implications for clinical use of CAD.

Methods

47 naïve observers in two studies were asked to search for a target, embedded in 1/f^2.4 noise while we monitored their eye-movements. For some observers, a CAD system marked 75% of targets and 10% of distractors while other observers completed the study without CAD. In Experiment 1, the CAD system’s primary function was to tell observers where the target might be. In Experiment 2, CAD provided information about target identity.

Results

In Experiment 1, there was a significant enhancement of observer sensitivity in the presence of CAD (t(22)=4.74, p<.001), but there was also a substantial cost. Targets that were not marked by the CAD system were missed more frequently than equivalent targets in No CAD blocks of the experiment (t(22)=7.02, p<.001). Experiment 2 showed no behavioral benefit from CAD, but also no significant cost on sensitivity to unmarked targets (t(22)=0.6, p=n.s.). Finally, in both experiments, CAD produced reliable changes in eye-movements: CAD observers examined a lower total percentage of the search area than the No CAD observers (Ex 1: t(48)=3.05, p<.005; Ex 2: t(50)=7.31, p<.001).

Conclusions

CAD signals do not combine with observers’ unaided performance in a straight-forward manner. CAD can engender a sense of certainty that can lead to incomplete search and elevated chances of missing unmarked stimuli.

Introduction

Computer-aided detection (CAD) algorithms are designed to assist radiologists during medical image interpretation. For instance, in mammography, a typical CAD system marks potential abnormalities on the image to encourage additional evaluation by the radiologist before the radiologist makes a final recommendation. In the USA, CAD is currently used on nearly 75% of all mammograms (1). A number of large studies have assessed the efficacy of CAD (2, 3). While most studies show that hit rate increases when CAD is introduced to a practice, false alarm rate also tends to increase, making it unclear whether the benefits of CAD outweigh the costs (4, 5). From a signal detection perspective, the relatively small benefit of CAD is surprising because the CAD system should be increasing the total amount of information available to the radiologists, yielding increased performance. The size of the hypothetical benefit would be larger if CAD and radiologists were making use of independent signals and smaller if they are using the same noisy signals. Even if CAD and radiologists are not independent, the hypothetical benefit seems to be larger than what is observed (3). The fact that the use of CAD produces only modest improvement in signal detection measures such as area under the ROC curve, suggests that radiologists are unable to optimally combine the information conveyed by the CAD system and information they gather from the image itself.

In the current study, we use eye-tracking to study the costs and benefits of the presence of a simultaneous CAD system. The laboratory task we created was designed to emulate critical aspects of a typical radiologic search for a difficult to find target. In both experiments, half of the observers completed the experiment without a CAD system while the other half searched the same trials with the help of our artificial CAD system that marked 75% of all targets and 10% of non-targets. In Experiment 1 targets were difficult to find because they were embedded in a field of noise. Here, the CAD system primarily aided target detection (CADe). In Experiment 2, we manipulated the appearance of our target ‘Ts’ and distractor ‘Ls’, making the Ts and Ls more similar to each other. At the same time, we decreased the opacity of the background noise the items so that the items were easier to find. Our intent was to keep the overall difficulty roughly the same across the two experiments. In this case, the CAD system primarily aided target diagnosis (CADx).

Materials and Methods

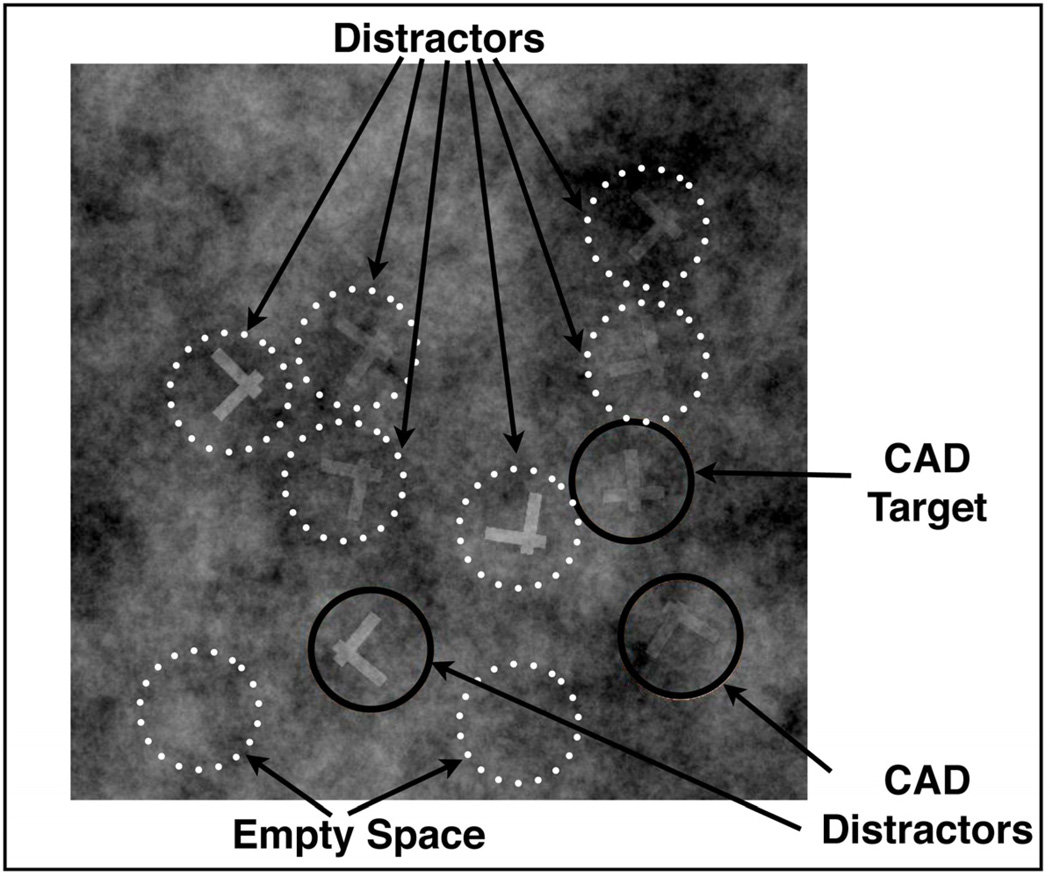
Observers were instructed to search for a target letter, T, among distractor, Ls. All of the stimuli were embedded in a 16.5° square texture of cloudlike 1/f^2.4 noise (see Figure 1). This noise roughly simulates the spatial frequency of radiologic images. Mammograms, for example, can be roughly characterized as 1/f³ stimuli (6). The similarity to real medical images is not critical in this case. The noise was merely designed to make the search task more demanding. The stimuli consisted of Ts and Ls of a random orientation that were made up of two perpendicular lines slightly offset from each other. These stimuli allowed us to manipulate the difficulty of differentiating targets and distractors by changing the offset of bars comprising these items. T’s and L’s subtended 1.35 degrees visual angle. CAD marks were pink circles with a diameter of 1.5°. Target and distractor locations were chosen at random from a 4×4 grid of possible locations. Position within this grid was randomly jittered (up to .25°) to avoid predictable locations (See Figure 1).

Figure 1.

Representative example of the search stimulus. Dotted circles represent predefined interest areas that were not visible during the experiment.

Observers were instructed to click on the T when detected and to click on an ‘absent’ button if no target was found. Half of the trials contained a single target. A confidence rating was collected at the conclusion of each trial using a 6-point scale with 6 denoting highest confidence in target presence and 1, lowest. On CAD blocks, observers were instructed to use the CAD to help them find the target, however they were told that the CAD would sometimes miss the target or mark a distractor. In this artificial situation, we could set the performance of our simulated CAD to any level. In this case, our CAD marked the target 75% of the time and marked 10% of the distractor Ls; equivalent to a d-prime value of 1.95. Each trial contained an average of 5 Ls (range: 0–15), meaning that the CAD made an average of 0.5 false positive marks per image. CAD marks appeared simultaneously with stimulus onset. This differs from the FDA-approved protocol of showing CAD marking after an initial CAD-free reading.

Both experiments employed a between-subjects design where half of the observers were assigned to a CAD condition and the other half to a No CAD condition. Observers in both conditions began with a 50 trial practice block that did not contain CAD markings. This was followed by a block of 100 experimental trials. All observers saw the same 150 “cases” though the order of cases was different for each observer. In the CAD condition, the 100 experimental trials had CAD marks added. We then compared performance across observers in the CAD / No CAD block. This design allowed us to equate the amount of experience the observers had with our task when they undertook the critical CAD/No CAD block of trials.

Differences between Experiment 1 and 2

Experiments 1 and 2 differed in the opacity of the 1/f^2.4 noise and the similarity between targets and distractors. Higher noise opacity makes the items harder to detect. Increased similarity makes targets harder to discriminate from distractors. The effects of these manipulations are not independent since noise also makes the items harder to discriminate. However, separately manipulating these two factors allows us to produce two tasks with similar performance for different reasons. Experiment 1 had high noise and low similarity between targets and distractors while Experiment 2 had lower noise and higher similarity between targets and distractors. Thus, the targets in Experiment 1 were difficult to detect but easy to “diagnose”. Here CAD would aid detection (CADe). The targets in Experiment 2 were easy to detect and hard to identify. In this case, CAD would aid diagnosis (CADx).

Observers

Twenty-three observers were tested in Experiment 1 and 24 in Experiment 2. Observers ranged in age from 18 to 54 (average = 24.3, standard deviation = 5.7, 11 male). All had at least 20/25 acuity (with correction as needed) and could pass the Ishihara Color-Blindness test. All gave informed consent and were paid $10/hr for their time.

Apparatus

Eye movements were recorded with an EyeLink1000 tower system (SR Research, Canada) at a sampling rate of 1000Hz. Each block within the experiment was preceded by a randomized, 9-point calibration and validation procedure. Experimental Sessions were carried out on a Macintosh G4 computer running Mac OS 10.5 and written in Matlab 7.5 (The Mathworks) using the Psychophysics Toolbox (7, 8), version 3. Stimuli were presented on 20” CRT monitor (Mitsubishi Diamond Pro 91TXM) with resolution set to 1280×960 pixels, and an 85 Hz refresh rate. Observers were 57.4 cm from the monitor. At this viewing distance, 1 cm subtends 1° of visual angle (°). We measured eye-movements from the onset of the stimulus material until the observer clicked on either the target or a ‘no target’ button.

Eye-Tracking Interest Areas

To quantify the amount of time spent on different types of stimuli during whilst searching for targets, we pre-defined a number of regions of interest (ROIs) on each trial and measured the amount of time spent by the eyes in each region. Each ROI was a circle that subtended 1.5°. ROIs included each distractor on the trial, 2 regions of Empty Space and, when present, the target. As noted, items and, thus, their ROIs were located on an invisible jittered 4×4 grid. Empty space ROIs were randomly chosen from among the possible item locations that did not contain an item.

Results

In Experiment 1, we compared performance for the CAD and No CAD groups. Recall that Observers clicked on the target or on an “absent” box on each trial. Based on those responses, there was a modest but significant increase in sensitivity from 80% in the No CAD to 87% in the CAD blocks (t(22)=4.74, p<.001). There was a small, statistically insignificant decrease in specificity: (No CAD 91%; CAD 88%; t(22)=1.05, p>.2). D-prime was 2.20 in the No CAD condition and 2.26 in the CAD condition. The difference was not significant (t(22)=.97, p>.3). The 6-point rating scale data was used to compute an area under the ROC curve. Again, there was no significant benefit from the CAD (AUC: CAD= .71, No CAD=.67, t(22)=0.4, p> 0.6).

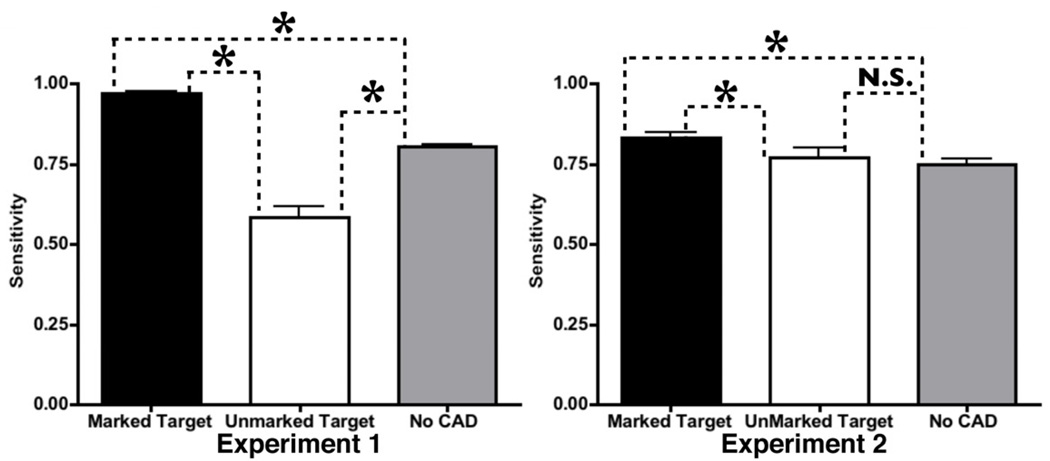
Insight into the lack of benefit appears in Figure 2. Here sensitivity is shown separately for marked and unmarked targets in the CAD condition as well as for the No CAD condition. As would be expected, sensitivity was considerably higher for targets that were marked by CAD (No CAD condition 81%, CAD-marked 97%: t(22)=15.75,p<.001). However, sensitivity for unmarked targets in the CAD block was dramatically lower, just 56%; significantly lower than performance in the No CAD block (t(22)=7.02,p<.001). The difference in sensitivity between marked and unmarked targets was also significant (t11)=13.16, p<.001).

Figure 2.

Sensitivity for different trial types in Experiment 1 and 2. Stars denote significant differences (p<.05) between sensitivity for a given condition and the No CAD block. Errors bars here and throughout the paper represent standard error of the mean.

Experiment 2 (CADx version) decreased noise opacity and increased similarity of target Ts and distractor Ls. The targets were easier to find but harder to identify. CAD effects were smaller in this CADx simulation than they were in the CADe simulation. There was a marginally significant increase in sensitivity from 79% (No CAD) to 84% (CAD) (t(22)=2.00, p=.06). Specificity did not change significantly (CAD: 83%, No CAD 87%, t(22)=1.11, p>.2) nor did d-prime (CAD: 1.65, No CAD 1.56: t(22)=0.98, p>.3) or the area under the ROC curve, calculated from the rating data (CAD: .68, No CAD .66: t(23) = 0.17, p = 0.87).

Turning to marked and unmarked targets in the CAD block, we see that, as in Experiment 1, marked targets are found more frequently (83%) than unmarked-targets (77%: t(11)=2.23, p<.05). The sensitivity to marked targets is higher than the sensitivity in the No CAD block (CAD:87%, No CAD: 82%, (t(22)=3.64, p<.005). However, unlike Experiment 1, sensitivity to the unmarked targets in the CAD block was not significantly lower than in the No CAD block (t(22)=0.6, p>.5.; See Figure 2).

Perhaps the increased miss rate for CAD observers is due to a tendency to spend less overall time due to an over-reliance on the CAD system. This hypothesis was not supported by the response time data in either experiment. In both experiments the overall mean response time did not differ between the CAD and No CAD groups (Experiment 1: t(21)=1.67, p=.11; Experiment 2: t(22)=1,45,p=.16). The same result held for trials that did not contain a target (Experiment 1: t(21)=1.23, p=.21; Experiment 2: t(22)=1.46, p=.16). CAD seems to have changed the way observers spent their time; not the amount of time that they spent.

Eye Movements

We quantified eye movements by analyzing overall coverage of the search area, cumulative dwell time on specific regions of the search images (Targets, Distractors or Empty Space) and frequency with which these interest areas were simply never fixated.

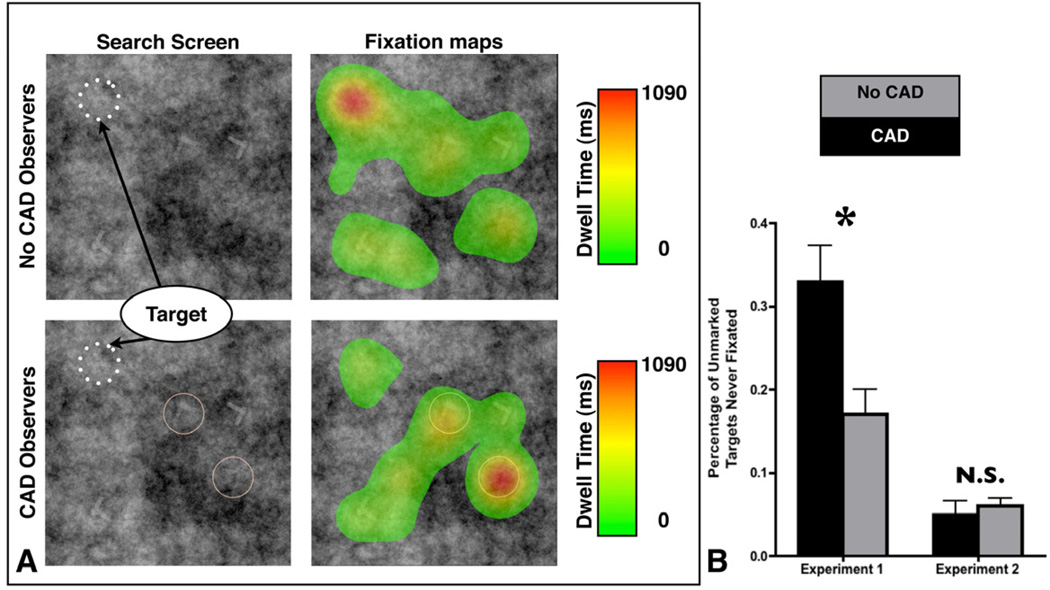
The most dramatic finding in the behavioral data is the reduction in sensitivity for unmarked targets in the CAD condition of Experiment 1, the CADe simulation. Intuitively, it would seem that Observers put too much faith in an imperfect CAD, assuming that the CAD marked all targets. An analysis of eye movements can substantiate this intuition. The two primary results of our analysis of the eye-movements are previewed in Figures 3a & 4a. We created heat maps that represent the amount of time spent in each position of the search area for two representative trials from Experiment 1. The trial is shown on the left with the eye movement heat map overlaid on the right. The upper fields show an example without CAD. The lower fields show the same display in a condition where it received two CAD marks, neither one marking the target, in this case. Each map is a composite of the eye movements of 11 observers. The final No CAD observer was excluded so that the two groups were equal.

Figure 3.

A: Heat maps for a target present trial where the CAD system did not mark the target. Search array and heat maps for the No CAD observers and CAD observers respectively. Color indicates the amount of time spent on a particular region of space. Note that the scale for these heat maps is the same. B: Percentage of unmarked targets that were never fixated in Experiment 1 and 2. Star denotes a significant difference between the percentage of targets missed in the CAD and No CAD block during Experiment 1.

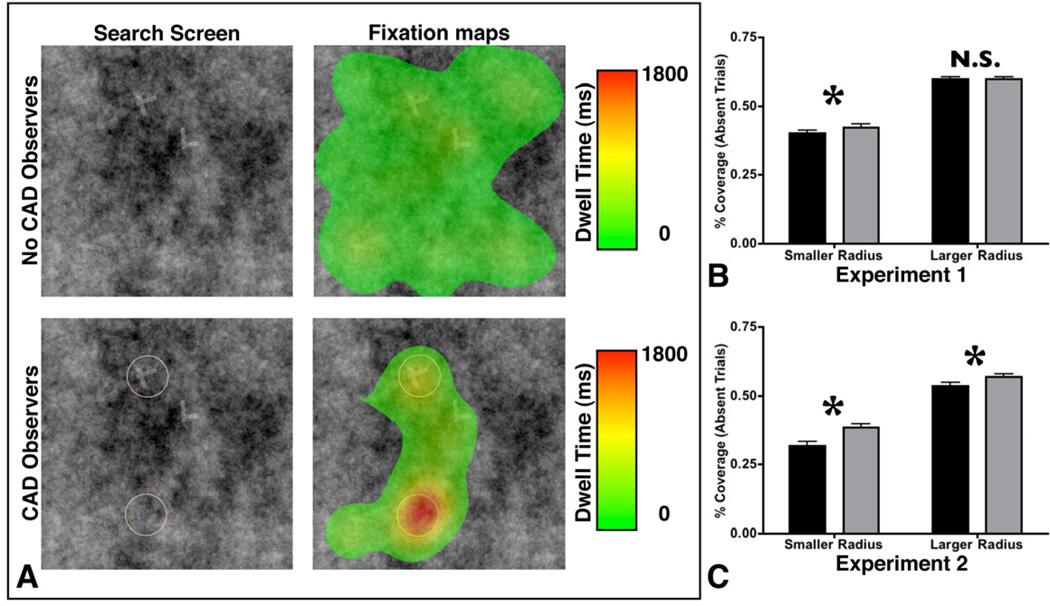
Figure 4.

A: Heat maps for a target absent trial. Search array and heat maps for the No CAD observers and CAD observers respectively. Color indicates the amount of time spent on a particular region of space. Note that the scale for these heat maps is the same. B: Percent coverage for absent trials for Experiment 1 and 2. Coverage was computed using a 2.1° (smaller) and 5° (larger) circle. See text for additional details.

The figure suggests that when a target is present but unmarked, Observers in the CAD condition spend less time looking at it. Indeed, observers fail to fixate unmarked targets at all more frequently in the CAD than in the No CAD conditions. To quantify this result, we analyzed the percentage of unmarked targets that were never fixated by the observer for Experiment 1 and 2 (See Figure 3b). There was a significant interaction between Experiment and CAD presence on the percentage of targets that were never fixated (F(1,43)=8.72, p<.01) as well as main effects for both CAD presence (F(1,43)=7.49, p<.01) and Experiment (F(1,43)=49.3, p<.001). There was a significant effect of CAD presence in Experiment 1 (F(1,21)=9.01, p<.01), but no effect in Experiment 2 (F(1,22)=.05, p=.83.), suggesting that the interaction was driven by the increased miss rate in the absence of CAD in Experiment 1. This result is consistent with the heat maps in Figure 3, suggesting that the present of CAD increased the rate of target misses when the target was unmarked.

As noted, we designed the two experiments so that our CAD system would play a different role in the two experiments. The CAD was set to the same performance level in both experiments (75% of targets marked, 10% of distractors), but the primary difficulty in the first experiment was to detect the target in the high opacity 1/f^2.4 noise, while Experiment 2 primarily challenged the observer’s ability to differentiate between similar targets and distractors. If we restrict our analysis to the No CAD observers from both experiments, the rate of targets that were never fixated was higher in Experiment 1 than in Experiment 2 (F(1,22)=15.00,p<.001): clear evidence for the increased detection difficulty in Experiment 1.

In Figure 4a, we created heat maps for a trial without a target and found that, again, the presence of the CAD strongly influenced how the area was searched. In this example, the observers in the No CAD condition appeared to do a more comprehensive job of searching the entire search display while the CAD observers spent much of their time closely examining the low salience item that was marked by the CAD system. To assess the completeness of search, we aggregated the list of all fixations across observers and computed the overall coverage of the search area for each trial as a function of the experimental condition (CAD or No CAD). The estimate of coverage is dependent on an assumption about the “useful field of view”, the region surrounding the point of fixation within which the task can be accomplished. Without additional follow-up experiments, it is difficult to determine what the useful field of view should for this set of stimuli. Here, we report this analysis with using two different useful field of view (UFOV) estimates: a circle with a 2.1° diameter adapted from the visual psychophysical literature (e.g. 9) and a larger 5° circle adapted from the medical image perception literature (e.g. 10). In computing percentage of coverage for a given trial, we marked all pixels that fell within the diameter around the center of each fixation as ‘covered’ and repeated this process for each fixation on a given trial. Coverage percentage is computed as the number of ‘covered’ pixels / total pixels for the entire search area. To assess the reliability of observed effects we analyzed coverage for each trial and compared across observer groups (CAD or No CAD). We focused our analyses on absent trials, because observers typically terminate search as soon as they find a target, making coverage metrics for target present trials more difficult to interpret. Using the smaller UFOV estimate, we found that overall coverage of the search area was significantly higher for the No CAD observers in both Experiment 1 (40.5% to 42.4%; t(48)=3.36, p<.01) and Experiment 2 (31.8% to 38.5%; t(50)=8.33, p<.001). Using the larger UFOV, the different was no longer significant for Experiment 1 (59.7% to 59.8%; t(48)=0.05, p>.8), but remained reliable for Experiment 2 (53.6% to 56.9%; t(50)=4.06, p<.001; see Figure 4b). It is not surprising that the effect of CAD on total coverage appears to decrease as the UFOV estimate is increased: as the UFOV estimate increases so does the percentage of pixels that are ‘covered’ by multiple fixations, decreasing the influence of additional fixations that are relatively close.

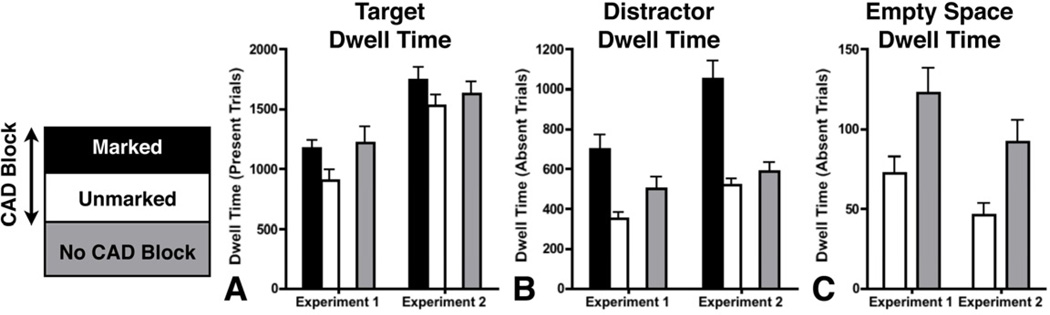
Dwell time analysis

While overall coverage is a good metric for the total amount of the space that the observers searched, we can go a step further in understanding the effects that CAD has on search behavior by measuring the amount of time spent fixating different ROIs on each trial. Recall that “Empty Space” interest areas served as control interest areas and, on each trial, consisted of two empty areas having the same size and location as Target or Distractors on other trials. We categorized each ROI in terms of whether or not it was marked or unmarked by the CAD system. This allowed us to compare time spent fixating different regions of interest (i.e. dwell time) as a function of A) whether the observer was in the CAD or No CAD condition, and B) whether the ROIs for CAD observers were or were not marked by the CAD system. Items which were not marked for the CAD observers thus allowed us to compare these items to the dwell times for visually identical regions viewed by the No CAD observers. Under these circumstances, it seems likely that any differences found in the dwell time for these unmarked areas are due to differences in the observers’ experimental context.

In Figure 5, we display the average time spent in Target, Distractor and Empty Space regions of interest for Experiment 1 and 2. Regions of interest for the CAD observers are separated based on whether or not they were marked by the CAD system. In Experiment 1, dwell time on unmarked Targets for the CAD observers was marginally lower than dwell time on always unmarked targets for the No CAD observers (t(21)=1.88, p>.05), consistent with the picture painted by the heat maps and the rate of targets that were never fixated in Figure 3a and 3b respectively. Within the CAD block, we found that observers tended to spend more time looking at marked targets than targets that were not marked ((t(10)=2.51,p<.05; See Figure 5a). However, dwell time for marked targets in the CAD block was not significantly higher than dwell time for targets (that were all unmarked) in the No CAD block (t(21)=.3, p>.7). Dwell time on targets followed a similar pattern in Experiment 2. Dwell time on marked targets was longer than unmarked targets in the CAD block (t(11)=2.28, p<.05), but the marked targets for the CAD observers were not fixated longer than the targets in the No CAD block (t(22)=.72, p=.49).

Figure 5.

Mean dwell time for targets, distractors and empty space in both experiments. Data are broken down as a function of whether the ROI was marked by the CAD system, unmarked by the CAD system, or data from the No CAD observers. Data on distractors and empty space is from target absent trials. Empty Space regions were never marked by the CAD system.

In order to analyze dwell time on non-target items, we restricted our analyses to trial where there was no target present. This is to avoid those trials where a target was found, leading to search termination prior to complete investigation of the search area. Under these circumstances, the presence of CAD led to a significant decrease in dwell time on unmarked Distractors (t(21)=2.18, p<.05) and Empty Space (t(21)=2.60, p<.05; see Figure 5b, c). In both cases, as predicted by the heat maps and the overall coverage shown in Figure 4, more time was spent fixating non-target items in the No CAD observers, indicating more extensive search of the area. We also found that dwell time was much higher for marked distractors than unmarked distractors for CAD observers (t(10)=8.74, p<.001), or distractors (that were all unmarked) for the No CAD observers (t(21)=4.05, p<.001).

Similar to Experiment 1, in Experiment 2, we found evidence of less extensive search in presence of CAD despite our finding of no behavioral benefit of CAD. As in Experiment 1, observers spent significantly less time on Empty Space in the presence of CAD (t(22)=2.88, p<.01), However, unlike Experiment 1, we found no effect of CAD presence on Target dwell time (t(22)=.72, p>.4) or Distractor dwell time ((t(22)=1.11, p>.2). As in Experiment 1, we found increased dwell time devoted to marked distractors as compared to unmarked distractors for the CAD observers (t(11)=8.7, p<.001). We also found that dwell time was higher for marked distractors than distractors for the No CAD observers (t(22)=4.91, p<.001).

We also used our eye-movement data to assess whether or not our manipulation of noise opacity and target ambiguity was able to modulate how the CAD markings were used in Experiment 1 and Experiment 2. Due to the nature of the CAD signal, we hypothesized that the CAD marks would attract more attention in Experiment 1 than in Experiment 2 despite the fact that, in terms of d-prime, the two systems were equivalent. One way to quantify this effect is to examine the time when an item is first fixated on a given trial. In Experiment 1, targets with a CAD marking were first fixated after 530 ms, and this increased to 1918 ms in the same observers on those trials when the target was not marked (t(11)=9.38, p<.001). Although the same trend was present in Experiment 2, the effect did not approach significance (marked targets time to first fixation: 1409 ms; unmarked targets: 1572 ms; t(11)=.35 p>.9). It seems that the CAD marks in Experiment 1 served to guide attention to a given area quickly, while, in Experiment 2 the same marks were used to support the difficult “diagnosis” of ‘T’ vs ‘L.’ Together with the large difference in the percentage of targets that were never fixated across the two experiments (see Figure 3b), our data suggest that we were successful in creating two CAD systems that behaved in a manner analogous to CADe (Experiment 1) and CADx (Experiment 2).

Discussion

This study used eye-tracking to better understand the costs and benefits associated with the presence of CAD marks in a simulation of a radiological search task. Despite finding no overall benefit of the presence of our CAD system and no difference in terms of the amount of time spent searching these images, we found that naïve observers consistently explored images less completely in the presence of two different CAD systems. Furthermore our data suggest that the uses of CAD may depend greatly on the nature of the task that is being undertaken. We found that when CAD’s primary function was to aid target detection, it led to a large cost for those targets that were not marked. In this situation, unmarked targets were detected much less frequently than visually identical unmarked target in a block of trials without CAD. This replicates previous work that found that radiologists were less likely to recommend further evaluation of lesions that were not marked by CAD (11). However, no such effect was found when the CAD system’s primary function was diagnosis. These results have implications for both how CAD is currently used and how to design more effective CAD systems.

It is important to note that our experiments used a simultaneous rather than second-reader CAD system that is most common usage of CAD (12, 13). Our rationale for this decision was to focus on the role that the presence or absence of a CAD system has on how a given image is searched. While this design admittedly moves us away from the current recommended usage of CAD, our goal was design a task that concentrated on the influence of CAD markings on visual search strategies and performance. Future research will need to determine whether this result generalizes to sequential CAD systems where the reader assesses the image, then turns the CAD system on. According to the rationale of second-reader design, the first read should resemble the pattern of search observed for unaided search. However, this is empirical prediction that has not yet been tested. It would very interesting to see whether the first read in a second-reader design resembles proper unaided search or a truncated version of search in anticipation of the second read. Another limitation of the current study is that our observers were naïve and further work will be necessary to determine whether the tendency to search less completely holds true for radiologists searching medical images. Furthermore, this study was conducted using a sample of images that include a much higher prevalence of targets that is typically found in the clinic (14). However, Gur and colleagues have suggested that target prevalence does not influence area under the ROC curve in observer studies (15). Still, we might expect that the tendency to fail to fully search each image in the presence of CAD may be exacerbated the very low prevalence found for many tasks in the radiology clinic. Further work is necessary to determine whether this intuition holds true.

Although it is imperative to continue to improve performance by CAD systems, we believe that understanding how observers are influenced by the presence or absence of CAD is equally important. While in theory giving an observer a CAD signal should only increase d-prime, in practice (and as we have seen in the current study), this is not always the case (e.g. (3)). A number of explanations have been proposed for this situation including ignoring of CAD prompts, trusting CAD marks too much thereby decreasing specificity, or a false sense of security in the absence of CAD marks (16). For instance, previous research has shown that there was a large decrease in sensitivity for cancers that were not marked by a CAD system (3, 17). Our results confirm and extending this finding, suggesting that CAD steers observers away from searching exhaustively through empty space. This could lead to an increased miss rate for unmarked targets when the target is missed by the CAD system, but in our experiments this effect was only clearly observed when the CAD system’s primary role was detection rather than diagnosis.

Given that our observers spent roughly the same amount of time searching in the presence or absence of CAD and that more time was spent evaluating items that were marked by the CAD system, one simple way to explain our results is through a fixed resource allocation model. If an observer is willing to search a given image for a specific period of time before moving on the next trial irrespective of the presence or absence of a CAD system, then to the extent that marked items lead to longer dwell times on those items, marked items will lead to less time that can be spent exploring the image and examining unmarked items. As observed in Experiment 1 the extra time afforded to marked items is useful when the target is marked, and detrimental when the target is not marked. Unmarked targets led to a large decrease in hit rate in Experiment 1. More generally, the presence of CAD appears to lead to the less complete search observed in both Experiments.

In the current study, we focused most of our analyses on absent trials because we did include any trials with more than one target. As a result, observers should have terminated search as soon a single target was found, therefore making coverage metrics from present trials difficult to interpret. Including trials with multiple targets would fundamentally change this situation, and might enable us to test whether our fixed resource allocation model can account for search in the presence or more than one target. There is a sizable amount of evidence that even when the observer knows there may be more than one target, detection of additional targets may suffer: a phenomenon known as Satisfaction of Search (e.g. 18). In an eye-tracking study with radiologists searching chest radiographs, Berbaum and colleagues (19) found that dwell time on native abnormalities was not affected by the presence of an additional target that was added to radiographs. It would be interesting to see if the additional coverage metrics discussed in the current paper are also unaffected by the presence of the additional target.

No CAD system is perfect and observer studies may be provides the means necessary to improve CAD usage by studying how to convey this imperfect information source to users in the most efficient manner. While the current methodology of using artificial images and naïve observers requires additional work to determine whether these effects generalize to medical practice, they are ideal for investigating the cause of these sorts of interesting and unexpected results. We believe that naïve observer studies using advanced experimental methods such as eye-tracking can serve as a valuable first step in guiding future research in medical imaging.

In sum, our data point to two distinct causes of underperformance in the presence of CAD. CAD appears to induce observers to investigate the search area less thoroughly than in the absence of CAD. In cases where the target is hard to detect, such as Experiment 1, this can lead to significantly decreased performance for any targets that the CAD misses. Furthermore, we have demonstrated strong evidence that observers sometimes fail to properly combine information from the CAD system and the stimulus signal, leading to no behavioral benefit of CAD. This failure of data fusion suggests a re-examination of CAD display techniques so that an expert observer can more readily combine the two signals. Some recent work has suggested that CAD may be more effective if the CAD marks convey more information than a simple on or off signal and this may be one way to address this concern (16).