Using Enhanced Sampling and Structural Restraints to Refine Atomic Structures into Low-resolution Electron Microscopy Maps

Abstract

For a variety of problems in structural biology, low-resolution maps generated by electron microscopy (EM) imaging are often interpreted with the help of various flexible-fitting computational algorithms. In this work, we systematically analyze the quality of final models of various proteins obtained via molecular dynamics flexible fitting (MDFF) by varying the map-resolution, strength of structural restraints, and the steering forces. We find that MDFF can be extended to understand conformational changes in lower-resolution maps if larger structural restraints and lower steering forces are used to prevent overfitting. We further show that the capabilities of MDFF can be extended by combining it with an enhanced conformational sampling method, temperature-accelerated molecular dynamics (TAMD). Specifically, TAMD can be either used to generate better starting configurations for MDFF fitting, or TAMD-assisted MDFF (TAMDFF) can be performed to accelerate conformational search in atomistic simulations.

INTRODUCTION

Single-particle electron microscopy (EM) is a powerful technique to characterize biological complexes, which provides valuable information on both the architecture and the conformational dynamics of macromolecular assemblies. Intermediate-resolution maps of biomolecules obtained by EM are often interpreted with a judicious combination of high-resolution structures (of individual components or homologous members) and structural fitting techniques (Frank, 1990, 2002; Mitra and Frank, 2006; Frank, 2009; Frank and Gonzalez, Jr., 2010). These techniques can be classified into either rigid-body docking (Wriggers et al., 1999; Wriggers and Chacón, 2001), or flexible fitting computational algorithms (Tama et al., 2004a,b; Trabuco et al., 2008, 2009, 2011; Whitford et al., 2010, 2011; Ratje et al., 2010). Normal mode flexible fitting (NMFF) is a computationally efficient flexible fitting method based upon normal mode analysis (NMA) (Tama and Sanejouand, 2001; Tirion, 1996), which has been previously applied successfully to large biological complexes such as viruses, the ribosome, the GroEL chaperonin, and the protein-conducting channel (Tama and Brooks, C. L., III, 2002; Tama et al., 2002, 2003; Tama and Brooks, C. L., III, 2005, 2006). NMFF often uses a coarse-grained representation (though, in principle, the method is not limited to such representation) of the system to compute normal modes for flexible fitting, and can be performed using only a small number of degrees of freedom, thereby, decreasing the potential for overfitting. More recently, however, a flexible fitting technique that incorporates the information from an EM map directly into an all-atom molecular dynamics (MD) simulation, known as molecular dynamics flexible fitting (MDFF), has been developed and applied successfully to a number of important biological systems (Trabuco et al., 2008, 2009, 2010, 2011; Chan et al., 2011; Schreiner et al., 2011; Armache et al., 2010a,b; Strunk et al., 2011; Gumbart et al., 2009; Hsin et al., 2009; Li et al., 2009, 2011; Sener et al., 2009; Villa et al., 2009).

Though MDFF was originally tested for simulated maps of upto 15 Å resolution (Trabuco et al., 2008), and has been applied to even lower resolution experimental maps by us (Strunk et al., 2011) and others (Sener et al., 2009), the quality of structural models obtained for map resolutions lower than 15 Å has not been systematically analyzed before. A key issue here is related to over-fitting of atomic positions to the low-resolution electron density maps. Another known limitation of MDFF is its inability to capture the large-scale rotations of structural elements (Trabuco et al., 2008); a misoriented domain is likely to be fitted as it was initially docked. The present work is motivated by two questions that have the potential to extend the capabilities of MDFF: (a) to what extent can we describe conformational changes if MDFF-based refinement is used for maps with a resolution lower than 15 Å?, and (b) how does one study conformational changes that require large-scale domain rotations using MDFF?

In this work, we systematically analyze the quality of final models of four different proteins (adenylate kinase (ADK), maltose-binding protein (MBP), the nucleotide-binding domains of an ATP-binding cassette transporter (NBD), and a subunit of the GroEL chaperonin (GroEL)) obtained via molecular dynamics flexible fitting (MDFF) by varying the map-resolution, strength of structural restraints, and the steering forces. All of these proteins are known to undergo closed to open structural transitions elicited via domain rotations and translations. We start with their known closed crystal conformations and generate final models via multiple independent MDFF fitting simulations performed into maps with resolution of 5Å, 18Å, 20Å, 22Å, and 24Å. Simulated target-maps were used for ADK, MBP, and NBD, while experimental maps (EM Data Bank code EMD-2000) filtered to different resolutions were used for the GroEL example (Clare et al., 2012). For all four proteins, we also performed independent MDFF runs with different values of structural restraints and steering forces to demonstrate the sensitivity of fitting simulations to these parameters. Furthermore, we take an example of the G_α-subunit from the recently published crystal structure of a pharmacologically-relevant (Salon et al., 2011) β₂-adrenergic-receptor-Gs protein complex (PDB code 3SN6) (Rasmussen et al., 2011), where the flexible α-helical (αH) domain (Westfield et al., 2011) is significantly translated and rotated away in comparison to its known nucleotide-bound closed conformation (PDB codes 1CIP and 1GP2). We find that starting with multiple independent SITUS-docked (Wriggers et al., 1999) configurations of G_α, MDFF (Trabuco et al., 2008, 2009, 2010, 2011) simulations improve the fit, but are unable to find the correct orientation of αH into a simulated map of the closed conformation, even at 5 Å resolution. The backbone C_α-RMSD from known closed-state conformation of G_α for MDFF-generated final models remains ~30 Å with relatively low correlation coeffcients. However, we instead demonstrate that an enhanced conformational sampling algorithm for proteins (Abrams and Vanden-Eijnden, 2010), based upon temperature-accelerated molecular dynamics (TAMD) (Maragliano and Vanden-Eijnden, 2006, 2008), is first able to generate a relatively closed-like conformation of the G_α-subunit, which subsequently could be easily fitted via MDFF in the precise crystallographic orientation with simulated maps of the nucleotide-bound conformation of G_α(PDB code 1CIP). Motivated by this, we performed multiple independent explicit-solvent TAMD-assisted MDFF (TAMDFF) simulations by taking ADK as an example. These results show that the conformational search via MDFF can be accelerated when TAMD is judiciously combined with MDFF in a single atomistic simulation.

RESULTS

MDFF Fitting of Four Proteins with High Structural Restraints

To test the effect of varying map resolution on MDFF refinement with significantly large structural restraints (k = 300 kcal mol⁻¹ rad⁻²), we carried out fitting of the closed states of four different proteins (ADK, MBP, NBD, and a GroEL-subunit; see introduction) into maps of their respective open states at 5 Å (8.5 Å for GroEL), 18 Å, 20 Å, 22 Å, and 24 Å resolution (simulation details appear in Methods). We carried out four independent MDFF runs for each map resolution and for all four proteins. The quality of final models generated via independent MDFF trajectories can be measured by computing the root-mean-squared-deviation (RMSD; C_α) of the final structural model from the known open-state crystal structures of each protein, which were used to generate maps of different resolution, except for the GroEL-subunit where an 8.5 Å resolution experimental map (EMDB code EMD-2000) of the open-conformation was filtered to lower map resolutions. We report the C_α-RMSD traces with respect to known initial (closed) and final (open) states of each protein (Figure 1A), and superimposed cartoon representations of a final conformation (with highest correlation coefficient in four runs) for each map resolution of all proteins (Figure 1B). For all MDFF runs presented in Figure 1, the initial/final cross-correlation-coefficients are also tabulated (Table S1), and the overlay of final conformations in target-maps is shown in Figure S1.

Figure 1. MDFF Fittings of Four Example Proteins Starting from their Closed Conformations.

(A) Root-mean-squared-deviation (RMSD; C_α) as a function of simulation time (ns) during MDFF fitting of each protein into five maps of different resolutions (5Å (8.5 Å for GroEL), 18Å, 20Å, 22 Å, and 24 Å). Top panels for each protein show the RMSD from the initial closed-state crystal structures and bottom panels show the RMSD from the final open-state crystal structures. Different colors for traces indicate four independent MDFF runs for each map. For the case of GroEL chaperonin, RMSD only from the starting structure is reported for the 8.5 Å map resolution MDFF fitting due to the absence of structural information on the target open-state conformation. The RMSD from the target open-state conformation in 18 Å to 24 Å maps of GroEL were computed by using as a basis the structure with the highest correlation-coefficient obtained from the MDFF fitting in 8.5 Å map. The numbers in italics on bottom RMSD panels for each protein represent the final average RMSD with respect to known target crystal structures. (B) Cartoon representations of two different views of the overlay of final conformations generated via MDFF fitting of each protein at each map resolution is shown. Out of four independent runs for each map resolution, only the structure with the highest correlation-coefficient is rendered. Black cartoons correspond to the known target crystal conformations which are used as a basis to judge the quality of all fitting simulations, while colored cartoons correspond to the fitting with the highest correlation-coefficient for each map of each protein. See also Figures S1 (the final conformations for each of the four runs at all map resolutions), S2, and S3, and Table S1 (correlation-coefficients).

Vashisth, Skiniotis, and Brooks, 2012

From four independent runs for each map resolution, we also computed final average RMSD from known target crystal structures of each protein (numbers in italics in lower RMSD panels of Figure 1A). An RMSD of 0.0 Å from target structure will indicate the perfect overlap between MDFF-generated conformation and the crystallized final open-state structures of each protein. In general, the final achievable (via MDFF) average RMSD from known target structures indicates that the quality of final conformations generated via MDFF decreases with decreasing map resolution. For example, initial RMSD from the target open-state structure of ADK is 7.02 Å, and the final average RMSDs (in Å) for each map resolution are: 0.84 (5 Å map), 2.82 (18 Å map), 3.17 (20 Å map), 4.11 (22 Å map), and 5.06 (24 Å map). These numbers indicate that while ~88% of the conformational change could be achieved at 5 Å resolution for ADK, only ~27% is achieved at 24 Å resolution. Similar trends were observed for MBP and NBD, where conformational changes could be captured to the following extent for the highest (5 Å) and the lowest (24 Å) map resolutions considered here: 88%/31% (5Å/24Å; MBP), and 89%/41% (5Å/24Å; NBD). For the GroEL-subunit where we used an experimentally obtained target map filtered to different resolutions for MDFF fitting, initial RMSD from the target open-state structure of the GroEL-subunit is 5.98 Å, and the final average RMSDs (in Å) for each map resolution are: 1.90 (18 Å map), 2.23 (20 Å map), 2.59 (22 Å map), and 2.88 (24 Å map). We point out that the crystal structure of the final open-state conformation corresponding to the 8.5 Å EM-map of GroEL (Clare et al., 2012) is not available, and hence the RMSDs from the target open-state conformation in 18 Å to 24 Å maps of GroEL were computed by using as a basis the structure with the highest correlation-coefficient obtained from the MDFF fitting in the 8.5 Å map.

Furthermore, we also analyzed the close interplay between weakening the secondary structure restraints and lowering the map resolution. Specifically, for each map resolution of all proteins we carried out MDFF simulations with harmonic restraining spring constants of k = 0, 5, 10, 50, 100, and 300 kcal mol⁻¹ rad⁻². The C_α-RMSDs measured from the initial and final structures of each protein during MDFF runs with varying structural restraints are shown in Figure S2. These RMSD trends indicate that on lowering k-values, MDFF can overfit the structures (as indicated by RMSDs from initial structures; top panels in Figure S2) at the expense of structural distortions because over-fitted final structures diverge from the actual final crystal conformations (as indicated by RMSDs from final structures; bottom panels in Figure S2). This effect is even more pronounced beyond the map resolution of 20 Å and for k-values below 100 kcal mol⁻¹ rad⁻². Additionally, we also find that MDFF simulations at lower map resolutions can be sensitive to the steering forces tuned via force-scaling parameter ξ. Particularly, we carried out MDFF simulations with ξ = 0.2, 2.0, 5.0, and 10.0 at 18 Å and 20 Å map resolution for each protein. The C_α-RMSD traces for these simulations are shown in Figure S3. As indicated by RMSDs from the target conformations (bottom panels in Figure S3 for each protein), we find that MDFF-generated final conformations of each protein closer to the known target conformations occur at the slowest steering of ξ = 0.2, while MDFF structures obtained at ξ values beyond 2.0 significantly diverge from the known target conformations; MDFF simulations for more than one protein are highly unstable at ξ = 5.0 and 10.0.

MDFF Fails to Correctly Orient the α-Helical Domain of G_α

The crystal structure of the β₂-adrenergic-receptor-Gs protein complex (PDB code 3SN6) (Rasmussen et al., 2011) shows that the α-helical domain (αH) of the G_α-subunit in the absence of nucleotide is displaced by ~45Å/127° with respect to its nucleotide-bound closed-conformation (PDB codes 1CIP and 1GP2). Furthermore, electron microscopy (EM) maps of this complex also indicate significant flexibility in this domain (Westfield et al., 2011). Hence, the G_α-subunit is an excellent example to test if starting with the nucleotide-free open-conformation of G_α, MDFF can find the correct orientation of αH even in a noise-free simulated map of the nucleotide-bound closed-conformation at a resolution of 5 Å.

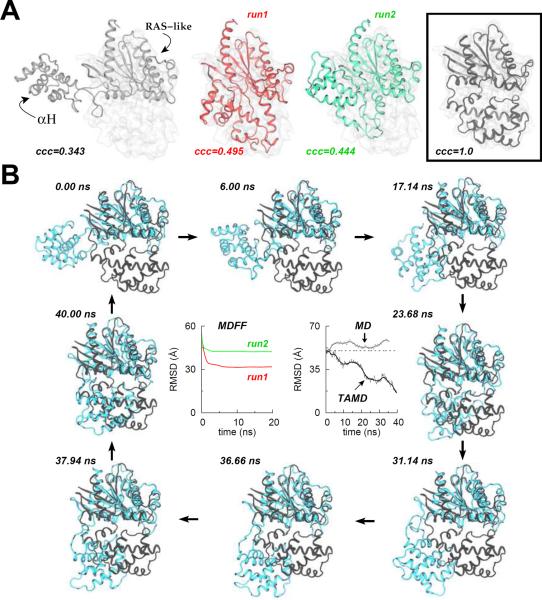
Starting with four different initial orientations of the open-conformation of G_α, we performed two independent 20-ns MDFF simulations for each starting orientation in a 5 Å target-map of the closed-conformation (Figure 2A and Figure S4). For each MDFF run, we also measured the C_α-RMSD from the target crystal structure (PDB code 1CIP) of G_α to judge the correct orientation of αH. In each case, we find that although MDFF is capable of improving the initial fit with the target-map, it is unable to find the correct orientation of αH as represented in the target-map (see middle panels in Figure 2A and Figure S4 for MDFF-generated conformations, and the right-most panel in Figure 2A for the desired final conformation). The maximum achievable correlation coefficient for the 5 Å target-map in all MDFF runs with independent starting orientations is 0.495, while final RMSDs from the known closed-states are at least 30 Å or greater, both indicating final structures that are significantly different from the one represented by the 5 Å map. We also observe that after the first ~2–3 ns of each MDFF run, the RMSD saturates and remains so towards the end of simulation, indicating that the MDFF simulations have converged. Continuing the MDFF simulations is unlikely to improve the fit because the visual analysis of MDFF trajectories shows a nearly linear movement of the αH-domain into the density with no significant change in its orientation.

Figure 2. Conformational Change in the Gα-Subunit of a GTP-Binding-Protein (G-protein) studied via MDFF and TAMD Simulations.

(A) Cartoon representations for MDFF fitting of G_α at 5 Å target-map resolution: initial docked open-state crystal conformation (white cartoon; left panel), final conformations generated via two independent 20-ns MDFF simulations (red and green cartoons; middle panels), and the known target closed-state crystal conformation with perfect correlation-coefficient of 1.0 (black cartoon; boxed right-most panel). The C_α-RMSD (w.r.t. the final crystal structure) traces for each 20-ns MDFF run are shown in panel B. (B) Representative snapshots from a 40-ns TAMD simulation of G_α are shown at various time-points during the simulation. TAMD-generated conformation is shown in cyan and the known closed-state crystal structure conformation in black. The C_α-RMSD (w.r.t. the final crystal structure) trace from the ~40-ns TAMD simulation is shown in the central right-panel along with the RMSD trace from an unbiased ~36-ns explicit-solvent MD simulation of G_α. See also Figure S4 (for additional MDFF simulations starting with independent initial docked-orientations) and Figure S5 (for additional TAMD simulation details).

Vashisth, Skiniotis, and Brooks, 2012

To explore the possibility of observing this conformational change and to generate better starting orientations for MDFF, we also conducted a ~36-ns long explicit-solvent unbiased molecular dynamics (MD) simulation of the open-conformation of G_α. This simulation also fails to generate this conformational change as shown by the RMSD from the target structure (see RMSD trace labeled as “MD” in the central-right panel of Figure 2B), which does not change significantly. This is not surprising because observing large-scale conformational transitions in proteins on reasonable time-scales via unbiased simulations remains difficult due to the underlying free-energy barriers. However, an enhanced conformational sampling algorithm for proteins (Abrams and Vanden-Eijnden, 2010), based upon temperature-accelerated molecular dynamics (TAMD) (Maragliano and Vanden-Eijnden, 2006, 2008), was recently shown to be a promising approach to understand conformational changes involving significant domain movements (rotations and/or translations). Hence, we resorted to an un-targeted TAMD simulation (see Methods for details) for conformational sampling of G_α to achieve this conformational change.

TAMD-Generated Conformation of G_α can be Fitted with MDFF

For conformational sampling of G_α, we conducted a ~40-ns long TAMD simulation of the open-state conformation of G_α (see Methods for simulation details, and Figure S5 for system-setup). We observe that TAMD is able to generate a closed-like conformation of G_α spontaneously, where the RMSD (w. r. t. the target-structure) decreases from ~50 Å to ~15 Å (see RMSD trace labeled as “TAMD” in the central-right panel of Figure 2B). A major consequence of the TAMD run is that the angle (θ; see Figure S5C for the definition of θ) between the αH-domain and the Ras-like domain changes from ~110° to ~54°, which places the αH in nearly the crystallographic orientation (see Figure S5D for the evolution of θ during the 36-ns MD and 40-ns TAMD run). At 8 different time-points during TAMD (Figure 2B), we also show the snapshots of the overlay of TAMD-generated conformations (cyan cartoons) and the target crystal conformation (black cartoons). We observe that the αH-domain begins to rotate from the beginning of TAMD simulation (see snapshots at t = 6.00, 17.14, and 23.68 ns in Figure 2B) as indicated by the decreasing RMSD (Figure 2B) and θ (Figure S5D). After about ~31.14 ns, the orientation of αH does not change significantly and it only experiences translational movement that places it within ~15 Å RMSD from the target crystal conformation.

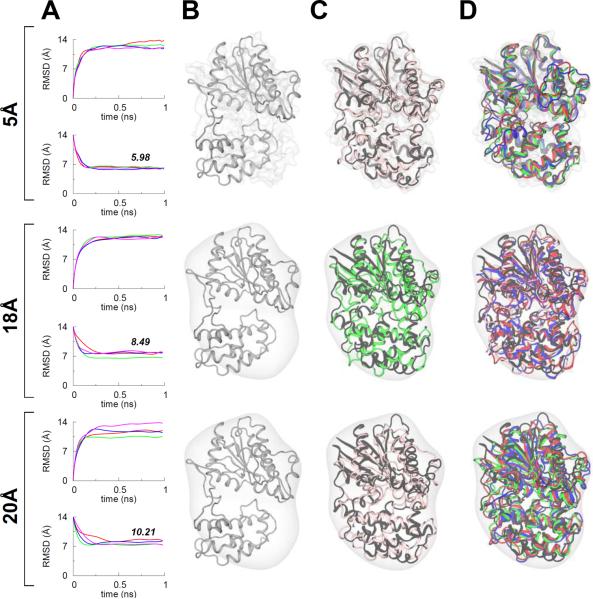
When docked into the closed-state simulated map of G_α, we observe that the TAMD-generated conformation of G_α is still partially outside the density, and hence we further test if MDFF can now be used to improve the fit further with the TAMD-generated conformation as the starting coordinates. In a next step, we also test the effect of map resolution on MDFF fitting of G_α into target-maps at 5 Å, 18 Å, and 20 Å resolution. We conducted four independent MDFF runs for each map resolution, and find that MDFF is further able to improve the fit into simulated maps with correct orientation of αH. Similar to the four other proteins (vide supra), we observe that the quality of final models generated via MDFF decreases with decreasing map resolution as indicated by the final average RMSDs (Å) from the known target structure of G_α (PDB code 1CIP) for each map resolution which are: 5.98 (5 Å), 8.49 (18 Å), and 10.21 (20 Å) (see Figure 3 for details and Table S2 for correlation coefficients of all MDFF runs). Taken together, these data demonstrate that TAMD can be used to generate better starting configurations for MDFF simulations if the conformational changes involve large-scale domain rotations as observed in the G_α-subunit of the β₂-adrenergic-receptor-Gs protein complex. In the following, we test whether TAMD can be incorporated within an MDFF simulation to accelerate conformational search during fitting.

Figure 3. Post-TAMD MDFF Fittings of the G_α-Subunit.

(A) RMSD traces from four independent MDFF simulations of the TAMD-generated conformation of G_α for three different target map resolutions. As in Figure 1, the top and bottom panels for each map resolution show the C_α-RMSD traces from the known initial and final crystal conformations of G_α. The numbers in italics on bottom RMSD panels represent the final average (of four MDFF runs) RMSD with respect to the known target crystal structure (B) Cartoon representation of the TAMD-generated conformation of G_α is shown docked in the target maps at three different resolutions. (C) For each map, overlay of MDFF-generated conformations with highest correlation-coefficients (among four independent runs) and the closed-state target crystal structure (black cartoons) of G_α. MDFF-generated conformations are in the same color as RMSD traces in panel A. (D) For three additional MDFF runs, overlay of MDFF-generated conformations and the target crystal structure. See also Table S2 for correlation-coefficients.

Vashisth, Skiniotis, and Brooks, 2012

MDFF vs. TAMD-Assisted MDFF Fitting of Adenylate Kinase in Explicit-Solvent

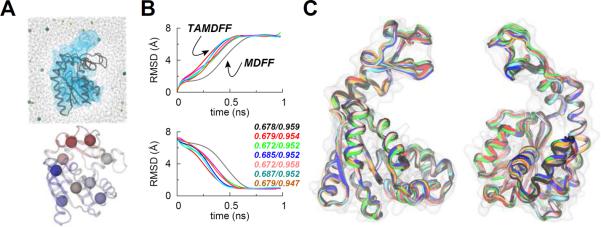
As TAMD is an enhanced conformational sampling technique and MDFF is also a conformational fitting method, it is likely that the conformational search via MDFF can be accelerated if TAMD-assisted MDFF (TAMDFF) is performed in a single atomistic simulation. To test this, we constructed an explicit-solvent system for ADK as an example (Figure 4A). ADK is the smallest protein (1661 atoms) considered in this work with its starting/final structures known at significantly higher-resolutions (1.9 Å; 1AKE, and 2.2 Å; 4AKE), while the small system-size (~29,000 atoms) for the solvated ADK allows us to perform multiple TAMDFF simulations. We performed six independent TAMDFF simulations (see Methods for details) starting with ADK in its closed-conformation, which is fitted into a 5 Å resolution simulated map of its open-conformation. We show the C_α-RMSD traces from the initial and final crystal structures of ADK during these TAMDFF runs and a typical explicit-solvent MDFF run in Figure 4B. We observe consistently in all TAMDFF runs that the convergence to the final conformation of ADK encoded in the map is faster than the MDFF run as indicated by the change in the slope of the RMSD traces. Moreover, the final correlation-coefficients for TAMDFF-generated conformations are similar to the MDFF run indicating that the quality of structures generated by TAMDFF (Figure 4C) is highly similar to the MDFF run; the only difference is that the final conformations could be achieved in shorter simulation time due to the enhanced conformational search in TAMDFF. These data suggest that TAMD can be used not only to generate better starting configurations for MDFF (as in the case of the G_α-subunit), it can also be used to enhance the conformational search for target conformations if combined with MDFF.

Figure 4. MDFF vs. TAMD-Assisted MDFF (TAMDFF) Fitting of Adenylate Kinase in Explicit-Solvent.

(A; top panel) Schematic representation of the simulation domain (29416 atoms) of the adenylate kinase (ADK) as viewed along the z-axis: starting docked closed-conformation of ADK (black cartoon), 5 Å resolution target map (blue surface), water molecules (wireframe), and ions (spheres). (A; bottom panel) Subdomain partitions of ADK are shown for the TAMD simulation. Each sphere represents the center-of-mass (COM) of a mutually exclusive subdomain. Entire ADK structure was divided into 9 subdomains. Residue memberships for each subdomain of ADK are listed in Table S4. (B) Top and bottom panels respectively show the C_α-RMSD traces from the known initial and final crystal conformations of ADK. The black trace is from an MDFF simulation, while the traces of other color are from six independent TAMD-assisted MDFF (TAMDFF) simulations. Initial/final correlation-coefficients for all seven simulations are shown in the bottom panel. (C) Cartoon representations of two different views of the overlay of final conformations generated via MDFF and TAMDFF simulations are shown. Cartoon colors are same as the RMSD traces in panel B.

Vashisth, Skiniotis, and Brooks, 2012

DISCUSSION

A key finding of this work is the observation that MDFF helps in improving the initial fit of a protein even in a 24 Å resolution target-map. However, the quality of final models generated via MDFF decreases with decreasing map-resolution because the final achievable RMSDs (w. r. t. the known target conformations of the four proteins considered here) increase with decreasing map-resolution. We also find that at lower map-resolutions the quality of final models generated via MDFF deteriorates if the restraints on the secondary structural elements are softened or steering forces are increased likely due to the over-fitting (Tama et al., 2004a,b; Trabuco et al., 2008) of structures. Although we have performed MDFF simulations on proteins of different shapes (in terms of secondary and flexible structural elements) and sizes (1661 atoms; ADK, 5737 atoms; MBP, 5993 atoms; G_α, 7835 atoms, the GroEL-subunit, and 11648 atoms, NBD), application of MDFF at lower-resolutions can be dependent on the size and shape of a specific protein under consideration. For example, the flexible non-secondary structural elements (such as the loops, coils, and turns) in a protein, often missing in experimental structures and modeled in simulations, cannot be restrained according to the secondary structure, and hence the quality of final models generated via MDFF at lower-resolutions can be dependent upon the distribution of flexible structural parts on the entire structure of a protein. Based upon the MDFF simulations conducted on simulated maps as well as the experimental maps, we recommend that better final models can be generated by maintaining significantly higher secondary structure restraints and employing lower steering forces at any map-resolution; these requirements however become necessary for lower map-resolutions. In fact, MDFF has been used successfully even at map-resolutions of 18 Å or beyond for large macromolecular assemblies (Sener et al., 2009; Strunk et al., 2011). We have carried out MDFF simulations both in vacuum as well as explicit-solvent for test cases here, but implicit solvent in MDFF simulations can also be used as has been demonstrated recently (Tanner et al., 2011). In our earlier work on the eukaryotic ribosome (Strunk et al., 2011), we used explicit-solvent in MDFF runs because solvation in addition to restraints might play a significant role in maintaining the structural integrity in such systems even though such applications rapidly become computationally infeasible. Because the quality of final models generated decreases with the decreasing map-resolution, we suggest that one can only understand the overall nature of conformational changes for intermediate map resolutions, while inferences about atomic positions of molecular structure are difficult to propose. However, precise structural details at atomistic resolution are not straightforward to infer with confidence from 5 Å resolution maps either.

Furthermore, it was originally suggested that MDFF can be combined with enhanced sampling techniques (Trabuco et al., 2008), but to our knowledge no such example application yet exists in the literature. Here, we have used a relatively new conformational sampling technique (TAMD) in combination with MDFF to study the open (nucleotide-free) to closed (nucleotide-bound) conformational change in the G_α-subunit of the β₂-adrenergic-receptor-Gs protein complex. Beginning with the open-state crystal conformation of G_α in multiple different orientations, we observe that MDFF improves the initial fit, but is unable to generate this conformational change largely due to the limitations in capturing rotations of structural elements (Trabuco et al., 2008). In contrast, a TAMD-generated conformation of G_α can readily be fitted via MDFF into simulated maps of its closed conformation. This suggests that MDFF simulations can be sensitive to the initial placement, especially orientation, of the structural elements, and enhanced conformational sampling methods like TAMD can be used to alleviate such limitations. We also note that a ~36-ns long unbiased explicit-solvent MD simulation of G_α is also unable to show any significant conformational change likely due to the underlying free-energy barriers. Even though the excised H and the Ras-like domains of G_α could be fitted correctly by MDFF into their respective excised simulated maps independently, properly excising densities from the experimental maps is neither trivial nor desirable. In fact, the need to not divide a molecular structure into individual parts for flexible fitting was originally suggested to be a major advantage of MDFF (Trabuco et al., 2008) and NMFF (Tama and Brooks, C. L., III, 2002; Tama et al., 2002, 2003; Tama and Brooks, C. L., III, 2005, 2006) over other techniques. By taking ADK as an example, we also show that TAMD can be incorporated inside an explicit-solvent MDFF simulation to accelerate the conformational search for target conformations. We believe that this work reports the first examples of the combination of TAMD with MDFF for flexible fitting into EM maps, which may be useful for other applications.

CONCLUSIONS

In this work, we have attempted to understand the effect of varying map resolution on fitting via MDFF of the closed conformations of four different proteins into the simulated/experimental maps of their open conformations. In independent simulations for each case, we find that MDFF in fact helps in improving the initial fit even at 24 Å resolution, but the quality of MDFF-generated final models decreases with decreasing map-resolution as measured by the RMSD from the target known conformations of each protein. We also find that the quality of final models generated via MDFF at low-resolution is sensitive to the strength of structural restraints and the steering forces employed. For the G_α-subunit of the β₂-adrenergic-receptor-Gs protein complex, we find that MDFF improves the initial fit, but is unable to capture the open→closed conformational change in G_α, likely due to limitations in capturing large-scale domain rotations. Because this conformational change could not be captured in a ~36-ns long unbiased MD simulation of the open-conformation of G_α, we used TAMD (Abrams and Vanden-Eijnden, 2010) for enhanced conformational sampling of G_α, which is able to generate this conformational change to a significant extent. We futher show that the TAMD-generated conformation of G_α could be easily refined via MDFF into simulated maps of the closed conformation. Finally, we perform TAMD-assisted MDFF (TAMDFF) simulations in an explicitly-solvated system of adenylate kinase (ADK), and find that conformational search for the target conformation of ADK encoded in the map can be accelerated when TAMD and MDFF are combined judiciously in a single simulation.

METHODS

Molecular Dynamics Flexible Fitting

In the molecular dynamics flexible fitting (MDFF) method of Trabuco et al. (Trabuco et al., 2008, 2009, 2011), external steering forces arising from the potential encoded in the electron microscopy (EM) map in addition to the underlying molecular dynamics (MD) force-field are applied. In addition, restraining forces are applied to prevent significant structural distortions, and to maintain the correct stereochemistry (Schreiner et al., 2011), or symmetry of the complex (Chan et al., 2011). Therefore, the resulting potential function for MDFF is:

$$U_{total}=U_{MD}+U_{EM}+U_{SS}+\cdots$$ (1)

where U_MD is the underlying MD force-field, U_EM is the potential derived from the target EM map, and U_{S S} is a harmonic restraining potential to preserve secondary structure; additional potential terms can be added if required. A scaling factor ξ > 0 is typically used to uniformly tune the effect of the EM map on the molecular system.

We generated all MD trajectories using NAMDv2.8 (Phillips et al., 2005; Kalé et al., 1999) and the CHARMM force-field (MacKerell, Jr. et al., 1998) with the CMAP correction (MacKerell, Jr. et al., 2004). VMDv1.9 was used for system creation and protein rendering (Humphrey et al., 1996). The mdff plugin of VMDv1.9 was used to prepare the simulated maps and the input files, as well as for the analyses. The initial rigid-body docking of structures was performed using SITUS (Wriggers et al., 1999). We performed all MDFF simulations in vacuum (except for the ADK case described in Figure 4 where explicit-solvent was used). For MDFF runs in Figures 1, 2, 3, and S4, a scaling factor of ξ = 0.2 kcal/mol, and the secondary structure restraints with k = 300 kcal mol⁻¹ rad⁻² were used. For runs described in Figures S2, a scaling factor of ξ = 0.2 kcal/mol structural restraints with k = 0, 5, 10, 50, 100, and 300 kcal mol⁻¹ rad⁻² were used. For runs described in Figures S3, scaling factors of ξ = 0.2, 2.0, 5.0, and 10.0 kcal/mol, and structural restraints with k = 0 and 5 kcal mol⁻¹ rad⁻² were used. For runs described in Figure 4, a scaling factor of ξ = 0.1 kcal/mol, and the secondary structure restraints with k = 300 kcal mol⁻¹ rad⁻² were used. A grid spacing of 1Å was used for all simulated maps. Other than secondary structure restraints, we also used restraints to maintain the correct chirality of all chiral centers as well as the trans-configurations of peptide bonds. Initial coordinates (for MDFF fitting) and final coordinates (for target map generation) for different proteins were taken from the following coordinate files (initial/final): NBD (2R6G/3FH6), MBP (3MBP/1LLS), ADK (1AKE/4AKE), and G_α (3SN6/1CIP). For the GroEL subunit, an experimental map of 8.5 Å resolution (EMDB code EMD-2000) was filtered to lower map resolutions for all MDFF simulations. The entire symmetric map was box-segmented around one subunit (using software Chimera), as also done in the original work (Clare et al., 2012). Bound-ligands were deleted from the closed conformations of all proteins before fitting. A 1-fs time-step was used for all MDFF runs, and the MDFF-generated final configuration of each protein was energy-minimized for 2000 steps with a scaling factor ξ = 10.

Temperature Accelerated Molecular Dynamics

For the conformational sampling of the G_α subunit, we carried out a 40-ns long explicit-solvent temperature-accelerated molecular dynamics (TAMD) simulation of its open state as seen in the crystal structure (PDB 3SN6) (Rasmussen et al., 2011). The theoretical basis of TAMD was originally presented by Maragliano and Vanden-Eijnden (Maragliano and Vanden-Eijnden, 2006, 2008; Vanden-Eijnden, 2009). More recently, a novel conformational sampling algorithm for proteins based upon TAMD was developed and applied successfully (Abrams and Vanden-Eijnden, 2010; Vashisth et al., 2012). We have used this conformational sampling algorithm as originally implemented in NAMD (Phillips et al., 2005; Kalé et al., 1999). Therefore, we simply describe the underlying equations here. The coupled system of equations describing TAMD are as follows:

$$\begin{array}{c}\hfill m_i{\ddot{x}}_i=-\frac{\partial V\left(x\right)}{\partial x_i}-k\sum _{j=1}^m[{\theta }_j^{\ast }\left(x\right)-{\theta }_j]\frac{\partial {\theta }_j^{\ast }\left(x\right)}{\partial x_i}-\gamma m_i{\stackrel{.}{x}}_i+{\eta }_i(t;\beta )\hfill \\ \hfill \stackrel{‒}{\gamma }{\stackrel{‒}{m}}_j{\stackrel{.}{\theta }}_j=k[{\theta }_j^{\ast }\left(x\right)-{\theta }_j]+{\xi }_j(t;\stackrel{‒}{\beta })\hfill \end{array}$$ (2)

where ${\theta }^{\ast }\left(x\right)=({\theta }_1^{\ast }\left(x\right),{\theta }_2^{\ast }\left(x\right),\dots \dots ,{\theta }_m^{\ast }\left(x\right))$ are collective variables (CVs) that are functions of the atomic Cartesian coordinates, m_i are the masses of x_i, V(x) is the interatomic MD potential, κ is the “coupling spring-constant”, γ is the Langevin friction coefficient, η is the white noise satisfying fluctuation-dissipation theorem at physical temperature β⁻¹, $\stackrel{‒}{\gamma }$ and ${\stackrel{‒}{m}}_j$ respectively are fictitious friction and masses of the variables θ_j, and ξ is the thermal noise at artificial temperature ${\stackrel{‒}{\beta }}^{-1}$.

The aforementioned set of equations describe the motion of x(t) and θ(t) over the extended potential

$$U_x(x,\theta )=V\left(x\right)+\frac{\kappa }{2}\sum _{j=1}^m{[{\theta }_j^{\ast }\left(x\right)-{\theta }_j]}^2$$ (3)

As shown before (Maragliano and Vanden-Eijnden, 2006), by choosing κ so that θ*(x(t)) ≈ θ(t) and the fictitious friction coefficient $\stackrel{‒}{\gamma }$ so that θ moves slower than x, we can generate a trajectory θ(t) which moves at artificial temperature ${\stackrel{‒}{\beta }}^{-1}$ on the free energy landscape computed at the physical temperature β⁻¹. In this work, we have chosen a TAMD friction ($\stackrel{‒}{\gamma }$) of 500 ps⁻¹ and a spring constant (κ) of 100 kcal/mol·Å² to guarantee that the slow variables indeed evolve slower than the fundamental variables. For the G_α-subunit, each of the Ras-like and the α-helical domain was divided into 3 subdomains with a total of 6 subdomains for the entire G_α (Figure S5B) and therefore 18 CVs (the Cartesian coordinates of the center of mass of each subdomain are CVs). The missing linker-residues in the open crystal conformation (PDB code 3SN6) of G_α were modeled. For the TAMDFF simulations of ADK described in Figure 4, the entire ADK structure was divided into a total of 9 subdomains (bottom panel in Figure 4A) and hence 27 CVs. Other parameters for the TAMD part of the TAMDFF simulations of ADK were same as those for G_α, and parameters for the MDFF part of the TAMDFF simulations are described above. The identity of residues in each subdomain of G_α and ADK are listed in Tables S3 and S4, respectively. Before applying TAMD, the G_α subunit was equilibrated for ~5 ns via MD simulation in the NVT ensemble. Further, a 40-ns long TAMD simulation in explicit solvent was carried out at a fictitious thermal energy ${\stackrel{‒}{\beta }}^{-1}=7$ kcal/mol, where $\stackrel{‒}{\beta }=1∕k_B\stackrel{‒}{T}$, k_B is Boltzmann's constant, and $\stackrel{‒}{T}$ is the fictitious temperature. We note that TAMD runs at thermal energies lower than used here fail to generate this conformational change on similar time-scales, presumably because the underlying free-energy barriers are comparable or higher than the thermal energies needed to overcome them. The final TAMD-generated conformation of G_α was further fitted using MDFF into the simulated maps of the closed state (PDB code 1CIP) filtered to 5Å, 18Å, and 20Å resolution using same simulation protocols as described above.

Highlights

• Effect of map resolution and structural restraints on MDFF fitting is tested

• Use of large structural restraints is recommended for lower map resolutions

• Conformational change is studied in the G_α-subunit of a GPCR-Gs-protein complex

• MDFF is combined with enhanced conformational sampling technique TAMD

Abbreviations used

MD

molecular dynamics

MDFF

molecular dynamics flexible fitting

TAMD

temperature accelerated molecular dynamics

EM

electron microscopy

RMSD

root-mean squared deviation