Complex tiling patterns in liquid crystals

Abstract

In this account recent progress in enhancing the complexity of liquid crystal self-assembly is highlighted. The discussed superstructures are formed mainly by polyphilic T-shaped and X-shaped molecules composed of a rod-like core, tethered with glycerol units at both ends and flexible non-polar chain(s) in lateral position, but also related inverted molecular structures are considered. A series of honeycomb phases composed of polygonal cylinders ranging from triangular to hexagonal, followed by giant cylinder honeycombs is observed for ternary T-shaped polyphiles on increasing the size of the lateral chain(s). Increasing the chain size further leads to new modes of lamellar organization followed by three-dimensional and two-dimensional structures incorporating branched and non-branched axial rod-bundles. Grafting incompatible chains to opposite sides of the rod-like core leads to quaternary X-shaped polyphiles. These form liquid crystalline honeycombs where different cells are filled with different material. Projected on an Euclidian plane, all honeycomb phases can be described either by uniformly coloured Archimedean and Laves tiling patterns (T-shaped polyphiles) or as multi-colour tiling patterns (X-shaped polyphiles). It is shown that geometric frustration, combined with the tendency to segregate incompatible chains into different compartments and the need to find a periodic tiling pattern, leads to a significant increase in the complexity of soft self-assembly. Mixing of different chains greatly enhances the number of possible ‘colours’ and in this way, periodic structures comprising up to seven distinct compartments can be generated. Relations to biological self-assembly are discussed shortly.

1. Introduction: liquid crystal self-assembly

Liquid crystals (LCs) represent truly fascinating materials in terms of their properties, their importance for the fundamental understanding of molecular self-assembly and their tremendous success in commercial applications [1]. The constituent molecules of LC phases are sufficiently disordered to generate softness, yet comprising varying degrees of ordering, in this way providing a state of matter which in a unique way combines order and mobility [2–9]. Owing to the inherent fluidity, these self-organized LC structures have the ability to change their configuration under the influence of external stimuli (surfaces, electric, magnetic and mechanical fields) and to eliminate defects by self-healing. Therefore, this special state of matter provides a very general way to assemble functional molecules into well-defined superstructures. This can be used in technology, as well as providing an important concept of molecular self-assembly in biosystems, as, for example, found in cell membranes [10] and DNA [11–13].

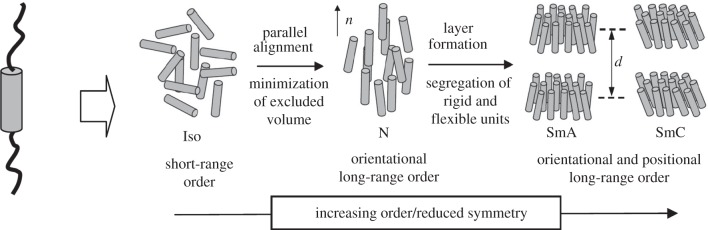
Order in LCs can be based on a rigid and anisometric (rod- or disc-like [6]) shape of the molecular or supramolecular architecture, leading to orientational long-range order as found in nematic, smectic and columnar phases (figure 1) [14].

Figure 1.

Organization of rod-like molecules in LC phases (for clarity, the alkyl chains are not shown in the models of the phase structures). Iso, isotropic liquid state; N nematic LC phase; SmA, smectic A phase; SmC, smectic C phase (tilted).

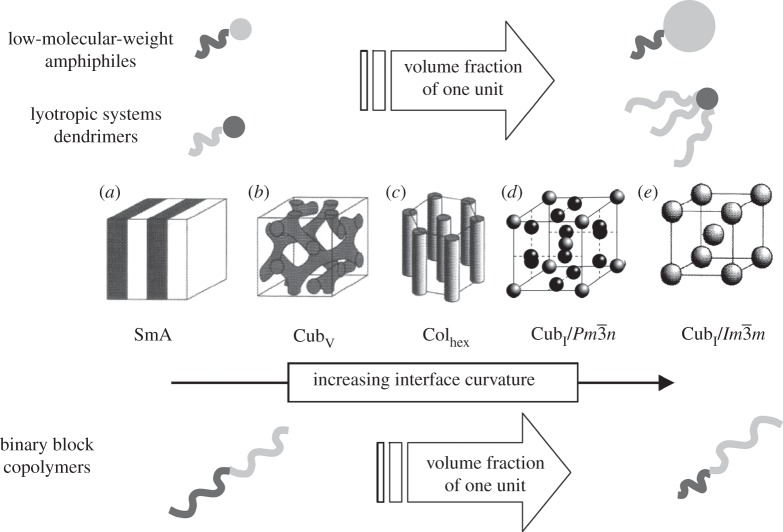
Positional long-range order is usually generated by amphiphilicity, resulting from the combination of two mutually immiscible (incompatible) segments in one molecule. Nanoscale segregation [15,16] of these incompatible molecular segments leads to the formation of distinct nanometre-sized compartments that are organized on a one-dimensional, two-dimensional or three-dimensional periodic lattice, separated by interfaces. These interfaces tend to be minimal in order to reduce the interfacial energy stored in the system. Therefore, for flexible amphiphiles, the mesophase type is mainly determined by the relative volume of the two incompatible segments leading to structures with minimum interfacial energy, as shown in figure 2 [17–19].

Figure 2.

Modes of self-assembly of binary amphiphiles depending on the volume ratio of the two incompatible units; in the amphiphiles, the incompatible units (e.g. hydrophilic/hydrophobic) are indicated by different shades of grey and in the morphologies shown, the dark units are located inside the aggregates separated by or embedded in the spaces filled by the light grey units. SmA, smectic A phase (i.e. lamellar phase); Cub_V, bicontinuous cubic phase (the gyroid phase is shown as a representative example); Col_hex, hexagonal columnar phase; Cub_I, discontinuous (micellar) cubic phase (the cubic Pm3̄n and Im3̄m cubic lattices are shown as representative examples).

The above two basic principles, shape anisotropy and amphiphilicity, can on their own lead to only a few relatively simple modes of self-assembly, as shown in figures 1 and 2. However, combined in the same molecule in a competitive manner, they can produce completely new LC phase structures [7,15]. In such molecules, the number of mutually incompatible units usually becomes larger than only two, hence such molecules are polyphilic.

In block copopolymers, linear as well as branched, polyphilicity is achieved by combining more than only two different and incompatible blocks. This leads to new morphologies, more complex than those shown in figure 2. Morphologies of linear [20,21] and branched block copolymers [22–25], rod-coil polymers [26], dendrimers [27,28] and also oligomers containing mesogenic units [29] have been reviewed previously in the cited references and therefore will not be discussed here.

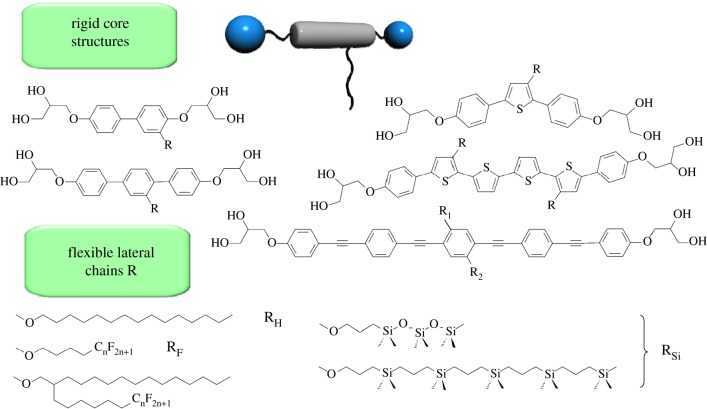
Herein, we will focus on new modes of LC soft matter self-assembly achieved with T-shaped and X-shaped low-molecular-mass polyphiles, developed in our laboratories during the last decade. In most of these molecules, a rod-like rigid core is used, which is decorated at both ends with a hydrophilic glycerol group providing sufficiently strong attractive intermolecular interaction by hydrogen bonding (blue dots in figure 3). One or two flexible chain(s), incompatible with the polar groups as well as with the rigid cores were attached laterally to the rod-like moiety leading to T-shaped (one chain) or X-shaped (two chains at opposite sides of the rod) polyphiles, as shown in figure 3 [8,25]. Figure 4 shows selected examples of molecular structures of these polyphiles. Typically, not only alkyl chains (R_H) [30,31], semiperfluoroalkyl chains (R_F) [32–39], but also silicon-containing chains (siloxanes and carbosilanes = R_Si) were used [40] as lateral groups.

Figure 3.

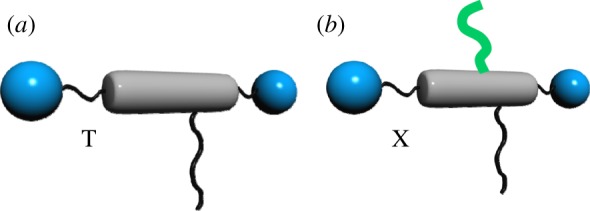
Fundamental structures of the (a) T-shaped and (b) X-shaped polyphiles under discussion.

Figure 4.

Examples of molecular structures of selected polyphilic molecules under discussion.

2. Liquid crystal honeycombs

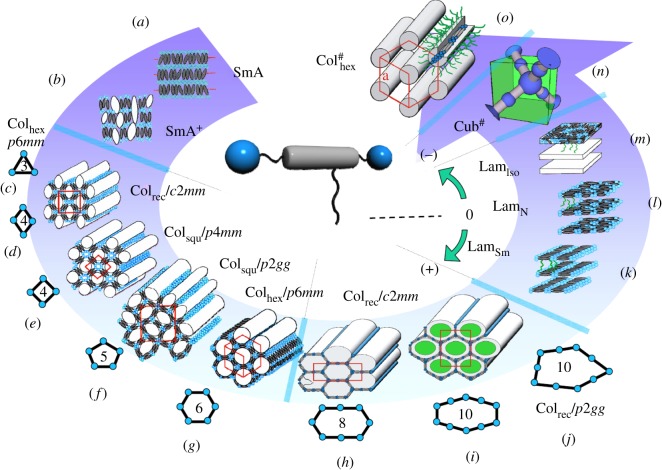
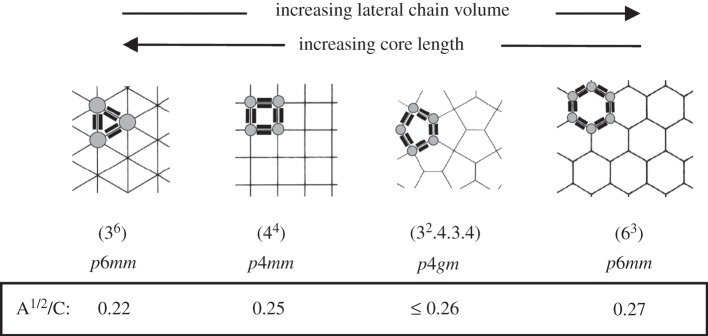
Let us first focus on the T-shaped molecules having only one lateral chain. These molecules, bearing three types of mutually incompatible groups were found to form many different types of fluid self-assembled structures, as outlined in figure 5. The most prominent are the honeycomb LC phases also known as polygonal cylinder phases. These honeycomb LC phases can be divided into the simple honeycomb phases shown in figure 5c–g and the giant honeycomb phases shown in figure 5h,i [8]. In the simple LC honeycomb phases, rod-like cores form cell walls connected at the ‘seams’ by the hydrogen-bonding glycerol groups. The resulting honeycomb cells of polygonal cross section and infinite length are filled by the fluid lateral chains. Depending on the ratio of the volume of the chains to the length of the rod-like core, cells ranging from triangular [41] via rhombic, square and pentagonal to hexagonal were obtained [32]. Projected on a Euclidian plane, most observed honeycombs are Archimedean tilings [42] by polygons, i.e. tilings in which all vertices are the same or their duals the Laves tilings, where all tiles are the same (figure 6) [7,42].

Figure 5.

Sequence of LC phases formed by self-assembly of T-shaped polyphiles as observed on increasing the size of the lateral chain: (a,b) smectic phases, (c–g) simple polygonal LC honeycomb phases, (h–j) giant polygonal honeycomb phases (cylinders of (c) and (j) not shown), (k–m) Lam phases, (n) bicontinuous cubic rod-bundle phases and (o) columnar rod-bundle phases; SmA, smectic A phase, the rod-like cores are organized in layers with the long axis on average perpendicular to the layer planes; SmA⁺, distorted layer structure, where the lateral chains form disordered regions in the layers (mesh phases); Col, columnar phases, the subscripts rec, squ and hex identify a rectangular, square or hexagonal lattice, respectively, after a slash, the plane group of the two-dimensional lattice is given; Lam, lamellar phases in which the rod-like cores are organized parallel to the layer planes; in Lam_N, there is a nematic-like, in Lam_Sm, a smectic-like in-plane order of the rod-like cores, in Lam_Iso, the cores are completely disordered; Cub^#, bicontinuous cubic phase (branched axial rod-bundles); 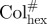, hexagonal columnar phase formed by non-branched axial rod-bundles [7].

Figure 6.

Tiling patterns formed by self-assembly of T-shaped polyphiles, their net-notations (top line), the plane group symmetries (highest possible symmetries, middle line) and the square root area to circumference ratios (A^1/2/C) of the constituting polygonal tiles.

The general trend with increasing length of the lateral chain or with rising temperature (thermal expansion of the lateral chains) is to undergo a phase transition from smaller to larger polygons, i.e. moving anticlockwise around the diagram in figure 5. This is because the ratio of the square root of the area to the circumference of the regular polygons is increasing from triangles to hexagons (figure 6). Extension of the rod-like cores at constant volume of the lateral chain has the opposite effect. As longer rods provide more space inside the cylinders, the number of walls in the cross section of the cylinder must be reduced, i.e. moving clockwise around the diagram in figure 5 [7,41,43,44]. Especially pentagonal and hexagonal cylinders are easily formed by a wide range of molecules [7,32].

The easy formation of honeycombs with a pentagonal cylinder cross section is a special feature of these liquid crystalline systems, whereas pentagonal organizations are rarely found in solid-state systems. This is due to the fact that regular pentagons cannot tile a plane periodically. However, the fluid LC state allows easy deformation of regular pentagons and for non-regular pentagons there are numerous different tiling patterns. The most symmetric is the square p4gm lattice, but also the lower symmetry rectangular p2gg lattice is often found.

It is interesting to note that besides the T-shaped polyphiles shown in figure 7a, there are also T-shaped polyphiles with a reversed position of hydrophilic and lipophilic units [45–51] as shown in figure 7b. These compounds also form polygonal cylinder phases with cells ranging from triangular to hexagonal [32]. In this case, the flexible lipophilic chains form the nodes interconnecting the cylinder walls and the polar groups fill the interior of the cylinder cells, as shown in figure 7 for the pentagonal cylinder phases. As the positions of the different groups in the molecules are exchanged, also the cylinder structures formed by these polyphiles are reversed [45,48].

Figure 7.

Exchanging the positions of the groups attached in lateral and terminal positions of the rod-like anisometric units leads to LC phases with the same tiling pattern and symmetry, but with reversed positions of the distinct chains either in the cylinder cells or at the vertices interconnecting the cylinder walls (colour isomers) [7,45].

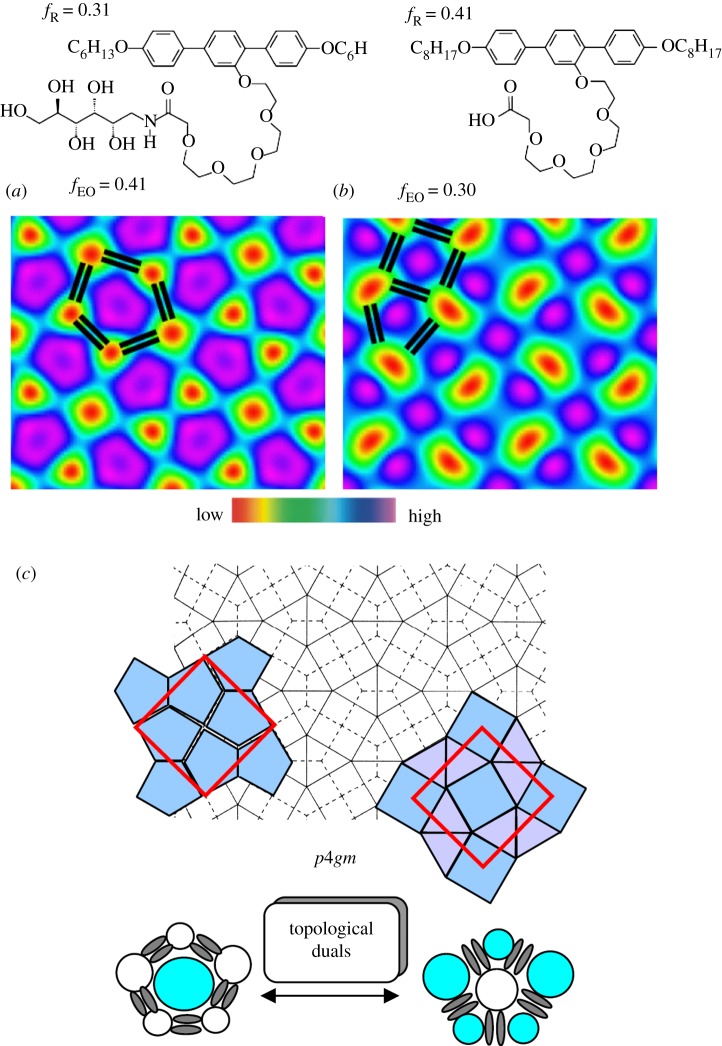
Besides the cell interior and the nodes swapping ‘colour’, there is also the possibility of topological duality of the entire tiling pattern, as shown in figure 8 [48]. This is achieved by reversing the volume fractions of lateral and end-chains. The resulting two apparently very different cylinder networks with p4gm lattice, the pentagonal cylinder phase and the cylinder phase composed of a 1 : 2 mixture of triangular and square cylinders represent duals of the same topological class (3².4.3.4; i.e. threefold-threefold-fourfold-threefold-fourfold vertices going around each pentagon, or triangle-triangle-square-triangle-square going around each fivefold vertex). This means that in the two tessellations (full and dotted lines), the nodes and tiles are exchanged. In the resulting tessellation, there are exclusively fivefold vertices exactly at the positions of the pentagonal tiles in the dual, and the triangles and squares developed from the threefold and fourfold vertices, respectively. In principle, topological duals can be constructed for any periodic edge-to-edge tiling (for example, hexagons versus triangles), except for the (4⁴) tiling by squares which is its own dual [42].

Figure 8.

Topological duality of LC phases formed by two different T-shaped polyphiles depending on the volume fraction of the terminal alkyl chains (f_R) and polar lateral chains (f_EO); (a,b) the experimental electron density maps for the two different honeycomb phases with p4gm symmetry representing topological duals; (a) pentagonal honeycombs and (b) honeycomb formed by square and triangular cylinders in ratio 1 : 2 (blue/purple, highest electron density, polar lateral groups; red/yellow, lowest electron density, terminal alkyl chains; the positions of the rod-like cores are indicated by black lines). (c) Laves tiling composed of pentagonal tiles (left) is superimposed on the dual Archimedean tiling composed of squares and triangles (right). Note that each vertex of the Laves tiling is in the centre of one tile of the Archimedean Tiling and vice versa. [48].

3. Giant cylinder honeycombs and laminated phases

Further extension of the lateral chains beyond the hexagonal cylinders would lead to cylinders with a number of sides greater than 6. If these polygons were to be regular, as in the case of pentagons, a periodic tiling would be impossible. However, the fluidity in the self-assembled LC systems allows them to adjust their cross-sectional shape in such a way as to allow periodic tiling. This leads to a series of giant cylinder phases with rectangular lattices (figure 5h–j) [32,39]. In these phases, some or all cylinder walls have double lengths, being formed by two end-to-end connected molecules instead of just one. For example, elongated hexagons with eight [32] or even 10 rod-like cores [39,52] around the circumference were observed (figure 5h,i). Giant pentagonal cylinders, where each side contains two end-to-end molecules, represent another mode of organization of 10 molecules in the circumference (figure 5j) [32].

Further enlargement of the lateral chain volume causes the cylinders to burst [39]; the side walls are removed leaving only disconnected layers, as shown in figure 5k–m. Unlike the usual smectic phases (figure 5a) formed by rod-like molecules without lateral chains, in these lamellar phases, the rod-like cores are oriented parallel to the layer plane (denoted as Lam phases) [7,33,34,37,38,53,54]. In the two lamellar phases occurring adjacent to the polygonal cylinder phases (Lam_Sm and Lam_N), the biphenyl cores remain parallel to the layer planes and retain in-plane positional and orientational order (Lam_Sm, figure 5k) or only orientational order (Lam_N, figure 5l), before the in-plane molecular order is completely lost in the Lam_Iso phase occurring at higher temperature or for longer side chain lengths (figure 5m) [53–55]. These Lam phases are of significant interest for condensed matter physics in general, as they offer the possibility to investigate phase transitions in quasi-two-dimensional systems [55].

4. Linear and branched axial rod-bundle phases

Further increasing the volume of the lateral chains, for example, by using branched chains or two chains at the same side of a rod-like core can lead to the disruption of the infinite rafts of rod-like cores in the Lam phases into laterally isolated bundles [56,57]. These bundles can form branched networks embedded in the continuum formed by the lateral chains, leading to new types of bicontinuous cubic phases (figure 5n) [58]. In these cubic phases, the rod-bundles are interconnected by threefold or fourfold nodes, forming Gyroid or double-diamond-type bicontinuous interwoven nets (Cub^#). In the case shown in figure 5n, two end-to-end rod-bundles are located between adjacent nodes and two of such infinite networks of tetrahedra form a double-diamond structure. Further increase of lateral chain volume leads to non-branched rod-bundle arrays, where linear rafts of these bundles organize on a hexagonal lattice, creating a unique type of columnar LC phases in which rod-like aromatics are arranged parallel to the column long axis, referred to as axial rod-bundle phases (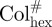) and shown in figure 5o [56,57]. This orientation of the aromatic cores contrasts the organization of the rod-like segments in the LC honeycomb phases (figure 5c–j), where the aromatics are always oriented perpendicular to the column long axis. In the rod-bundle phases, the aromatic cores and the polar end groups are segregated, leading to a periodicity along the columns. These modulated columns can lock into register with each other with or without a defined longitudinal shift on a rhombohedral (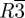m) or hexagonal (P6/mmm) three-dimensional lattice, respectively [57,59].

Overall, the Lam phases with zero interface curvature divide the columnar phases into two inverted structures with opposite sign of the curvature of the interface between the regions comprising the rod-like cores and the regions formed by the flexible chains (figure 5, right). The reversal of the position of flexible and rigid parts in these rigid/flexible amphiphiles can be considered as analogous to swapping the polar and non-polar moieties in polar/apolar amphiphiles, as, for example, known in lyotropic systems. This is associated with a complete reorganization of the rod-like moieties with respect to the column long axes, which takes place in two steps; in the first step, the polygonal cylinders burst with the formation of layers (Lam phases) [39]. In the second step, the layers of these Lam phases split into infinite ribbons, giving rise to the axial-bundle phases.

5. X-shaped polyphiles and multi-colour tilings

Attaching two lateral chains to opposite sides of the aromatic core (X-shaped polyphiles) generates polygonal honeycombs with walls that are only one molecule thick (figure 9b) [60]. In contrast, T-shaped polyphiles with only one lateral chain always give rise to honeycombs where the cross section of the walls contains two rods arranged side-by-side, i.e. these honeycombs have double walls (figure 9a). The reason is that in the X-shaped molecules, the back-to-back alignment of the rod-like units in the walls is distorted by the additional chain. As a consequence of the thinner walls, effectively more space is left available for the lateral chains inside the cells. Hence, honeycombs with smaller cells could be achieved by using two short lateral chains instead of only one chain with the same total volume [41].

Figure 9.

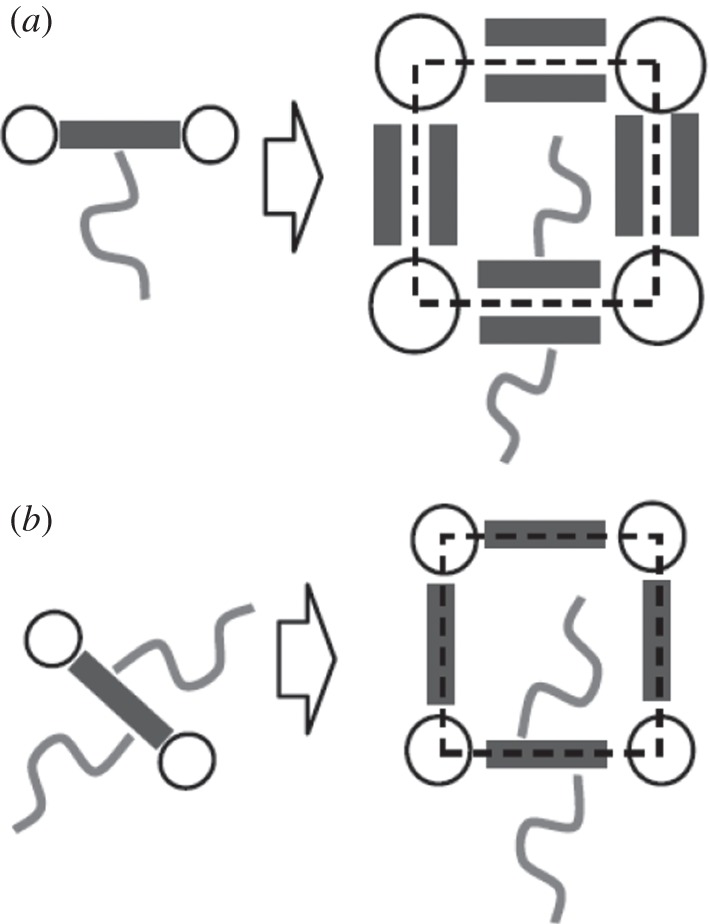
Dependence of honeycomb wall thickness on the type of polyphile, shown for the case of a square cylinder phase; (a) double wall structure of T-shaped polyphiles; (b) single wall cylinders formed by X-shaped polyphiles [41,60].

More importantly, these X-shaped molecules offer the possibility to attach two different and incompatible groups to opposite sides of the rod-like core and thus provides an opportunity to create liquid crystalline honeycombs with cells of different composition. If projected on a Euclidian plane, such structures can be described as tessellations by two or even more differently coloured tiles (multi-colour tilings) [61,62].

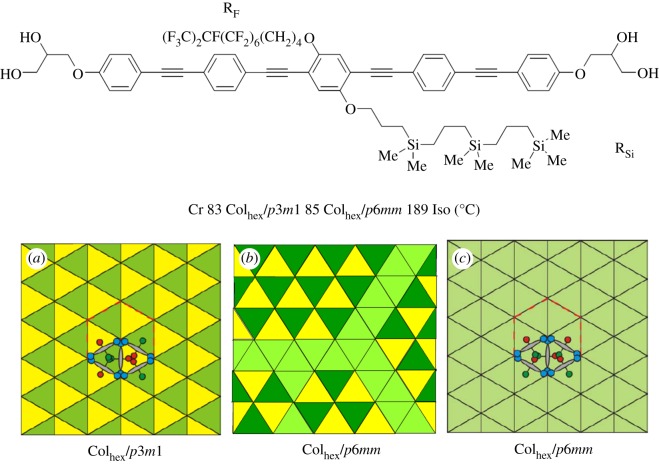
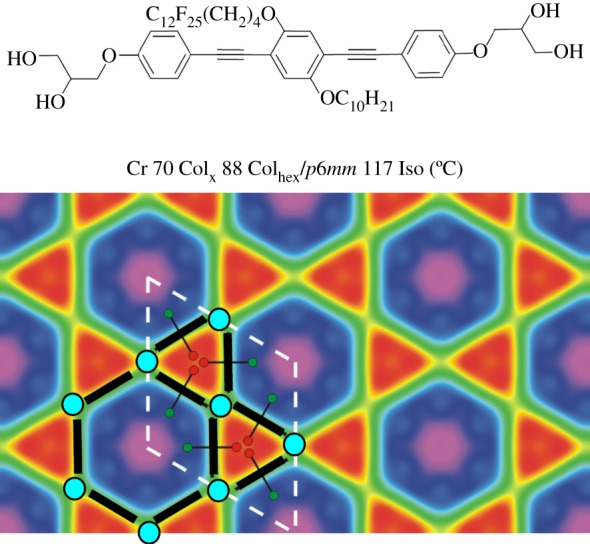
For example, the molecule shown in figure 10 has a fluorinated chain (R_F-chain) and a carbosilane chain (R_Si) at opposite sides of a long oligo(p-phenylene ethinylene) core. R_F and R_Si chains beyond a certain length do not mix readily, i.e. they are incompatible [61]. The molecule in figure 10 forms two hexagonal columnar phases separated by a thermo-reversible continuous (second-order) phase transition with critical behaviour upon approaching the transition temperature. Based on X-ray diffraction (XRD) data, it was confirmed that in both Col_hex phases, the molecules are arranged in honeycombs composed of triangular cylinders. The Col_hex phase at low temperature is a periodic two-colour tiling composed of two types of triangular cylinders with ratio 1 : 1, one type is filled with the R_F-chains, the other with the R_Si-chains (figure 10a). The long-range periodic packing of these two types of cylinders reduces the symmetry of the Col_hex phase to trigonal (p3m1). Above the phase transition temperature T_c, the correlation of the triangular cylinders forming the honeycomb is also long range, but the correlation of the ‘colours’ of the honeycomb cells becomes only short range (figure 10b), so that the p3m1 lattice is only local and on a larger scale it is averaged to p6mm. This means that above the critical temperature, there are local clusters of two-colour trigonal-like tiling (figure 10b) that decrease in size as the temperature is increased further away from T_c [61].

Figure 10.

X-shaped quaternary polyphile forming triangular cylinder phases with models showing: (a) the p3m1 phase with long-range order of the segregated two-colour tiling, (b) the structure with only short-range order of the two-colour tiling above T_c and (c) the completely mixed p6mm structure as observed for related molecules with shorter R_F segments which have a reduced incompatibility and therefore easily mix with the R_Si-chains: green, R_F-chains; yellow, R_Si-chains; green/yellow, mixed cells [61].

It is interesting to note here that there is an analogy of this phase transition with magnetic systems. The LC systems are highly dynamic with the molecules flipping around their long axis, analogous to spin flips in magnetic materials. In this analogy, the side chain interactions replace the magnetic interactions and the LC phase transition temperature is analogous to the Curie temperature at which the paramagnets change into ferromagnets.

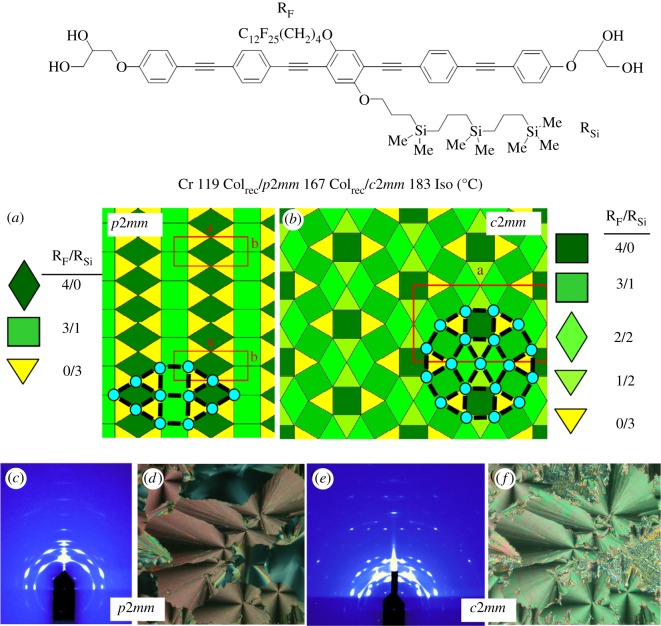
Complexity of LC phase structures can be further increased by introducing geometric frustration. In the case of the compound shown in figure 11, the size of the R_F-chain was further increased, compared with the compound shown in figure 10, so that an organization in a tiling pattern formed exclusively by triangular cylinders is no more possible and hence, square cylinders are also formed. Because of the large difference in area between equilateral triangles and squares, the system experiences a frustration, the triangular cylinders being too small and square cylinders being too large. In addition to this purely steric frustration, this compound must simultaneously relieve the frustration owing to the incompatibility of the side chains and their tendency to segregate into distinct cylinders; at the same time, a periodic tiling pattern is required. The two LC phases formed by this compound, shown in figure 11, are separated by a first-order phase transition at which not only the distribution of the chains (colours), but also the tiling pattern itself changes. In the low-temperature phase with plane group symmetry p2mm (figure 11a), there are three distinct types of cylinders, triangular-, rhombic- and square-shaped, each having a different composition. The triangular cylinders are filled exclusively with the R_Si-chains, the rhombus exclusively with the R_F-chains, whereas the squares must contain a 3 : 1 mixture of R_F and R_H. The latter is because the molecules located between adjacent squares have no option to give their R_Si-chains into one of the adjacent R_F-filled squares (figure 11a) [61]. Note that in this structure, the number of different cylinder cell types is larger than the number of incompatible chains attached to the rod-like core. This means that mixing of different chains gives rise to additional ‘colours’ that further enhances the complexity of LC self-assembly.

Figure 11.

(a) Three-colour tiling and (b) five-colour tiling of the LC phases formed by a quaternary X-shaped polyphile; dark green, R_F-chains; yellow, R_Si-chains; different green/yellow scales, mixed cells with different mixing ratios as indicated beside the models; (black rods, rod-like cores; blue dots, glycerols); (c,e) experimental GISAXS patterns of aligned samples of (c) the three-colour tiling LC phase with p2mm symmetry at T = 150°C and (e) the five-colour tiling LC phase with c2mm symmetry at T = 175°C; (d,f) show the corresponding textures as observed by polarizing microscopy between crossed polarizers for (d) the three-colour tiling LC phase at T = 150°C and (f) the five-colour tiling LC phase at T = 175°C [61].

Upon increasing the temperature, the lateral chains expand and also the miscibility of the incompatible chains (R_F and R_Si) increases. This leads to an even more complex tiling pattern, shown in figure 11b. It is composed of five distinct types of cylinders, triangular cylinders filled only by R_Si-chains, square-shaped filled exclusively by the R_F-chains and three other types of cylinders with different triangular and quadrangular shapes, in which R_F- and R_Si-chains are mixed in different proportions. Hence, the number of colours was further increased to five by the different mixing ratios of the lateral chains inside the cylinders [61]. The complexity of this self assembled nano-scale structure is unprecedented, especially if it is considered that beside the five different cylinder cells the honeycomb framework itself also represents a segregated structure composed of cylinder walls formed by the rod-like cores and columns containing the glycerols at the edges. Thus, this c2mm phase actually represents a well-defined periodically ordered fluid, composed of seven different compartment types in total.

In the tiling patterns reported above, polygonal cylinders with similar size were combined (triangles, rhombus and squares), but it is also possible to combine cylinders of very different size and shape, as, for example, triangles and hexagons in the so-called kagome pattern, shown in figure 12 [62]. This indicates the potential for creating a huge variety of additional highly complex multi-colour tiling patterns that are presently under investigation in our groups.

Figure 12.

Experimental electron density map of a LC kagome lattice formed by a quaternary X-shaped polyphile (blue, highest electron density, R_F-chains; red, lowest electron density, R_H-chains, green positions of the rod-like aromatic cores forming the cylinder walls) [62].

It should be noted here that the reported LC phase structures have been determined by a combination of experimental methods such as optical investigations (polarizing microscopy), calorimetry and different XRD techniques and have been further confirmed by modelling and simulations. For illustration, representative examples of optical textures and grazing-incidence small-angle X-ray scattering (GISAXS) patterns are shown in figure 11c–f. Examples of electron density maps, reconstructed from experimental XRD patterns, are displayed in figures 8a,b and 12. More experimental details and the analysis of these experimental data are described in the cited references.

Simulations by coarse-grained and dissipative particle dynamics methods confirmed a large part of the phases shown in figure 5 [63–67] and some of the two-colour tilings [68]. These simulation methods also can be used to predict new tiling patterns [68]. Nevertheless, molecular design by synthetic chemist combined with sophisticated structure elucidation methods are still required to produce ‘intelligent’ molecules that would provide new superstructures with even higher complexity.

6. Summary and discussion of analogies

As shown above, relatively simple polyphilic molecules, if correctly designed, can spontaneously arrange into highly complex soft matter structures representing periodic multi-compartment arrays. Despite of their complexity, the dynamics of these structures is still fast with the molecules flipping and changing their positions. In this respect, the LC honeycombs differ from related cellular structures in solid-state materials and in morphologies of block polymers [24,25].

As shown in figure 13a, all these complex soft matter structures were obtained with a single class of relatively simple polyphiles by only slight modification of the basic molecular structure, mainly by tailoring the number, polarity, compatibility and size of the lateral chains R attached to a rod-like backbone. In a similar manner, during biological evolution, only about 20 distinct residues R attached to the peptide backbone, varying in size, hydrophilicity, compatibility and sequence, have been used to tailor the numerous biological functions of peptides (figure 13b). Though the mechanism of self-assembly of polyphiles into long-range-ordered mesophases and folding of individual protein molecules into their tertiary and quaternary structures are different, they have in common that only slight mutation of a once successful basic structure leads to a huge number of different useful structures.

Figure 13.

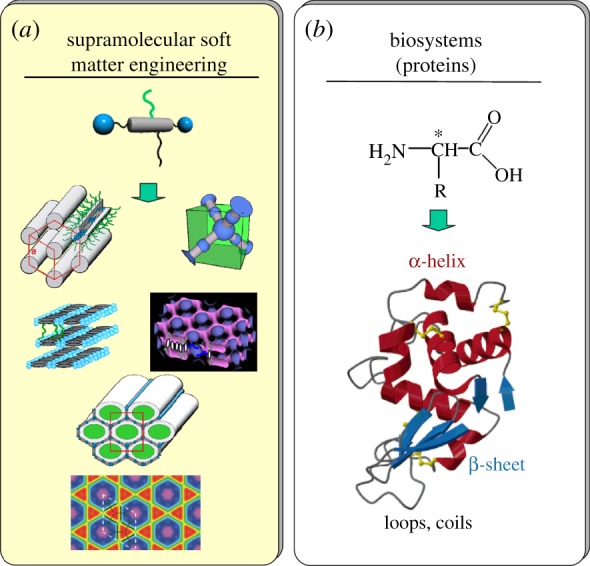
(a) Slight variation of the molecular structure of polyphiles leads to a huge variety of quite diverse soft matter structures with one-dimensional, two-dimensional and three-dimensional periodicities, similarly nature uses slight variation of the structure of the α-amino acids by permutation of only about 20 different residues R along the peptide backbones (b) to tailor the ternary and quaternary protein structures of all functional and structural proteins required in biological systems.

It is acknowledged that simple honeycombs, including tilings by pentagons and squares + triangles, were also reported for ternary star polymers and also a hexagonal three-colour tiling was recently found in a lyotropic system formed by a flexible low-molecular-weight polyphile with water [69]. Nevertheless, we suggest that the high degree of complexity achieved with the polyphiles reported herein is largely the result of the combination of amphiphilicity and shape of the rigid moiety. The analogy with biological systems is also brought to notice, as in the case of peptides, which combine in their functional structures rigid rod-like α-helices with disordered coils and loops. Hence, the proper combination of rigid and flexible molecular units in a specific topology seems to be a successful approach to functionality by self-assembly. In LC systems, this combination is manifested on a macroscopic scale and it is widely used for technical devices [1], whereas in biological systems, it is present on a microscopic level, providing a fundamental basis for biological self-assembly involved in the formation of membrane channels, receptor sites and catalytically active sites in enzymes, etc.

Similarities to biosystems can even be drawn for the two distinct modes of organization of T-shaped polyphiles, the honeycombs with shells of ordered rods enclosing a disordered interior (figure 5c–j), and the axial-bundle phases where ordered rods form a core skeleton surrounded by a disordered continuum (figure 5n,o). They can be considered as analogous to the fundamental construction principles in distinct biological species; insects, for example, having hard shells filled by a soft interior, and mammals, fishes, etc., where bones form a hard inner skeleton around which soft tissue is organized.