A look through ‘lens’ cubic mitochondria

Abstract

Cell membranes may fold up into three-dimensional nanoperiodic cubic structures in biological systems. Similar geometries are well studied in other disciplines such as mathematics, physics and polymer chemistry. The fundamental function of cubic membranes in biological systems has not been uncovered yet; however, their appearance in specialized cell types indicates a role as structural templates or perhaps direct physical entities with specialized biophysical properties. The mitochondria located at the inner segment of the retinal cones of tree shrew (Tupaia glis and Tupaia belangeri) contain unique patterns of concentric cristae with a highly ordered membrane arrangement in three dimensions similar to the photonic nanostructures observed in butterfly wing scales. Using a direct template matching method, we show that the inner mitochondrial membrane folds into multi-layered (8 to 12 layers) gyroid cubic membrane arrangements in the photoreceptor cells. Three-dimensional simulation data demonstrate that such multi-layer gyroid membrane arrangements in the retinal cones of a tree shrew's eye can potentially function as: (i) multi-focal lens; (ii) angle-independent interference filters to block UV light; and (iii) a waveguide photonic crystal. These theoretical results highlight for the first time the significance of multi-layer cubic membrane arrangements to achieve near-quasi-photonic crystal properties through the simple and reversible biological process of continuous membrane folding.

1. Introduction

It is generally assumed that mitochondria are rather homogeneous in their shapes and sizes localized throughout the cytoplasm. However, application of transmission electron microscopy (TEM) and confocal microscopy for visualization of mitochondria has established that the structure of mitochondria in cells is highly dynamic. The inner mitochondrial membrane arrangements may vary from simple lamellar, tubular, vesicular, zigzag or reticular structure to highly convoluted cubic membrane arrangements [1,2]. The mechanisms underlying mitochondrial inner membrane organization and whether this morphological heterogeneity is concomitant with functional diversity remain unclear.

Cubic membrane arrangements represent highly curved, three-dimensional nanoperiodic structures that correspond to mathematically well-defined triply periodic minimal surfaces, or the corresponding periodic nodal surfaces with constant mean curvature. So far, three surface families have been identified to exist in biological systems. They are designated according to their corresponding triply periodic minimal surfaces as gyroid (G), double diamond (D) and primitive (P) surfaces [3]. Cubic membranes have been observed in all kingdoms of life, and they do not appear to be associated with any particular biomembrane, such as the plasma membrane, endoplasmic reticulum, nuclear envelope, chloroplasts or inner mitochondrial membrane. Although they have been observed in numerous cell types and under different conditions, particularly in stressed or diseased cells, knowledge about the formation and function of such non-lamellar, cubic structures in biological systems is scarce, and research so far is restricted to the descriptive level. The frequent appearance of cubic membranes in differentiated and highly specialized cell types poses the intriguing question as to their specific function(s). It is possible that cubic membranes are but an inevitable self-assembled product of the complex molecular mixture of the lipids and proteins, the result of ‘simple’ molecular packing considerations and inter-molecular interactions. However, an increasing body of evidence suggests that these structural organizations might have to fulfil a specific purpose and their formation cannot be rationalized solely by spontaneous molecular packing.

The mitochondria in the inner segment of the cone photoreceptor of certain tree shrew species are unique in size and ultrastructural arrangement of their inner membranes [4]. The average size of mammalian mitochondria is about 0.5 to 1 µm in diameter; however, larger-sized mitochondria (about 5 µm in diameter) have been reported in the retinal cones of at least two mammals, Scandentia: common tree shrew (Tupaia glis) [4] and northern tree shrew (Tupaia belangeri) [5–7]. The retina of Tupaia is vastly different from retina in other mammals and contains up to 95 per cent cone cells, with only a few interspersed rods. In addition, the inner segment of retinal cones of adult Tupaia contains several layers of mega-sized mitochondria (MG), measuring 6–8 µm in diameter [4]. These mitochondria contain a unique pattern of multi-layer cristae in a highly ordered configuration (figure 1a). Although these morphologically striking mitochondria have been studied intensively in the past and some speculation regarding their potential function in the photoreceptors has been proposed [7], little work has been directed to reveal their genuine three-dimensional structures and their potential function in the optical path.

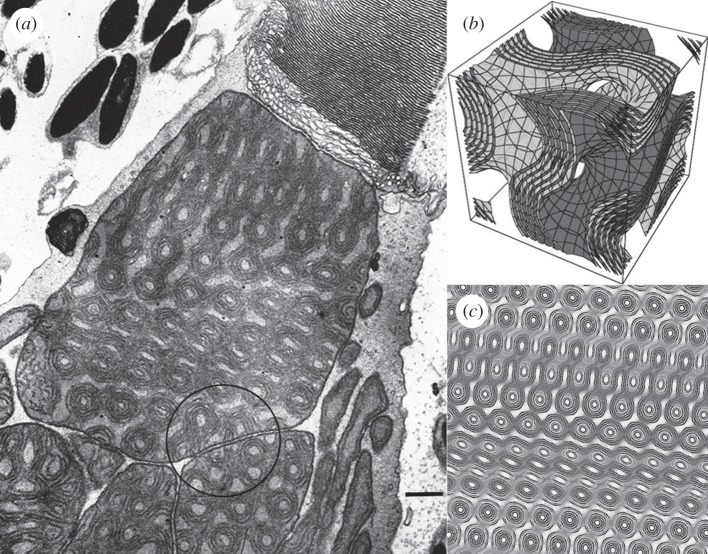
Figure 1.

Direct template-matching method to identify cubic membrane arrangements in transmission electron microscopy (TEM) images (a) at the outer segment of the photoreceptor in tree shrew retina. Note the continuity of the inner mitochondrial membrane organization across the apical mitochondrion and the adjacent mitochondria (encircled). The original TEM micrograph is from fig. 10 of Samorajski et al. [4], with permission (scale bar, 500 nm). (b) Three-dimensional level-surface plot of the multi-layer gyroid cubic membrane arrangement; and (c) the corresponding computer-simulated two-dimensional projection of a thick slice using the same gyroid model as (b). The TEM micrograph of lens mitochondria matches the theoretical projection generated from multi-layer G-based level surfaces (±0.2, ±0.4, ±0.7, ±0.9, ±1.2) with 0.15 unit cell section thickness, viewed from the lattice direction [h, k, l] = [9, 8, 1].

Since the retina in the tree shrews is defined as all-cone retina with less than 5 per cent rods [4], several concerns about the unsatisfactory function of such all-cone retina arise. Firstly, the maximum diameter of the inner segments of the cones of Tupaia is much wider than the diameter of the outer segments. Therefore, the outer segments are not densely packed, as in the retina of most mammals that is rich in rods, but rather widely spaced. As a matter of fact, the cut surface of the outer segment is only about one-quarter to one-third of the inner segments. Secondly, the epithelial cytoplasmic extensions rich in melanin pigments are projecting deeply into the spaces between cone photoreceptors (figure 1a). This means that a considerable percentage of the light penetrating the inner segment would miss the receptors in the outer segment and rather be absorbed by melanin pigments, if the light were not refracted strongly towards the central longitudinal axis of the outer segment. Thirdly, mammalian pupil constriction is controlled through rod–rod appositions in the peripheral retina. As retina of Tupaia has a limited number of rods compared with higher primates, the wavelength limit of the visual response of a retina rich in rod cells might be shifted towards the biologically damaging UV region in retina that is rich in cone cells. Since blue wavelength controls pupillary constriction, a broader range of wavelengths extending into the UV-A region (i.e. wavelengths shorter than 400 nm extending to 320 nm) would be allowed to enter the eyes. Although the melanin present in the pigment epithelial layer absorbs UV close to the visible spectral wavelengths (the extinction coefficient of eumelanin is about 20 cm² mg⁻¹ at 400 nm) [8], other protective mechanisms against overexposure to shorter wavelengths of UV might be required for a retina of Tupaia that is devoid of rod photoreceptors. The experimental measurement of the spectra absorbance of Tupaia retina shows a significant absorbance within the UV range, with peak absorption/sensitivity close to 420 nm [9]. As such, a ‘curious photostable pigment’ was suggested in the inner segment of Tupaia retina close to the base of the outer segment [9] to protect the inner segment from UV damage. However, the nature and the characteristics of the pigment have not been identified yet.

Owing to the above-mentioned unsatisfactory conditions, it has been proposed that the unique size, dense matrix and specialized multi-lamellar system of cristae of the highly refractive MG of Tupaia might have accessory optical functions to optimize the all cone retina function. The main proposed function for these MG is to act as microlenses to enhance the photon capture of the outer segments [7] and, accordingly, they were named as ‘lens mitochondria’. However, the foremost drawback in characterizing their optical function theoretically and experimentally is perhaps owing to the lack of knowledge about their physical structure. Indeed, identifying the three-dimensional structure of these mitochondria is the key to investigate their potential optical role in the photoreceptors.

2. Methods

2.1. Identifying three-dimensional structure of lens mitochondria

A simple yet reliable method for identifying the three-dimensional configuration of highly convoluted and complicated structures with cubic symmetry in TEM images has been developed [10–13]. Briefly, a theoretical two-dimensional projection map is computer-generated from a mathematical three-dimensional model and matched to a TEM micrograph of interest. From this template-matching process, theoretical conclusions about the three-dimensional definition and shape are drawn. This procedure is known as direct template-matching method and is mainly based on pattern recognition [10,11,13]. The reliability of this method in predicting the three-dimensional cubic membrane structure as inferred from two-dimensional TEM images has been further evaluated and confirmed by the three-dimensional reconstruction technique of electron tomography [2].

2.2. Three-dimensional simulator for light transport across multi-layer cubic membranes

As both lens mitochondria and three-dimensional photonic crystals share the same geometry (gyroid), it is interesting to speculate that cubic membrane architecture in the lens mitochondria of tree shrew may act as a nanolens to focus light at the narrow outer segment. More importantly, it may function as a three-dimensional biophotonic crystal with a lattice size close to UV wavelength; thus, its optical property might be able to block or direct UV light away from reaching the outer segment of cone photoreceptors. The multi-layer gyroid-surface-based cubic membrane arrangement of lens mitochondria in Tupaia photoreceptors may enable the mitochondria to amplify, filter or re-direct selectively certain wavelengths of light, while discriminating other wavelength ranges.

To explore the presumed optical properties of the lens mitochondria beyond light collection and focusing, we programmed a simplified model of the lipid membrane layers that tessellate the volume of the mitochondrion. The dimension of the layers within each membrane is of the same magnitude as optical coatings for anti-reflecting surfaces or interference filters. As the refractive indices (RIs) of all the lipids and interstitial spaces within the biological membrane are known [14,15], the membrane can be modelled as special case of a stratified medium [16], where the layers have constant thickness but are strongly spatially curved.

We tested two paradigms (different models) for the simulator setup: (i) the transport of spherical waves across the unit cell of the cubic membrane where all the input and output light is described in terms of monochromatic spherical waves travelling into and out of the unit cell. The other setup is a (ii) modified Monte Carlo simulator in which rays carry the energy and the phase of the light. Upon traversing an interface, the ray splits into a forward and a reflected portion (or optionally into several forward portions to account for higher orders of diffraction). Upon leaving the confinement sphere, the amplitudes and phases are integrated on the image planes and then finally merged. As we are less interested in the proper shape of the resulting focal regions rather than in the energy transmitted through such a system, we implemented both versions for our simulation study (for details refer to Xu et al. [17]).

3. Results and discussion

3.1. ‘Lens mitochondria’ with multi-layer gyroid-based cubic membrane arrangement

We have previously identified complex gyroid membrane organization with six pairs (12 layers) in the retina of Tupaia belangeri [3]. In this report, we use a published TEM micrograph of a lens mitochondrion of Tupaia glis photoreceptors [4] to define the type of inner membrane arrangements by using the above-mentioned template-matching method. The TEM micrograph of interest (patterned membranes) is shown in figure 1a. The first step is the pattern recognition by eye through looking into our collected two-dimensional projection library followed by matching the density details through modifying the parameters such as number of membranes, section thickness and viewing directions [11,13]. Each type of cubic membrane has its own unique patterned signature, and this becomes evident when the gyroid configuration is extrapolated to its TEM two-dimensional counter form (figure 1c). After careful inspection and evaluation, the order membrane domain appears to be of a multi-layer (8–12 layers) gyroid-based cubic membrane arrangement (figure 1).

As shown in figure 1a, the inner membrane cristae of lens mitochondria have 8–12 parallel and closely packed gyroid-surface cubic membrane arrangements. The estimated lattice size of this complicated multi-layer cubic membrane structure is about 400 nm. To the best of our knowledge, this mitochondrial inner membrane organization represents the highest number of multi-layer cubic membrane structures reported in biological systems. In most of the observed cubic membranes, the membranous structure consists of either a single membrane or, more commonly, one pair of parallel membranes [3]. Similar structures, however, have been generated and extensively studied in surfactant and water–lipid systems [18,19]. The significance of these multi-layer cubic membrane arrangements might be correlated with amplification, multiplication or fine manipulation of the proposed function. The tree shrew's ‘lens mitochondria’ morphology is based on a multi-layer gyroid-based cubic membrane arrangement. The apparent three-dimensional geometric similarity between these unique ‘lens mitochondria’ and three-dimensional photonic crystals may spark more interest in investigating and understanding potential functions of these intriguing membrane arrangements in living systems.

3.2. Optical properties of multi-layer gyroid-based cubic membrane arrangements

The photonic properties of cubic phases based on triply periodic-level surfaces (gyroid, G; double diamond, D; and primitive, P) have been studied theoretically [20–22] and experimentally [23,24]. The same G-surfaces are used to describe cubic membrane organization of lens mitochondria in this report. In general, the lattice size of the photonic crystal has to be equal to the wavelength of the light or electromagnetic wave that one wants to manipulate. Three-dimensional simulation data show that the unique 12-layer gyroid cubic membrane arrangements observed in the retina of tree shrew may act as multi-focal lens, angle-independent interference filters that disperse short waves including UV light, and waveguide photonic crystal as well (for details see Xu et al. [17]).

3.2.1. Photon focus and dispersion

The three-dimensional simulation data [17] show that MG with cubic membrane organization is able to focus the incident light at different focal points. The shift of the geometric focus is dependent on the wavelength. The short waves are focused in close proximity to cubic MG, while the long waves are focused far from the MG (figure 2). All the focal points are located within the long axis of the folded membrane in the outer segment of the retina. However, for wavelengths approaching 800 nm (twice the lattice constant), the geometric focus is lost or nearly lost.

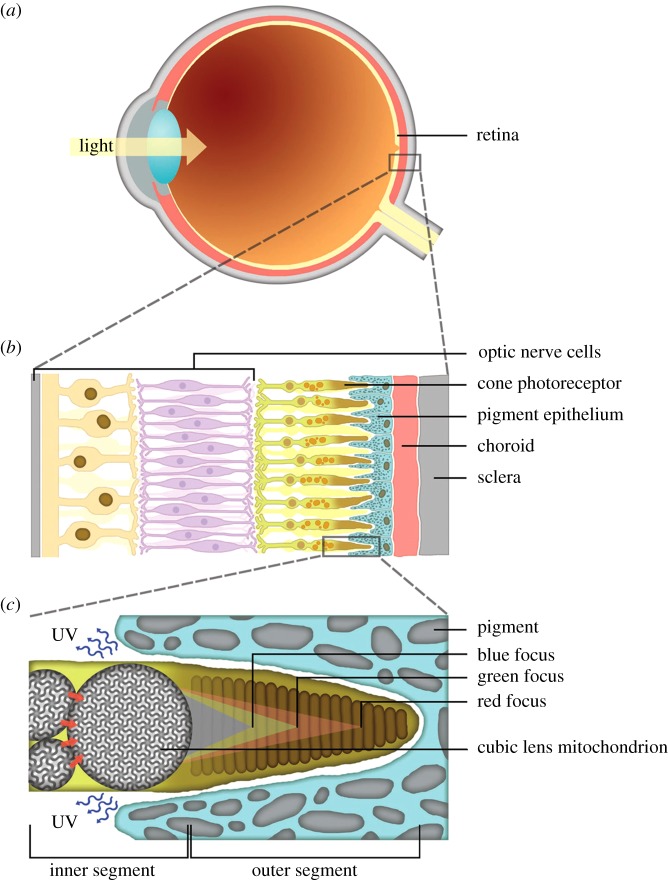
Figure 2.

Schematic of the all-cone retina in the eye of tree shrew (Tupaia glis). (a) A simplified cross section of an eye; (b) level of sensor cells in the retina layer; (c) inner segment containing a large cubic mitochondrion adjacent to a couple of smaller mitochondria. Multi-focal points of red, green and blue wavelengths; UV may be rejected backward in the outer segment based on the quasi-photonic properties of the cubic membrane arrangement in lens mitochondria. Arrows indicate cubic membrane orientation and contact across the mitochondria supporting waveguide properties of multi-layer cubic membrane arrangement.

Multi-focal capacity of MG may enhance colour perception of the tree shrew animals. It is well known that tree shrews are diurnal animals, with voracious appetites and unusually high metabolic rates. Shrews may consume food up to 80–90% of their own body weight daily. Without trichromacy ability, the tree shrews would share the difficulty of the mammalian dichromat in detecting ripe fruit against the dappled background of forest foliage [25,26]. It is primarily at wavelengths above 500 nm that the spectral reflectance curves of yellow or orange fruit differ from those of background leaves [27]. Thus, the dichromatic consumer can seldomly detect such fruit by colour, since the colour vision depends on their short-wave cones, which absorb negligibly above 500 nm.

Interestingly, we also found that light of wavelengths above 650 nm yield second, elongate, region in depth where the light is relatively focused (second focus), but only for the range around twofold lattice constant; the power flux in the second focus exceeds the one in the (lost) focal region. The biological significance of this second focus region is currently unknown.

3.2.2. Interference filter

The striking similarity between the three-dimensional arrangement of ‘lens mitochondria’ inner membranes and certain experimentally produced photonic crystals with photonic bandgap (PBG) or wave guidance is obvious [20,28]. Photonic crystals are periodic dielectric composite nanostructures that are designed to affect the propagation of electromagnetic waves in the same way as the periodic potential in a semiconductor crystal affects the electron motion by defining allowed and forbidden electronic energy bands [29]. The simplest form of a photonic crystal is a one-dimensional periodic structure, such as a multi-layer film. A photonic crystal with hexagonal lattice represents a typical two-dimensional photonic crystal. However, strong confinement (or control) of photons can be possible by using three-dimensional periodic crystals with corresponding three-dimensional PBG that forbid propagation of light waves, in any direction and for any polarization, for a certain frequency range. As both lens mitochondria and photonic crystals with PBG properties share the same geometry (gyroid type), it is tempting to speculate that cubic membrane architecture in the lens mitochondria of Tupaia species may function as a photonic crystal with a lattice size close to UV wavelength, and that their PBG property might be able to block or direct UV light from reaching the outer segment of photoreceptors in the rod-deficient retina.

Our work on simulating the light transport through the multi-layer cubic membrane arrangement shows that photonic crystal properties might not be required for the lens mitochondria to operate as a wide-angle, broad-band UV filter in front of the outer segment of the photoreceptors. Our simulations ascribe to a simplified assembly of such membranes the power to reduce UV transmission by as much as 50 per cent by dispersing the UV light. We were not able to identify a definitive focus point for the wavelengths less than 400 nm or more than 800 nm. The interference filters also show sufficiently steep transitions not to block the visible light from the eye (figure 2). MG with cubic membrane arrangement may not act as a perfect quasi-photonic crystal maybe because the changes in refractive index are too small and the lipid-bilayer-based membrane (approx. 5 nm) is too narrow to create bandgaps; however, it works as a decently effective bandpass that suppresses a majority of the short wavelengths yet allows the longer wavelengths to be transported much more efficiently through a multi-layer cubic membrane arrangement. Furthermore, our simulation data may explain the experimental results which show the ability of Tupaia retina to prevent the transmission of near-blue and UV light to the outer segment [9].

3.2.3. Waveguide properties

The TEM images often show that an apical MG is usually placed on top of three to six closely packed MG. Together, the MG form a solid mass that fills the conical upper region of the inner segment. Multiple contact points are also observed between the densely packed MG (figure 2). Furthermore, cubic membrane orientation seems to be maintained across the adjacent MG (figure 1a). These observations in the published TEM images may suggest that MG with cubic membrane arrangement might have waveguide properties to direct the light from the inner mitochondrial layer towards the apical MG where the light might be further focused on the narrow outer segment. Our three-dimensional simulation data support this notion and, as expected, the two separate compartments of the MG with different RIs, the channels inside the compartment with the higher RI, form a mild waveguide that preferentially propagates light inside that compartment (figure 3). The capturing angle for light into these channels is astonishingly large and the efficiency of the waveguide transport increases with the wavelength of the light (figure 3).

Figure 3.

Three-dimensional simulation plot of the intensity patterns for various wavelengths of light as they are transmitted through a ‘lens mitochondrion’ with a multi-layer gyroid-based cubic membrane arrangement. After leaving the mitochondrion, the light leaves the pattern illustrated in the figure. The vertical axis is the distance from the mitochondrion and the shape of the blob is a surface of constant intensity (constant power flux). The images are projections from the three-dimensional distribution without perspective distortion and are hence to scale in all axes. The total power of the transmission increases dramatically for longer wavelengths but focus and bundling and hence the peak intensity is higher for shorter wavelengths. Marked by red arrows is the emission from waveguides created by straight single-compartment channels inside the mitochondrion present for all wavelengths examined. The shape of this light emission ‘blob’ including the waveguide peaks strongly depends on the orientation of the mitochondrion and polarization of the light. The mitochondrion exhibits an overly simple and imperfect photonic bandgap which is achieved despite very low changes of refractive indices in the membranes.

4. Conclusions

Previous studies suggested that membrane-bound ‘ellipsosomes’, lipid droplets and MG [7] might play a role in altering the spectral sensitivity of the photoreceptors to act as microlenses to enhance the photon capture in the outer segment of the photoreceptors. Apparently, cubic membrane structures are linked to light reactive biomembranes in plant tissues as well, such as the cubic structures found in the green algae Zygnema chloroplasts and in the prolamellar body (PLB) of photosynthetic cells in higher plants [3]. A physical role has been proposed for the selection of D-surface geometry [30], based on theoretical considerations on how the geometry of crystals controls the emission or absorption of certain wavelengths of light through the existence of photonic bandgaps [20]. Although the D-surface is isotropic, its geometry is such that it may potentially trap photons. The absorbed energy could then be used by certain molecules that are positioned along a particular lattice direction, and, for instance, trigger conformational changes to transform PLB into an active thylakoid membrane geometry. A similar structural role can be considered for the selection of different subtypes of cubic membrane architectures (photosome) in bioluminescent scale worms [31,32]. Interestingly, the photosome membrane organization has a D subtype cubic membrane in the resting, un-stimulated state; however, upon electrical or optical stimulation, the membrane configuration changes and acquires a P subtype. This suggests that different cubic membrane subtypes indeed respond to, or manipulate different wavelengths of light. This also raises the possibility that cubic membranes change their geometrical configuration upon interaction with light. These questions clearly deserve further investigation. In this report, we have shown that the MG, categorized as ‘lens mitochondria’, are indeed ‘cubic mitochondria’ from the ultrastructural point of view. The apparent three-dimensional ultrastructural similarity of lens (cubic) mitochondria to photonic crystals and our computational simulation results strongly suggest a role of cubic membranes as ‘optical filters’. Our three-dimensional simulation of the light transport across the cubic membranes in lens mitochondria further suggests multiple roles for MG: they may act as: (i) multi-focal lens; (ii) angle-independent interference filters to block UV light; and (iii) waveguide photonic crystal. Experimental investigations are necessary to further test this hypothesis.