Hierarchical self-assembly of chiral fibres from achiral particles

Abstract

We investigate, by molecular dynamics simulation, the behaviour of discotic particles in a solvent of Lennard-Jones spheres. When chromonic disc–sphere interactions are imposed on these systems, three regimes of self-assembly are observed. At moderate temperatures, numerous short threads of discs develop, but these threads remain isolated from one another. Quenching to low temperatures, alternatively, causes all of the discs to floc into a single extended aggregate which typically comprises several distinct sections and contains numerous packing defects. For a narrow temperature range between these regimes, however, defect-free chiral fibres are found to freely self-assemble. The spontaneous chirality of these fibres results from frustration between the hexagonal packing and interdigitation of neighbouring threads, the pitch being set by the particle shape. This demonstration of aggregate-wide chirality emerging owing to packing alone is pertinent to many biological and synthetic hierarchically self-assembling systems.

1. Introduction

The mechanism by which molecular handedness leads to optical chirality on macroscopic length scales is the stuff of high-school physics. An issue of more contemporary interest, though, is the onset of mesoscopic or macroscopic twist in systems for which the self-assembling objects have no underlying handedness. Experimental systems that exhibit such behaviour include helically mesostructured silica nanofibres templated by achiral surfactants [1,2], twisted ribbons of self-assembled tetrahedral cadmium telluride nanoparticles [3], certain fibre-forming dendrimer systems [4] and achiral benzene triesters [5].

Both theory [6] and simulation [7] have been used to examine the onset of spontaneous chirality in model achiral polymeric systems. More recently, particle-based simulation studies have observed the development of regularly twisted superstructures in systems comprising achiral particles. Specifically, rods with both spherical end-chains [8] and bolaamphiphilic sphere chain systems [9] have been shown to exhibit such behaviour, apparently driven by local packing mismatch between the different particle types involved.

Here, we examine spontaneous chiral symmetry breaking in the context of free self-assembly of fibrillar structures. Such fibrils are found in many biological and synthetic systems; they are both important nanocomponents in their own right and, apparently, significant intermediate arrangements in certain hierarchical self-assembly processes. For example, it has been hypothesized that protofibrils, which are intermediate structures involved in the production of amyloid fibrils, may themselves be pathogenic with respect to neurodegenerative conditions such as Alzheimer's and Parkinson's diseases [10,11]. Hierarchical self-assembly of fibres and elongated micelles is also central to the generation of many templated silica structures [12]. There is some debate, however, as to the origins of the chirality observed in various of these structures [2,13]

A number of simulation studies of fibre self-assembly have been published in recent years employing coarse-grained models of cylindrically symmetric particles. Bolhuis [14] considered the behaviour of hard spheres decorated with attractive interaction sites on their poles. This patch potential not only promoted thread formation but also led to weak thread–thread interactions. Thus, Monte Carlo simulations showed the spheres polymerizing into threads, which subsequently condensed into bundles or fibres. In a subsequent study, Li et al. [15] developed a mesoscale simulation model which was used to investigate the self-assembly of soft disc-like micelles in dilute solutions. This model was found to form flexible threads and, for some solvent conditions, these threads underwent further self-assembly into flexible and twisted hexagonal bundles. More recently, in a mixed experimental/simulation study, the self-assembly kinetics of colloidal Janus spheres have been investigated [16]. Both approaches observed formation of extended multi-thread fibres, some with chiral character, and the competing growth mechanisms were identified. They represent exciting manifestations of theoretical work explaining the emergence of chirality in systems involving both intercalation and hexagonal packing [17,18].

Here, we use molecular dynamics (MD) simulation to investigate fibre formation by discotic pseudo-ellipsoidal particles in a solvent of Lennard-Jones spheres. From these, we show that, in appropriate conditions, the types of chiral clusters predicted by the zero temperature energy landscape calculations of the study of Chakrabarti et al. [19] can be realized in finite-temperature systems. This is achieved by following kinetic crossover ideas [20], whereby the yield of states which are thermodynamically stable but kinetically restricted is optimized at intermediate temperatures.

In §2, we present details of the model system and simulation parameters used in this study. Following this, we present results obtained with one parametrization of this model in four temperature quenches. In this, we concentrate on structural aspects of the resultant aggregates. Finally, we characterize the structure of the defect-free fibre formed at intermediate temperature, discuss its origins and draw some conclusions.

2. Model and simulation details

We consider behaviour of oblate Gay–Berne ellipsoids mixed in a solvent of Lennard-Jones spheres. The disc–disc interaction employed is the variant introduced by Bates & Luckhurst [21]

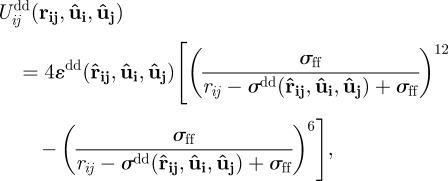2.1

where 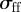characterizes the thickness of the discs i and j and the anisotropic shape and well-depth functions 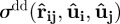and 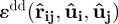take the standard forms given in the study of Bates & Luckhurst [21]. Here and in what follows, the suffix f denotes the disc face and the suffix e denotes its edge. In this study, we consider moderately discotic particles with aspect ratio 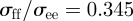. The energetic anisotropy of the disc–disc interaction is set by the parametrization .

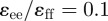Lennard-Jones solvent particles, of size 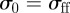and well-depth 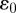, interact with the discs through a tuneable form of the generalized Gay–Berne interaction [22]. For a disc 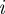and sphere 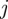, equation (2.1) simplifies to

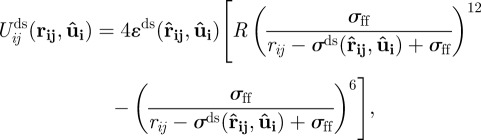2.2

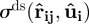and 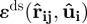adopting the forms given in the study of Cleaver et al. [22]. It is straightforward to adjust the nature of the disc–sphere interaction by varying the ratio 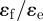. Here, we consider the case 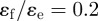, such that the edges of the discs are solvophilic and the faces solvophobic; this symmetry of amphiphilic behaviour promotes what is termed chromonic self-assembly in which stacking of disc-like molecules is promoted by the desire to shield their solvophobic faces. Chromonic stacking is exhibited by, for example, many dyestuffs, as summarized in an earlier insightful review [23]. The additional parameter 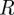tunes the relative influence of the repulsive and attractive components. The interaction potentials (2.1) and (2.2) are illustrated in figures 1 and 2.

Figure 1.

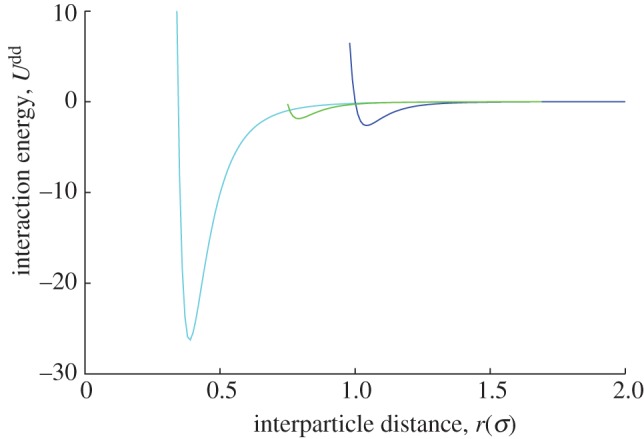
The disc–disc interaction potential for three combinations of relative particle orientations. Face-to-face, light blue; edge-to-edge, dark blue; face-to-edge, green.

Figure 2.

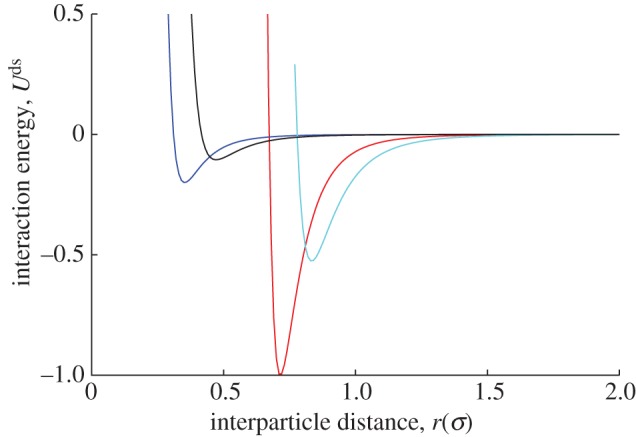
The R = 1 (sphere-to-edge, red; sphere-to-face, dark blue) and R = 5 (sphere-to-edge, light blue; sphere-to-face, black) disc–sphere interaction potentials for two relative orientations of the disc symmetry axis and the inter particle vector.

Following the standard convention for molecular simulations [24], in what follows, we express system parameters and observables in terms of the length 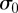, the energy 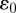and the particle mass m. On adopting this scheme, reduced temperature is expressed in units of 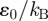, where 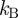is Boltzmann's constant and the unit of reduced time is 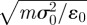. The MD time step used here was 0.0015.

Initial simulation results for this model, obtained from small system runs, showed that R provides an effective means by which to vary the quality of the solvent and, so, control the formation of fibrillar structures. With R = 1, cooling initially isotropic mixtures led to the development of numerous linear stacks of discs, consistent with previous simulations of chromonic self-assembly [25–27]. These stacks were well solvated and did not condense into a single aggregate on further cooling—lateral aggregation of the stacks was inhibited by the strongly associated solvation shells. With R = 5, the equilibrium arrangement at temperatures ≥1.8 was, again, a solution of monomer discs and length-polydisperse threads of discs. Quenching below 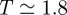with R = 5 led, however, to the development of anisotropic multi-thread aggregates. We employ R = 5 in all of the simulations described below.

In §3, we present results from a series of constant number, volume, temperature MD simulations performed to investigate the behaviour of the model just described. To reduce the influence of the periodic boundary conditions, a large simulation box length was used (L_x = 34.18); this proved significantly larger than any of the fibre lengths observed in this study. To prepare an equilibrated high-temperature configuration, an initial system of 8788 particles (7908 spheres and 880 discs) was melted from a face-centred cubic lattice arrangement and simulated for 7 000 000 MD time-steps at T = 2.3. Once memory of the original lattice had been lost, no further transitions were observed in this equilibration run; the system remained isotropic and well mixed throughout. The final configuration from this T = 2.3 run was then used as the starting point for all other runs; in all cases, this isotropic arrangement was quenched to a lower temperature.

As well as standard thermodynamic observables, a number of structural characteristics were monitored in each quench simulation. Threads of discs were identified via a standard cluster-identification algorithm using a short cut-off distance. Higher order structures were then determined via a second-level cluster-monitoring process which found adjacent threads. The findings of this analysis were cross-checked against animations showing system evolution. At regular intervals, the largest aggregate identified at each given time step was further analysed via calculation of its size, its principal moments of inertia and the orientational order of its constituent discs. In addition to this, post-processing analysis was performed on fully formed fibres to identify further structural details.

3. Results

An initial quench was made to a temperature of 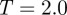. On cooling to this temperature, it was found that short thread-like assemblies of two to three discs occasionally developed. Each of these was found to persist for a relatively short time before dissociating into monomers and dimers.

Performing a deeper quench, to 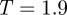, led to more noteworthy self-assembly processes. Here, significantly more and longer threads were observed. These threads were dynamic objects, with monomers joining and leaving on a regular basis. Once established, these threads proved long-lived and several could be traced over hundreds of thousands of time steps. A typical configuration from this run is shown in figure 3.

Figure 3.

A typical configuration from the equilibrated phase of the T = 1.9 quench. For clarity, only discs in threads of length 4 or more are shown.

Disaggregation of these longer threads commonly involved a split into two shorter threads. Another occasional feature seen at this temperature was lateral association, leading to second-generation double-thread mini-bundles. At 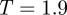, these mini-bundles proved meta-stable as they always re-divided into separate threads. This initial observation of mini-bundle formation was, though, significant since it signposted the general propensity of this system to develop multi-thread assemblies.

In an attempt to encourage the formation of more involved assemblies, a lower temperature of 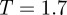was used in the next quench simulation. At this temperature, after an initial period in which numerous individual threads were formed (each comprising up to eight monomers), several larger bundles developed. The threads in each of these bundles were approximately parallel, leading to nascent fibres which gradually developed both laterally and longitudinally. When these assemblies had relatively few threads (i.e. approx. three to five), they exhibited considerable flexibility, the threads exploring various packing arrangements. This flexibility reduced, however, as the bundles grew. Also, subsequent to this, a small number of bundle–bundle aggregation events took place. One of these is apparent from the jump at 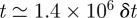in the moment of intertia time lines shown in figure 4. These time lines show that, even before this jump, the largest bundle was elongated as two of its moments of inertia were larger than the third. This difference was accentuated by the bundle–bundle aggregation event, showing that the two bundles attached end-to-end. Subsequent to this, the three moments of inertia all grew in near monotonic fashion, but the smallest grew significantly more slowly than the other two. Very little change was seen over the last two million time steps of the run; by this stage, virtually all of the discs in the system had joined the fibre.

Figure 4.

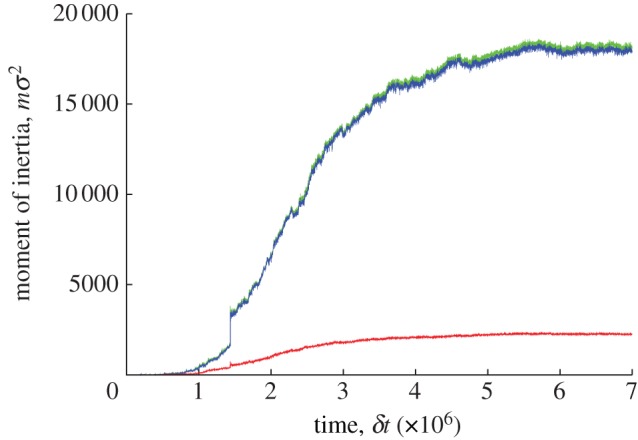
Time lines of the principal moments of inertia of the largest cluster in the T = 1.7 quench (largest eigenvalue I_l, green; middle eigenvalue I_m, blue; smallest eigenvalue I_s, red).

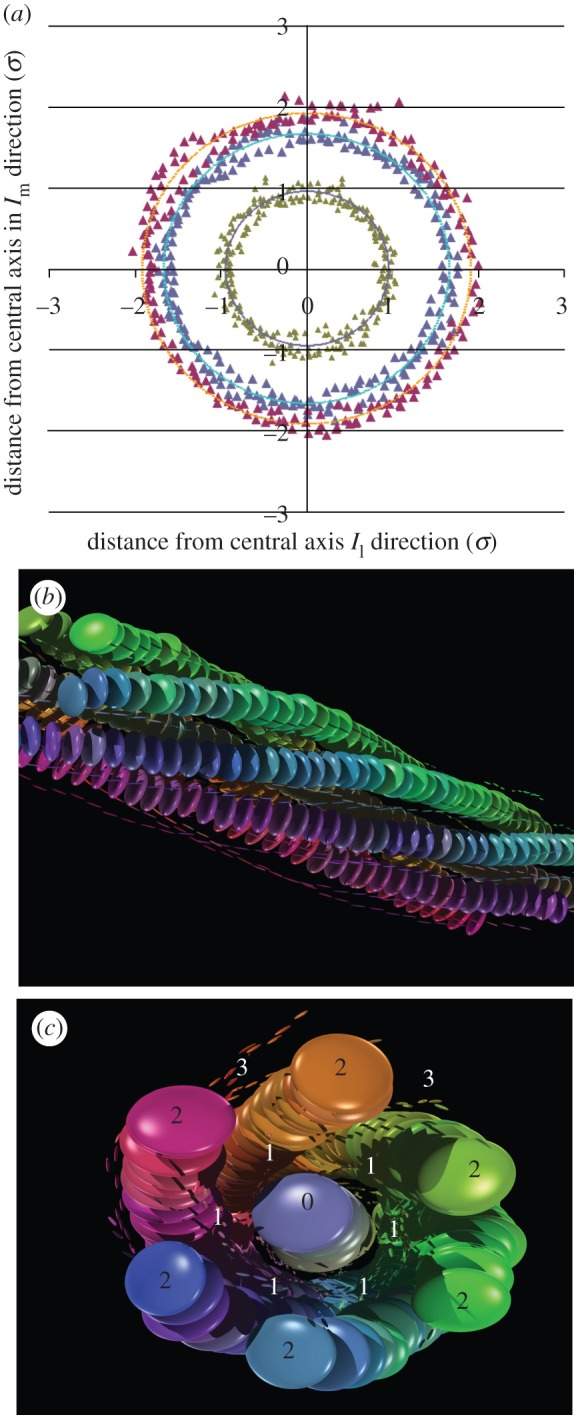
A configuration snapshot from the end of this run is shown in figure 5. Here, the discs are colour-coded according to their orientations, so as to make it easier to recognize differing local packing arrangements. Thus, segments of uniform colour are straight, whereas segments with gradually changing hue are chiral. As expected from the moment of inertia data, the final aggregate is certainly fibre-like. However, at least three distinct segments can be identified: a central straight region and twisted segments (of opposite handedness) at each end. Stacking defects between these segments can also be identified. Animations of the self-assembly process confirm that this segmental structure originated owing to the evolutionary steps experienced by the fibre. Specifically, in this quench, three significant multi-thread bundles developed independently in the middle stage of the self-assembly. Each of these grew to a sufficient size that it retained its own local packing arrangement throughout bundle–bundle aggregation. This multi-segment-fibre arrangement was found to be long-lived when the run-time of this simulation was extended, the main segments and defect regions persisting indefinitely.

Figure 5.

Final aggregate formed in the T = 1.7 quench. For clarity, no spheres are shown. Discs are colour-coded according to their orientation; neighbouring threads in chiral segments therefore have differing colours.

On the time scales accessible here, the final aggregate obtained from this 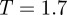quench proved to be kinetically arrested; while the thermal energy in the system was sufficient to allow a degree of single particle-dissociation type relaxations, the stronger bundle–bundle interaction strengths were too great for large-scale rearrangements to take place. As a result, the fibre had no kinetically accessible route by which to adopt a defect-free structure.

In view of this, subsequent quenching runs were undertaken at a range of temperatures intermediate between 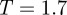and 1.9. Of these, the run at 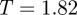proved optimal in that only one multi-thread bundle was nucleated. As evidenced by the corresponding moment of inertia time lines (figure 6), this then grew into an elongated fibre without exhibiting any of the discontinuities seen at 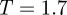. Interestingly, the growth time scales apparent from these time lines proved relatively insensitive to, for example, changes to the initial configuration. The final configuration from this run, shown in figure 7, was a defect-free, chiral fibre which again contained virtually all of the discs in the system. As we show in the following section, the chirality in this fibre of achiral particles resulted from frustration between hexagonal packing and interdigitation of neighbouring threads.

Figure 6.

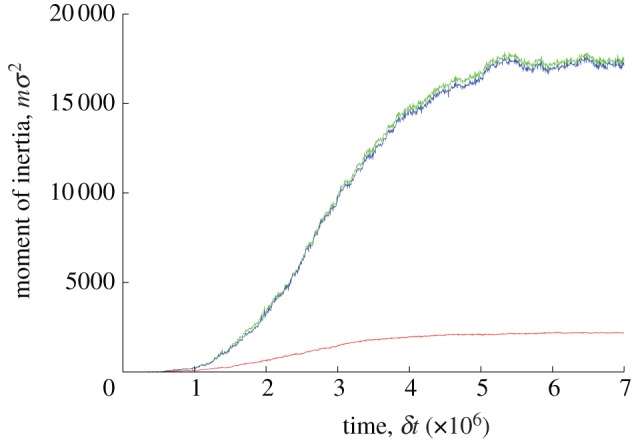
Time lines of the principal moments of inertia of the largest cluster in the T = 1.82 quench (largest eigenvalue I_l, green; middle eigenvalue I_m, blue; smallest eigenvalue I_s, red).

Figure 7.

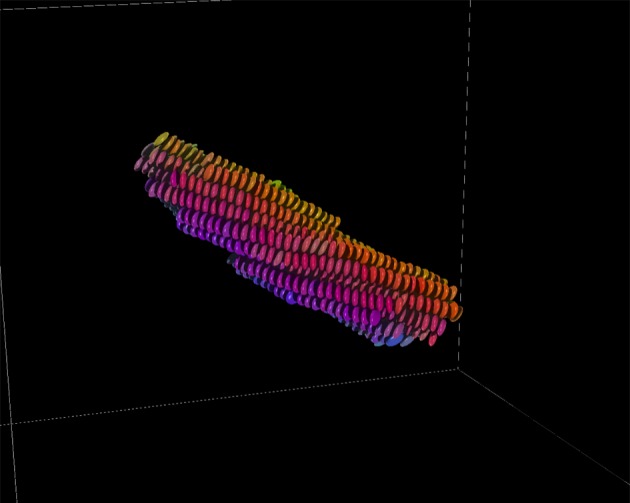
Final configuration from the T = 1.82 quench. For clarity, no spheres are shown. Discs are colour-coded according to their orientation; defect-free helical threads therefore have gradually changing colours.

4. Characterization and discussion

To characterize the defect-free chiral fibre more fully, each of its threads was fitted to the locus of a helix with centre-line running along the eigenvector corresponding to the fibre's smallest moment of inertia. Using this approach, parametric fits yielded independent helical pitch and radius values for 21 of the fibre's 22 threads (the central thread was found to be straight and so no fit was performed). These fits are given in table 1. All of these give a consistent value of 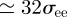for the emergent length scale that is the fibre pitch. Furthermore, their radial fit parameters show a tendency to adopt certain preferred values, the first 18 thread radii falling into three distinct groups.

Table 1.

Parametric radius and pitch fits of individual threads of the T = 1.82 fibre to ideal helices.

thread	radius (σee)	pitch (σee )
1	0.939 ± 0.005	32.8 ± 0.4
2	0.960 ± 0.004	30.2 ± 0.9
3	0.942 ± 0.009	31.6 ± 0.7
4	0.923 ± 0.009	33.5 ± 0.8
5	0.976 ± 0.005	30.5 ± 0.4
6	1.017 ± 0.003	31.7 ± 0.4
7	1.637 ± 0.008	32.1 ± 0.3
8	1.734 ± 0.003	31.0 ± 0.3
9	1.726 ± 0.004	31.8 ± 0.2
10	1.626 ± 0.007	33.1 ± 0.3
11	1.640 ± 0.006	31.5 ± 0.2
12	1.669 ± 0.006	31.8 ± 0.3
13	1.890 ± 0.007	31.8 ± 0.9
14	1.907 ± 0.007	32.3 ± 0.3
15	1.980 ± 0.001	31.5 ± 0.2
16	1.949 ± 0.004	32.0 ± 0.3
17	1.974 ± 0.005	31.8 ± 0.1
18	1.868 ± 0.013	33.3 ± 0.1
19	2.511 ± 0.003	32.7 ± 0.1
20	2.484 ± 0.006	33.8 ± 0.2
21	2.458 ± 0.003	30.4 ± 0.2

The reason for this grouping is made apparent by figure 8a, which shows all of the disc centres projected onto a plane perpendicular to the fibre axis. This illustrates that the fibre had a straight central thread (‘layer 0’) surrounded by six ‘layer 1’ helical threads. Six ‘layer 2’ threads then resided in the grooves provided by layer 1 and, similarly, the locations of the six ‘layer 3’ threads were templated by the grooves in layer 2. Finally, three ‘layer 4’ threads lay in grooves outside the fibre. Snapshots showing the layer 0 and layer 2 particles in full and (so as to give unobstructed views of these threads) the other particles as short lines are given in figure 8b,c. Both these reinforce the absence of defects in this self-assembled structure and, through their orientation-dependent colour coding, show the smooth helices traced out by the layer 2 threads.

Figure 8.

Views of the T = 1.82 chiral fibre (a) showing particle centres only, projected onto a plane perpendicular to the main thread axis and coloured for layer: green, 1; blue, 2; red, 3; (b,c) different views showing the particles in layers 0 and 2 fully resolved and colour-coded for orientation.

This structural characterization also indicates why the fibre formed here was chiral. The chirality was founded on the structural stability of a hexagonal 7-thread nucleus comprising a straight central thread sheathed in six columns of slightly tilted discs, the outer threads spiralling around so as to maintain the integrity of the fibre. This arrangement was identified by Chakrabarti et al. [19] as the optimal cluster for 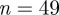discotic ellipsoids.

The discs in the layer 1 threads were obliged to tilt because they had to interdigitate (with each other and with the central thread) in order to achieve their radial displacements from the central axis (note, from table 1, that the radial fit values for layer 1 particles are generally less than 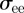). As hexagonal packing requires triplets of neighbouring threads to cooperatively interdigitate, a consistent handedness developed naturally in the stacking adopted at these triplet junctions. This arrangement is characterized by a 7-particle propeller-like motif—this motif is the structurally chiral object from which the large-scale fibre pitch originated. Once formed, the chiral seven-thread core acted as a seed for the subsequent fibre growth.

As predicted earlier [17,18], the chirality observed here develops owing to the interplay of packing entropy and the inter- and intra-thread enthalpic contributions. Provided that the enthalpic contributions are in the correct regime, the helical pitch is controlled by packing, i.e. details of the disc-particle shape. We will describe the complex kinetics of this hierarchical growth process in a future publication. We also defer our contribution to the intriguing debate regarding the suggestion that chiral fibres may have self-limiting radii [28,29] to this subsequent paper.

It is noteworthy that, for all but the outermost layers, the threads formed in the 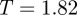fibre had no defects. In contrast, anisotropic charge transport in discotic liquid crystals [30,31] via electron hopping has only achieved limited mobilities owing to the marked impact of occasional in-column defects. This suggests that experimental realization of defect-free fibres of the sort simulated here may offer a route to significantly higher electron mobilities than those achieved using bulk discotics.

In summary, we have shown that a defect-free chiral fibre can self-assemble from achiral disc-shaped particles provided that the temperature is set so as to limit the system to a single nucleation process. The fibre chirality observed here results from the frustration that arises when both hexagonal packing and interdigitation of neighbouring threads are sought. This spontaneous symmetry-breaking through self-assembly also has more general implications for nanostructure formation. It demonstrates that it is not always necessary for the constituent particles to manifest all of the properties required of a desired nanostructure—given appropriately controlled conditions, such properties and symmetries can simply develop spontaneously via structural chirality.