Abstract
Phagocyte transmigration is the initiation of a series of phagocyte responses that are believed important in the formation of fibrotic capsules surrounding implanted medical devices. Understanding the molecular mechanisms governing phagocyte transmigration is highly desired in order to improve the stability and functionality of the implanted devices. A hybrid computational model that combines control theory and kinetics Monte Carlo (KMC) algorithm is proposed to simulate and predict phagocytes responses at molecular level. In order to mimic various biological knockout experiments, a general external control scenario is designed. The stochastic nature inherent to phagocyte transmigration is captured by KMC. A new formula is derived to calculate the transition rates as inputs to KMC. This formulation might quantify biological interactions in a general manner which is beyond the scope of the traditional chemical reaction kinetics.
I. INTRODUCTION
In the practice of medicine, the use of a number of implanted medical devices, such as breast implants, eye implants, drug delivery systems and biosensors, is becoming increasingly important. However, these devices often induce a wide variety of unwanted responses, including inflammation, thrombosis, infection, and fibrosis. As a result, fibrotic capsules may form and surround the implanted medical devices. It has a direct impact on the stability and compatibility of the implanted medical devices, and it may leads to implant failure[1], [2], [3]. In many cases, the fibrotic tissue formation is associated with the rapid accumulation of large numbers of phagocytic cells[4], [5]. It begins with the recruitment of phagocytes from capillary to implants sites, which is referred as phagocyte transmigration. Having an insight into the molecular mechanisms governing phagocyte transmigration is the jumping-off point in the studying of how phagocyte responses may alter the extent of fibrotic tissue formation so that we can learn from it to improve the stability and functionality of the implanted devices.
It is well accepted that phagocyte transmigration is a multistep cascade process, involving initial margination in the vessels, rolling and firm adhesion of phagocytes to the vessel wall, and extravasation. Phagocyte rolling on the vessel wall is mediated by members of the selectin family via continuous formation and rupturing of receptor-ligand bonds between phagocytes and endothelial cells (ECs). Rolling rapidly leads to trans-membrane signaling and the formation of a second set of shear resistant adhesion bonds, enabling phagocyte cells to become arrested prior to migration into the extravascular space.
Over years, mechanical and thermodynamic models have been developed to study how physical parameters influence the behavior of phagocyte or leukocyte rolling and adhesion. One well-known model used to describe the kinetics of single bio-molecular bond failure was established 20 years ago[6]. At the same time, biomedical engineers have developed and applied a variety of optical and electronic technologies (i.e., intravital and conventional light microscopy, flowcytometry, rotational and translational viscometry, and molecular force and optical spectroscopy) so that real-time imaging of phagocyte rolling and arrest can be obtained, and an inner view of the intercellular adhesive contact region can been achieved. Along with the progress of experimental methods that enable quantification of the relevant kinetic and mechanical parameters, studies[7], [8], [9], [10], [11] have been done in adhesive dynamics simulations. These models focus on studying the dynamical characteristics of receptor-ligand bonds under various physical parameters, such as rolling velocity and shear rate. It is difficult for these models to answer the questions like what is the response of phagocytes transmigration if the concentrations of selectins decrease. Therefore, models that can explain a variety of interactions at the level of individual molecular pairs are highly demanded. More importantly, the multistep process of phagocytes transmigration should be taken into account as a whole. But aforementioned models fail to do it. The multi-step process of phagocytes transmigration can be viewed as a biological system that comprises a number of elements to form a complex network. How each individual bio-molecular behaves over time? What is system traffic pattern? How can we control this traffic? These questions are most wanted to be known by us. To gain a system-level understanding of a biological process, system and control theory has been re-adopted in system biology. The first application of system theory and control theory to study cellular responses to implanted devices[12] was published in 1979. Besides this model, a variety of related modeling works have been done in the areas of inflammatory reactions[13], [14], thrombosis[15], coagulation[16], and fibroblast proliferation[17]. Despite these interesting models, most of them were based on in vitro results and none of these models can be directly used to simulate phagocyte responses to implanted devices in vivo.
Another important issue about phagocytes transmigration process is its stochastic nature. For example, phagocyte rolling shows a stop-and-go type of jerky motion along with highly fluctuating rolling velocity[18]. The randomness appears because of the small number of receptor-ligand bonds. Even small change in the number of bonds, it might alter rolling behavior dramatically. Besides the small-scale rolling, the lack of quantitative information on heterogeneous cell properties, such as receptor number and class, contributes to the randomness appeared in phagocytes transmigration. This randomness is not due to measurement error but a manifestation of the stochastic nature inherent to the physics and chemistry of receptor-ligand binding. This situation calls for a probabilistic model other than a deterministic model in the study of phagocytes transmigration.
In system biology, a basic probabilistic description of dynamic system is master equation. A master equation is a probabilistic differential equation that describes a system defined by discrete configurations. Master equations are useful in describing systems at small length scales when continuum assumptions break down, particularly when fluctuations are important. For example, a chemical system of N reacting species can be described by a master equation that is a differential-difference equation in N dimensions governing the dynamics of the probability distribution for the system. One common drawback of master equations is that they suffer from the well-known “curse of dimensionality”. Each species adds one dimension to the problem leading in many cases to a prohibitive computational complexity. Instead of numerically integrating the master equation, stochastic realizations are usually obtained through Monte Carlo simulation. The most referred method is Gillespie’s SSA method[19] and variations of it. The Monte Carlo approaches have been shown to be mathematically equivalent to the master equations[20]. Almost all of these methods describe biological interactions using chemical reaction kinetics. This might narrow the scope of the interactions appeared in a biological system.
Rule based methods are also popular in simulating stochastic dynamic systems. Recent work of[21] applied a multilevel, agent based, in silico model to represent the dynamics of rolling, activation, and adhesion of individual leukocytes in vitro. It provides the links between sub-cellular molecular level events and the variety of systemic phenotypic attributes. However, agent based methods (ABMs) looks at a system not at the aggregate level but at the level of its constituent units. The interpretation of interactions between each of the components in the system might not be explicit. And the high computational requirements of ABMs remain a problem when it comes to modeling large systems. In this paper, we set up the following objectives. (1) Understand links from molecular level events to system phenotype. (2) Provide a general external control scenario to mimic various biological knockout experiments, and even to provide possible suggestions in future experimental design. (3) Capture the stochastic nature appeared in the system. (4) Quantify biological interactions in a general manner which might be beyond the scope of chemical reaction kinetics. To achieve these goals, we divide the whole biological system into two sub-systems. The first sub-system comprises all the molecular species that are involved in phagocytes transmigration, except phagocyte cells. The second sub-system includes phagocyte cells and all the molecular species that directly effect phagocytes rolling, adhesion and migration. A control theory based deterministic model is applied to the first sub-system. On the other hand, a Monte Carlo based stochastic model is utilized to the second sub-system. The output of the first model will serve as the input of the second model.
II. Model-1: Control Theory Based Deterministic Model
In control theory, a dynamic system is described by a finite number of variables, x1, …, xn called the “state”. The canonical mathematical form for a nonlinear time varying system with control is given by a differential equation system of the type:
| (1) |
| (2) |
where t is the independent variable “time”, x is the state vector of dimension n, u is the control vector (or called input) of dimension m, y is the output vector of dimension p. f and h are the functions of the state and control variables. This is an m input and p output system. A fundamental assumption in using this model is that the initial condition, will be sufficient, together with the differential equation, to determine the future evolution of the system uniquely.
In this part, four computational issues are addressed. (1) For the molecular species that stimulate other molecular species to be activated, their concentrations over time are modeled by a damped harmonic oscillator. (2) The differential equation system that describes the biological system is formulated based on mass action kinetics and singularly perturbed versions of mass action (Michaelis-Menten kinetics). (3) A general external control scenario is provided.
A. The releasing of bio-molecules can be modeled by a damped harmonic oscillator as follows
| (3) |
where C stands for released bio-molecule. ω(t) indicates the oscillator frequency. q is the damped parameter. A reasonable hypothesis about releasing of bio-molecules is that they are released periodically with a decreasing amount. This is because periodical oscillation phenomenon is common in biological system and this periodical pattern is indeed observed from experimental data.
B. The phagocytes transmigration is modeled by a differential equation system
The differential equation system that describes the biological system is formulated based on mass action kinetics and singularly perturbed versions of mass action (Michaelis-Menten kinetics). Specific format of differential equations depend on the biological problems to be studied. For the case study of this paper, the bio-molecules of histamine, H1/H2 receptor, and P/E selectins can be modeled as:
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
where Chmr(T) is released histamine that can be modeled by a damped harmonic oscillator, equation (3). u(t)’s are control variables that can be modeled according to the following control scenario.
C. A general external control scenario
The control variable in equations (1) and (2) are designed to model block/unblock actions in biological knockout experiments. The form of the control variables is given by:
| (9) |
or it takes the form as:
| (10) |
where Hε is a regularized Heaviside function to regulate the control variable so that it is continuous for second derivative with respect to time t. The variable T in (9) and (10) represents the time when control begins to be taken. The representation of (9) and (10) stands for the block/unblock action in knockout experiments. Specifically, the control variable in (9) represents the situation that block action is taken at the beginning and unblock is conducted after certain time T. On the other hand, the control variable in (10) describes an opposite case that unblock is taken at the beginning and block is applied after certain time T.
III. Model-2: Kinetics Monte Carlo Algorithm Based Stochastic Model
Other than using chemical reaction kinetics that is the basis for most of existing stochastic models in system biology, a physical barrier-jumps kinetics model that is known as the Bortz-Kalos-Liebowitz (BKL) algorithm or the kinetic Monte Carlo (KMC) algorithm is adopted by us. The first publication which described the basic features of the KMC method was by Young and Elcock in 1966 [22]. The KMC method is intended to simulate the time evolution of some processes occurring in nature. It is commonly used in physics, such as modeling surface diffusion and surface growth.
In this section, three computational issues are discussed. (1) Derive a new formula of transition rates to replace the traditional computation in physics. (2) Determining parameters by Maximum likelihood estimation. (3) Outline the procedure of KMC algorithm.
A. Derive the new formula of transition rates that are inputs to the KMC algorithm
Consider a system includes n states x1, …, xn and a set of transitions Wi(xa → xb) from a state xa into other possible states xb, i = 1, …, m. For each Wi there is a transition probability per unit time, i. e. transition rate ri. The transition probability ri is determined by a set of variables {Zj}, j = 1, …, q(i). q(i) is a nature number that is associated with i. It is to say that each transition might be influenced by different groups of factors. Our goal is to formulate the transition probability ri as a function of s.
In a general case, the function of s can be a polynomial of degree at most q(i):
| (11) |
The value of fi(z) belongs to (−∞, ∞). But the range of the transition probability ri is [0, 1]. Therefore, fi(z) and ri can not be set equal at this point. To build a equation in terms of fi(z) and ri, two transformations are made in the follows:
At first, we notice that the probability that the ith transition does not occurs is 1 − ri. Then the odds of the ith transition occurring vs not occurring is . The range of the odds value is (0, ∞). Take logarithm transform on the odds, we have whose range is (−∞, ∞) that is same range of fi(z).
Assume the following equation hold.
| (12) |
Then the transition probability ri can be calculated by:
| (13) |
The parameters of β’s in fi(z) are determined by maximum likelihood estimation.
B. Maximum likelihood estimation
Let y1, …, ym be variables that indicate whether the ith transition occurring. It is assumed that yi = 1 indicates the ith transition occurring. On the other hand, if yi = 0, it stands for the ith transition not occurring. Then the likelihood function can be written as:
| (14) |
Based on the definition of ri, we have: Pr(yi = 1) = ri, and Pr(yi = 0) = 1 − ri. Therefore, . The likelihood function becomes:
| (15) |
Consider the Log likelihood function:
| (16) |
Plug equation (13) into (16), we obtain:
| (17) |
We want to maximize the Log likelihood function, equation (11), according to the parameters of β’s.
| (18) |
In general case, the solving of (18) is not straightforward. Newton-Raphson method, an iterative method, is conducted here.
A number of biological systems comprise a series of molecular level events. Therefore, in practice, the “state” mentioned in above context actually is “event”. Various factors represented by variables z’s effect the probability of event occurring and the extent of event. The specific format of fi(z) in many cases can be obtained through a priori biological knowledge. If this kind of information is not available, then the optimal format of fi(z) can be derived through the above procedure where parameters are determined for equation (11).
C. Outline the procedure of KMC algorithm
Set the time t = 0.
Calculate ri for all i.
Calculate the cumulative function for i = 1, …, m where m is the total number of transitions. Denote R = Rm.
Get a uniform random number u ∈ [0, 1].
Find the event that carry out transition i by find i for which Ri−1 < uR ≤ Ri.
Carry out the found event.
Get a uniform random number u ∈ [0, 1].
Update the time with t = t + Δt, where .
Got back to step (b) or stop.
The explanation and proof of the KMC algorithm procedure can be found at[22].
IV. Case Study of Phagocyte Transmigration by Using Hybrid Model
As we known, phagocytes transmigration is a multi-step process, including initial margination in the vessels, rolling and firm adhesion of phagocytes to the vessel wall, and extravasation. During the time of rolling and firm adhesion, phagocytes are captured from blood stream. This multi-step process is illustrated in Figure 1. In the reduced biological process, it is assumed that three biological events occur: (1) Phagocytes are captured. (2) Detachment of phagocytes. (3) Phagocytes migrate into the extravascular space. A subset of bio-molecules involved in phagocytes transmigration, i.e. histamine, P selectin, E selectin, H1 receptor and H2 receptor are considered.
Fig. 1.
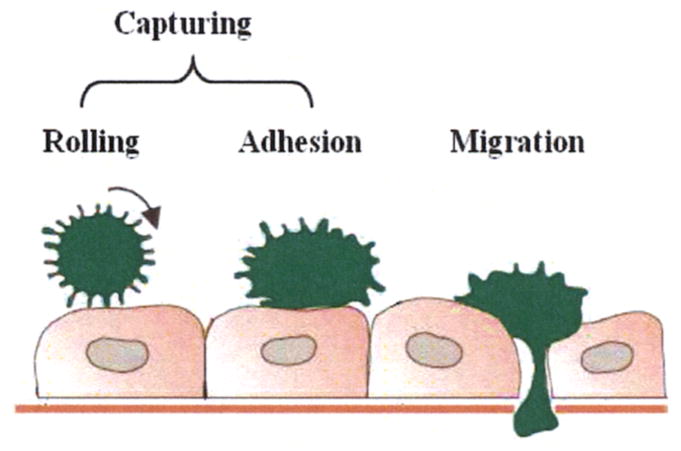
Multi-step process of phagocyte transmigration.
The phagocytes transmigration process is divided into two sub-systems. (1) The first sub-system includes components of histamine, P selectin, E selectin, H1 receptor and H2 receptor. The basic interactions among these components are that histamine up-regulates P and E selectins and histamine enhances H1 and H2 receptors. (2) The second subsystem comprises aforementioned three biological events and bio-molecules of phagocytes (polymorphonuclear leukocyte (PMN)), P selectin, E selectin, H1 receptor and H2 receptor. P and E selectins mediate the events of phagocytes capturing and detachment. H1 and H2 receptors facilitate the event of phagocytes migration into the extravascular space. The effects of bio-molecules on biological events are verified through a variety of biological knockout (KO) experiments conducted in implanted mice.
In this section, we utilize hybrid model to simulate and predict a reduced biological process of phagocytes transmigration. Computational model-1 mentioned in section 2 is applied to simulate dynamic of the first sub-system. On the other hand, computational model-2 discussed in section 2 is utilized to the second sub-system. The outputs of model-1 are served as inputs of model-2.
Computational simulation by the hybrid model is presented in the following. Simulation shows agreement with the experimental results. Furthermore, predictions for some un-explored knockout experiments are carried out.
A. Histamine modeling
The histamine residual measurement experiment up to 16 hours was carried out. Computational simulation is conducted by a damped harmonic oscillator described as equation (3) in section 2. Certain periodic pattern can be observed in experimental data (Figure 2(a)). The simulation result exhibits the same pattern (Figure 2(b)).
Fig. 2.
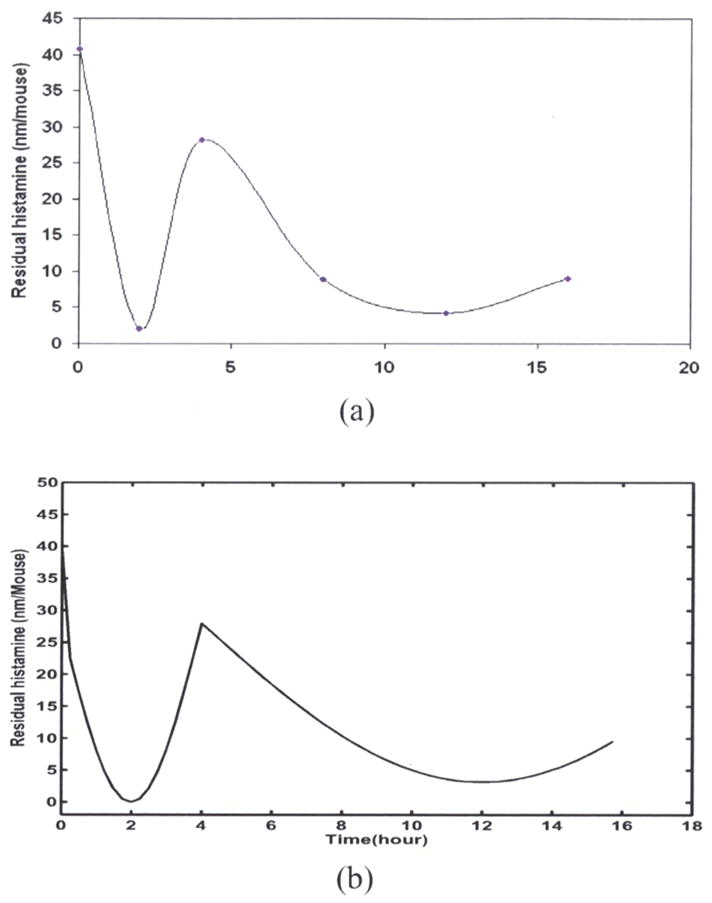
(a) Experimental data of histamine residual measurement. (b) Computational simulation of histamine residual measurement.
B. Modeling stochastic events of phagocytes capturing and migration
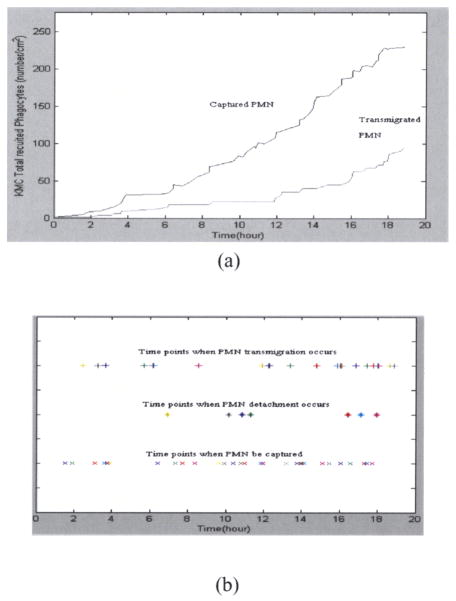
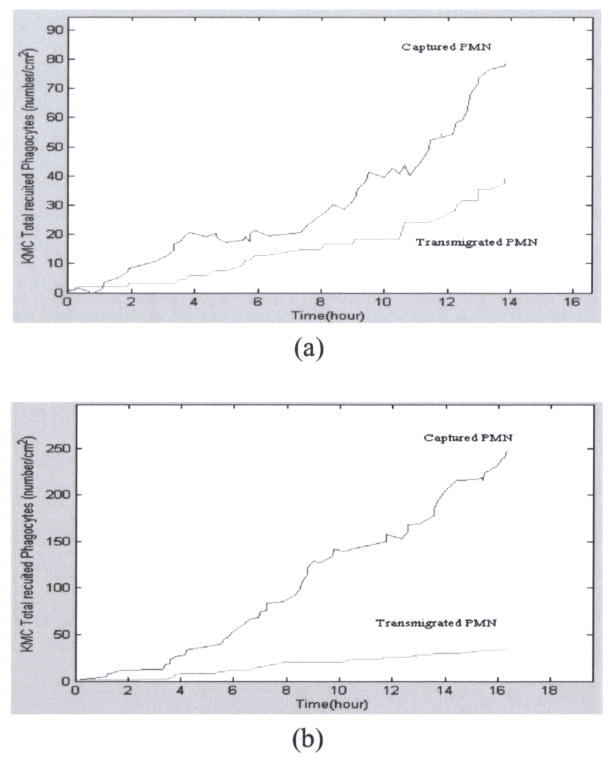
The time courses of biological events, such as capturing of phagocytes, detachment of phagocytes and phagocytes migration into the extravascular space, are predicted by KMC simulation in the case of polymorphonuclear leukocyte (PMN) transmigration (Figure 3(a)). The corresponding time points when biological events occur are plotted (Figure 3(b)). The importance of P and E selectins in mediating the capturing of PMN is supported by P/E selectins knockout experiments. KMC simulation results of such P/E selectins knockout experiments indicate that the captured PMN are significantly reduced. As a result, the number of PMN migration into the extravascular space is much reduced. This can be seen by comparing Figure 4(a) to Figure 3(a). On the other hand, the KMC simulation of H1/H2 receptors knockout experiments shows that the captured PMN remains the same level as usual, but the PMN migration into the extravascular space is dramatically reduced (Figure 4(b)). These two different simulation results reveal the fact that P/E selectins and H1/H2 receptors effect the phagocytes transmigration differently by their mediating different biological events.
Fig. 3.
(a) Dynamics of polymorphonuclear leukocyte (PMN) capturing and migration. (b) Time points that various events occurring.
Fig. 4.
(a) Dynamics of PMN capturing and migration when P and E selectins were blocked. (b) Dynamics of PMN capturing and migration when H1 and H2 receptors were blocked.
C. Prediction of un-explored knockout experiments
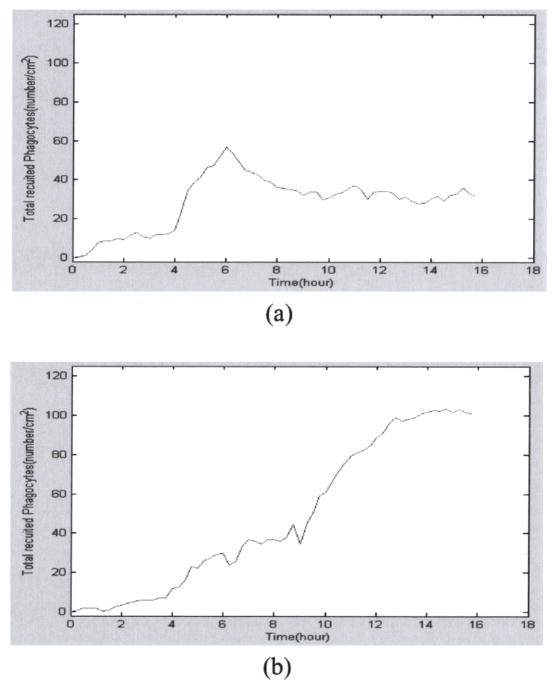
Certain un-explored knockout experiments can be predicted by the mathematical model. For example, a knockout experiment can be designed as that no any knockout at beginning and H1/H2 are blocked after the 6th hour. Then the time course of recruited PMN might looks like Figure 5(a). Another knockout experiment can be the case that P and E selectins are blocked at beginning, but they are recovered after the 9th hour. Figure 5(b) presents this situation.
Fig. 5.
(a) Prediction of PMN at the situation that H1 and H2 receptors are blocked after the 6th hour. (b) PMN at the situation that P and E selectins are blocked at beginning, but they are recovered after the 9th hour.
V. Conclusion
A hybrid computational model that combines control theory and kinetics Monte Carlo (KMC) algorithm is built to study in silico the molecular mechanisms governing phagocyte transmigration. The simulation reveals the facts of histamine, H1/H2 receptors, and P/E selectins play important roles in phagocyte transmigration process. These computational results agree with the experimental reports. The stochastic nature inherent to phagocyte transmigration is captured by KMC algorithm. Various biological knockout experiments are mimicked, and un-explored knockout experiments are predicted. The ability to predict un- explored knockout experiments may facilitate experiment design itself. For example, different combinations of interested components can be chosen to be blocked/unblocked; various block/unblock time can be tested; the temporal order of block/unblock can be specified.
Contributor Information
Jiaxing Xue, Email: jxx6599@exchange.uta.edu, Department of Computer Science, University of Texas, Arlington, TX 76019, USA.
Jean Gao, Email: gao@uta.edu, Faculty of Computer Science, University of Texas, Arlington, TX 76019, USA.
Liping Tang, Email: ltang@uta.edu, Faculty of Bioengineering, University of Texas, Arlington, TX 76019, USA.
References
- 1.Carro LP, Suarez GG. Intracondylar notch fibrous nodule after total knee replacement. Arthroscopy. 1999;15:103–105. doi: 10.1053/ar.1999.v15.015010. [DOI] [PubMed] [Google Scholar]
- 2.Cutroneo KR, White SL, Chiu JE, Ehrlich HP. Tissue fibrosis and carcinogenesis; divergent or successive pathways dicatate multiple molecular therapeutic targets for oligo decoy therapies. J Cell Biochem. 2006;97:1161–1174. doi: 10.1002/jcb.20750. [DOI] [PubMed] [Google Scholar]
- 3.Hu WJ, Eaton JW, Tang LP. Molecular basis of biomaterial-mediated foreign body reactions. Blood. 2001;98(4) doi: 10.1182/blood.v98.4.1231. [DOI] [PubMed] [Google Scholar]
- 4.Christenson L, Aebischer P, McMillan P, Galletti PM. Tissue reaction to intraperitoneal polymer implants: species difference and effects of corticoids and doxorubicin. J Biomed Mater Res. 1989;23:705–18. doi: 10.1002/jbm.820230704. [DOI] [PubMed] [Google Scholar]
- 5.Tang LP, Wu Y, Timmons RB. Fibrinogen adsorption and host tissue responses to plasma functionalized surfaces. J Biomed Mater Res. 1998;42:156–63. doi: 10.1002/(sici)1097-4636(199810)42:1<156::aid-jbm19>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
- 6.Bell GI. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 7.Hammer DA, Apte SM. Simulation of cell rolling and adhesion on surfaces in shear flow: general results and analysis of selectin-mediated neutrophil adhesion. Biophysics Journal. 1992;63:35–57. doi: 10.1016/S0006-3495(92)81577-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Caputo KE, Lee D, King MR, Hammer DA. Adhesive Dynamics Simulations of the Shear Threshold Effect for Leukocytes. Biophysical Journal. 2007;92:787–797. doi: 10.1529/biophysj.106.082321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Evans E, Leung A, Heinrich V, Zhu C. Mechanical switching and coupling between two dissociation pathways in a P-selectin adhesion bond. PNAS. 2004;101(31):11281–11286. doi: 10.1073/pnas.0401870101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Simon SI, Green CE. Molecular mechanics and dynamics of leukocyte recruitment during inflammation. Annu Rev Biomed Eng. 2005;7:151–85. doi: 10.1146/annurev.bioeng.7.060804.100423. [DOI] [PubMed] [Google Scholar]
- 11.Cozens-Roberts C, Lauffenburger DA, Quinn JA. Receptor-mediated cell attachment and detachment kinetics 1. Probabilistic model and analysis. Biophys J. 1990;58:841–856. doi: 10.1016/S0006-3495(90)82430-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nichols MF, Greller LD, Hahn AW. A Mathematical Model of the Foreign Body Reaction to Implanted Materials. Biomed Sci Instrum. 1979;15:1–5. [PubMed] [Google Scholar]
- 13.Reynolds A, Rubin J, Clermont G, Day J, Vodovotz Y, Ermentrout GB. A Reduced Mathematical Model of the Acute Inflammatory Response: I. Derivation of Model and Analysis of Anti-inflammation. Journal of Theoretical Biology. 2006;242:220–236. doi: 10.1016/j.jtbi.2006.02.016. [DOI] [PubMed] [Google Scholar]
- 14.Vodovotz Y, Clermont G, Chow C, An G. Mathematical Models of the Acute Inflammatory Response. Current Opinion in Critical Care. 2004;10:383–390. doi: 10.1097/01.ccx.0000139360.30327.69. [DOI] [PubMed] [Google Scholar]
- 15.Goodman PD, Barlow ET, Crapo PM, Mohammad SF, Solen KA. Computational Model of Device-Induced Thrombosis and Thromboembolism. Annals of Biomedical Engineering. 2005;13(6):780–797. doi: 10.1007/s10439-005-2951-z. [DOI] [PubMed] [Google Scholar]
- 16.Ataullakhanov FI, Panteleev MA. Mathematical Modeling and Computer Simulation in Blood Coagulation. Pathophysiol Haemost Thromb. Biomed Sci Instrum. 2005;34:60–70. doi: 10.1159/000089927. [DOI] [PubMed] [Google Scholar]
- 17.Mcdougall S, Dallon J, Sherratt J, Mainti P. Fibroblast migration and collagen deposition during dermal wound healing: mathematical modelling and clinical implications. Phil Trans R Soc A. 2006;364:1385–1405. doi: 10.1098/rsta.2006.1773. [DOI] [PubMed] [Google Scholar]
- 18.Zhu C, Bao G, Wang N. Cell mechanics: mechanical response, cell adhesion, and molecular deformation. Annu Rev Biomed Eng. 2000;2:189–226. doi: 10.1146/annurev.bioeng.2.1.189. [DOI] [PubMed] [Google Scholar]
- 19.Gillespie DT. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J Comput Phys. 1976;22(4):403–434. [Google Scholar]
- 20.Long M, Goldsmith HL, Tees DFJ, Zhu C. Probabilistic modeling of shear-induced formation and breakage of doublets cross-linked by receptor-ligand bonds. Biophysics Journal. 1999;76:1112–1128. doi: 10.1016/S0006-3495(99)77276-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tang J, Ley KF, Hunt CA. Dynamics of in silico leukocyte rolling, activation, and adhesion. BMC Systems Biology. 2007;1:14. doi: 10.1186/1752-0509-1-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Young WM, Elcock EW. Proceedings of the Physical Society. BMC Systems Biology. 1966;89:735. [Google Scholar]