Abstract
This article considers a broad class of kernel mixture density models on compact metric spaces and manifolds. Following a Bayesian approach with a nonparametric prior on the location mixing distribution, sufficient conditions are obtained on the kernel, prior and the underlying space for strong posterior consistency at any continuous density. The prior is also allowed to depend on the sample size n and sufficient conditions are obtained for weak and strong consistency. These conditions are verified on compact Euclidean spaces using multivariate Gaussian kernels, on the hypersphere using a von Mises-Fisher kernel and on the planar shape space using complex Watson kernels.
Keywords: Nonparametric Bayes, Density Estimation, Posterior consistency, Sample dependent prior, Riemannian manifold, Hypersphere, Shape space
1 Introduction
Density estimation on compact metric spaces, such as manifolds, is a fundamental problem in nonparametric inference on non-Euclidean spaces. Some applications include directional and axial data analysis, spatial modeling, shape analysis and dimensionality reduction problems in which the data lie on an unknown lower dimensional space. However, the literature on statistical theory and methods of density estimation in non-Euclidean spaces is still under-developed. Our focus is on Bayesian nonparametric approaches.
For nonparametric Bayes density estimation on the real line ℜ, there is a rich literature, with Dirichlet process mixtures of Gaussian kernels providing a commonly-used approach (Escobar and West (1995)[6]) that leads to dense support (Lo (1984)[14]) and weak and strong posterior consistency (Ghosal et al. (1999)[8]). From the celebrated theorem of Schwartz (1965)[16], weak posterior consistency results when the true density f0 is in the Kullback-Leibler (KL) support of the prior, meaning that all KL neighborhoods around f0 are assigned positive probability. In general, it is quite difficult to show KL support for new priors for a density, though Wu and Ghosal (2008)[20] provide useful conditions for a class of kernel mixture priors, with Bhattacharya and Dunson (2010a)[2] extending these conditions to general compact metric spaces. It is widely accepted that weak consistency is an insufficient property when the focus is on density estimation. For example, if f0 is a density with respect to Lebesgue measure, weak consistency does not even ensure that the posterior assigns positive probability to the set of densities with respect to Lebesgue measure. Hence, it is important to provide stronger results.
Until very recently, essentially all the literature on theory of nonparametric Bayes density estimation focused on one-dimensional Euclidean spaces. An important development in multivariate Euclidean spaces is the article of Wu and Ghosal (2010)[21] who provide sufficient conditions for strong consistency in nonparametric Bayes density estimation from Dirichlet process mixtures of multivariate Gaussian kernels. However severe tail restrictions are imposed on the kernel covariance, which become overly restrictive when the data are very high dimensional. Also the theory developed in their paper is specialized and cannot be easily generalized to arbitrary kernel mixtures on more general spaces.
We are particularly interested in density estimation in the special case in which the compact metric space M corresponds to a Riemannian manifold. In order to extend kernel mixture models used in Euclidean spaces to manifolds M, the kernel needs to be carefully chosen. One approach is to introduce an invertible coordinate map between a subset of M and a Euclidean space (Hirsch (1976)[10]). Under such an approach, the density prior on M can be induced through a kernel mixture model in a Euclidean space. However, several major problems arise in using such an approach. Firstly, it is not possible to cover the entire manifold with a single smooth coordinate chart except for very simple manifolds, so unless the data are very concentrated one may obtain poor performance. Different local charts can be patched together to form an atlas, but this may introduce artifactual discontinuities in the resulting density. Because the coordinate map is not isometric, the geometry of the manifold can be heavily distorted. As good choices of coordinate frames necessarily depend on the observations, additional uncertainty is automatically induced. Due to these and other shortcomings of coordinate based methods, we focus on modeling approaches that are coordinate free in the sense that we build density models with respect to the invariant volume form on the manifold.
In Bhattacharya and Dunson (2010a)[2], a density model is presented on a general compact metric space with respect to any fixed base measure using a random mixture of probability kernels. Under mild conditions on the kernel and the mixing prior, it is shown that the prior probability of any uniform neighborhood of any continuous density f0 is positive and if f0 is positive everywhere, it lies in the KL support of the prior. This inturn implies posterior consistency in the weak sense. Density estimation on the planar shape space is presented as a special case. However strong posterior consistency is not addressed. The everywhere positivity restriction on the true density cannot be easily relaxed. Also besides the location mixing distribution, the only other parameter in the model is a scalar band-width. This restricts the flexibility when the sample size is small.
Focusing on kernel mixture priors for densities on a compact metric space M, in this article, we provide sufficient conditions on the kernel, prior and the underlying space to ensure strong consistency. Theorem 2 and Corollary 1 provide sufficient conditions to ensure that all total variation neighborhoods around f0 will be assigned probability converging to one as the sample size increases. The theoretical development relies on the method of sieves and exponentially consistent tests discussed in Barron (1989)[1]. However, applying this framework outside multivariate spaces is not standard and requires careful use of differential geometry. Through Theorem 1, we prove weak consistency for a bigger class of kernels than Bhattacharya and Dunson (2010a)[2]. The only requirement on the true density is that it is continuous everywhere. To illustrate the theory, we focus on density estimation on the unit hypersphere using von Mises-Fisher kernels and on the planar shape space using complex Watson kernels. In both these cases, it is shown that the kernels satisfy the sufficient conditions. The results also apply to Gaussian mixture densities on ℜd whenever the true density has compact support. In that case, a truncated and transformed Wishart prior on the covariance inverse, the transformation depending on the data dimension is shown to suffice as in Wu and Ghosal (2010)[21]. Appropriate kernel choices are presented on other manifolds such as axial spaces, Stiefel manifolds and Grasmannians which arise as generalisations of the two manifolds.
When the manifold is high-dimensional, priors satisfying conditions for strong consistency tend to put too little probability near bandwidths close to 0, which is undesirable for applications. A gamma prior on the inverse-bandwidth, for example, cannot be shown to satisfy the conditions. Hence, we extend the consistency results to cover cases with priors depending on the sample size n. Theorem 3 extends the Schwartz theorem to prove weak consistency, while Theorem 4 proves strong consistency using such priors. A gamma prior with scale decreasing with n at an appropriate rate satisfies the conditions for both weak and strong posterior consistency at an exponential rate. When using multivariate Gaussian mixtures, a truncated Wishart prior with hyper-parameters depending on n, is shown to work.
To mantain a free flow while reading, we put all the proofs together at the end in a section called Appendix.
2 Consistency theorems on compact metric spaces
2.1 Weak posterior consistency
Let (M, ρ) be a compact metric space, ρ being the distance metric, and let X be a random variable on M (from some measurable space (Ω,
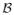 , Q)). We assume that the distribution of X has a density with respect to some fixed finite base measure λ on M. The natural choice for such a λ when M is a Riemannian manifold is the invariant volume form. We are interested in modelling this unknown density via a flexible model. Let K(m; μ,
, Q)). We assume that the distribution of X has a density with respect to some fixed finite base measure λ on M. The natural choice for such a λ when M is a Riemannian manifold is the invariant volume form. We are interested in modelling this unknown density via a flexible model. Let K(m; μ,
 ) be a probability kernel on M with location μ ∈ M and other parameters
) be a probability kernel on M with location μ ∈ M and other parameters
 ∈ N, N being a Polish space, that is, it is homeomorphic to a complete seperable metric space. In the special case, we choose N = (0, ∞) and then K may be called a location-scale kernel.
∈ N, N being a Polish space, that is, it is homeomorphic to a complete seperable metric space. In the special case, we choose N = (0, ∞) and then K may be called a location-scale kernel.
Given the parameters (μ,
 ), K satisfies ∫M K(m; μ,
), K satisfies ∫M K(m; μ,
 )λ(dm) = 1. Then a location mixture density model for X is defined as
)λ(dm) = 1. Then a location mixture density model for X is defined as
| (1) |
with parameters P in the space
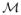 (M) of all probability distributions on M and
(M) of all probability distributions on M and
 ∈ N. We call P the location mixing distribution. When N = (0, ∞), we view
∈ N. We call P the location mixing distribution. When N = (0, ∞), we view
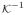 as the band-width of the kernel and hence call
as the band-width of the kernel and hence call
 the precision or inverse band-width parameter. More generally
the precision or inverse band-width parameter. More generally
 comprises of many other parameters in different spaces determining the kernel shape, modality etc, and the precision is a particular function of
comprises of many other parameters in different spaces determining the kernel shape, modality etc, and the precision is a particular function of
 . The upcoming consistecy theorems and examples will illustrate that function. Kernel mixture models are used routinely in Bayesian density estimation in Euclidean spaces, with Lennox et al.(2009)[13] applying such an approach to bivariate angular data and Bhattacharya and Dunson (2010a)[2], (2010b)[3] considering kernel mixtures on general metric spaces.
. The upcoming consistecy theorems and examples will illustrate that function. Kernel mixture models are used routinely in Bayesian density estimation in Euclidean spaces, with Lennox et al.(2009)[13] applying such an approach to bivariate angular data and Bhattacharya and Dunson (2010a)[2], (2010b)[3] considering kernel mixtures on general metric spaces.
A prior Π1 on (P,
 ) induces a prior Π on the space of densities
) induces a prior Π on the space of densities
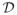 (M ) on M through the model (1). Given a random realization X1, …, Xn of X, we can compute the posterior of f. The Schwartz theorem provides a useful tool in proving that the posterior assigns probability converging to one in arbitrarily small neighborhoods of the true density f0 as the sample size n → ∞. Let F0 denote the probability distribution corresponding to f0, let KL(f0; f ) = ∫M f0(m) log{f0(m)/f(m)}λ(dm) denote the KL divergence of another density f from f0, and let Kε(f0) denote the KL neighborhood {f ∈
(M ) on M through the model (1). Given a random realization X1, …, Xn of X, we can compute the posterior of f. The Schwartz theorem provides a useful tool in proving that the posterior assigns probability converging to one in arbitrarily small neighborhoods of the true density f0 as the sample size n → ∞. Let F0 denote the probability distribution corresponding to f0, let KL(f0; f ) = ∫M f0(m) log{f0(m)/f(m)}λ(dm) denote the KL divergence of another density f from f0, and let Kε(f0) denote the KL neighborhood {f ∈
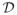 (M): KL(f0; f ) < ε}. f0 is said to be in the KL support of Π or Π is said to satisfy the KL condition at f0 if Π{Kε(f0)} > 0 for all ε > 0.
(M): KL(f0; f ) < ε}. f0 is said to be in the KL support of Π or Π is said to satisfy the KL condition at f0 if Π{Kε(f0)} > 0 for all ε > 0.
Proposition 1 (Schwartz Theorem)
If (1) f0 is in the KL support of Π, and (2) U ⊂
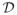 (M) is such that there exists a uniformly exponentially consistent sequence of test functions for testing H0: f = f0 versus H1: f ∈ Uc, then Π(U |X1, …, Xn) → 1 as n → ∞ a.s.
.
(M) is such that there exists a uniformly exponentially consistent sequence of test functions for testing H0: f = f0 versus H1: f ∈ Uc, then Π(U |X1, …, Xn) → 1 as n → ∞ a.s.
.
The posterior probability of Uc can beexpressed as
| (2) |
Condition (1), known as the KL condition, ensures that for any β > 0,
| (3) |
while condition (2) implies that
for some β0 > 0 (depending on U ) and therefore
Hence Proposition 1 provides conditions for posterior consistency at an exponential rate. Theorem 1 derives sufficient conditions on the kernel and the prior so that f0 is in the uniform support and hence KL support of Π. They are
-
A1
The kernel K is continuous in its arguements.
For any continuous function f: M → ℜ (written as f ∈ C(M)), for any ε > 0, there exists a compact subset Nε of N with non-empty interior, such that
-
A2
supm∈M,
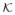 ∈Nε|f(m) − ∫M K(m; μ,
∈Nε|f(m) − ∫M K(m; μ,
 )f (μ)λ(dμ)| < ε.
)f (μ)λ(dμ)| < ε. -
A3
For any ε > 0, the set intersects with the (weak) support of Π1. Here Ao denotes the interior of a set A.
-
A4
f0 is a continuous density.
Theorem 1
Under assumptions A1–A4, for any ε > 0,
which implies that f0 is in the KL support of Π.
As a corollary, we obtain the KL property for the location-scale kernel, derived in Bhattacharya and Dunson (2010a)[2]. However unlike in there, we need not assume f0 to be positive everywhere.
When U is a weakly open neighborhood of f0, condition (2) in Proposition 1 is always satisfied. Hence under assumptions A1–A4, weak posterior consistency at an exponential rate follows. Assumptions A1 and A2 impose some mild conditions on the kernel choice, which are easily satisfied by several parametric families. In particular, A2 implies that as a probability distribution on M, K(; μ,
 ) can be made arbitrarilly close in weak sense to the degenerate point mass at μ, uniformly in μ, for appropriate
) can be made arbitrarilly close in weak sense to the degenerate point mass at μ, uniformly in μ, for appropriate
 choice, thereby justifying the name ‘location’ for μ. When the compact neighborhood Nε can be represented as the inverse image under some function ψ(ψ: N → ℜ+) of some neighborhood around infinity, then ψ(
choice, thereby justifying the name ‘location’ for μ. When the compact neighborhood Nε can be represented as the inverse image under some function ψ(ψ: N → ℜ+) of some neighborhood around infinity, then ψ(
 ) can be viewed as the precision parameter. We will provide examples of kernels on some non-Euclidean manifolds arising in shape and directional data analysis which satisfy A1 and A2. A common choice for Π1 satisfying A3 can be a full support product prior such as a Dirichlet process DP(w0P0) prior on P satisfying supp(P0) = M and an independent everywhere positive density prior on
) can be viewed as the precision parameter. We will provide examples of kernels on some non-Euclidean manifolds arising in shape and directional data analysis which satisfy A1 and A2. A common choice for Π1 satisfying A3 can be a full support product prior such as a Dirichlet process DP(w0P0) prior on P satisfying supp(P0) = M and an independent everywhere positive density prior on
 .
.
2.2 Strong consistency
When U is a total variation neighborhood of f0, LeCam (1973)[12] and Barron (1989)[1] show that condition (2) of Proposition 1 will not be satisfied in most cases. In Barron (1989)[1] (also see Ghosal et al.(1999)[8]), a sieve method is considered to obtain sufficient conditions for the numerator in (2) to decay at an exponential rate and hence get strong posterior consistency at an exponential rate. This is stated in Proposition 2. In its statement, for
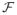 ⊆
⊆
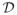 (M) and ε > 0, the L1-metric entropy N (ε,
(M) and ε > 0, the L1-metric entropy N (ε,
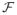 ) is defined as the logarithm of the minimum number of ε-sized (or smaller) L1 subsets needed to cover
) is defined as the logarithm of the minimum number of ε-sized (or smaller) L1 subsets needed to cover
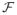 .
.
Proposition 2
If there exists a
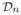 ⊆
⊆
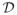 (M) such that (1) for n sufficiently large,
for some β > 0, and (2) N (ε,
(M) such that (1) for n sufficiently large,
for some β > 0, and (2) N (ε,
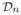 )/n → 0 as n → ∞ for any ε > 0, then for any total variation neighborhood U of f0, there exists a β0 > 0 (depending on U) such that
a.s.
. Hence if f0 is in the KL support of Π, the posterior probability of any total variation neighborhood of f0 converges to 1 almost surely.
)/n → 0 as n → ∞ for any ε > 0, then for any total variation neighborhood U of f0, there exists a β0 > 0 (depending on U) such that
a.s.
. Hence if f0 is in the KL support of Π, the posterior probability of any total variation neighborhood of f0 converges to 1 almost surely.
Theorem 2, which is the main theorem of this paper, describes a
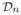 which satisfies condition (2). We assume that there exists a continuous function φ: N → [0, ∞) for which the following assumptions hold.
which satisfies condition (2). We assume that there exists a continuous function φ: N → [0, ∞) for which the following assumptions hold.
-
A5There exists positive constants κ1, a1, A1 such that for all κ ≥ κ1, μ, ν ∈ M,
-
A6There exists positive constants a2, A2 such that for all
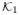 ,
,
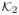 ∈ φ−1 [0, κ], κ ≥ κ1,
∈ φ−1 [0, κ], κ ≥ κ1,
ρ2 metrizing the topology of N.
-
A7
For any κ ≥ κ1, the subset φ−1 [0, κ] is compact and given ε > 0, the minimum number of ε (or smaller) radius balls covering it (known as the ε-covering number) can be bounded by (κε−1)b2 for appropriate positive constant b2 (independent of κ and ε).
-
A8
There exists a3, A3 > 0 such that the ε-covering number of M is bounded by A3ε−a3 for any ε > 0.
For two positive sequences {an} and {bn}, {an} is said to be ‘little-o’ of {bn}, written as an = o(bn), if the sequence {an/bn} converges to 0 as n → ∞.
Theorem 2
For a positive sequence {κn} diverging to ∞, define
Under assumptions A5–A8, given any ε > 0, for n sufficiently large,
for some C(ε) > 0. Hence N(ε,
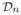 ) is o(n) whenever κn is o (n(a1a3)−1).
) is o(n) whenever κn is o (n(a1a3)−1).
As a corollary, we derive conditions on the prior Π1 on (P,
 ) under which strong posterior consistency at an exponential rate follows.
) under which strong posterior consistency at an exponential rate follows.
Corollary 1
Under the hypothesis of Theorems 1 and 2 and
-
A9
Π1(
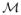 (M ) × φ−1 (na, ∞)) < exp(−nβ) for some a < (a1a3)−1 and β > 0,
(M ) × φ−1 (na, ∞)) < exp(−nβ) for some a < (a1a3)−1 and β > 0,
the posterior probability of any total variation neighborhood of f0 converges to 1 a.s. .
Theorem 1 ensures that f0 is in the KL support of Π. Theorem 2 and assumption A9 ensure that
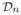 satisfies conditions (1) and (2) of Proposition 2. Hence from the Proposition, the proof follows.
satisfies conditions (1) and (2) of Proposition 2. Hence from the Proposition, the proof follows.
When we use a location-scale kernel, that is, when N = (0, ∞), choose a prior Π1 = Π11⊗π1 having full support, set φ to be the identity map, then a choice for π1 for which Assumption A9 is satisfied is a Weibull density W eib(
 ; α, β) ∝
; α, β) ∝
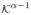 exp(−β
exp(−β
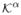 ) whenever the shape parameter α exceeds a1a3 (a1, a3 as in Assumptions A5 and A8).
) whenever the shape parameter α exceeds a1a3 (a1, a3 as in Assumptions A5 and A8).
Remark 1
A gamma prior on
 satisfies the requirements for weak consistency but not A9 (unless a1a3 < 1). However that does not prove that it is not eligible for strong consistency because Corollary 1 provides only sufficient conditions. In Section 2.3, we prove it to be eligible as long as the hyperparameters are allowed to depend on sample size n in a suitable way.
satisfies the requirements for weak consistency but not A9 (unless a1a3 < 1). However that does not prove that it is not eligible for strong consistency because Corollary 1 provides only sufficient conditions. In Section 2.3, we prove it to be eligible as long as the hyperparameters are allowed to depend on sample size n in a suitable way.
When the underlying space is non-compact such as ℜd, Corollary 1 applies to any true density f0 supported on a compact set, say M. Then the kernel can be chosen to have non-compact support, such as Gaussian, but to apply Theorem 2, we need to restrict the prior on the location mixing distribution to have support in
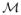 (M). We can weaken assumptions A5 and A6 to
(M). We can weaken assumptions A5 and A6 to
-
A5′
sup
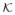 ∈φ−1[0, κ]||K(μ,
∈φ−1[0, κ]||K(μ,
 ) − K(ν,
) − K(ν,
 )|| ≤ A1κa1ρ (μ, ν) and
)|| ≤ A1κa1ρ (μ, ν) and -
A6′
μ∈M||K(μ,
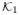 ) − K(μ,
) − K(μ,
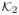 )|| ≤ A2κa2ρ2(
)|| ≤ A2κa2ρ2(
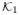 ,
,
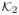 ) ∀
) ∀
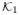 ,
,
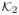 ∈ φ−1 [0, κ] respectively. Here ||f −g|| denotes the L1 distance between densities f and g. The proof of Theorem 2 can be easily modified to show consistency under the new assumptions and is left to the reader.
∈ φ−1 [0, κ] respectively. Here ||f −g|| denotes the L1 distance between densities f and g. The proof of Theorem 2 can be easily modified to show consistency under the new assumptions and is left to the reader.
The multivariate Gaussian kernel can be represented as
M+(d) being the space of all d × d positive matrices. Hence
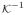 is the kernel covariance. It satisfies A5′ and A6′ as shown in Proposition 3. Here by λ1(
is the kernel covariance. It satisfies A5′ and A6′ as shown in Proposition 3. Here by λ1(
 ), …, λd(
), …, λd(
 ), we denote the eigen-values of
), we denote the eigen-values of
 in increasing order.
in increasing order.
Proposition 3
The multivariate Gaussian kernel satisfies A5′ with φ being the largest eigen-value function, φ(
 ) = λd(
) = λd(
 ) and a1 = 1/2. It also satisfies A6′ once we restrict N to be the space of all positive matrices with the least eigen-value being bounded below by some pre-specified positive constant, say, λ1, i.e., N = {
) and a1 = 1/2. It also satisfies A6′ once we restrict N to be the space of all positive matrices with the least eigen-value being bounded below by some pre-specified positive constant, say, λ1, i.e., N = {
 ∈ M+ (d): λ1(
∈ M+ (d): λ1(
 ) ≥ λ1}. The space M+(d) (and hence N) satisfies A7 while any compact subset M of ℜd satisfies A8 from Theorem 2 with a3 = d. Hence if
) ≥ λ1}. The space M+(d) (and hence N) satisfies A7 while any compact subset M of ℜd satisfies A8 from Theorem 2 with a3 = d. Hence if
for some a < 2/d and β > 0, and if f0 is in the KL support of Π, strong posterior consistency follows.
Theorem 4 in Ghosal et al.(1999)[8] provides sufficient conditions on f0 and Π1 for the KL condition to be satisfied while using a Gaussian mixture model in the univariate setting to model a compactly supported density. It assumes Π1 = Π11⊗π1 with F0 ∈ supp(Π11) and ∞ ∈ supp(π1). The theorem can be extended to multivariate setting with the condition on Π1 relaxed to, for any κ > 0, there exists a
 ∈ M
+ (d) with λ1(
∈ M
+ (d) with λ1(
 ) ≥ κ such that (F0,
) ≥ κ such that (F0,
 ) ∈ supp(Π1). Therefore λ1(
) ∈ supp(Π1). Therefore λ1(
 ) can be viewed as the kernel precision in this case. A full support product Π1 on
) can be viewed as the kernel precision in this case. A full support product Π1 on
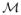 (M ) × N will satisfy these requirements. Using a product prior, a choice for π1 for which strong consistency also follows can be the so called truncated transformed Wishart defined as follows. Set
(M ) × N will satisfy these requirements. Using a product prior, a choice for π1 for which strong consistency also follows can be the so called truncated transformed Wishart defined as follows. Set
 = Λa for any a ∈ (0, 2/d) with Λ following a Wishart distribution restricted to N. Then
= Λa for any a ∈ (0, 2/d) with Λ following a Wishart distribution restricted to N. Then
 is said to follow a truncated transformed Wishart with transformation power a.
is said to follow a truncated transformed Wishart with transformation power a.
Remark 2
The truncation restriction on the space N is not undesirable, because for more precise fit, we are interested in low bandwidths and the least eigen-value of
 can be viewed as the inverse of the band-width. However, lower the transformation power, lower is the prior probability for high precisions which is undesirable when sample sizes are not high.
can be viewed as the inverse of the band-width. However, lower the transformation power, lower is the prior probability for high precisions which is undesirable when sample sizes are not high.
In Wu and Ghosal (2010)[21], strong consistency is proved in the special case of Dirichlet process Gaussian mixtures used to model density f0 having support as ℜd. It requires a to be less than 1/d resulting in even smaller precision. In the next section, we prove that no transformation is required (a = 1) as long as the hyper-parameters are allowed to depend on the sample size appropriately.
2.3 Consistency with sample size-dependent priors
When the dimension of the manifold is large, as is the case in shape analysis with a large number of landmarks, the constraints on the shape parameter in the proposed Weibull prior on the inverse bandwidth become overly-restrictive. In particular, for strong posterior consistency, the shape parameter needs to be very large in high-dimensional cases, implying a prior on the bandwidth that places very small probability in neighborhoods close to zero, which is undesirable in many applications. By instead allowing the prior to depend on sample size n, we can potentially obtain priors that may have better small sample operating characteristics, while still leading to strong consistency. However, for n-dependent priors, the KL condition is no longer sufficient to ensure that (3) holds and hence the Schwartz theorem breaks down. In this section, we will modify the conditions and derive weak and strong consistency results for n-dependent priors.
As recommended in earlier sections, we let P and
 be independent under Π1. Then, assuming P ~ Π11 is a constant prior, we focus on the case in which
be independent under Π1. Then, assuming P ~ Π11 is a constant prior, we focus on the case in which
 has a sample size-dependent prior density πn with respect to some base measure λ1 on N,
has a sample size-dependent prior density πn with respect to some base measure λ1 on N,
 ~ πn(
~ πn(
 )λ1(d
)λ1(d
 ). We pick λ1 to have full support. Depending on the context, πn will refer to both the density and distribution of
). We pick λ1 to have full support. Depending on the context, πn will refer to both the density and distribution of
 . Denote the resulting sequence of induced priors on
. Denote the resulting sequence of induced priors on
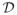 (M) as Πn. Theorem 3 proves weak posterior consistency under the following assumptions on the prior.
(M) as Πn. Theorem 3 proves weak posterior consistency under the following assumptions on the prior.
-
A10
The prior Π11 contains F0 in its support.
-
A11For any ε > 0, for all
 ∈ Nε,
∈ Nε,
Here Nε is as defined in Assumption A2.
Theorem 3
Under assumptions A1 and A2 on the kernel, A4 on the true density f0, and, A10 and A11 on the prior, the posterior probability of any weak neighborhood of f0 converges to one a.s. .
The proof is immediate from the following two lemmas.
Lemma 1
Under assumptions A1–A2, A4 and A10–A11, for any ε > 0,
| (4) |
a.s. .
Lemma 2
If there exists a uniformly exponentially consistent sequence of test functions for testing H0: f = f0 versus H1: f ∈ Uc, and Πn(Uc) > 0 for all n > C with C a sufficiently arge constant, then for some β0 > 0,
a.s. .
The proof of Lemma 2 is related to that of Lemma 4.4.2. from Ghosh and Ramamoorthi (2003)[9] which is stated for a constant prior Π but with the set Uc depending on n, they call this Vn. There it is assumed that lim infn→∞Π(Vn) > 0 but that is not necessary as long as Π(Vn) > 0 for all large n. Lemma 1 is proved in the Appendix.
With a location-scale kernel, N being (0, ∞), a gamma prior πn(
 ) ∝ exp(−βn
) ∝ exp(−βn
 )
)
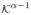 , α, βn > 0, denoted by Gam(α, βn), satisfies Assumption A11 on entire of N, as long as βn is o(n).
, α, βn > 0, denoted by Gam(α, βn), satisfies Assumption A11 on entire of N, as long as βn is o(n).
With a multivariate Gaussian kernel on ℜd with dispersion
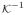 , a Wishart prior on
, a Wishart prior on
 ,
,
denoted as satisfies A11 on entire M+(d), as long as βn is o(n). Here Γd(.) denotes the multivariate gamma function defined as
For strong consistency, we impose the following additional condition on πn. Let a1 and a3 be as in Assumptions A5 (or A5′) and A8 respectively.
-
A12For some β0 > 0 and a < (a1a3)−1,
This assumption is in place of A9 used for constant priors.
Theorem 4
Under Assumptions A1–A2 and A4–A8 and A10–A12, the posterior probability of any total variation neighborhood of f0 converges to 1 a.s .
The proof is very similar to that of Corollary 1. This is because under assumptions A1–A2, A4 and A10–A11, the conclusion (4) of Lemma 1 holds. The other assumptions are to show that the L1-metric entropy of
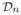 is o(n) while
is exponentially small,
is o(n) while
is exponentially small,
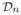 being defined in Theorem 2. Under these assumptions, the proof of Proposition 2 goes through to prove strong consistency with sample size dependent priors. This is also mentioned in §5 of Ghosal et al.(1999)[8]. They require lim infn→∞Πn(Kε(f0)) > 0 in place of of the assumption Π(Kε(f0)) > 0 for constant priors but this is only to ensure that (4) holds.
being defined in Theorem 2. Under these assumptions, the proof of Proposition 2 goes through to prove strong consistency with sample size dependent priors. This is also mentioned in §5 of Ghosal et al.(1999)[8]. They require lim infn→∞Πn(Kε(f0)) > 0 in place of of the assumption Π(Kε(f0)) > 0 for constant priors but this is only to ensure that (4) holds.
Again as in §2.2, we can weaken assumptions A5 and A6 to A5′ and A6′ respectively.
For a location-scale kernel, a Gam(α, βn) prior on precision
 satisfies A12 when n
1−a is o(βn) for some a ∈ (0, (a1a3)−1). Hence, for example, we have weak and strong posterior consistency with βn = b1n/{log(n)}b2 for any b1, b2 > 0.
satisfies A12 when n
1−a is o(βn) for some a ∈ (0, (a1a3)−1). Hence, for example, we have weak and strong posterior consistency with βn = b1n/{log(n)}b2 for any b1, b2 > 0.
For a multivariate Gaussian kernel, to satisfy assumption A6′, we need to truncate the space N to {
 ∈ M
+ (d): λ1(
∈ M
+ (d): λ1(
 ) ≥ λ1}, as proved in Proposition 3. Then we may set a truncated Wishart prior on
) ≥ λ1}, as proved in Proposition 3. Then we may set a truncated Wishart prior on
 , defined as
, defined as
| (5) |
Then for Assumption A12 to be satisfied, we require n1−a to be o(βn) for some a ∈ (0, (a1a3)−1). This is shown in Proposition 4. Hence we have weak and strong posterior consistency once we set βn = b1n/{log(n)}b2 for any b1, b2 > 0. Unlike in §2.2, we impose no transformation constraints, which is very helpful especially when sample sizes are not that high while the data dimensions are huge.
Proposition 4
For a positive sequence {βn} diverging to infinity, Assumption A12 is satisfied for the Truncated-Wishart density sequence πn in (5) if there exists an a ∈ (0, (a1a3)−1) for which βn satisfies n1−a/βn → 0 as n → ∞.
In the subsequent sections, we present kernel choices for density estimation on some specific non-Euclidean manifolds that arise in several applications. We illustrate how to apply Theorems 1, 2, 3 and 4 and obtain weak and strong posterior consistency.
3 Application to unit hypersphere
Let M be the unit sphere Sd embedded in ℜd+1. It is a compact Riemannian manifold of dimension d and a compact metric space under the chord distance ρ(u, v) = ||u−v||2, ||.||2 denoting the L2-norm. Spherical data on S2 arise in the context of directional data analysis. Most of the shape spaces are quotients of high dimensional spheres. Hence it is important to develop consistent inference procedures on this space, and very few results exist in the context of Bayesian nonparametrics.
To define a probability density model as in (1) with respect to the volume form V, we need a suitable kernel which satisfies the assumptions in Section 2. One of the most commonly used probability densities on this space is the von Mises-Fisher (vMF) density which is given by
| (6) |
with c being the normalizing constant which can be derived to be
| (7) |
The vMF density on S1 was first derived in Von Mises (1918)[18] and the density in case of S2 was given by Fisher (1953)[7]. Watson and Williams (1953)[19] generalized this distribution to Sd and examined many of its properties. It can be shown that the parameter μ is the extrinsic mean (as defined in Bhattacharya and Patrangenaru (2003)[4]), and hence can be interpreted as the distribution location. The parameter
 is a measure of concentration, with
is a measure of concentration, with
 = 0 corresponding to the uniform distribution having constant density equal to 1/∫SdV (dm). As
= 0 corresponding to the uniform distribution having constant density equal to 1/∫SdV (dm). As
 diverges to ∞, the vMF distribution converges to a point mass at μ in an L1 sense uniformly. This is proved in Theorem 5.
diverges to ∞, the vMF distribution converges to a point mass at μ in an L1 sense uniformly. This is proved in Theorem 5.
Theorem 5
The vMF kernel satisfies Assumptions A1 and A2.
Hence from Theorem 1, weak posterior consistency follows using the location mixture density model (1) with a Dirichlet Process prior on P and an independent gamma prior on
 . In the d = 2 special case, Lennox et al.(2009)[13] proposed a closely related model but did not consider theoretical properties. Theorem 6 verifies the assumptions for strong consistency.
. In the d = 2 special case, Lennox et al.(2009)[13] proposed a closely related model but did not consider theoretical properties. Theorem 6 verifies the assumptions for strong consistency.
Theorem 6
With φ(
 ) =
) =
 , the vMF kernel on Sd satisfies assumption A5 with a1 = d/2 + 1 and A6 with a2 = d/2. The compact metric-space (Sd, ρ) satisfies assumption A8 with a3 = d.
, the vMF kernel on Sd satisfies assumption A5 with a1 = d/2 + 1 and A6 with a2 = d/2. The compact metric-space (Sd, ρ) satisfies assumption A8 with a3 = d.
As a result a Weibull prior on
 with shape parameter exceeding (d + d2/2)−1 satisfies the condition of Corollary 1 and strong posterior consistency follows. The proofs of Theorems 5 and 6 use the following lemma which establishes certain properties of the normalizing constant.
with shape parameter exceeding (d + d2/2)−1 satisfies the condition of Corollary 1 and strong posterior consistency follows. The proofs of Theorems 5 and 6 use the following lemma which establishes certain properties of the normalizing constant.
Lemma 3
Define c̃(
 ) = exp(−
) = exp(−
 )c(
)c(
 ),
),
 ≥ 0. Then c̃ is decreasing and for
≥ 0. Then c̃ is decreasing and for
 ≥ 1,
≥ 1,
for some appropriate positive constant C.
When d is large, as is often the case for spherical data, a more appropriate prior on
 for which weak and strong consistencies hold can be Gam(α, βn) as mentioned at the end of §2.3.
for which weak and strong consistencies hold can be Gam(α, βn) as mentioned at the end of §2.3.
It is easy to check that the vMF density is the conditional distribution, given ||X|| = 1, of a Gaussian random vector X on ℜd+1 with mean μ and dispersion matrix
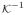 Id+1. A more general family of distribution on Sd may be obtained as the conditional distribution, given ||X|| = 1, of a Normal X on ℜd
+1 with mean μ and dispersion matrix
Id+1. A more general family of distribution on Sd may be obtained as the conditional distribution, given ||X|| = 1, of a Normal X on ℜd
+1 with mean μ and dispersion matrix
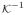 ,
,
 in the space M
+ (d + 1) of (d + 1) × (d + 1) positive matices. Then we obtain the Fisher-Bingham family of kernels. It can be interesting to show that the resulting kernel mixture satisfies the assumptions of Theorems 1, 2, 3 and 4 and obtain posterior consistency. We postpone that to later works.
in the space M
+ (d + 1) of (d + 1) × (d + 1) positive matices. Then we obtain the Fisher-Bingham family of kernels. It can be interesting to show that the resulting kernel mixture satisfies the assumptions of Theorems 1, 2, 3 and 4 and obtain posterior consistency. We postpone that to later works.
A generalization of the sphere is the Stiefel manifold Vd+1,k, the space all k dimensional orthonormal frames in ℜd+1. One can easily extend the vMF kernel to the so called Fisher kernel on this manifold and carry out density estimation. Again, proving that consistency holds is postponed for future works.
Another important manifold arising in axial data analysis is RPd, the space of all rays in ℜd+1. This manifold can be obtained as the quotient of Sd after identifying antipodal points p and −p as identical. In the next section, we illustrate density estimation on its complex analogue, the complex projective space. It is easy and simpler to obtain analogous results on the real version.
4 Planar Shape Space
4.1 Background
Let M be the planar shape space
which is defined as follows. Consider a set of k landmark locations, k > 2, on a 2D image, not all points being the same. We refer to such a set as a k-ad. The similarity shape of this k-ad is what remains after removing the Euclidean rigid body motions of translation, rotation and scaling. We use the following shape representation first proposed by Kendall (1984)[11]. Denote the k-ad by a complex k-vector z in
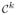 . To remove the effect of translation from z, let zc = z − z̄, with
being the centroid. The centered k-ad zc lies in a k − 1 dimensional complex subspace, and hence we can use k − 1 complex coordinates. The effect of scaling is then removed by normalizing the coordinates of zc to obtain a point w on the complex unit sphere
. To remove the effect of translation from z, let zc = z − z̄, with
being the centroid. The centered k-ad zc lies in a k − 1 dimensional complex subspace, and hence we can use k − 1 complex coordinates. The effect of scaling is then removed by normalizing the coordinates of zc to obtain a point w on the complex unit sphere
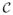
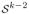 in
in
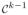 . Since w contains the shape information of z along with rotation, it is called the preshape of z. The similarity shape of z is the orbit of w under all rotations in 2D which is
. Since w contains the shape information of z along with rotation, it is called the preshape of z. The similarity shape of z is the orbit of w under all rotations in 2D which is
This represents a shape as the set of all intersection points of a unique complex line passing through the origin with
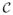
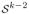 and the planar shape space
is then the set of all such shapes. Hence
can be identified with the space of all complex lines passing through the origin in
and the planar shape space
is then the set of all such shapes. Hence
can be identified with the space of all complex lines passing through the origin in
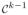 which is the complex projective space and is a compact Riemannian manifold of dimension 2k − 4. The
can be embedded into the space of all order k − 1 complex Hermitian matrices via the embedding J([w]) = ww*, * denoting the complex conjugate transpose. This embedding induces a distance on
called the extrinsic distance which generates the manifold topology and is given by
which is the complex projective space and is a compact Riemannian manifold of dimension 2k − 4. The
can be embedded into the space of all order k − 1 complex Hermitian matrices via the embedding J([w]) = ww*, * denoting the complex conjugate transpose. This embedding induces a distance on
called the extrinsic distance which generates the manifold topology and is given by
For more details, see Bhattacharya and Dunson (2010a)[2] and the references cited therein.
4.2 Density model
We define a location-mixture density on as in (1) with respect to the Riemannian volume form V and the kernel being a complex Watson density. This complex Watson density was used in Dryden and Mardia (1998)[5] for parametric density modelling and is given by
| (8) |
| (9) |
It is shown in Bhattacharya and Dunson (2010a)[2] that the complex Watson kernel satisfies assumptions A1 and A2 in §2. Using a Dirichlet Process prior on the location mixing distribution and an independent gamma prior on the precision parameter, Theorem 1 implies that the density model (1) has full support in the space of all positive continuous densities on in uniform and KL sense and hence the posterior is weakly consistent.
Theorem 7 verifies that the complex Watson kernel also satisfies the regularity conditions in A5 and A6.
Theorem 7
The complex Watson kernel CW(m; μ,
 ) on the compact metric space
endowed with the extrinsic distance dE satisfies assumption A5 with a1 = k − 1 and A6 with a2 = 3k − 8.
) on the compact metric space
endowed with the extrinsic distance dE satisfies assumption A5 with a1 = k − 1 and A6 with a2 = 3k − 8.
The proof uses Lemma 4 which verifies certain properties of the normalizing constant.
Lemma 4
Let c(
 ) be the normalizing constant for CW(μ,
) be the normalizing constant for CW(μ,
 ) as defined in (9). Then c is decreasing on [0, ∞) with
) as defined in (9). Then c is decreasing on [0, ∞) with
If we define
it follows that c̃ is increasing with
The proof follows from direct computations.
Theorem 8 verifies that assumption A8 holds on .
Theorem 8
The compact metric space ( ,dE) satisfies assumption A8 with a3 = 2k − 3.
As a result, Corollary 1 implies that strong posterior consistency holds with Π1 = (DP)(ω0P0)⊗π1, for Weibull π1 with shape parameter exceeding (2k − 3)(k − 1). Alternatively one may use a gamma prior on
 with inverse-scale increasing with n at a suitable rate and we have consistency using Theorems 3 and 4.
with inverse-scale increasing with n at a suitable rate and we have consistency using Theorems 3 and 4.
The complex Watson kernel is a special case of the complex Bingham kernel which has density proportional to exp(z*Az) with respect to the volume form. This kernel has location corresponding to the shape of a eigen-vector corresponding to the largest eigen-value of A. Since it has more parameters, we expect better fit in smaller samples. We will prove that weak and strong posterior consistency holds while using this kernel in a later work.
When the landmarks are obtained from a 3D object, it is more appropriate to carry out an affine shape analysis, that is identify two k-configurations as identical if they are related by an affine transformation. One can identify the resulting shape space with the Grassmanian manifold - the space of all 3D subspaces of ℜk−1, a result of Sparr (1992)[17]. The Grassmanian is an extension of the real projective space and hence one may consider (real) Bingham kernels and construct kernel mixture density models on this space.
5 Summary & Future Work
We consider kernel mixture density models on general compact manifolds and obtain sufficient conditions on the kernel, priors and the space for the density estimate to be strongly consistent. Thereby we extend the existing literature on strong posterior consistency on ℜd using Gaussian kernels to more general non-Euclidean manifolds. The conditions are verified for specific kernels on two important manifolds, namely the hypersphere and the planar shape space. It is discussed how to extend the kernel choice on these manifolds and construct their counterparts on other manifolds arising as generalisations. The multivariate Gaussian mixture model with an appropriate truncated and transformed Wishart prior on the within cluster covariance inverse is also shown to satisfy the consistency conditions when used to model a compactly supported density on ℜd. We also allow the prior to depend on the sample size and obtain sufficient conditions for weak and strong consistency, while expecting better small sample operating characteristics. As a result a truncated Wishart prior on the covariance inverse of a multivariate Gaussian kernel is shown to satisfy the requirements for strong consistency.
In later works we plan to prove the results for other kernels on additional manifolds arising in applications. We also plan to extend the results to cover densities with non-compact support, in particular ℜd. Since most of the non-Euclidean manifolds arising in applications are compact, that is not a high priority.
6 Appendix
6.1 Proof of Theorem 1
The proof runs on the lines of that of Theorem 1 in Bhattacharya and Dunson (2010a)[2].
Proof
First of all we show that the set
| (10) |
contains a weakly open neighborhood of F0, F0 being the distribution corresponding to f0. The kernel K being continuous from assumption A1, for any (m,
 ) ∈ M × Nε,
) ∈ M × Nε,
defines an open neighborhood of F0. The mapping from (m,
 ) to f (m; P,
) to f (m; P,
 ) is a uniformly equicontinuous family of functions on M × Nε, labeled by P ∈
) is a uniformly equicontinuous family of functions on M × Nε, labeled by P ∈
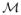 (M), because, for m1, m2 ∈ M;
(M), because, for m1, m2 ∈ M;
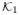 ,
,
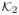 ∈ Nε,
∈ Nε,
and K is uniformly continuous on M × M × Nε. Therefore there exists a δ > 0 such that ρ12((m1,
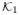 ), (m2,
), (m2,
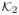 )) < δ implies that
)) < δ implies that
Here ρ12 denotes any distance on M × N inducing the product topology. Cover M × Nε by finitely many balls of radius
. Let
which is an open neighborhood of F0. Let P ∈
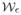 and (m,
and (m,
 ) ∈ M × Nε. Then there exists a (mi,
) ∈ M × Nε. Then there exists a (mi,
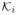 ) such that (m,
) such that (m,
 ) ∈ B{(mi,
) ∈ B{(mi,
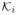 ), δ}. Then |f(m; P,
), δ}. Then |f(m; P,
 ) − f(m; F0,
) − f(m; F0,
 )|
)|
This proves that the set in (10) contains
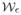 , an open neighborhood of F0.
, an open neighborhood of F0.
For P ∊
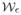 and
and
 ∊ Nε, supm|f0(m) − f(m; P,
∊ Nε, supm|f0(m) − f(m; P,
 )|
)|
because of assumptions A2 and A4. Hence
because of assumption A3 and the fact that int(
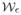 × Nε) interects with supp(Π1). This implies the KL property when f0 is strictly positive (and hence bounded below), as shown in Corollary 1 of Bhattacharya and Dunson (2010a) [2].
× Nε) interects with supp(Π1). This implies the KL property when f0 is strictly positive (and hence bounded below), as shown in Corollary 1 of Bhattacharya and Dunson (2010a) [2].
In case f0 is not bounded below, we use Lemma 4 in Wu and Ghosal (2008)[20] to get a continuous everywhere positive density f1 (depending on f0 and ε) for which . From what we have proved above, Π(Kε(f1)) > 0 and as a result the KL condition follows for f0.
6.2 Proof of Theorem 2
In this proof and the subsequent ones, we shall use a general symbol C for any constant not depending on n (but possibly on ε).
Proof
Given δ1 > 0 (≡ δ1(ε, n)), cover M by N1 (≡ N1(δ1)) many disjoint subsets of diameter at most . Assumption A8 implies that for δ1 sufficiently small, . Pick μi ∈ Ei, i = 1, …, N1, and define for a probability P,
| (11) |
Denoting the L1-norm as ||.||, for any
 with φ(
with φ(
 ) ≤ κn,
) ≤ κn,
| (12) |
| (13) |
The inequality in (13) follows from (12) using Assumption A5.
For
 ,
,
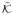 in φ−1 [0, κn], P ∈
in φ−1 [0, κn], P ∈
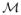 (M),
(M),
| (14) |
the inequality in (14) following from Assumption A6. Given δ2 > 0 (≡ δ2(ε, n)), cover φ−1 [0, κn] by finitely many subsets of diameter at most δ2, the number of such subsets required being at most , from Assumption A7. Call the collection of these subsets W (δ2, n).
Letting Sd = {x ∈ [0, 1]d: Σxi ≤ 1}, Sd is compact under the L1-metric (||x||L1 = Σ|xi|, x ∈ ℜd), and hence given any δ3 > 0 (≡ δ3(ε)), can be covered by finitely many subsets of the cube [0, 1]d each of diameter at most δ3. In particular cover Sd with cubes of side length δ3/d lying partially or totally in Sd. Then an upper bound on the number N2 ≡ N2(δ3, d) of such cubes can be shown to be , λ denoting the Lebesgue measure on ℜd and Sd(r) = {x ∈ [0, ∞)d: Σxi ≤ r}. Since λ(Sd(r)) = rd/d!, hence
Let
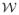 (δ3, d) denote the partition of Sd as constructed above.
(δ3, d) denote the partition of Sd as constructed above.
Let dn = N1(δ1). For 1 ≤ i ≤ N2(δ3, dn), , define
with
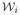 and Wj being elements of
and Wj being elements of
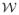 (δ3, dn) and W (δ2, n) respectively. We claim that this subset of
(δ3, dn) and W (δ2, n) respectively. We claim that this subset of
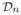 has L1 diameter of at most ε. For f(P,
has L1 diameter of at most ε. For f(P,
 ), f(P̃,
), f(P̃,
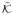 ) in this set, ||f(P,
) in this set, ||f(P,
 ) − f(P̃,
) − f(P̃,
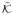 )|| ≤
)|| ≤
| (15) |
From inequality (13), it follows that the first and third terms in (15) are at most . The second term can be bounded by
and from the inequality in (14), the fourth term is bounded by
. Hence the claim holds if we choose
, and δ3 = C. The number of such subsets covering
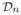 is at most
. From Assumption A8, it follows that for n sufficiently large,
is at most
. From Assumption A8, it follows that for n sufficiently large,
Using the Stirling’s formula, we can bound log(N2(δ3, dn)) by Cdn. Also
is bounded by
, so that N(ε,
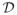 ) ≤
) ≤
for n sufficiently large.
6.3 Proof of Proposition 3
Proof
In Lemma 5 of Wu and Ghosal (2010)[21], it is shown that
for all μ, ν ∈ ℝd and
 ∈ M+(d). This means that A5′ is satisfied with a1 = 1/2. Also by the geometry of ℜd, A8 is satisfied with a3 = d.
∈ M+(d). This means that A5′ is satisfied with a1 = 1/2. Also by the geometry of ℜd, A8 is satisfied with a3 = d.
To show A7, note that φ−1 [0, κ] is a subset of M + (d) consisting of those positive matrices whose eigen values are bounded by κ. We equip M + (d) with the L2 norm distance, i.e.
and view it as a subset of M(d) - the space of all order d real matrices. Then φ−1 [0, κ] is contained in a ball of radius around the zero matrix. The ε-covering number of a such a ball is of the order . Hence A7 is also satisfied.
Remains to check A6′. Since φ−1 [0, κ] is a convex subset of M(d), use the Taylor’s theorem to get
for all x, μ ∈ ℜd, and
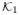 ,
,
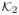 ∈ φ−1 [0, κ]. This in turn implies that
∈ φ−1 [0, κ]. This in turn implies that
Some calculation will show that
C being some constant independent of x, μ or
 . Since φ−1 [0, κ] consists of all positive matrices
. Since φ−1 [0, κ] consists of all positive matrices
 whose eigen values lie in [λ1, κ], this will imply that
whose eigen values lie in [λ1, κ], this will imply that
which means that A6′ is also satisfied with a2 = d/2. Here C denotes a constant independent of μ,
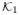 ,
,
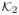 or κ. The rest of the proof follows from Theorem 2 and Proposition 2.
or κ. The rest of the proof follows from Theorem 2 and Proposition 2.
6.4 Proof of Lemma 1
Proof
Fix ε > 0. Under assumptions A1, A2 and A4, it follows from the proof of Theorem 1 that there exists a weakly open neighborhood
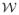 of F0 (depending on ε) such that Kε(f0) contains {f (P,
of F0 (depending on ε) such that Kε(f0) contains {f (P,
 ): P ∈
): P ∈
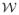 ,
,
 ∈ Nε}. Hence
∈ Nε}. Hence
By the law of large numbers, for any f ∈ Kε(f0),
a.s.
as n → ∞. Therefore for any P ∈
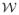 and
and
 ∈ Nε,
∈ Nε,
Also from Assumption A11, lim infn exp(nε)πn(
 ) = ∞ ∀
) = ∞ ∀
 ∈ Nε and hence
∈ Nε and hence
By Fubini-Tonelli theorem, there exists a Ω0 ⊂ Ω with probability 1 such that for any ω ∈ Ω0,
for all (P,
 ) ∈
) ∈
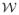 × Nε outside of a Π11(dP)⊗λ1(d
× Nε outside of a Π11(dP)⊗λ1(d
 ) measure 0 subset. By Assumption A10, and since λ1 has full support and Nε has a non-empty interior, (Π11⊗λ1)(
) measure 0 subset. By Assumption A10, and since λ1 has full support and Nε has a non-empty interior, (Π11⊗λ1)(
 × Nε) > 0. Therefore using the Fatou’s lemma, we conclude that
× Nε) > 0. Therefore using the Fatou’s lemma, we conclude that
Since ε was arbitrary, the proof is completed.
6.5 Proof of Proposition 4
Proof
For any a > 0,
| (16) |
the last identity following because X equals to in distribution. The numerator in (16) is less than Pr(Tr(Z) > βnna). The trace of Z follows a Gam(1/2, qd/2) distribution which has exponentially decaying tail. Hence the numerator is less than exp(−Cβnna) for some C > 0 when n is sufficiently large.
Now we derive a lower bound for the probability in the denominator of (16). In Mallik (2003)[15], the joint density of λ1(Z), …, λd(Z) has been shown to be
Hence Pr(λ1(Z) ≥ βnλ1) = Pr(λj (Z) ≥ βnλ1 ∀j) =
| (17) |
for n sufficiently large. Integrate (17) by parts to get Pr(λ1(Z) ≥ βnλ1) ≥ exp(−Cβn) for appropriate C > 0 when n is sufficiently large. Hence there exists a C > 0 such that the ratio in (16) is less than exp(−Cβnna). If we pick a as in the Proposition, for any β0 > 0, it follows that
which converges to zero because βnna−1 diverges to infinity. This verifies Assumption A12 with a as in the Proposition and β0 being any positive constant.
6.6 Proof of Theorem 5
Proof
Denote by M the unit sphere Sd and by ρ the chord distance on it. Express the vMF kernel as
Since ρ is continuous on the product space M × M and c is continuous and non-vanishing on [0, ∞), K is continuous on M × M × [0, ∞) and assumption A1 follows.
For a given continuous function f on M, m ∈ M,
 ≥ 0, define
≥ 0, define
Then assumption A2 follows once we show that
To simplify I(m,
 ), make a change of coordinates μ ↦ μ̃ = U(m)T μ, μ̃ ↦ θ ∈ Θd ≡ (0, π)d−1× (0, 2π) where U(m) is an orthogonal matrix with first column equal to m and θ = (θ1, …, θd)T are the spherical coordinates of μ̃ ≡ μ̃(θ) which are given by
), make a change of coordinates μ ↦ μ̃ = U(m)T μ, μ̃ ↦ θ ∈ Θd ≡ (0, π)d−1× (0, 2π) where U(m) is an orthogonal matrix with first column equal to m and θ = (θ1, …, θd)T are the spherical coordinates of μ̃ ≡ μ̃(θ) which are given by
Using these coordinates, the volume form can be written as
and hence I(m,
 ) equals
) equals
| (18) |
where t = cos(θ1), μ̃ = μ̃(θ(t)) and θ(t) = (arccos(t), θ2, …, θd)T. In the integrand in (18), the distance between m and U(m) μ̃ is
. Substitute t = 1 −
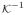 s in the integral with s ∈ (0, 2
s in the integral with s ∈ (0, 2
 ). Define
). Define
Then
Since f is uniformly continuous on (M, ρ), therefore Φ is bounded on (ℜ+)2 and lim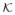 →∞
Φ(s,
→∞
Φ(s,
 ) = 0. Hence from (18), we deduce that supm∈M |I(m,
) = 0. Hence from (18), we deduce that supm∈M |I(m,
 )| ≤
)| ≤
| (19) |
From Lemma 3, it follows that
This in turn, using the Lebesgue Dominated Convergence Theorem implies that the expression in (19) converges to 0 as
 → ∞. This verifies assumption A2.
→ ∞. This verifies assumption A2.
6.7 Proof of Theorem 6
In the proof, Bd(r) denotes the ball of radius r around 0 in ℜd:
and Bd refers to Bd(1).
Proof
It is clear from (6) and (7) that the vMF kernel K is continuously differentiable on ℜd+1 × ℜd +1× [0, ∞). Hence
Since
its norm is bounded by
 c̃−1 (
c̃−1 (
 ). Lemma 3 implies that this in turn is bounded by
). Lemma 3 implies that this in turn is bounded by
for
 ≤ κ and
≤ κ and
 ≥ 1. This proves assumption A5 with a1 = d/2 + 1.
≥ 1. This proves assumption A5 with a1 = d/2 + 1.
To verify A6, given
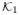 ,
,
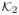 ≤ κ, use the inequality,
≤ κ, use the inequality,
By direct computations, one can show that
Therefore, using Lemma 3,
for any
 ≤ κ and κ ≥ 1. Hence A6 is verified with a2 = d/2.
≤ κ and κ ≥ 1. Hence A6 is verified with a2 = d/2.
Finally to verify A8, note that Sd ⊂ Bd+1 ⊂ [−1, 1]d +1 which can be covered by finitely many cubes of side length ε/(d + 1). Each such cube has L2 diameter ε. Hence their intersections with Sd provides a finite ε-cover for this manifold. If ε < 1, such a cube intersects with Sd only if it lies entirely in Bd+1(1 + ε) ∩ Bd+1(1 − ε)c. The number of such cubes, and hence the ε-cover size can be bounded by
for some C > 0 not depending on ε. This verifies A8 for appropriate positive constant A3 and a3 = d.
6.8 Proof of Lemma 3
Proof
Express c̃(
 ) as
) as
and it is clear that it is decreasing. This expression suggests that
if
 ≥ 1.
≥ 1.
6.9 Proof of Theorem 7
Proof
Express the complex Watson kernel as
Given
 ≥ 0, define
≥ 0, define
Then , so that
which implies that
| (20) |
For
 ≤ κ, from Lemma 4, it follows that
≤ κ, from Lemma 4, it follows that
provided κ ≥ 1. Hence for any κ ≥ 1,
and from inequality (20), a1 = k − 1 follows.
By direct computation, one can show that
| (21) |
Denote by S the sum in the second line of (21). Since , it can be shown that
so that
Plug the above inequality in (21) to get
| (22) |
For
 ≤ κ and κ ≥ 1, using Lemma 4, we bound the expression in (22) by
≤ κ and κ ≥ 1, using Lemma 4, we bound the expression in (22) by
| (23) |
for κ sufficiently large. Since K is a continuously differentiable in
 , from (23) it follows that there exists κ1 > 0 such that for all κ ≥ κ1,
, from (23) it follows that there exists κ1 > 0 such that for all κ ≥ κ1,
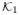 ,
,
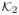 ≤ κ,
≤ κ,
This proves Assumption A6 with a2 = 3k − 8.
6.10 Proof of Theorem 8
In the proof, Ci, i = 1, 2, … denote positive constants possibly depending on k.
Proof
The preshape sphere
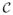
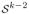 , as a real manifold, can be identified with the real unit sphere S2k−3. Endow it with the chord distance induced by the L2-norm
, as a real manifold, can be identified with the real unit sphere S2k−3. Endow it with the chord distance induced by the L2-norm
Then from Theorem 6, it follows that given any δ > 0,
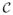
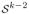 can be covered by finitely many subsets of diameter less than or equal to δ, the number of such subsets being bounded by C1δ−(2k−3) + C2. The extrinsic distance dE on
can be bounded by the chord distance on
can be covered by finitely many subsets of diameter less than or equal to δ, the number of such subsets being bounded by C1δ−(2k−3) + C2. The extrinsic distance dE on
can be bounded by the chord distance on
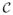
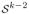 as follows. For u, v ∈
as follows. For u, v ∈
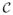
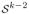 ,
,
Hence
, so that given any ε > 0, the shape image of a δ-cover for
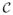
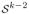 with
provides an ε-cover for
. Hence the ε-covering size for
can be bounded by C1ε−(2k−3)+ C2.
with
provides an ε-cover for
. Hence the ε-covering size for
can be bounded by C1ε−(2k−3)+ C2.
Contributor Information
Abhishek Bhattacharya, Email: ab-hishek@isical.ac.in, Indian Statistical Institute, 203 B.T. Road, Kolkata, W.B. 700108, India.
David B. Dunson, Email: dun-son@stat.duke.edu, Department of Statistical Science, Duke University, Durham, NC 27708, U.S.A
References
- 1.Barron AR. Uniformly powerful goodness of fit tests. Annals of Statistics. 1989;17:107–24. [Google Scholar]
- 2.Bhattacharya A, Dunson D. Nonparametric Bayesian density estimation on manifolds with applications to planar shapes. Biometrika. 2010a;97(4):851–865. doi: 10.1093/biomet/asq044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bhattacharya A, Dunson D. Discussion Paper. Department of Statistical Science, Duke University; 2010b. Nonparametric Bayes classification and hypothesis testing on manifolds. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bhattacharya RN, Patrangenaru V. Large sample theory of intrinsic and extrinsic sample means on manifolds. Annals of Statistics. 2003;31:1–29. [Google Scholar]
- 5.Dryden IL, Mardia KV. Statistical Shape Analysis. Wiley; N.Y: 1998. [Google Scholar]
- 6.Escobar MD, West M. Bayesian density-estimation and inference using mixtures. Journal of the American Statistical Association. 1995;90:577–588. [Google Scholar]
- 7.Fisher RA. Dispersion on a sphere. Proceedings of the Royal Society of London A. 1953;1130:295–305. [Google Scholar]
- 8.Ghosal S, Ghosh JK, Ramamoorthi RV. Posterior consistency of dirichlet mixtures in density estimation. Annals of Statistics. 1999;27:143–158. [Google Scholar]
- 9.Ghosh JK, Ramamoorthi RV. Bayesian Nonparametrics. Springer; N.Y: 2003. [Google Scholar]
- 10.Hirsch M. Differential Topology. Springer Verlag; New York: 1976. [Google Scholar]
- 11.Kendall DG. Shape manifolds, procrustean metrics, and complex projective spaces. Bulletin of the London Mathematical Society. 1984;16:81–121. [Google Scholar]
- 12.LeCam L. Convergence of estimates under dimensionality restrictions. Annals of Statistics. 1973;1:38–53. [Google Scholar]
- 13.Lennox KP, Dahl DB, Vannucci M, Tsai JW. Density estimation for protein conformation angles using a bivariate von Mises distribution and Bayesian nonparametrics. Journal of the American Statistical Association. 2009;104:586–596. doi: 10.1198/jasa.2009.0024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lo AY. On a class of Bayesian nonparametric estimates. 1. density estimates. Annals of Statistics. 1984;12:351–357. [Google Scholar]
- 15.Mallik RK. The pseudo-wishart distribution and its application to mimo systems. IEEE Transactions on Information Theory. 2003;49(10):2761–2769. [Google Scholar]
- 16.Schwartz L. On Bayes procedures. Z Wahrsch Verw Gebiete. 1965;4:10–26. [Google Scholar]
- 17.Sparr G. Depth-computations from polihedral images. Proceedings of 2nd European Conference on Computer Vision, ECCV-2; 1992. pp. 378–386. [Google Scholar]
- 18.von Mises RV. Uber die “Ganzzahligkeit” der Atomgewicht und verwandte Fragen. Physik Z. 1918;19:490–500. [Google Scholar]
- 19.Watson GS, Williams EJ. Construction of significance tests on the circle and sphere. Biometrika. 1953;43:344–52. [Google Scholar]
- 20.Wu Y, Ghosal S. Kullback-Leibler property of kernel mixture priors in Bayesian density estimation. Electronic Journal of Statistics. 2008;2:298–331. [Google Scholar]
- 21.Wu Y, Ghosal S. The L1 - consistency of dirichlet mixtures in multivariate bayesian density estimation on bayes procedures. Journal of Mutivariate Analysis. 2010;101:2411–2419. [Google Scholar]


