CROSS-CURRENTS BETWEEN BIOLOGY AND MATHEMATICS: THE CODIMENSION OF PSEUDO-PLATEAU BURSTING

Abstract

A great deal of work has gone into classifying bursting oscillations, periodic alternations of spiking and quiescence modeled by fast-slow systems. In such systems, one or more slow variables carry the fast variables through a sequence of bifurcations that mediate transitions between oscillations and steady states. A rigorous classification approach is to characterize the bifurcations found in the neighborhood of a singularity; a measure of the complexity of the bursting oscillation is then given by the smallest codimension of the singularities near which it occurs. Fold/homoclinic bursting, along with most other burst types of interest, has been shown to occur near a singularity of codimension three by examining bifurcations of a cubic Liénard system; hence, these types of bursting have at most codimension three. Modeling and biological considerations suggest that fold/homoclinic bursting should be found near fold/subHopf bursting, a more recently identified burst type whose codimension has not been determined yet. One would expect that fold/subHopf bursting has the same codimension as fold/homoclinic bursting, because models of these two burst types have very similar underlying bifurcation diagrams. However, no codimension-three singularity is known that supports fold/subHopf bursting, which indicates that it may have codimension four. We identify a three-dimensional slice in a partial unfolding of a doubly-degenerate Bodganov–Takens point, and show that this codimension-four singularity gives rise to almost all known types of bursting.

1. Introduction

Fast-slow systems, particularly oscillators with fast activation and slow inhibition, are ubiquitous in biology (see, for example, [14]); this is likely because cells are replete with mechanisms on a wide range of time scales and because negative feedback is powerfully selected by evolution to maintain homeostasis. The combination of these ingredients leads naturally to oscillations that break away from homeostasis, i.e., lose stability by bifurcation, in order to support homeostasis on a longer time scale. When oscillations on different time scales become interlinked, bursting oscillations, which consist of alternating active and silent periods, often ensue.

Electrically excitable cells, such as neurons and secretory cells, display a wide variety of bursting rhythms. One reason is that single cycles of fast oscillations (spikes or action potentials) are ineffective at mediating the build-up of calcium, which is needed to trigger release of neurotransmitters and hormones. A particularly favorable form of bursting for this purpose is plateau bursting, which provides a prolonged period of high membrane potential to mediate calcium entry [9]. Plateau bursting both resembles and shares features of mathematical structure with relaxation oscillations, but the excited, high-voltage state is adorned with small-amplitude spikes.

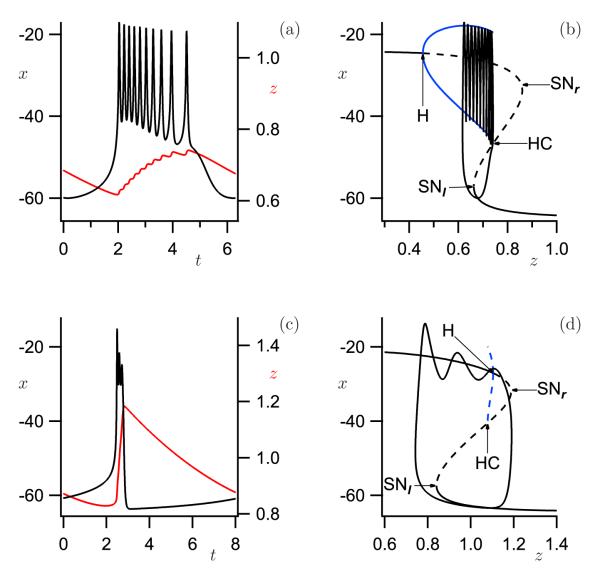
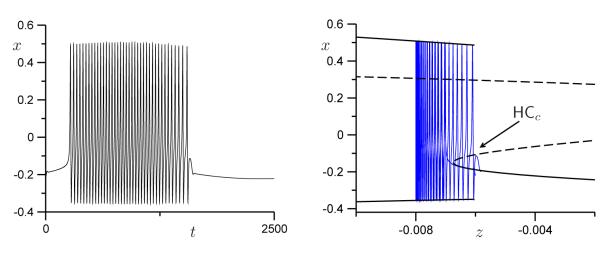
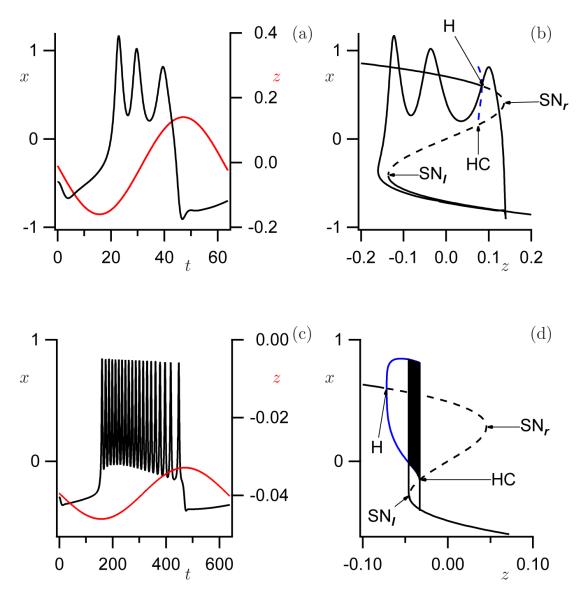
The first mathematical models for bursting were guided by this simple intuition of spike trains modulated by a slow process. An early fruitful example was the model for insulin-secreting pancreatic beta cells of Chay and Keizer [4]. Rinzel [18] pioneered the bifurcation analysis of these systems, showing that such bursts could be generated by a so-called frozen system or fast subsystem that had bi-stability between a low-voltage steady state and a high-voltage spiking state. Upward transitions were initiated by a saddle-node bifurcation and downward transitions by passage through a homoclinic orbit. A simple example of such a burster, informally called a square-wave burster, is the plateau burster shown in Figure 1(a), with the corresponding bifurcation diagram in Figure 1(b). Rinzel also began the process of classifying the various burst patterns that were emerging at that time in terms of the bifurcations marking the transitions [19].

Figure 1.

Time series (a) and bifurcation diagram (b) for square-wave (fold/homoclinic) bursting in a conductance-based model. Time series (c) and bifurcation diagram (d) for pseudo-plateau (fold/subHopf) bursting. Parameters as in [27, Fig. 1], except that here the square-wave bursting trajectory is calculated for f_c = 0.0052.

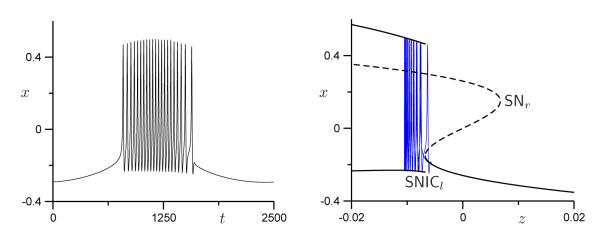
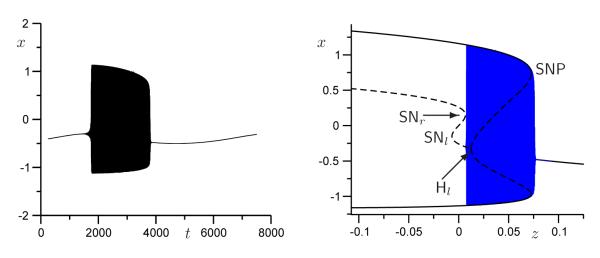
Another formative example was the bursting observed in R15 neurons of the sea snail Aplysia, which is characterized by a spike frequency that first increases and then decreases during the active (spiking) phase [1]. This was dubbed parabolic bursting and was elegantly demonstrated to be explained by passage in the frozen system through a curve of saddle-node-on-invariant-cycle (SNIC) bifurcations at both the beginning and end of the active phase [21]; an example of this type of bursting is illustrated in Figure A5 of the Appendix. A model for a third form of bursting, observed in an oscillating chemical reaction, was shown to be mediated by bi-stability generated by a subcritical Hopf bifurcation with active phases terminated by a saddle-node of periodics bifurcation (SNP) [19]; an example of this type of bursting is illustrated in Figure A9 of the Appendix. Hoppensteadt and Izhikevich [12] pointed out that there should be many more burst types, sixteen if one considers just the bifurcations of planar fast subsystems that can mediate transitions between fixed points and limit cycles, and up to 120 if one defines bursting more broadly. In their nomenclature, square-wave bursting became “fold/homoclinic” bursting.

Figure A5.

Parabolic (circle/circle) bursting with ν = −0.08, A = 0.008, ${\stackrel{‒}{\mu }}_1$ = −0.0025 and ε = 0.0025.

Figure A9.

“Type III” (subHopf/fold-cycle) bursting with ν = 0.35, A = 0.043, ${\stackrel{‒}{\mu }}_1$ = 0.05 and ε = 0.001.

These early successes in modeling and in classifying the diverse patterns prompted an ongoing effort to ascertain mathematically what other burst types might exist and what are the simplest mathematical models that can instantiate them. Cells perform vastly different tasks and so diversity is to be expected as cells randomly explore the bifurcation landscape. Simplicity, on the other hand, is not a priority for Nature and, indeed, redundancy is generally preferable in order to buffer cells from imperfections such as noise and heterogeneity in the components at their disposal, as well as provide sites of regulation. Nonetheless, it has been of both mathematical and biological interest to know what the limits of such exploration are.

One type of plateau bursting that was not appreciated at the time of previous classification efforts is that of fold/subHopf bursting, shown in Figures 1(c) and 1(d); in contrast to the bifurcation diagram in Figure 1(b) that corresponds to squarewave plateau bursting, the Hopf bifurcation for fold/subHopf bursting is subcritical. This type of plateau bursting had, in fact, been predicted as a missing element in the tables of Hoppensteadt and Izhikevich [12, 13], but did not show up in a biophysical model until the papers by Tsaneva-Atanasova et al. [28] and Stern et al. [23] on pituitary somatotrophs. (Van Goor et al. [8] had previously published a model for somatotrophs with this bifurcation structure but did not show the bifurcation diagram.) Fold/subHopf bursting had been overlooked because its appearance as in Figure 1(c) is similar to that of square-wave bursting in Figure 1(a), except for the suspiciously small spike amplitude. However, hewing closely to the data revealed the fold/subHopf structure and showed that the small spike amplitude was a consequence of not having any stable limit-cycle attractors in the frozen system. The spikes then are only seen if the speed ∈ of the slow variable is not very small. This seems paradoxical, as bursting trajectories were previously understood to be a sequence of states of the system that exist in the limit ∈ → 0 and are visited as the slow variable(s) evolve in time. In contrast, the states visited during fold/subHopf bursting are transients of the frozen system, not attractors. As shown in Figure 1(d) at the end of the active phase, the plateau can persist even when there is no stable solution at all. Such bursting with transient spikes has been called pseudo-plateau bursting to distinguish it from square-wave bursting [23]. Cells, not being scrupulous about observing the neat formulations of mathematicians, readily exploit the fold/subHopf structure, which has now turned up in models for another pituitary cell, namely, the lactotroph [24, 26].

In this paper we follow [2, 7] and investigate the complexity of burst types in terms of the smallest codimension of the singularities in whose unfolding it appears. We briefly recall this approach in the next section and discuss that most known burst types are found in the codimension-three unfolding of a degenerate Bogdanov–Takens point. However, fold/subHopf bursting does not occur alongside these other known burst types. Therefore, in Section 3 we focus our attention on a partial unfolding of a codimension-fourdoubly-degenerate Bogdanov–Takens point as studied in [15]. We are able to identify fold/subHopf along with almost all known burst types in a neighborhood of this codimension-four singularity. We believe that fold/subHopf bursting has codimension four and explain this in Section 4. We end with conclusions in Section 5 and include an Appendix with illustrations of all burst types discussed in this paper that are not visualized in the main text.

2. Towards a normal form for bursting

In the original Chay–Keizer model [4] the four equations of the classical Hodgkin–Huxley system [11] were modified to provide for a parameter regime with three steady states, and an equation for calcium was added. It was quickly realized that two variables could be set to equilibrium, leaving two variables to mediate spiking and one for negative feedback, leading to equations of the form

$$\{\begin{array}{c}\begin{array}{ccc}\hfill \stackrel{.}{x}\hfill & \hfill =\hfill & \hfill f(x,y,z),\hfill \\ \hfill \stackrel{.}{y}\hfill & \hfill =\hfill & \hfill \varphi g(x,y),\hfill \\ \hfill \stackrel{.}{z}\hfill & \hfill =\hfill & \hfill \epsilon h(x,z).\hfill \end{array}\hfill \end{array}\phantom{\}}$$ (1)

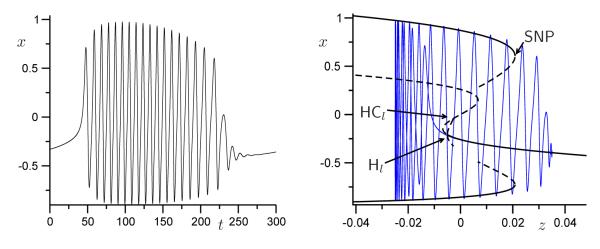
This is the minimum number of equations for bursting; some types, such as parabolic bursting, require a second slow variable [19, 21]. The parameter ϕ has to be sufficiently small to yield spiking, and ε has to be much smaller than ϕ to allow for multiple spikes per burst. Figure 1 shows examples of fold/homoclinic and fold/subHopf bursting for a model that was made using the Hodgkin–Huxley formalism, with x representing membrane potential, y activation of a voltage-dependent potassium current, and z cytosolic calcium; the slow rise in calcium acts on a calcium-activated potassium channel to terminate the active phase. We used the equations and parameters as in [27, Fig. 1], except that f_c = 0.0052 for the squarewave bursting shown in Figures 1(a) and 1(b). Figures 1(a) and 1(c) show the time series of x and z for both square-wave and pseudo-plateau bursting, respectively; in panels (b) and (d) the respective bursting orbits are overlaid on the bifurcation diagrams that are obtained by considering only the (x, y)-equations in (1) and using the slow variable z as a bifurcation parameter.

If one is willing to give up biophysically identifiable ion currents then the functions f, g, and h in (1) can be replaced by polynomials. Hindmarsh and Rose [10] adopted for f the cubic of the Fitzhugh–Nagumo system, originally introduced as a model for simple spiking, which allows for three steady states. They found, however, that g needed to be quadratic to break the symmetry between the upper and lower states, allowing one to be a fixed point and the other a limit cycle. The function h need only be linear.

2.1. Classification of bursters by unfolding

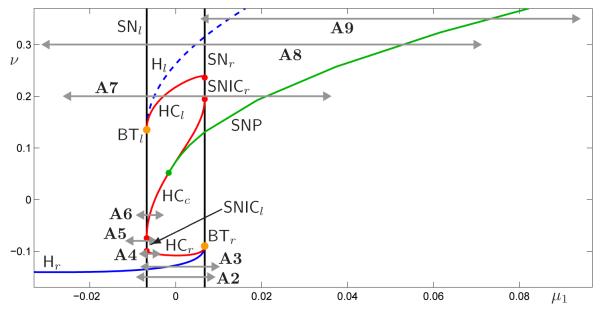
The next advance in classification was by Bertram et al., who showed that the three burst patterns identified by Rinzel could be located in a single two-parameter bifurcation diagram [2] of the two-dimensional frozen system involving only the equations for x and y above; here, one parameter plays the role of a slow negative feedback variable (which represents z above) and the other determines the burst pattern — these two parameters correspond to μ₁ and ν in system (4) of this paper. Bertram et al. pointed out that the two-parameter plane in [2, Fig. 7] was a slice of the unfolding of a codimension-three singularity, namely, a degenerate Bogdanov–Takens point of focus type; this singularity had been studied by Dumortier et al. [6], who were not concerned about bursting but sought to categorize all singularities of planar vector fields.

Figure A1.

Bifurcation diagram of (4) in the (μ₁, ν)-plane with b = 0.75 and μ₂ = 0.0675 fixed; see also Figure 6. The horizontal paths indicated in the figure correspond to the bursters shown in Figures A2–A10 and have been labeled accordingly.

Apart from unifying the known burst patterns, [2, Fig. 7] revealed two additional types of bursting that emerged naturally as the parameter corresponding to ν was varied. One of these was a second type of fold/homoclinic burster that did not take the form of a square wave because the limit cycles surrounded all three steady states. This burst type had previously been found by Pernarowski [17] in a cubic Liénard system augmented by a slow variable and described as “nearly parabolic” bursting, because of the large-amplitude spikes. The bifurcation diagram, however, revealed that this burster does not involve passage across a SNIC, but rather is of fold/homoclinic type; an example of this type of bursting is illustrated in Figure A6 of the Appendix. It was called type Ib in [2, 7] to distinguish it from the classical fold/homoclinic bursting with square-wave appearance (historically called type I). The bifurcations of this cubic Liénard system were later systematically studied by De Vries [30].

Figure A6.

Fold/homoclinic bursting with no plateau because the limit cycles surround all three steady states. The path satisfies ν = −0.03, A = 0.002, ${\stackrel{‒}{\mu }}_1$ = −0.006 and ε = 0.002.

The work in [2] suggested that additional types of bursters were possible and that unfolding would be a way to find and classify them. This approach involves finding an unfolding that contains the required bifurcations of the fast subsystem as well as a path through the parameter space representing an evolution of the slow variable(s) to visit the bifurcations in the appropriate order. This was implemented systematically for the first time by Golubitsky et al. [7], who pointed out that unfolding would also provide an unambiguous way to define the complexity of a burst type in terms of the codimension of the singularity in whose unfolding it first appears. They showed, in particular, that fold/homoclinic bursting appears for the first time in the unfolding of a codimension-three singularity, namely, the degenerate Bogdanov–Takens point studied in [6]. Golubitsky et al. [7] used the following normal form

$$\{\begin{array}{c}\begin{array}{cc}\stackrel{.}{x}\hfill & =y,\hfill \\ \stackrel{.}{y}\hfill & =-{\mu }_1+{\mu }_{2}x-x^3+y(\nu +\mathit{bx}+x^2),\hfill \end{array}\hfill \end{array}\phantom{\}}$$ (2)

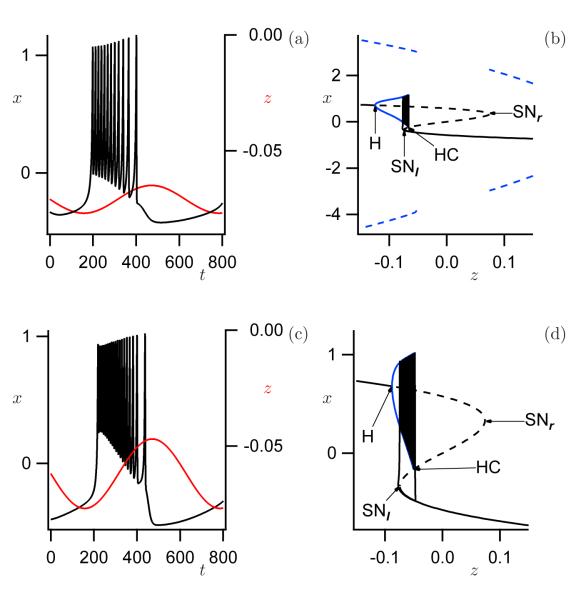
with b = 3, which puts the system into the elliptic case studied in [6], instead of the focus case identified by Bertram et al. [2]. Nonetheless, they were able to identify a path for fold/homoclinic bursting in the (μ₁, ν)-plane with μ₂ = ⅓ fixed. Note that we use the notation –μ₁, instead of +μ₁, because we view μ₁ as the inhibitory slow variable z; see Figure 2(b). Parabolic bursting could be obtained by choosing a different path in this same plane. The subHopf/fold-cycle burster, in contrast, was determined to have codimension two.

Figure 2.

Time series (a) and bifurcation diagram (b) for the square-wave (fold/homoclinic) burster defined in Golubitsky et al. [7] with μ₂ = 1/3 and b = 3 in (2). For the slow path we set ν = −1.4+10 μ₁ and identified μ₁ with the slow variable z as in (3) with ${\stackrel{‒}{\mu }}_1$ = −0.071, A = 0.006 and ∈ = 0.01. Time series (c) and bifurcation diagram (d) for a ‘clean’ fold/homoclinic burster with no large surrounding periodic orbit. This case is obtained from (4) with μ₂ = ⅓ and b = 3, which is (2) with time reversed as well as the orientations of μ₁, ν and x. Here, we used ν = —0.7 + 10 μ₁ and z as in panels (a) and (b), with ${\stackrel{‒}{\mu }}_1$ = −0.062, A = 0.015 and ∈ = 0.01.

In order to make the normal form (2) into a burster, we assume that μ₁ is slowly oscillating and identify μ₁ with the slow variable z in (1). Hence, we define μ₁ = μ₁(t) = z(t), where

$$z\left(t\right)≔{\stackrel{‒}{\mu }}_1-A\sin \left(\epsilon t\right),$$ (3)

The fold/homolinic burst path identified by Golubitsky et al. [7] has the disadvantage that system (2) exhibits an unstable limit cycle of large amplitude surrounding the region in phase space that is involved in the burst; this is not seen in the biophysical models. Figure 2(a) shows a square-wave burster obtained using the fold/homoclinic burst path found by Golubitsky et al. [7]. The underlying bifurcation diagram, shown in Figure 2(b), illustrates the presence of a large-amplitude unstable periodic orbit that coexists in the regime that gives rise to the square-wave burster. Furthermore, there always exists a Hopf bifurcation on the lower branch that gives rise to a family of periodic orbits; for the choice of path in [7] this additional family ends in a SNIC. Note that neither family affects the actual shape of the square-wave bursting pattern, but the phase portraits sampled during the oscillation differ from those found in typical models; the large-amplitude unstable periodic orbit influences the flow and its sensitivity to perturbations. A ‘clean’ fold/homolinic burst path can be found in the time-reversed system, which is system (4) that we study in this paper (technically one also reverses the orientations of μ₁, ν and x, so that the net effect is only a change of sign for the cubic term y x², and the Hopf bifurcation again occurs on the “upper” branch; see Section 4). Figures 2(c) and 2(d) illustrate a fold/homoclinic burst path in the (μ₁, ν)-plane for the time-reversed system with μ₂ = ⅓ and b = 3 as before. For this time-reversed case there exist no large surrounding periodic orbits within the path of the oscillation.

3. Fold/subHopf bursting has codimension at most four

Pseudo-plateau (fold/subHopf) bursting is a new type of plateau bursting that was identified relatively recently and whose codimension has not yet been determined. In this section, we identify a path for fold/subHopf bursting in the unfolding of a particular codimension-four singularity; hence, the codimension of fold/subHopf bursting is at most four. Furthermore, we show that this singularity gives rise to a bifurcation diagram in which paths for almost all known bursters can be identified. We actually believe that fold/subHopf bursting has codimension four, which we discuss in detail in Section 4.

We found fold/subHopf bursting in the (partial) unfolding of the doubly-degenerate Bogdanov–Takens singularity studied by Khibnik et al. [15]. A Bogdanov–Takens point can be thought of as a bifurcation point where a Hopf bifurcation occurs at the same time as a saddle-node bifurcation, which automatically gives rise to a family of homoclinic orbits in the bifurcation diagram. A degenerate Bogdanov–Takens singularity is a Bogdanov–Takens point that occurs at a cusp point, rather than an ordinary saddle-node bifurcation. The doubly-degenerate Bogdanov–Takens singularity is characterized by the fact that the Hopf bifurcation at the degenerate Bogdanov–Takens bifurcation point is itself degenerate. As we will see, the degeneracy of the Hopf bifurcation at the singularity creates an additional (generic) Bogdanov–Takens bifurcation not found in the codimension-three scenarios and this creates the appropriate bifurcations in the appropriate order for fold/subHopf bursting.

A partial unfolding of the doubly-degenerate Bogdanov–Takens singularity has been studied by Khibnik et al. [15], who used the cubic Liénard form:

$$\{\begin{array}{c}\begin{array}{cc}\stackrel{.}{x}\hfill & =y,\hfill \\ \stackrel{.}{y}\hfill & =-{\mu }_1+{\mu }_{2}x-x^3+y(\nu +\mathit{bx}-x^2).\hfill \end{array}\hfill \end{array}\phantom{\}}$$ (4)

Here, we preserve the notation used in (2); equation (4) can be obtained from (2) by reversing time as well as the orientations of x, μ₁ and ν. It is important to realize that in this codimension-four unfolding the parameter b is no longer fixed and we study the entire four-dimensional parameter space.

As is always the case in unfolding theory, the singularity under consideration lies at the origin (μ₁, μ₂, ν, b) = (0, 0, 0, 0) in the four-dimensional parameter space (and the bifurcation also occurs at the origin in phase space). The codimension-one saddle-node, Hopf and homoclinic bifurcations form three-dimensional manifolds in this four-dimensional parameter space. In order to understand how these bifurcations organize the possible phase portraits of (4), it helps to reduce the effective parameter space, preferably without limiting the possible dynamics. Note that the b-axis, except for the origin itself, consists entirely of codimension-three degenerate Bogdanov–Takens points of the types studied in [6]. However, the unfoldings described in [6] are only a local theory, i.e., additional bifurcations may occur for parameters outside a neighborhood of the origin in (μ₁, μ₂, ν)-space. On the other hand, these additional bifurcations are present in an arbitrarily small neighborhood of the codimension-four singularity in (μ₁, μ₂, ν, b)-space. Hence, for each fixed b it suffices to consider a large enough neighborhood around the origin in (μ₁, μ₂, ν)-space; or conversely, any fixed neighborhood around the origin in (μ₁, μ₂, ν)-space contains the additional bifurcations, provided b is chosen small enough.

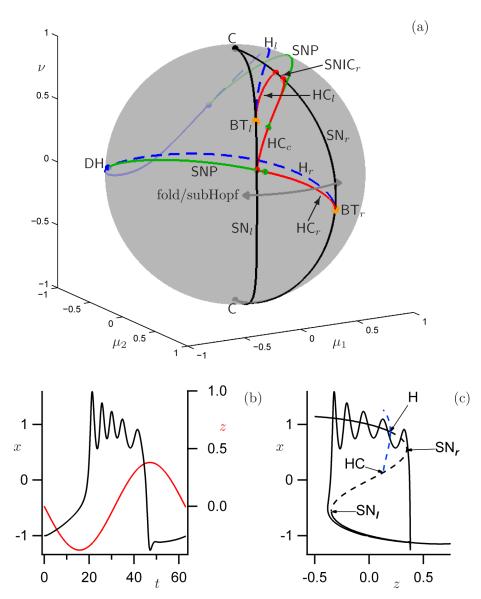
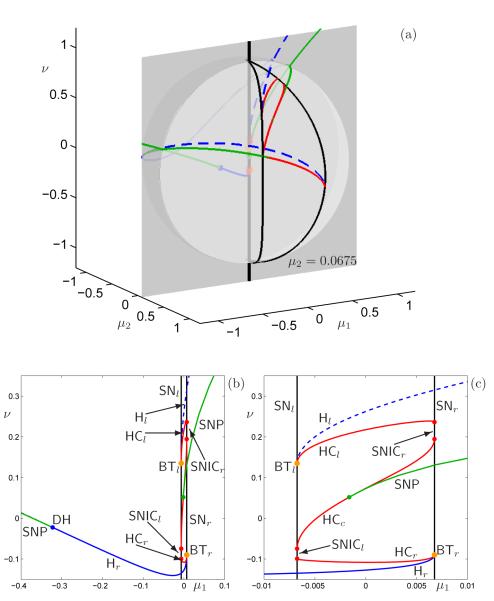
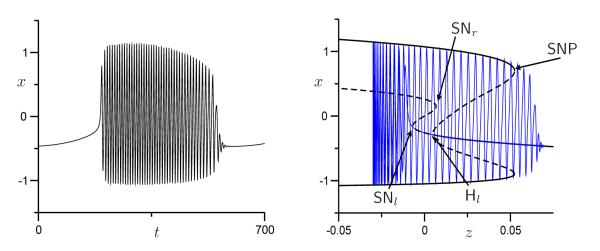
We consider the unit sphere, that is, a sphere with radius one centered around the origin in (μ₁, μ₂, ν)-space, as the boundary of such a fixed neighborhood. We found that b = 0.75 is small enough that we can identify a fold/subHopf burst path of (4) on this unit sphere; Figure 3(a) shows the corresponding bifurcation diagram. There are two cusp points C on the ν-axis that give rise to two curves of saddle-node bifurcations, denoted SN_l and SN_r for the left and right knees, respectively; inside the smaller region delimited by SN_l and SN_r there are three coexisting steady states. A (generic) Bogdanov–Takens point BT_r (BT_l) exists on SN_r (SN_l) that gives rise to curves of Hopf H_r (H_l) and homoclinic bifurcations HC_r (HC_l). The curves HC_r and HC_l end on SN_l and SN_r, respectively, which gives rise to segments on SN_l and SN_r that correspond to SNICs; the other end points of the SNIC segments are formed by the end points of a third homoclinic bifurcation curve HC_c. We denote these SNIC segments SNIC_l and SNIC_r; note that SNIC_l is so small that it is not labeled but is indicated by the (red) dot on SN_l in Figure 3(a). As shown by the dashed curves in Figure 3(a), the Hopf bifurcations H_l and H_r are both subcritical, but the two curves are connected via a segment of supercritical Hopf bifurcations and two degenerate Hopf points DH (one on the left side of the sphere, labeled, and the other on the back side, μ₂ < 0, unlabeled); this gives rise to two curves of saddle-nodes of periodics (SNP) that end on HC_r and HC_c.

Figure 3.

Pseudo-plateau bursting exists in the (partial) unfolding (4) of a doubly-degenerate Bogdanov–Takens singularity. Panel (a) shows the bifurcation diagram on the unit sphere in (μ₁, μ₂, ν)-space with b = 0.75. Color in on-line version: red, homoclinic (HC); blue, Hopf bifurcation (H; solid: supercritical, dashed: subcritical); black, saddle-node (SN); orange, Bogdanov–Takens point (BT); green, saddle node of periodics (SNP); degenerate Hopf and cusp are labeled DH and C, respectively. Panels (b) and (c) show time series and underlying bifurcation diagram of pseudo-plateau bursting corresponding to the path indicated in panel (a).

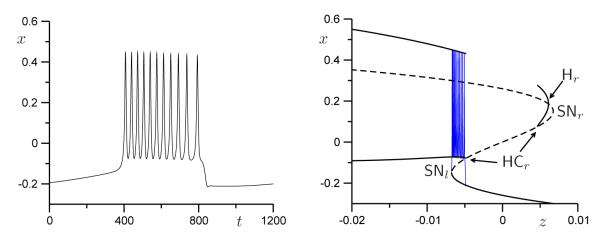
Pseudo-plateau bursting is defined by any path that crosses SN_l below SNIC_l and crosses SN_r between BT_r and SNIC_r such that it only intersects the curves H_r and HC_r; such a path is indicated in Figure 3(a) and corresponding time series and bifurcation diagram are illustrated in Figures 3(b) and 3(c). More specifically, we chose the circle segment with ν = 0.1 fixed and ${\mu }_2=\sqrt{1-{\nu }^2-{\mu }_1^2}$, where μ₁ ranges between ±0.38. As before, we identified μ₁ with the slow variable z as in (3) with ${\stackrel{‒}{\mu }}_1=0$, A = 0.38 and ε = 0.1. The bursting oscillation associated with this path is shown in Figure 3(b); it has all the characteristics of a pseudo-plateau burster and the underlying bifurcation diagram, shown in Figure 3(c), illustrates that this is indeed a fold/subHopf burster.

3.1. Transition from pseudo-plateau to square-wave bursting

The cells that exhibit pseudo-plateau bursting (or, at least, whose models do so), such as pituitary somatotrophs and lactrotrophs, are closely related functionally and developmentally to cells that exhibit square-wave bursting, such as pituitary corticotrophs and pancreatic β cells. This leads us to expect that the two burst patterns are also related mathematically. In fact, the fold/homoclinic and fold/subHopf bursters shown in Figure 1 were obtained from the same model by changing a single parameter, namely, one that controls the activation of the calcium current. Shifting this activation to lower voltages has the consequence that greater activation of the calcium-activated potassium channels is needed to destabilize the steady, highvoltage plateau. This shifts the supercritical Hopf bifurcation in Figure 1(b) to the right and also causes it to flip to subcritical, i.e., it passes through a degenerate Hopf bifurcation. It was shown in [25] that shifting the activation of the voltage-dependent potassium channel causes the same transition, which, thus, seems easily available to cells.

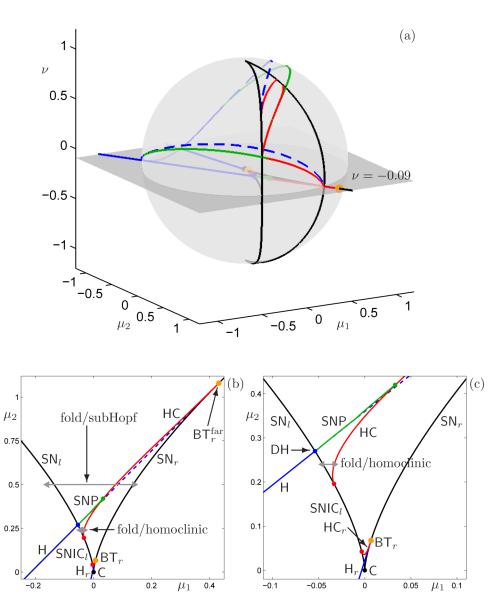
There is no path on the sphere in Figure 3(a) that represents square-wave bursting. (For this, the curve H_r from BT_r must become supercritical before it crosses the homoclinic HC_c, that is, DH should lie between SN_l and SN_r.) However, we know that the origin in Figure 3(a) is a degenerate Bogdanov–Takens point and expect that a fold/homoclinic path exists for μ₁, μ₂ and ν small enough [6, 7, 15]. In order to visualize bifurcations inside the unit sphere we choose a slice with ν = −0.09 fixed. The bifurcation diagram of (4) with b = 0.75 and ν = −0.09 is shown in Figure 4; the location of the (μ₁, μ₂)-plane in (μ₁, μ₂, ν)-space relative to the unit sphere of Figure 3 is shown in panel (a) and the slice itself in panel (b), with an enlargement in panel (c). Note that there are two Bogdanov–Takens points in this slice that are both located on SN_r; we denote these points BT_r and ${\mathsf{BT}}_r^{\mathrm{far}}$. The point BT_r that lies very close to the origin (μ₁, μ₂) = (0, 0) is part of the unfolding of a degenerate Bogdanov–Takens singularity with b = 0.75 fixed [6, 7, 15], but the transition from square-wave to pseudo-plateau bursting is organized by ${\mathsf{BT}}_r^{\mathrm{far}}$, which is not part of that unfolding. That is, as the sphere is shrunk with b fixed, ${\mathsf{BT}}_r^{\mathrm{far}}$ is not guaranteed to persist. ¿From ${\mathsf{BT}}_r^{\mathrm{far}}$ emanates a subcritical Hopf bifurcation H that becomes supercritical at the point DH, which lies just to the right of SN_l; the degenerate Hopf point DH gives rise to a curve of saddle-nodes of periodics (SNP) that ends on the curve of homoclinics HC, which also emanates from ${\mathsf{BT}}_r^{\mathrm{far}}$. Paths for both fold/subHopf and fold/homoclinic bursting that involve only the Hopf H and homoclinc bifurcations HC originating from ${\mathsf{BT}}_r^{\mathrm{far}}$ are indicated in Figures 4(b) and 4(c).

Figure 4.

Bifurcation diagram of (4) with b = 0.75 and ν = −0.09; the bifurcation diagram on the unit sphere with b = 0.75 from Figure 3(a) is shown for reference in panel (a) with the (μ₁, μ₂)-plane shown in panel (b) and an enlargement in panel (c). Note that there are two Bogdanov–Takens points, BT_r and ${\mathsf{BT}}_r^{\mathrm{far}}$, on the same side SN_r of the cusp point C. Two burst paths are indicated, which are the fold/subHopf and fold/homoclinic bursters illustrated in Figure 5. Colors and symbols as in Figure 3.

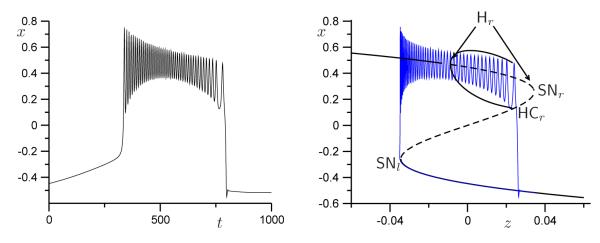
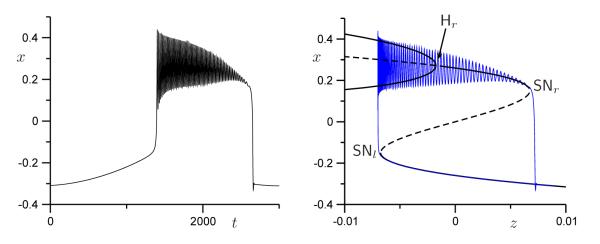
The path for fold/subHopf (pseudo-plateau) bursting is horizontal, with μ₂ fixed such that it lies above the point on HC where SNP ends and below ${\mathsf{BT}}_r^{\mathrm{far}}$. Figure 5(a) shows the time series for x and z corresponding to the path labeled fold/subHopf in Figure 4(b) with μ₂ = 0.5, and Figure 5(b) shows the one-parameter bifurcation diagram. Fold/homoclinic (square-wave) bursting can be obtained by choosing μ₂ below the point DH, but above the segment SNIC_l on SN_l in Figure 4(c). An example with μ₂ = 0.24 is shown in Figures 5(c) and 5(d).

Figure 5.

Time series and one-parameter bifurcation diagrams illustrating the two path segments indicated in Figure 4; we used (4) with b = 0.75 and ν = −0.09, and μ₂ = 0.5 for pseudo-plateau bursting in panels (a) and (b), and μ₂ = 0.24 for square-wave bursting in panels (c) and (d), respectively. The slow variable z = μ₁ is defined in (3); we used ${\stackrel{‒}{\mu }}_1$ = −0.01, A = 0.15 and ε = 0.1 for μ₂ = 0.5, and ${\stackrel{‒}{\mu }}_1$ = −0.0395, A = 0.0066 and ε = 0.01 for μ₂ = 0.24.

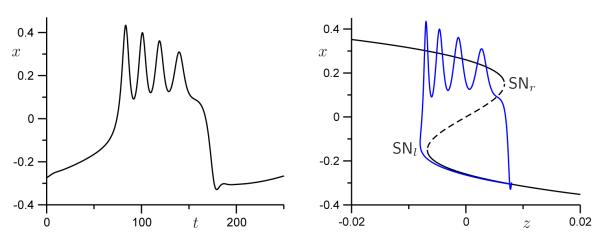
For intermediate values of μ₂, in between DH and the point on HC where SNP ends in Figure 4(c), a transitional form of bursting with square-wave appearance is found in which the Hopf bifurcation is subcritical but becomes stable via an SNP before going homoclinic. The stable branch then carries the spikes of the active phase and the unstable branch is not involved. The canonical square-wave example that has introduced a generation of computational neuroscientists to bursting [20, Fig. 7.9] is of this type, albeit with the SNP outside the knees; it does not occur in the unfolding of the degenerate Bogdanov–Takens singularity [2, 6] but rather appears as a transitional form between the classical supercritical fold/homoclinic and fold/subHopf types in the scenario of Figure 4.

For values of μ₂ that intersect the segment SNIC_l, no type of bursting is possible with one very slow variable but may be possible for non-small ∈. Parabolic bursting would be possible with two (also very) slow variables. This has not been observed in pituitary cells, but the diagram is compatible with the beating (repetitive large spikes) seen spontaneously in lactotrophs and in somatotrophs when the large conductance voltage- and calcium-dependent (BK) channel is blocked [8].

3.2. Transition to other known burst patterns

As mentioned above, the point (μ₁, μ₂, ν) = (0, 0, 0) with b = 0.75 is, in fact, a degenerate Bogdanov–Takens singularity classified in [6]. We can recover the bifurcation diagram of this unfolding as part of the unfolding of the doubly-degenerate Bogdanov–Takens singularity by considering a slice with μ₂ fixed. Figure 6 shows the bifurcation diagram of (4) for b = 0.75 and μ₂ = 0.0675; the value for μ₂ is precisely the μ₂-value of BT_r in Figure 4, so that BT_r in Figure 6 is the same Bogdanov–Takens bifurcation point. As in Figure 4, we illustrate the relative location of the μ₂-slice in (μ₁, μ₂, ν)-space with respect to the unit sphere of Figure 3(a) in Figure 6(a); the slice itself is shown in panel (b) with an enlargement in panel (c). The bifurcation diagram is organized by the degenerate Bogdanov–Takens singularity at the origin in (μ₁, μ₂, ν)-space because all ingredients that are important for the bifurcation structure on this slice are present in a small neighborhood of the origin (μ₁, ν) = (0, 0), which is also a small neighbhorhood of the origin in (μ₁, μ₂, ν)-space, since μ₂ = 0.0675 is small. Figure 6(c) is similar to the bifurcation diagrams shown in [2, Fig. 7] and [30, Fig. 18], but with the top-down orientation reversed. Hence, we expect to obtain fold/homoclinic bursting by selecting a path that crosses SN_l and SN_r such that it only intersects the curves HC_r and H_r that emanate from BT_r; it is illustrated in Figure A4. Note that this fold/homoclinic burster is not generated by the same bifurcation curves as the fold/homoclinic burster marked in Figure 4 and we distinguish between fold/homoclinic bursters that are near fold/subHopf bursters (Figure 4) and those that are not (Figure 6).

Figure 6.

Bifurcation diagram of (4) with b = 0.75 and μ₂ = 0.0675; the bifurcation diagram on the unit sphere with b = 0.75 from Figure 3 is shown for reference in panel (a) with the (μ₁, ν)-plane shown in panel (b) and an enlargement in panel (c); the Bogdanov–Takens point BT_r is the same point as the one labeled BT_r in the ν-slice shown in Figure 4. Colors and symbols as in Figure 3.

Figure A4.

Square-wave (fold/homoclinic) bursting with ν = −0.105, A = 0.0013, ${\stackrel{‒}{\mu }}_1$ = −0.006 and ε = 0.005.

Apart from fold/subHopf bursting, the bifurcation diagram in Figure 6 contains most known burst types. We describe these briefly here, and refer to the Appendix and the literature for pictures and details. Let us again choose horizontal path segments with ν constant and μ₁ playing the role of the slow variable. As already mentioned, for ν-values between the minimum of HC_r and the bottom of the SNIC region SNIC_l we get square-wave bursting. Note that the Hopf bifurcation required for square-wave bursting occurs (far) to the left of SN_l in Figure 6; if both Hopf bifurcations lie between SN_l and SN_r, which happens if the minimum of H_r lies between SN_l and SN_r, then the spike envelope of the burst first shrinks in amplitude then grows; see Figure A10. This was termed “parabolic amplitude bursting” in the Liénard model of Pernarowski [17, Fig. 1(c)] and was also found in a Hodgkin-Huxley model for pituitary corticotrophs [16]. Mathematically, these cases are topologically equivalent and the latter is considered a minor variant of fold/homoclinic bursting because it does not involve any change in the bifurcation structure. Put another way, the transition of the far left Hopf bifurcation across SN_l is not a bifurcation and is not even required if curved paths are allowed.

Figure A10.

“Parabolic amplitude” bursting, a phenomenological variant of fold/homoclinic bursting, with μ₂ = 0.2, ν = −0.132, A = 0.006, ${\stackrel{‒}{\mu }}_1$ = 0.023 and ε = 0.05. This case does not correspond to a path in Figure A1; μ₂ was changed to move both Hopf bifurcations to the right of the left knee (small periodic branch corresponding to the right Hopf bifurcation not displayed).

Moving ν up so that horizontal path segments cross SNIC_l gives parabolic bursting (Figure A5); and moving ν further up to cross the middle homoclinic curve HC_c gives fold/homoclinic with large limit cycles (Figure A6). Other bursters with large limit cycles are found as ν is increased further (Figures A7 and A8), as described in detail in [2].

Figure A7.

Fold/fold-cycle bursting, historically called “Type 4″, with ν = 0.2, A = 0.03, ${\stackrel{‒}{\mu }}_1$ = 0.005 and ε = 0.02.

Figure A8.

A form of subHopf/fold-cycle bursting with folds in the steady-state curve so that some of the fast-subsystem limit cycles surround three steady states. The path satisfies ν = 0.3, A = 0.05, ${\stackrel{‒}{\mu }}_1$ = 0.02 and ε = 0.01.

If ν is chosen below the minimum of HC_r but above the minimum of H_r, there are two Hopf bifurcations on the upper steady-state branch of the frozen system that are joined by a closed curve of periodic orbits. The shape of the active-phase spike envelope again depends on whether both Hopf bifurcations on H_r occur between SN_l and SN_r or one lies to the left of SN_l. The latter is the case in Figure 6 and results in tapered bursting; see Figure A3 as well as [17, Fig. 1(e)] and [5, Fig. 7]. An example with both Hopf bifurcations between the knees is given in [25, Fig. 2]. In the nomenclature of Izhikevich and Hoppensteadt [12, 13] these are both variants of fold/fold bursting, which also occurs for ν-values below the minimum of H_r, when there are no longer any limit cycles in the frozen system (Figure A2). In the limit ∈ → 0, this last case is just a classic relaxation oscillator, but if ∈ is not very small compared to the rate of attraction to the upper stable steady state, transient spikes can appear on the plateau.

Figure A3.

Tapered (fold/fold) bursting with ν = −0.13, A = 0.008, ${\stackrel{‒}{\mu }}_1$ = 0.001 and ε = 0.002.

Figure A2.

Fold/fold bursting in which there is no Hopf bifurcation of the fast subsystem but spikes are generated by transients of the fast subsystem. The path satisfies ν = −0.15, A = 0.008, ${\stackrel{‒}{\mu }}_1$ = 0 and ε = 0.025. The spikes disappear as ε ↔ 0.

We emphasize again that the location of the Hopf bifurcations relative to the knees is only of phenomenological interest. All of the burst types mentioned above can be found in Figure 6, provided one allows for curved paths, for which the value of ν depends linearly or even nonlinearly on μ₁. Nonetheless, the options with ν fixed, where μ₁ is directly identified with the slow variable z, are very easy to identify and already account for most of the wide range of burst types reported in the literature.

4. The codimension of fold/subHopf bursting

We have shown above that fold/subHopf bursting can be obtained by unfolding a codimension-four doubly degenerate Bogdanov-Takens singularity. We now examine more closely whether it is possible to find this burst pattern in the neigbhorhood of a singularity with smaller codimension. Unfortunately, not all possible unfoldings are known and already the list of unfoldings of codimension-three singularities is incomplete. In this section we show that fold/subHopf bursting does not appear in any of the known unfoldings, which indicates that its codimension is likely equal to four.

The main ingredients for fold/subHopf bursting are very similar to those for fold/homoclinic bursting: the bifurcation structure must include three coexisting steady-state branches, with a Hopf as well as a homoclinic bifurcation on the “upper” branch. The Hopf bifurcation for fold/subHopf bursting is subcritical, whereas for fold/homoclinic bursting it is supercritical. The requirement of three coexisting steady states implies that the singularity must lie at a cusp point. Furthermore, the presence of a Hopf bifurcation together with a homoclinic bifurcation on the same branch can only be realized with a Bogdanov–Takens point. Hence, in our opinion, the only codimension-three candidate for fold/subHopf is the degenerate Bogdanov–Takens singularity; such a singularity also gives rise to fold/homoclinic bursting. However, we show here that fold/subHopf bursting cannot be realized near a degenerate Bogdanov–Takens singularity.

The degenerate Bogdanov–Takens singularity was studied systematically by Dumortier et al. in [6]. They defined the unfolding

$$\{\begin{array}{c}\begin{array}{cc}\stackrel{.}{x}\hfill & =y,\hfill \\ \stackrel{.}{y}\hfill & =-{\mu }_1+{\mu }_2\pm x^3+y(\nu +\mathit{bx}\pm x^2),\hfill \end{array}\hfill \end{array}\phantom{\}}$$ (5)

with b > 0 fixed and unfolding parameters μ₁, μ₂, and ν. Here, we use –μ₁ instead of μ₁ conforming to our notation. Note that systems (2) and (4) are examples of (5) with –x³, whereas (2) uses +y x² and (4) uses –y x². As we have stated previously, the sign of the cubic term y x² can be changed by reversing time, which also transforms stable equilibria and periodic orbits into unstable ones and vice versa; more precisely, apart from the stability properties, system (5) with ±x³ and +y x² is equivalent to system (5) with ±x³ and –y x² via the transformation (x,y,μ₁,μ₂,ν,t) ↔ (–x,y,–μ₁,μ₂,–ν,–t). Hence, strictly speaking, the sign of yx² not lead to a different case; it only affects the stability of the invariant objects. Dumortier et al. used +y x² in their analysis [6], whereas we have consistently used –y x² in this paper.

Dumortier et al. [6] identified three canonical cases: system (5) with +x³ leads to the saddle case, where b > 0 is unrestricted; system (5) with –x³ leads to the focus case, if 0 < b < 2$\sqrt[]{2}$, or the elliptic case, if b > $2\sqrt[]{2}$. The focus case is contained in the bifurcation diagrams for this paper, except for Figure 2, because we use b = 0.75 < $2\sqrt[]{2}$ in our analysis of the codimension-four singularity at b = 0; Golubitsky et al. [7] studied the elliptic case with b = 3 > $2\sqrt[]{2}$; see also Figure 2. The saddle case can be dismissed immediately, because all of the phase portraits that have three steady states consist of two saddles separated by a node or a focus; see [6, page 6]. Fold/subHopf bursting requires two foci or nodes and only one saddle.

Hence, it suffices to consider system (5) with –x³. We first consider the focus case. One can get an idea of the bifurcation diagram for the focus case from the slice at constant μ₂ in Figure 6(c), in which the cusp points are located at infinity. While the unfolding (5) involves the full three-dimensional parameter space, it is argued in [6, 15] that this two-dimensional slice contains all possible phase portraits for the focus case, provided we do not prescribe the definitions of “upper” and “lower” branches. Fold/subHopf bursting requires a path that crosses one of the Hopf curves, H_l or H_r, the associated curve of homoclinic bifurcation, HC_l or HC_r, respectively, and, in order to create a silent phase, it should cross the “opposite” saddle-node curve, SN_r or SN_l, respectively. The Hopf bifurcation should be subcritical, which can be achieved by reversing time when necessary. Furthermore, the branch that corresponds to the silent phase should consist of stable steady states. There are other stability requirements — for example, the segment of the “upper” steadystate branch in between the Hopf and homoclinic bifurcations should be stable as well — but we do not need them for our arguments. The saddle-node bifurcations SN_l and SN_r give rise to a saddle and a stable steady state when crossed below BT_l and BT_r in Figure 6(c), respectively; otherwise, we get a saddle-focus pair. Of course, these stability properties are reversed if we reverse time.

Figure 6(c) has a subcritical Hopf bifurcation H_l, but the phase portraits locally near H_l do not support fold/subHopf bursting. The parameter regime bounded by the curves SN_l, H_l and SN_r gives rise to a saddle and two foci; one of the foci becomes stable in a subcritical Hopf bifurcation as we cross H_l from the left (see examples in Figures A7–A9). However, this steady-state branch should correspond to the “upper” branch or active phase of the burst, and this makes the “lower” branch, which should correspond to the silent phase, unstable. Furthermore, in this region of Figure 6(c) there is an attracting periodic orbit that surrounds all three steady states, also evident in Figures A7–A9, which removes any hope for generating fold/subHopf bursting.

Alternatively, if we consider the time-reversed version of Figure 6(c), then the family of Hopf bifurcations H_r becomes subcritical; this means that we need to cross H_r, HC_r and SN_l. The phase portraits corresponding to the two parameter regimes on either side of H_r and bounded by SN_l, SN_r and HC_c do not exhibit a large periodic orbit surrounding all three steady states. However, the time reversal renders the silent phase arising from SN_l unstable, so bursting is again not possible; for example, consider the time-reversed version that corresponds to Figure A10, in which the Hopf bifurcation is conveniently between the knees. We refer to [15] for a complete overview of all possible phase portraits for the focus case.

The elliptic case is different from the focus case, but not at the level of the phase portraits locally near the Bogdanov–Takens points BT_l and BT_r. In fact, the two paths discussed above for the focus case are illustrated for the fold/homoclinic case of system (5) with +x³ and b = 3 in Figures 2(b) and 2(d). If we reverse time in these two figures, the Hopf bifurcation becomes subcritical, but we lose the silent phase; as in the focus case, there also exists a large attracting periodic orbit in the time-reversed version of Figure 2(b).

Paths crossing H_l or H_r are the only possible candidates for fold/subHopf bursting in the unfolding of the degenerate Bogdanov–Takens singularity. Hence, we conclude that the right combinations for the fold/subHopf case do not exist near such a codimension-three singularity. It is tempting to conclude from Figure 4 that fold/subHopf bursting and its cousin fold/homoclinic bursting appear in the same unfolding of a different codimension-three singularity, namely, the one that gives rise to the point ${\mathsf{BT}}_r^{\mathrm{far}}$ and associated bifurcations SN_r, H and HC. Such a singularity could be thought of as a Bogdanov–Takens point that occurs at a degenerate Hopf point, rather than a generic Hopf bifurcation. An entire curve of such codimension-three singularities exists in the unfolding of the codimension-four doubly-degenerate Bogdanov–Takens singularity. However, as a single codimension-three point, this singularity does not give rise to three coexisting steady states. Only the doubly-degenerate Bogdanov–Takens singularity guarantees both saddle-node bifurcations SN_l and SN_r, which provides the possibility of a stable silent phase. Hence, we conclude that the codimension of fold/subHopf bursting is four.

5. Conclusions

The development of the theory of bursting serves as a valuable case study of the interplay between biology and mathematics. The impetus to examine bursting in the first place came from the experimental observation of it in cells. Through mathematical analysis the diverse experimental phenomena were assembled into a beautiful and coherent theory of considerable explanatory power and in turn facilitated modeling by providing ready-to-use templates. Rapid progress was made possible by the prior existence of a body of theory cataloguing the possible behaviors of planar systems without regard to bursting; the strong separation of time scales allowed this to be leveraged into a theory of bursting.

In this paper we have extended the theory of bursting by classifying fold/subHopf (pseudo-plateau) bursting in terms of the codimension of the singularity in whose unfolding it first occurs. We identified a fold/subHopf burst path in the partial unfolding of a codimension-four doubly-degenerate Bogdanov–Takens singularity and believe that this is the smallest codimension of singularities that give rise to pseudo-plateau bursting. Furthermore, since the unfolding of this codimension-four singularity includes a curve of codimension-three degenerate Bogdanov–Takens bifurcation points of focus type, it also gives rise to all the codimension three bursters, which include most known burst types.

Prior biological observation and modeling experience indicated that pseudoplateau and square-wave bursting should be cousins. Figure 4 illustrates the existence of a one-parameter transition between these two burst types as part of the partial unfolding of the codimension-four doubly-degenerate Bogdanov–Takens singularity. This transition is organised by a second Bogdanov–Takens bifurcation point on the “upper” branch, denoted ${\mathsf{BT}}_r^{\mathrm{far}}$ in Figure 4(b), the occurrence of which is in turn organized by a codimension-three bifurcation point that exists as part of the unfolding of the doubly-degenerate Bogdanov–Takens singularity.

Our analysis illustrates that not all fold/homoclinic bursters are the same — some can be converted to fold/subHopf bursters by small changes in a single parameter (e.g.,Figure 4) and others cannot (e.g., Figure 6). This highlights a difference between classification of bursters by unfolding and classification in terms of the bifurcations that initiate and terminate the active phase [13]. Although all the bursters disclosed by unfolding had previously been identified by the classification system of [13], additional distinctions are made by unfolding that reflect bifurcations that do not participate in the burst mechanism but may influence its properties and what other patterns it has as neighbors. Other examples in this study include the two types of fold/homoclinic in Figure 2 and the two types of subHopf/fold-cycle in Figure A8 and A9.

The two slices shown in Figures 4 and 6 combined provide a fairly complete picture of possible burst types that have been found in models. In principle, one should be able to define a single two-dimensional curved slice in (μ₁, μ₂, ν)-space that contains a combination of the two bifurcation diagrams with ν, respectively μ₂ fixed. There are other known burst types, such as fold/fold-cycle with small limit cycles [22], that do not occur in either of the slices we have considered, but it may be possible to find this and additional known or unknown burst types in other unexplored slices of the unfolding of the codimension-four doubly-degenerate Bogdanov–Takens singularity. We propose that bursting cells explore a bifurcation landscape in the neighborhood of this codimension-four singularity.

Despite the fact that burst types appear to be generated by planar fast subsystems, cells likely operate with non-planar fast subsystems. Indeed, cells have to serve a variety of functions under different conditions and, therefore, incorporate a non-minimal set of ion channels. Coupling of bursters also naturally generates higher-dimensional fast subsystems. Instructive examples of single [2] and coupled cells [3] have been described, but the surface has only been scratched.

Some common forms of bursting (e.g., pseudo-plateau and fold/fold with no or only vestigial limit cycles) depend on the separation of time scales not being too great, otherwise spikes would not be seen in the active phase. This has led to consideration of pseudo-plateau bursting as a form of mixed-mode oscillation, in which y and z are considered slow and x fast. This approach has advantages for some purposes, such as predicting a priori how many spikes occur per burst, and cases exist in which the traditional fast-slow method fails completely [29]. Mixed-mode oscillations in systems with two slow variables can similarly be viewed as generated via bifurcation diagrams of particular unfoldings. We leave it as challenging future work to extend the classification theory for bursting to such higher-dimensional paths.

Appendix.

The figures in this appendix were all made with system (4), repeated here for convenience:

$$\{\begin{array}{c}\begin{array}{cc}\stackrel{.}{x}\hfill & =y,\hfill \\ \stackrel{.}{y}\hfill & =-{\mu }_1+{\mu }_{2}x-x^3+y(\nu +\mathit{bx}-x^2).\hfill \end{array}\hfill \end{array}\phantom{\}}$$

Except for Figure A10, μ₂ is fixed at 0.0675 and b at 0.75, corresponding to the μ₂-slice in Figure 6, which is reproduced, enlarged and annotated in Figure A1. The parameter ν is varied to select an appropriate horizontal slice in the (μ₁, ν)-plane in order to produce each form of bursting that was not previously illustrated in the main text. Time series and one-parameter diagrams are displayed in increasing order of ν.

As before, μ₁ is identified with the slow variable z; we use the sinusoidal oscillation defined in (3) in the main text, i.e.,

$$z\left(t\right)≔{\stackrel{‒}{\mu }}_1-A\sin \left(\epsilon t\right),$$

where A, ${\stackrel{‒}{\mu }}_1$, and ε are chosen to produce an appropriate path for the desired burst pattern, as listed in each figure caption; all paths are also indicated in Figure A1 and labeled with the associated figure number. In each figure, the left panel shows the time series of the (fast) variable x and the right panel shows this trajectory overlayed in the (z, x)-plane on top of the bifurcation diagram of the fast subsystem, where z is considered a parameter. Solid curves in the bifurcation diagrams correspond to stable solutions and dashed ones to unstable solutions. The bifurcations are labeled as follows: SN for saddle-node bifurcations, H for Hopf, HC for homoclinic, SNIC for saddle-node-on-invariant-cycle, and SNP for saddle-node of periodics; the subscripts l and r indicate whether these involve the upper (x > 0), lower (x < 0) equilibrium branches, respectively, while the subscript c indicates that the bifurcation involves a large periodic orbit surrounding all three steady states.