Error-correcting barcoded primers allow hundreds of samples to be pyrosequenced in multiplex

Abstract

We have constructed error-correcting DNA barcodes that allow one run of a massively parallel pyrosequencer to process up to 1544 samples simultaneously. We have used these barcodes to process 16S ribosomal DNA sequences representing 286 microbial communities, correct 92% of sample assignment errors, and nearly double the known 16S rRNA sequences. In principle, our approach has myriad applications.

Pyrosequencing¹ has the potential to revolutionize many sequencing efforts, including assessments of microbial community diversity throughout our planet^2–4, by eliminating the laborious step of producing clone libraries and generating hundreds of thousands of sequences in a single run. Use of pyrosequencing for culture-independent 16S rRNA-based analysis of microbial community composition has been limited by the expense of each individual run, and by the difficulty of splitting a single plate across multiple runs. One way around this problem is to use a barcoding approach, in which a unique tag is added to each primer before PCR amplification^5,6. Because each sample is amplified with a known tagged primer, sequencing can be performed on an equimolar mixture of PCR-amplified DNA from each sample, and sequences can be assigned to samples based on the unique barcode. To date, this technique has been used successfully to sequence up to thirteen samples in the same lane in a single pyrosequencing run⁵.

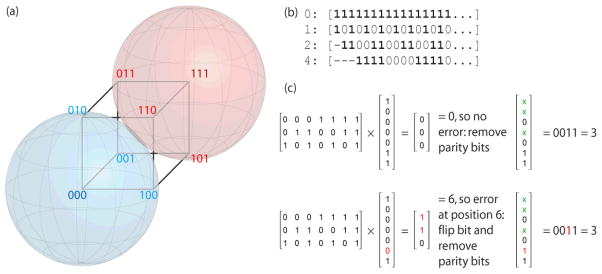
Existing barcoding methods are limited both in the number of unique barcodes they use and in the ability to detect sequencing errors that change sample assignments. We have developed a new set of barcodes based on error-correcting codes⁷, which are widely used in applications ranging from cell phones to CDs. Briefly, Hamming codes, like all error-correcting codes, are based on the principle of redundancy and are constructed by adding redundant parity bits to data that is to be transmitted over a noisy medium. Here we want to encode sample identifiers with redundant parity bits, and “transmit” these sample identifiers as codewords. If each base is encoded by two bits, and we use 8 bases for each codeword, we will be transmitting 16-bit codewords. Hamming codes use only a subset of the possible codewords, choosing those that lie at the center of multidimensional spheres (hyperspheres) in a binary subspace. Single bit errors fall within hyperspheres associated with each codeword and can thus be corrected (Fig. 1a), whereas double bit errors do not and thus can be detected but not corrected.

Figure 1.

(a) A Hamming code to transmit one bit of information (k=1, n=3). Consider a hypersphere centered at 000 (blue): any single-bit error (010, 001, and 100) falls within a radius of 1 and thus can be corrected. Likewise with the hypersphere centered at 111 (red). (b) Regions of a codeword of length 16 (or longer) checked by parity bits at positions 0, 1, 2, and 4: bits that are checked by each position are marked with 1. (c) Example of decoding a “received” codeword containing the binary value of 3 (0011) (n=7, k=4): the first case contains no errors; the second contains a single-bit error at position 6 that is detected and corrected.

Let n be the total number of bits in the codeword being transmitted, and k be the number of bits of information to be transmitted. Hamming codes use n-k bits of redundancy, and because not all 2ⁿ possible codewords are used, there are 2^k valid, error-correcting codewords is 2^k that form a k-dimensional subspace. The Hamming distance is defined as the number of bits that differ between two vectors in this subspace, and the relevant parameter for error-correction is the minimum Hamming distance. Let t be the radius of a sphere in this subspace where any change within this sphere can be corrected. The error-correcting capability is the largest radius such that all Hamming spheres are disjoint: t = floor((d_min−1)/2), where d_min is the minimum Hamming distance (Fig. 1). Thus, the minimum Hamming distance between codewords needed to correct a single error is 3. Hamming codes can be efficiently constructed and decoded using standard linear algebra techniques: for further details, see ref. 8.

To apply Hamming codes to biological problems, we have encoded sample identifiers as DNA translations of each binary codeword using 2 bits/base. Thus, our 8-base codewords (n=16) use 11 bits for sample identifiers (k=11), and 5 bits of redundancy (n-k=5). There are thus 2¹¹ = 2048 possible 8-base codewords (for comparison, 4-base barcodes can encode up to 16 codewords, and 16-base barcodes can encode up to 67 million, so the technique is readily scalable). To pick our maximal set of 1544 codewords (Supplementary Data), we chose an encoding scheme for ATCG that resulted in the most valid “candidate” codewords, then filtered these candidates to optimize PCR and sequencing performance based on GC content (40–60%), and eliminating consecutive triples of the same base and self-complementarity or complementarity to the primer.

To test these barcodes, we determined the bacterial composition of 286 environmental samples by PCR amplifying, sequencing, and analyzing 681,688 16S rRNA gene sequences⁹ from a single sequencing run of the Genome Sequencer FLX (454 Life Sciences, Branford, CT.). We used 286 of the 1544 candidate codewords to synthesize barcoded PCR primers to use in PCR reactions amplifying a region (27F–338R) of the 16S rRNA gene that we previously determined to be the optimal region of the 16S rRNA to use for phylogenetic analysis from pyrosequencing reads¹⁰.

For each sample, the 16S rRNA gene was amplified using the composite forward primer 5′-GCCTTGCCAGCCCGCTCAGTCAGAGTTTGATCCTGGCTCAG-3′: the underlined sequence is 454 Life Sciences^® primer B, and the sequence in italics is the broadly conserved bacterial primer 27F. A two-base linker sequence (‘TC’) that was not observed in >250,000 aligned 16S rRNA sequences was inserted between the 454 primer B and 27F to help mitigate any effect the composite primer might have on PCR efficiency. The reverse primer was 5′-GCCTCCCTCGCGCCATCAGNNNNNNNNCATGCTGCCTCCCGTAGGAGT-3′: the underlined sequence is 454 Life Sciences’ primer A, and the sequence in italics is the broad-range bacterial primer 338R. NNNNNNNN designates the unique eight-base barcode used to tag each PCR product, with ‘CA’ inserted as a linker between the barcode and rRNA primer. Total DNA was extracted from samples of human lung, river water, the Guerrero Negro microbial mat, particles filtered from air, and hot spring water using a modified bead-beating solvent extraction¹¹.

PCR reaction conditions were as follows: 8 μl 2.5X HotMaster PCR Mix (Eppendorf), 0.3 μM each primer, and 10–100 ng template DNA in a total reaction volume of 20 μl. PCR was performed with an Eppendorf Mastercycler: 2 min at 95°C, followed by 30 cycles of 20s at 95°C (denaturing), 20s at 52°C (annealing) and 60s at 65°C (elongation). Four independent PCR reactions were performed for each sample, along with a no template (water) negative control. For each of 286 samples, the four replicate PCR reactions were combined, purified with Ampure magnetic purification beads (Agencourt), quantified with the Quant-iT PicoGreen dsDNA Assay Kit (Invitrogen) and a fluorospectrometer (Nanodrop ND3300), and combined to create a master DNA pool with a final concentration of 21.5 ng/μl, which was sent for pyrosequencing with primer A at 454 Life Sciences (Branford, CT) as described^1,4. After removal of low-quality sequences and trimming of primer sequences, 437,544 sequences remained, each representing between ~240–280 bases of 16S rRNA sequence. The quality determination of each sequencing read was based on criteria previously described¹².

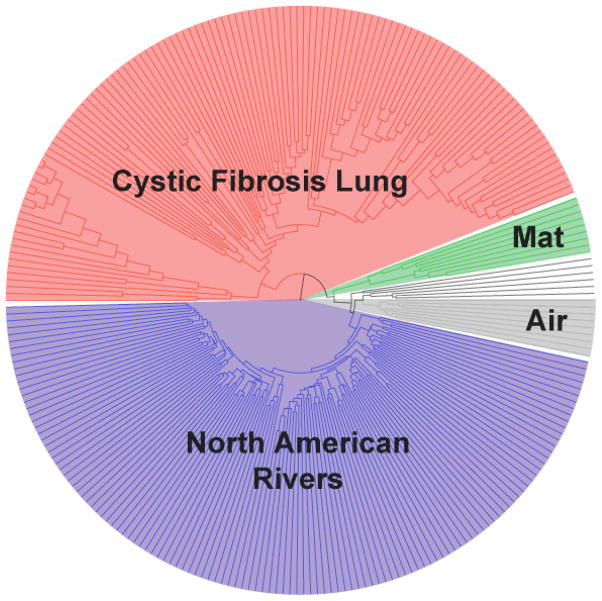
We assigned each remaining sequence to a sample based on the barcodes, picked OTUs (operational taxonomic units) at 96% identity, aligned one sequence representing each of the 25,351 OTUs with NAST¹³, built a “relaxed neighbor-joining” tree with clearcut¹⁴, and clustered the samples based on their similarities in bacterial phylogenetic diversity with UniFrac^15,16. The clustering (Fig. 2) correlated perfectly with sample type: all the lung samples clustered together, as did all the North American rivers, the microbial mat samples, air samples, hot spring samples, and two African river samples. Nineteen DNA samples were analyzed in triplicate with three independent barcode primers, and in each case the replicate samples clustered together in the UniFrac analysis. This suggests that these barcoded primers amplified equivalently in PCR. 1345 sequences (0.3%) had decoding errors, of which 1241 (92.2%) could be corrected to valid barcodes.

Figure 2.

UniFrac clustering of samples from cystic fibrosis lung (red), Guerrero Negro microbial mat (green), air (gray), and North American rivers (blue) demonstrates the essentially perfect clustering by community when using UniFrac on samples obtained by pyrosequencing. Of 61 replicate samples, all but one pair clustered.

These results demonstrate that we can use the tagged barcoding strategy to obtain sequences from hundreds of samples in a single sequencing run, and to perform phylogenetic analyses of microbial communities from pyrosequencing data. In the present study, we sequenced nearly as many 16S rRNAs as the total number determined to date by Sanger sequencing. This strategy should be useful for many applications. The combination of error-correcting barcodes and massively parallel sequencing will rapidly revolutionize our understanding of microbial habitats located throughout our biosphere, as well as those associated with our human bodies.