Transcriptional and metabolic data integration and modeling for identification of active pathways

Abstract

With the growing availability of omics data generated to describe different cells and tissues, the modeling and interpretation of such data has become increasingly important. Pathways are sets of reactions involving genes, metabolites, and proteins highlighting functional modules in the cell. Therefore, to discover activated or perturbed pathways when comparing two conditions, for example two different tissues, it is beneficial to use several types of omics data. We present a model that integrates transcriptomic and metabolomic data in order to make an informed pathway-level decision. Since metabolites can be seen as end-points of perturbations happening at the gene level, the gene expression data constitute the explanatory variables in a sparse regression model for the metabolite data. Sophisticated model selection procedures are developed to determine an appropriate model. We demonstrate that the transcript profiles can be used to informatively explain the metabolite data from cancer cell lines. Simulation studies further show that the proposed model offers a better performance in identifying active pathways than, for example, enrichment methods performed separately on the transcript and metabolite data.

1. Introduction

The development of different omics technologies in molecular biology has advanced the characterization of cells and tissues. In addition to the complete sequence of the genome, the overall collection of gene transcripts (the transcriptome), proteins (the proteome), and metabolites (the metabolome) can be investigated with various high-throughput technologies, including microarrays and mass-spectrometry. Thus, thousands of genes and hundreds of proteins and metabolites (molecules like sugars, amino acids, and vitamins) can be measured under different experimental conditions or cell states and we can hence obtain insight into their regulatory mechanisms. Taking cancer as an example, tumors originate from alterations in the DNA sequence of cells transforming them to carcinogenic ones (Stratton and others, 2009). In addition to more routine gene expression analyses, recent efforts have been focused on understanding the metabolome of cancer cells (see, e.g. Sreekumar and others, 2009). Since alterations on the genomic level often manifest themselves as downstream variations in metabolite concentrations, the metabolites can be viewed as end-points of perturbed (active) pathways and the information on the often relatively few measured metabolites is very important (Abate-Shen and Shen, 2009). Therefore, a combined analysis of the different omes of the cell holds much promise in understanding disease mechanisms.

In addition, the focus in the analysis of high-throughput data has shifted from identifying individually active genes, proteins, and metabolites to sets of them. Examples include enrichment of functional categories using the gene ontology (GO) hierarchy (http://www.geneontology.org) or of pathways. Pathways encode sets of reactions involving genes, metabolites, and proteins by connecting them in an intricate network, and can be viewed as functional groups with a more complex structure than GO groups. The KEGG database (http://www.genome.jp/kegg) contains collections of pathway information for a large set of species, which can be used in enrichment analysis for genes, as well as proteins, and metabolites.

The availability of multiple omics datasets in an experiment poses a challenge on how to effectively combine the various data sources for enrichment analysis, especially of pathways. Previous investigations employing an integrative approach for different types of omics data include several studies on plants, particularly Arabidopsis thaliana (e.g. Gibon and others, 2006; Allen and others, 2010), tomato (Carrari and others, 2006), and hybrid aspen (Bylesjö and others, 2009), a study on the yeast Saccharomyces cerevisiae (Bradley and others, 2009), and studies on rat or mouse (e.g. Frey and others, 2007; Xu and others, 2008). A breast cancer profiling study has also recently been published in which an integrative approach is undertaken for transcriptomic and metabolomic data (Borgan and others, 2010). The two main approaches for data integration in these studies are correlation analysis and/or unsupervised multivariate techniques like principal component analysis (PCA) and partial least squares (PLS). In the correlation approach, significant correlations between transcripts and metabolites are extracted, followed by clustering and network visualization or enrichment analysis of functional groups (generally using only genes). Overall, previous work relies on identifying co-expressed connections between transcripts and metabolites and afterwards integrating them into a pathway/functional group decision.

The objective of this study is to instead build a global model using directly the information present in the different data sources with the purpose of identifying active or enriched pathways, as opposed to a two-step individual modeling. We model the metabolite and transcript data jointly to pick out active pathways (what we refer to as making an informed pathway decision). The interpretation of the data becomes more straightforward since the need for post-analysis is reduced. Further, given the overall complexity of the model, our model selection strategy is based on information theoretic concepts that directly incorporate the composition of the pathways. The end goal of the methodology is to highlight pathways in which there is a considerable difference between treatment groups manifested both on the mRNA and metabolite levels.

The remainder of the paper is organized as follows: Section 2 describes the proposed model and model selection procedures. Extensive simulation studies as a proof of concept are presented in Section 3, including comparisons with other methods. Section 4 illustrates the model applied to an Arabidopsis dataset, and Section 5 contains the discussion.

2. Pathway model of transcript – metabolite connections

We propose a global model with the purpose of making decisions on active or enriched pathways by joint modeling of transcript and metabolite data. We base our model on the availability of transcriptional and metabolic data from the same samples, which in turn belong to a control or a treatment group, for example matched normal and cancer tissue, or wild-type and mutant. A generalization to the model is to include more treatment groups, which we touch briefly upon in Section 5.

Two frameworks are presented below; a linear model which is a special case of a richer mixed model framework. We have chosen to present mainly the linear model for two reasons. First, the mixed model framework is, due to the need to estimate mixed effects, more unstable in the fitting for smaller sample sizes, and hence less applicable to real-world examples. Secondly, with the linear model, we employ a richer model selection procedure that cannot as easily be attached to the mixed model framework. This model selection procedure improves the performance of the linear model greatly, making it competitive with the mixed model in almost all scenarios.

Pathway information is directly incorporated into the model, specifically, let c_k, for k=1,…,K, represent pathway activity, so that c_k equals one if pathway k is active (perturbed between control and treatment), and equals zero otherwise. The goal is to select the pathways, i.e. find the non-zero c_k indicators, that the experimental data most support. The prior information on pathways is incorporated into the global model in the form of membership indicator variables. The variables are denoted by a_ik and b_jk and defined as a_ik=1 if gene i is in pathway k and b_jk=1 if metabolite j is in pathway k.

The transcriptional and metabolic data contains levels of expression for a set of genes and metabolites, respectively. The expression level of gene i in condition t is denoted by g_it, while the level of metabolite j in condition t is denoted by f_jt. The control and treatment groups (t=1 and 2, respectively) are distinguished by the indicator variable x_t; x₁=0,x₂=1.

The gene model specifies a dependence of the gene expressions on pathway membership:

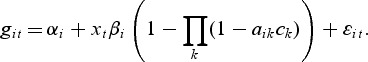(2.1)

The gene level includes an intercept term denoted by α_i while the second term with the parameters β_i represents a direct effect from a potential pathway membership. If gene i is a member of one or more active pathways, the direct effect can be included in the model for the observations from the treatment group. The model selection procedure (see Section 2.1) determines if β_i≠0 for gene i. Similarly, the metabolite model includes an intercept 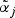for each metabolite:

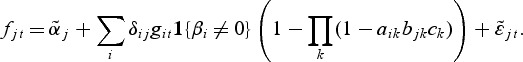(2.2)

The second term in the metabolite model accounts for a potential effect of gene expression on the metabolite expression. The expression of metabolite j can be affected by gene i if both are members of the same pathway, provided that the direct effect for gene i was included in the gene model. The parameters δ_ij estimate the relationship between gene i and metabolite j. Since we aim at modeling the hierarchical structure of regulation, in which genes affect metabolites, we will not include a treatment effect for the metabolites if no genes are selected as differential. We assume that we have n replications of observations in each model in which the biological material used in both the transcriptional and metabolic profiling comes from the same individual or pool.

One may also consider the following extension of the model that includes random effects on the metabolite level. The reasoning behind this is that genes within a pathway can still affect the metabolite expression, although they are not selected on the gene level. Hence, the metabolite mixed model is

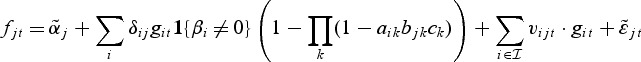(2.3)

with 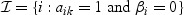. We make the assumption that the random effects v_ijt are normally distributed with mean zero and a diagonal covariance matrix (for details and parameter estimation, see Appendix A of the supplementary material available at Biostatistics online).

The complete model framework is designed to produce as much interpretative power as possible in different scenarios. The linear framework, in which genes are selected as active and used to explain the metabolite data, is efficient when we have a distinct differential signal on a set of genes. However, when we cannot exactly identify (in a linear way) the connection between genes and metabolites, the mixed model framework allows for small, cooperative effects in the model.

2.1. Model selection and parameter estimation for the linear model

Model selection is needed on two levels in the estimation procedure. First, within pathways to select differentially expressed genes and subsequently which genes are allowed to influence the metabolite expression. Secondly, on the global pathway level to pick out the active pathways.

Algorithm 1.

Model selection within a pathway

Preliminaries: Center and scale the data. Select active genes in pathway k. Regress the metabolites in pathway k on the active genes under regularization. Calculate a score (indicating level of activity) for pathway k.

The procedure for selection within pathways is displayed in Algorithm 1. In step (a) we select active genes in each pathway by comparing the null (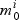, not active) and non-null (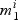, active) gene models. For a given pathway k and gene i:a_ik=1, we have:

(2.4)

(2.5)

A rate-distortion criterion (for details, see Appendix B of the supplementary material available at Biostatistics online) is used to choose the model for each gene. The rate-distortion theory, originally intended for data compression in the information theory field, can be adjusted to work as a model selection criterion in significance testing or cluster analysis on high-dimensional data (Jörnsten, 2009). Briefly, the aim is to do model selection simultaneously for all genes in pathway k by minimizing the overall distortion (the residual sum-of-squares) under the constraint that the total number of parameters used in the models must not exceed a certain bound. In effect this means that we are optimizing the number of parameters we pay for a certain explanatory power. The rate-distortion slope 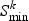(i.e. the bound for the number of parameters) that minimizes the overall Bayesian information criterion (BIC) is selected, and this determines the choice between m₀ and m₁ simultaneously for all genes in pathway k:

(2.6)

In using BIC to select models, we make the assumption that the model errors are Gaussian.

In step (b), we do model selection for the metabolites within pathway k. Active genes (i.e. genes with β_i≠0), as chosen in step (a), are allowed to work as potential predictors for metabolite j. The number of genes may be large (and the number of replicates small), and hence we use regularization with the elasticnet penalty (Zou and Hastie, 2005), with a high level of sparsity, to select predictors.

For each metabolite we have the null model 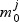and a set of increasingly complex models 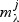indexed by the elastic net penalty parameter (large penalty results in small models); for a given pathway k and metabolite j:a_ikb_jk=1:

(2.7)

(2.8)

Rate-distortion is used to choose between the models 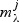, i.e. which λ to use, simultaneously for all metabolites. Instead of minimizing the overall BIC (which is unstable in a p>n context), we maximize the overall predictive likelihood by using cross validation over the different rate-distortion slopes. The slope that minimizes the overall residual sum-of-squares is selected.

In step (c), the overall distortion is calculated by extracting the residual sum-of-squares SS_E, and the total sum-of-squares SS_T in the gene and metabolite models. The coefficient of determination R²=1−(SS_E/SS_T) for both models (giving 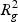and 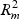) is calculated and a weighted combined 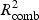for pathway k is

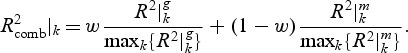(2.9)

The weight parameter 0≤w≤1 defines how much the gene and metabolite model influences the combined R². If w=1, only the gene model influences the choice, and conversely if w=0, only the metabolite model does so. Equal contribution of the two data sources implies w=0.5 as a sensible choice, but we also explore an alternative weighting procedure in Appendix C of the supplementary material available at Biostatistics online. For all the simulations and the real data application presented in this paper, we use w=0.5.

To make the informed pathway decision, i.e. globally select the most active pathways, we could stop the procedure here, after one round, and then select a set of top-ranking pathways based on the R² scores. An alternative would be to run the estimation several rounds in a stepwise procedure, as described in Algorithm 2. In each round (repeat) of the stepwise procedure, one pathway is output as the most active. A set of active pathways can be picked by running several rounds of estimation. When performing repeated rounds of estimation, the data need to be re-processed before entering another iteration. First, the picked pathway k′ is removed from the set of pathways for which to do estimation in subsequent rounds. Secondly, the genes in pathway k′ for which the non-null model was chosen (step (a) in Algorithm 1) are excluded from the data set. Thirdly, the residuals from the metabolite model (step (b) in Algorithm 1) are calculated and used as responses in subsequent rounds.

The stepwise procedure is repeated until we meet a stopping criterion, for example after a fixed number of rounds of estimation, or after the combined R² for any pathway falls under a certain threshold. A discussion on a reasonable cutoff for the R²-statistic is outlined in Section 3.

Algorithm 2.

Global stepwise pathway selection

repeat

for pathway k=1→K do

within model selection procedure

end for

return pathway k′ with highest score.

re-process data

until stop

Either model selection choice, using one or several rounds of estimation, may be preferable in different scenarios, as we can have different goals with the analysis. For example, if we wish to identify a set of tightly regulated cross-talking pathways (with several active genes and metabolites in common), it would be reasonable to rank the pathways by only running one round of estimation, since the chance of selecting overlapping pathways is high in that scenario. However, if we suspect that the active pathways form, for example, a cascade, with little overlap with each other, then running the estimation method for the model several rounds to produce a set of pathways with the highest ranks would be more wise. This highlights the fact that the same enrichment method or model may work better at detecting active pathways with certain regulation scenarios than others. In Section 3.2, we further explore the inner workings of the model selection procedure, and compare it to simpler versions of the same framework.

The estimation procedure was implemented in the open-source software R, and the elastic net paths in the metabolite model calculated via the glmnet algorithm (Friedman and others, 2010). The code for the estimation algorithm can be found in the supplementary material available at Biostatistics online.

3. Simulation studies

3.1. NCI-60 simulation study

A simulation study based on the NCI-60 data of human cancer cell lines was designed to test our model under various scenarios for pathway activity. Details concerning the study can be found in Appendix D of the supplementary material available at Biostatistics online.

Data from four cell lines (divided into two groups) from the NCI-60 set was used to assess the overall performance of the model and to judge the predictive power in the gene expression data on the metabolite expression data. In the case of poor predictive power in the gene expression data, the overall rate-distortion model selection criterion should frequently pick null models, or models with few parameters.

In addition, three simulated datasets were created with the aim to mimic different scenarios of pathway activity; one in which a majority of the genes and metabolites are moderately perturbed between the treatment and control groups (“all active”, or shorter, ss1), one having a small set of genes with a strong signal, and similarly a strong signal on correlated metabolites (“a third active”, or ss2), and one in which we observe differential expression between the groups on half of the genes and metabolites (“half active”, or ss3). Five pathways were spiked in each set.

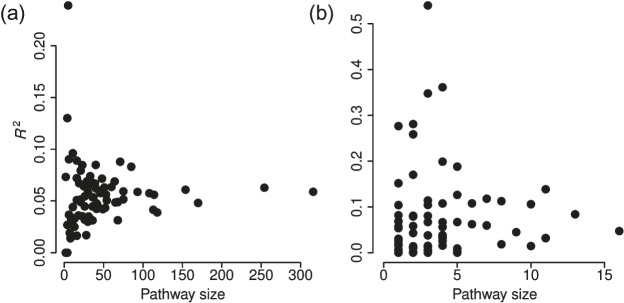
Figure 1 displays results from the linear model used on the original (non-spiked) NCI-60 data. Small pathways are generally scored highly, especially in the metabolite model, since they can be easily explained in R² sense if they contain just one or two metabolites, and we happen to have a strong signal on those metabolites in the data. Non-null models are frequently picked on the metabolite level, which motivates our model formulation of genes having a predictive power of the metabolite levels. We would expect the explanatory values in the gene model to be higher if the observations truly came from two distinct groups (instead of pools of several sample types).

Fig. 1.

Overall R² scores for pathway activation versus pathway size for each of the 80 included pathways estimated using the linear model in the gene (a) and metabolite (b) models on the original NCI-60 data. The limited availability of detailed metabolite data is clearly illustrated, as many of the pathways only contain one or two mapped metabolites. Each dot represents an average of the R²-values from 100 replicated runs.

Similar plots for the simulated datasets for the first round of estimation are depicted in Figures S3–S4 in Appendix E of the supplementary material available at Biostatistics online. The general trend is that the 5 spiked pathways have a high rank in the simulated sets especially on the gene model. For all the other pathways, the increase in precision on the member genes also leads to higher R² values in the metabolite model.

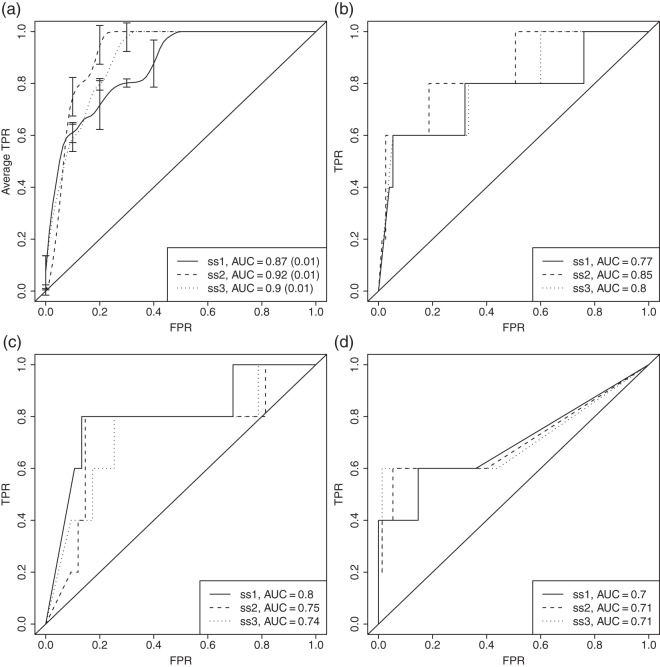
In Figure 2(a) the results from our method are presented for the three simulated datasets after one round of estimation. Our method performs well on all sets, with the all active set a bit worse. One possible explanation is that the rate-distortion criterion is a bit restrictive when it comes to selecting genes if they are only moderately differentially expressed. Results from running the estimation several rounds are illustrated in Figure S5 in Appendix E of the supplementary material available at Biostatistics online.

Fig. 2.

Results in the form of ROC curves on the NCI-60 data for our method (a), together with the scoring from GSEA (b), GSA (c), and correlation analysis (d). The ROC curves for our method were generated from 100 replicated runs on each dataset in order to assess the variability from the cross-validation step. The average true positive rate (TPR) is assessed for each fixed false positive rate (FPR) and an average AUC (and its standard deviation) is calculated for each dataset. The error bars show the standard deviation. For GSEA, GSA, and correlation analysis the ROC curves are based on a ranking from a combined p-value using Stouffer’s method (Stouffer and others, 1949).

An alternative to equal weights (w=0.5) between the gene and metabolite models is to use a weighting scheme that is dependent on the relative number of metabolites and genes in each pathway. For example, for a pathway with a relatively large number of genes and a small number of metabolites, the gene model would have more weight in the overall score, thus avoiding the problem of an inflated R² in the metabolite model. See Appendix C of the supplementary material available at Biostatistics online for a discussion and an example.

In Section 2, we touched briefly upon the question of selecting a reasonable cutoff for the R² statistic. We implemented a permutation test, which takes care of the correlation structure in the data, to investigate this, and evaluated it on the all active set. The results and a more detailed description are given in Appendix F of the supplementary material available at Biostatistics online. For this particular dataset, a reasonable cutoff could be in the range 0.45–0.5, and we also see that the number of pathways with relatively high R²-statistics are quite rare.

Next, we compare the results from the estimation to the gene set enrichment analysis (GSEA) and gene set analysis (GSA) methods, and correlation analysis to integrate transcriptomic and metabolomic data. See Appendix E of the supplementary material available at Biostatistics online for details.

Figures 2(b)–(d) summarize the enrichment results from the competing methods. The receiver operating characteristic (ROC) curves are based on ranking the pathways using a combined p-value. ROC plots for the rankings among genes and metabolites separately can be found in Figure S6 in Appendix E of the supplementary material available at Biostatistics online.

The simulated datasets were spiked to increase the differences in the gene and metabolite models between the groups. If this difference is present among many of the genes/metabolites within one pathway, GSEA and GSA should perform well. However, as the maxmean score in GSA is designed to pick up one-tailed expression changes well (perturbations mainly in one direction), we can expect it to perform a bit worse under such circumstances.

Both GSA and GSEA have problems detecting the all active set on the metabolite level, most likely due to the moderate signal in this set. Since the genes are scored well on this set for GSA, the overall area under the curve (AUC) is better than that for GSEA. The maxmean statistic is designed to avoid situations where few strong signals could dominate the score, which may be the reason that it performs a bit worse than GSEA on the a third active set.

For the correlation analysis, we would expect the method to pick up at least some of the signal in the gene dataset since genes with a differential expression between the treatment and control groups were chosen in the first step and hence are present in the clustered groups. However, we see that correlation analysis generally performs slightly worse than GSEA and GSA, and this is due to the lower scoring in of the enrichment among genes mainly. Some spiked genes within the sets were most likely excluded from the clusters, affecting the overall enrichment. Also, the fact that the gene–metabolite connections may be induced by between-pathway correlations, instead of correlations within pathways, may raise concerns.

In summary, gene set enrichment techniques work well to detect differentially expression within one data type, but as single source methods, they are inadequate to address the integrated enrichment problem at hand. Although correlation analysis is an attempt to integrate the two data types, the simulations show that that our model generally performs better at identifying active pathways. The fact that some spiked pathways are poorly detected by competing methods show that the signal in the spiked sets is not overly enhanced, and that our simulated scenarios function as proofs of concept for our modeling approach.

3.2. Variations of the pathway model

The second simulation study was designed to investigate the inner workings of our method and compare it to simpler versions of the same framework. 30 pathways, with each 20 genes and 3 metabolites were simulated, among which the first 5 pathways were active, i.e. perturbed between the control and treatment groups. Small overlaps were induced between the active pathways and a set of 10 other pathways for a realistic (biological) setting.

The genes in pathway 1–5 were simulated so as to mimic scenarios in which a few genes were active with a strong signal, to many genes differentially expressed, but with lower intensity. The metabolites levels were simulated from the genes within the same pathway (as well as from one spurious non-active gene from a another pathway). Ten datasets were simulated in total under this scenario. More details on the study are presented in Appendix G of the supplementary material available at Biostatistics online.

The pathway model is designed to detect enrichment in pathways, with the level of activity in a detected pathway depending on the differential expression of the genes, and how well these genes explain the metabolite expressions within the same pathway. The differential expression on the metabolite level is implicitly modeled by only allowing genes that have a differential expression to influence the metabolite expression. The metabolites can show both high differential expression, or rather small levels of differential expression, as long as we can find genes that relevantly influence their expression.

Our estimation method was run for all 10 sets of data with 10 repeats each to assess the cross-validation variability. We compared the output to the results from four simpler versions of the methodology. In these simpler versions, genes are ranked using the moderated t-statistic, and we select (i) genes with p-value <0.1, (ii) genes with p-value <0.05, (iii) genes with p-value <0.001, or (iv) all genes as differential. The differential genes are allowed to influence the metabolites within the same pathway. The metabolite models are chosen via the elasticnet penalty with cross-validation on each individual metabolite (but not using rate-distortion).

The data from the 10 simulated sets are presented in Figure 3 by a mean ROC curve where each underlying R² value has been averaged over 10 repeated runs. By choosing a conservative cutoff (0.001) in the simple framework, too few differential genes are selected, and the average performance suffers. On the other hand, by not filtering the genes, the non-active pathways also receive high scores, with the result that some of these pathways are picked before the active ones. Consequently, the average AUC for the non-filtered version is also lower.

Fig. 3.

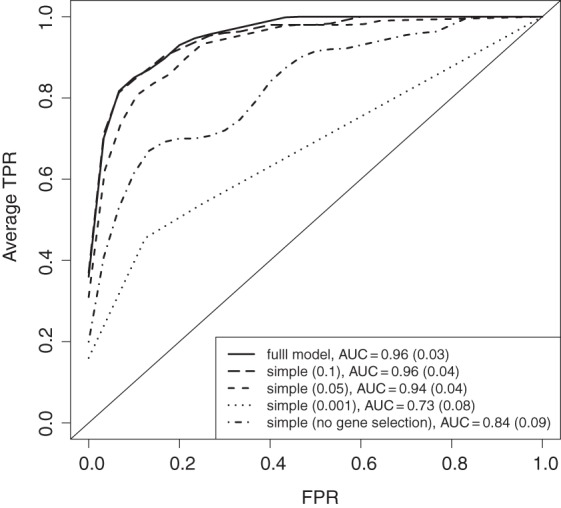
Results from the simulation study investigating different versions of the pathway model framework. The simple version is based on ranking with the moderated t-statistic (cutoffs used are 0.1, 0.05, 0.001, and 1) for genes and selection using elasticnet for metabolites (no rate-distortion). The different ROC curves are the average from 10 simulated data sets. In each simulated set, 10 repeats of the estimation were run to assess the cross-validation variability. Error bars have been excluded for easier visualization. The average AUC is given with associated standard deviation.

In comparing the simple (0.1) version to the full framework, the simple version is slightly more generous on the selection of genes (data not shown). For pathways 1–3 and the non-active pathways, this means that non-differential genes are picked, but on the other hand for pathways 4–5, this is beneficial since all genes have some differential signal. We argue that a suitable cutoff for the simple framework is dependent on, for example, sample size and signal strength, and should vary between different studies. In comparing the results for the simple framework when using p-value 0.05 and 0.1, we can conclude that the simple framework is subject to some sensitivity concerning the cutoff. The global rate-distortion that we use to select differential genes in the full framework is a robust alternative to the p-value cutoff.

3.3. Evaluation of the mixed model

Since the mixed model is more complex compared with the linear model and demands the estimation of random effects, using the NCI-60 simulation data is hard due to the relatively small sample size. Instead, a simulation study was used to compare the two models (see Appendix H of the supplementary material available at Biostatistics online).

All pathways have a fixed size (20 genes and 3 metabolites) and no overlap with each other for a controlled setting. A few of the genes in pathway 1 are active, but with a strong signal. For pathway 2, half of the genes are active with a moderate signal, while in pathway 3, all genes have a low intensity signal (which can be troublesome for the linear model). The metabolites in each pathway were simulated from selected genes within the same pathway (as well as one spurious active non-pathway gene). The explanatory power of each metabolite from the genes within the pathway was designed to be approximately the same. The remaining three pathways were simulated to function as negative controls.

In Table 1, the results for the linear and mixed model formulations are compared for the metabolite model. The linear model picks up the signal well for the two first pathways, but as expected, the third pathway is troublesome. Only 12 of the 20 active genes are picked up in the gene model, and since some of the metabolites in the pathway were simulated from the non-picked genes, the explanatory power is lower. On the other hand, the mixed model has a tendency to overfit the data by selecting too many random variables.

Table 1.

Explanatory power (R²) for the metabolite model in the simulation study for the mixed and linear models. The first 3 pathways contain differential signal, which in pathway 3 is of low intensity. Pathways 4–6 function as negative controls. The data used is simulated in its entirety and not based on the NCI-60 set.

Pathway	Mixed model	Linear model
1	0.879	0.776
2	0.883	0.828
3	0.875	0.430
4	0.158	5.67×10−5
5	0.183	2.2×10−3
6	0.114	1.21×10−4

4. Real data application

The methodology presented in this paper was also applied to a dataset on Arabidopsis containing transcriptional and metabolic profiles for seeds or seedlings harvested from imbibition to 8 days old (Allen and others, 2010). The methodology for analysis in Allen and others (2010) was to look at differential expression in the transcriptional and metabolic profiles separately, as well as doing correlation analysis between the two data types.

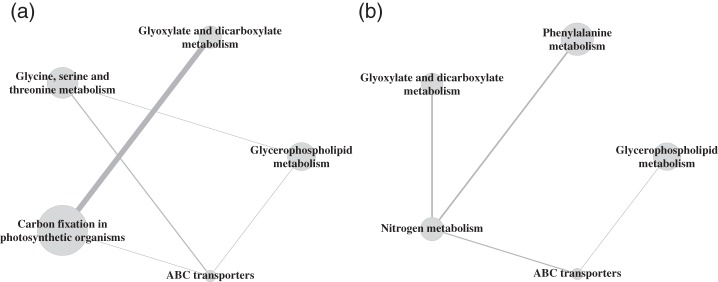
We take a slightly different approach in the analysis (see Appendix I of the supplementary material available at Biostatistics online) and compare early (days 1–4) versus late (days 5–8) samples to find pathways that are up- or down-regulated in early or late stages of development (but not both). Figure 4 presents both the results when running the method several consecutive runs and using rankings after one round. It is clear that pathways that do not overlap are selected to a larger extent if we run the stepwise procedure, compared with using one round of estimation.

Fig. 4.

Active pathways identified when comparing early versus late samples in the seedling germination data from Arabidopsis (visualization as in Merico and others, 2010). The top 5 identified pathways from (a) just using the first round of estimation, and (b) using five consecutive rounds in which one pathway is picked in each round. The node sizes are scaled to reflect the total pathway size, including both genes and metabolites. The edges connecting the nodes have been scaled to represent the overlap between the pathways. Interesting biological pathways like ABC transporters and Glycerophospholipid metabolism are identified.

However, three of the pathways appear among the top five ranked pathways in both selection methods, and these are Glycerophospholipid metabolism, Glyoxylate and dicarboxylate metabolism, and ABC transporters. In the original paper, clusters of metabolites were identified with similar trends over the different time points. Interestingly, four metabolites, namely valine, isoleucine, leucine, and choline, belong to a cluster that shows a peak in concentration early in the development (days 2–3), and then declines, and these metabolites are mapped to the ABC transporters pathway. In Footitt and others (2002), it is reported that the transition of a seed into germination is regulated by a locus called CTS which encodes a protein of the ABC transporter class. Moreover, CTS affects the metabolism of stored lipids, and that may be a reason we also see the Glycerophospholipid metabolism to be regulated. Previous reports also show that glyoxylate metabolism is involved in the germination process (Brownleader and others, 1997). Based on this example our method seems to perform well in picking up key regulated pathways.

5. Discussion

The model we propose in this paper aims to identify perturbed pathways (sets of reactions involving genes, metabolites, and proteins) when comparing two different experimental conditions. We integrate two different omics data types, while also integrating the pathway-level decision in the modeling procedure.

We chose to do model selection using a rate-distortion criterion, which works well in a situation in which a small set of features, for example genes, show a strong signal. If a larger set of features instead exhibits moderate to low signals, the rate-distortion criterion tends to select a subset of the features, but generally not all of them. As the simulation study comparing the mixed and linear models shows, there are some scenarios where the mixed model outperforms the linear one. The drawback of the mixed model is its’ tendency to overfit the data, and with small samples sizes it is hard to fit. In a situation with only small to moderate sample sizes, the linear model performs satisfactory in most scenarios.

The rate-distortion criterion functions as a robust model selection criterion for choosing active genes and metabolites, as the simulation study on variations of the pathway model shows, when we compare it to ranking genes using the moderated t-statistic and selecting them based on a p-value cutoff.

The elasticnet penalty is used for model selection in the metabolite model, since it works better in a p>n setting than for example the lasso (Zou and Hastie, 2005). The elasticnet penalty was set to a fixed value so as to largely mimic the behavior of the lasso, but still allow for highly correlated genes to function as predictors together. Undesirable lasso effects like model saturation and the restriction of the maximum number of included predictors can thus be circumvented. However, using BIC for selection of the penalty parameter in p>n situations is unstable and we fit using cross-validation techniques within the metabolite model instead. The cross-validation introduces some inherent variability in the model, but this mainly results in overlapping pathways “swapping” places with each other in the rankings.

To make a global pathway-level decision, we can either run the stepwise procedure or rank pathways by the R²-criterion after one round. If there are correlated active overlapping pathways present, the stepwise procedure tends to choose one of the pathways, and leaves the others outside the active set. By comparing the results after several rounds of estimation with the results after one round, it is possible to detect this.

The approach used in the NCI-60 simulations with spiked subsets of pathway genes and metabolites was motivated by our desire to generate a more controlled setting with known signals in the data (although the original data may of course be informative to differentiate between cancer types). To enhance existing signals in a real dataset also has the benefit of preserving correlations between genes and metabolites. The combined analysis in our method demonstrates the strength of using an integrated approach when there are different data sources available for analysis. The proposed method is also good at picking up small active pathways due to the R² criterion. However, pathways that are active only on the metabolite level will not be detected by this methodology.

The metabolite data in the NCI-60 set contain characterization of a relatively large set of metabolites, although many of the features, i.e. peaks in the spectra, could not be identified uniquely. Unfortunately it is often the case that missingness in the data is present. The missing metabolite concentration values can be imputed from the other replicates within treatment groups, which also has been done in the NCI-60. As an alternative to imputation our model and estimation procedure can handle moderate levels of data missingness, as long as there are a sufficient number of data points left to do estimation for each gene and metabolite (with larger variance in prediction as a result). Incompleteness in the pathway information also induces some problems in the modeling. In effect, we reduce the sizes of the pathways to match the detectable gene and metabolite sets, but this is the standard procedure in enrichment analysis.

A potential application of the current model is to extend it to jointly analyze transcription factor binding site data coupled with gene expression or microRNA expression, for which a similar biological ordering is inherent. Another possibility is to generalize the model to handle several treatment groups and include more data sources, for example adding copy number variation data to the current setting. Extending the model to handle more than two treatment groups can be done in several ways, for example re-parametrizing to penalize contrasts of regression coefficients.

Supplementary material

Supplementary material is available at http://biostatistics.oxfordjournals.org.

Funding

This work was supported by the National Institutes of Health (1 RC1 CA145444-01 to G.M.) and the Swedish Research Council (Vetenskapsrådet) (90583001 to R.J.).