Robust inference in discrete hazard models for randomized clinical trials

Abstract

Time-to-event data in which failures are only assessed at discrete time points are common in many clinical trials. Examples include oncology studies where events are observed through periodic screenings such as radiographic scans. When the survival endpoint is acknowledged to be discrete, common methods for the analysis of observed failure times include the discrete hazard models (e.g., the discrete-time proportional hazards and the continuation ratio model) and the proportional odds model. In this manuscript, we consider estimation of a marginal treatment effect in discrete hazard models where the constant treatment effect assumption is violated. We demonstrate that the estimator resulting from these discrete hazard models is consistent for a parameter that depends on the underlying censoring distribution. An estimator that removes the dependence on the censoring mechanism is proposed and its asymptotic distribution is derived. Basing inference on the proposed estimator allows for statistical inference that is scientifically meaningful and reproducible. Simulation is used to assess the performance of the presented methodology in finite samples.

1 Introduction

It is often the case in survival studies that the event of interest is not observed the instant it occurs due to a lack of obvious signals indicating event occurrence. In such settings, the realization of the event is usually only detectable by a complicated and costly screening test. For example, cancer diagnosis or disease progression are often not visibly identifiable and can only be detected through a screening procedure such as a CT scan, mammography, colonoscopy, or blood test. Repeated screenings at fine time intervals (e.g., daily) to determine the “exact” event time are impractical due to limited resources and the adverse impact on quality of life for the patients. When it is of interest to monitor such events, a more practical approach would be to screen for the event of interest at coarsened time intervals (e.g., monthly, quarterly or annually).

As a motivating example, consider the development of the drug Atrasentan in hormone-refractory prostate cancer (HRPC). A more detailed description of the drug’s development can be found in the Atrasentan briefing document presented to the Oncologic Drugs Advisory Committee (ODAC) of the United States Food and Drugs Administration (FDA) (Abbott Laboratories 2005). Briefly, the study sponsor carried out a phase 2 multi-arm clinical trial comparing a 10 mg dose and 2.5 mg dose regime to placebo using time to disease progression as the primary outcome, where disease progression was determined by either radiographic measures (performed at the investigator’s discretion and interpreted locally) or clinical measures (adjudicated by the investigator). Radiographic scans were not scheduled at regular intervals but were required at baseline and at the time of clinical progression. Because of this, the observed event times in the phase 2 study were scattered in a continuous fashion. Based on the promising results of the 10 mg dose regime in the phase 2 study, the study sponsor planned for a pivotal multi-center phase 3 trial comparing the 10 mg dose to placebo with the goal of establishing efficacy. However, for the phase 3 study the FDA insisted on a 12-week schedule for bone scans to determine disease progression. Regulators felt that regularly scheduled scans would provide a more precise definition and a more objective measure for the time to disease progression. As such, disease progression in the phase 3 trial would only be observed at weeks 12, 24, 36, etc. Of course, this protocol would result in each patient’s true event time being interval censored (disease progression occurs between visits) and the resulting observed event time (visit time where disease progression was determined) would be discrete. Scientific focus is placed on the observed event time and a proportional hazards (PH) model (Cox 1972) can be used for inference.

Since event times are grouped, ties are sure to occur and the approximate partial likelihood methods of Breslow (1974) or Efron (1977) are often employed to overcome the computational complexity that arises from maximizing the exact partial likelihood. However, when ties occur very frequently, e.g., when time between visits are wide relative to the distribution of event times, Kalbfleisch and Lawless (1991) noted that analysis should be based on discrete-time methods as opposed to the continuous-time proportional hazards model. Moreover, Farewell and Prentice (1980) described the inadequacy of approximate partial likelihood methods in the case-control setting when ties are frequent.

Common methods for the analysis of discrete failure times include the discrete-time proportional hazards model (Prentice and Gloeckler 1978), the continuation ratio model (Berridge and Whitehead 1991) and the proportional odds model (Bennett 1983). The former two models focus on the discrete hazard and hence, can incorporate right-censored observations whereas the proportional odds model focuses on the cumulative probability of failure and cannot readily account for right censoring. These discrete survival models are widely used in the social sciences (Singer and Willett 1993) and are becoming more common in the clinical trial setting.

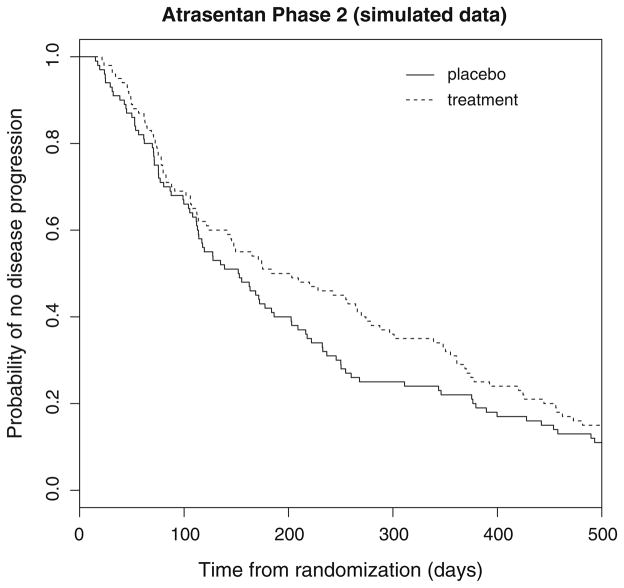
In the context of planning for the phase 3 Atrasentan trial, it would be natural to consider the discrete-time proportional hazards or continuation ratio model for quantifying the effect of treatment on time to disease progression. However, data from the phase 2 study indicated that the effect of Atrasentan may be delayed. For illustration, Fig. 1 depicts simulated survival curves comparing the 10 mg dose regime to placebo. The estimates in Fig. 1 are analogous to those observed in the actual phase 2 study as seen in Abbott Laboratories (2005). This delay in the separation of the survival curves could be attributed to a minimum time required for the treatment to show an effect in all patients or because there may have existed a subset of the sickest patients for which the occurrence of progression was inevitable regardless of treatment assignment. In either case, the phase 2 results indicate that data from a forthcoming phase 3 study may violate the proportional hazards and/or odds assumption.

Fig. 1.

Replicated progression-free survival curves for the Atrasentan phase 2 trial based on simulated data

It has long been known in the time-to-event literature that consistency of regression coefficients of survival models is dependent upon the observed censoring distribution and the maximum follow-up time when model assumptions fail to hold; Struthers and Kalbfleisch (1986) demonstrated this for the continuous-time proportional hazards model. In the absence of censoring and where there exists a time-varying treatment effect, the hazard ratio from a Cox model represents a weighted average of hazard ratios or a marginal hazard ratio over the support of the observable times. However, in the presence of right censoring the estimand is influenced by the observed censoring pattern of the current study. This leads to an estimand that varies with the observed censoring distribution. Consequently, it may be difficult to replicate results with another study as it is nearly impossible to replicate the censoring distribution. This is true because, besides drop-outs, censoring is a function of the accrual pattern and study length, which themselves are by-products of logistical constraints and are usually outside the investigator’s control. The estimand is only constant, and hence reproducible, if the censoring distribution is held constant. Noting this, a natural target estimand is the marginal hazard ratio over a fixed maximal time in the absence of intermittent censoring. That is, the estimand of the maximum likelihood estimator under no censoring.

The impact of this dependence on the observed censoring distribution is apparent in multi-center studies where accrual patterns, and hence censoring patterns, often differ by region. Thus, results from stratified estimation (by region) are not comparable when the time-invariant treatment effect assumption does not hold. This becomes particularly problematic when a sizable difference in the estimates is observed, as it may mislead investigators to conclude the presence of effect modification by region or center simply because accrual patterns have differed by these strata.

Similar issues can arise in comparative effectiveness research and meta-analyses of clinical trial results, where point estimates from different studies are compared or combined with one another. Because estimates are not scaled according to a reference censoring distribution, in the presence of a nonproportional hazards covariate effect the estimands may vary from study to study. The issue is exemplified in active control trials as described in Section E.10 of the International Conference on Harmonization (ICH 2000). In this case, we may have one trial demonstrating that treatment A is efficacious relative to placebo, and is approved for use in the population. Then in a separate trial, treatment B is compared to treatment A (the active control). Since the consistency of the estimators is determined by observed censoring distribution in each trial, transitivity in the comparison of the hazard ratios does not necessarily follow (Gillen and Emerson 2007). Thus, the relative effect of treatment B compared to placebo may not translate from the previous two trials. Solutions to the censoring problem associated with the continuous-time proportional hazards model have been proposed by Xu and O’Quigley (2000) for covariate-independent censoring and Boyd et al. (2012) for covariate-dependent censoring in the two-sample problem but have not seen widespread adoption.

In this manuscript, we take the planning of the phase 3 Atrasentan trial as motivation to study the implications of model misspecification for discrete hazards models in the randomized clinical trial setting. In Sect. 2, we show that the resulting estimators from commonly used discrete survival models are consistent for a parameter that depends on the underlying censoring distribution and the maximal follow-up time when the models are misspecified. Building on the work of Xu and O’Quigley (2000) and Boyd et al. (2012) for the continuous-time proportional hazards model, we propose a general estimator based on a weighted score equation that is robust to the underlying censoring distribution when the form of the hazard function is misspecified and derive its asymptotic distribution. In Sect. 3, we compare the proposed estimator to the usual estimator under various scenarios using simulation. In Sect. 4, we discuss the relevance of the proposed work to the design and analysis of clinical trials with discrete time-to-event outcomes and present avenues for future work.

2 Robust estimation and inference

2.1 Discrete hazards models

Let Λ₀ denote the baseline cumulative hazard function with masses λ₀₁, λ₀₂, …, λ_0J at times t₁, t₂, …, t_J for a random variable T > 0 such that

$${\mathrm{\Lambda }}_0(t)=\sum _{j=1}^J{{\lambda }_0}_{j}I(t_j\le t),$$

where I (A) is one if A is true and zero otherwise. Thus, the baseline hazard is dΛ₀(t_j) = λ₀(t_j) = λ_0j for j = 1, …, J. The number of mass points J is assumed to be fixed and finite since one can only observe up to a finite time in any data analysis.

Similar to the continuous case, we observe for subject i the response

$$\{T_i^{\mathit{obs}}=min(T_i,C_i),{\delta }_i=I(T_i\le C_i)\},$$

where δ_i = 1 indicates that the failure time was observed and C_i > 0 is the censoring time under random censorship. We further assume C_i is conditionally independent of T_i given bounded and predictable covariate vector R_i of length p that may or may not be time-dependent. The observed response for subject i can be transformed to the at-risk vector Y_i = (Y_i1, …, Y_iJ)^T and failure time vector X_i = (X_i1, …, X_iJ)^T, where Y_ij equals 1 if the i th subject was at risk just prior to time t_j and zero otherwise, and X_ij equals one if the i th subject failed at time t_j and zero otherwise. We focus on non-recurrent events so that at most one element of X_i will be 1. A subject that is right-censored in the interval [t_j, t_j+1) will have ones up to the jth element of Y and zeroes afterward, and zeroes for all of X. See Table 1 for an example of a subject’s possible response. The observed data for a sample of size n can hence be re-written as {(X_i, Y_i, R_i) : i = 1, …, n}.

Table 1.

Discrete survival data

Time	t1	t2	t3	t4	t5
Y1	1	1	1	0	0
X1	0	0	1	0	0
Y2	1	1	1	1	1
X2	0	0	0	0	0

Example of how a subject’s observed data might look like. Here, there are 5 discrete time points where a subject may fail. Subject 1 was at risk in for the first three time points and failed at time t₃. Subject 2 was censored and did not fail in these time points. In addition to these response data, each subject may have covariate data

An analog to the continuous-time proportional hazards model is obtained with the relationship

$$h[d\mathrm{\Lambda }(t_j\mid R)]={\alpha }_j+R{(t_j)}^T\beta ,$$ (1)

where dΛ(t | R) is the discrete hazard at time t given covariate vector R(t), α_j = h[dΛ₀(t_j)], and h is a monotone-increasing and twice-differentiable link function mapping [0, 1] into [−∞, ∞] such that h(0) = −∞. Common choices for h include the complementary-log-log link, h(x) = log[− log(1 − x)], which corresponds to the discrete-time proportional hazards model (Prentice and Gloeckler 1978), and the logit link, h(x) = log[x/(1 + x)], which corresponds to the continuation ratio model (Berridge and Whitehead 1991). Prentice and Gloeckler (1978) showed that grouped survival times in the Cox proportional hazards setting is equivalent to the complementary-log-log case. We refer to models satisfying Eq. 1 as discrete hazard models; see Kalbfleisch and Prentice (2002) for a further overview of these models.

For a 2-sample randomized clinical trial R is the treatment indicator and β captures the treatment effect. In the K groups setting, R = (R₁, …, R_{K −1})^T indicates group memberships and the kth element of β corresponds to the treatment effect of group k relative to the referent group. While the methods to be proposed are trivially extended to the K -sample setting, for ease of exposition we focus on the most common scenario of a 2-sample comparison for the remainder of the manuscript. As such, R will represent an indicator of treatment group membership. The parameter exp (β) is interpreted as a hazard ratio or a hazard-odds ratio for the discrete-time proportional hazards model and the continuation ratio model, respectively. For any data analysis, the choice of h should be guided by the scientific interest of the investigator, such as a covariate effect on the hazard ratio or a covariate effect on the hazard-odds ratio.

Equation 1 is often equivalently expressed as

$$h[d\mathrm{\Lambda }(t_j\mid R)]=Z{(t_j)}^T\theta ,$$

where Z(t_j) = [e_j, R(t_j)]^T, e_j = (0, …, 0, 1, 0, …, 0)^T is an indicator vector of length J consisting of all zeroes except for the jth element which equals 1, θ = (α, β)^T is of length J + p, and α = (α₁, …, α_J)^T. We adopt these notations to assist in the theoretical developments for the remainder of the manuscript.

The aforementioned class of models can be fit by maximizing

$$L(\theta )=\prod _{i=1}^n\prod _{j=1}^J{\left\{d\mathrm{\Lambda }{(t_j\mid R_i)}^{X_{ij}}{[1-d\mathrm{\Lambda }(t_j\mid R_i)]}^{Y_{ij}-X_{ij}}\right\}}^{Y_{ij}},$$

or equivalently, by obtaining the root θ̂ of the score function,

$$U(\theta )=\sum _{i=1}^n\sum _{j=1}^J\left\{\frac{Y_{ij}{Z}_i(t_j)[X_{ij}-Y_{ij}d\mathrm{\Lambda }(t_j\mid R_i)]}{[1-d\mathrm{\Lambda }(t_j\mid R_i)]d\mathrm{\Lambda }(t_j\mid R_i)h^{\prime }(d\mathrm{\Lambda }(t_j\mid R_i))}\right\}\equiv 0,$$

where L and U are functions of θ through dΛ. The reader should recognize that the likelihood looks very similar to that of Bernoulli data, with X_ij an indicator of success and dΛ (t_j | R_i) the probability of success. Because of this, discrete survival models can be fit using existing generalized linear models (GLM) software where only terms in the score equation with Y_ij = 1 contribute to the likelihood.

A counting process and martingale representation of the score equation aids in the development of large sample properties of the score and the maximum likelihood estimator (MLE) of θ when the model is correctly specified. Thus it is useful to note that the previous score equation can be re-written as a sum of stochastic integrals,

$$U(\theta )=\sum _{i=1}^n\underset{0}{\overset{t_J}{\int }}\left\{\frac{Y_i(u)Z_i(u)}{[1-d\mathrm{\Lambda }(u\mid R_i)]d\mathrm{\Lambda }(u\mid R_i)h^{\prime }(d\mathrm{\Lambda }(u\mid R_i))}\right\}{dM}_i(u),$$

where N_i (t_j) = I (T_i ≤ t_j, δ_i = 1), Y_i (t_j) = I (T_i ≥ t_j, C_i ≥ t_j), and $M_i(t_j)=N_i(t_j)-{\int }_0^{t_j}{Y}_i(t)d\mathrm{\Lambda }(t\mid R_i)$ is a discrete-time martingale with d N_i (t_j) = X_ij.

2.2 Impact of model misspecification

For mathematical convenience and ease of exposition, we assume the logit link for the remainder of the manuscript; the results follow in parallel for other link functions such as the complementary-log-log. In this case, the score function for the continuation ratio model reduces to

$$U(\theta )=\sum _{i=1}^n\underset{0}{\overset{t_J}{\int }}{Y}_i(u)Z_i(u)[{dN}_i(u)-Y_i(u)d\mathrm{\Lambda }(u\mid R_i)].$$ (2)

Theorem 1

Suppose the continuation ratio model is misspecified. That is, suppose dΛ(t | R) is the true hazard function for failure time random variable T | R. Then θ̂, the estimator obtained by solving the root of the score equation based upon the assumed hazard function dΛ(t | R), is consistent for ${\theta }_{t_J,S_C}^{\ast }$, such that ${\theta }_{t_J,S_C}^{\ast }$ solves

$$g({\theta }_{t_J,S_C}^{\ast })=\underset{0}{\overset{t_J}{\int }}{E}_R[Z(u)S_C(u\mid R)S_T(u\mid R)\{d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)-d\mathrm{\Lambda }(u\mid R)\}]du=0$$ (3)

where the expectation is taken with respect to the distribution of R, where the integral is with respect to the counting measure for u = t₁, …, t_J, and where S_T, S_C, and dΛ̃ refer to the true survival function of the failure time, the true survival function of the censoring time, and the true population hazard function, respectively.

The proof is presented in the manuscript’s appendix.

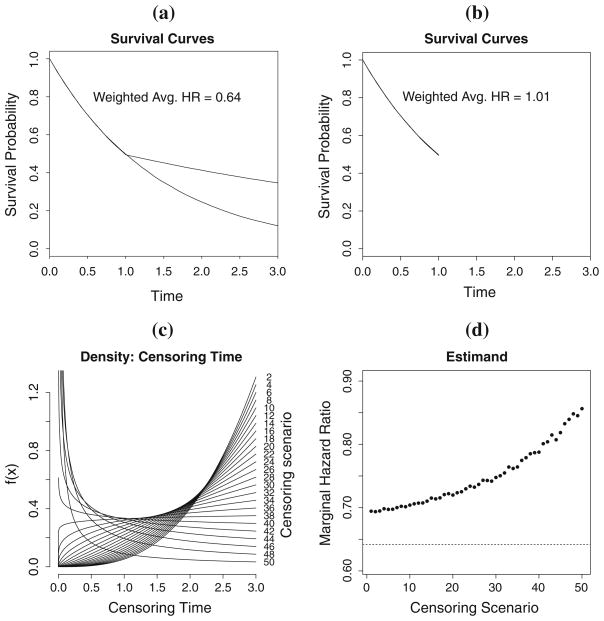
As a result of Theorem 1, θ̂ = (α̂, β̂)^T will be consistent for a parameter ${\theta }_{t_J,S_C}^{\ast }=({\alpha }^{\ast },{\beta }_{t_J,S_C}^{\ast })$ that depends on the underlying censoring distribution through the presence of S_C and the support of observable times, [0, t_J]. To illustrate this dependence, consider the four plots in Fig. 2. Figure 2(a) shows the survival curves of two groups exhibiting nonproportional hazards, namely, a case of late-diverging hazards, over the support [0,3] under no intermittent censoring; it corresponds to a marginal hazard ratio of 0.64. Figure 2(b) shows the same two curves over the support [0,1]; it corresponds to a marginal hazard ratio of 1.0 (the study ended prior to the diverging hazards could be observed). The estimands are thus different depending on the support of observable times.

Fig. 2.

Illustration of the censoring-dependence and maximum observable time. a shows the survival curves for two groups exhibiting nonproportional hazards over the support [0,3]. b shows the survival curves for the same two groups over the support over [0,1]. c shows varying densities for the censoring times that correspond to different estimands in d

Figure 2(c) shows different probability densities for the censoring time, and Fig. 2(d) shows the estimand for the maximum likelihood estimator corresponding to each censoring distribution. It is important to note that the estimated survival curves (not shown) for the failure time of interest under each censoring scenario are identical to that of Fig. 2(a). However, the estimand changes as a function of the censoring distribution. Thus, the presence of censoring could lead to non-reproducible results when studies are replicated as the censoring distribution is often different from study to study. A more rigorous derivation of the dependence on S_C in misspecified discrete hazard models is elaborated in Sect. 2.4.

This manuscript only addresses the dependence on the censoring distribution and not on the maximum follow-up time. We note that the choice of t_J should be guided by the scientific question of interest. For example, short-term survival may be sufficient if the patient population consists primarily of octogenarians. In contrast, long-term survival is often of interest when the patient population consists of infants.

2.3 Censoring-robust inference

To remove dependence on the censoring distribution, we propose an estimator θ̂_CR that solves the weighted score equation,

$$U_W(\theta )=\sum _{i=1}^n\underset{0}{\overset{t_J}{\int }}\widehat{W}(u\mid R_i)Y_i(u)Z_i(u)[{dN}_i(u)-Y_i(u)d\mathrm{\Lambda }(u\mid R_i)]$$

where Ŵ(u | R_i ) = 1/Ŝ_C (u | R_i) and Ŝ_C (· | R_i) refers to the left-continuous Kaplan–Meier estimator of the survival function of the censoring time obtained from group R_i (0 for control, 1 for treatment). Since covariate-independent censoring (i.e., S_C (t | R) = S_C (t)) is not assumed, the censoring distribution for each group is estimated separately as in Boyd et al. (2012). We note that our approach to weighting the score by the inverse of the probability of not-yet-censored is similar to Robins and Rotnitzky (1992), however, our goal is different from theirs. Specifically, their goal is to obtain a meaningful consistent estimator in the presence of informative censoring whereas we wish to obtain a meaningful consistent estimator when the hazard is misspecified in the presence of independent censoring. Put another way, Robins and Rotnitzky (1992) seeks to address the impact of data not missing at random while we wish to address model misspecification from an estimation perspective.

Theorem 2

Under mild regularity conditions, θ̂_CR is a consistent estimator for ${\theta }_{t_J}^{\ast }$ such that

$$g_W({\theta }_{t_J}^{\ast })=\underset{0}{\overset{t_J}{\int }}{E}_R[Z(u)S_T(u\mid R)\{d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)-d\mathrm{\Lambda }(u\mid R)\}]du=0.$$ (4)

Moreover,

$$\sqrt{n}({\widehat{\theta }}_{CR}-{\theta }_{t_J}^{\ast })$$

converges to a zero-mean Gaussian distribution with variance that can be consistently estimated by Â⁻¹ B̂Â⁻¹, where for the continuation ratio model (logit link),

$$\widehat{A}=-\frac{1}{n}\sum _{i=1}^n\underset{0}{\overset{t_J}{\int }}\widehat{W}(u\mid R_i)Y_i(u)Z_i(u)Z_i{(u)}^T\{d\mathrm{\Lambda }(u\mid R_i)[1-d\mathrm{\Lambda }(u\mid R_i)]\},$$

and

$$\widehat{B}=\frac{1}{n}\sum _{i=1}^n{\left[\underset{0}{\overset{t_J}{\int }}\widehat{W}(u\mid R_i)Y_i(u)Z_i(u){dM}_i(u)\right]}^{\otimes 2},$$

with θ̂_CR plugged in the dΛ’s and for a vector a, a^⊗2 = aa^T.

The proof is presented in the Appendix.

Note that the proposed estimator is consistent for a quantity that is independent of the censoring distribution as S_C does not appear in Eq. 4. Thus, we call θ̂_CR = (α̂_CR, β̂_CR ) the censoring-robust estimator. Also note that the estimand is the same as that of the usual estimator’s when no intermittent censoring is present since in the absence of censoring, S_C (t|Z) = 1 for all t, making (3) match (4).

When the model is correctly specified, ${\beta }_{t_J}^{\ast }$ from Eq. 4 equals β from Eq. 1 since in this case U_W is an unbiased estimating equation for β regardless of what weights are used. This is analogous to weighted least squares for linear regression when addressing heteroscedasticity or the choice of covariance structure for efficient estimation in generalized estimating (Liang and Zeger 1986).

2.4 Interpretations

In the two-sample setting, a failure of the constant treatment assumption implies that the true data generating mechanism can be expressed as a time-varying treatment effect,

$$h[d\stackrel{\sim }{\mathrm{\Lambda }}(t\mid R)]=Z{(t)}^T\theta (t),$$ (5)

where the regression coefficients

$$\theta (t)={[\alpha ,\beta (t)]}^T,$$

can vary with time. That is, the treatment effect on the hazard is not constant with time. In our discrete-time setting, we can express this relationship with J × 2 parameters. This is achieved by including the baseline hazard components and the interaction of treatment with the J possible time points, yielding J treatment effects, one for each time point. It is similarly true for the K -sample case. This parameterization is true even if the link function was misspecified as there is a one-to-one correspondence between the J × 2 parameters of any link function to the J × 2 parameters of any other link function.

Let us compare the interpretations of ${\beta }_{S_C,t_J}^{\ast }$, the estimand of the usual/naive estimator, and ${\beta }_{t_J}^{\ast }$, the estimand of the censoring-robust estimator, given in the previous section. Using a first order Taylor approximation of dΛ (t | R) about β(t) for the argument ${\beta }_{S_C,t_J}^{\ast }$, we obtain from Eq. 3,

$$\begin{array}{l}0\approx \underset{0}{\overset{t_J}{\int }}{E}_R\left[{RS}_C(u\mid R)S_T(u\mid R)\{d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)-d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)-[{\beta }_{S_C,t_J}^{\ast }-\beta (u)][(\partial /\partial \beta )d\mathrm{\Lambda }(u{\mid R)\mid }_{\beta =\beta (u)}]\}\right]du\\ =\underset{0}{\overset{t_J}{\int }}{E}_R[{RS}_C(u\mid R)S_T(u\mid R)\{-[{\beta }_{S_C,t_J}^{\ast }-\beta (u)][(\partial /\partial \beta )d\mathrm{\Lambda }(u{\mid R)\mid }_{\beta =\beta (u)}]\}]du.\end{array}$$ (6)

When h is the logit link, we have

$${\frac{\partial }{\partial \beta }d\mathrm{\Lambda }(u\mid R)|}_{\beta =\beta (u)}=d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)[1-d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)]R.$$

Note that

$$d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)S_T(u\mid R)=f_T(t\mid R),$$

where f denotes the probability mass function. Solving for ${\beta }_{S_C,t_J}^{\ast }$ in Eq. 6, substituting the previous two identities, and exchanging the order of integration, we arrive at

$${\beta }_{S_C,t_J}^{\ast }\approx \frac{E_{T,R}[\beta (T)R^2(T)(1-d\stackrel{\sim }{\mathrm{\Lambda }}(T\mid Z))S_C(T\mid R)I(T\le t_J)]}{E_{T,R}[R^2(T)(1-d\stackrel{\sim }{\mathrm{\Lambda }}(T\mid Z))S_C(T\mid R)I(T\le t_J)]}.$$ (7)

When R is binary, this reduces to

$$\frac{E_{T\mid R}[\beta (T)\{1-d\stackrel{\sim }{\mathrm{\Lambda }}(T\mid R=1)\}{S}_C(T\mid R)I(T\le t_J)\mid R=1]}{E_{T\mid R}[\{1-d\stackrel{\sim }{\mathrm{\Lambda }}(T\mid R=1)\}{S}_C(T\mid R)I(T\le t_J)\mid R=1]}.$$

The parameter ${\beta }_{S_C,t_J}^{\ast }$ is thus a weighted average of the time-varying treatment effect β(t) that depends upon the distribution of R, the maximum follow-up time t_J, the distribution of failure times T, and the nuisance parameter S_C.

Similarly, using a first order Taylor approximation of dΛ(t | R) about β(t) for the argument ${\beta }_{t_J}^{\ast }$ for each t, we obtain from Eq. 4

$${\beta }_{t_J}^{\ast }\approx \frac{E_{T,R}[\beta (T)R^2(T)(1-d\stackrel{\sim }{\mathrm{\Lambda }}(T\mid Z))I(T\le t_J)]}{E_{T,R}[R^2(T)(1-d\stackrel{\sim }{\mathrm{\Lambda }}(T\mid Z))I(T\le t_J)]}.$$ (8)

When R is binary, this reduces to

$$\frac{E_{T\mid R}[\beta (T)\{1-d\stackrel{\sim }{\mathrm{\Lambda }}(T\mid R=1)\}I(T\le t_J)\mid R=1]}{E_{T\mid R}[\{1-d\widehat{\mathrm{\Lambda }}(T\mid R=1)\}I(T\le t_J)\mid R=1]}.$$

Similar to Xu and O’Quigley (2000), ${\beta }_{t_J}^{\ast }$ can be interpreted as a weighted average or marginal regression effect of β(t) over the distribution of (T, R), which in the logit link case reduces to a marginal log-hazard-odds ratio regression effect. The estimand can be thought of as a weighted average of the treatment effect over time, where the weights depend directly on the distribution of R and the distribution of failure time and is independent of S_C.

The parameter ${\beta }_{t_J}^{\ast }$ is most meaningful in the case of stochastically ordered hazards, i.e., when β(t) is either positive or negative for the entire support of the data. When β(t) takes on both positive and negative values, one should clearly use caution in concluding an overall positive or negative covariate effect since the effect is qualitatively differential depending upon time. As this is a general weakness of hazard regression models, in cases where one pre-hypothesizes a qualitatively differential covariate effect over time (e.g., in the case of heavily invasive surgery where the hazard is expected to rise immediately following the intervention then reduce rapidly with time), a different parameter of interest such as the difference in restricted mean survival (Irwin 1949; Karrison 1987) may be preferred.

3 Numerical studies

Using simulation, we evaluate the usual/naive and censoring-robust estimators based on bias and coverage probabilities of 95% confidence intervals for n = 100 and n = 400 for a variety of cases. We generate survival times under 4 different conditions (null, proportional hazards, early difference in survival, and late difference in survival) and censoring times under 5 different scenarios in order to illustrate the impact of censoring as described in this manuscript. This yields a total of 20 scenarios (4 × 5) for each n. For each data set, we apply the usual estimator and the censoring-robust estimator based on the discrete-time proportional hazards model with the complementary-log-log link. Thus, the model is correctly specified in the null and proportional hazards settings, and misspecified in the early and late differences in the survival distributions. We repeat the estimation 5,000 times for each scenario, and compare their operating characteristics; results for the continuation ratio model (logit link) were similar.

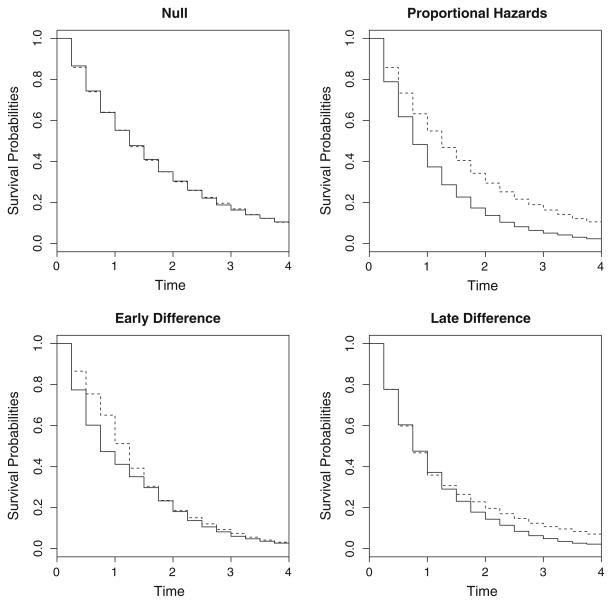
Figure 3 displays the survival curves of the different data-generating conditions. Survival times for the null and proportional hazards case were generated from exponential distributions, and the times for the early difference and late difference cases were generated from piecewise exponential distributions. The times were then discretized to every 0.25, i.e., rounded up to every multiple of 0.25.

Fig. 3.

Survival curves of the different scenarios under consideration for the simulation study. Solid line indicates the control group and dotted line indicates the treatment group

The first censoring case in our simulation study is that of Type 1 censoring (Klein and Moeschberger 2003), where C = ∞ for all subjects and administrative censoring occurs at time 4; this represents the case of no intermittent censoring over the interval [0,4]. Administrative censoring at time 4 is also present in all remaining censoring cases to ensure the support is constant across all censoring scenarios since our proposed methodology did not address the dependency on the support of observable times. A reliable estimate of the target estimand ${\beta }_{t_J}^{\ast }$ is the Monte Carlo average of the usual estimator for censoring case 1 with n = 10, 000; we use it to assess the operating characteristics (bias and coverage probabilities) of the two estimators.

Censoring times for cases 2 and 3 were generated based on a power-function distribution with cdf F_C (t) = (t/b)^r, where b > 0 and r > 0. For case 2, b = 3.75 and r = 1, which reduces to the uniform distribution, with 0.25 added to the generated times to prevent censoring from occuring before the first time point. For case 3, b = 3.75 and r = 1 for the treatment group and r = 1.5 for the control group, also with 0.25 added to the generated times. The censoring times of case 4 and 5 were generated based on the lognormal and loglogistic distributions, respectively.

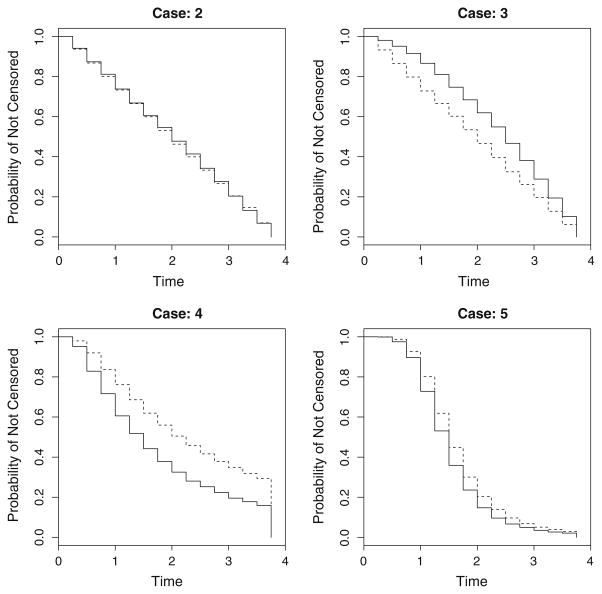
In all scenarios, censoring differs by treatment (covariate-dependent censoring) except for cases 1 and 2. Figure 4 shows the censoring distributions from cases 2–5. In practice, censoring patterns are most likely best described by the power-function distribution (cases 2 and 3) arising from staggered entry and administrative censoring; cases 4 and 5 are included to assess the performance of the proposed estimator under extreme censoring patterns.

Fig. 4.

Different censoring distributions, S_C (· | R), under consideration for the simulation study. Case 1 is that of C = ∞ and administrative censoring occurs at t = 4

Convergence issues stemming from the Newton-Raphson algorithm can sometimes (rarely) arise due to the incorporation of weights. To mitigate this problem, we suggest using the estimate based on the usual estimator as starting values. The simulation results are presented in Table 2.

Table 2.

Simulation results (# simulations = 5,000) for n = 100 and n = 400 under different censoring and treatment mechanisms

Scenario	${\beta }_{t_J}^{\ast }$	bias of β̂	% bias	SD (β̂)	% Cov.	bias of β̂CR	% bias	SD (β̂CR)	% Cov.
n = 100
Null
Case 1 (Cens = 9.0%)	0.000	−0.003	–	0.217	94.4	−0.003	-	0.217	94.4
Case 2 (Cens = 36.9%)	0.000	−0.004	–	0.265	94.6	−0.006	-	0.294	93.3
Case 3 (Cens = 32.8%)	0.000	−0.003	–	0.253	95.0	−0.001	-	0.274	93.9
Case 4 (Cens = 37.0%)	0.000	−0.001	–	0.264	94.4	−0.003	-	0.292	93.7
Case 5 (Cens = 40.9%)	0.000	0.000	–	0.272	94.5	−0.002	-	0.339	92.4
Proportional Hazards
Case 1 (Cens = 5.5%)	−0.511	−0.018	3.4	0.218	94.2	−0.018	3.4	0.218	94.2
Case 2 (Cens = 29.9%)	−0.511	−0.017	3.2	0.253	94.5	−0.024	4.7	0.269	94.1
Case 3 (Cens = 26.1%)	−0.511	−0.016	3.2	0.246	94.4	−0.023	4.4	0.261	93.9
Case 4 (Cens = 30.0%)	−0.511	−0.017	3.4	0.256	94.5	−0.028	5.4	0.272	94.1
Case 5 (Cens = 32.5%)	−0.511	−0.015	2.9	0.257	94.3	−0.025	4.8	0.290	93.4
Early Difference
Case 1 (Cens = 2.5%)	−0.105	−0.004	3.3	0.215	94.1	−0.004	3.3	0.215	94.1
Case 2 (Cens = 27.5%)	−0.105	−0.068	64.6	0.249	92.9	−0.020	19.6	0.265	92.9
Case 3 (Cens = 23.7%)	−0.105	−0.054	51.4	0.241	93.6	−0.014	13.6	0.252	93.7
Case 4 (Cens = 27.7%)	−0.105	−0.088	84.3	0.250	92.3	−0.036	34.6	0.269	92.8
Case 5 (Cens = 30.3%)	−0.105	−0.087	83.4	0.251	92.7	−0.038	36.0	0.283	92.3
Late Difference
Case 1 (Cens = 4.0%)	−0.172	−0.006	3.4	0.213	94.8	−0.006	3.4	0.213	94.8
Case 2 (Cens = 25.0%)	−0.172	0.057	−33.1	0.245	93.3	0.019	−10.8	0.257	93.5
Case 3 (Cens = 21.2%)	−0.172	0.047	−27.3	0.237	93.8	0.016	−9.0	0.248	93.6
Case 4 (Cens = 25.2%)	−0.172	0.063	−36.6	0.241	94.1	0.017	−10.1	0.251	94.6
Case 5 (Cens = 26.1%)	−0.172	0.090	−52.1	0.242	93.0	0.048	−27.7	0.262	93.5
n = 400
Null
Case 1 (Cens = 9.1%)	0.000	−0.001	–	0.105	94.9	−0.001	-	0.105	94.9
Case 2 (Cens = 36.9%)	0.000	−0.002	–	0.128	94.4	−0.003	-	0.142	94.3
Case 3 (Cens = 32.9%)	0.000	−0.001	–	0.124	94.5	−0.001	-	0.135	94.9
Case 4 (Cens = 37.0%)	0.000	0.000	–	0.129	94.5	−0.001	-	0.138	94.6
Case 5 (Cens = 41.0%)	0.000	−0.001	–	0.131	94.8	−0.001	-	0.182	93.5
Proportional hazards
Case 1 (Cens = 5.5%)	−0.511	−0.007	1.3	0.105	95.1	−0.007	1.3	0.105	95.1
Case 2 (Cens = 30.0%)	−0.511	−0.006	1.2	0.119	95.5	−0.010	2.0	0.128	95.0
Case 3 (Cens = 26.1%)	−0.511	−0.004	0.8	0.118	95.2	−0.005	1.0	0.126	94.5
Case 4 (Cens=30.0%)	−0.511	−0.007	1.3	0.123	95.4	−0.010	2.0	0.129	95.0
Case 5 (Cens=32.4%)	−0.511	−0.005	1.0	0.124	95.2	−0.010	2.0	0.150	93.9
Early Difference
Case 1 (Cens = 2.5%)	−0.105	−0.002	1.9	0.102	94.8	−0.002	1.9	0.102	94.8
Case 2 (Cens=27.4%)	−0.105	−0.063	60.6	0.118	91.5	−0.014	13.7	0.125	94.3
Case 3 (Cens=23.6%)	−0.105	−0.052	49.4	0.115	93.1	−0.013	12.2	0.120	94.8
Case 4 (Cens=27.6%)	−0.105	−0.081	77.7	0.120	89.2	−0.024	23.4	0.128	93.5
Case 5 (Cens=30.3%)	−0.105	−0.085	81.0	0.121	88.9	−0.030	29.0	0.143	92.8
Late Difference
Case 1 (Cens= 4.0%)	−0.172	0.000	0.1	0.104	95.0	0.000	0.1	0.104	95.0
Case 2 (Cens=25.0%)	−0.172	0.060	−34.9	0.119	91.4	0.018	−10.7	0.124	94.3
Case 3 (Cens=21.2%)	−0.172	0.051	−29.8	0.117	91.6	0.015	−8.5	0.123	93.8
Case 4 (Cens=25.3%)	−0.172	0.068	−39.6	0.119	90.8	0.022	−12.6	0.122	95.1
Case 5 (Cens=26.2%)	−0.172	0.093	−54.0	0.120	87.2	0.039	−22.8	0.136	93.1

The true ${\beta }_{t_J}^{\ast }$ is determined based on the monte carlo average of β̂ under the scenario n = 10, 000 with administrative censoring occuring at time = 4 (case 1). Bias and % bias of an estimator β̂ are defined to be $\widehat{E(\widehat{\beta })}-{\beta }_{t_J}^{\ast }$ and $(\widehat{E(\widehat{\beta })}-{\beta }_{t_J}^{\ast })/{\beta }_{t_J}^{\ast }\times 100$, respectively

Under correct model specification, i.e. null and PH, both the usual estimator and the censoring-robust estimator are seen to be roughly unbiased for ${\theta }_{t_J}^{\ast }$. For n = 100, the maximum absolute bias in the null case was 0.004 for the usual estimator and 0.006 for the censoring-robust estimator; under the PH scenario, the maximum % bias of the usual estimator and censoring-robust estimator were 4.4% and 5.4%, respectively. However, under non-PH (early difference and late difference), the bias is much larger for the usual estimator compared to the censoring-robust estimator. For example, in one of the extreme censoring scenario (case 5: loglogistic censoring), we observe a bias of 29.0% for the censoring-robust estimator and an 81.0% in bias for the usual estimator in the early difference and n = 400 simulation; this translates to a 2.8-fold improvement in the relative bias for the censoring-robust estimator. In the late difference scenario with n = 400 and case 5 censoring, we observe a bias of −22.8% for the censoring-robust estimator and a bias of −54.0% for the usual estimator; this translates to a 2.4-fold improvement in the relative bias for the censoring-robust estimator. As previously mentioned, loglogistic and lognormal censoring times are probably not representative of censoring in real-world applications; power-function censoring arising from staggered entry are more realistic. Thus, cases 2 and 3 are what one might expect in practice. For example, when there is early difference in survival under censoring case 2 with n = 400, the censoring-robust estimator and the usual estimator biases of 13.7% and 60.6%, respectively. This translates to a 4.4-fold improvement in the relative bias for the censoring-robust estimator.

Confidence intervals from both estimators have approximately the nominal coverage under the null and PH conditions. However, as expected, confidence intervals obtained from the usual estimator have poor coverage for the target estimand when the survival curves differ early or later in time. For example, coverage for the usual estimator was 87.2% in the late difference scenario (n = 400, censoring: case 5), whereas the coverage for the censoring-robust estimator was 93.1%. Coverage probabilities for confidence intervals based on the usual estimator are worse as the sample size increases (results not shown).

Noting that the usual unweighted estimator is asymptotically efficient when the model is correctly specified, we considered the asymptotic relative efficiency (ARE) of the proposed estimator in this case. Table 3 presents the ARE comparing the usual estimator to the censoring-robust estimator for the PH case. As expected, the censoring-robust estimator can be inefficient compared to the usual estimator for the null and PH conditions. The re-weighting allows for robust estimation but, as can be seen by comparing columns 5 and 9 of Table 2, introduces additional variability to the estimation.

Table 3.

Asymptotic Relative Efficiency (ARE): We estimate Var(β̂)/Var(β̂_CR) for the null and the proportional hazards case based on n = 10,000

Censoring Case	1	2	3	4	5
Null: Avg. Cens. Rate	0.091	0.369	0.328	0.370	0.409
ARE	1.000	0.807	0.843	0.872	0.462
PH: Avg. Cens. Rate	0.054	0.299	0.261	0.299	0.324
ARE	1.000	0.863	0.880	0.914	0.616

4 Discussion

In this manuscript, we have demonstrated that consistency of the usual estimator in the discrete hazards models is dependent on the censoring distribution when the model is misspecified. In order to remove this censoring-dependence, we have proposed a censoring-robust estimator that is consistent for an average regression effect in the absence of intermittent censoring. To the best of our knowledge, this dependence and the proposed modification has not previously been considered in the case of discrete survival models.

The proposed methodology is useful in clinical research since model assumptions (e.g., proportional hazard or proportional odds of hazard) are not known a priori to hold, and the probability model and test statistic is generally required to be pre-specified prior to data collection. Model-checking and model-building are generally not acceptable when the goal is to formally address a scientific question based on a population parameter (estimation and testing) as doing so can alter the pre-conceived question and inflate Type I error. The research presented here is particularly relevant to the Atrasentan trial described in Sect. 1. Based upon the observed phase 2 data, a delayed treatment effect may be present in later investigation. Also, due to regulatory requirements, scheduled radiologic follow-up assessments would be required in confirmatory investigations and this would result in discrete time-to-event data. Since it is impossible to know whether a time-invariant effect would be observed in later investigations, in our opinion it is imperative that the potential influence of the censoring distribution on future trial conclusions be investigated and that a censoring-robust estimator, as we have proposed, be used to limit such influence.

The censoring-robust estimator can be used to consistently estimate the root of Eq. 4, an average regression effect in the absence of intermittent censoring regardless of whether model assumptions hold. Although the censoring-robust estimator can be inefficient relative to the usual unweighted estimator when the model is correctly specified, we believe the tradeoff with robustness is worthwhile, especially in the clinical trials setting. Moreover, the proposed methodology allows for legitimate comparison of point estimates in stratified estimation that is often done in large, multi-center trials. In such a setting, accrual patterns often differ by region, impacting the consistency of the usual unweighted estimator when the treatment effect is misspecified. Results from comparative effectiveness research and meta-analyses can be meaningful should the censoring-robust estimator be used, assuming the inclusion, exclusion, and the maximal observable time remain constant.

The censoring-robust estimator essentially gives higher weights to later observations based on the censoring distribution. In order for the estimator to work well, the censoring distribution must be estimated adequately, i.e., it requires at least a moderate risk-set size. We have seen in the simulation study that n = 100 – 400 are reasonable sample sizes and moreover, are typical of mid- to late-phase trials. A larger sample should be used to increase the efficiency of the estimator should that be a concern to account for increased variability in the re-weighting.

The proposed methodology will not give a different estimate when there is no variability in the censoring time (i.e., when censoring occurs only at a fixed time) since the left-continuous Kaplan–Meier estimator of the censoring distribution will give weights of 1 to all observations in this case. In such a setting, censoring-robust estimation is not needed since the fixed censoring time can be thought of as administrative censoring due to the ending of a study. Hence, both estimators would yield the same estimate of the marginal log-hazard-ratio (or odds) for the observed support.

We advocate the censoring-robust estimator since it estimates a single target, is well-defined, and is generalizable to a population of interest by removing a nuisance parameter (censoring) that is often ignored and unaccounted for. That is, we are acknowledging the censoring-dependence when the model is misspecified and attempt to remove it through the proposed estimator as opposed to ignoring it and using the naive estimator as in the status quo. One might argue that the estimand in Eq. 8 is a complicated beast, but it is no more complicated than the censoring-dependent estimand in Eq. 7 that is widely estimated when the misspecified model is used for inference.

We note that the proposed methodology is easily implemented using existing software. One would need a GLM package that can incorporate weights into the score equation and allow for the specification of a starting value and a survival package that can compute Kaplan–Meier estimates. Robust standard errors can be computed by modifying the inner portion of the sandwich estimator in existing robust standard error software for GLM’s.

In future work we plan to develop methods for implementing the censoring-robust estimator in a group sequential context providing clinical trialists with the ability to periodically monitor outcomes over time. The implementation will not be straightforward as information growth will not be linear due to the introduction of weights (Gillen and Emerson 2005) and the interim estimates will not have asymptotic independent increments since the censoring distribution (weights) changes from interim analysis to interim analysis (Tsiatis 1982). We also plan to incorporate adjustment variables (possibly continuous variables) into the model for use with observational studies. In this setting, estimation of S_C (· | R) is not obvious unless a parametric assumption is placed on the censoring distribution.

Appendix: Consistency of the usual estimator and the Censoring-Robust estimator

We outline the proof to the consistency of the usual estimator first and then the censoring-robust estimator. Letting dΛ̃ denote the true hazard function in a misspecified model setting. Adding and subtracting by Z_i (t_j)Y_i (t_j) dΛ̃(t_j | R_i) in Eq. 2, we obtain

$$\frac{1}{n}U(\theta )=\frac{1}{n}\sum _{i=1}^n\underset{0}{\overset{t_J}{\int }}{Z}_i(u)Y_i(u)\{{dN}_i(u)-Y_i(u)d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R_i)\}+\frac{1}{n}\sum _{i=1}^n\underset{0}{\overset{t_J}{\int }}{Z}_i(u)Y_i(u)\{d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R_i)-d\mathrm{\Lambda }(u\mid R_i)\}.$$

As n → ∞, the first term converges to 0 in probability since it is an average of zero-mean independent and identically distributed random variables (the integral is a martingale as a function of the upper limit).

Let f denote the probability density/mass function so that f_T,C,Z denotes the joint density of (T, C, Z). By the Weak Law of Large Numbers (WLLN) the second term converges to the expectation of a single term in the sum,

$$\begin{array}{l}\underset{0}{\overset{t_J}{\int }}\int \int \int Z(u)Y(u)\{d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)-d\mathrm{\Lambda }(u\mid R)\}{f}_{T,C,Z}(t,c,z)dtdcdzdu\\ =\underset{0}{\overset{t_J}{\int }}\int Z(u)\{d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)-d\mathrm{\Lambda }(u\mid R)\}\int \int Y(u)f_{T,C,Z}(t,c,z)dtdcdzdu\\ =\underset{0}{\overset{t_J}{\int }}\int Z(u)\{d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)-d\mathrm{\Lambda }(u\mid R)\}\left[\underset{C>u}{\int }\underset{T>u}{\int }{f}_T(t\mid R)f_C(c\mid R)dtdc\right]\times f_Z(z)dzdu\\ =\underset{0}{\overset{t_J}{\int }}\int Z(u)\{d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)-d\mathrm{\Lambda }(u\mid R)\}{S}_C(u\mid R)S_T(u\mid R)f_Z(z)dzdu\\ =\underset{0}{\overset{t_J}{\int }}{E}_Z[Z(u)S_C(u\mid R)S_T(u\mid R)\{d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)-d\mathrm{\Lambda }(u\mid R)\}]du,\end{array}$$ (9)

where the expectation is taken with respect to the distribution of Z, the last integral is respect to the counting measure for u = t₁, …, t_J, and where S_T and S_C refer to the true survival function of the failure time and the true survival function of the censoring time, respectively. Note that if dΛ is correctly specified, then (9) reduces to 0 and censoring will not influence the estimand. Under mild regularity conditions, and by the same argument as the proof of Theorem 2.1 of Struthers and Kalbfleisch (1986), θ̂ can be shown to converge to ${\theta }_{t_J,S_C}^{\ast }$ that solves for (9) when set to 0. This completes the proof for the consistency of the usual estimator in Theorem 1.

The proof of the consistency of the censoring-robust estimator makes use of the fact that the Kaplan–Meier estimator Ŝ_C (t) is consistent for S_C (t) for all t. Let W (t | R) = 1/S_C (t | R). Ŵ(t | R) is consistent for W (t | R) for any t by the Continuous Mapping (Mann-Wald) theorem. Similar to the original score function, we have

$$\frac{1}{n}{U}_W(\theta )=o_p(n)+\frac{1}{n}\sum _{i=1}^n\underset{0}{\overset{t_J}{\int }}\widehat{W}(u\mid R_i)Z_i(u)Y_i(u)\{d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R_i)-d\mathrm{\Lambda }(u\mid R_i)\}du$$

By consistency of the weight function, the second term is asymptotically equivalent to

$$\frac{1}{n}\sum _{i=1}^n\underset{0}{\overset{t_J}{\int }}W(u\mid R_i)Z_i(u)Y_i(u)\{d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R_i)-d\mathrm{\Lambda }(u\mid R_i)\}du$$

As in the case of the naive estimator, by the WLLN, we have the previous term converging to

$$\begin{array}{l}\underset{0}{\overset{t_J}{\int }}\int \int \int S_C{(u\mid R)}^{-1}Z(u)Y(u)\{d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)-d\mathrm{\Lambda }(u\mid R)\}{f}_{T,C,Z}(t,c,z)dtdcdzdu\\ =\underset{0}{\overset{t_J}{\int }}\int S_C{(u\mid R)}^{-1}Z(u)\{d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)-d\mathrm{\Lambda }(u\mid R)\}\int \int Y(u)f_{T,C,Z}(t,c,z)dtdcdzdu\\ =\underset{0}{\overset{t_J}{\int }}\int S_C{(u\mid R)}^{-1}Z(u)\{d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)-d\mathrm{\Lambda }(u\mid R)\}\times \left[\underset{C>u}{\int }\underset{T>u}{\int }{f}_T(t\mid R)f_C(c\mid R)dtdc\right]f_Z(z)dzdu\\ =\underset{0}{\overset{t_J}{\int }}\int S_C{(u\mid R)}^{-1}Z(u)\{d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)-d\mathrm{\Lambda }(u\mid R)\}{S}_C(u\mid R)S_T(u\mid R)f_Z(z)dzdu\\ =\underset{0}{\overset{t_J}{\int }}{E}_Z[Z(u)S_T(u\mid R)\{d\stackrel{\sim }{\mathrm{\Lambda }}(u\mid R)-d\mathrm{\Lambda }(u\mid R)\}]du.\end{array}$$

Again, applying the argument from Struthers and Kalbfleisch (1986) completes the proof for consistency in Theorem 2.

Asymptotic normality of the Censoring-Robust estimator

We outline the proof for asymptotic normality of the censoring-robust estimator for the logit link in the two-sample case. The proof for other link functions and K -sample follows in parallel.

Consider the weighted score estimating function

$$U_W(\theta )=\sum _{i=1}^n\underset{0}{\overset{t_J}{\int }}\widehat{W}(u\mid R_i)P_i(u)du\equiv \sum _{i=1}^n{U}_W^{(i)}(\theta ),$$

where

$$P_i(u)=Z_i(u)[{dN}_i(u)-Y_i(u)d\mathrm{\Lambda }(u\mid R_i)]$$

and

$$U_W^{(i)}(\theta )=\underset{0}{\overset{t_J}{\int }}\widehat{W}(u\mid R_i)P_i(u)du.$$

P_i is different for different link functions.

Let θ* denote the “true” θ, i.e., what θ̂_CR is consistent for. Now, by the Mean Value theorem,

$$U_W({\widehat{\theta }}_{CR})=U_W({\theta }^{\ast })+U_W^{\prime }(\stackrel{\sim }{\theta })({\widehat{\theta }}_{CR}-{\theta }^{\ast }),$$

where θ̂_CR is the root of the estimating function and θ̃ lies on the segment connecting θ* and θ̂_CR. Since U_W (θ̂_CR) = 0, we obtain

$$\sqrt{n}({\widehat{\theta }}_{CR}-{\theta }^{\ast })={\left[-\frac{U_W^{\prime }(\stackrel{\sim }{\theta })}{n}\right]}^{-1}\left[n^{-1/2}{U}_W({\theta }^{\ast })\right].$$

Since θ̂_CR is consistent for θ* and θ̃ is on the segment connecting the two, θ̃ is also consistent for θ*. Next, we derive asymptotic normality for the second factor on the right hand side.

Levy’s Central Limit theorem does not apply to $\sqrt{n}{U}_W({\theta }^{\ast })$ because the n terms are not independent due to the Ŵ_i ’s. The Martingale Central Limit theorem does not apply because we do not have a sum of martingales (misspecified model setting). To prove asymptotic normality for this term, we show that U_W can be written as a sum of n independent and identically distributed random variables and terms that converge to 0 in probability. To do so, add and subtract the “true weights” to obtain

$$n^{-1/2}{U}_W(\theta )=n^{-1/2}\sum _{i=1}^n\int W(u\mid R_i)P_i(u)du+n^{-1/2}\sum _{i=1}^n\int \{\widehat{W}(u\mid R_i)-W(u\mid R_i)\}{P}_i(u)du.$$

The second term converges to 0 in probability by noting that n^−1/2 converges to 0, Ŵ(u | R_i) − W (u | R_i) converges to 0, and by application of Slutsky’s theorem. The first term is a normalized sum of n independent and identically distributed random variables; asymptotic normality follows from Levy’s Central Limit theorem.

Thus, n^−1/2 U_W (θ*) converges to a zero-mean Gaussian distribution with variance

$$B=\underset{n\to \infty }{lim}\frac{1}{n}\sum _{i=1}^n{\left[\underset{0}{\overset{t_J}{\int }}W(u\mid R_i)Y_i(u)Z_i(u){dM}_i(u)\right]}^{\otimes 2},$$

where the dΛ’s are evaluated at θ*. By the Weak Law of Large Numbers, $-U_W^{\prime }(\stackrel{\sim }{\theta })/n$ will converge to

$$\begin{array}{l}A=\underset{n\to \infty }{lim}-\frac{1}{n}\sum _{i=1}^n{U}_W^{{(i)}^{\prime }}(\stackrel{\sim }{\theta })\\ =\underset{n\to \infty }{lim}-\frac{1}{n}\sum _{i=1}^n\underset{0}{\overset{t_j}{\int }}W(u\mid R_i)Y_i(u)Z_i(u)Z_i{(u)}^T\{d\mathrm{\Lambda }(u\mid R_i)[1-d\mathrm{\Lambda }(u\mid R_i)]\}du.\end{array}$$

Applying Slutsky’s theorem, we have $\sqrt{n}({\widehat{\theta }}_{CR}-{\theta }^{\ast })$ converging to a zero-mean Gaussian distribution with variance A⁻¹ B A⁻¹. A can be consistently estimated by

$$\widehat{A}=-\frac{1}{n}\sum _{i=1}^n\underset{0}{\overset{t_J}{\int }}\widehat{W}(u\mid R_i)Y_i(u)Z_i(u)Z_i{(u)}^T\{d\mathrm{\Lambda }(u\mid R_i)[1-d\mathrm{\Lambda }(u\mid R_i)]\},$$

and B can be consistently estimated by

$$\widehat{B}=\frac{1}{n}\sum _{i=1}^n{\left[\underset{0}{\overset{t_J}{\int }}\widehat{W}(u\mid R_i)Y_i(u)Z_i(u){dM}_i(u)\right]}^{\otimes 2},$$

where the dΛ’s are evaluated with θ̂_CR plugged in.

To ensure the limits exist, we require the Z_i (u)’s and the weights to be bounded and predictable. Bounded covariates ensure the dΛ(u | R_i)’s are bounded away from 0 and 1 in the complementary-log-log and logit links. The weights are predictable by design since we use the left-continuous version of the Kaplan–Meier to estimate S_C. To ensure that not one term in the estimating equation dominates due to re-weighting, we require

$$\underset{i,j}{max}\frac{\widehat{W}(t_j\mid R_i)}{{\sum }_{l,k}\widehat{W}(t_k\mid R_l)}\to 0.$$

This completes the proof of asymptotic normality in Theorem 2.