Abstract
We describe an approach to the high-resolution three-dimensional structural determination of macromolecules that utilizes ultrashort, intense x-ray pulses to record diffraction data in combination with direct phase retrieval by the oversampling technique. It is shown that a simulated molecular diffraction pattern at 2.5-Å resolution accumulated from multiple copies of single rubisco biomolecules, each generated by a femtosecond-level x-ray free electron laser pulse, can be successfully phased and transformed into an accurate electron density map comparable to that obtained by more conventional methods. The phase problem is solved by using an iterative algorithm with a random phase set as an initial input. The convergence speed of the algorithm is reasonably fast, typically around a few hundred iterations. This approach and phasing method do not require any ab initio information about the molecule, do not require an extended ordered lattice array, and can tolerate high noise and some missing intensity data at the center of the diffraction pattern. With the prospects of the x-ray free electron lasers, this approach could provide a major new opportunity for the high-resolution three-dimensional structure determination of single biomolecules.
X-ray protein crystallography is currently the primary methodology used for determining the three-dimensional (3D) structure of protein molecules at near-atomic or atomic resolution (the other being NMR). However, typically around 20–40% of all protein molecules, including most of the important membrane proteins, are difficult or impossible to crystallize, and hence their structures have not been accessible by crystallography. NMR has limitations on the size of the molecules that can be structurally characterized. Overcoming these challenging limitations requires the development of new techniques and methods. One approach under rapid development is single-molecule imaging using cryo-electron microscopy (EM). The highest resolution currently achievable by this technique is ∼7 Å for highly symmetrical viruses (1) and 11.5 Å for the asymmetrical ribosome (2). The main limitations to achieving better resolution by cryo-EM are radiation damage, specimen movement, and low contrast. Here we describe an approach that combines continuous diffraction images recorded with the unique properties of proposed x-ray free electron lasers (X-FELs) (3, 4) with oversampling, an ab initio approach to solving the classical “phase problem” made possible by the recording of continuous (molecular) transforms. The feasibility of recording such single biomolecule diffraction patterns by using X-FELs, including pushing beyond the traditional radiation damage barrier, has been discussed (5, 6). The phase problem with continuous diffraction patterns from noncrystalline specimens is somewhat different than that for a crystal Bragg diffraction pattern. For a crystal, the interference among a large number of unit cells generates strong Bragg peaks. The Bragg peaks facilitate data acquisition, in that they are discrete and often well above background, but they do not sample the molecular transform finely enough for the phases to be directly retrieved without additional information (hence the “phase problem”). For a noncrystalline specimen, the diffraction intensity forms a continuous pattern, which, if sampled in discrete arrays with the sampling spacing at the Nyquist frequency (i.e., the inverse of the size of the specimen), can be expressed as
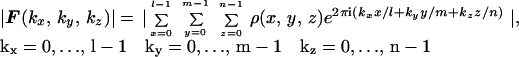 |
1 |
where |F(kx, ky, kz)| represents the magnitude of the Fourier transform, and ρ(x, y, z) the electron density of the specimen. Eq. 1 actually consists of a series of independent equations, and the phase problem is to solve these for ρ(x, y, z) at each pixel, where the pixel is the element of the discrete arrays. When the electron density is complex, the number of equations is lmn, and the number of unknown variables is 2lmn, because each density point has two unknown valuables, the real and imaginary parts. When the density is real, the number of unknown variables reduces to lmn, whereas the number of independent equations also goes down to lmn/2 because of the centro symmetry of the diffraction pattern. This explains why, without additional information, the electron density cannot be directly recovered from a diffraction pattern sampled at the Nyquist frequency. For a noncrystalline specimen, however, the diffraction pattern can be sampled at a spacing finer than the Nyquist frequency (7), which corresponds to surrounding the electron density with a no-density region (8, 9). The higher the sampling frequency, the larger the no-density region. Oversampling the diffraction pattern more finely than the Nyquist frequency thus increases the number of independent equations while retaining the same number of unknown variables (corresponding to the data points inside the electron density region). To characterize the sampling frequency, we have introduced the concept of ratio (σ), which is defined as (8),
 |
2 |
where the volume of a region represents the total grid points inside the region. When σ > 2, the number of independent equations is more than the number of unknown variables. Enough information is recorded so that, in principle, the phase information can be directly retrieved from the diffraction pattern by using an iterative algorithm (8–10). One may argue that, because of the nonlinearity of the equations, a unique solution cannot be guaranteed by the number of independent equations being more than the number of unknown variables. However, this is often not the case. Mathematically, it has been shown that multiple solutions are rare for two-dimensional (2D) and 3D specimens (11). By using this oversampling method, the phase information has recently been retrieved ab initio from the experimental diffraction pattern of a 2D noncrystalline specimen (a series of dots of 1/10th micron dimensions) (12). By using molecular transforms, this approach can in principle be used to image single macromolecules in three dimensions, but there are potentially serious radiation damage issues because of the loss of the large number of unit cells (and hence copies of the molecules) in a crystal. This radiation damage problem can be mitigated by using an ultra-short pulse and extremely bright X-FEL. Theoretical simulations show that, within about 10 fsec, biomolecules can withstand an x-ray intensity of ∼3.8 × 106 photons/Å2 with minimal structural changes (5). The combination of the oversampling phasing method with the femtosecond X-FEL for image recording makes it possible to directly determine the 3D structures of single biomolecules at high resolution.
Methods
Obtaining 3D Diffraction Patterns from Single Biomolecules by Utilizing a Simulated X-FEL.
We used a simulated X-FEL with a wavelength of 1.5 Å, a per-pulse flux of 2 × 1012 photons, and a pulse length of 10 fsec (13). Although it is not yet well established whether X-FEL pulses this short can be achieved in practice, we assume 10-fsec pulses in our simulation for the sake of consistency with prior published studies on the feasibility of recording such patterns. The X-FEL was then focused down to a 0.1-μm diameter spot (14) (which corresponds to 2.55 × 106 photons/Å2 and is a value that is about at the state of the art). By using the spraying techniques from mass spectrometry (15, 16), identical biomolecules can be selected and inserted one by one in random orientation into the X-FEL beam. With the simulated X-FEL exposures, we calculated 2D diffraction patterns from single biomolecules, each generated from a single pulse before the radiation damage manifests itself. To assemble a 3D diffraction pattern from these 2D patterns, we have to first determine the molecular orientation, which can be carried out by two methods. One is to use laser fields to physically align each molecule before the exposure. It has been demonstrated, theoretically and experimentally, that an elliptically polarized and nonresonant laser field can simultaneously force all three axes of a molecule to align along given axes fixed in space and inhibit the free rotation in all three Euler angles (17). Another is to determine the molecular orientation on the basis of 2D diffraction patterns, which has been developed in cryo-electron microscopy (18–20). The concept is that two arbitrary projections in reciprocal space intersect on a line through the origin, e.g., common line (when the Ewald sphere is curved, the common line becomes a common curve). Theoretically, a third projection, provided it is nonplanar with either of the first two, will lead to a complete determination of the relative angles of the projections. Although either method may result in high noise of each orientation determination, the signal-to-noise ratio can be greatly improved by averaging a large number of molecules at the same orientation. We hence anticipate that the misorientation noise will be within the Poisson noise of the diffraction intensity. For the second method, the misorientation noise can also be reduced by using larger molecules (e.g., molecular mass >100 kDa) because of the larger scattering cross sections and hence higher signal-to-noise-ratio of the diffraction pattern (21). In this simulation, we assumed that the individual orientations have already been determined by either method. The large number of 2D diffraction patterns was then assembled to a 3D diffraction pattern. The number of individual 2D patterns required for the assembly process is determined by multiplying the number of necessary projections, which is characterized by πD/d, where D is the diameter of the molecule and d the desired resolution (18), by the number of 2D patterns needed to raise the signal-to-noise ratio in each projection to a satisfactory level.
The Phasing Algorithm.
We have developed an iterative phasing algorithm (8, 9) by modifying that of Fienup (10).¶ Each iteration of the algorithm consists of the following four steps. (i) By combining the known magnitude of the Fourier transform and a guessed phase set, we assemble a new Fourier transform. For the initial iteration, we use a random phase set. (ii) We then calculate a new electron density by applying the inverse discrete Fourier transform (DFT) on the assembled Fourier transform. (iii) On the basis of the oversampling ratio (σ), we define a finite support in real space to separate the no-density and electron density regions. The finite support we usually choose is somewhat bigger than the envelope of the specimen, because practically it may be difficult to locate the true envelope of the specimen.‖ Outside the finite support, we drive the electron density close to zero. Inside the finite support, we retain the positive electron density and push the negative electron density close to zero. The positivity constraint is to separate the correct and conjugate phases. We hence get a new electron density. (iv) By applying DFT on the new electron density, we get a new Fourier transform and adopt its phase set. We then restore the phase of the central pixel to zero and obtain a new guessed phase set. Usually, after a few hundred iterations, the correct phase set can be retrieved. The computing time of 100 iterations for a 160 × 160 × 160 3D array is about 90 minutes on a Pentium III 750 MHz Dell workstation.
Results and Discussion
We simulated the process here by using a subunit of the protein rubisco with molecular mass of 106,392 Da (22), whose atomic coordinates were obtained from the RCSB Protein Data Bank (2RUS). Fig. 1 A and B show a stereoview of the 3D electron density map and the active site of the molecule with the refined atomic model of the rubisco molecule superimposed. By using the parameters of the focused X-FEL described above, we obtained an oversampled 3D diffraction pattern (i.e., a 160 × 160 × 160 pixel array), with resolution extending to 2.5 Å. The high-resolution 3D diffraction pattern was generated from ∼106 identical copies of the molecules with a total of 251 projections and 3,984 2D diffraction patterns in each projection. The sampling frequency of the diffraction pattern is at 0.4 Å−1 in each dimension, which is somewhat finer than the inverse of the diameter of the rubisco molecule. The oversampling was carried out by surrounding the molecule with a no-density region and then applying the discrete Fourier transform on it, which is mathematically equivalent to directly calculating the oversampled diffraction pattern by using the Fourier integral (23). To examine the applicability of the phasing method to experimental data, we have also investigated the sensitivity of the reconstruction to noise. For this purpose, Poisson statistical noise was added to the 3D diffraction pattern (not to each individual 2D pattern). The average percentage difference between the calculated and noisy intensity (RI) is defined
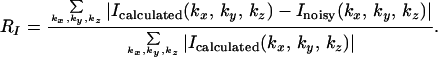 |
3 |
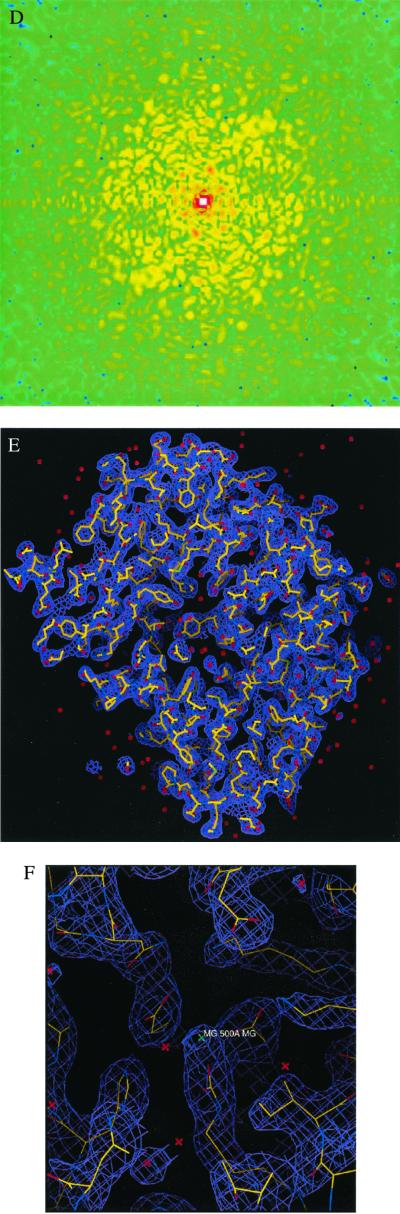
We also removed some intensity points at the center of the diffraction pattern to simulate the diffraction intensity lost in the direct x-ray beam. Fig. 1C shows one section (kz = 0) of the 3D diffraction pattern with Poisson noise (RI = 9.7%) and the central 3 × 3 × 3 pixel intensity removed. The vertical axis in Fig. 1C shows the number of diffracted photons, and the diffraction pattern extends to a resolution of 2.5 Å at the edge. Fig. 1D shows the top view of Fig. 1C.
Figure 1.
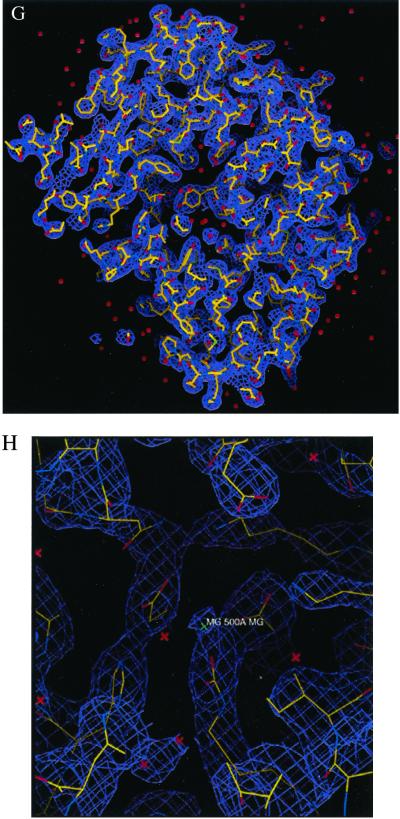
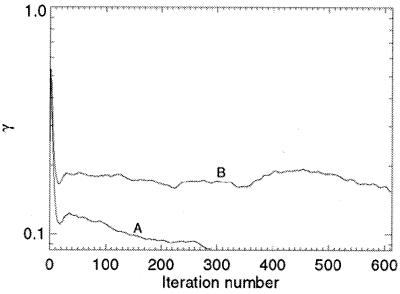
3D structural determination of single rubisco molecules utilizing a simulated X-FEL and direct phase retrieval by the oversampling technique. (A) Stereoview of the 3D electron density map of the rubisco molecule (contoured at two sigma), on which the refined atomic model of the rubisco molecule is superimposed. The red dots represent the location of water molecules. (B) The active site with a Mg(II). (C) One section (kz = 0) of the 3D diffraction pattern processed from 106 identical copies of the rubisco molecules with Poisson noise added (RI = 9.7%) and 3 × 3 × 3 pixel intensity removed. The edge of the diffraction pattern corresponds to 2.5-Å resolution. We assume here a 100% quantum efficiency for the detector. (D) Top view of C, where the central white area represents the intensity removed. (E) Stereoview of the 3D electron density map of the rubisco molecule (contoured at two sigma), reconstructed from C, on which the same atomic model is superimposed. (F) The active site reconstructed from C. (G) The 3D electron density map of the rubisco molecule (contoured at two sigma) reconstructed from the 3D diffraction pattern of 3 × 105 identical copies of the rubisco molecules, with Poisson noise added (RI = 16.6%) and central 3 × 3 × 3 pixel intensity removed. (H) The reconstructed active site corresponding to G.
To retrieve the phase information from the noisy 3D diffraction pattern, we first defined an orthorhombic-shaped finite support of 80 × 86 × 124 pixels (i.e., 100 × 107.5 × 155 Å3) in real space, which corresponds to σ = 4.8. This finite support is a little larger than the molecular envelope of the rubisco molecule. By using a random initial phase set and enforcing the positivity constraint in real space, after 300 iterations we successfully retrieved the correct phase set from the noisy diffraction pattern. Fig. 1 E and F show a stereoview of the reconstructed 3D electron density map and the active site on which the same atomic model is superimposed. The reconstructed electron density map is almost identical to the true one except for some very small differences. To quantitatively characterize the reconstruction, we adopt a quantity (γ) in each iteration
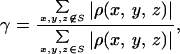 |
4 |
where S represents the finite support. We adopt γ instead of the R factor to characterize the reconstruction in that the oversampling method uses σ times more intensity points than the number of the Bragg peaks in the x-ray crystallography. It is hence not informative to compare the R factor in the oversampling method with that in x-ray crystallography. When the correct phase set is retrieved, γ should converge to a number very close to 0. Fig. 2A shows the convergence of the reconstruction of γ vs. the iteration number, which indicates that the correct phase set was converged upon after about 20 iterations and refined after another 280 iterations. That γ did not converge to a smaller number is a reflection of the Poisson noise and the intensity missing in the diffraction pattern. We also performed 10 more reconstructions with the same finite support and different initial random phase sets. The convergence speed of the reconstructions was somewhat different, but each reconstructed electron density map was almost identical to the true one. To investigate the reconstruction quality vs. the Poisson noise, we also processed a 3D diffraction pattern from 3 × 105 identical copies of the rubisco molecules. Poisson noise was then added to the diffraction pattern with RI = 16.6%, and the central 3 × 3 × 3 pixel diffraction intensity was removed. By using the same finite support, we carried out 10 additional reconstructions with different initial random phase sets, and each reconstruction was again successful. Because of the high Poisson noise, the reconstruction process was a little slower as shown in Fig. 2B, and γ did not converge to a value as small as that in Fig. 2A. The quality of the reconstructed electron density map (Fig. 1 G and H) also deteriorates somewhat, as some of the electron density positions in Fig. 1H shift a little relative to that in Fig. 1B.
Figure 2.
The convergence of the reconstruction from the 3D diffraction pattern (A) of 106 identical copies of the rubisco molecules and (B) of 3 × 105 identical copies of the rubisco molecules.
Conclusion
This computer modeling demonstrates that, when utilized with continuous diffraction patterns, the oversampling method can ab initio retrieve phase information from complex large macromolecules even with the presence of high noise and some data missing in the center of the diffraction pattern. It requires no information about the molecule except for a finite support, which can be larger than the molecular envelope. Unlike the direct methods approach (24), this method can, in principle, phase the diffraction pattern of both small and large molecules and does not require diffraction patterns at atomic resolution (although it can use such data if present). As a second important point, with the design of an X-FEL such as the planned Linac Coherent Light Source (3), and with its planned repetition rate of 120 Hz (13), we can estimate the data acquisition time for 106 copies of the molecules at about 2.3 hr, a reasonable time for such experiments. The powerful combination of the X-FEL-enabled diffraction imaging and the oversampling phasing method could therefore have an important impact on structural biology. It should be emphasized that this approach is a general 3D structural determination method and can, in principle, be applicable to electron and neutron diffraction for imaging both biomolecules and nanoscale materials.
Acknowledgments
We thank Janos Kirz, Henry Bellamy, and Mike Soltis for reading the first draft of this report and making many valuable suggestions. We are grateful to Joachim Stöhr, Peter Kuhn, Paul Ellis, Ingolf Lindau, John Arthur, Janos Hajdu, Chris Jacobsen, and Max Cornaccia for many helpful and stimulating discussions. This work was supported by the Stanford Synchrotron Radiation Laboratory, which is operated by the U.S. Department of Energy (DOE), Office of Basic Energy Sciences, with the structural biology program supported by the DOE Office of Biological and Environmental Research and the National Institutes of Health, National Center for Research Resources, and National Institute of General Medical Science programs.
Abbreviations
- 3D
three-dimensional
- 2D
two-dimensional
- X-FEL
x-ray free electron laser
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
See commentary on page 6535.
Given the diffraction pattern, one can calculate the Patterson function of the molecule. This function can provide an approximate envelope of the molecule, which could be a better finite support for the algorithm.
Another potential algorithm is the holographic reconstruction method. See, e.g., ref. 25.
References
- 1.Bottcher B, Wynne S A, Crowther R A. Nature (London) 1997;386:88–91. doi: 10.1038/386088a0. [DOI] [PubMed] [Google Scholar]
- 2.Gabashvili I S, Agrawal R K, Spahn C M T, Grassucci R A, Svergun D I, Frank J, Penczek P. Cell. 2000;100:537–549. doi: 10.1016/s0092-8674(00)80690-x. [DOI] [PubMed] [Google Scholar]
- 3.Winick H. J Elec Spec Rel Phenom. 1995;75:1–8. [Google Scholar]
- 4.Wiik B H. Nucleic Instrum Methods Phys Res B. 1997;398:1–8. [Google Scholar]
- 5.Neutze R, Wouts R, Spoel D, Weckert E, Hajdu J. Nature (London) 2000;406:752–757. doi: 10.1038/35021099. [DOI] [PubMed] [Google Scholar]
- 6.Hajdu J. Curr Opin Struct Biol. 2000;10:569–573. doi: 10.1016/s0959-440x(00)00133-0. [DOI] [PubMed] [Google Scholar]
- 7.Sayre D. In: Direct Methods of Solving Crystal Structures. Schenk H, editor. New York: Plenum; 1991. pp. 353–356. [Google Scholar]
- 8.Miao J, Sayre D, Chapman H N. J Opt Soc Am A. 1998;15:1662–1669. [Google Scholar]
- 9.Miao J, Kirz J, Sayre D. Acta Crystallogr D. 2000;56:1312–1315. doi: 10.1107/s0907444900008970. [DOI] [PubMed] [Google Scholar]
- 10.Fienup J R. Appl Opt. 1982;21:2758–2769. doi: 10.1364/AO.21.002758. [DOI] [PubMed] [Google Scholar]
- 11.Barakat R, Newsam G. J Math Phys. 1984;25:3190–3193. [Google Scholar]
- 12.Miao J, Charalambous P, Kirz J, Sayre D. Nature (London) 1999;400:342–344. [Google Scholar]
- 13.Arthur J, Bane K, Bharadwaj V, Bowden G, Boyce R, Carr R, Clendenin J, Corbett W, Cornacchia M, Cremer T, et al. Linac Coherent Light Source (LCLS) Design Study Report. Stanford University, Stanford, CA: Stanford Linear Accelerator Center; 1998. [Google Scholar]
- 14.Tatchyn R. Proceedings of the Workshop on Scientific Applications of Short Wavelength Coherent Light Sources. Stanford University, Stanford, CA: Stanford Linear Accelerator Center; 1993. [Google Scholar]
- 15.Tito M A, Tars K, Valegard K, Hajdu J, Robinson C V. J Am Chem Soc. 2000;122:3550–3551. [Google Scholar]
- 16.Siuzdak G, Bothner B, Yeager M, Brugidou C, Fauwuet C M, Hoey K, Chang C M. Chem Biol. 1986;3:45–48. doi: 10.1016/s1074-5521(96)90083-6. [DOI] [PubMed] [Google Scholar]
- 17.Larsen J J, Hald K, Bjerre N, Stapelfeldt H, Seideman T. Phys Rev Lett. 2000;85:2470–2473. doi: 10.1103/PhysRevLett.85.2470. [DOI] [PubMed] [Google Scholar]
- 18.Crowther R A. Philos Trans R London B. 1971;261:221–230. doi: 10.1098/rstb.1971.0054. [DOI] [PubMed] [Google Scholar]
- 19.van Heel M. Ultramicroscopy. 1987;21:111–124. doi: 10.1016/0304-3991(87)90078-7. [DOI] [PubMed] [Google Scholar]
- 20.Frank J. Three-Dimensional Electron Microscopy of Macromolecular Assemblies. San Diego: Academic; 1996. pp. 182–202. [Google Scholar]
- 21.Henderson R. Q Rev Biophys. 1995;28:171–193. doi: 10.1017/s003358350000305x. [DOI] [PubMed] [Google Scholar]
- 22.Lundqvist T, Schneider G. Biochemistry. 1991;30:904–908. doi: 10.1021/bi00218a004. [DOI] [PubMed] [Google Scholar]
- 23.Miao J, Sayre D. Acta Crystallogr A. 2000;56:596–605. doi: 10.1107/s010876730001031x. [DOI] [PubMed] [Google Scholar]
- 24.Woolfson M M. Acta Crystallogr A. 1987;43:593–612. [Google Scholar]
- 25.Szöke A. Chem Phys Lett. 1999;313:777–788. [Google Scholar]