Diversification rates and the latitudinal gradient of diversity in mammals

Abstract

The latitudinal gradient of species richness has frequently been attributed to higher diversification rates of tropical groups. In order to test this hypothesis for mammals, we used a set of 232 genera taken from a mammalian supertree and, additionally, we reconstructed dated Bayesian phylogenetic trees of 100 genera. For each genus, diversification rate was estimated taking incomplete species sampling into account and latitude was assigned considering the heterogeneity in species distribution ranges. For both datasets, we found that the average diversification rate was similar among all latitudinal bands. Furthermore, when we used phylogenetically independent contrasts, we did not find any significant correlation between latitude and diversification parameters, including different estimates of speciation and extinction rates. Thus, other factors, such as the dynamics of dispersal through time, may be required to explain the latitudinal gradient of diversity in mammals.

1. Introduction

The distribution of biodiversity on Earth is neither uniform nor random. Rather, it is structured into distinctive patterns that seem to be associated with geographical and climatic conditions [1]. On a global scale, one of the best-known patterns is the latitudinal gradient of diversity. Indeed, the increasing species richness from the poles to the tropics is a trend that has been recognized for more than two centuries in almost every group of organisms where it has been studied [2,3]. Paradoxically, even with so much focus on the topic, a full explanation of the latitudinal gradient of diversity remains elusive. In fact, multiple hypotheses have been proposed to date, but none has been completely proved [3–6].

During the last few decades, the study of the latitudinal gradient of diversity has been dominated by an ecological point of view [3,6]. Ecological hypotheses explain the existence of the latitudinal gradient as a consequence of differences in the species-carrying capacity of the ecosystems [6]. This way, testing these hypotheses usually involves the evaluation of the main limiting factors for species richness. Nevertheless, the main problem with these hypotheses is that it is not clear that niches are saturated in current ecosystems [7–9]. Moreover, even though a combination of ecological variables may be the ultimate cause behind the highest diversity found in the tropics, this does not tell us much about the processes that led to the latitudinal gradient of diversity.

Contrary to ecological hypotheses, evolutionary hypotheses are related to the birth and death of lineages through time and to the dispersal dynamics of species [5,6,10]. In fact, most of the evolutionary hypotheses assume that net diversification rates are higher in the tropics either because of increased speciation rates or decreased extinction rates, which have been respectively conceptualized in the metaphors of the tropics as a ‘cradle’ or as a ‘museum’ of diversity [11,12]. To justify differences in speciation or extinction rates between tropical and temperate groups, a number of explanations have been raised: differences in physiological tolerance ranges, evolutionary rates, environmental stability, area availability, etc. [6]. Nevertheless, it is still unclear whether differences in diversification rates are behind the latitudinal gradient of species richness. In fact, recent analyses have rendered inconsistent results: whereas some works have found higher diversification rates in the tropics for some primates [13], birds [14–17], amphibians [18] or plants [19], others have not shown appreciable differences for mammals and birds [20], or some groups of amphibians [21,22].

In this study, we used data from a mammalian supertree [23,24] and reconstructed a comprehensive and curated set of species-level time-calibrated phylogenies of mammalian genera specifically assembled for this study. In order to evaluate whether a latitudinal gradient of diversification rates parallels the latitudinal gradient of species richness, we did several correlation analyses of latitude and different diversification parameters. Our results show that there are no differences in diversification rates for genera living at different latitudes and therefore suggest that other factors may be necessary to explain the current spatial patterns of diversity in mammals.

2. Material and methods

(a). Datasets of genera

We used a recently updated supertree of mammals that comprises 5020 species [24] and extracted the genera that were monophyletic using a custom Perl script that uses Bioperl subroutines [25]. The genus was chosen as our taxonomic unit of study because mammalian genera present sufficiently restricted geographical distributions to allow comparisons of latitudinal ranges. Marine genera were excluded from the analyses because they follow a completely different pattern of distribution, with species richness peaks at high latitudes [26]. We also discarded the genus Mazama because it presented an abnormally low divergence time. This mammalian supertree is poorly resolved towards the present [23,24] and no reliable internal branching times can be obtained for most genera. Thus, we only used the divergence times of the genera for diversification analyses.

We also assembled a dataset of individual phylogenetic trees of terrestrial genera reconstructed with cytochrome b sequences. We used cytochrome b for the phylogenetic analyses because this gene has been sequenced in a much higher number of species of mammals than any other [27,28]. Following the taxonomy of Wilson & Reeder [29], we retrieved sequences from GenBank [30] for as many species as possible. We carried out a thorough process of curation and alignment using several programs in a semi-automated pipeline [31–34]. A detailed description of the methods followed is available in the electronic supplementary material, §S1.

(b). Reconstruction and calibration of phylogenetic trees

Since no calibration information exists for most of the analysed genera, we obtained secondary calibrations by carrying out a mammalian phylogenetic reconstruction, including a species pair for each genus used here as well as a set of other species needed for the placement of calibrations. This way, we assembled a dataset of 270 species by retrieving sequences from GenBank for five nuclear markers: growth hormone receptor (GHR), interstitial retinol-binding protein (IRBP), recombination activation gene 1 (RAG1), recombination activation gene 2 (RAG2) and von Willebrand factor (vWF), along with mitochondrial cytochrome b. Alignments were made for each gene using Mafft v. 6.833b [35] and Gblocks v. 0.91b [36]. We selected the best-fit substitution model by the Bayesian information criterion using jModeltest v. 0.1.1 [37] and reconstructed a Bayesian phylogenetic tree using BEAST v. 1.6.2 [38], which allows the co-estimation of tree topology (including the position of the root) and divergence times assuming an uncorrelated relaxed molecular clock model. We used the BEAGLE library [39] to speed up analyses. To date the tree, we used 63 fossil-based calibrations previously described by Meredith et al. [40]. Details on the procedure and priors, along with the position of the calibrations in the tree, can be found in the electronic supplementary material (§S2, tables S1–S4 and figure S1). Divergence times obtained for the species pair of each genus were then used as secondary calibrations for dating individual trees of genera. To that end, we fitted a gamma distribution to the posterior distribution of divergence times using the R package MASS v. 7.3 [41]. The estimated parameters were later used for calibration of each genus tree (electronic supplementary material, table S4).

Bayesian phylogenetic tree reconstructions of each genus were conducted using the BEAST package. As before, we selected the substitution model for each genus by the Bayesian information criterion (electronic supplementary material, table S5). We did not include any outgroup and therefore the root was estimated along with the rest of the parameters. For each genus, we performed between two and four runs of Markov chain Monte Carlo (MCMC) for 20 million generations, sampling every 1000 steps. To check for convergence, we compared chains visually with Tracer v. 1.5. We combined the runs with Logcombiner, removing the first five million generations of each one as burn-in and resampling every 3000 generations. Effective sample size of the posterior distribution of trees was over 1000 in all cases (over 200 for all parameters). The maximum credibility summary tree with median node heights was obtained using Treeannotator.

(c). Diversification rates estimation

Owing to the high number of polytomies present in the most recent part of the mammalian supertree, we estimated diversification rates using the method of moments of Magallon & Sanderson [42], which only requires knowing the number of species and the age of a given clade. To avoid underestimating diversification rates because of incomplete sampling in some genera, we considered the number of species described for each genus in the taxonomy of Wilson & Reeder [29]. Crown group diversification rates were estimated assuming no extinction (μ = 0) or a high extinction fraction (μ = 0.9).

The dataset of well-resolved trees of genera allowed the application of more sophisticated methods. Thus, apart from the Magallon & Sanderson estimator, we also used the maximum-likelihood coalescent approach of Morlon et al. [43], which allows the estimation of diversification rates with incomplete sampling using different models. As before, we considered the number of species described for each genus in the taxonomy of Wilson & Reeder [29]. In particular, we fitted two biologically realistic models: a constant birth–death model and a variable birth–death model with exponential variation in speciation and constant extinction. In this variable diversification model, the speciation rate is regulated by the α parameter, which is positive if there is a progressive decrease in speciation rate and vice versa. Models of gradual diversification have been found to be adequate for describing the diversification patterns of different groups [43–46]. Moreover, this model allows discerning between initial and current diversification rates of the genera. We used different combinations of initial values of the parameters to prevent getting trapped in local maxima.

(d). Geographical data and latitude assignment

We retrieved distribution maps of terrestrial mammals publicly available in ESRI Shapefile format from the IUCN website [47]. The maps covered the extent of occurrence for 5279 species, but we found nomenclatural correspondence with the Wilson & Reeder [29] taxonomy for only 4857 species.

In order to assign a latitudinal value to each genus, we divided the world in 15° latitudinal bands and calculated the number of species of the genus present in each band. Then we assigned the mode latitude to each genus, defined as the midpoint of the latitudinal band with the highest number of species. In cases of equal intervals, we assigned the midpoint between intervals.

Alternatively, we used the individual phylogenetic trees of genera to reconstruct the ancestral latitudinal state of the root. Thus, we used the midpoint of the latitudinal range of each species and reconstructed ancestral states using the method of Felsenstein [48], which assumes a Brownian model of evolution, as implemented in the R package APE v. 3.0 [49].

These tasks were automated by means of Perl scripts, which make extensive use of the Geo::ShapeFile v. 2.52 and Geo::Shapelib v. 0.20 modules (available at http://www.cpan.org).

(e). Correlation analysis and phylogenetically independent contrasts

It is well known that phylogeny can have a deep impact on correlation analyses [48,50], and it could happen that genera inhabit similar latitudes and show similar diversification rates because of shared ancestry rather than correlation among both variables. For this reason, we obtained standardized phylogenetically independent contrasts with the R package APE and performed the correlation analyses between latitude and diversification parameters. Following the standard procedure [48,51], we fitted regression lines through the origin by ordinary least squares. For obtaining the contrasts, we compared different genera using the mammalian supertree or the phylogenetic reconstruction of mammals, depending on the dataset.

3. Results

(a). Data overview

The dataset derived from the mammalian supertree comprised 232 genera (2976 species, 67 families and 17 orders), with an average species sampling coverage of 93 per cent (electronic supplementary material, table S6). The dataset of individual phylogenetic reconstructions consisted of 100 genera (1198 species, 37 families and 10 orders), with an average sampling of 67.5 per cent. The divergence times of the 84 genera shared by both datasets were moderately correlated (Pearson's r = 0.504, p < 0.0001).

(b). Phylogenetic reconstructions and diversification rates

We estimated net diversification rates for each of the 232 genera extracted from the mammalian supertree using the Magallon & Sanderson estimator, with and without extinction (electronic supplementary material, table S6). As expected, diversification rates were higher when no extinction was assumed (mean of 0.184 versus 0.070 Myr⁻¹). However, both estimates were highly correlated (r = 0.988, p < 0.0001), suggesting that assuming extinction with this estimator has little impact on comparative analyses.

We also reconstructed calibrated Bayesian phylogenetic trees of 100 genera using secondary calibrations (electronic supplementary material, figure S1 and table S4) and calculated diversification parameters using different approaches (electronic supplementary material, table S7). First, we used the Magallon & Sanderson estimator for comparative purposes, obtaining a mean diversification rate of 0.326 Myr⁻¹ (without assuming extinction). Diversification rates in the dataset of Bayesian trees were higher than in the supertree genera, probably owing to the selection of more species-rich genera, for tree reconstructions. Second, we inferred diversification rates by fitting a constant birth–death model by maximum likelihood, obtaining similar results (mean = 0.287 Myr⁻¹). The correlation between these estimates was very high (r = 0.934, p < 0.0001). In addition, estimated extinction rates were very low for most genera; in fact, only seven genera showed extinction rates greater than zero (electronic supplementary material, table S7). Finally, we fitted a model that assumed exponential variation in speciation and constant extinction. Initial diversification rates were moderately correlated with both the Magallon & Sanderson estimates (r = 0.513, p < 0.0001) and the constant birth–death estimates (r = 0.446, p < 0.0001). Final diversification rates were also moderately correlated with previous estimates (r = 0.440, p < 0.0001 and r = 0.437, p < 0.0001, for Magallon & Sanderson and constant birth–death estimates, respectively) but, interestingly, both initial and final diversification rates were uncorrelated. Using this model, 59 genera showed positive extinction rates. The parameter α was positive for all but one of the genera, indicating that a decline in speciation rate is the most common trend in mammalian genera, in agreement with previous results [45].

(c). Assignment of latitudes to genera

We assigned as the representative latitude for each genus the mode of the distribution of the species latitudes discretized in 15° latitudinal bands. This approach has significant advantages over the widely used midpoint latitude using the global distribution of the genus, because it associates to each genus the latitude value where most species of that genus live, which probably represents the latitude with optimal conditions for the group. We chose 15° as the most reasonable latitudinal interval for discretizing distributions based on the precision that we can achieve with our data, and because it is an adequate range to recover climatic and ecological variables that may ultimately be behind the distribution of species. Furthermore, other intervals such as 10° or 5° rendered similar results (data not shown).

In the case of the dataset based on individual phylogenetic trees of genera, we alternatively assigned to each genus the reconstructed ancestral latitude for the root inferred from the midpoint latitude of the species. Latitudes assigned using both methods were strongly correlated (r = 0.954, p < 0.0001), suggesting a very limited effect on the subsequent comparative analyses. Latitudinal values assigned to each genus are shown in the electronic supplementary material, tables S6 and S7.

Using these latitude assignments, we confirmed that the distributions of species richness conform to the latitudinal gradient of diversity (electronic supplementary material, figure S2).

(d). Is there a conspicuous latitudinal gradient of diversification rates in mammals?

If the latitudinal gradient of species richness was due to differences in diversification rates, we should observe that diversification rates are higher in the tropics. In the dataset of genera derived from the supertree, box plots of diversification rates in every 15° latitudinal band did not show any noticeable trend (figure 1a). In the case of the Bayesian phylogenetic trees, a slight increase in diversification rate is observed at lower latitudes with the two different calculation methods (figure 1b,c), although no difference was significant (the Tukey–Kramer test at a level of 0.05), neither between the latitudinal bands nor when they were grouped in two classes (two central latitudinal bands and the rest). In addition, correlation between diversification rate and absolute latitude did not show significance in any of the three analysed cases.

Figure 1.

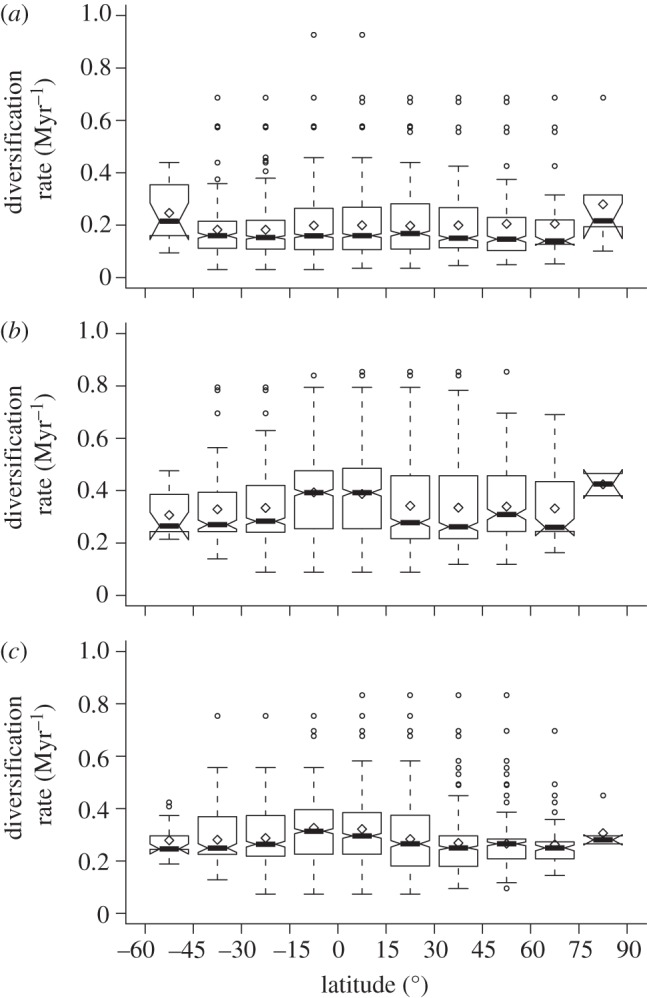
Distribution of diversification rates of genera present in each latitudinal 15° band. Results are shown for (a) the diversification rates for the 232 monophyletic genera extracted from the mammalian supertree [24], estimated using the method of Magallon & Sanderson [42]; (b) the diversification rates for the 100 genera whose trees where specifically reconstructed for this study, estimated using the method of Magallon & Sanderson; and (c) the diversification rates for these 100 genera, estimated by fitting a constant birth–death model. The box plots show median values (bold lines) and quartile values. Notches denote 95% confidence intervals (overlapping notches suggest that medians do not differ significantly). Outliers are defined as points beyond 1.5 times the interquartile range and are indicated by white circles. White diamonds represent means.

When latitude assignments were based on the ancestral reconstruction, results were similar, and also none of the correlations between diversification rate and absolute latitude was significant.

(e). Is there a correlation between diversification rates and latitude?

In order to account for the possible incidence of phylogeny on the correlation analyses, we obtained 463 phylogenetic contrasts from the mammalian supertree. For the Magallon & Sanderson estimator assuming no extinction, the regression line showed a regression coefficient (R²) of 0.0022, which was not statistically significant (p = 0.4741).

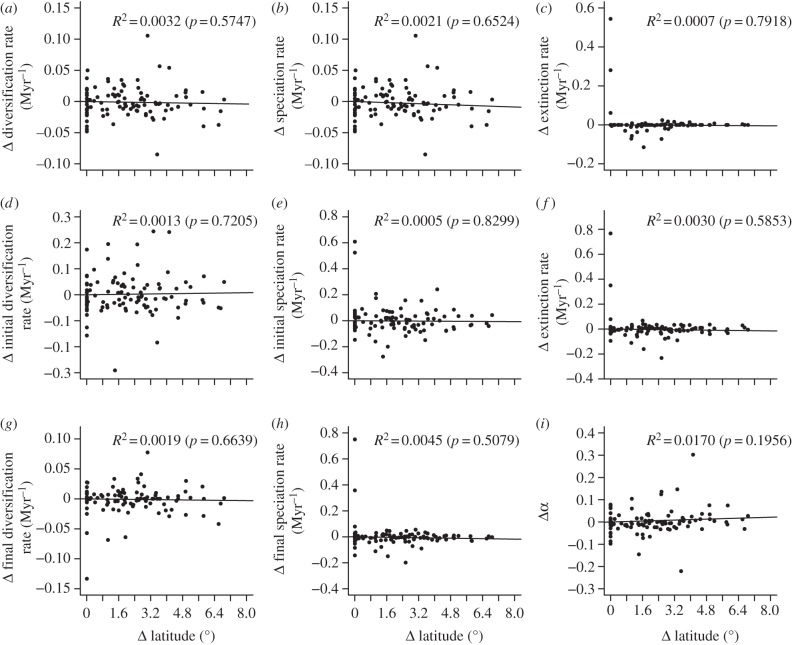
For the 100 genera with individual phylogenetic reconstructions, we obtained 199 phylogenetic contrasts. The regression coefficient for contrasts using diversification estimated with the Magallon & Sanderson method was very low and not significant (R² = 0.0001, p = 0.9041). For analyses of estimates coming from fitting a constant birth–death model (figure 2a–c), regressions were not significant for diversification rate (R² = 0.0032, p = 0.5747), speciation rate (R² = 0.0021, p = 0.6524) nor extinction rate (R² = 0.0007, p = 0.7918). Analyses using estimates by fitting a variable birth–death model (figure 2d–i) were also not significant for any of the parameters: initial diversification rate (R² = 0.0013, p = 0.7205), initial speciation rate (R² = 0.0005, p = 0.8299), extinction rate (R² = 0.0030; p = 0.5853), final diversification rate (R² = 0.0019, p = 0.6639), final speciation rate (R² = 0.0045, p = 0.5079) and α (R² = 0.0170, p = 0.1956).

Figure 2.

Regression analysis of standardized phylogenetically independent contrasts between latitude and diversification parameters estimated by fitting (a–c) a constant birth–death model and (d–i) a variable birth–death model with exponential variation in speciation and constant extinction. Results are shown for (a) diversification rate, (b) speciation rate, (c) extinction rate, (d) initial diversification rate, (e) initial speciation rate, (f) extinction rate, (g) final diversification rate, (h) final speciation rate and (i) α. Regression coefficients (R²) and corresponding p-values are displayed on the top right of each panel. Regression lines fitted by least squares forcing regression through the origin are also shown.

Although the method employed for the estimation of diversification parameters can be used with incomplete sampling, the coverage was low for some of the 100 genera of this dataset. Therefore, we repeated the correlation analyses using only 75 genera (151 contrasts) for which we had a sampling coverage greater than or equal to 50 per cent. Results using this subset of genera were very similar, and no significant correlation was found between latitude and any of the diversification parameters. Likewise, we carried out additional analyses using ancestral latitude assignments, which rendered similar results, with no significance between any of the estimated diversification parameters and latitude. Detailed information on all phylogenetic contrasts analyses can be found in the electronic supplementary material, table S8.

4. Discussion

(a). Diversification rates do not explain the latitudinal gradient of diversity in mammals

Diversification rates are commonly assumed to drive the latitudinal gradient of biodiversity. Furthermore, many hypotheses have been raised in an attempt to explain how differences in diversification rates across latitude might have been generated. A recent review [6] listed nine hypotheses considering why the tropics might exhibit either higher speciation rates (including genetic drift, climatic variation, differences in area or differences in evolutionary rates, among other triggering factors) or lower extinction rates (because of higher stability or larger ranges in tropical areas). Nevertheless, we have shown here that, at least in mammals, net diversification rates of genera are very similar for different latitudes; thus, there is apparently no need for any of these explanations. Even after considering a complex model that allows for the variation of diversification rates and takes into account both extinction and incomplete sampling, we did not find any evidence of significant differences in either initial or final diversification rates for genera that inhabit different latitudes. We also found no latitudinal patterns in any of the two components of diversification: speciation and extinction.

Our results are in agreement with a recent study of mammals that found that the gradient in diversification rates (estimated from distributions of divergence times between sister species) was not significantly different from zero [20]. Likewise, analyses of diverse groups of vertebrates and invertebrates showed that net diversification rates did not correlate with species richness, suggesting that differences in species richness must be driven by other factors [52]. However, different results have been obtained in analyses of amphibians and birds. In the first case, a global analysis of amphibians showed an inverse correlation between diversification rates and latitude [18], although this correlation was lost when particular families of anurans were examined [21,22], indicating that different taxonomic levels could reflect the impact of different forces in the generation of biodiversity. In the case of birds, although several analyses indicated that a gradient of diversification rates parallels the gradient of species richness [14,15], a more recent analysis did not find any significant correlation [20]. All these different results seem to suggest that the trend that we found for mammals might not be applicable to all taxa and that, in spite of the apparent universality of the latitudinal gradient of diversity, it might have been generated by different combinations of ecological and evolutionary forces for different groups [53]. However, such a taxonomically and geographically pervasive global pattern is likely to have a general explanation involving a few common primary causes, justifying the need for further investigations with a global perspective [54].

(b). Other explanations for the latitudinal gradient in mammals

Although we did not observe a significant correlation between diversification rate and latitude, it could be that small differences in rates remain undetected in current phylogenies. Moreover, it is true that even slight differences in diversification rates could produce a strong latitudinal gradient, provided that they are sustained over a long period of time. Better species coverage of all mammals may help to detect these possible small differences in diversification rates and to analyse the possibility that they played a role in generating the latitudinal gradient of diversity.

It is also known that latitudinal gradients of diversity can be traced back in the fossil record to the Palaeozoic, and the current latitudinal gradient probably originated in the early Cenozoic [55]. If the latitudinal gradient originated in these early times and in a very short period, it might be that the factors that contributed to its origin ceased to operate far before the time span covered by mammalian genera. If this was the case, the analyses of genera might not be able to detect differences in diversification rates. Thus, analyses at higher taxonomic levels might be necessary to reveal such ancient forces (provided that the difficulties in the assignment of latitudes to groups with very wide ranges can be overcome). In summary, since diversification rates are likely to have changed through time, analyses at different taxonomic levels can provide complementary information about the different evolutionary forces that have been contributing through time to the generation of biodiversity patterns.

Differences in extinction rates have also been proposed to explain the latitudinal gradient of diversity [3,6]. In this respect, we have not found evidence of correlation between latitude and extinction rate in the phylogenies of mammalian genera, assuming constant background extinction and random species sampling. Nevertheless, it has been noted for a long time that, whereas tropical areas are climatically stable through extended periods of time, temperate areas are much more affected by episodes of large climatic changes [56,57]. During these catastrophic episodes, whole clades (e.g. genera or subgenera) might have disappeared from high latitudes, leaving no signal at all in molecular phylogenies at low taxonomic levels [18,22]. In fact, the recent study of Weir & Schluter [20] pointed to a faster turnover of mammal species at high latitudes, which might mean that whole clades go extinct more frequently in temperate and boreal zones. If this is the case, the exclusion of such extinct clades from analyses might result in a biased estimation of the average diversification rates for these regions. This extinction pattern might be detected using more inclusive phylogenies at higher taxonomic levels. Nevertheless, caution must be exercised in the interpretation of these results, because the estimation of extinction is very difficult from molecular phylogenies alone [58,59]. Consequently, only the examination of fossil data in an appropriate phylogenetic framework will allow discerning the influence of extinction on the generation of the species richness gradients.

All the hypotheses considered so far ignore the dispersal dynamics of species and clades. However, frequent changes in the geographical distributions of species through time are well documented [60,61], suggesting that these range shifts might have also played a key role in the generation and maintenance of the latitudinal gradient of diversity. The relevance of dispersal as a driver of diversity gradients has been highlighted by simulation analyses using models that incorporate the contribution of dispersal and macroevolutionary dynamics together [62]. In addition, a few studies have already examined empirical data considering the relative contributions of diversification rates and the timing of dispersal to the latitudinal gradient of diversity, and strongly supported the importance of dispersal relative to diversification rates [21,22,60]. Certainly, it has been proposed that tropical lineages might have developed strong physiological constraints derived from a high specialization in stable environments, limiting their dispersal ability to other climatic regions [63,64]. This has given rise to the so-called tropical conservatism hypothesis [10]. Conversely, temperate and boreal groups are thought to have wider ecological tolerances because of their evolution under harsh and changing environments, which would have enabled them to colonize other regions more frequently than their tropical counterparts [57,65]. According to these hypotheses, we would expect to find an evolutionary trend consisting of lineages producing descendants that shift towards lower latitudes more frequently than the opposite. However, trends can be much more complex than that, as it has been shown that patterns can vary among groups and through time [53,66]. Given that our results suggest that differences in diversification rates might not have played a key role in the generation of the latitudinal gradient, it seems that further research on the dynamics of dispersal through time, and not only on diversification trends, will be necessary to fully understand the factors that shaped the spatial distribution of diversity in mammals.