Abstract
The N-H stretching vibrations of adenine, one of the building blocks of DNA, are studied by combining infrared absorption and nonlinear two-dimensional infrared spectroscopy with ab-initio calculations. We determine diagonal and off-diagonal anharmonicities of N-H stretching vibrations in chemically modified adenosine monomer dissolved in chloroform. For the single quantum excitation manifold, the normal mode picture with symmetric and asymmetric NH2 stretching vibrations is fully appropriate. For the two-quantum excitation manifold, however, the interplay between intermode coupling and frequency shifts due to a large diagonal anharmonicity leads to a situation where strong mixing does not occur. We compare our findings with previously reported values obtained on overtone spectroscopy of coupled hydrogen stretching oscillators.
1.Introduction
Nucleic acid bases, building blocks of DNA and RNA, have been investigated with numerous experimental and theoretical methods. In light of the hydrogen bonding interactions between complementary nucleic acid bases, linear vibrational spectroscopy has been one of the favoured techniques, as N-H stretching modes provide a direct local probe of these interactions. Typically one follows either a top-down approach, where a DNA (or RNA) double helix formed by a specific base pair sequence is studied,1–3 or a bottom-up approach, where only a limited number of building blocks, i.e. nucleic acid bases, are included in the study. In recent years, individual bases and base pairs have been studied in the gas phase4–7 and in solution.8–12 Despite the fact that both in the gas phase and in solution such a bottom-up approach involves the existence of several different hydrogen-bonded complexes, a characterization of infrared (IR) spectra has been possible by applying a comparison to theoretical spectra resulting from density functional theory calculations.
Until now, most of these studies have relied on linear IR spectra which give insight into the frequencies and cross sections of the fundamental v=0 to 1 transitions. Apart from leaving much ambiguity in the assignment of N-H stretching bands, the diagonal anharmonicities and the couplings between different modes, i.e., the off-diagonal anharmonicities have remained unspecified. Ultrafast nonlinear pump-probe and two-dimensional (2D) infrared spectroscopy give direct insight into such behaviour, as has been demonstrated for N-H and C=O stretching excitations of DNA sequences and oligomers.2,3,13–19 To a lesser extent, nucleobase pairs and monomers in solution12,20–22 have been studied by such techniques. As a result the diagonal and off-diagonal anharmonicities of uncomplexed nucleic bases have so far remained elusive.
In this article, the N-H stretching modes of adenosine monomer in chloroform solution (Figure 1) are studied by a combination of ultrafast nonlinear infrared spectroscopy and ab-initio calculations of vibrational modes and couplings. The adenosine monomer contains a NH2 group with two local N-H stretching oscillators. We deduce from linear and 2D-IR spectra the diagonal and off-diagonal anharmonicities of the N-H stretching modes. We analyse the observed frequency shifts in the linear and 2D-IR spectra using both normal and local mode representations, the latter allowing for a detailed comparison with theory. We substantiate these results by ab-initio calculations which provide local diagonal anharmonicities and intermode couplings.
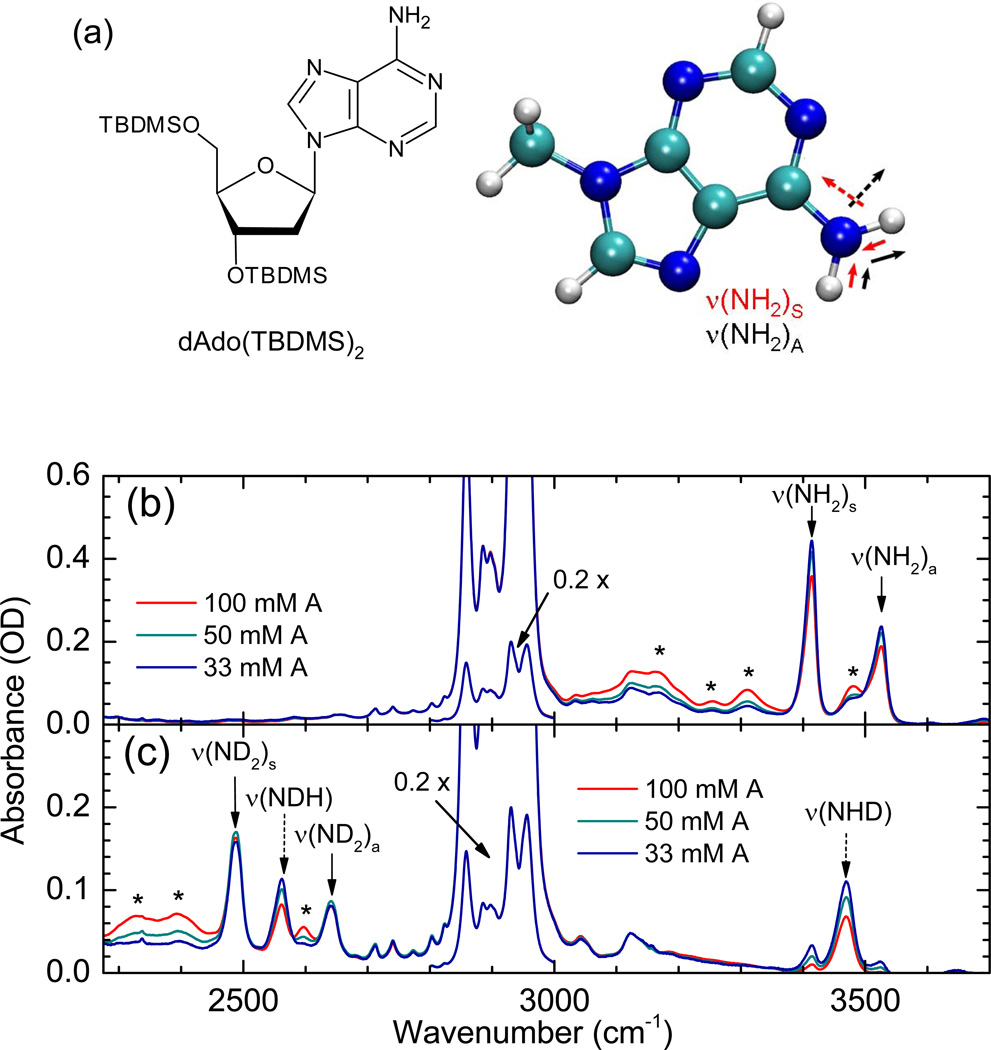
Figure 1.
(a) Molecular structure of A, incl. TBDMS-ribose side group. The symmetric and asymmetric N-H stretching normal modes of 9-mA are also shown. (b) Linear FT-IR spectrum of A in CDCl3. (c) Linear FT-IR spectrum of partially H/D-exchanged A in CDCl3. Relevant N-H and N-D stretching modes are assigned with arrows; asterisks denote bands of A•A complexes; the spectral region between 2800 and 3000 cm−1 showing the C-H stretching modes of the TBDMS-ribose side groups have been scaled by a factor of 0.2.
2. Experimental and Theoretical Methods
Linear and nonlinear IR spectroscopy
Chemically modified 2’-deoxyadenosine nucleoside was synthesized in a similar fashion as reported before.11 To increase the solubilities in weakly polar solvents, the hydroxyl groups of the ribose units were substituted with tert-butyldimethylsilyl (TBDMS) groups. We denote the chemically modified nucleic base 3’,5’-TBDMS protected 2’-deoxyadenosine as species A (Fig. 1a). CHCl3 (Uvasol, ≥ 99.0% purity) was obtained from Aldrich and CDCl3 from Deutero. The solvent was dried over molecular sieves with pore diameters of 0.3 nm. Deuteration of the amino-group of adenosine was obtained by dissolving A in a hundred-fold excess amount of methanol-d1. After a few minutes, the solvent was removed in vacuum. This procedure was repeated once before the substance was taken up in chloroform and the solution was transferred to a cuvette, leading to about a 70% degree of deuteration.
Linear IR spectra were recorded at room temperature with a Varian 640 FT-IR spectrometer (resolution 1 cm−1). The solutions were held between 1 mm CaF2 windows with absorption path lengths of 0.2 mm using Teflon spacers. Femtosecond IR pump-probe and 2D-IR photon echo experiments were performed as described before.12 In short, the mid-IR pulses, generated by parametric down-conversion of the output of an amplified Ti:sapphire laser system, had a centre frequency of 3350 cm−1 and a pulse energy of 500 nJ, the pulse duration was 50 fs. In the pump-probe experiments, the probe pulses were spectrally dispersed after interaction with the sample (resolution 4 cm−1). The 2D-IR spectra have a resolution of 10 cm−1 along the excitation frequency ν1, and 9 cm−1 along the detection frequency ν3. For the ultrafast experiments, we use a 0.04 M solution of A in CHCl3 which was held between 1 mm CaF2 windows with an absorption path length of 0.2 mm.
Quantum chemical calculations
Ab-initio calculations were performed on 9-methyladenine (9-mA) and 9-methyladenine-d2 (9-mA-d2), where the amino hydrogens have been exchanged with deuterium. All calculations were preformed in the gas-phase, at the HF/6-311++G** level of theory using Gaussian 09.23 Linear absorption and absorptive 2D IR spectra (kI + kII) were calculated using the sum over states expressions as implemented in SPECTRON.24 All calculations were performed in the impulsive limit using a homogeneous dephasing of 4 cm−1. For the 2D-IR calculations, the sum over states expressions were used (for a complete description see reference25) with the population time (t2) fixed to 0 fs. To account for inhomogeneous broadening, a stochastic gaussian frequency fluctuation was added to the symmetric and asymmetric fundamental (eigenstate) frequencies over 500 snapshots.24 Anharmonic shifts were fixed to the gas-phase value.
3. Experimental Results and Discussion
Figure 1 shows the linear FT-IR spectra of A in chloroform, before and after partial H/D exchange of the hydrogen atoms in the adenosine NH2-group. In a normal mode picture, the infrared band of non-deuterated A at 3413 cm−1 is assigned to the symmetric NH2 stretching mode ν(NH2)S while the asymmetric stretching band ν(NH2)A occurs at 3525 cm−1. From the frequency difference between these two transitions, i.e., 2JH = ν(NH2)S − ν(NH2)A = −112 cm−1, a ‘mechanical’ coupling of JH = −56.0 cm−1 between the two local N-H stretching modes can be deduced. Slightly larger values for JH of −57.5 to −59.0 cm−1 are found for gas-phase 9-H-adenine and 9-methyl-adenine,26–28 9H-adenine in Helium nanodroplets6 and in Ar matrices,29 and 9-ethyladenine in CDCl3 solution.8
In the partially H/D exchanged sample the symmetric ND2 stretching mode ν(ND2)s is observed at 2489 cm−1 and the asymmetric ND2 stretching mode ν(ND2)A at 2639 cm−1, leading to a value for the splitting of 2JD = ν(ND2)S − ν(ND2)A = −154 cm−1, i.e., JD = −77.0 cm−1). The H/D exchange yield is estimated to be ~70%, with the result that not only A monomers with fully exchanged ND2-groups contribute to the spectrum, but also partially exchanged A monomers, for which both the local N-H and the N-D stretching modes of an NHD-group are observed. This partial exchange allows for determining the transition frequencies of the virtually decoupled local N-H and N-D stretching modes of the NHD-group: ν(NH) = 3469 cm−1 and ν(ND) = 2565 cm−1. These values lie perfectly halfway the symmetric and asymmetric normal mode stretching frequencies, showing that the exchange of a single hydrogen atom with a deuterium effectively decouples the two local N-H stretching modes. Moreover, it explicitly confirms the validity of regarding the normal modes as linear combinations of the local N-H(D) modes, with a splitting caused by the extracted couplings. From the decoupled local mode frequencies it follows that the H/D-isotope effect on the local NH stretching mode frequency is equal to 1.352, whereas the isotope effect on the coupling between the two local modes is JH / JD = (1.375)−1.
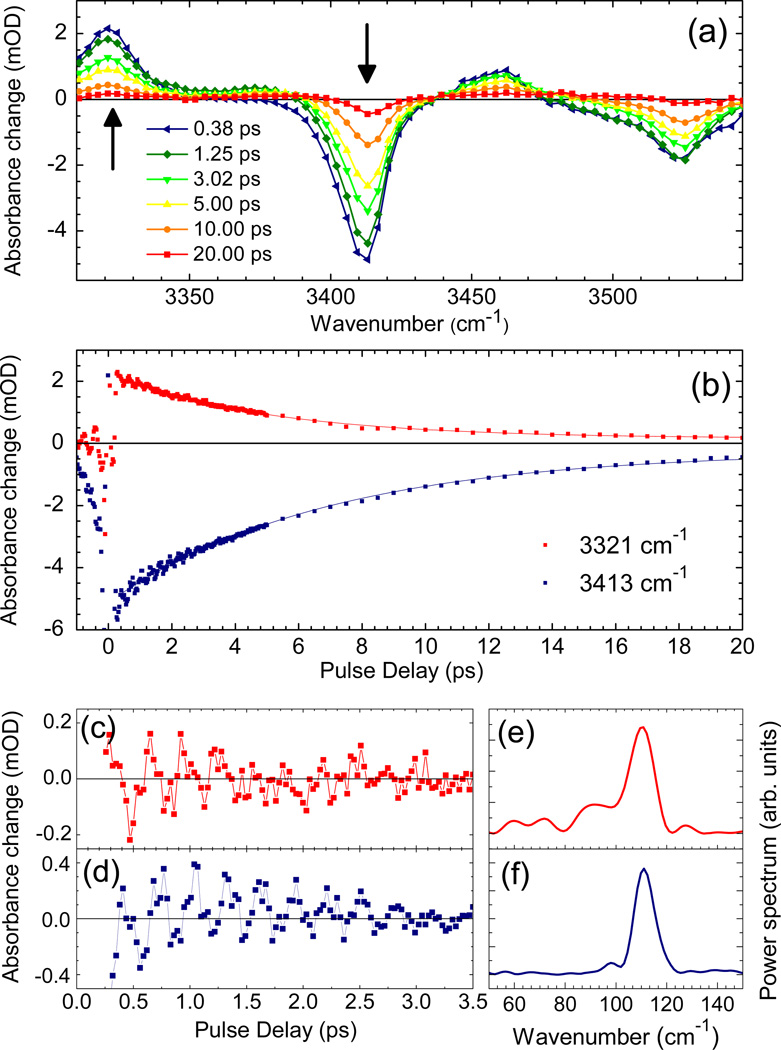
To determine the vibrational population dynamics, we performed time- and frequency-resolved pump-probe measurements. In Figure 2a, transient pump-probe spectra are plotted for delay times between 0.2 and 40 ps. On the fundamental transitions at ν(NH2)S ≈ 3415 cm−1 and ν(NH2)A ≈ 3525 cm−1, one observes a prominent decrease of absorption which is due to the depletion of the respective v=0 ground state and stimulated emission from the respective v=1 state. The bleaching components below 3380 and 3500 cm−1 are caused by transitions of complexed A molecules (cf. asteriks in Fig. 1a). The complexed molecules which will not be considered in the following, show a somewhat higher transition dipole μt than the (monomeric) species A. Thus, their relative intensity in the pump-probe spectra proportional to (μt)4 is higher than in the linear infrared absorption spectra proportional to (μt)2. The enhanced absorption below 3340 cm−1 is due to the v=1 to 2 absorption of the two normal modes. Figure 2b shows the time-resolved bleach recovery at ν(NH2)S=3415 cm−1 and excited state absorption decay measured at 3319 cm−1 which display a similar time evolution. From an exponential fit (solid lines), we derive a v=1 lifetime of the ν(NH2)S mode T1 = 6 ± 1 ps. The time-resolved bleach recovery at 3526 cm−1 (not shown) gives a T1 =10 ± 2 ps for the ν(NH2)A mode. Comparable values for the vibrational lifetime of N-H stretching modes have been found for other heterocyclic compounds having free N-H modes in chloroform solution.12,30,31 There is a weak residual bleaching signal on the (fundamental) v=0 to 1 transitions of ν(NH2)S and ν(NH2)A which we assign to a vibrationally heated ground state formed after the decay of the v=1 states.
Figure 2.
Pump-probe results for A dissolved in CHCl3 (concentration 40 mM). (a) Transient pump-probe spectra for different delay times. (b) Kinetic traces of signals (symbols) in the range of the symmetric NH2 stretching mode ν(NH2)s: v=1 to 2 excited state absorption at 3315 cm−1 and v=0 to 1 absorption decrease at 3419 cm−1. The solid lines represent a single exponential fit with a 6 ± 1 ps time constant, the v=1 lifetime. (c,d) Oscillatory components of the pump-probe signals and (e,f) respective Fourier transforms showing the 112 cm−1 beat frequency.
The oscillatory component on the pump-probe transients of Figure 2b, obtained after correction for the slow picosecond exponential population decay, is shown in Figure 2c,d, and the corresponding Fourier transforms are given in Figure 2,e,f. From this analysis we derive an oscillation frequency of 112 cm−1 (corresponding to a period of 298 fs), with a dephasing time of ~ 1 ps. The pump spectrum covers both the v=0 to 1 transitions of the ν(NH2)S and ν(NH2)A modes. An excitation scheme where spectrally distinct components of the pump field induce the two transitions simultaneously, generates a coherent superposition of quantum states. As a result, the coherent superpositions induced by the pump pulse results in quantum beats between the ν(NH2)S and ν(NH2)A normal modes with a frequency of 2|JH| = ν(NH2)A − ν(NH2)S = 112 cm−1 in the subsequent time period.32 The relatively long dephasing time of this quantum beat is fully in line with the observed difference in line widths of the inhomogeneously broadened transitions of the ν(NH2)S and ν(NH2)A modes (FWHM 21 and 30 cm−1, respectively).
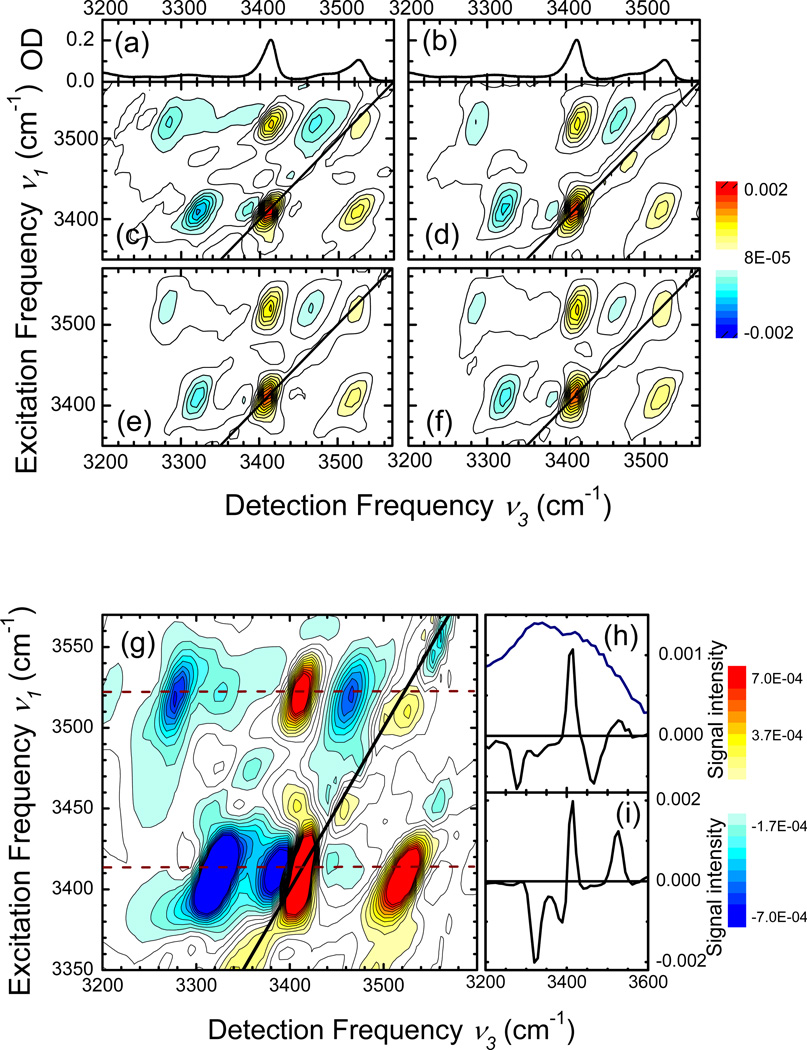
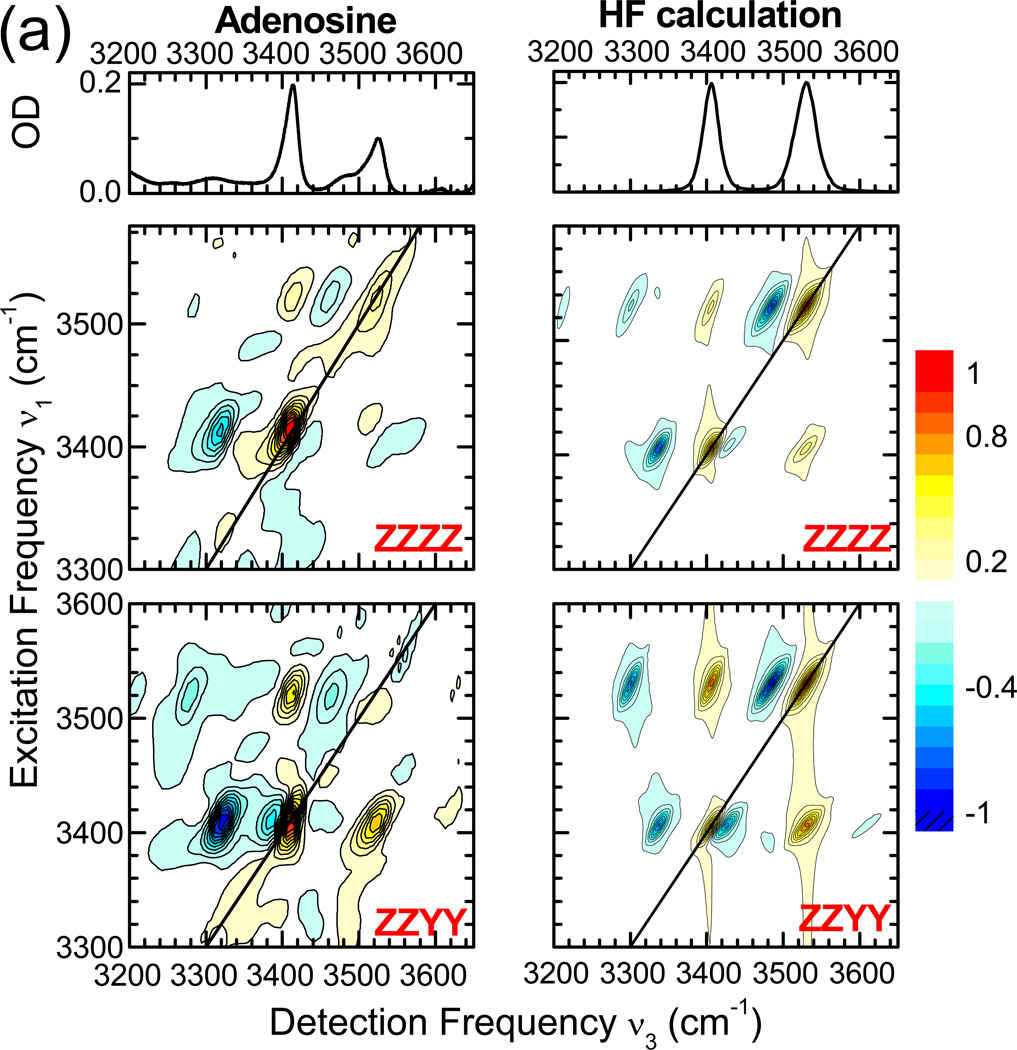
Figure 3 shows 2D-IR spectra of A dissolved in CHCl3, obtained with the (k1,k2,k3,kLO) = (ZZYY) polarisation geometry. We plot absorptive 2D-IR spectra, i.e. the sum of the rephasing and non-rephasing signals. The 2D spectra were recorded for (population) waiting times of (c) T = 0.2 ps, (d) 0.3 ps, (e) 0.5 ps, and (f) 1.0 ps. Each 2D spectrum is normalized to the maximum positive signal at (ν1[cm−1], ν3[cm−1]) = (3413, 3413). The 2D spectra display two prominent positive diagonal peaks at (3413,3413) and (3525,3525) which originate from the v=0 to 1 transitions of the ν(NH2)S and ν(NH2)A normal modes (cf. linear infrared spectra in Figs. 3a,b). In addition, there are positive cross peaks at (3413,3525) and (3525,3413) and negative off-diagonal peaks at (3413,3320), (3413,3390), (3525,3280), and (3525,3465). As a function of population time T, the spectral positions, lineshapes and relative intensities of the different peaks display minor changes. This observation suggests a minor role of spectral diffusion on this time scale and a negligible energy transfer from the ν(NH2)A mode at 3525 cm−1 to the ν(NH2)S mode at 3413 cm−1, as is to be expected given the 6 and 10 ps lifetimes.
Figure 3.
2D-IR spectra of adenosine monomer as a function of the waiting time T, using the (ZZYY) polarisation condition: (c) 0.2 ps, (d) 0.3 ps, (e) 0.5 ps, (f) 1.0 ps. The linear FT-IR spectra are shown in the top panels (a,b). The 2D-IR spectrum measured at T = 0.2 ps is shown on a blown-up scale in panel (g) together with cross cuts (solid lines) for (h) ν3 = 3525 cm−1 and (i) ν3 = 3525 cm−1. The blue line indicates the laser spectrum of the IR pulses used.
In Fig. 3g, we show the spectrum of Fig. 3c on a magnified intensity scale. Cuts along the detection frequency axis for ν1 = 3525 and 3413 cm−1 (dashed lines in Fig. 3g) are plotted in Figs. 3h,i, together with the (intensity) spectrum of the femtosecond infrared pulses in Fig. 3h. In addition to the strong peaks originating from the monomeric species A, there are a number of weaker peaks caused by complexed molecules.
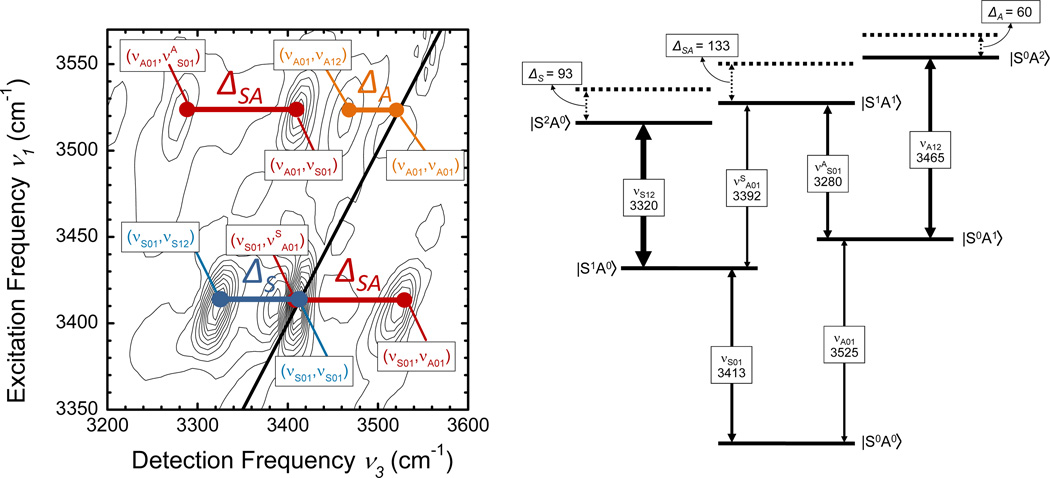
We now interpret the 2D spectra by assigning the different peaks to different vibrational transitions in the normal-mode picture. The corresponding level scheme is shown in Figure 4, together with a schematic 2D spectrum including the assignments. The fundamental v=0 to 1 transitions of ν(NH2)S and ν(NH2)A give rise to the diagonal peaks at (νS01,νS01) = (3413, 3413) and (νA01,νA01) = (3525,3525). In addition, there are the v=1 to 2 transitions of each of the two normal modes and the transition to the combination state in which both modes are excited on their fundamental transition. The frequency spacing of the positive peak at (νA01,νS01) = (3525,3413) and the negative peak at (νA01,νSA12) = (3525,3280) has a value of ΔSA ≈ 133 cm−1. The detection frequency spacing between the positive peak at (νS01,νA01) = (3413,3525) and the negative peak at (νS01,νAS01) = (3413,3392) has the same value within the experimental accuracy. Thus, we assign the two peak patterns to the two quantum excitation of the coupled normal modes where both modes are excited on the fundamental transition and the combined excitation is anharmonically down-shifted by ΔSA ≈ 133 cm−1 compared to the sum of the two fundamental frequencies of 3413 + 3525 = 6938 cm−1. The pairs of positive and negative off-diagonal peaks at the two excitation frequencies νS01 = 3413 cm−1 and νA01 = 3525 cm−1 is characteristic for this double excitation.33 In addition to such pairs of off-diagonal peaks, there are negative peaks at (νS01,νS12) = (3413,3320) and (νA01,νA12) = (3525,3465) which represent the v=1 to 2 contributions of ν(NH2)S and ν(NH2)A. From their detection frequency values, we derive a diagonal anharmonicity ΔS = 3413-3320 = 93 cm−1 and ΔA = 3525-3465 = 60 cm−1.
Figure 4.
The level scheme in the normal mode representation is shown together with the strongly allowed n=0 → n=1 and n=1 → n=2 transitions, together with the anharmonic frequency shifts for the n=2 excitation manifold.
4. Theoretical Analysis and Discussion
The measured 2D spectra are in qualitative agreement with the normal mode description, discussed in Section 3. An alternative choice of vibrational coordinates are the local N-H stretching modes. In principle, the two types of mode descriptions lead to equivalent predictions of the observed transitions, as they are linked by a mere basis set transformation. For a more detailed analysis with the help of theoretical calculations, we now introduce the local mode picture, which has been used extensively in overtone spectroscopy.34–37 Using local modes has been shown to be advantageous in the explanation of the interplay of couplings and anharmonic shifts of overtone states of in particular hydrogen stretching modes. Comparison of the results obtained on the local N-H stretching modes of A with previously published data on O-H and N-H stretching modes of a variety of molecules is therefore straightforward.
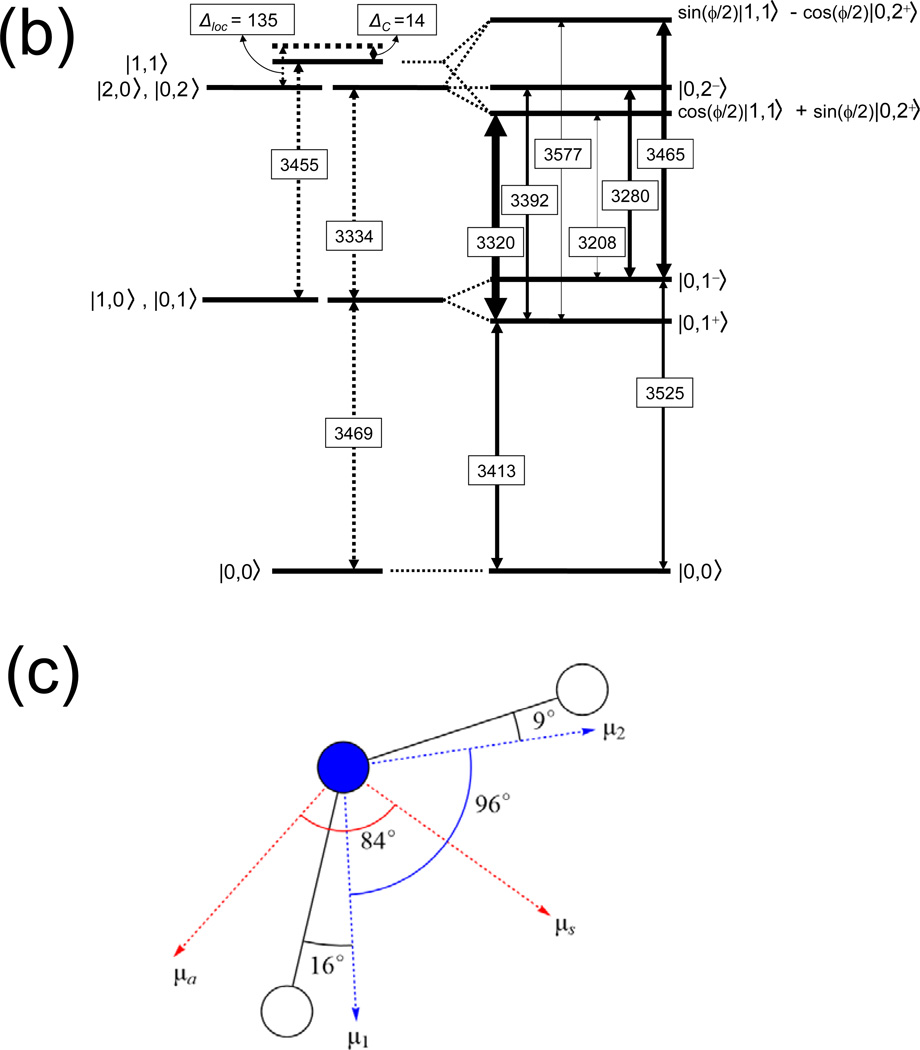
In Fig. 5, we show an energy level scheme appropriate for a discussion of the local mode picture. On the left hand side, the ground state, the (degenerate) one-quantum and two-quantum states as well as the combination tone are shown for the uncoupled local oscillators. The right-hand side of the scheme represents the coupled oscillators with arrows indicating the transitions between the single and double excitation manifolds and n indicating the number of excitation quanta in the system. We analysed this level scheme with the n=1 and n=2 manifolds in the local mode representation,33,35–41 by adopting the symmetrized local mode basis with the elements:
| (1a) |
| (1b) |
Figure 5.
(a) 2D-IR spectra of adenosine monomer (left column) recorded at a population waiting time of 200 fs, using the (ZZZZ) and (ZZYY) polarisation conditions (second and third row, respectively). Calculated 2D-IR spectra for A monomer are given in the second column. The linear FT-IR spectra are depicted in the top panels. (b) Level scheme in the local mode representation with the uncoupled levels shown on the left and the coupled levels on the right. The thicknesses of the n=0 → n=1 and n=1 → n=2 transitions are scaled to the intensities in the 2D-IR spectra calculated with the coupled local mode model. (c) Orientational information on bond vectors and dipole moments.
The fundamental n=0 → n=1 transitions occur at 3413 and 3525 cm−1. From each of these n=1 states, two excited-state n=1 → n=2 absorption transitions are strongly allowed. With these excited-state absorption transitions, the energy location of the three levels in the n=2 manifold can be accurately determined: 6735 cm−1, 6805 cm−1 and 6990 cm−1 (accuracy ± 5 cm−1). Furthermore, realizing that the uncoupled fundamental local N-H stretching frequency is equal to 3469 cm−1, we can deduce from this level scheme that the total diagonal anharmonicity in the double excitation manifold is (6×3469 − 6735 − 6805 − 6990) = 284 ± 13 cm−1.
Using the intermode coupling JH = −56.0 cm−1 as input, we obtain a local mode diagonal anharmonicity of Δloc ~135 cm−1, which leaves for the diagonal anharmonic downshift of the combination mode |1,1> about Δc ~14 cm−1. The local mode anharmonicity Δloc ~ 135 cm−1 is comparable to those of free (non hydrogen-bonded) N-H stretching vibrations in heterocyclic nucleic bases or base model systems.12,30,31 We note that, in contrast to Cho,40,41 Child and Halonen35–37 as well as Hamm and Zanni33 do not introduce an anharmonic shift Δc for the combination level |1,1>. The 14 cm−1 value obtained here suggests that this anharmonic shift is small for the N-H stretching local modes of adenosine. In fact, the value barely exceeds the error margin on the total anharmonicity for the n=2 manifold.
To obtain insight into the microscopic origin of the anharmonicities and couplings of A, we now discuss results from ab-initio quantum chemical calculations. The HF/6-311++G** potential energy surface was expanded to sixth order in the two local N-H stretching coordinates:42,43
| (2) |
where Gij are elements of the Wilson G-Matrix44,45 and are the n-th order force constants:
| (3) |
mkx and ωkx are the reduced mass and harmonic local mode frequency of the internal coordinate rkx. The nuclear dipole moment was truncated at linear order:
| (4) |
The equilibrium force constants and transition dipole moments were determined by least squares fits to the computed potential energy surface and electric dipole respectively. The optimized geometry agrees well with previous results.46 The NH2 group is roughly 10 degrees out of plane with respect to the ring. The potential energy surface and the electric dipole moment were calculated on a grid whose points are displacements from equilibrium ranging from −0.2 to 0.2 Å in steps of 0.05 Å.
The Hamiltonian can be written in an equivalent form by transforming the internal coordinates using:
| (5a) |
| (5b) |
where Bi and are the bosonic annihilation and creation operators which satisfy the commutation relation Using these relations, the Hamiltonian can now be written as:
| (6) |
where the dimensionless force constants are related to those in Eq. 2 by . The bilinear (‘mechanical’) coupling, which causes the splitting between the symmetric and asymmetric fundamentals, includes both a kinetic and potential energy (φ12) contribution:44,45
| (7) |
where is the kinetic energy contribution and φ12 is the potential energy contribution. the observed splitting for 9-mA is dominated by rather than φ12 (Table 2). The vibrational eigenstates were obtained by diagonalizing the Hamiltonian (Eq. 6) in a harmonic basis, which was truncated at 15 quanta (136 basis states).
Table 2.
Anharmonic expansion coefficientsa of 9-mA in cm−1. Values for 9-MA-d2 are given in parantheses.
| g1 | −0.2 (−0.2) | g11111 | −140.1 (−64.0) |
| g2 | −0.1 (−0.1) | g11112 | 14.9 (6.8) |
| ω1 | 3901.8 (2851.0) | g11122 | 22.6 (10.3) |
| ω2 | 3900.7 (2850.2) | g11222 | 22.9 (10.4) |
| γ12’ | 64.6 (88.3) | g12222 | 15.1 (6.9) |
| φ12 | −6.7 (−4.9) | g22222 | −140.1 (−64.0) |
| g111 | −816.2 (−509.8) | g111111 | 58.4 (22.8) |
| g112 | 6.6 (4.1) | g111112 | −8.2 (−3.2) |
| g122 | 5.9 (3.7) | g111122 | −24.2 (−9.4) |
| g222 | −815.8 (−509.6) | g111222 | −23.7 (−9.2) |
| g1111 | 319.6 (170.7) | g112222 | −24.5 (−9.5) |
| g1112 | −17.4 (−9.3) | g122222 | −8.4 (−3.3) |
| g1122 | −13.5 (−7.2) | g222222 | 58.5 (22.8) |
| g1222 | −17.3 (−9.2) | ||
| g2222 | 319.4 (170.6) |
The force constants are listed as
The calculated anharmonic energy levels and the expansion coefficients of the Hamiltonian for 9-mA and 9-mA-d2 are listed in Tables 1 and 2. All frequencies and anharmonicities are scaled by a factor of 0.9183. This factor, which is greater than the standard harmonic scaling factor47 and less than the recently determined anharmonic scaling factor, based on second-order vibrational perturbation theory calculations,48,49 was chosen to match with experiment. The calculated anharmonic energy levels match qualitatively with the anharmonicity parameters derived from the 2D-IR experiments (Figure 4). Due to the negative bilinear coupling, the symmetric stretch is lower in energy than the asymmetric stretch, as previously assigned.6,8,26–29 Upon isotopic substitution, increases by a factor of √2, which explains the greater splitting in 9-mA-d2. A similar effect has recently been observed for water.50
Table 1.
Comparison of calculated and experimentally determined fundamental frequencies and anharmonic shifts of 9-mA in cm−1. Values for 9-MA-d2 are given in parantheses.
| Experiment | HF/6-311+G** | |
|---|---|---|
| νa | 3525 | 3530 (2861) |
| νs | 3413 | 3406 (2704) |
| Δaa | 60 | 46 (31) |
| Δss | 93 | 69 (35) |
| Δas | 133 | 106 (68) |
| Δtot | 284 | 219 (134) |
| Δloc | 135 | 107 (65) |
| Δc | 14 | 6 (5) |
The intensity ratio R of the symmetric and asymmetric peaks in the linear absorption spectrum (Figure 1) is estimated at ~1.45 ± 0.2. Regarding these modes as positive and negative linear combinations of N-H local modes the angle θ between the local mode transition dipoles is predicted from cos θ = (R−1)/(R+1) to be ~79 ± 4 degrees. Our ab-initio calculations produce an angle between the local mode transition dipoles of 95 degrees, which confirms that the N-H stretching local mode dipoles are not parallel to the bond vectors (Figure 5). This is similar to the amide I mode, where the transition dipole moment makes a 20 degree angle with the C=O bond vector.51 The angle between the symmetric and asymmetric transition dipoles is 84 degrees.
Figure 5 compares the measured and calculated 2D-IR spectra for (k1,k2,k3,kLO) = (ZZZZ) and (ZZYY) polarisation geometries. The nearly perpendicular orientation of the two transition dipole moments is reflected in the relative intensities of the cross peaks compared to those of the diagonal peaks in the 2D-IR spectra for these polarisation geometries.52 The local mode diagonal anharmonicity, Δloc, was calculated by expanding Equation 2 in one-dimension and calculating the resulting anharmonic shift. A comparison of the ab-initio results to the experimental parameters values derived using the coupled local mode model is shown in Table 1. Our calculations confirm that the total diagonal anharmonicity is dominated by Δloc, while Δc is small. Whereas the main features observed in the experiments are reproduced in the calculated 2D-IR spectra, the absolute value of the total diagonal anharmonicity, a measure of the three anharmonic shifts, is underestimated by a factor of 1.3, resulting in smaller spectral shifts of peaks in the 2D-IR spectra related to excited-state n=1 → n=2 absorption transitions. The relative magnitudes of the three anharmonic shifts are roughly equal to the experimentally measured values, suggesting that a further refinement of the calculations should point at a better estimation of the N-H stretching anharmonicities.
We now discuss our findings on the diagonal anharmonicities and couplings of the N-H stretching modes of A, relating to previously reported work on hydrogen stretching oscillators, as well as indicating the repercussions the obtained parameter values have on the fundamental n=0 → n=1 and excited state n=1 → n=2 absorption transitions. It has been shown that for hydrogen stretching overtone states with n = 2 … 5 of molecules such as H2O and C2H2, quenching of the intermode JH coupling by the anharmonicity of the individual bond potentials Δloc causes a localisation of vibrational excitation, i.e. a local mode representation provides a better description for the experimentally determined frequency shifts of these overtone transitions.34,35,37,53 For C2D2 and SO2 rather the normal mode picture is more beneficial to describe the observed features. Child and Halonen35–37 have provided the formalism to connect the local mode and normal mode representations. Depending on the relative magnitudes of coupling JH = −56 cm−1 and diagonal anharmonicity Δloc it follows which mode description is closer to the real situation for the overtone states. In particular, when for the parameter ξ, defined as:
| (8) |
the value is close to zero, the local mode limit applies (i.e. |J| >> Δloc). In contrast, when ξ becomes equal to ± 1, that is when |J| << Δloc, the normal mode limit is reached. For A monomer, with JH = −56 cm−1 and Δloc = 135 cm−1, we find ξ = −0.44, indicating that the character of the N-H stretching modes of A in overtone states is intermediate between local and normal limits. The characteristics of the N-H stretching modes of A monomer can at best be compared with the O-H stretching modes of gas phase H2O, with ξ = −0.34, where similar diagonal anharmonicities and couplings have been derived using the local mode picture.35–37,53 The local mode basis has also been applied in the interpretation of overtone spectra of amines and anilines.54,55 From such studies it has been derived that for aliphatic amines such as methylamine and cyclopropylamine |JH| = 32 cm−1 and Δloc = 158 cm−1.55,56 For aromatic amines such as aniline, where the resonance between the nitrogen lone pair and the π-molecular orbitals leads to a planarization of the NH2-group, the local mode coupling increases to |JH| = 43.65 cm−1 and Δloc = 163.4 cm−1.54 Comparing these literature values with those we have found for A monomer suggests that the magnitude of the local mode coupling increases upon increased interaction of the nitrogen lone pair with an extended aromatic π -molecular orbital system, whereas the magnitude of the local diagonal anharmonicity remains similar. To validate this, N-H stretching parameters for other molecular systems having the NH2-functionality should be investigated.
The coupling JH = −56.0 cm−1 leads to strong mixing of the resonant v=1 states of the two local modes (i.e. |JH| >> |ω1 – ω2| = 0) and therefore the normal modes are the proper eigenstates in the n=1 manifold, and, thus, the strong coupling regime applies to the single-excitation manifold.33,41 In the double-excitation manifold, on the other hand, the |1,1> local mode state is coupled to the local mode states |0,2>, |2,0> that are both lowered by the large diagonal anharmonicity Δloc. Transforming the basis set to |1,1 >, |0,2+ >, and ‖0,2− >, eliminates the coupling between |0,2− > and the other two states, and produces a modified coupling of 2JH between |1,1 > and |0,2+ >, with uncoupled energies of 2ω0-Δc and 2ω0-Δloc, respectively. Thus, in the double-excitation manifold the symmetric stretch overtone is only a proper eigenmode if (Δloc-Δc)/ 2|JH| >> 1. In the present case this ratio is (135-14)/(2*56)~1.1, so clearly the intermediate coupling regime applies to the double-excitation manifold, and neither the local nor the normal mode representations provide an accurate description of these vibrational overtone eigenstates. As a result, the |1,1 > and |0,2+ > states of A are strongly mixed (see Figure 5), with the mixing angle ϕ defined as:
| (9) |
Finding ϕ = 118° for A, such strong mixing results also in the weak allowance of the harmonically forbidden three-quantum transitions. Even though in our 2D-IR experimental data sets we find indications of these forbidden transitions becoming weakly allowed, that would lead to negative cross peaks located at (3525,3210) and (3413,3575), the minute signal strengths are just above detection threshold – and of similar magnitude as peaks due to A complexes – prevents us from making definitive statements on this. The calculated 2D-IR spectra indicate that the magnitudes of these additional cross peaks are within a few percent of the main peaks. Such behaviour of “forbidden” transitions having small cross sections has been observed before for the excited-state n = 1 → n = 2 transitions in 2D-IR spectra obtained on the C≡O stretching modes of Rh(CO)2(C5H7O2) (I) complexes.42,57–59 For such complexes with carbonyl stretching modes, however, Δloc ~ |J| and mixing between the symmetric stretching overtone and the combination state is less pronounced with concomitant weaker cross sections for these “forbidden” transitions.
Therefore, we feel that such rich effects of vibrational spectroscopy can grasped best on hydrogen stretching oscillators, i.e. C-H, N-H and O-H stretching modes, with additional features that may take place upon formation of hydrogen bonds. Here ultrafast 2D-IR spectroscopy provides a clear alternative to overtone spectroscopy to obtain direct insight into these vibrational coupling effects for molecules in the condensed phase. With ultrafast 2D-IR spectroscopy one not only discerns the information on vibrational frequency shifts and band intensities into two spectral dimensions (as opposed to overtone spectroscopy where the transitions are recorded in one dimension), but additional orientational degrees of freedom can be explored using the polarisation properties of the femtosecond IR laser pulses. A difference between the N-H and O-H stretching modes is the typically much larger spectral broadening for O-H stretching modes upon formation of hydrogen bonds, a consequence of a larger susceptibility of O-H stretching modes to fluctuations imposed by the surrounding solvent shells.60,61 Dynamical decoupling effects may then be expected to hinder a full determination of the interplay between coupling and diagonal anharmonicities. As a result, full characterisation of the rich spectral structure of the nonlinear 2D-IR spectra is likely to happen for N-H stretching manifolds of hydrogen-bonded nucleobase pairs rather than for O-H stretching bands of hydrogen-bonded topographies consisting of multiple OH groups.
5. Conclusions
We have investigated the linear FT-IR and nonlinear femtosecond 2D-IR spectra of the N-H stretching modes of adenosine (A) monomer in chloroform solution. Based on the frequency positions of the symmetric and asymmetric NH2-stretching, of symmetric and asymmetric ND2-stretching and of the N-H and N-D stretching modes of NHD groups, couplings JH = − 56 cm−1 and JD = − 77 cm−1 were found. We have applied the local mode representation to fully explore the first n=1 and second n=2 excitation manifolds using the formalism developed to describe results from overtone spectroscopy of stretching oscillators. Whereas the local N-H stretching modes of A are degenerate in frequency, i.e. |JH| >> |ω1 – ω2| = 0, making them strongly coupled in the n=1 single excited states and the symmetric and asymmetric normal modes are proper eigenmodes of the molecular system, the large local diagonal anharmonicity Δloc ~135 cm−1 leads to a distinctly different behaviour for the n=2 double excitation manifold, where intermediate coupling leads to the situation that neither local nor normal modes are the appropriate eigenmodes for A. We anticipate that the analysis presented here can be further refined when comparing 2D-IR spectra of N-H stretching modes in A monomer with N-D stretching modes of deuterated A monomer, as well as extending to linear and 2D-IR spectroscopy on hydrogen bonded A.
Acknowledgements
The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP7/2007–2013 / ERC grant agreement n° 247051; TE), the German Science Foundation (Deutsche Forschungsgemeinschaft; FT), the National Institutes of Health (grants GM059230 and GM091364; SM) as well as the National Science Foundation (grant CHE-1058791; SM). NKP is supported by a National Science Foundation Graduate Research Fellowship. We cordially acknowledge assistance in the pump-probe experiments by Dr. Ismael A. Heisler.
References
- 1.Szyc Ł, Yang M, Nibbering ETJ, Elsaesser T. Angew. Chem. Int. Ed. 2010;49:3598. doi: 10.1002/anie.200905693. [DOI] [PubMed] [Google Scholar]
- 2.Yang M, Szyc Ł, Elsaesser T. J. Phys. Chem. B. 2011;115:1262. doi: 10.1021/jp1090697. [DOI] [PubMed] [Google Scholar]
- 3.Yang M, Szyc Ł, Elsaesser T. J. Phys. Chem. B. 2011;115:13093. doi: 10.1021/jp208166w. [DOI] [PubMed] [Google Scholar]
- 4.Nir E, Kleinermanns K, de Vries MS. Nature. 2000;408:949. doi: 10.1038/35050053. [DOI] [PubMed] [Google Scholar]
- 5.Plützer C, Hünig I, Kleinermanns K, Nir E, de Vries MS. ChemPhysChem. 2003;4:838. doi: 10.1002/cphc.200300648. [DOI] [PubMed] [Google Scholar]
- 6.Dong F, Miller RE. Science. 2002;298:1227. doi: 10.1126/science.1076947. [DOI] [PubMed] [Google Scholar]
- 7.de Vries MS, Hobza P. Annu. Rev. Phys. Chem. 2007;58:585. doi: 10.1146/annurev.physchem.57.032905.104722. [DOI] [PubMed] [Google Scholar]
- 8.Biemann L, Haber T, Maydt D, Schaper K, Kleinermanns K. J. Chem. Phys. 2008;128 doi: 10.1063/1.2912064. [DOI] [PubMed] [Google Scholar]
- 9.Biemann L, Haber T, Kleinermanns K. J. Chem. Phys. 2009;130 doi: 10.1063/1.3098352. [DOI] [PubMed] [Google Scholar]
- 10.Schwalb NK, Temps F. J. Am. Chem. Soc. 2007;129:9272. doi: 10.1021/ja073448+. [DOI] [PubMed] [Google Scholar]
- 11.Schwalb NK, Michalak T, Temps F. J. Phys. Chem. B. 2009;113:16365. doi: 10.1021/jp904883n. [DOI] [PubMed] [Google Scholar]
- 12.Yang M, Szyc L, Rottger K, Fidder H, Nibbering ETJ, Elsaesser T, Temps F. J. Phys. Chem. B. 2011;115:5484. doi: 10.1021/jp110561d. [DOI] [PubMed] [Google Scholar]
- 13.Krummel AT, Mukherjee P, Zanni MT. J. Phys. Chem. B. 2003;107:9165. [Google Scholar]
- 14.Krummel AT, Zanni MT. J. Phys. Chem. B. 2006;110:24720. doi: 10.1021/jp063227a. [DOI] [PubMed] [Google Scholar]
- 15.Krummel AT, Zanni MT. J. Phys. Chem. B. 2006;110:13991. doi: 10.1021/jp062597w. [DOI] [PubMed] [Google Scholar]
- 16.Lee C, Cho M. J. Chem. Phys. 2006;125 doi: 10.1063/1.2213257. [DOI] [PubMed] [Google Scholar]
- 17.Lee C, Park KH, Cho M. J. Chem. Phys. 2006;125 doi: 10.1063/1.2213257. [DOI] [PubMed] [Google Scholar]
- 18.Lee C, Park KH, Kim JA, Hahn S, Cho M. J. Chem. Phys. 2006;125 doi: 10.1063/1.2213259. [DOI] [PubMed] [Google Scholar]
- 19.Lee C, Cho MH. J. Chem. Phys. 2007;126 doi: 10.1063/1.2715602. [DOI] [PubMed] [Google Scholar]
- 20.Krishnan GM, Kühn O. Chem. Phys. Lett. 2007;435:132. [Google Scholar]
- 21.Yan YA, Krishnan GM, Kühn O. Chem. Phys. Lett. 2008;464:230. [Google Scholar]
- 22.Peng CS, Jones KC, Tokmakoff A. J. Am. Chem. Soc. 2011;133:15650. doi: 10.1021/ja205636h. [DOI] [PubMed] [Google Scholar]
- 23.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery JA, Jr, Peralta JE, Ogliaro F, Bearpark M, Heyd JJ, Brothers E, Kudin KN, Staroverov VN, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam JM, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K, Zakrzewski VG, Voth GA, Salvador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas Ö, B FJ, V O, Cioslowski J, Fox DJ. Gaussian 09, Revision A.1. Wallingford CT: Gaussian, Inc.; 2009. [Google Scholar]
- 24.Mukamel S. Principles of Nonlinear Optical Spectroscopy. Vol. 6. Oxford: Oxford University Press; 1995. [Google Scholar]
- 25.Abramavicius D, Palmieri B, Voronine DV, Sanda F, Mukamel S. Chem. Rev. 2009;109:2350. doi: 10.1021/cr800268n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Plützer C, Nir E, de Vries MS, Kleinermanns K. Phys. Chem. Chem. Phys. 2001;3:5466. [Google Scholar]
- 27.Plützer C, Kleinermanns K. Phys. Chem. Chem. Phys. 2002;4:4877. [Google Scholar]
- 28.Kabeláč M, Plützer C, Kleinermanns K, Hobza P. Phys. Chem. Chem. Phys. 2004;6:2781. [Google Scholar]
- 29.Nowak MJ, Lapinski L, Kwiatkowski JS, Leszczynski J. J. Phys. Chem. 1996;100:3527. [Google Scholar]
- 30.Woutersen S, Cristalli G. J. Chem. Phys. 2004;121:5381. doi: 10.1063/1.1785153. [DOI] [PubMed] [Google Scholar]
- 31.Dwyer JR, Dreyer J, Nibbering ETJ, Elsaesser T. Chem. Phys. Lett. 2006;432:146. [Google Scholar]
- 32.Khalil M, Demirdöven N, Tokmakoff A. J. Chem. Phys. 2004;121:362. doi: 10.1063/1.1756870. [DOI] [PubMed] [Google Scholar]
- 33.Hamm P, Zanni M. Concepts and Methods of 2D Infrared Spectroscopy. Cambridge: Cambridge University Press; 2011. [Google Scholar]
- 34.Sage ML, Jortner J. Adv. Chem. Phys. 1981;47(Pt. 1):293. [Google Scholar]
- 35.Child MS, Halonen L. Adv. Chem. Phys. 1984;57:1. [Google Scholar]
- 36.Child MS. Acc. Chem. Res. 1985;18:45. [Google Scholar]
- 37.Halonen L. Adv. Chem. Phys. 1998;104:41. [Google Scholar]
- 38.Lim M, Hochstrasser RM. J. Chem. Phys. 2001;115:7629. [Google Scholar]
- 39.Hamm P, Lim M, Hochstrasser RM. J. Phys. Chem. B. 1998;102:6123. [Google Scholar]
- 40.Cho MH. Chem. Rev. 2008;108:1331. doi: 10.1021/cr078377b. [DOI] [PubMed] [Google Scholar]
- 41.Cho M. Two-Dimensional Optical Spectroscopy. Boca Raton: CRC Press; 2009. [Google Scholar]
- 42.Moran AM, Dreyer J, Mukamel S. J. Chem. Phys. 2003;118:1347. [Google Scholar]
- 43.Hayashi T, Mukamel S. J. Phys. Chem. A. 2003;107:9113. [Google Scholar]
- 44.Wilson EB, Decius JC, Cross PC. Molecular Vibrations. New York: Dover Publications; 1980. [Google Scholar]
- 45.Kjaergaard HG, Garden AL, Chaban GM, Gerber RB, Matthews DA, Stanton JF. J. Phys. Chem. A. 2008;112:4324. doi: 10.1021/jp710066f. [DOI] [PubMed] [Google Scholar]
- 46.Hobza P, Šponer J. Chem. Rev. 1999;99:3247. doi: 10.1021/cr9800255. [DOI] [PubMed] [Google Scholar]
- 47.Merrick JP, Moran D, Radom L. J. Phys. Chem. A. 2007;111:11683. doi: 10.1021/jp073974n. [DOI] [PubMed] [Google Scholar]
- 48.Barone V. J. Chem. Phys. 2005;122 doi: 10.1063/1.1824881. [DOI] [PubMed] [Google Scholar]
- 49.Johnson RD, Irikura KK, Kacker RN, Kessel R. J. Chem. Theor. Comput. 2010;6:2822. doi: 10.1021/ct100244d. [DOI] [PubMed] [Google Scholar]
- 50.Li F, Skinner JL. J. Chem. Phys. 2010;132 doi: 10.1063/1.3430518. [DOI] [PubMed] [Google Scholar]
- 51.Torii H, Tasumi M. J. Chem. Phys. 1992;96:3379. [Google Scholar]
- 52.Zanni MT, Ge N-H, Kim YS, Hochstrasser RM. Proc. Natl. Acad. Sci. USA. 2001;98:11265. doi: 10.1073/pnas.201412998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lemus R. J. Mol. Spectrosc. 2004;225:73. [Google Scholar]
- 54.Howard DL, Robinson TW, Fraser AE, Kjaergaard HG. Phys. Chem. Chem. Phys. 2004;6:719. [Google Scholar]
- 55.Marom R, Zecharia U, Rosenwaks S, Bar I. J. Chem. Phys. 2008;128 doi: 10.1063/1.2907738. [DOI] [PubMed] [Google Scholar]
- 56.Niefer BI, Kjaergaard HG, Henry BR. J. Chem. Phys. 1993;99:5682. [Google Scholar]
- 57.Golonzka O, Khalil M, Demirdöven N, Tokmakoff A. Phys. Rev. Lett. 2001;86:2154. doi: 10.1103/PhysRevLett.86.2154. [DOI] [PubMed] [Google Scholar]
- 58.Golonzka O, Khalil M, Demirdöven N, Tokmakoff A. J. Chem. Phys. 2001;115:10814. doi: 10.1103/PhysRevLett.86.2154. [DOI] [PubMed] [Google Scholar]
- 59.Venkatramani R, Mukamel S. J. Chem. Phys. 2002;117:11089. [Google Scholar]
- 60.Jansen TLC, Cringus D, Pshenichnikov MS. J. Phys. Chem. A. 2009;113:6260. doi: 10.1021/jp900480r. [DOI] [PubMed] [Google Scholar]
- 61.Knop S, Jansen TL, Lindner J, Vöhringer P. Phys. Chem. Chem. Phys. 2011;13:4641. doi: 10.1039/c0cp02143a. [DOI] [PubMed] [Google Scholar]