Beyond ROC curvature: Strength effects and response time data support continuous-evidence models of recognition memory

Abstract

A classic question in the recognition memory literature is whether retrieval is best described as a continuous-evidence process consistent with signal detection theory (SDT), or a threshold process consistent with many multinomial processing tree (MPT) models. Because receiver operating characteristics (ROCs) based on confidence ratings are typically curved as predicted by SDT, this model has been preferred in many studies of recognition memory (Wixted, 2007). Recently, Bröder and Schütz (2009) argued that curvature in ratings ROCs may be produced by variability in scale usage; therefore, ratings ROCs are not diagnostic in deciding between the two approaches. From this standpoint, only ROCs constructed via experimental manipulations of response bias (‘binary’ ROCs) are predicted to be linear by threshold MPT models. The authors claimed that binary ROCs are linear, consistent with the assumptions of threshold MPT models. We compared SDT and the double high-threshold MPT model using binary ROCs differing in target strength. Results showed that the SDT model provided a superior account of both the ROC curvature and the effect of strength compared to the MPT model. Moreover, the bias manipulation produced differences in RT distributions that were well described by the diffusion model (Ratcliff, 1978), a dynamic version of SDT.

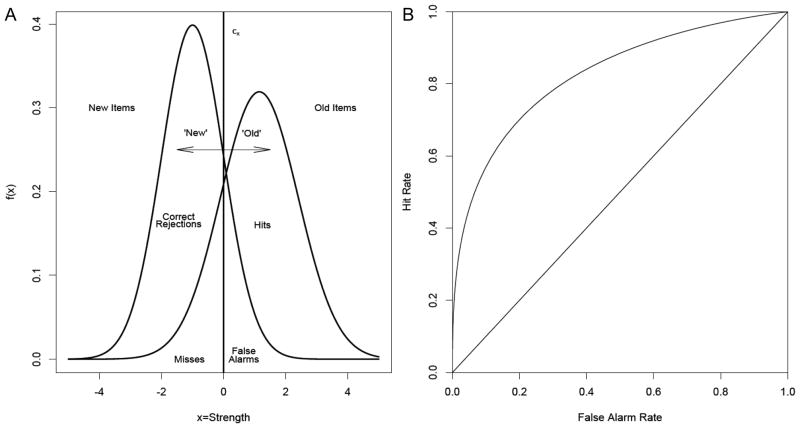
Is the recognition of previously-encountered stimuli accomplished by exceeding a fixed threshold, or do participants experience fine-grained differences in memory evidence? The experiments that attempt to answer this question typically involve presentation of words or other items for study, followed by a test containing the previously studied items and new items. Participants are asked to judge whether each item is ‘Old’ (from the study event) or ‘New.’ Variations on this simple task have resulted in sophisticated quantitative models of recognition, and many of these models share the assumption that participants respond based on gradations in memory strength rather than fixed transition points (Benjamin, Diaz, & Wee, 2009; Criss, 2010; Dennis & Humphreys, 2000; Hautus, Macmillan, & Rotello, 2008; Malmberg, 2008; Mickes et al., 2009; Mueller & Weidemann, 2008; Ratcliff, 1978; Ratcliff & Starns, 2009; Ratcliff, Sheu, & Gronlund, 1992; Sekuler & Kahana, 2007; Shiffrin & Steyvers, 1997; Yonelinas, 1994). For example, this assumption forms the basis of the unequal-variance signal detection model displayed in Figure 1A.

Figure 1.

The unequal-variance signal detection model (A) and its implied ROC (B).

Signal detection theory (SDT) assumes that participants operate on continuous distributions of memory strength that are almost always assumed to be Gaussian in form, with higher average strength (μ_o) assigned to Old items. The variance of the old item distribution (σ_o) exceeds that of the new item distribution, consistent with the notion that strength increases by a variable amount across learning trials (Wixted, 2007).¹ Participants compare test probes to a criterion level of strength, labeled c_x in the figure. Items that pass this level of strength, falling right of the criterion, are declared ‘Old.’ Those that fall to the left of the criterion are declared ‘New.’ Importantly, this model assumes that participants experience a single, continuous range of strengths, and the criterion does not represent a fixed transition point between states, but a level of response bias that can be influenced experimentally.

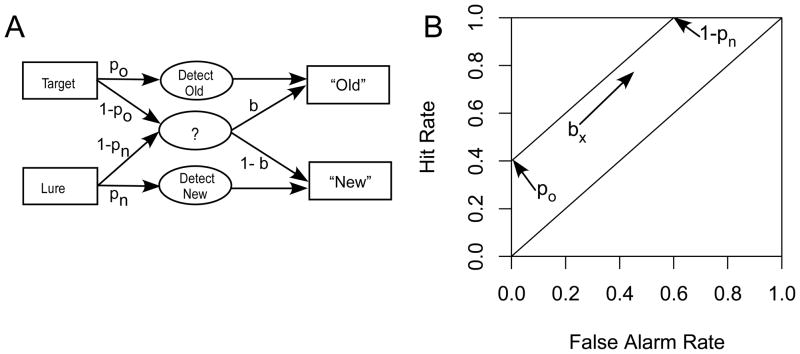
Although the continuous-evidence approach is popular, some researchers have challenged this idea and instead proposed a discrete-state, or ‘threshold’ framework for recognition (Bröder & Schütz, 2009; Klauer & Kellen, 2010; Malmberg, 2002). Threshold theories (Krantz, 1969; Batchelder & Riefer, 1990) differ from continuous-evidence theories by assuming that participants respond on the basis of a small number of discrete mental states. Consider, for example, the double high-threshold model (2HTM) depicted in Figure 2A. This model assumes that old items vary on some metric analogous to signal strength, but decisions are primarily based on whether a fixed transition point or ‘threshold’ level of strength is achieved for a given item. If an old item is high enough in strength, it will exceed the memory threshold and present some signal in conscious awareness. As illustrated in Figure 2A, this ‘detect’ state is entered with probability p_o. With probability 1 − p_o the participant remains in a ‘non-detect’ state and is assumed to have no information about the status of the item. Since participants are presumably aware that they may sometimes fail to remember an old item, they may then guess that the item is old according to the bias parameter b. An advantage of the 2HTM over simpler threshold models is its application of the same logic to new items. That is, new (‘lure’) items can be detected as new with probability p_n. Lure detection fails with probability 1 − p_n, leading again to reliance on the guessing parameter b.

Figure 2.

The double high-threshold model (A) and its implied ROC (B).

To date, continuous and threshold recognition models have been evaluated by assessing the curvature of receiver-operating characteristic (ROC) functions. These functions plot the hit rate (HR) against the false alarm rate (FAR) across multiple levels of response bias with constant accuracy. ROCs can be formed by manipulating response bias experimentally, producing a ‘binary’ or ‘Yes/No’ ROC, or they can be formed by asking participants to make confidence ratings following their Old/New decisions. SDT predicts that ROCs will be curved for both methods, while threshold models predict they will be linear for the binary method, as shown in Figures 1B and 2B, respectively (Green & Swets, 1966; Bröder & Schütz, 2009; Klauer & Kellen, 2010; Klauer & Kellen, 2011). In recognition, ratings ROCs have most often been found to be curved, which has been taken as support for the continuous-evidence approach of SDT (Wixted, 2007).

Unfortunately, previous research has not always considered the fact that threshold models can produce curvature for confidence-rating ROCs under certain assumptions about how the response stage is modeled (Erdfelder & Buchner, 1998; Krantz, 1969; Malmberg, 2002). As noted by Bröder and Schütz (2009), arguments in favor of SDT have been based largely on ratings ROCs. If curvature in these functions is not diagnostic, the validity of arguments favoring SDT rests on the form of binary ROCs, which are not commonly collected in recognition. The authors reported that existing binary ROCs were well-described by both models, and that binary ROCs from three newer experiments were linear, consistent with threshold models. Dube and Rotello (2012) argued that Bröder and Schütz’s meta-analysis was weakened by the inclusion of non-diagnostic 2-point ROCs, and that when these were excluded the data clearly favored SDT. Dube and Rotello also reported data from two new experiments that modified several aspects of Bröder and Schütz’s experimental design. They found the binary ROCs resulting from their experiments were generally curved and well-described by SDT at both the group and individual-participant levels. A meta-analysis of individual-participant ROCs from the perception literature showed similar results.

Although ROC curvature has been the focus of the debate thus far, this aspect of the data is unlikely to definitively discriminate between continuous and threshold approaches to recognition. Indeed, binary ROC procedures often produce relatively subtle changes in bias, and model recovery simulations demonstrate that the models are difficult to discriminate in this situation (Dube, Rotello, & Heit, 2011). For instance, Dube and Rotello found that participants sometimes appeared to be less willing to follow biasing instructions than to assign different confidence ratings, which produced a clustering of the points in their binary ROCs. They noted that curvature can be more difficult to detect in this case, and in fact the few cases in which the ROCs appeared to be linear were also ones that fell into this category.

The Current Study

In the present study, we examine ROCs formed by manipulating the proportion of target items at test, and we expand on previous approaches by considering aspects of recognition data beyond ROC curvature. Specifically, we tested the models’ predictions for the effect of strengthening target items on ROC functions, and we considered how the debate can be informed by including RT data in addition to the response proportions used to form ROCs (Ratcliff & Starns, 2009; Starns, Ratcliff, & McKoon, 2012). To foreshadow, our results were consistent with those of Dube and Rotello (2012) in terms of ROC curvature, but they revealed additional problems for the threshold framework. Specifically, the SDT model produced more appropriate predictions for the effect of target strength on ROC functions than did the 2HTM. Moreover, we observed patterns in the RT data that cannot be readily explained by the 2HTM but were predicted naturally by the diffusion model, a dynamic extension of SDT.

Varying Target Strength

In our experiments, we varied the number of presentations at encoding to create different levels of memory strength. At test, strong items and weak items were randomly intermixed with a single set of lures. These manipulations allowed us to construct binary ROC functions differing in target strength, but with a single set of false alarm rates contributing to both functions. For the SDT model, increasing target strength implies shifting the target distribution to a higher average strength value, thus increasing the hit rate at each bias level. For the threshold model, increasing target strength increases the probability that target items will produce the detect state without affecting the probability that lures will produce the detect state. That is, because strong and weak targets are mixed into a test with a single class of lure items, it is not possible for responses to lures to vary between the strong and weak functions. This imposes the constraint of equal p_n across the strong and weak ROCs, and thus a single upper x-intercept equal to 1 − p_n.

Figure 3 illustrates the distinct predictions of the models. We generated predictions from the SDT model across two levels of target strength, and these predictions are shown as circles in Figure 3. We then fit the SDT-generated data in Fig. 3 with the 2HTM (predictions shown as plusses). As is clear in the figure, the constraint of equal lure detection in the 2HTM prevents this model from matching the data, with especially large misfits for the leftmost point of the strong function and the rightmost point of the weak function (the threshold model predicts a higher hit rate than the SDT model in both cases). Thus, the target strength variable should help to discriminate the models. To determine how well the data discriminated the models, we performed model recovery simulations for each dataset (Jang, Wixted, & Huber, 2011; Wagenmakers, Ratcliff, Gomez, & Iverson, 2004). As will be seen, some data did not discriminate the models, in which case the models provided comparable fits. Other data, however, clearly discriminated the models. All of these diagnostic datasets strongly supported the continuous model.

Figure 3.

A hypothetical scenario, in which data generated with SDT (circles) are erroneously fit with the 2HTM (plusses, lines).

Response Times

Another goal of the current study is to demonstrate how RT data can facilitate model selection. Notably, there has been limited research on the ability of threshold models to accommodate RT data. Hu (2001), following Link (1982), proposed that mean RTs could be generated for each decision path in an MPT model by assuming that each transition probability has a certain associated processing time. For example, the mean RT for a hit made from the state of uncertainty would depend on the sum of the processing times to fail to detect the stimulus and to subsequently guess ‘old’. Mean RT for a hit made from the detect-old state would depend only on the time to detect the stimulus. Averaged together in appropriate proportions (according to the parameters estimated with the response rates), these two path-based processing times would yield the predicted mean RT for hits. This approach requires a large number of additional free parameters; indeed, it requires more free parameters than there are degrees of freedom in the model, as Hu noted. For this reason, we did not attempt to explicitly fit our RT data with an MPT model, and it is difficult to even make general predictions based on the threshold assumption. However, we entertain some tentative predictions based on the most straight-forward implications of Hu’s approach.

If each traversed link adds processing time, then it is reasonable to expect that a response made from a detect state will be faster overall than the same response made from the combination of entering an uncertain state and then guessing. As Figure 2 shows, the former involves traversing one link, and the latter involves traversing two. From a threshold standpoint, this assumption also makes sense psychologically: entering the detect state removes all ambiguity regarding the decision, and participants can respond immediately. For a design in which the target base rate is manipulated, some general predictions can be made about the mean RT for hits (and analogously for correct rejections). When targets occur rarely on the test, subjects should be biased to guess ‘new’ rather than ‘old,’ and hit responses should depend more heavily on the detect-old state. Since responses based on the detect state have a shorter path, faster RTs should result. In contrast, when targets dominate the test list, subjects should be biased to guess ‘old’ and hits should depend more heavily on the longer, guessing path. In this case, the overall RT associated with hits should be slowed. The approach to RT proposed by Hu (2001) is quite flexible, so other predictions are possible. However, there is good psychological motivation for our assumption that entering a state of uncertainty and then guessing should take longer than entering the detect state and responding.

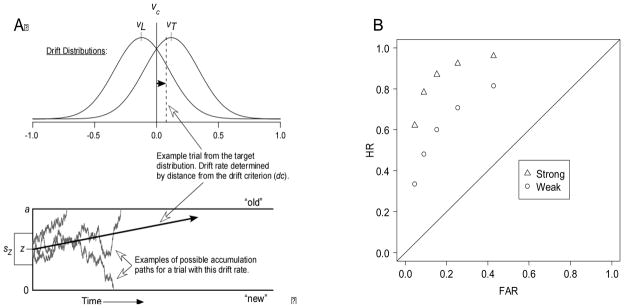
In contrast to the relative inattention to RT data in threshold modeling, the continuous approach has been extensively tested in this domain (for reviews, see Ratcliff & McKoon, 2008; Wagenmakers, 2009). To evaluate the continuous assumption under joint constraints from accuracy and RT, we fit our data with the diffusion model (Ratcliff, 1978). Figure 4A displays the diffusion model applied to a recognition memory task. Memory evidence for a given test item accumulates toward one of two boundaries at 0 and a, corresponding to ‘New’ and ‘Old’ decisions. The distance between boundaries (a) can be varied to produce speed-accuracy tradeoffs, with wider boundary separation corresponding to more emphasis on accuracy. The starting point of evidence accumulation is sampled across trials from a uniform distribution with mean z and range s_Z. The position of the starting point reflects decision bias; that is, decisions will be biased toward the “old” response if the starting point is near the top boundary or the “new” response if it is near the bottom boundary. The drift criterion (labeled v_c in the figure) determines whether each individual evidence sample supports an “old” or “new” response (much like the criterion in SDT). The accumulated evidence moves toward the top boundary for samples that fall above the drift criterion or moves toward the bottom boundary for samples that fall below. There is considerable variability from one sample to the next within a given trial, creating the wandering paths displayed in Figure 4. New evidence samples are taken continuously in time, leading to an average drift rate (v) in the decision process determined by the strength of evidence from the stimulus (e.g., a target studied 5 times should tend to approach the top boundary faster than a target studied 1 time). The average drift rate for a given item class varies across trials with standard deviation η, creating distributions of drift rate as shown in the top panel of Figure 4.

Figure 4.

The Ratcliff diffusion model (A) and its implied ROCs, generated by varying the starting point and mean target drift rates in the diffusion process (B).

An example ROC generated with the diffusion model is shown in Figure 4B. The five ROC points were produced by varying the starting point of the diffusion process (z) over five levels.² The diffusion model produces curvilinear ROCs similar to those predicted by signal detection theory, which is perhaps not surprising given that both assume continuous evidence. Changing bias in the diffusion model also leads to large changes in RT. When participants are biased to say “old,” they should make “old” responses more quickly than “new” responses. That is, if the starting point is near the top boundary, then fewer evidence samples are needed to reach the top boundary than the bottom boundary. In contrast, “new” responses should be fastest when people are biased to say new. Thus, RTs for hits (“old” responses) should decrease when there is a higher proportion of targets on the test, and RTs for correct rejections (“new” responses) should increase. This prediction, which follows directly from the geometry of the diffusion model, opposes our tentative 2HTM prediction of slower RTs with increased reliance on the guessing path.

Starns et al. (2012) recently reported data consistent with diffusion predictions for ROC shape and RTs. In their study, participants completed an “old”/”new” recognition task where the proportion of targets on the test varied across five levels. Participants completed 20 hour-long sessions of data collection, and the diffusion model was fit to both ROC functions and RT distributions at both the individual-participant and group levels. For every participant, increasing the proportion of targets on the test produced faster “old” responses and slower “new” responses in addition to increasing the overall willingness to respond “old.” The model matched the form of the binary ROCs while also providing a good fit to the position, shape, and spread of the RT distributions.

We adopted the basic design used by Starns et al. (2012) for our experiments, but extended the explanatory models under evaluation to include the 2HTM. We retained their general strategy of using RTs as an additional constraint on model selection. Given that our participants completed only one session of data collection in a design with relatively few observations in some conditions (e.g., lure items in the 80% target condition), we did not have a sufficient number of observations to estimate RT distributions for all of our conditions. Therefore, we used a more limited application of the diffusion model that targeted the aspects of our data that we can estimate reliably. Specifically, we fit the model to the ROC data and to RT medians for correct responses. Given the limitations in the data, we reduced the complexity of the model by fixing at standard values parameters that are primarily constrained by distribution shape and/or the relative speed of correct and error responses. Our design should not be considered a full test of the model, and is not appropriate for accurate estimation of all of the parameter values. However, our design does allow us to determine if our ROC and RT data are consistent with the general predictions of a continuous sequential-sampling model.

Experiment 1

The goal of Experiment 1 was to evaluate the continuous-evidence assumption by considering both ROC and RT data. First, we sought to compare the 2HTM and SDT in fits to ROCs differing in target strength. Strength was manipulated by varying the number of times items were presented at study. At test, both strong and weak items were presented, along with a set of new items. From the standpoint of the 2HTM, lure detection should be unaffected by target strength, as all of the items were presented in the same test. This constrains the 2HTM to ensure that p_n does not respond to aspects of the data unrelated to recognition accuracy, as has been suggested by Dube and Rotello (2012). Second, we fit the diffusion model to both the response time and ROC data. This allowed us to assess the validity of the continuous-evidence assumption under constraints from multiple dependent variables.

Methods

Participants

29 undergraduates at the University of Massachusetts participated. They received course credit for their participation. Eight participants were excluded for producing many trials with very short (< 300ms) or very long (> 3000ms) RTs.³

Design

Experiment 1 used a 3 (item type: strong, weak, or lure) × 5 (old item proportion: .25, .33, .50, .67, .75) within-subjects design. Each participant completed a single session comprising 20 study-test cycles. In a given cycle, participants studied a list of 20 words (18 critical items, and a primacy and recency buffer). Half of the critical items were shown 5 times each, for a total of 56 study trials per list; study trials were randomly ordered for each participant and cycle. The test list contained 24 items, with the number of targets and lures varying depending on the base rate condition (18, 16, 12, 8, or 6 targets, with half strong targets and half weak in all cases). Participants were given 4 consecutive study-test cycles for each of the 5 base rate conditions. The order of the test conditions was counterbalanced across participants using a 5 × 5 Latin square.

Stimuli

The stimulus pool consisted of 640 singular nouns taken from the MRC psycholinguistic database (Coltheart, 1981). The words were 5–8 letters in length, with an average written frequency of 61.04 (Kučera & Francis, 1967). Stimuli were randomly sampled without replacement in order to construct 20 sets of 20 study words and a total of 240 lures, with the precise number in each of the 20 lure sets varying according to the base rate condition.

Procedure

Participants were tested individually, and were seated approximately two feet in front of a computer monitor. At the beginning of the experiment, participants were told that they would study several lists of words and that, following each list, their memory for the words on the list would be tested. In the first study phase, participants were presented with a list of 56 items (primary and recency words, 9 words shown once, and 9 words shown 5 times) in a random order. The words were shown one at a time, in the center of the monitor, for 500ms each. The rather short 500ms presentation rate was chosen to establish a low level of performance for the weak items (Ratcliff, Clark, & Shiffrin, 1990), which could potentially increase the effectiveness of our target strength manipulation.

In the test phase, participants were told they would be a shown a list containing a mixture of items from the study list and new items. They were instructed to respond ‘Old’ or ‘New’ using the f and j keys. Participants were informed of the percentage of items on the test that would be old (either 25%, 33%, 50%, 67%, or 75%) and were also asked to balance speed and accuracy. Following these instructions, participants were presented with the 24 test words, one at a time, with the response options ‘Old’ (f key) and ‘New’ (j key) displayed beneath each one. Half of the studied words on each test were strong, and half were weak. To help participants track the base rates at test, they were given feedback on the accuracy of each response.

Following the test phase, participants were given the option to take a short break, and to resume the experiment by pressing the spacebar. The next cycle began by informing participants that none of the words in the previous study and test lists would be presented in the current study-test cycle. The procedure was otherwise the same as in the first cycle. This continued for a total of four cycles, following which the same procedure was used for the next four, except that the bias condition was changed. This procedure repeated until all 5 bias conditions were completed, for a total of 20 study-test cycles.

Results

ROC fits: SDT and the 2HTM

The response proportions from the 5 bias conditions were used to construct binary ROCs, which are plotted in Figure 5. The ROC data were fit with the 2HTM and the unequal-variance SDT model by using the optim procedure in R (R Development Team, 2006) to minimize G² for each model. For the SDT fits, parameters for strong (μ_st) and weak (μ_wk) old item means, a single old item variance parameter, and a total of 5 criteria were used. For the 2HTM, two old item detection parameters for strong (p_str) and weak (p_wk) were used, along with a single lure detection parameter and a set of 5 bias parameters. Thus, both models used 8 parameters to fit a total of 15 freely-varying response proportions and can be compared via the resulting group and individual-level G² statistics with df = 7. The fit statistics and parameter values for the group data are displayed in Table 1. The fit results for individual participants are displayed in Table 2.

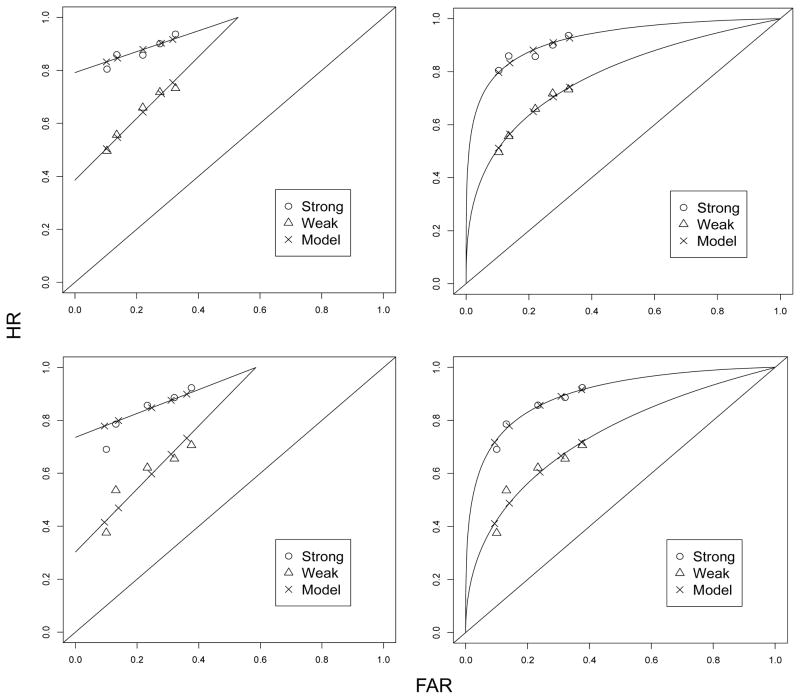
Figure 5.

Observed and model-predicted ROC data for Experiment 1 (top row) and Experiment 2 (bottom row). Lines are fits from the 2HTM, curves are fits from SDT. Specific operating point predictions are shown as crosses.

Table 1.

Fit statistics and best-fitting parameter values for SDT and the 2HTM in Experiments 1–2.

Experiment	Signal Detection Model
	G2(3)	μst	μwk	σo	c1	c2	c3	c4	c5
1	8.29	2.37	1.30	1.33	1.26	1.09	.79	.59	.44
2	12.40	2.04	1.04	1.25	1.32	1.08	.71	.50	.32
	Double High-Threshold Model
Experiment	G2(7)	pst	pwk	pn	b1	b2	b3	b4	b5
1	11.21	.79	.39	.47	.60	.53	.42	.26	.19
2	44.04***	.74	.30	.41	.16	.24	.42	.53	.62

^***p<.001.

Table 2.

Fit statistics and best-fitting parameter values for SDT and the 2HTM fit to individual data in Experiment 1.

		Signal Detection Model									Double high-threshold Model
ID	G2(3)	μstr	μwk	σo	c1	c2	c3	c4	c5	G2(3)	pstr	pwk	pn	b1	b2	b3	b4	b5
1	5.04	1.27	0.54	0.75	0.34	0.11	0.07	0.75	1.12	7.02	0.65	0.00	0.38	0.62	0.76	0.75	0.37	0.20
2	16.45*	1.14	0.90	0.20	0.80	0.81	0.90	0.89	0.95	18.98**	0.79	0.00	0.65	0.71	0.64	0.59	0.49	0.44
3	5.41	6.73	2.24	3.00	0.89	1.26	1.39	1.58	1.24	4.86	0.96	0.53	0.43	0.34	0.19	0.15	0.09	0.19
4	14.40*	3.88	1.57	2.02	0.66	1.09	1.23	1.63	1.44	13.49	0.85	0.25	0.70	0.60	0.49	0.45	0.18	0.26
5	7.84	5.01	1.92	3.00	0.39	0.91	1.10	0.90	1.34	8.02	0.89	0.55	0.00	0.34	0.18	0.14	0.18	0.08
6	7.46	2.03	0.97	1.35	0.30	0.24	0.24	0.85	0.76	8.35	0.79	0.40	0.20	0.47	0.51	0.52	0.23	0.29
7	4.09	2.56	1.32	1.16	0.06	0.69	0.63	1.12	0.82	6.03	0.91	0.52	0.34	0.71	0.37	0.41	0.20	0.30
8	15.48*	4.52	2.38	3.00	−0.19	0.57	0.75	0.81	1.04	16.93*	0.86	0.62	0.00	0.54	0.29	0.23	0.20	0.15
9	27.92	2.77	1.66	3.00	−0.36	−0.09	0.96	0.89	2.06	21.89**	0.66	0.46	0.00	0.57	0.54	0.18	0.19	0.00
10	13.10	2.16	1.52	0.56	0.97	1.04	1.44	1.42	1.51	14.94*	0.85	0.29	0.80	0.81	0.71	0.40	0.41	0.28
11	3.42	3.31	1.73	2.57	−0.09	0.55	0.55	1.40	1.37	2.87	0.78	0.49	0.08	0.57	0.33	0.32	0.09	0.09
12	11.72	2.10	1.23	0.99	0.54	0.55	0.79	1.68	1.39	9.93	0.71	0.15	0.64	0.74	0.71	0.68	0.10	0.27
13	15.02*	5.38	2.44	3.00	0.77	0.61	0.46	0.54	1.30	13.96	0.92	0.63	0.00	0.20	0.28	0.32	0.30	0.09
14	20.61**	3.42	1.82	3.00	0.06	−0.42	0.96	0.95	1.66	20.76**	0.74	0.45	0.05	0.52	0.66	0.18	0.18	0.06
15	14.97*	1.94	1.45	1.21	0.26	0.49	0.93	0.91	1.54	15.18*	0.66	0.46	0.48	0.75	0.61	0.38	0.35	0.11
16	5.75	2.63	1.37	0.92	0.67	0.50	1.16	1.48	1.32	6.35	0.91	0.36	0.60	0.66	0.74	0.36	0.13	0.24
17	12.80	2.27	1.22	2.86	0.35	0.10	0.60	1.16	1.58	13.72	0.60	0.40	0.00	0.39	0.42	0.28	0.12	0.06
18	8.43	2.19	1.54	0.95	1.06	1.03	1.06	0.87	1.62	7.40	0.69	0.20	0.75	0.60	0.66	0.61	0.71	0.22
19	7.38	2.05	0.90	1.38	0.64	0.99	0.88	1.23	0.70	8.45	0.73	0.34	0.25	0.35	0.19	0.27	0.14	0.32
20	4.51	2.81	1.93	0.91	0.71	1.00	1.17	1.56	1.80	5.79	0.90	0.54	0.75	0.84	0.67	0.53	0.25	0.11
21	4.41	5.07	2.63	3.00	0.17	0.99	0.96	1.50	1.69	3.05	0.88	0.60	0.23	0.56	0.21	0.22	0.09	0.06

^*p<.05,

^**p<.01,

^***p<.001. Bold values denote the better fitting model.

As can be seen in Figure 5, the strength manipulation was effective: the ROC points for strong items fall higher in the space than the points for weak items. The form of these functions is not entirely clear, however. Both ROCs show a fairly close grouping of the operating points, and while there appears to be curvature in the weak function, the strong function appears to be more linear. As the strong and weak items were presented in the same test, it is likely that apparent inconsistencies in form are random. (Recall also that Dube et al., 2011, found that closely-clustered operating points rendered model selection between SDT and 2HTM difficult). Consistent with this assumption, the fit results showed that both models fit the group data closely, with a slight edge for the SDT model (G²(7) = 8.29, p = .31) over the 2HTM (G²(7) = 11.21, p = .13). The individual participant data in Table 2 were also best described in more cases by SDT (13 of 21), though the SDT advantage was not reliable by a sign test (p < .10). Summing G² over individuals also produced similar results for the two models: 226.21 (SDT) and 227.97 (2HTM).

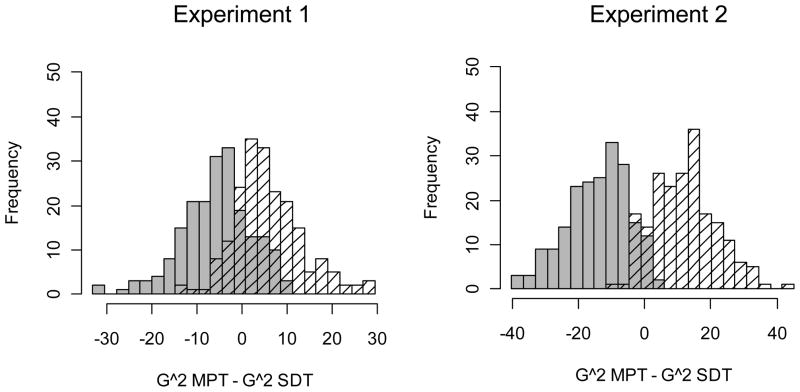
One interpretation of these results is that both models perform adequately (Bröder & Schütz, 2009, drew similar conclusions in the absence of large fit differences). Another interpretation is that the data do not provide strong constraints on the models, and thus do not allow strong conclusions to be drawn about the validity of the two approaches. In other words, the diagnosticity of the data must be considered before drawing any conclusions in the absence of a large difference in model fit (Jang, Wixted, & Huber, 2011). To assess the diagnosticity of our data, we performed bootstrap analyses to assess model recovery (Jang et al., 2011; Wagenmakers, Ratcliff, Gomez, & Iverson, 2004). Specifically, we simulated 200 datasets using the best-fitting parameters from Experiment 1 for each model. We then fit each dataset with both models to assess the degree of error in model recovery for the generated data. The results are displayed in Figure 6. There is considerable overlap in the distributions of fit differences for SDT and the 2HTM, which shows that the models are difficult to discriminate with data like those in Experiment 1. This could indicate that the small difference in fit favoring SDT is not a reflection of the validity of the 2HTM, but a consequence of lack of constraint on the models.

Figure 6.

Results of model recovery simulations using parameter values obtained in fits to the data from Experiment 1 and 2.

In sum, the observed ROC data were not entirely informative as to the form of the underlying functions or the validity of the continuous-evidence assumption. A clearer assessment requires more data. In what follows, we will use response time data in addition to the ROCs to provide a more rigorous test of the assumption. We will fit these data with the diffusion model, a dynamic version of SDT.

Diffusion Modeling

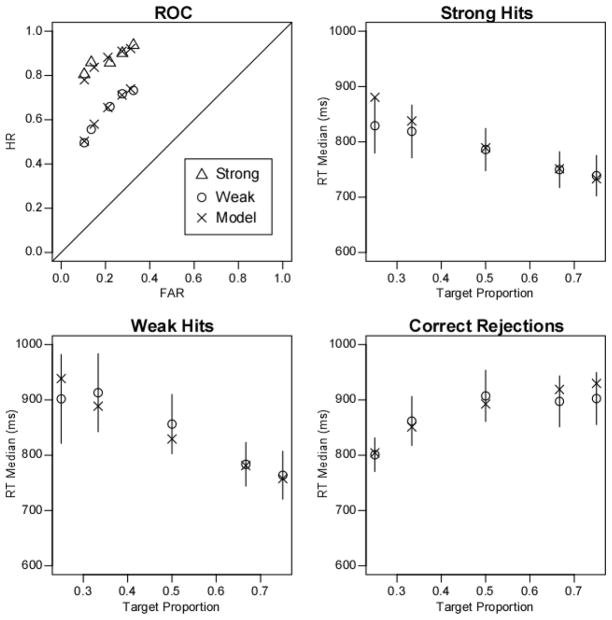
Due to the relatively low number of observations in the extreme bias conditions (and low number of errors in the strong condition), full distributional analyses are not practical. However, our main interest is in whether the core assumption of continuous evidence in the diffusion model is consistent with both ROC shape and the effect of target proportion on response latency. For this reason, we chose to concentrate on the ROC functions and median RTs for correct responses, which we fit with a restricted version of the diffusion model. Observed RT medians are displayed as circles in Figure 7, along with their 95% confidence intervals. Model predictions are shown as crosses.

Figure 7.

Observed ROCs and RT medians for correct responses in Experiment 1, and corresponding predictions from the diffusion model.

As can be seen in Figure 7, the observed hit RTs decreased steadily as the proportion of old items at test increased. For correct rejections, the opposite pattern emerged: RTs increased as base rate increased. This is consistent with previous results reported for recognition memory base rate manipulations by Criss (2010), Ratcliff and Smith (2004), and Starns et al. (2012), but it is in direct conflict with our tentative prediction for RTs based on the 2HT model.

To capture the effects of our base rate manipulation, we varied the starting point in the diffusion process over 5 levels. To capture the item strength effect, we allowed the mean target drift rates to vary with strength. We assumed a single mean drift rate for lures. One boundary width a, one value of η for target items, and one value of T_er were estimated. Parameters that cannot be estimated in the absence of full RT distributions (s_t, s_z, and η for lures) were fixed to standard values (specifically, s_t = 200 ms, s_z = .02, and lure η = .08). In sum, the restricted diffusion model used 11 free parameters to fit 30 freely-varying datapoints: 10 hit rates, 5 false alarm rates, and 15 RTs (median RTs for hits to strong targets, hits to weak targets, and correct rejections each at 5 levels of P(Old)). This resulted in 19 degrees of freedom for the fitting procedure. We estimated the median RT by averaging the medians from each participant, and the total number of correct responses in each condition was evenly divided into RT bins representing responses before and after the median. Incorrect responses were tallied into a third bin. To fit the model, we used the SIMPLEX routine to maximize goodness-of-fit by minimizing χ² across the resulting 45 frequency bins (3 item types × 5 probability conditions × 3 RT bins; see Ratcliff & Tuerlinckx, 2002).

Predicted values are shown in Figure 7 as crosses, and the resulting parameter values are shown in Table 3. As is clear in the figure, the diffusion model provided a good fit to our data: χ²(19) = 24.84, p = .17. The model nicely captured the form of the observed ROCs, the effects of target strength, and the effects of our bias manipulation. The same fits also produced a tight fit to the RT medians: all predictions fall within the 95% CIs around the observed points. Although there is a small deviation apparent in the low target proportion condition for strong hits, this is likely a trade-off in the fits that reflects differential sensitivity of the χ² statistic at different sample sizes. For the 30% target condition, there are relatively few target trials, meaning there is more room for flexibility in this condition. Even in this case, however, the model prediction still falls within the margin of error.

Table 3.

Best-Fitting parameters of the diffusion model fit to data from Experiments 1–2.

Parameter	Exp. 1	Exp. 2
a	0.133	0.123
z1	0.095	0.092
z2	0.097	0.086
z3	0.081	0.078
z4	0.069	0.059
z5	0.056	0.051
vstong	0.152	0.136
vweak	0.027	0.002
vlure	−0.164	−0.169
ηtarget	0.095	0.099
ηlure*	0.080	0.080
sz*	0.020	0.020
ter	0.497	0.575
st*	0.200	0.200

Asterisks denote fixed parameters.

Although we could not estimate RT quantiles and error RTs across all of the conditions, a subset of the conditions had sufficient observations to validly estimate these measures. We checked these conditions to make sure they were consistent with two critical assumptions that we made in applying the diffusion model. The first assumption was that the bias conditions affected the starting point parameter. Changes in starting point should produce large shifts in the leading edge (.1 quantile) of the RT distributions across the probability conditions, which distinguishes this account from the relatively constant leading edges produced by the model’s other bias parameter, the drift criterion (Ratcliff & McKoon, 2008; Ratcliff, Van Zandt, & McKoon, 1999). Only correct responses for strong targets and lures had enough observations to reliably estimate the leading edge for each participant across all five bias conditions. Data from both of these items types supported the starting point account by showing large changes in leading edge as the proportion of targets increased. Specifically, the .1 quantiles for “old” responses to strong targets were 625, 604, 569, 520, and 523 ms across the 25% to 75% target proportion conditions [F(4,80) = 13.37, p < .001], and the .1 quantiles for “new” responses to lures were 558, 611, 631, 652, and 667 ms [F(4,80) = 7.82, p < .001]. The proportion effect for the .1 quantiles was similar in size to the effect on the medians. This pattern replicates previous results (Criss, 2010; Ratcliff & Smith, 2004; Starns et al., 2012).

The second assumption was that drift rates varied continuously across trials as well as within trials (that is, η > 0). Between-trial variation in drift rates produces slower median RTs for errors than for correct responses in unbiased conditions (Ratcliff, 1978; Ratcliff & McKoon, 2008). To check for this pattern, we looked at RT medians for correct and error responses in the 50% targets condition for lures and weak targets (some participants never made errors for strong targets, making it impossible to estimate their median RT). As expected, errors were slower than correct responses for weak targets (900 vs. 756 ms; t(20) = 3.95, p < .001), and a non-significant trend in the same direction was apparent for lures (876 vs. 807 ms; t(20) = 1.58, p = .13). Previous recognition results also indicate that median RTs are slower for errors than correct responses unless participants are pressured to respond very quickly (Criss, 2010; Ratcliff & Smith, 2004; Ratcliff, Thapar, & McKoon, 2004; Starns et al., 2012).

Discussion

Although the observed ROC data were well described by both SDT and the 2HTM, numerically a better fit was obtained for SDT. When the continuous-evidence assumption of SDT was constrained by a wider range of data, however, the approach remained successful: the diffusion model accurately described all aspects of the ROC data as well as the effects of the base rate manipulation on the observed RT medians. Moreover, the pattern of RTs across base rate conditions was inconsistent with Hu’s (2001) proposal that traversing more links in a threshold model should increase mean RT.

Experiment 2

The aim of Experiment 2 was to improve upon the design of Experiment 1 in two ways, with the goal of producing ROC data that more definitely discriminate between the continuous and threshold models. First, we attempted to increase the effectiveness of our strength manipulation by doubling the number of study presentations in the strong condition. Second, we attempted to increase the effectiveness of our bias manipulation by modifying the feedback procedure. Whereas in Experiment 1, trial-by-trial accuracy feedback was given, in Experiment 2 we provided feedback only when participants made errors. Additionally, the feedback duration was longer when errors were inconsistent with the bias condition (e.g., a miss in the 80% targets condition or a false alarm in the 20% targets condition). Duration was equated for the different error responses in the 50% targets condition. This essentially adds a “payoff” manipulation (or, reinforcement contingency; Skinner, 1953) to encourage bias shifts in addition to varying target proportion. That is, participants were penalized with longer error messages when their responding was inconsistent with the prevailing target proportion. We expected that the form of the ROC would be more apparent with a wider spacing in the operating points, and that a larger difference in accuracy across strength conditions would provide a more stringent test of the threshold model’s prediction that the strong and weak ROCs converge to the same point on the right of the function.

Participants

28 undergraduates at the University of Massachusetts participated. They received course credit for their participation. Two participants were excluded for producing many trials with unusually fast (< 300ms) or slow (> 3000ms) RTs⁴.

Design and Procedure

Experiment 2 used the same design as Experiment 1, except that strong items were studied 10 times rather than 5. The procedure was also the same, with two exceptions. First, the presentation duration at study was reduced to 250 ms rather than 500ms. This change was expected to encourage a larger strength difference by weakening encoding for items presented once. Second, accuracy feedback was only given following erroneous responses, and the duration of the feedback varied. For responses inconsistent with the bias condition (e.g. a false alarm in a conservative condition) the feedback remained on screen for 3500ms. For error responses consistent with the condition, the duration was 1000ms. The duration was always 1000ms in the .50 condition.

Results

ROC fits: SDT and the 2HTM

The observed and model-predicted ROCs are plotted in Figure 5. Although the functions are similar to those of Experiment 1 in terms of accuracy, the feedback manipulation in the present experiment produced a slightly greater spread in the operating points. We hypothesized that with a greater spread in the operating points, there would be a clearer difference in model fit. This appears to be the case. The group results in Table 1 indicate a good fit for SDT (G²(7) = 12.40, p = .09) but rejection for the 2HTM (G²(7) = 44.04, p < .001). These empirical functions appear to be curved, consistent with the continuous-evidence assumption of SDT. Additionally, the value of σ_o obtained in this study, 1.25, is the same value that is approximated in many fits of the unequal-variance SDT model to ratings data (Wixted, 2007). This indicates further that there is good agreement in the form of recognition ROCs generated with base rate manipulations and confidence ratings, as had previously been observed in the perception literature (Egan, et al., 1959). Finally, note that the largest misfits for the 2HTM were as predicted from the simulated data in Figure 3.

The individual-participant data (model fits and parameters) are reported in Table 4. Of the 26 participants in the table, 19 were better fit by SDT than the 2HTM. This result is significant by a sign test at the .01 level. Additionally, a test of the magnitude of the differences in fit (SDT – 2HTM) also supports SDT, t(25) = 2.10, p<.05. Summing G² across participants also reveals an advantage for SDT (G²(147) = 276.70 vs. 300.74 for the 2HTM). Thus, the individual results are consistent with the group results: both levels of the analysis support the continuous-evidence assumption over the discrete-state assumption of the 2HTM.

Table 4.

Fit statistics and best-fitting parameter values for SDT and the 2HTM fit to individual data in Experiment 2.

		Signal Detection Model									Double high-threshold Model
ID	G2(3)	μstr	μwk	σo	c1	c2	c3	c4	c5	G2(3)	pstr	pwk	pn	b1	b2	b3	b4	b5
1	3.18	1.45	1.19	0.29	0.90	0.89	0.93	1.16	1.32	3.36	0.68	0.00	0.77	0.86	0.86	0.83	0.50	0.35
2	14.92*	3.73	1.48	1.90	0.79	0.80	1.53	1.69	1.56	16.92*	0.88	0.45	0.35	0.34	0.32	0.07	0.07	0.10
3	17.07*	2.34	1.32	1.38	0.58	0.90	0.49	0.90	1.88	19.39**	0.61	0.07	0.68	0.66	0.60	0.74	0.78	0.14
4	5.80	5.65	2.42	2.79	0.54	1.39	1.60	2.03	0.73	6.15	0.92	0.57	0.39	0.45	0.14	0.10	0.03	0.39
5	15.74*	2.42	1.72	1.17	1.05	0.34	0.81	1.10	1.49	13.98	0.87	0.68	0.25	0.00	0.56	0.27	0.20	0.10
6	7.06	1.54	0.61	0.81	0.07	0.20	0.94	0.82	1.16	8.23	0.71	0.01	0.42	0.77	0.72	0.30	0.40	0.19
7	22.27**	4.25	1.54	3.00	0.05	0.27	0.97	1.21	0.97	22.58**	0.84	0.47	0.00	0.48	0.37	0.16	0.12	0.17
8	15.48*	1.58	0.85	1.77	−0.37	0.14	0.29	1.34	1.31	10.47	0.56	0.25	0.14	0.73	0.52	0.45	0.09	0.12
9	4.80	5.33	1.74	3.00	−0.88	0.67	1.30	1.43	1.10	5.50	0.91	0.50	0.00	0.74	0.26	0.09	0.07	0.14
10	4.62	1.87	1.46	0.61	0.95	0.88	1.20	1.43	1.81	8.21	0.57	0.12	0.80	0.80	0.82	0.65	0.43	0.19
11	5.62	4.60	1.78	3.00	0.83	1.28	1.46	1.50	1.86	4.72	0.85	0.51	0.00	0.22	0.11	0.06	0.06	0.03
12	9.56	5.23	1.23	3.00	0.65	0.30	1.58	1.76	1.84	9.39	0.90	0.41	0.00	0.26	0.39	0.04	0.03	0.04
13	8.10	1.43	0.84	1.14	−0.31	−0.15	−0.03	0.30	1.26	10.67	0.60	0.24	0.27	0.81	0.76	0.72	0.54	0.15
14	8.27	4.10	1.01	2.84	−0.25	0.09	0.95	0.97	0.93	10.19	0.85	0.38	0.00	0.55	0.44	0.17	0.17	0.18
15	13.41	0.65	0.44	0.77	−0.09	−0.16	0.17	0.81	1.05	15.27*	0.17	0.03	0.30	0.77	0.79	0.63	0.28	0.22
16	6.79	4.81	2.24	3.00	0.26	0.71	0.06	0.66	1.11	6.87	0.89	0.59	0.00	0.38	0.25	0.47	0.26	0.13
17	12.29	1.56	1.28	0.20	1.17	1.17	1.17	1.19	1.37	15.72*	0.87	0.00	0.82	0.70	0.73	0.70	0.61	0.42
18	28.81	2.93	0.56	3.00	1.15	1.05	0.72	1.18	1.70	29.79	0.51	0.00	0.72	0.48	0.40	0.41	0.65	0.27
19	4.97	2.53	0.94	1.40	0.60	0.29	0.72	1.23	1.75	5.51	0.79	0.17	0.47	0.53	0.63	0.49	0.23	0.07
20	7.72	0.95	0.53	0.54	0.02	0.17	0.44	0.87	0.95	13.50	0.46	0.00	0.42	0.85	0.78	0.60	0.32	0.25
21	4.81	6.48	2.65	3.00	1.04	1.24	1.50	1.50	1.65	4.33	0.95	0.63	0.00	0.16	0.10	0.07	0.07	0.04
22	5.27	1.66	1.13	1.45	−0.53	−0.08	0.01	0.55	1.52	8.43	0.60	0.41	0.19	0.81	0.67	0.63	0.36	0.08
23	9.10	0.45	0.17	0.77	−0.43	0.03	0.03	0.71	0.51	8.42	0.26	0.00	0.14	0.80	0.59	0.58	0.26	0.33
24	11.38	2.37	0.96	1.24	0.26	0.39	0.62	1.34	1.98	8.27	0.76	0.00	0.55	0.74	0.70	0.64	0.28	0.04
25	19.82**	0.82	0.37	0.78	0.20	0.58	0.61	0.76	1.51	21.98**	0.32	0.00	0.30	0.62	0.37	0.40	0.34	0.08
26	9.84	2.40	1.48	0.81	1.31	1.20	1.26	1.91	1.86	12.89	0.78	0.22	0.79	0.47	0.57	0.50	0.09	0.18

^*p<.05,

^**p<.01,

^***p<.001. Bold values denote the better fitting model.

To assess the diagnosticity of our data, we again carried out model recovery simulations following the procedure from Experiment 1. The results are in the right panel of Figure 6. These distributions of fit differences indicate that model recovery was improved in this dataset relative to Experiment 1: there is less overlap in the distributions of simulated data for SDT and the 2HTM. In other words, the data in Experiment 2 produced values in the model parameters that more clearly highlight the models’ differences. This indicates that the current experiment, which attempted to produce a larger spread in the operating points, produced ROC data that were more diagnostic than those of Experiment 1.

Diffusion Modeling

We fit the diffusion model to our results following the procedure described in Experiment 1. Predicted values are shown in Figure 8 as crosses, and the resulting parameter values are shown in Table 3. Although the fit of the diffusion model was significant according to the standard χ₂ calculation (namely, 37.14, p < .01), this statistic is driven by a very large number of observations, which can result in significant results even if the differences between the observed and expected data are trivial (Myers, Well, & Lorch, 2010; Ratcliff, Thapar, Gomez, & McKoon, 2004).

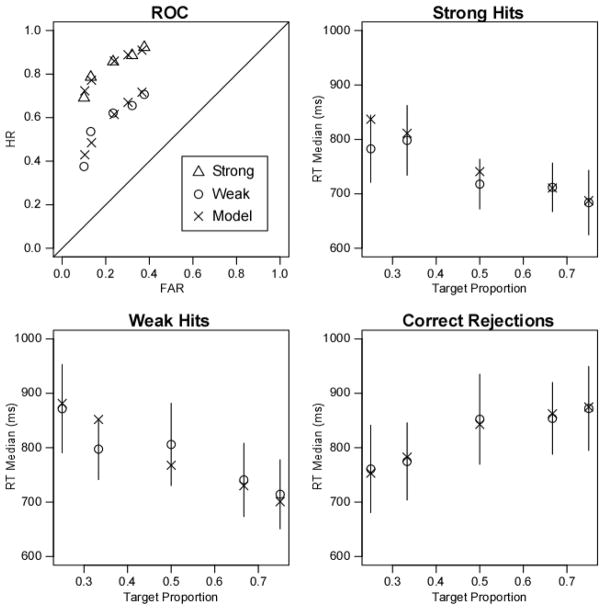
Figure 8.

Observed ROCs and RT medians for correct responses in Experiment 2, and corresponding predictions from the diffusion model.

The results in Figure 8 show a good correspondence between the observed and predicted ROCs and RT data. The diffusion model captured the form of the ROC data, the effects of bias on the operating points, and the effect of target strength on sensitivity. In the RT plots, the pattern observed in Experiment 1 is evident again: “Old” responses become faster as P(Old) increases, and “New” responses become slower. All of the predicted RTs fall within the margins of error in Figure 8, consistent with the model. In sum, the diffusion model provided a good fit to our data, which shows that the continuous evidence approach is successful even when constraints from multiple dependent variables are applied.

As in the first experiment, we evaluated the leading edge data (.1 quantile) to validate our decision to model biases as a change in starting point. Only correct responses for strong targets and lures consistently had enough observations to estimate the leading edge. Replicating Experiment 1, there were big shifts in leading edge as the proportion of targets increased, as predicted by the starting point model (“old” responses to strong targets: M = 670, 652, 594, 570, and 536 ms, F(4,100) = 21.96, p < .001; “new” responses to lures: M = 577, 602, 651, 700, and 714 ms, F(4,100) = 11.28, p < .001). We also examined RT medians for correct and error responses in the 50% targets condition to check for between-trial variability in drift rates. As in Experiment 1, only lures and weak targets supported the estimation of error RTs across all participants. Errors were slower than correct for both lures (975 vs. 852 ms; t(25) = 2.59, p < .05) and weak targets (917 vs. 806 ms; t(25) = 3.11, p < .01), consistent with between-trial variation in drift.

Discussion

The present experiment improved upon Experiment 1 by including a feedback manipulation intended to produce a greater effect of P(Old) on response bias. This manipulation was successful in producing a more decisive result: the ROC data were clearly better described by SDT than the 2HTM, at both the group and individual-participant levels. When the continuous-evidence assumption was instantiated in the diffusion model, we were able to account simultaneously for the form of the observed ROCs, the effects of response bias and target strength on the response proportions, and the patterns in RTs for strong hits, weak hits, and correct rejections at all levels of P(Old). The results for the comparison between SDT and the 2HTM, and the fits of the diffusion model, are consistent with Experiment 1. These data argue in favor of continuous-evidence models as opposed to discrete-state models such as the 2HTM.

Re-analysis of Starns, Ratcliff, and McKoon (2012)

Although we find the results show overall agreement across our two experiments, the comparison between SDT and the 2HTM in Experiment 1 did not show a statistical advantage for either model. It is important to ensure that the present results were in fact influenced by the spread in the operating points and do not reflect random differences across the experiments. For this reason, we have conducted a similar analysis using binary ROC data collected previously by Starns et al. (2012). This data set has several properties that make it particularly promising for discriminating continuous and threshold ROC models. First, participants in this experiment each completed 20 sessions of data collection, allowing detailed model comparison at the individual-participant level. Second, the design included a range of target strengths mixed into the same test, as in the current two experiments. Specifically, targets were studied once, twice, or four times, and each list also included words of both high and low natural-language frequency. Third, ROCs were formed using a target proportion manipulation in an old/new paradigm, a situation in which the threshold model unambiguously predicts linear functions (Bröder & Schütz, 2009). Specifically, across study/test cycles either .21, .32, .50, .68, or .79 of the test items were targets. Participants were asked to emphasize speed for half of the sessions and accuracy for the remaining sessions.

For both models, memory evidence parameters were free to vary for high and low frequency, speed- versus accuracy-emphasis instructions, and number of learning presentations (1, 2, or 4). Bias parameters were free to vary across the target-proportion variable and between speed- and accuracy-emphasis instructions. Fitting SDT to these data requires a total of 30 parameters: 14 means (12 for old items, and 2 for lures), 6 variance parameters (high vs. low frequency targets crossed with speed vs. accuracy emphasis, and 2 variances for low frequency lures; variances were fixed across number of target repetitions), and 10 criteria (5 each for the speed and accuracy sessions). For the 2HTM, 26 parameters were required: 12 old and 4 new detection probabilities, and 10 bias parameters.

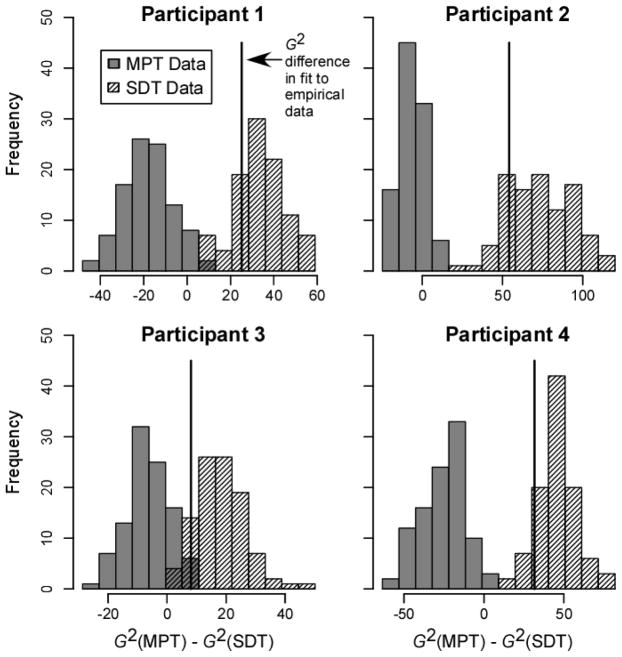
To assess the diagnosticity of this dataset for discriminating the models, we again conducted model recovery simulations. We generated 100 simulated datasets from each model (SDT and 2HTM) for each participant’s parameters and the parameters for the group data. The resulting data were fit with both models. The histograms in Figure 9 show the difference in G² for the data generated by each model. The vertical lines in the plots mark the difference in G² that was actually observed in the data. With these parameters, the models are fairly easy to discriminate at the individual participant level. In other words, the data provide good diagnosticity for selecting between the models (Jang et al., 2011; Wagenmakers et al., 2004). In all cases, the observed difference in G² fell near the mean of the distribution for SDT-generated data. In contrast, for three of the four participants the observed difference in G² was completely outside the distribution of fits to data generated by the threshold model. These results are consistent with our main contention: the ROC functions are more consistent with the continuous-evidence model.

Figure 9.

Results of model recovery simulations using parameter values obtained in fits to the data collected by Starns, Ratcliff, and McKoon (2012).

Another method for selecting among models that differ in complexity is to apply statistics that subtract a penalty term for each free parameter in a given model. The Akaike information criterion (AIC; Akaike, 1973) and Bayesian information criterion (BIC; Schwarz, 1978) are often used for this purpose. AIC and BIC include a penalty for complexity that is more stringent in the latter statistic. We used the model recovery simulations to evaluate the accuracy of AIC and BIC in selecting between SDT and the 2HTM in the Starns et al. dataset.

Table 5 shows the model selection results we observed for each participant, and Table 6 shows the proportion of cases in which each measure selected the generating model in our simulations. As shown in Table 5, all four participants and the overall data are better described by SDT than the 2HTM in G² as well as AIC. However, the harsher penalty in BIC produces results that favor the 2HTM for 3 out of 4 participants, although even BIC favored the SDT model for the overall data. The results seem to be equivocal, but Table 6 shows that the accuracy of these fit statistics varies greatly depending on how strictly complexity is penalized. AIC (like G²) nearly always recovers the generating model, but BIC does not. In fact, BIC appears to fare quite poorly in this scenario, with accuracy rates dropping as low as 2%. Importantly, the poor performance in BIC is restricted to SDT-generated data: BIC always recovers the 2HTM when that model generated the data. In other words, there is a pronounced bias in BIC that is driven by the number of parameters in the two models. This is consistent with a model recovery study conducted by Jang et al. (2009) which showed that, in deciding between different signal detection models of recognition, BIC overpenalized for additional parameters to the point of suggesting implausible conclusions (also see Wagenmakers et al., 2004 for more evidence of bias in model recovery). The bias we have observed in BIC indicates that the conflicting results that we observed in BIC are probably due to the pronounced bias in this statistic, which indicates more weight should be placed on AIC. As we have noted, AIC was lower in every case for SDT than the 2HTM.

Table 5.

Fit statistics for SDT and the 2HTM fit to individual and group data from Starns, Ratcliff, and McKoon (2012).

	G2		AIC		BIC
	SDT	2HTM	SDT	2HTM	SDT	2HTM
Participant 1	55.12	80.28	528.12	545.28	759.91	746.16
Participant 2	61.23	115.4	540.32	586.5	772.08	787.35
Participant 3	60.23	68.32	523.59	523.67	755.5	724.66
Participant 4	49.94	81.6	525.17	548.82	756.82	749.59
Average	47.51	113.3	636.05	693.89	909.41	930.75

^*p<.05,

^**p<.01,

^***p<.001. Bold values denote the better fitting model. Degrees of freedom are 130 for SDT, and 134 for the 2HTM.

Table 6.

Model selection and recovery accuracy for SDT and the 2HTM for individuals in Starns, Ratcliff, and McKoon (2012).

Participant and Fit Statistic	Modeling Results
	Winner in fits to empirical data	Model recovery accuracy for SDT data	Model recovery accuracy for 2HTM data
Participant 1
G2	SDT	1.00	0.92
AIC	SDT	0.98	1.00
BIC	MPT	0.30	1.00
Participant 2
G2	SDT	1.00	0.75
AIC	SDT	1.00	0.99
BIC	SDT	0.98	1.00
Participant 3
G2	SDT	1.00	0.81
AIC	SDT	0.92	0.98
BIC	MPT	0.02	1.00
Participant 4
G2	SDT	1.00	0.97
AIC	SDT	1.00	1.00
BIC	MPT	0.77	1.00

The results from the Starns et al. (2012) data are consistent with our results in Experiment 1 and 2. This suggests the greater differences in fit observed in Experiment 2 were in fact due to the somewhat greater spread in the operating points produced via our feedback manipulation. Taken together, our accuracy-only modeling results support the continuous evidence model over the discrete-state model.

General Discussion

The results of the present study support continuous-evidence models of recognition memory. In two experiments, we manipulated item strength and old item base rates in order to discriminate between SDT and the 2HTM. We found that the resulting binary ROC data were consistent with SDT but not the 2HTM. Although the comparison of SDT and the 2HTM in Experiment 1 was not decisive, it was nonetheless consistent with that of Experiment 2. As noted previously (Dube et al., 2011) the SDT and 2HT models are more difficult to discriminate when the operating points are more closely grouped. We encouraged larger differences in “Old” rates across conditions in Experiment 2 by penalizing error responses that were inconsistent with the bias conditions. This resulted in a larger difference in model fit, which favored SDT. We found similar results in fits to individual-participant data and in re-analyses of data collected previously by Starns et al. (2012).

The current results add to a growing body of data that suggests binary ROCs are curved, contrary to the conclusions reached by Bröder and Schütz (2009). First, as pointed out by Dube and Rotello (2012), the meta-analysis reported by Bröder and Schütz contained a large number of 2-point ROCs. These functions can generally be equally well described by a line or a curve. When those data are removed, it is clear that the remaining cases are better described by SDT than the 2HTM. Second, a meta-analysis of binary ROCs in the perception literature strongly favored the SDT model. Third, the new experiments Bröder and Schütz (2009) reported potentially confounded changes in sensitivity and response bias. Dube and Rotello reported two new experiments that were generally better described by SDT than the 2HTM, even at the individual-participant level.

Thus far, the existing data from Bröder and Schütz’s meta-analysis (excluding 2-point data), the perception data analyzed by Dube and Rotello, the new data collected by Dube and Rotello, the data collected in two experiments in the present study, and the re-analysis of binary ROC data collected by Starns et al. (2012) converge on a single conclusion: binary ROCs are curvilinear and consistent with continuous-evidence theories such as SDT and the diffusion model. These data contradict arguments against ratings ROCs as a valid model selection tool as well: not only were the binary ROCs curvilinear, as in the ratings case, but the SDT models we fit (unequal-variance SDT) generally produced values of σ_o greater than 1. This is the same result that is typically obtained in fits of the model to ratings data (Wixted, 2007). We conclude that the curvature observed in ratings ROCs is not due to the ratings task, but reflects an essential aspect of the process by which participants assess memory evidence.

Nonetheless, a strict focus on binary ROCs imposes a number of limitations on model selection. Because binary ROCs require relatively large numbers of observations in order to produce stable data and require participants to consistently adhere to biasing instructions, their form can be difficult to discern. This was the case in Experiment 1. For this reason, we expanded our focus to include response time data. We used these data, along with the ROC data, to test the continuous evidence assumption as it is embodied in the diffusion model (Ratcliff, 1978; Starns et al., 2012). In both of our experiments we found that the diffusion model provided a good fit to both the RTs and the ROCs. The model captured the effects of item strength and old item base rates on RT medians via the drift rate and starting point parameters, and was able to simultaneously account for the form of the observed ROCs as well as the effects of target strength and old item base rates on the operating points. This suggests that, even under the constraints imposed by multiple forms of data, the continuous-evidence assumption still provides an excellent account.

In contrast to the success of continuous-evidence models applied to RT data, these data might prove particularly challenging for a threshold approach. One difficulty is how to terminate the decision when evidence does not pass the detection threshold; that is, what signals to the decision maker that it is time to make a random guess? If guesses are only made on trials that fail to generate the detect state after some criterial length of time, then the threshold account would make the strong prediction that errors are always slower than correct responses (that is, only entering a detect state could trigger the early termination of a trial). This constraint would lead to misfits in the RT data for some conditions, especially conditions that engender strong biases. For example, in Starns et al.’s (2012) .21-target condition, error responses for target items were up to 100 ms faster than correct responses. This pattern is naturally accommodated by the diffusion model, given that a bias to say “new” means that the starting point is close to the “new” boundary and far from the “old” boundary (error and correct responses for targets, respectively). The 2HT models, in contrast, might be fundamentally inconsistent with fast errors.

Beyond capturing the relative speed of correct and error responses, the threshold account would also need to accommodate the shape and spread of RT distributions and predict how these characteristics change with variables influencing task difficulty, decision biases, and speed-accuracy tradeoffs – all of which are successfully accounted for by continuous sequential-sampling models (Ratcliff & McKoon, 2008; Wagenmakers, 2009). Such achievements might be out of reach of the threshold approach. At the least, they will require substantial theoretical development. For these reasons, we suspect RT data will play a significant role in the continuous versus threshold debate.

Recent advances in ROC modeling have explored variation across participants and items in a hierarchical modeling structure, and modeling results can sometimes change substantially when averaging over these variables as opposed to directly modeling them (Pratte, Rouder, & Morey, 2010). As a result, we cannot rule out the possibility that a hierarchical version of the threshold model might provide a better account of ROC shape than the non-hierarchical model. That is, if we assume that different items vary in their probability of producing a detect state, then even the threshold approach might be able to match curved binary ROC functions. Of course, such an implementation would blur the line between the alternative approaches, because items would fall along a continuum of strength even in the threshold model (except that strength would be expressed as the probability of producing a detect state). Even if a hierarchical approach could more closely match the data, the ROC results still refute the non-hierarchical versions of the threshold model that are currently being applied to ROC data (Bröder & Schütz, 2009; Klauer & Kellen, 2010, 2011). Moreover, even a hierarchical version of the threshold model would not address the RT data that are well matched by continuous sequential-sampling models.

Implications for Threshold Models Treated as Measurement Models

One argument in favor of discrete-state models like the 2HTM is that they may still provide reasonably good measures of memory accuracy and response bias, even if participants do not respond on the basis of discrete mental states as the models assume. In other words they may serve well in their limited capacity as ‘measurement models’ (Batchelder & Reifer, 1990; Klauer & Kellen, 2010). We find there are good reasons to be skeptical of arguments that attempt to separate models into the ‘measurement’ and ‘processing’ categories. Even if such a distinction can be agreed upon, this does not mean that the processing and measurement aspects are independent in these models. In fact, this is not true from the standpoint of either an SDT or threshold framework. Ignoring this dependence, or failing to evaluate the processing assumptions of a given model when applying it for measurement purposes, may produce serious statistical errors that are not remedied by increases in sample size or through replication.

For instance, Rotello, Masson, and Verde (2008) showed that when accuracy is compared across conditions differing only in bias, the probability of erroneously concluding that accuracy differs is elevated when statistics that generate the wrong underlying ROC form are applied. They simulated recognition data from two conditions differing in bias, using either Gaussian distributions consistent with SDT or rectangular distributions consistent with threshold theory. The resulting data were then compared via statistics consistent with either the SDT model (d′) or threshold models (percent correct). The authors found that, when statistics consistent with the generating model were compared, Type I error rates remained near the nominal alpha level of .05. When the wrong statistic was applied, however, error rates soared, in some cases to near unity.

That such errors can be predictable and prevalent in pre-existing data was demonstrated by Dube, Rotello, and Heit (2010). Their study examined the belief bias effect in deductive reasoning. In belief bias studies, participants are presented with logical arguments that vary in conclusion validity and believability. These studies show that when conclusions are not believable (e.g. ‘Some cigarettes are not addictive’) participants are more successful in valid/invalid discrimination (Evans, Barston, & Pollard, 1983). However, the effect is nearly always measured with a contrast comparing H – F across conditions differing in believability. Crucially, the finding of higher accuracy in H – F has driven much of the theoretical work on belief bias (e.g. Ball, Phillips, Wade, & Quayle, 2006; Evans, Barston, & Pollard, 1983; Evans & Curtis-Holmes, 2005; Evans, Newstead, Allen, & Pollard, 1994; Morley, Evans, & Handley, 2004; Newstead, Pollard, Evans, & Allen, 1992; Quayle & Ball, 2000; Roberts & Sykes, 2003; Shynkaruk & Thompson, 2006; Stupple & Ball, 2009; Thompson, Striemer, Reikoff, Gunter, & Campbell, 2003). Dube et al. (2010) provided the first ROC analysis of data from belief bias experiments and found that all of the data for believable and unbelievable arguments fell on a single curve. This suggests that the sensitivity difference that has driven over 30 years of theoretical work on belief bias may be a predictable Type I error. Such errors result from inappropriate application of a statistic, H – F, that is consistent with a restricted version of the double high-threshold model. When more appropriate SDT-based statistics were applied, no errors resulted in the analysis and sensitivity was found to be equal for both argument types. The studies by Dube et al. (2010) and Rotello et al. (2008) together show that there is a dependence between the measurement and process aspects of MPT and SDT models, and that a failure to evaluate the processing level when applying models for measurement can have quite severe consequences for data analysis.

One need look no further than the current dataset for an example of the kinds of measurement errors that can occur when processing assumptions are ignored during measurement. When the data from Experiment 2 are fit allowing p_n to vary with target strength, the values are .52 and .34 for the functions with strong versus weak targets, a difference of .18. In other words, the 2HTM concludes there is a difference in lure detection when the same responses to lures are replotted in the strong and weak target functions, an impossible result. This is yet another example of how incorrect processing assumptions lead to inaccuracies in measurement and incorrect conclusions regarding the effects of independent variables.

Despite the disadvantages of the 2HTM analyses in the domains we have considered, the MPT framework offers the advantage of applicability across tasks differing widely in complexity (e.g. Erdfelder & Buchner, 1998; Smith & Bayen, 2004). Indeed, the continuous-evidence models we have considered here are typically applied to a binary response format and/or ratings data (see Ratcliff & Starns, 2009 for an extension of the diffusion model to ratings), and do not provide an obvious application to phenomena such as prospective memory or hindsight bias.

Nonetheless, if threshold models are to be considered tools for data analysis, then we must acknowledge that they are tools that largely ignore a major dependent variable in decision tasks, namely response time (although see Hu, 2001). Continuous sequential-sampling models offer tools that handle all aspects of decision making in an integrated framework. The ability to jointly model accuracy and decision time has redefined interpretations and research questions in a number of domains (Ratcliff & McKoon, 2008; Wagenmakers, 2009), and RT models promise to do the same for recognition memory.

Conclusion

People do not appear to respond purely on the basis of detection thresholds in recognition memory tasks. Our data support continuous-evidence models such as SDT and the diffusion model, both in terms of ROC and RT data. Given the success of continuous models, interpretations based on models that assume threshold memory retrieval should be viewed with caution.

Highlights.

• We compare continuous and threshold models using binary ROCs and response times.

• We manipulate target strength to add additional constraints to the models.

• We test continuous/SDT assumptions further via the Ratcliff Diffusion model.

• Of the two ROC models, only SDT describes the ROCs and strength effects.

• SDT assumptions applied via the Diffusion model capture all of our data.