A bone marrow toxicity model for ²²³Ra alpha-emitter radiopharmaceutical therapy

Abstract

Purpose

Ra-223, an α-particle emitting bone-seeking radionuclide, has recently been used in clinical trials for osseous metasteses of prostate cancer. We investigated the relationship between absorbed fraction-based red marrow dosimetry and cell level-dosimetry using a model that accounts for the expected localization of this agent relative to marrow cavity architecture. We show that cell level-based dosimetry is essential to understanding potential marrow toxicity.

Methods

The GEANT4 software package was used to create simple spheres representing marrow cavities. Ra-223 was positioned on the trabecular bone surface or in the endosteal layer and simulated for decay, along with the descendants. The interior of the sphere was divided into cell-size voxels and the energy was collected in each voxel and interpreted as dose cell histograms. The average absorbed dose values and absorbed fractions were also calculated in order to compare those results with previously published values.

Results

The absorbed dose was predominantly deposited near the trabecular surface. The dose cell histograms results were used to plot the percentage of cells that received a potentially toxic absorbed dose (2 or 4 Gy) as a function of the average absorbed dose over the marrow cavity. The results show (1) a heterogeneous distribution of cellular absorbed dose, strongly dependent on the position of the cell within the marrow cavity; and (2) that increasing the average marrow cavity absorbed dose, or equivalently, increasing the administered activity resulted in only a small increase in potential marrow toxicity (i.e., the number of cells receiving more than 4 or 2 Gy), for a range of average marrow cavity absorbed doses from 1 Gy to 20 Gy.

Conclusion

The results from the trabecular model differ markedly from a standard absorbed fraction method while presenting comparable average dose values. These suggest that increasing the amount of radioactivity may not substantially increase the risk of toxicity, a result unavailable to the absorbed fraction method of dose calculation.

I. INTRODUCTION

Although α-emitters have been studied for many decades, their current use in humans for targeted therapy is an important milestone (1). One of the more promising specific cases is the use of ²²³Ra to treat metastatic prostate cancer in the skeleton (2, 3); however, the localization of ²²³Ra to the bone matrix raises concerns about potential acute hematologic toxicity and depletion of bone marrow reserve. Initial clinical studies have shown toxicities well below those expected (4, 5). As such, we have investigated the relationship between absorbed fraction-based red marrow dosimetry and cell level-dosimetry using a model that accounts for the expected localization of this agent relative to marrow cavity architecture. We show that cell level-based dosimetry is essential to understanding potential marrow toxicity. Recognizing that the traditional absorbed fraction-based approach gives the average red marrow absorbed dose, and that this average dose is an unreliable predictor of marrow toxicity, we present an alternative basic approach to α-emitter dosimetry for the tissues of human bone marrow.

Advances in the targeted delivery of radionuclides and radionuclide conjugation chemistry, as well as the increased availability of α-emitters appropriate for clinical use, have recently led to patient trials of radiopharmaceuticals labeled with α-particle emitters (1). Alpha-particle emitters have the advantages of high potency and localized energy deposition. These advantages arise from the densely ionizing track and short path length, respectively, of the emitted positively charged helium nucleus in tissue. The linear energy transfer (LET) of α-particles can be 2 or 3 orders of magnitude greater than that of β-particles (1). Cell survival studies have shown that cell death may result from as few as one to three α-particle tracks across the nucleus (6). Furthermore, the ability of high LET radiation to kill cancer cells is less compromised by hypoxia, dose rate effects or cell cycle position than low LET β-radiation, enhancing its potential effectiveness in targeted radionuclide therapy (1, 7).

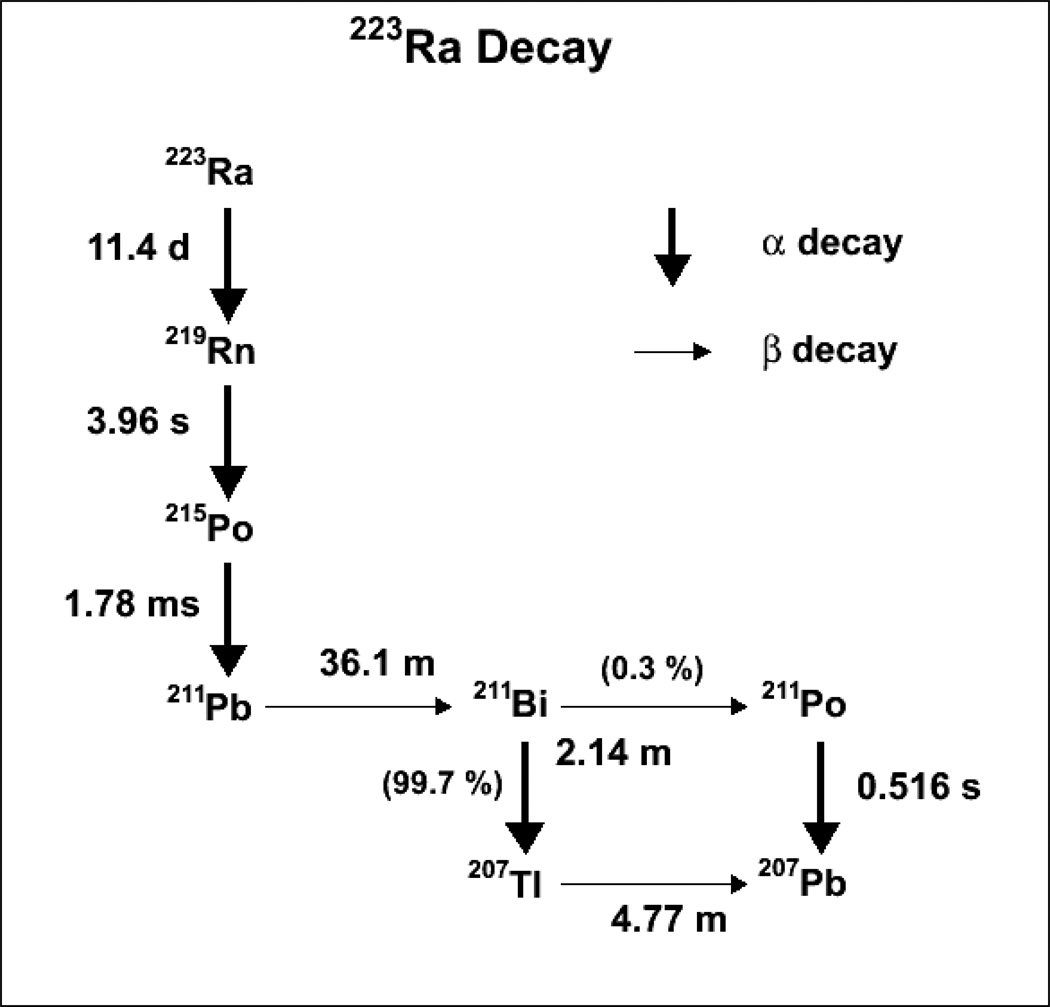
The incidence of bone metastases in patients with cancer is most commonly associated with primary cancers of the breast (47–85 %), prostate (33–85 %) and lungs (32–60 %). Bone metastases contribute to the death of over 350,000 individuals a year in the US alone (8). As calcium and radium share the same chemical properties, ²²³Ra localizes to areas of active bone formation found in both bone metastases and in the matrix of normal bone mineral. For this reason also, acute red marrow toxicity becomes a prime concern. Ra-223 decays to several short-lived α-particle emitting daughters, for a total of 4 α-particles emitted per ²²³Ra ion, thereby increasing the amount of energy deposited per nuclide. This decay chain is shown in Figure 1. While the half-life of the daughter ²¹¹Pb (36.1 min) is in theory long enough for the ion to relocate to a different part of the patient’s body, dosimetry/biodistribution studies have shown that this is not the case for the majority of the ions (9).

Figure 1.

²²³Radium decay chain. A total of four α-particles and two β-particles are emitted.

Absorbed dose (D) is a measure of damage to tissue, and is defined as the ratio of the mean energy deposited by the decaying particle to the mass of the target tissue. To simplify the implementation of absorbed dose calculations, in particular for risk assessment, the MIRD Committee established a dosimetry schema that incorporates the concept of absorbed fraction, the fraction of energy absorbed by a target volume from radiation emissions in a source region (surface or volume) (10, 11). This schema is by far the most widely adopted method of absorbed dose calculation. Its implementation requires the user to calculate the time-integrated activity from longitudinal source activity data in the different source regions (organs) that could irradiate the target volume (organ). The absorbed dose to the target volume is then calculated by considering the fraction of energy that is emitted in each contributing source volume and is absorbed in the target volume, hence the appellation “absorbed fraction”. This approach is commonly applied using the software package OLINDA/EXM (12). As currently implemented, the fundamental assumption in this approach, however, is of a uniform distribution of emitters in the source volume and a calculation that gives the average absorbed dose to the target volume. In principle, this formalism could also apply to highly non-uniform activity and dose distributions, such as the distributions created by localized α-particles, whose range is on the order of 50–80 µm, and where the localization of activity is on a scale that is substantially smaller than: (a) the resolving power of clinical imaging detectors and modalities, and (b) the scale of human organs. The MIRD formalism could potentially overcome this complication as long as a sufficiently large number of very small target and source volumes are defined. However, in such scenarios, the MIRD committee (1), along with others (6) have recommended cell-level and microdosimetry calculations that are based on a priori biodistribution information obtained from preclinical or, when the sub-cellular distribution is also relevant, cell-based studies. Such cell-level and microdosimetric approaches have been implemented for laboratory animal ex vivo and cellular in vitro studies (9, 13–15), including most recently an S-value methodology applied to the testes (16).

Bone marrow is often the dose-limiting organ in radioimmunotherapy (17). Accurate dosimetry of bone marrow is difficult because of its complex geometry and the presence of tissue inhomogeneities (18). This is especially true for radionuclides that bind to either blood or bone (19) when commonly used simple blood to bone marrow activity conversions (17) are no longer valid.

II. METHODS

Modeling

Simple geometrical modeling can often provide valuable insight and assistance for dosimetry of regions of interest with dimensions smaller than the scanning resolution (20). Here, modeling has been performed with GEANT4, a general-purpose Monte Carlo code, originally developed within and for the high energy physics community. GEANT4 modeling has already been implemented in radiopharmaceutical therapy (RPT) (21).

More specifically, GEANT4 α-particle modeling has been validated by comparison to MCNPX (22) and been used for a-particle microdosimetry (22, 23). The continuous energy losses along the track of the α-particle range are modeled by the Bethe-Bloch equation, which is modified by taking into account various corrections including multiple scattering of charged particles as well as knock-on electron (delta ray) production, which was implemented by lowering the threshold of electron production to 1 nm.

Trabecular model

The simplified trabecular model, developed in this work, consists of a sphere of tissue composition and density (1.06 g/cm³) of varying size (250–500 µm radius), the marrow space, surrounded by bone (density equal to 1.95 g/cm³) (24). The outer shell (10 µm) (25) of the marrow space was considered to be the endosteal layer, composed of osteoblasts. Osteoprogenitor cells are presumed to be present in the first 50 µm (26) of the bone surfaces – a region termed “shallow marrow”, which includes the aforementioned endosteal layer. The hematologic stem and progenitor cells occupy the entire cavity, including both the endosteal and shallow marrow layers, as do the marrow adipocytes (27). The region beyond the shallow marrow is termed the “deep marrow”.

This model, originally derived to address the target geometry for stochastic effects, is illustrated in Figure 2. The cavity is binned into cubes of approximately a cellular volume (10×10×10 µm³). Since the absorbed dose is calculated for each cell (actually for every fixed potential cellular position), variations in the actual total number or concentration of cells in the marrow cavity, i.e.: the cellularity of the marrow cavity, will not affect the absorbed dose values, as long as the distribution of cells is homogenous. Furthermore, the results are not dependent on the assumption of cuboidal voxels, or cellular positions, as opposed to true spherical shape of the cells.

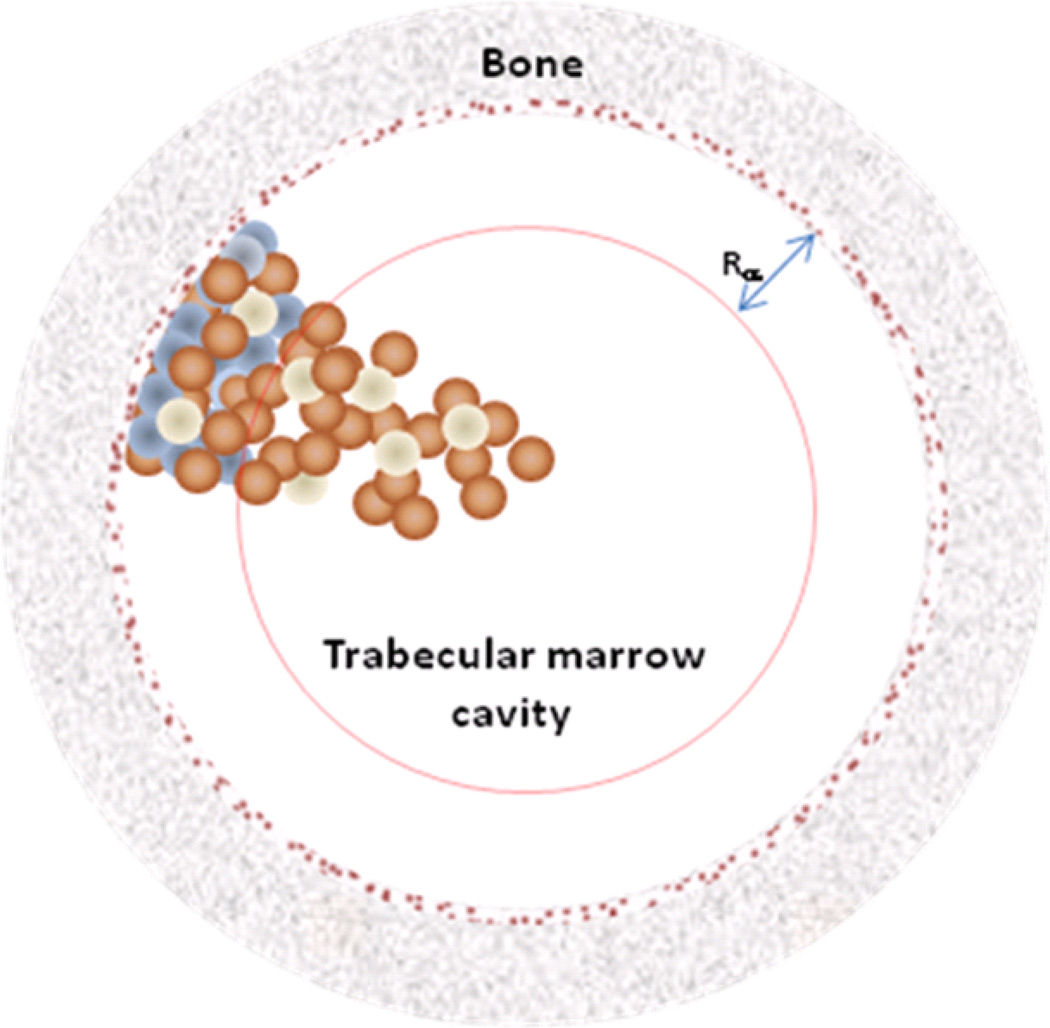
Figure 2.

Representation of the marrow cavity model (not drawn to scale). The cavity is represented by a sphere of radius R_c. R_α is the range of the α-particles from ²²³Ra decay. The blue spheres are osteoprogenitor cells, present only within shallow marrow, while the brown spheres are hematopoietic stem and progenitor cells and the white spheres are adipose cells, both present throughout the marrow cavity. The 10 µm endosteal layer is represented by the brown speckled ring.

Model validation

In order to compare this model with existing α-particle absorbed fraction results, activity was placed independently in the different compartments: (a) in the endosteal layer (EL), (b) on the surrounding bone matrix (TBS, trabecular bone surface), and (c) in the marrow cavity (MC) for a marrow cavity radius of 400 µm. The deposited energy was collected over the entirety of the MC assuming a cellularity of 100 %, and divided by the total emitted energy. The resulting absorbed fractions were compared to those calculated by Watchman et al (28) based upon chord-length distributions measured in human trabecular spongiosa. From these results the absorbed fractions for different cellularity values can be obtained by scaling to the cellularity value, i.e.: the S-values for a cellularity of 50 % are 50 % of those calculated for the 100 % scenario. This is consistent with the idea that individual cellular dose does not vary with cellularity.

Dose Calculations

The exact localization of ²²³Ra within the trabecular bone is still not known to the authors’ knowledge, however the activity is generally assumed to localize to regions of calcium uptake: either in the bone matrix or, as a worst case scenario for acute red marrow toxicity which is typical of dosimetric studies to date, in the endosteal layer. Therefore, two sets of simulations were performed, one for activity located on the trabecular bone surface and one for activity in the endosteal layer. For both sets of simulation scenarios, the energy deposited in each cell was collected and the absorbed dose to each cell in the marrow cavity was calculated using a number of events calculated to deliver different average absorbed doses to the marrow cavity volume (for an average dose range of 1–20 Gy to the marrow cavity). A 400 µm marrow cavity radius was used for these calculations. For marrow cavities with different radii (250–500 µm), the cumulated activity (number of simulated events) was scaled based on the cumulated activity concentration in the 400 µm marrow cavity model (i.e.: concentration of events was kept constant).

The distribution of hematopoietic stem and progenitor cells (HSPCs) has been shown to have a dependence on distance from the trabecular surfaces (29, 30); consequently, as a second step, a percentage of the cuboidal “cells” was determined to be inactive (either occupied by adipocytes or other non-HSPCs); this probability increases as a function of distance from the bone surface, the parameters used for this radial dependency were taken from reference (30), in order to mimic the desired distribution. Additionally, a blood activity component was added, although the contribution to the marrow dose from blood has been shown to be minimal (9). A conservative example is presented using a value derived from pre-clinical bio-distribution measurements at 1 h post-injection (9), where the ratio of blood activity concentration to femur activity concentration is approximately 1 % at 1 h post-injection as well as a more extreme case where the blood activity is twice the preceding derived value. By considering the total trabecular bone surface in the body (1.05·10⁵ cm² (31)) as well as the total trabecular bone mass (1100 g (31)), a conversion from endosteal layer activity concentration to femur concentration was calculated, from which the activity concentration for blood was calculated for an average MC absorbed dose of 2 Gy, assuming a MC plasma concentration of 40 %. The distribution of activity was assumed to mimic the distribution of red marrow cells, that is with a radial distribution and a higher concentration closer to the bone surface.

Dose cell histograms

The energy deposited in all cell positions (voxels) was collected and converted to absorbed dose and stored in dose cell histograms. The percentage of cells with an absorbed dose less than two different reference doses, generally regarded as thresholds for whole body bone marrow toxicity (2 Gy, threshold for possible major hematotoxicity and 4 Gy, threshold for almost certain major hematotoxicity (32)), the “spared cell percentage”, was calculated, with the results plotted as a function of average absorbed dose.

Dynamic Considerations

In addition to the spatial micro-level dosimetric approach, the temporal consideration of absorbed dose deposition can be modeled. This is especially important for a longer-lived (on the scale of RPT) isotope such as ²²³Ra, whose half-life (11.4 days) is on the order of hematopoiesis (7 days), the process by which hematopoietic progenitor cells develop to mature blood cells. In particular, if specific regions receive a much greater absorbed dose than the average, cells occupying those regions may die and be replaced by other cells, potentially migrating from a region of lesser radiation, which may in turn receive potentially lethal absorbed doses even though they did not occupy that position for the duration of the absorbed dose delivery. Thus the radiation may be potentially toxic to a greater number or percentage of cells than that predicted by the initial or static distribution.

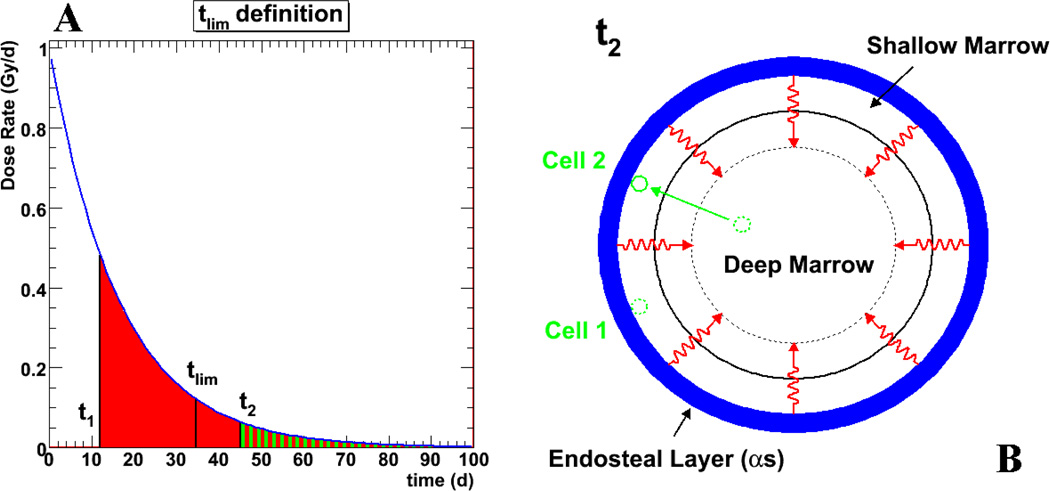
In order to estimate the length of time after injection a certain cellular position (i.e. a region of the marrow cavity which may or may not be occupied by a cell) remains potentially toxic, or equivalently, the time point at or beyond which a spatial cellular position receives less than the reference threshold absorbed dose, a “reference time point”, t_lim, is defined for each cellular position. This reference time point is the time point at which a cell arriving in this position will receive no more than the reference absorbed dose, D_ref, i.e: 2 Gy, whereas a cell occupying this position prior to this time point will receive more than 2 Gy (see Figure 3).

Figure 3.

The notion of reference time point, t_lim, is illustrated. Figure 3a depicts the absorbed dose rate to a potential cellular position (i.e. a region of the marrow cavity that the cell may or may not occupy) as a function of time after the start of exposure. For every cellular position (physical space) within the range of the α-emissions, there is a time after the start of irradiation (taken to be the injection time) beyond which the number of decays emanating from the trabecular surface are insufficient to deliver a reference dose to a target cell occupying that position. Prior to this time, any cell moving to the considered position will receive a reference dose. This is illustrated in Figure 3b. At a certain time t₂, cell 2 migrates from the deep marrow to position where the absorbed dose received is represented by the green area under the curve shown in Figure 3a. Cell 1 is already in a similar position and has been there since time t₁. The total dose that cell 1 has or will receive is greater than the reference dose since t₁ < t_lim. On the other hand, cell 2, arrives after t_lim and will receive less than the reference dose.

The numeric value of the reference time point may be derived in the following way. The total absorbed dose, D, received by a cell at a given position is given by:

$$D={\displaystyle {\int }_0^{\infty }}{\mathit{Ḋ}}_0{e}^{-\lambda t}\mathit{\text{dt}}=\frac{{\mathit{Ḋ}}_0}{\lambda }$$ (1)

where λ is the rate of decay for ²²³Ra and Ḋ₀ is the initial dose rate. The first equality in this equation assumes instantaneous uptake of activity, a reasonable approximation given the scale of ²²³Ra decays (11.4 days). The time t_lim is then defined as:

$$D_{\mathit{\text{ref}}}={\displaystyle {\int }_{t_{\mathit{\text{lim}}}}^{\infty }}{\mathit{Ḋ}}_0{e}^{-\lambda t}\mathit{\text{dt}}={\mathit{\text{De}}}^{-\lambda t_{\mathit{\text{lim}}}}$$ (2)

from which the relation:

$$t_{\mathit{\text{lim}}}=\frac{1}{\lambda }\mathit{\text{ln }}\left(\frac{D}{D_{\mathit{\text{ref}}}}\right)$$ (3)

is derived. These equations are illustrated in Figure 3. Note that in the case where the integral definitions do not reduce to (or are not well approximated by) simple expressions, as for example in the case of a prolonged pharmacokinetic distribution of ²²³Ra, tlim may still be obtained by solving Equation (2) numerically.

III. RESULTS

Absorbed fraction comparison

Calculated absorbed fractions are compared to the values in reference (28), which were calculated from sampling measured pathlength distributions in human cadavers, for mono-energetic α-particles for a cellularity of 100 % and an endosteal thickness of 10 µm. The comparisons are given in Table I for mono-energetic α-particles as well as for ²²³Ra, whose decay includes 4 α–particles (with 6.0, 6.9, 7.5, and 7.6 MeV initial energies) and two β-particles (see Figure 1). The mono-energetic value comparison shows very comparable results, although the GEANT4 values for EL source are 10–30 % different (with more self-dose) than the University of Florida values. Note that the range in the University of Florida values reflects the different pathlength distributions attributed to variations in marrow cavity size within different body spongiosa regions of the skeleton - ribs, cervical vertebrae, and parietal bone. The absorbed fractions were compared for 100 % cellularity; because of the nature of the simple marrow cavity model of the present study, results for a different specific marrow cellularity may be obtained by taking the appropriate fraction of the 100 % cellularity results (results not shown). As Watchman et al. show (28), there is a slightly non-linear variation in the absorbed fraction as a function of cellularity making linear scaling an approximation.

Table 1.

Absorbed fraction (ϕ) comparisons to University of Florida (UF) published (28) results. The comparative reference values are for individual monoenergetic α-particles; GEANT4 (G4) results for the entire ²²³Ra decay chain (including photons and electrons) are also given. Note that in the Watchman et al. paper (28), the marrow cavity (MC) is known as the trabecular active marrow and the endosteal layer (EL) is termed the trabecular endosteum. TBS stands for the trabecular bone surface.

ϕ	223Ra	6 MeV α		6.5 MeV α		7 MeV α
	G4	UF	G4	UF	G4	UF	G4
MC←MC	0.90	0.90–0.97	0.95	0.89–0.97	0.94	0.88–0.97	0.94
MC←EL	0.35	0.38–0.40	0.34	0.40–0.41	0.35	0.41–0.42	0.36
MC←TBS	0.27	0.23–0.26	0.24	0.25–0.28	0.26	0.27–0.30	0.28
EL←MC	0.03	0.01–0.06	0.03	0.01–0.06	0.03	0.01–0.06	0.03
EL←EL	0.23	0.20–0.22	0.28	0.18–0.19	0.25	0.15–0.17	0.22
EL←TBS	0.19	0.24–0.26	0.24	0.23–0.25	0.21	0.20–0.22	0.20

Geometrical considerations

Assuming that all radioactivity is located either within the endosteal layer or on the trabecular bone surface, and considering the range of the α-particles in soft tissue (~70 µm) and the dimensions of the marrow cavity space (250 µm – 500 µm radius), there are regions of the bone marrow which would not receive α-particle radiation. The theoretical limit of the percentage of cells that cannot be affected, the “spared cell percentage”, as a function of marrow cavity radius was calculated and used as a base-line comparison for the Monte Carlo results.

Spared cell percentage

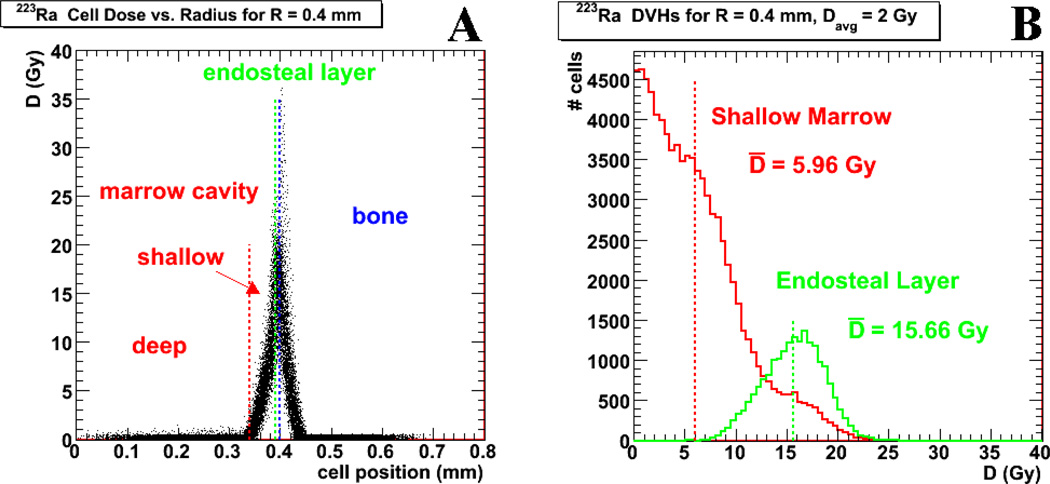
Dose cell histograms for the HSPCs and osteoprogenitor cells were created for different average absorbed dose, D_avg, simulations to the contents of the “typical” 400 µm radius marrow cavity. The results are shown in Figure 4 for activity confined to the endosteal layer. Figure 4a gives a plot of the absorbed dose, D, versus cellular radial position in the marrow cavity. The limited range of the dose deposition is clearly illustrated in this plot and is consistent with results from previous publications (9, 33). Figure 4b shows the dose cell histograms for cells within both the shallow marrow and endosteal layer. The cells located within the regions of deep marrow are not represented as they are all nearly zero (Figure 4a).

Figure 4.

shows results for simulations using activity localized to the endosteal layer. Figure 4a gives the relationship between the mean absorbed dose to the marrow cavity, D, versus the cellular radial position within the marrow cavity (0 mm for the center of the marrow cavity), where each dot represents a single cell value. The blue vertical line indicates the marrow cavity radius, while the green line indicates the limit of the endosteum. The region between these two lines is thus the marrow tissues where the decays have been placed. Figure 4b shows cell dose histograms for the cells within shallow marrow (red) and within the endosteal layer (green).

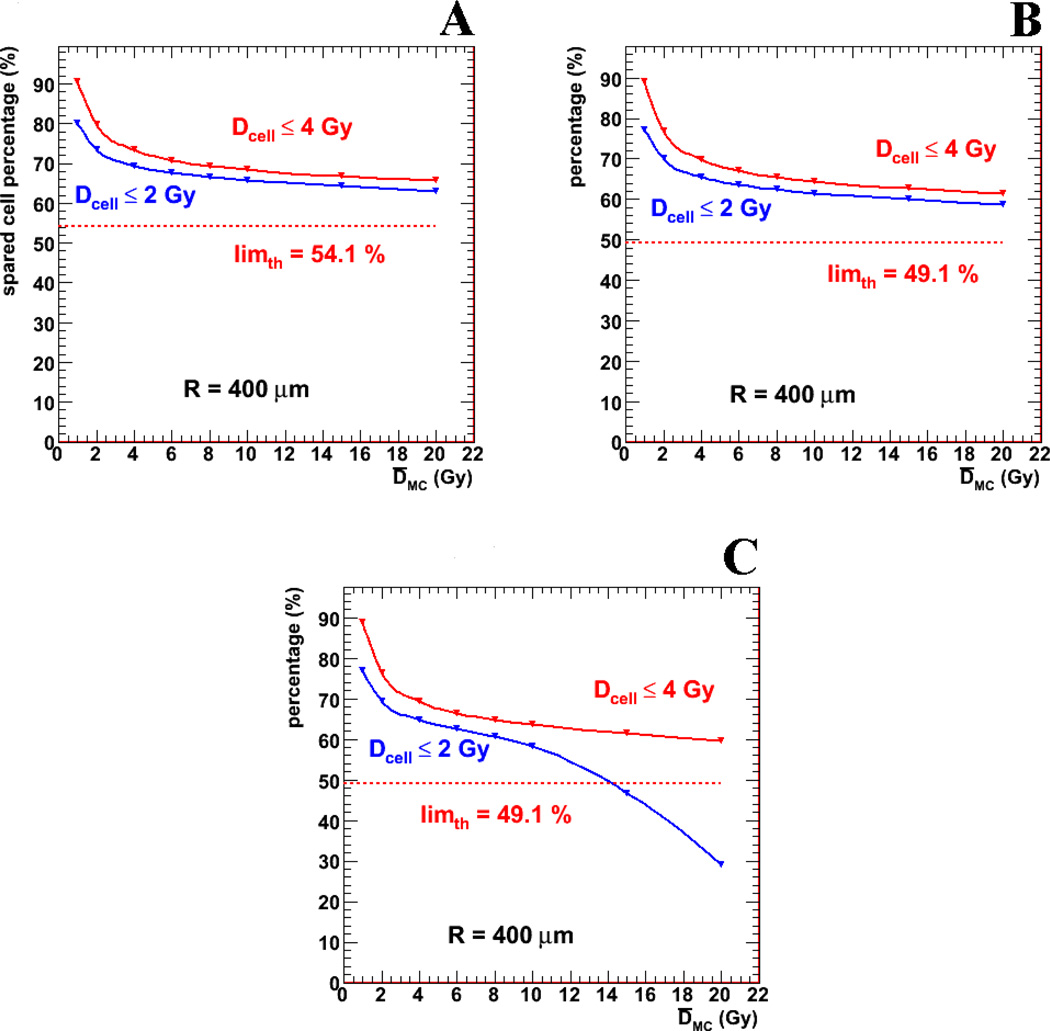
Figure 5a shows the spared cell percentage results for the purely geometrical case, i.e.: without a gradient of cellular distribution and for activity confined to the endosteal layer, defined as the percentage of HSPCs receiving less than the reference dose (2 Gy or 4 Gy) as a function of average absorbed dose to the entire marrow cavity. These percentages are plotted as a function of average MC dose and compared to theoretical limits. This figure illustrates a somewhat surprising, but logical, consequence of the dose distribution – namely that increasing the average dose to the bone marrow (or equivalently, the administered activity to the patient) even by an order of magnitude, does not substantially affect the number of HSPCs that receive a toxic dose of radiation.

Figure 5.

shows the percentage of hematopoietic stem and progenitor cells receiving less than the reference doses (2 Gy or 4 Gy) for different scenarios, all for activity localized to the endosteal layer. Figure 5a shows the strictly geometrical case with uniform cellular distribution on the marrow cavity. Figures 5b and 5c have added the radial dependence of hematopoietic stem and progenitor cell distribution and the red marrow (blood) activity contribution (average activity concentration for figure 5b and twice the average blood activity concentration for figure 5c).

Results are given (in Figures 5b, 5c and Table II for activity in the endosteal layer and in Table III for activity on the trabecular bone surface) including a HSPC cellular density proportional to the distance from the bone trabeculae surfaces, and the addition of a blood (MC) time integrated activity component equal to 0.0544 MBq-h/ml (based on a time integrated activity concentration of 58.7 MBq-h/ml in the endosteal layer). The presentation is similar to that given in Figure 5a; a new theoretical limit is shown, which also takes into account the HSPC radial probability distribution. Figure 5c shows the same graph as Figure 5b but with a blood activity level twice that of Figure 5b. The results as a function of average bone marrow absorbed dose differ from those of Figure 5a in that: (a) a slightly (~5 %) lower overall percentage of cells (and theoretical limit) receiving an absorbed dose below reference D_avg, due to the radial dependence of cells; and (b) a substantial decrease in values at high D_avg (10 Gy and above, only for the 2 Gy reference value, most evident for Figure 5c). This decrease, (or, equivalently, increase in percentage of cells receiving toxic absorbed dose), is a direct result of the activity in the blood and becomes even more apparent as the amount of activity present in the blood is increased.

Table 2.

Percentage of marrow cavity cells (“spared cell” percentages) receiving an absorbed dose below the reference value (2 Gy) as a function of marrow cavity radius, R_c, and average absorbed dose, D_avg, for activity localized in the endosteal layer. In this table, the average absorbed dose is calculated for the entire marrow cavity and assumes a distribution of decays as seen in the ²²³Ra studies (endosteal layer to marrow cavity cumulated activity ratio of ~100 to 1). “A_EL” indicates activity in the endosteal layer only, while “+A_MC” indicates that blood activity in the marrow cavity has been included. Both scenarios include the radial dependence of HSPC distribution.

(%)	Rc = 500 µm		Rc = 400 µm		Rc = 300 µm		Rc = 250 µm
Davg (Gy)	AEL	+AMC	AEL	+AMC	AEL	+AMC	AEL	+AMC
1	81.3	81.0	77.4	77.2	71.2	70.8	66.0	65.5
2	75.0	74.8	70.3	70.0	62.5	62.4	56.4	55.9
4	71.1	70.8	65.9	65.5	57.4	57.1	50.9	50.4
6	69.5	69.1	64.1	63.6	55.4	54.9	48.6	48.1
8	68.6	68.1	63.0	62.4	54.1	53.5	47.2	46.7
10	67.9	67.3	62.2	61.6	53.2	52.6	46.3	45.7
15	66.7	65.9	60.9	60.0	51.8	50.8	44.8	43.7
20	66.0	64.6	60.1	58.7	50.9	49.4	43.8	42.3

Table 3.

Percentage of marrow cavity cells (“spared cell” percentages) receiving an absorbed dose below the threshold (2 Gy) as a function of marrow cavity radius, R_c, and average absorbed dose, D_avg, for activity localized to the bone surface. In this table, D_avg is calculated for the entire marrow cavity and assumes a distribution of decays as seen in the ²²³Ra studies (endosteal layer to marrow cavity cumulated activity ratio of ~100 to 1). “A_TBS” indicates activity on the bone surface only, while “+A_MC” indicates that blood activity in the marrow cavity has been included. Both scenarios include the radial dependence of HSPC distribution.

(%)	Rc = 500 µm		Rc = 400 µm		Rc = 300 µm		Rc = 250 µm
Davg (Gy)	ATBS	+AMC	ATBS	+AMC	ATBS	+AMC	ATBS	+AMC
1	81.5	81.2	77.8	77.6	72.0	71.5	66.8	66.3
2	75.2	75.1	70.8	70.5	63.3	63.2	57.4	56.9
4	71.4	71.1	66.5	66.1	58.2	58.0	52.2	51.5
6	69.8	69.5	64.7	64.3	56.2	55.8	50.0	49.4
8	68.9	68.3	63.7	63.1	55.0	54.4	48.6	48.1
10	68.3	67.6	62.9	62.4	54.2	53.6	47.7	47.1
15	67.1	66.3	61.7	60.8	52.7	51.8	46.2	45.2
20	66.4	65.1	60.9	59.5	51.9	50.4	45.3	43.8

Dynamic Considerations

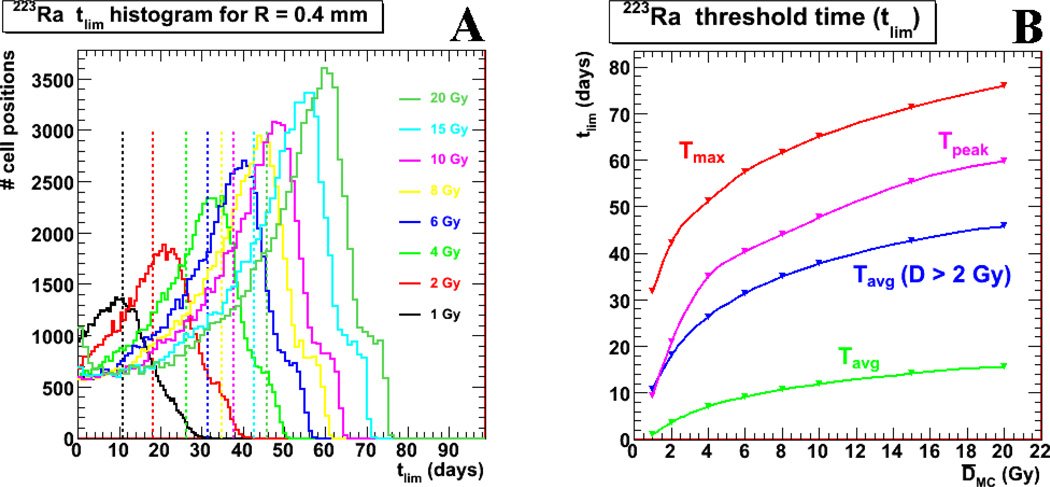
The t_lim values for each cellular position were calculated according to equation (3) for the different average absorbed dose D_avg scenarios, all for activity located in the endosteal layer. The values were then plotted as histograms shown in Figure 6, where the y-axis represents the number of cellular positions in the marrow cavity. The first figure (6a) shows the t_lim histograms by color representing increasing average absorbed dose to the marrow cavity. Note that only those positions (voxels) with an absorbed dose greater than the reference threshold of 2 Gy are plotted. For a D_avg of 2 Gy, there is a peak of voxels (potential cellular positions), t_PEAK, that are potentially toxic until 22 days, with certain voxels potentially toxic until 42 days (t_max); the average reference time point (t_lim) is 18 days, when taking into consideration the voxels not represented in the histogram, i.e.: those with a t_lim = 0, this average value becomes ~4 days. These results and the corresponding results calculated for different D_avg values are represented further in Figure 6b.

Figure 6.

illustrates the reference time point, t_lim, results from the current model for activity localized to the endosteal layer. Figure 6a shows t_lim histograms for different D_avg values. Only those cellular positions which receive a D greater than the reference 2 Gy are represented. Figure 6b synthesizes the values from Figure 6a. The red markers and line shows the max t_lim values (t_max) from Figure 6a as a function of D_avg, the average red marrow absorbed dose, while the pink markers and line shows the peak t_lim values (t_peak), and the blue markers and line shows the average t_lim values from the different histograms (seen as vertical dotted lines in Figure 6a). The green values are the average t_lim results, including the values for the cellular positions not shown on Figure 6a, i.e.: those for which t_lim = 0 (i.e., regions in the marrow that are outside the range of α-particles).

IV. DISCUSSION

Using a simple, first order model of a single bone marrow cavity, we have shown: (a) results that correlate with a lack of clinical trial hematotoxicity from ²²³Ra therapy (less than 1 % of patients showed grade IV hematological toxicity; 2–4 % had grade III toxicity for hemoglobin, platelets, neutrophils or WBC (4, 5)), results not predicted by the value of the mean absorbed dose to marrow tissues; and (b) that a significant (up to 10-fold) increase in administered activity or average absorbed dose will not necessarily lead to marrow toxicity. We have also shown that for a long-lived therapeutic emitter such as ²²³Ra, the duration of potential exposure to that portion of the marrow being irradiated needs to be considered in terms of its longer term impact on marrow function. According to this model, to first order (Figure 5), an increase in administered activity does not result in a greater fraction of marrow cells which receive toxic doses. To first order, the model is consistent with the absorbed fractions calculated in previously published results (Table I).

Red marrow histogram results

Table II shows that some fraction of the marrow cavity remains relatively unirradiated across a wide range of marrow cavity radii and average absorbed doses to the marrow cavity (corresponding to a range of administered activities).

As also seen in Figure 5b, the addition of a radial dependence on HSPC concentration reduces the percentage of cells receiving a non-toxic absorbed dose without affecting the shape of the overall absorbed dose vs. spared cell percentage (i.e., percentage of cells receiving < 2 or 4 Gy) curve. The addition of the marrow cavity (blood) activity (Figures 5b and 5c, and the A_MC columns of Table II) does, however, alter the shape of the curve. For combinations of large average absorbed dose values and relatively high blood activity concentrations, the spared cell percentage falls below the theoretical limit indicating a substantial contribution of absorbed dose arising from activity in the marrow cavity. The lack of effect at doses even up to 20 Gy (for average blood activity values) of average absorbed dose reflects the relatively low average blood cumulated activity (~1% of the endosteal layer cumulated activity). However, as shown in Figure 5c further increasing the dose contribution due to blood activity can rapidly reduce the sparing effect at high average marrow absorbed doses.

Impact of high LET

The greater energy deposition per decay typical of α-particles implies that the reference dose for toxicity can be delivered by a small number of events per cell. Consequently, the energy deposition in an individual cell is, depending upon the number of decays stochastic rather than continuous, which raises the question of the validity of the t_lim formalism and the equations (1–3) used to derive it. While the concept may be rather approximate for an individual voxel and should conceivably be replaced by a more probabilistic approach, when considering a large number of voxels the approximations of the formalism, on average are reasonably representative, as is the case for any conversion of individual probabilistic quantity (time of decay, e.g.) to a large population (macroscopic quantity of activity).

Dynamic considerations

Assuming that viable cells are indeed generated or migrate to occupy the space generated by the removal of cells killed by radiation, this means that potential toxicity may persist out to 40 days in the case when the average absorbed dose equals 2 Gy. These results should be factored in when considering the possibility of increasing dose, delivering multiple treatments or scheduling stem cell rescue in myeloablative protocols. These considerations are also relevant to understanding the possible effects of prior treatment (34). Since a significant fraction of voxel positions are still potentially toxic up until t_peak (22 days for D_avg = 2 Gy) with some voxel positions toxic until t_max (42 days for D_avg = 2 Gy), hematologic recovery will be logically affected until at least t_peak and possibly t_max, and subsequent treatments need to take this time into consideration. For instance, while doubling the initial administered activity (D_avg = 4 Gy) only increases the t_max from 42 to 50 days, a second administration equal to the initial amount 42 days after the first treatment would increase to 84 days the length of time a portion of the bone marrow would be exposed to potentially lethal radiation.

Potential osteogenic and other associated long-term toxicity

An additional caveat when considering an increase of administered activity is the absorbed dose to the osteoprogenitor cells. As seen in Figure 4b, the average osteoprogenitor cell dose is already 15.7 Gy for an average red marrow absorbed dose of 2 Gy and activity localized to the endosteal layer. Increasing the administered activity significantly could potentially increase the risk of long term deleterious effects to the bone or marrow, i.e.: secondary bone cancer or leukemia induction, assuming that such effects are indeed correlated with increasing absorbed dose (35–37). In general, the results obtained here are relevant to deterministic effects; long-term stochastic effects are less relevant in the context of cancer therapy of prostate bone metastases where the average survival time of patients after treatment is on the order of 9–13 months (5), significantly less than 2 years considered to be the latent period for induced leukemia or the 8 year average latent period for induced bone cancer (35,37).

Absorbed Fraction Validity

While the results in this paper are derived from cell-level dosimetry and are not amendable to an absorbed fraction methodology, this does not call into question the validity of this method in most cases. The particular circumstances which, when combined, predicated a different viewpoint, were: (a) the short range of the α-emitter ²²³Ra; and (b) the predominance of cross-terms in the evaluation of toxicity, i.e: that source volume and target volume were different. In most cases, the absorbed fraction methodology is expected to provide absorbed dose estimates relevant to expected biological effect. Furthermore, the absorbed fraction methodology could in theory simply be extended to encompass a wider range of compartments (marrow cavity radial bins), as proposed by Watchman et al. (28), thereby rendering more representative results than a two-volume model. However, the validity of small compartments with small statistics per compartment is questionable, and hence the advantage of a Monte Carlo-based methodology.

Scope and limitations

The literal interpretation of this model’s results states that any increase in activity will not lead to a significant increase in bone marrow toxicity, in spite of the presence of (a small amount) of activity in the blood stream and the bone marrow itself. However, several caveats are in order. Since there is such an imbalance in the absorbed dose as a function of distance from the bone surface, many cells will receive lethal doses of radiation within a few days. If cells farther from the bone marrow surface move closer and by doing so bring themselves into range, the number of cells receiving lethal doses could exceed expectations if possible cell trafficking is not taken into account (38). Moreover, although it has been determined that the descendant ²¹¹Pb does not substantially relocate away from the bone, it does not necessarily follow that it does not relocate to the marrow cavity, e.g., which if it were the case could potentially increase the dose to each marrow cavity cell by approximately one quarter of D_avg. These considerations plead in favor of a cautious approach to the conclusion that a large increase of administered activity will only minimally increase the red marrow toxicity, as well as for a more extended model which incorporates these dynamic features.

Furthermore, the model presented here makes the assumption that the ²²³Ra distributes either in the endosteal layer or along the trabecular surface. To the knowledge of the authors, no definitive measurements have been made determining the exact localization of the activity which differentiates between cell surface and endosteal layer, although with the advent of the α-Camera (39), such measurements could conceivably be made in the future. Consequently, it has been standard practice in dosimetric models to assume the worst case scenario, which in this case is for the activity to be located to the endosteal layer. From the model standpoint, activity localizing to the bone marrow surface or matrix would reduce even further the expected toxicity as can be seen by the comparing Tables II and III. However, given the small thickness (10 µm) of the endosteal layer compared to the marrow cavity radius, the results are not substantially different between those generated from activity localized to the endosteal layer and those derived from activity simulated on the trabecular bone surface.

The work presented here uses a simplistic spherical model for the red marrow. A more representative model would use human cord-length distributions as described by Watchman et al. (28), or direct use of 3D microimaging of trabecular bone as described in Hough et al. (40).

Ultimately, the true test of science is experiment (Feynman) and this model can only be truly validated by further experimental and clinical results. The comparison of the model with the previously published absorbed fraction S-values only validates the use of the single cavity model to adequately represent the trabecular bone architecture at the geometrical level – it does not take into consideration most of the subtleties of a highly complex system, such as the fact that different pluripotent cells within lineages could have different sensitivities to radiation killing, e.g., as well as the dynamic considerations mentioned above. All of these considerations should not detract from the value of this model which illustrates the importance of accounting for micron-scale anatomy and activity distributions in performing the dose calculations needed to examine the potential safety and efficacy of α-emitter. Since such data cannot be easily collected from humans (if at all), a combination of pre-clinical studies, a priori information regarding the distribution of the agent and modeling of the type shown will be needed.

V. CONCLUSIONS

The results from the marrow cavity model differ markedly from a standard absorbed fraction method while presenting comparable average dose values. The marrow cavity model offers an explanation for the clinical evidence suggesting that the average absorbed dose will not reflect biological outcome in the case of ²²³Ra RPT.