Theory for cross effect dynamic nuclear polarization under magic-angle spinning in solid state nuclear magnetic resonance: The importance of level crossings

Abstract

We present theoretical calculations of dynamic nuclear polarization (DNP) due to the cross effect in nuclear magnetic resonance under magic-angle spinning (MAS). Using a three-spin model (two electrons and one nucleus), cross effect DNP with MAS for electron spins with a large g-anisotropy can be seen as a series of spin transitions at avoided crossings of the energy levels, with varying degrees of adiabaticity. If the electron spin-lattice relaxation time T_1e is large relative to the MAS rotation period, the cross effect can happen as two separate events: (i) partial saturation of one electron spin by the applied microwaves as one electron spin resonance (ESR) frequency crosses the microwave frequency and (ii) flip of all three spins, when the difference of the two ESR frequencies crosses the nuclear frequency, which transfers polarization to the nuclear spin if the two electron spins have different polarizations. In addition, adiabatic level crossings at which the two ESR frequencies become equal serve to maintain non-uniform saturation across the ESR line. We present analytical results based on the Landau-Zener theory of adiabatic transitions, as well as numerical quantum mechanical calculations for the evolution of the time-dependent three-spin system. These calculations provide insight into the dependence of cross effect DNP on various experimental parameters, including MAS frequency, microwave field strength, spin relaxation rates, hyperfine and electron-electron dipole coupling strengths, and the nature of the biradical dopants.

INTRODUCTION

Dynamic nuclear polarization (DNP) offers a method to significantly boost the signal in nuclear magnetic resonance (NMR) experiments, which are often limited by low signal-to-noise. By transferring some of the larger electron spin polarization to the nuclear spins, the nuclear polarization and thus the NMR signal can be increased by as much as two orders of magnitude. This can enable experiments that would not be practical without DNP. DNP has a long history, beginning with its prediction¹ and discovery² in 1953. More recently, the development of high frequency microwave sources^{3, 4} and biradical dopants⁵ and the availability of commercial equipment⁶ has encouraged many research groups to use DNP for solid state NMR at high magnetic fields.^{3, 7, 8, 9}

Many of these solid state DNP-NMR experiments use magic-angle spinning (MAS), yet how MAS may affect DNP mechanisms has not been discussed in detail. There are many possible methods for transferring spin polarization from electrons to nuclei.^{10, 11} Here, we will focus on mechanisms which apply to solid state DNP at high magnetic field using continuous wave microwave excitation of the electron spins, as is typical for the experiments referenced above. The solid effect,¹² cross effect,¹³ and thermal mixing^{14, 15, 16} DNP mechanisms have been reviewed previously for non-rotating samples, for example, by Maly et al.¹⁰ These effects can be roughly differentiated by the role of electron-electron couplings and by the method of matching the energy of the nuclear spin flip. The solid effect does not require any electron-electron coupling. The electron-nucleus hyperfine coupling alone allows the microwaves to excite a nominally forbidden two-spin transition. The difference of the microwave frequency and the electron spin resonance (ESR) frequency matches the NMR frequency. For the cross effect, one electron-electron coupling is required, in addition to the hyperfine coupling. The difference between the two ESR frequencies matches the NMR frequency. For thermal mixing, energy matching with the nuclear spin flip is achieved by use of electron-electron couplings.

With the recent interest in DNP experiments, there has also been increased interest in theoretical analysis. Recent theoretical work has focused on DNP in static samples, primarily using quantum mechanical models, for the solid effect¹⁷ and the cross effect.^{18, 19}

In this article, we discuss a minimal model for cross effect DNP under MAS, with two electron spins and one nuclear spin. This three-spin model is sufficient to illustrate solid effect and cross effect DNP. The primary focus is on cross effect DNP involving a pair of electrons with wide ESR lines from g-anisotropy. Under these typical conditions, the cross effect is much stronger than the solid effect. In this model, cross effect DNP is composed of two time-dependent avoided crossings of the three-spin energy levels under MAS and microwave irradiation. The first crossing, when the microwave frequency matches one ESR frequency (ω_m ∼ ω_e1 or ω_m ∼ ω_e2), reduces the polarization of one of the electrons from its thermal equilibrium value, creating or altering the polarization difference between the electrons. The second crossing, when the difference of the ESR frequencies equals the NMR frequency (ω_e1 – ω_e2 ∼ ±ω_n), transfers some of the polarization difference between the two electrons to the nucleus. Below, we first discuss analytical estimates of the effects of these avoided level crossings on the spin polarizations. We then present numerical density matrix calculations for this three-spin model.

ANALYTICAL TREATMENT OF DNP MECHANISMS UNDER MAS

Three-spin Hamiltonian

For our model of cross effect DNP with MAS, we use two electron spins and one nuclear spin. In numerical calculations, the nucleus is a proton. In angular frequency units, the Hamiltonian is

$$\begin{array}{ccc}\hfill H& =& {\omega }_{e1}{S}_{1z}+{\omega }_{e2}{S}_{2z}+{\omega }_n{I}_z+d(2S_{1z}{S}_{2z}-S_{1x}{S}_{2x}-S_{1y}{S}_{2y})\hfill \\ & & +h_{zz}2I_z{S}_{1z}+h_{xz}2I_x{S}_{1z}+h_{yz}2I_y{S}_{1z}+{\omega }_1[(S_{1x}+S_{2x})\hfill \\ & & \times \cos \left({\omega }_{m}t\right)+(S_{1y}+S_{2y})\sin \left({\omega }_{m}t\right)].\hfill \end{array}$$ (1)

This Hamiltonian includes the interaction of the two electrons and one nucleus with the static field in the z direction, producing ESR and NMR frequencies ω_e1, ω_e2, and ω_n, the dipole-dipole coupling between the electrons, with coupling constant d, and the hyperfine coupling between the nucleus and one of the electrons, with coupling constants h_αβ. To simplify the equations, the weaker hyperfine coupling to the second electron is neglected. In addition, we apply a rotating microwave field, with strength ω₁ and frequency ω_m, near the ESR frequencies. The electron-electron dipole coupling and hyperfine coupling are expressed in the high field limit with respect to the ESR frequencies. However, the hyperfine coupling is not in the high field limit with respect to the NMR frequency, because the h_xz and h_yz terms (although small relative to ω_n) are not entirely negligible and are essential for DNP. Exchange coupling between the two electrons of the biradical is not included, because significant exchange coupling was not seen in the ESR spectrum of the Totapol nitroxide biradical,²⁰ which is a typical biradical used for cross effect DNP experiments. Under MAS, ω_e1, ω_e2, ω_n, d, and h_αβ are all time-dependent. For simplicity in our calculations, we neglect the time dependence of ω_n, since the time dependence of the spin energy levels is dominated by the much larger electron g-factor anisotropy. The detailed forms of the time dependence of these parameters are given in the supplementary information.²¹

This three-spin Hamiltonian has the eight energy levels sketched in Fig. 1. When the separations among the energy levels are large compared to the electron-electron and hyperfine couplings, the eigenstates are close to the direct-product states indicated in Fig. 1. The matrix representation of this Hamiltonian in the direct-product basis is

$$H=\begin{array}{c}|1⟩|2⟩|3⟩|4⟩|5⟩|6⟩|7⟩|8⟩\\ \begin{array}{c}\begin{array}{c}\\ |1⟩\hfill \\ \end{array}\\ |2⟩\\ \\ |3⟩\\ \\ |4⟩\\ \\ |5⟩\\ \\ |6⟩\\ \\ |7⟩\\ \\ |8⟩\\ \end{array}\left(\begin{array}{cccccccc}\begin{array}{c}\frac{1}{2}({\omega }_{e1}+{\omega }_{e2}+{\omega }_n\hfill \\ +d+h_{zz})\hfill \end{array}& \frac{1}{2}{\omega }_1{e}^{-i{\omega }_{m}t}& \frac{1}{2}{\omega }_1{e}^{-i{\omega }_{m}t}& 0& \frac{1}{2}(h_{xz}-i{h}_{yz})& 0& 0& 0\\ \frac{1}{2}{\omega }_1{e}^{i{\omega }_{m}t}& \begin{array}{c}\frac{1}{2}({\omega }_{e1}-{\omega }_{e2}+{\omega }_n\hfill \\ -d+h_{zz})\hfill \end{array}& -\frac{1}{2}d& \frac{1}{2}{\omega }_1{e}^{-i{\omega }_{m}t}& 0& \frac{1}{2}(h_{xz}-i{h}_{yz})& 0& 0\\ \frac{1}{2}{\omega }_1{e}^{i{\omega }_{m}t}& -\frac{1}{2}d& \begin{array}{c}\frac{1}{2}(-{\omega }_{e1}+{\omega }_{e2}+{\omega }_n\hfill \\ -d-h_{zz})\hfill \end{array}& \frac{1}{2}{\omega }_1{e}^{-i{\omega }_{m}t}& 0& 0& \frac{1}{2}(-h_{xz}+i{h}_{yz})& 0\\ 0& \frac{1}{2}{\omega }_1{e}^{i{\omega }_{m}t}& \frac{1}{2}{\omega }_1{e}^{i{\omega }_{m}t}& \begin{array}{c}\frac{1}{2}(-{\omega }_{e1}-{\omega }_{e2}+{\omega }_n\hfill \\ +d-h_{zz})\hfill \end{array}& 0& 0& 0& \frac{1}{2}(-h_{xz}+i{h}_{yz})\\ \frac{1}{2}(h_{xz}+i{h}_{yz})& 0& 0& 0& \begin{array}{c}\frac{1}{2}({\omega }_{e1}+{\omega }_{e2}-{\omega }_n\hfill \\ +d-h_{zz})\hfill \end{array}& \frac{1}{2}{\omega }_1{e}^{-i{\omega }_{m}t}& \frac{1}{2}{\omega }_1{e}^{-i{\omega }_{m}t}& 0\\ 0& \frac{1}{2}(h_{xz}+i{h}_{yz})& 0& 0& \frac{1}{2}{\omega }_1{e}^{i{\omega }_{m}t}& \begin{array}{c}\frac{1}{2}({\omega }_{e1}-{\omega }_{e2}-{\omega }_n\hfill \\ -d-h_{zz})\hfill \end{array}& -\frac{1}{2}d& \frac{1}{2}{\omega }_1{e}^{-i{\omega }_{m}t}\\ 0& 0& \frac{1}{2}(-h_{xz}-i{h}_{yz})& 0& \frac{1}{2}{\omega }_1{e}^{i{\omega }_{m}t}& -\frac{1}{2}d& \begin{array}{c}\frac{1}{2}(-{\omega }_{e1}+{\omega }_{e2}-{\omega }_n\hfill \\ -d+h_{zz})\hfill \end{array}& \frac{1}{2}{\omega }_1{e}^{-i{\omega }_{m}t}\\ 0& 0& 0& \frac{1}{2}(-h_{xz}-i{h}_{yz})& 0& \frac{1}{2}{\omega }_1{e}^{i{\omega }_{m}t}& \frac{1}{2}{\omega }_1{e}^{i{\omega }_{m}t}& \begin{array}{c}\frac{1}{2}(-{\omega }_{e1}-{\omega }_{e2}-{\omega }_n\hfill \\ +d+h_{zz})\hfill \end{array}\end{array}\right)\end{array}.$$ (2)

$\left(2\right)$

Figure 1.

Energy levels of a two-electron, one-nucleus system labeled with approximate z-axis spin states. The central four energy levels are colored to match Fig. 2b.

Behavior near level crossings

The energy levels change rapidly under MAS when the electrons have large g-anisotropy, as shown in Fig. 2b for the central four energy levels of a nitroxide biradical in a 9.4 T external field. At various points during the rotor period, the energies of direct-product states would cross if the off-diagonal Hamiltonian terms were zero. In fact, the energies of the eigenstates do not cross, because of the perturbation from the electron-electron dipole coupling, electron-nucleus hyperfine coupling, and microwaves. Instead, at these points in the rotor period, we get an avoided level crossing, resulting from a Hamiltonian with the following form for the relevant two-level system (see the inset to Fig. 2b):

$$H_{2\mathrm{L}}=\left(\begin{array}{cc}\hfill At& \hfill E\\ \hfill E& \hfill -At\end{array}\right),$$ (3)

where A and E are real constants, and t is time. In angular frequency units, the eigenvalues of H_2L are²²

$$E_{1,2}=\pm \sqrt{A^2{t}^2+E^2}.$$ (4)

For an avoided level crossing, if the time dependence is slow enough (adiabatic), the eigenstate populations will follow the energy levels. If the time dependence is very fast, there is no time for the weak interaction E to act, and the populations will stay in the same spin states across the level crossing. The probability of the energy level populations following the adiabatic path (thus producing a net transition between direct-product spin states in our analysis of DNP) is given by the Landau-Zener expression^{22, 23}

$$P_{\mathrm{adiabatic}}=1-\exp (-\pi E^2/A).$$ (5)

To first order in E, the eigenstates of H_2L are |a⟩ + (E/2At)|b⟩ and −(E/2At)|a⟩ + |b⟩, where |a⟩ and |b⟩ are the relevant direct-product states. Thus, the time during which the eigenstates significantly differ from the direct-product states is on the order of 2E/A, linear in the off-diagonal coupling E.

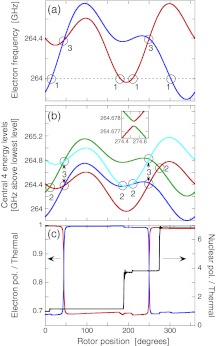
Figure 2.

As a function of the MAS rotor position angle, for one orientation of a nitroxide biradical: (a) ESR frequencies (blue and red lines) with microwave frequency indicated by dashed line; (b) central four energy levels of the three-spin system, colored to match Fig. 1; (c) electron and nuclear polarization from density matrix calculations during the first rotor period with hyperfine coupling, after equilibration of microwaves and electrons for 5T_1e. Parameters used for the calculations are listed in Table 1. Three types of energy level avoided crossings are circled in parts (a) and (b): (1) ESR frequency crosses microwave frequency; (2) ESR frequency difference crosses NMR frequency; (3) ESR frequencies cross. The inset of part (b) shows an expanded view of the last avoided crossing of the rotor period. For part (c), 100 sets of random T_2e fields were averaged.

We note that, in our three-spin system, the relevant two-level Hamiltonians near level crossings are not always real (or if partly imaginary, do not have a fixed complex phase for E), because, in our basis, I_xS_z is real, I_yS_z is imaginary, and their coefficients vary under MAS. However, we do not expect the resulting Berry's phase effects²² to be significant, especially over a powder average. In addition, such effects are automatically included in the numerical calculations below.

Adiabaticity at avoided level crossings can drive cross effect DNP under MAS. From Eq. 5, we can estimate the behavior of spin polarizations at the various level crossings. The three avoided crossings that are important for the cross effect are numbered in Fig. 2: (1) electron-microwave crossing, when the microwave frequency crosses an ESR frequency, ω_m ∼ ω_e1,2; (2) three-spin crossing, when the difference of the ESR frequencies crosses the NMR frequency, ω_e1 – ω_e2 ∼ ±ω_n; (3) electron-electron crossing, when ω_e1 ∼ ω_e2. (In addition, the solid effect can be driven by an avoided level crossing, when ω_m ∼ ω_e ± ω_n.)

Near an isolated electron-microwave crossing (labeled 1 in Fig. 2a), it is sufficient to consider a 2 × 2 subspace, spanned, for example, by direct-product states |1⟩ and |2⟩. In a rotating frame at the microwave frequency, the 2 × 2 Hamiltonian matrix has the form

$$H_{\mathrm{EM}}=\left(\begin{array}{cc}\begin{array}{c}\frac{1}{2}(-{\omega }_m+{\omega }_{e1}+{\omega }_{e2}\hfill \\ +{\omega }_n+d+h_{zz})\hfill \end{array}& \frac{1}{2}{\omega }_1\\ \frac{1}{2}{\omega }_1& \begin{array}{c}\frac{1}{2}({\omega }_m+{\omega }_{e1}-{\omega }_{e2}\hfill \\ +{\omega }_n-d+h_{zz})\hfill \end{array}\end{array}\right).$$ (6)

The avoided level crossing occurs when the difference of the diagonal elements of Eq. 6 (−ω_m + ω_e2 + d) crosses through zero. The adiabatic probability (i.e., electron spin-flip probability) is

$$P_{\mathrm{EM}}\approx 1-\exp \left(-\pi {\omega }_1^2/\left(2\frac{\partial |{\omega }_{e2}|}{\partial t}\right)\right)\approx \pi {\omega }_1^2/\left(2\frac{\partial \left|{\omega }_{e2}\right|}{\partial t}\right),$$ (7)

if the microwave frequency is fixed, and neglecting the small time dependence of d. The rate of change of the ESR frequency obviously depends on the MAS frequency ω_r, the magnetic field, the electron g-anisotropy tensor, the orientation of the radical, and the value of ω_m. Still, we can estimate a typical adiabatic probability for a nitroxide radical at 9.4 T (ESR lineshape shown in Fig. 3), with the other parameters relevant to our experiments as described below. For microwaves at 264 GHz and 7 kHz MAS, a typical value for ∂ω_e/∂t is 2π × 2 × 10¹³ s⁻². With 80 kHz microwave strength, a typical adiabatic probability is then P_EM ∼ 4 × 10⁻³. This relatively small probability for an electron spin flip induced by the microwave field at an electron-microwave crossing is nonetheless significant, because with electron spin-lattice relaxation time T_1e ∼ 2 ms, we have T_1e ≈ 14t_r, where t_r = 2π/ω_r is the MAS rotor period. With multiple level crossings per rotor period (1.3 on average for each electron spin for 264 GHz microwaves and the ESR lineshape in Fig. 3), the total probability of an electron spin flip is ∼14% within T_1e. This would result in a decrease of roughly 28% in the electron spin polarization. In agreement with this estimate, the numerical calculations described in Sec. 3 have an average total decrease in the electron polarization of 27%. Significant perturbation of the electron spin polarizations is produced, which can then be transferred to nuclear spin polarization as discussed below. In this simple adiabatic model, the electron spin saturation increases in proportion to the microwave power. For a 5 W gyrotron microwave source, the root-mean-squared ω₁ has been estimated as 0.84 MHz.²⁴ In this case, the probability of an adiabatic electron spin flip is ∼0.3 in a single level crossing.

Figure 3.

Nitroxide powder pattern lineshape used for calculations, shown at 9.4 T. The electron g-tensor principal values are 2.0061, 2.0021, 2.0094. The ¹⁴N hyperfine coupling principal values are 18.8, 92.4, 18.2 MHz, for the x, y, and z axes, respectively.²⁵

At the next important level crossing, the three-spin crossing (labeled 2 in Fig. 2b), the energies of direct-product states |2⟩ and |7⟩ (or |3⟩ and |6⟩) cross. These pairs of direct-product states differ by flipping all three spins. According to Eq. 2, no off-diagonal terms directly connect these pairs of direct-product states. However, numerical calculations show that there is an avoided level crossing at the three-spin crossing, caused by the combination of electron-electron and hyperfine couplings, which creates a second order off-diagonal interaction (see inset in Fig. 2). To analytically calculate the adiabatic probability of flipping all three spins, we can derive the lowest order off-diagonal coupling between these states by block diagonalizing the Hamiltonian matrix, following similar analyses by Vanhouten et al.,^{15, 26} and Hu et al.¹⁹ We only require the central four direct-product states (|2⟩, |3⟩, |6⟩, and |7⟩), because without the microwaves, these four states are not connected by off-diagonal elements with the outer four states. Also, for simplicity, we derive the analytical result for h_yz = 0. The resulting 4 × 4 section of the Hamiltonian is

$$\begin{array}{c}\hfill H_{\mathrm{CE}}=\begin{array}{c}\begin{array}{c}\left|2\right.⟩\hfill \\ \\ \end{array}\\ \begin{array}{c}\left|7\right.⟩\hfill \\ \\ \end{array}\\ \begin{array}{c}\left|3\right.⟩\hfill \\ \\ \end{array}\\ \left|6\right.⟩\end{array}\stackrel{\begin{array}{cccc}\hfill \left|2\right.⟩& \hfill \left|7\right.⟩& \hfill \left|3\right.⟩& \left|6\right.⟩\end{array}}{\left(\begin{array}{cccc}\begin{array}{c}\frac{1}{2}({\omega }_{e1}-{\omega }_{e2}+{\omega }_n\hfill \\ -d+h_{zz})\hfill \end{array}& 0& -\frac{1}{2}d& \frac{1}{2}{h}_{xz}\\ 0& \begin{array}{c}\frac{1}{2}(-{\omega }_{e1}+{\omega }_{e2}-{\omega }_n\hfill \\ -d+h_{zz})\hfill \end{array}& -\frac{1}{2}{h}_{xz}& -\frac{1}{2}d\\ -\frac{1}{2}d& -\frac{1}{2}{h}_{xz}& \begin{array}{c}\frac{1}{2}(-{\omega }_{e1}+{\omega }_{e2}+{\omega }_n\hfill \\ -d-h_{zz})\hfill \end{array}& 0\\ \frac{1}{2}{h}_{xz}& -\frac{1}{2}d& 0& \begin{array}{c}\frac{1}{2}({\omega }_{e1}-{\omega }_{e2}-{\omega }_n\hfill \\ -d-h_{zz})\hfill \end{array}\end{array}\right)}.\end{array}$$ (8)

To first order in the off-diagonal elements, the eigenstates of H_CE are

$$\begin{array}{c}\hfill \begin{array}{c}\left|2^{\prime }\right.⟩=N_{2^{\prime }}\left[\left|2\right.⟩-\frac{\frac{1}{2}d}{{\omega }_{e1}-{\omega }_{e2}+h_{zz}}\left|3\right.⟩+\frac{\frac{1}{2}{h}_{xz}}{{\omega }_n+h_{zz}}\left|6\right.⟩\right],\hfill \\ \left|3^{\prime }\right.⟩=N_{3^{\prime }}\left[\left|3\right.⟩+\frac{\frac{1}{2}d}{{\omega }_{e1}-{\omega }_{e2}+h_{zz}}\left|2\right.⟩-\frac{\frac{1}{2}{h}_{xz}}{{\omega }_n-h_{zz}}\left|7\right.⟩\right],\hfill \\ \left|6^{\prime }\right.⟩=N_{6^{\prime }}\left[\left|6\right.⟩-\frac{\frac{1}{2}d}{{\omega }_{e1}-{\omega }_{e2}-h_{zz}}\left|7\right.⟩-\frac{\frac{1}{2}{h}_{xz}}{{\omega }_n+h_{zz}}\left|2\right.⟩\right],\hfill \\ \left|7^{\prime }\right.⟩=N_{7^{\prime }}\left[\left|7\right.⟩+\frac{\frac{1}{2}d}{{\omega }_{e1}-{\omega }_{e2}-h_{zz}}\left|6\right.⟩+\frac{\frac{1}{2}{h}_{xz}}{{\omega }_n-h_{zz}}\left|3\right.⟩\right]\hfill \end{array}\end{array}$$ (9)

where N_i is the normalization constant for the state i. We now transform the Hamiltonian in Eq. 8 to the basis in Eq. 9. Keeping the lowest-order terms in d, h_xz, and h_zz, and ignoring any terms of third order and above, we obtain

$$H_{\mathrm{CE}}^{\prime }\approx \begin{array}{c}\begin{array}{c}\left|2^{\prime }\right.⟩\hfill \\ \end{array}\\ \begin{array}{c}\left|7^{\prime }\right.⟩\hfill \\ \end{array}\\ \begin{array}{c}\left|3^{\prime }\right.⟩\hfill \\ \end{array}\\ \left|6^{\prime }\right.⟩\end{array}\stackrel{\begin{array}{cccc}\hfill \left|2^{\prime }\right.⟩& \hfill \left|7^{\prime }\right.⟩& \hfill \left|3^{\prime }\right.⟩& \left|6^{\prime }\right.⟩\end{array}}{\left(\begin{array}{cccc}\begin{array}{c}\frac{1}{2}({\omega }_{e1}-{\omega }_{e2}+{\omega }_n\hfill \\ -d+h_{zz})\hfill \end{array}& -\frac{1}{4}d{h}_{xz}\left[\frac{{\omega }_{e1}-{\omega }_{e2}-{\omega }_n}{\left({\omega }_{e1}-{\omega }_{e2}\right){\omega }_n}\right]& 0& 0\\ -\frac{1}{4}d{h}_{xz}\left[\frac{{\omega }_{e1}-{\omega }_{e2}-{\omega }_n}{\left({\omega }_{e1}-{\omega }_{e2}\right){\omega }_n}\right]& \begin{array}{c}\frac{1}{2}(-{\omega }_{e1}+{\omega }_{e2}-{\omega }_n\hfill \\ -d+h_{zz})\hfill \end{array}& 0& 0\\ 0& 0& \begin{array}{c}\frac{1}{2}(-{\omega }_{e1}+{\omega }_{e2}+{\omega }_n\hfill \\ -d-h_{zz})\hfill \end{array}& \frac{1}{4}d{h}_{xz}\left[\frac{{\omega }_{e1}-{\omega }_{e2}+{\omega }_n}{\left({\omega }_{e1}-{\omega }_{e2}\right){\omega }_n}\right]\\ 0& 0& \frac{1}{4}d{h}_{xz}\left[\frac{{\omega }_{e1}-{\omega }_{e2}+{\omega }_n}{\left({\omega }_{e1}-{\omega }_{e2}\right){\omega }_n}\right]& \begin{array}{c}\frac{1}{2}({\omega }_{e1}-{\omega }_{e2}-{\omega }_n\hfill \\ -d-h_{zz})\hfill \end{array}\end{array}\right)}.$$ (10)

In this basis, the lowest-order terms of the Hamiltonian have the avoided energy level crossing structure between states |2^′⟩ and |7^′⟩, and between states |3^′⟩ and |6^′⟩. To simplify the off-diagonal elements further, we can calculate their approximate values at the level crossings. For states |2^′⟩ and |7^′⟩, the crossing occurs when ω_e1 – ω_e2 ∼ −ω_n, and the off-diagonal element at the level crossing is ∼ –dh_xz/2ω_n. For states |3^′⟩ and |6^′⟩, the crossing condition is ω_e1 – ω_e2 ∼ ω_n, and the off-diagonal element is ∼dh_xz/2ω_n. A similar result has been derived previously as the parameter $\tilde{K}$ in Eqs. (41) and (44) of the paper by Hu et al.¹⁹ Numerical calculations, including both h_xz and h_yz, confirm that the adiabatic probability for a three-spin flip at the level crossing is

$$P_{\mathrm{TRIPLE}}\approx \pi d^2\left(h_{xz}^2+h_{yz}^2\right)/\left(2\frac{\partial \left|{\omega }_{e1}-{\omega }_{e2}\right|}{\partial t}{\omega }_n^2\right).$$ (11)

For a typical biradical orientation in our conditions, ω_n = 2π × 400 MHz, d = 2π × 9 MHz, $h=\sqrt{h_{xz}^2+h_{yz}^2}$ = 2π × 4.5 MHz, ∂|ω_e1-ω_e2|/∂t = 2π × 3 × 10¹³ s⁻², and thus P_TRIPLE ∼ 4 × 10⁻³. This typical probability of an adiabatic three-spin flip is low, but significant nuclear polarization can be built up from many three-spin level crossings. In the numerical simulations described below, typical DNP build-up times are 10–100 ms, corresponding to 100–1000 three-spin level crossings.

The third important energy level crossing is the electron-electron crossing (labeled 3 in Figs. 2a, 2b). This crossing occurs when the two ESR frequencies are equal (neglecting the small h_zz term), and the direct-product states |2⟩ and |3⟩ (and also |6⟩ and |7⟩) have the same energy. The electron-electron dipole coupling provides an off-diagonal Hamiltonian matrix element in the direct-product state basis, so an adiabatic electron spin flip-flop can occur during the avoided level crossing. For states |2⟩ and |3⟩, for example, the relevant 2 × 2 Hamiltonian matrix is

$$H_{\mathrm{EE}}=\left(\begin{array}{cc}\begin{array}{c}\frac{1}{2}({\omega }_{e1}-{\omega }_{e2}+{\omega }_n\hfill \\ -d+h_{zz})\hfill \end{array}& -\frac{1}{2}d\\ -\frac{1}{2}d& \begin{array}{c}\frac{1}{2}(-{\omega }_{e1}+{\omega }_{e2}+{\omega }_n\hfill \\ -d-h_{zz})\hfill \end{array}\end{array}\right).$$ (12)

The probability of an adiabatic flip-flop is

$$P_{\mathrm{EE}}\approx 1-\exp \left(-\pi d^2/\left(2\frac{\partial \left|{\omega }_{e1}-{\omega }_{e2}\right|}{\partial t}\right)\right).$$ (13)

For a typical level crossing (d = 2π × 9 MHz, ∂|ω_e1 − ω_e2|/∂t = 2π × 3 × 10¹³ s⁻²), P_EE ∼ 1 − exp(−28) ∼ 1, so the electrons trade their polarizations with very high probability. As we shall see, the high adiabaticity at electron-electron crossings is important for efficient cross effect DNP with wide-line radicals under MAS. However, because of the exponential form of P_EE, this depends sensitively on d, ω_r, and the electron g-anisotropy. If the MAS frequency increases from ω_r/2π = 7 kHz to ω_r/2π = 50 kHz, the non-adiabatic probability increases from nearly zero to ∼2%. This small probability, occurring for many electron-electron level crossings during T_1e, acts to equalize the polarization of the two electrons in the biradical. Because cross effect DNP relies on the polarization difference between the two electrons, the enhancement of steady-state nuclear spin polarization by DNP is reduced at large ω_r.

Also worth estimating is the probability that an electron spin in one biradical will exchange polarization with an electron spin in a neighboring biradical. This probability depends on the concentration of biradicals. For a 10 mM concentration of biradicals, the average distance between one electron spin and its nearest neighbor electron spin in a different biradical is 28 Å. This results in a typical dipole coupling of ∼2π × 0.9 MHz, implying P_EE ∼ 0.2. Thus, at 10 mM biradical concentration, electron spin polarization exchange between neighboring biradicals is significant, causing electron spin diffusion. Electron spin diffusion is not included in our three-spin model, but may be important in experiments.

Solid effect DNP

The solid effect can also be viewed as an adiabatic level crossing, occurring when the microwave frequency crosses the sum or difference of the ESR and NMR frequencies. The adiabatic level crossing is in the rotating frame of the microwaves, but otherwise the form of the 4 × 4 Hamiltonian for the solid effect is the same as in Eq. 8, but with ω₁ replacing d (see the supplementary information²¹). We can therefore perform a similar block diagonalization of the Hamiltonian and derive the adiabatic probability. At the solid effect crossing condition, ω_m ∼ ω_e ± ω_n,

$$P_{\mathrm{SE}}\approx \pi {\omega }_1^2\left(h_{xz}^2+h_{yz}^2\right)/\left(2\frac{\partial \left|{\omega }_e\right|}{\partial t}{\omega }_n^2\right).$$ (14)

Comparing this to P_TRIPLE in Eq. 11, the most significant difference is that the solid effect has ω₁ in place of d. Because d in the biradical is typically much larger than ω₁, the solid effect is weaker. For our parameters and a typical radical orientation, P_SE ∼ 3 × 10⁻⁷. In addition, if the microwave frequency is chosen so that ω_m = ω_e – ω_n at some rotor position, for many radical orientations there will be other rotor positions where ω_m = ω_e. If T_1e is long compared to 1/ω_r, then the electrons will tend to be saturated at the “allowed” transition, and the electron polarization available to drive the solid effect will be strongly reduced. The solid effect is thus expected to be weak for wide-line radicals with MAS. Solid effect DNP can be seen in our numerical calculations if the microwave strength is high and the electron-electron dipole coupling is removed. However, the contribution to the total DNP build-up rate and steady-state nuclear polarization is negligible under our conditions, as expected from this analytical estimate.

NUMERICAL SIMULATIONS OF CROSS EFFECT DNP UNDER MAS

Algorithm

Beyond the above analytical treatment, the time evolution of the three-spin model can be calculated numerically using an 8 × 8 density matrix description of the system. For the numerical calculations, t_r is divided into time steps δt (typically 1 ns, unless otherwise specified) during which the Hamiltonian is taken to be the constant operator H(t_k) in the kth time step, and the propagator is calculated as U(t_k) = exp[−iH(t_k)δt]. The time dependence of the density matrix is calculated as ρ(t_k+1) = U(t_k)ρ(t_k)U(t_k)⁻¹. This calculation is carried out in the rotating frame of the microwaves. It was verified that reducing δt by a factor of ten did not significantly affect the results.

To include spin relaxation, two different calculation methods are used, depending on whether the relaxation is caused by fast or slow fluctuations of local fields (relative to the time step). For fast fluctuations, we assume that the values of the spin-lattice relaxation time T₁ and the transverse relaxation time T₂ result from isotropic random fields, represented by single spin operators (S_1x, etc.). Since this contribution to relaxation results from fast fluctuations, there is no frequency dependence. Relaxation effects are evaluated in the eigenstate basis, so that T₁ relaxation affects the populations of instantaneous eigenstates and T₂ relaxation affects coherences between eigenstates. For each pair of eigenstates |a⟩ and |b⟩ with initial populations p_a = ⟨a|ρ|a⟩ and p_b = ⟨b|ρ|b⟩ and energies E_a and E_b, the population change due to T₁ relaxation during time interval Δt is calculated from the electron and nuclear spin-lattice relaxation times, T_1e and T_1n, as

$$\begin{array}{ccc}\hfill \Delta p_a& =& \frac{\left(p_b{e}^{-E_a/kT}-p_a{e}^{-E_b/kT}\right)}{\left(e^{-E_a/kT}+e^{-E_b/kT}\right)}\frac{2}{{\hslash }^2}\hfill \\ & & \times \left[\frac{\Delta t}{T_{1e}}\sum _{\underset{k=x,y,z}{i=1,2}}{\left|⟨a\left|S_{ik}\right|b⟩\right|}^2+\frac{\Delta t}{T_{1n}}\sum _{k=x,y,z}{\left|⟨a\left|I_k\right|b⟩\right|}^2\right].\hfill \end{array}$$ (15)

T₂ relaxation of off-diagonal elements p_a,b = ⟨a|ρ|b⟩ is calculated from the electron and nuclear transverse relaxation times, T_2e and T_2n, as

$$\begin{array}{ccc}\hfill \Delta p_{a,b}& =& -p_{a,b}\left(\sum _{\underset{k=x,y,z}{i=1,2}}\frac{\Delta t}{T_{2e}{\hslash }^2}{\left|⟨a\left|S_{ik}\right|a⟩-⟨b\left|S_{ik}\right|b⟩\right|}^2\right.\hfill \\ & & \left.+\sum _{k=x,y,z}\frac{\Delta t}{T_{2n}{\hslash }^2}{\left|⟨a\left|I_k\right|a⟩-⟨b\left|I_k\right|b⟩\right|}^2\right).\hfill \end{array}$$ (16)

Δt is taken to be 1% or less of the shortest relaxation time from fast local field fluctuations (T_2n in our calculations, as discussed below). It was confirmed that calculating the relaxation at these intervals did not yield significantly different results from calculating the relaxation at every time point. This was confirmed both for the standard parameters described below and for relaxation times that were ten times shorter, at MAS frequencies of 0.1, 7, and 50 kHz.

Relaxation from slow local magnetic field fluctuations is treated by explicitly including a randomly varying field in the Hamiltonian. T_2e relaxation is treated in this way because ESR experiments on similar nitroxide radicals in frozen solution at lower magnetic field show a Gaussian T_2e decay, characteristic of slowly varying local magnetic fields from nearby nuclei.²⁷ In order to reproduce the 4 μs T_2e value measured in the ESR experiments, a longitudinal field with random sign was applied to each electron independently to provide a ±65 kHz interaction with a correlation time of 2 μs. The calculations were averaged over ten different sets of random magnetic fields, except where noted in the figure caption.

We expect T_1e to be dominated by fast lattice fluctuations.²⁷ In addition, a T_2e rate equal to T_1e was included to represent the T_2e contribution from fast fluctuations. T_2n relaxation may be dominated by slow local field fluctuations (from couplings to nearby ¹H and electron spins). However, because T_2e and T_2n relaxation from slow fluctuations does not affect the numerical results (discussed below), T_2n was treated as arising from fast fluctuations for the sake of calculational efficiency. T_1n also does not affect the numerical results because it is much longer than the length of any of the simulations, and T_1n was treated as arising from fast fluctuations.

Powder averaging was performed by choosing random orientations of the electron spin g-tensor, electron-electron dipole coupling tensor, and electron-nucleus hyperfine coupling tensor principal axes in the MAS rotor. No correlations among the various orientation angles were used. In addition to electron-¹H hyperfine coupling, the electron-¹⁴N hyperfine coupling of each nitroxide moiety is included, with the ¹⁴N spin state randomly chosen for each nitroxide and kept fixed during the calculations. (The electron-¹⁴N hyperfine coupling effectively modifies the electron g-tensor, but has no other effect.) In the following text, each “biradical orientation” is one random choice of all interaction tensor orientations in the MAS rotor. Powder averaging was done with the same set of 200 orientations for all of the calculations, except where noted in figure captions that the first 100 orientations were used.

For each biradical orientation, the time dependence of the density matrix was calculated starting from two different initial conditions: (1) thermal equilibrium of all three spins at 25 K, based on instantaneous energy levels at the beginning of a MAS rotor period and (2) thermal equilibrium of the electrons and the nucleus polarized to the thermal electron polarization at 264.4 GHz, defined to be e_pol,th. By having two different initial nuclear polarizations, we avoid the problem of distinguishing between a biradical orientation which has no DNP effect and an orientation with DNP that happens to have a final steady-state nuclear polarization close to the initial nuclear polarization. For each of these two initial conditions, the time dependence of the density matrix was first calculated for 5T_1e, without any electron-¹H coupling or nuclear relaxation. This allowed the electron polarizations to equilibrate with the microwaves, without affecting the nuclear polarization. This was done to simulate typical experimental conditions in which the microwaves are applied continuously, while the ¹H polarization is initially destroyed by a train of radio-frequency pulses, then allowed to build up through DNP. After this equilibration period, the calculation was continued with the complete Hamiltonian, typically for 71 ms (500t_r at 7 kHz MAS) unless otherwise noted. The simulation program was written in C using the Intel Math Kernel Library which includes LAPACK and CBLAS libraries for linear algebra functions. A sample version of the program and an input file are given in the supplementary information.²¹ The Biowulf Linux cluster at NIH (Ref. ²⁸) enabled us to run simulations for many different parameter sets in parallel. The longest calculations (1.4 s = 10⁴ × t_r) took ∼18 h for each biradical orientation using one core of an Intel Xeon X5550 CPU.

In order to summarize the behavior of the nuclear polarization, we can look at the nuclear polarization, n_pol, at the end of every rotor period (or within the rotor period for slow MAS), as shown in Fig. 4. At typical MAS frequencies, the change in n_pol per level crossing is small, so we get a reasonably smooth curve with an exponential form. We take the two curves from the two initial conditions, and fit them simultaneously to the following equations to get a single time constant t_DNP and steady-state nuclear polarization n_pol,ss, normalized to the thermal equilibrium polarization of an isolated proton n_pol,th:

$$n_{\mathrm{pol}}\left(t\right)=1+\left(n_{\mathrm{pol},\mathrm{ss}}-1\right)\left(1-\exp \left(-t/t_{\mathrm{DNP}}\right)\right),$$ (17a)

$$n_{\mathrm{pol}}\left(t\right)=e_{\mathrm{pol},\mathrm{th}}+\left(n_{\mathrm{pol},\mathrm{ss}}-e_{\mathrm{pol},\mathrm{th}}\right)\left(1-\exp \left(-t/t_{\mathrm{DNP}}\right)\right).$$ (17b)

At low MAS frequencies, the nuclear polarization curves are not smooth exponentials, but rather a series of step changes in the nuclear polarization at the three-spin crossings, but the same exponential fitting functions were used for consistency.

Figure 4.

Time dependence of nuclear spin polarization for four different biradical orientations for (a) nuclear spin polarization starting at thermal polarization and (b) nuclear spin polarization starting at thermal electron spin polarization. In these simulations, the hyperfine coupling (h_zz,max) and the nuclear spin-lattice relaxation are not included for 5T_1e (10 ms), then turned on at time 0 to initiate DNP. Level crossings for each orientation: blue circles, both electron-microwave and three-spin crossings (shown in Fig. 2); light blue squares, no three-spin crossing; red crosses, no electron-microwave crossing, but has three-spin crossing; green diamonds, electron-microwave crossing for higher frequency electron. 100 sets of random T_2e fields were averaged. For clarity, only some of the data points are shown.

To complete the powder average, once the fitting is done for each radical orientation, an overall average steady-state polarization is calculated by weighting the steady-state polarization with the inverse time constant, as shown by Eq. 18. Also, the average time constant is calculated by averaging the inverse time constants:

$$n_{\mathrm{pol},\mathrm{av}}=\frac{{\sum }_{k=1}^N{\left(\frac{n_{\mathrm{pol},\mathrm{ss}}}{t_{\mathrm{DNP}}}\right)}_k}{{\sum }_{k=1}^N{\left(\frac{1}{t_{\mathrm{DNP}}}\right)}_k},$$ (18a)

$$\frac{1}{t_{\mathrm{DNP},\mathrm{av}}}=\frac{1}{N}\sum _{k=1}^N{\left(\frac{1}{t_{\mathrm{DNP}}}\right)}_k,$$ (18b)

where the index k represents a single orientation and N is the number of orientations. In Eq. 18a, weighting by (1/t_DNP)_k is motivated by experimentally relevant situations in which many biradicals with different orientations contribute to the polarization of bulk nuclei through nuclear spin diffusion. The fitting of the nuclear polarization curves, and the averaging of the results was done using MATLAB.

Choice of parameters

The standard parameter values used for the calculations, unless stated otherwise, are listed in Table 1. These parameters were chosen to be typical for our current experimental conditions.^{9, 29} The microwave frequency of 264 GHz provides the maximum positive nuclear polarization at our magnetic field of 9.4 T. The microwave strength and T_1e are estimates from our non-spinning DNP experiments at 25 K with a 30 mW microwave source. The electron-electron dipole coupling is from experiments on Totapol biradicals by Song et al.^{5, 20} The ¹H hyperfine coupling is the strongest coupling measured in an ESR experiment on Tempo radicals.³⁰T_2e is from lower field ESR measurements.²⁷ The nuclear relaxation times, T_1n and T_2n, account for ¹H relaxation from mechanisms outside our three-spin model. T_1n is chosen to be long enough to have no effect on the calculations, and for T_2n, we choose a reasonable value for the contribution to transverse relaxation of ¹H polarization arising from fast local field fluctuations (not ¹H–¹H dipolar couplings).

Table 1.

Standard values of parameters for numerical calculations.

Parameter	Standard value	Justification
Microwave frequency, ωm/2π	264.0 GHz	Thurber et al.9
Microwave strength, ω1/2π	80 kHz	Thurber et al.9
NMR frequency, 1H, ωn/2π	−400.9 MHz	Thurber et al.9
Temperature, T	25 K	Thurber and Tycko29
MAS frequency, ωr/2π	7 kHz	Thurber and Tycko29
Electron-electron coupling, dmax/2π	23 MHz	Hu et al.20
Hyperfine coupling, hzz,max/2π	9 MHz	Ohzeki et al.30
g-tensor principal values	2.0061, 2.0021, 2.0094	Snipes et al.25
14N hyperfine coupling principal values	18.8, 92.4, 18.2 MHz	Snipes et al.25
T1e	2 ms	Thurber et al.9
T2e from slow fluctuations	4 μs	Sato et al.27
T2e from fast fluctuations	2 ms	Thurber et al.9
T1n	1000 s	Undoped 1H T1
T2n	0.2 ms	Transverse 1H relaxation

Numerical results

Figures 2a, 2b show the ESR frequencies and central four energy levels for one biradical orientation. Figure 2c shows the time dependence of the spin polarizations for this orientation, during the first rotor period that the hyperfine coupling is present (after the electron polarizations have been equilibrated with the microwaves for 5T_1e as discussed above). The time dependence of the polarizations over many rotor periods is shown in Fig. S1 of the supplementary information.²¹ The numerical calculations show results at the level crossings that agree quantitatively with the analytical model. At the electron-microwave level crossings (1), the polarization of one electron is reduced, creating a polarization difference between the two electrons. At the three-spin crossings (2), an adiabatic transition reduces this electron polarization difference and increases the nuclear polarization. Both of these level crossings are weakly adiabatic, as expected from the analytical estimates. Some three-spin crossings are more adiabatic and provide more nuclear polarization than others. This depends primarily on the orientations of the electron-electron dipole coupling and the hyperfine coupling at that rotor position, as well as the speed of the level crossing. At the electron-electron level crossings (3), the two electrons typically swap their polarization with very high probability. As a result, for our standard parameter values and most biradical orientations, the polarizations of the two electrons have one value for the higher-frequency electron and another value for the lower-frequency electron, even as the identity of the higher-frequency electron changes at each electron-electron crossing (see Fig. 2). This exchange of polarization at the electron-electron crossings is beneficial for DNP in two ways. First, a polarization difference between the electrons can be efficiently created by electron-microwave crossings with either or both electrons, as long as the microwave frequency always crosses the lower ESR frequency (or always the higher ESR frequency, for the opposite sign of DNP). Figure 2 illustrates this with an example where the microwave frequency crosses the ESR frequencies of both electrons, yet the polarization difference adds constructively (rather than tending to cancel out) because all the electron-microwave crossings are with the lower ESR frequency at that point in the rotor period. Second, the sign of the polarization difference between the higher-frequency electron and the lower-frequency electron is constant over the entire rotor period. As a result, the polarization transfer to the nucleus has the same sign at each three-spin level crossing.

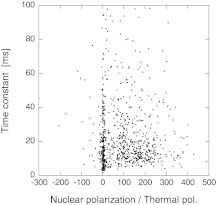
As shown in Fig. 4, numerical results for the time dependence of the nuclear polarization for different biradical orientations can mostly be categorized into four types: (1) If both three-spin and electron-microwave crossings occur during the rotor period, efficient DNP can take place; (2) If no three-spin crossing occurs, the electrons are decoupled from the nucleus, and little DNP happens; (3) If no electron-microwave crossing occurs, but a three-spin crossing does occur, there is little electron polarization difference, and the nuclear polarization is driven to a small value; (4) If an electron-microwave crossing involves the higher-frequency electron at that point in the rotor period (even though the microwave frequency is on the low-frequency side of the ESR line), the DNP can be negative, working against the majority of the orientations. The distribution of n_pol,ss and t_DNP values from 1000 random biradical orientations is shown in Fig. 5. Roughly half of the orientations are effective (arbitrarily defined as n_pol,ss > 15n_pol,th and t_DNP < 100 ms), while ∼2% of the orientations produce significant nuclear polarization with the opposite sign (n_pol,ss < −15n_pol,th). We emphasize that these results are for biradicals with uncorrelated g-tensor orientations for the two electron spins. The probability of effective DNP could be altered by correlation between the two g-tensor orientations, as would occur in a conformationally constrained nitroxide biradical.²⁰

Figure 5.

Steady-state nuclear spin polarizations (as a ratio to thermal polarization) (n_pol,ss) and time constants (t_DNP) for 787 of 1000 random biradical orientations. The remaining 213 orientations are not shown because their values of t_DNP exceeded 100 ms.

Using the numerical calculations, we can see how DNP depends on the system parameters. First, we find that the only relaxation rate that affects DNP under our conditions is T_1e. A shorter T_1e requires larger ω₁ in order to achieve the same differential electron polarization, as shown in Fig. 6. At large ω₁, there is a plateau in the value of n_pol,av. At these points, the electron polarization difference has been saturated, with one electron at roughly zero polarization, while the other is at roughly thermal polarization.

Figure 6.

Average steady-state nuclear spin polarization (n_pol,av, solid symbols) and time constant (t_DNP,av, open symbols) as a function of microwave field strength (ω₁/2π) for T_1e = 2 ms (circles) and T_1e = 0.2 ms (diamonds). Lines are drawn to guide the eye.

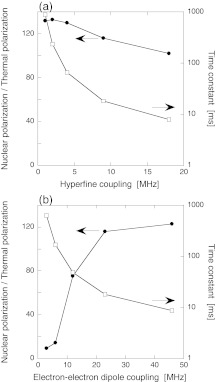
Figure 7 shows the dependence of DNP on h_zz,max and d_max. From Eq. 11, we expect t_DNP,av to scale as the inverse square of both h_zz,max and d_max. t_DNP,av does follow this scaling for small hyperfine and electron-electron couplings, but for larger couplings t_DNP,av is not as short as this scaling would predict. Presumably, this is because t_DNP becomes comparable to T_1e. Figure 6 shows that reducing T_1e also reduces t_DNP,av. n_pol,av decreases as d_max decreases, due to behavior at electron-electron level crossings. When d_max is reduced, the electron-electron crossing is no longer strongly adiabatic, and the electron polarization difference is not maintained.

Figure 7.

Average steady-state nuclear spin polarization (n_pol,av, solid symbols) and time constant (t_DNP,av, open symbols) as a function of (a) hyperfine coupling (h_zz,max/2π) and (b) electron-electron dipole coupling (d_max/2π). 100 biradical orientations are calculated for 1.4 s (10⁴ × t_r). Lines are drawn to guide the eye.

The effect of the adiabaticity of the electron-electron crossing can also be seen in the dependence on ω_r in Fig. 8. As ω_r increases, the electron-electron crossing becomes less adiabatic and there are more crossings per unit time. The electron polarization difference then decreases (see Fig. S2 of the supplementary information²¹), and n_pol,av decreases. However, t_DNP,av also decreases, which means the build-up rate of nuclear spin polarization at high ω_r does not drop as much as the steady-state polarization. At low ω_r, n_pol,av decreases and t_DNP,av increases. This is a consequence of the need to cross both the electron-microwave crossing and the three-spin crossing within ∼T_1e, so the electron saturation has not relaxed by the time of the three-spin crossing.

Figure 8.

(a) Average steady-state nuclear spin polarization (n_pol,av) and (b) time constant (t_DNP,av), as a function of MAS frequency (ω_r/2π) for simulations with ω₁/2π = 0.08 MHz and T_1e = 2 ms (circles), with ω₁/2π = 0.8 MHz and T_1e = 2 ms (squares), and with ω₁/2π = 0.8 MHz and T_1e = 0.2 ms (diamonds). 100 biradical orientations were used for the powder average and the calculations were run for 71 ms or longer. MAS frequencies below 210 Hz were calculated with a 10 ns timestep. Lines are drawn to guide the eye.

Figure 9a shows the dependences of t_DNP,av and n_pol,av on ω_m for a nitroxide biradical. The calculations show a dependence on ω_m very similar to that seen in experiments, both with MAS (Refs. ⁵ and ³¹) and without MAS.⁹ When ω_m is near the middle of the ESR lineshape, n_pol,av is small because both positive and negative DNP enhancements occur with similar probabilities. The shape of the dependence of n_pol,av on ω_m (i.e., the DNP excitation spectrum) is not altered significantly by changing ω_n, as shown in Fig. S3 of the supplementary information.²¹ This result indicates that the DNP excitation spectrum is determined primarily by the electron-microwave level crossings, which (depending on ω_m) produce either a net positive or a net negative difference in spin polarizations between higher-frequency and lower-frequency electrons.

Figure 9.

Average steady-state nuclear spin polarization (n_pol,av, solid symbols) and time constant (t_DNP,av, open symbols) as a function of microwave frequency (ω_m/2π) for (a) a Totapol biradical²⁰ and (b) a hypothetical narrow-line biradical, composed of two radicals with different g-factors (both with 30 MHz axially symmetric g-anisotropy), so that the ESR frequencies are separated by ω_n. Lines are drawn to guide the eye.

Figure 9b shows results for a hypothetical biradical composed of two different narrow-line radicals, with their different isotropic g-factors chosen so that the two ESR frequencies are separated by ω_n and with relatively small g-anisotropies. The simulations show that a narrow-line biradical should be more efficient for cross effect DNP, as expected for two reasons: (1) The microwaves create a larger net electron spin polarization difference, because the electron-microwave crossings are more strongly adiabatic and only one sign of electron spin polarization difference is created. (2) The three-spin crossings are more strongly adiabatic.^{32, 33}

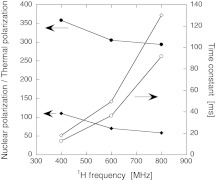
Figure 10 shows the dependence of DNP on the static magnetic field B. As B is increased from 9.4 T, the level crossing model predicts that t_DNP,av increases as B³ [see Eq. 11], if the adiabatic probability of the three-spin flip is the dominant contribution to t_DNP,av. The numerical calculations do show a strong increase in t_DNP,av with increasing B, close to B³. n_pol,av depends more weakly on B, decreasing with increasing B due to less efficient saturation of electron spin polarizations at electron-microwave crossings. However, the magnetic field dependence presented here is only a partial description of the dependence of cross effect DNP on B because it does not include changes in relaxation rates or electron spin diffusion that would be expected to occur.

Figure 10.

Dependence of the average steady-state nuclear spin polarization (n_pol,av, solid symbols) and time constant (t_DNP,av, open symbols) on magnetic field for microwave field strengths (ω₁/2π) of 2 MHz (circles) and 80 kHz (diamonds). Calculations were performed for ¹H NMR frequencies of 400.9, 600.0, and 800.0 MHz, with ω_m/2π equal to 264.0, 395.1, and 526.8 GHz, respectively (corresponding to the maximum positive DNP enhancements). The calculations were run for 2000 × t_r (286 ms). Lines are drawn to guide the eye.

DISCUSSION

Conditions for validity of the level crossing model

The level crossing model for cross effect DNP described in Sec. 2 relies on several conditions being satisfied. Some of these conditions are specific to the analytical estimates of adiabatic spin flip probabilities, and can be verified by comparison with the numerical calculations. First, the analytical estimates are in the high field limit where the electron-electron dipole coupling and hyperfine coupling can be treated as perturbations to the Zeeman energies. The numerical calculations support this approximation by showing the same quantitative results at level crossings when the full Hamiltonian is included.

Second, the analytical estimates treat the electron-microwave and three-spin level crossings separately. To justify this numerically, we can calculate that the probability of the two level crossings happening simultaneously is small. For example, for random nitroxide biradical orientations, there is only a ∼2% probability that the three-spin crossing condition, ω_e1 – ω_e2 = ±ω_n, is matched at the same time that a coupled electron transition is resonant with the microwaves (defined as being within 1 MHz of 264 GHz) at some point over the entire rotor period. This small fraction of biradical orientations could still dominate the DNP if their polarization rate was much faster than the other orientations. However, the numerical results show that the few orientations with overlapping level crossings have values of t_DNP and n_pol,ss that are similar to other biradical orientations without overlapping level crossings. One reason for this was pointed out by Hu et al.¹⁹ as their Example 3. During the three-spin crossing, if the microwaves are strong enough to excite transitions to both central eigenstates simultaneously, the nuclear polarization time scale is slowed down to ∼dh/ω_n, rather than ${\omega }_1/\sqrt{2}$.¹⁹

Third, the Landau-Zener formula does not include relaxation during the level crossing. One possible justification for neglecting relaxation during the level crossing is that the relaxation times T₁ and T₂ are very long compared with the level crossing time. This is true in our case for T_1e, T_1n, and T_2n. On the other hand, T_2e is short enough to potentially cause significant relaxation during a level crossing. However, ESR experiments show that the T_2e decay is Gaussian.²⁷ This implies that the local field fluctuations driving T_2e relaxation are on a time scale comparable to T_2e. This means that the local magnetic fields on the two electrons are essentially fixed for the duration of the electron-microwave and three-spin crossings (on the order of 10–100 ns and 10 ns, respectively), and do not cause relaxation during these level crossings. Closely related to the above discussion of T_2e relaxation is our treatment of the spin energies as discrete levels, rather than energy bands or lifetime-broadened levels arising from multiple-spin couplings. We expect the energy width of the states to be much larger than the energy level splitting at the three-spin crossing (∼dh/ω_n, typically of the order of 100 kHz). The electron spins in one biradical have ∼1 MHz couplings to electron spins in other biradicals, and also couplings of similar size to other nearby nuclei.³⁰ However, since the local fields from these couplings fluctuate slowly, we view the energy width as inhomogeneous (fixed local fields) for the time scale of the level crossings.

Another requirement for considering each level crossing separately and using the analytic Landau-Zener formula (which treats only populations) is that coherence between eigenstates generated at one level crossing does not significantly affect the next level crossing. For MAS frequencies typically in current use for cross effect DNP (up to ∼15 kHz),⁸ with T_2e ≈ 4 μs, any coherence that might be generated during one level crossing dephases before the next level crossing.

Spin diffusion

Spin diffusion is not included in this three-spin model of cross effect DNP. If electron and nuclear spin diffusion is weak, different regions of the sample surrounding differently oriented biradicals could have widely varying nuclear polarizations, even with opposite signs. However, for the biradical concentrations typically used in experiments, significant electron spin polarization exchange between neighboring biradicals is expected with MAS, as discussed above. This intermolecular polarization exchange may reduce the differences in DNP effects for different biradical orientations. Specifically, biradicals that do not have an electron-microwave crossing but do have a three-spin crossing could acquire an electron polarization difference through electron spin diffusion, which might enable these orientations to participate constructively in DNP. On the other hand, electron spin diffusion may also tend to decrease the average electron spin polarization difference within the biradicals, decreasing cross effect DNP, because (as discussed in the last paragraph of Sec. 2B) intermolecular electron-electron crossings are significant but not fully adiabatic.

Nuclear spin diffusion is also important in typical DNP experiments, transporting the nuclear spin polarization to nuclei that are far from any biradical (or far from biradicals that have large DNP effects).¹⁴ In the three-spin model, because the DNP time constant roughly scales as the inverse square of the hyperfine coupling, nearby nuclei are polarized much faster than distant nuclei. Roughly speaking, in terms of the distance r between the nucleus and the electron, the hyperfine coupling scales as r⁻³, while the number of nuclei in a spherical shell scales as r². The total DNP build-up rate to all nuclei at distance r should then scale roughly as r⁻⁴. This implies that nuclei close to biradicals will be the most important contributors to the total nuclear polarization. As discussed in previous work by others, a spin diffusion barrier may prevent the close nuclei (i.e., those with small r) from transferring their high polarization to bulk nuclei.^{14, 34} Due to the hyperfine coupling, which is primarily dipolar as seen in ESR experiments,³⁰ the close nuclei have large NMR frequency shifts from their neighboring nuclei, decreasing nuclear spin diffusion rates by reducing frequency overlap between neighboring nuclei. However, under MAS, the frequencies of pairs of nuclei will typically cross several times during the rotor period even with a large hyperfine coupling. We can treat this problem in terms of avoided level crossings, exactly as we did above when two ESR frequencies crossed during MAS. As a concrete example, we place the first nucleus at 2.08 Å from the electron, and the second nucleus 1.5 Å from the first, with random orientations, but requiring that the second nucleus be at least 0.5 Å further from the electron than the first nucleus, so that we are looking at outward spin diffusion from the first nucleus to the second. We find that, on average, the nuclear energy levels cross 2.7 times per rotor period. For a typical internuclear dipole coupling (d_nn = 2π × 14 kHz) and 7 kHz MAS (which implies ∂(ω_n1 − ω_n2)/∂t ∼ 2π × 3 × 10¹¹ s⁻²), the probability of an adiabatic polarization exchange between the coupled nuclei is ∼0.6%. This is small, but would result in a typical time for polarization exchange of ∼10 ms. So, while nuclear spin diffusion is attenuated considerably by the hyperfine coupling, the time scale for polarization to diffuse from a close nucleus to one of its neighbors is comparable to t_DNP. Once the polarization moves to nuclei further from any radical, nuclear spin diffusion generally becomes faster. Therefore, slow nuclear spin diffusion close to the radicals (i.e., a spin diffusion barrier) may not be a serious impediment to the transfer of nuclear polarization to the bulk. Experimentally, reducing the concentration of ¹H nuclei by using highly deuterated glycerol/water solvent has improved DNP signal enhancements,⁵ supporting the idea that a ¹H spin diffusion barrier is not the primary limiting factor for DNP under these experimental conditions.

Experimental implications

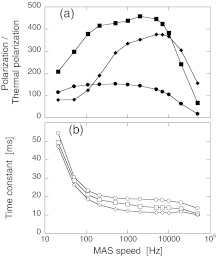
The level crossing model for cross effect DNP under MAS has several experimental implications. The first part of the cross effect process is the creation of electron polarization difference by the electron-microwave crossings. Electron polarization differences are preserved at highly adiabatic electron-electron crossings. The model predicts that the electron polarization difference depends primarily on ω₁, T_1e, and ω_r (and may also depend on electron spin diffusion when couplings between biradicals are considered). Saturation of the electron polarization difference is predicted at roughly ω₁/2π > 1 MHz for T_1e = 0.2 ms (Fig. 6), corresponding to an experimentally accessible microwave field strength, although detailed comparison to experiments requires consideration of the microwave field inhomogeneity over the sample.²⁴ Also, the model predicts significant changes in n_pol,av and in the electron spin saturation across the ESR lineshape as a function of ω_r for typical experiments (Figs. 8 and S2²¹). Experimental results do show a remarkably similar dependence of the DNP enhancement on ω_r, with a maximum at ω_r/2π ∼ 3 kHz.⁸ In principle, the electron spin saturation could be determined experimentally as a function of ω₁, ω_r, and T with two-frequency ESR measurements.

We can estimate the order of magnitude of the experimentally detected DNP enhancement if the dominant contribution to DNP is from the nuclei that are closest to biradicals. The calculations suggest that microwave saturation of randomly oriented biradicals (with parameters appropriate for Totapol⁵) produces a ∼10 ms time scale for polarization of the closest nuclei to ∼400 times n_pol,th (see Fig. 6). ESR measurements see two ¹H nuclei at the closest distance, with the 9 MHz hyperfine coupling used in our calculations.³⁰ For a 20 mM biradical concentration in a glycerol/water solution, there are roughly 5000 ¹H nuclei per biradical. Polarization of the two closest ¹H nuclei on a ∼10 ms time scale implies a rough time scale for polarization of all ¹H nuclei of (5000/2) × 10 ms = 25 s. This is a sensible order of magnitude, with experiments typically having polarization build-up times of 3–30 s and steady-state polarizations somewhat less than 400 times n_pol,th.^{5, 35} Nuclear spin-lattice relaxation mechanisms unrelated to the cross effect can reduce the final nuclear polarization and impose an upper limit on the experimental build-up times.

The dependence of cross effect DNP on B is expected to be influenced by various factors in this model. As discussed above and shown in Fig. 10, t_DNP scales roughly as B³, if t_DNP is primarily determined by the adiabatic probability of the three-spin flip. Dependence of T_1e on B can also affect t_DNP, as shown in Fig. 6. In addition, if the electron spin polarization difference is not saturated and the ESR linewidth is dominated by the g-anisotropy, the polarization difference scales as B⁻¹, from the effect of the ESR linewidth on the electron-microwave crossing [see Eq. 7]. In addition to these factors, spin relaxation rates and electron spin diffusion constants can depend on B. Experimentally, it has been reported that the net DNP enhancements under MAS are roughly proportional to B⁻¹.^{5, 8, 19, 36} However, extensive studies of field-dependent DNP enhancements and build-up rates have not yet been reported.

The numerical calculations in this article are for a nitroxide biradical dopant, but the two-step cross effect process is not limited to these specific biradicals. For example, the two-step cross effect process should also be relevant for experiments with nitroxide triradicals. Under our experimental conditions, a nitroxide triradical has produced higher nuclear polarization rates than a biradical.⁹ This may result from the reduced probability to have no electron-microwave crossing, or from the additional three-spin crossings, or from some other reason.

Even though the two-step process for cross effect DNP described here is derived with MAS, it is also likely to be relevant for some DNP experiments without MAS. The simplest model for cross effect DNP for a static sample requires that the three-spin transition condition (ω_e1 – ω_e2 ≈ ±ω_n) and the resonant microwave condition (ω_m ≈ ω_e1 or ω_m ≈ ω_e2) occur simultaneously.^{19, 32} However as discussed above, for a wide-line biradical, the probability of satisfying both conditions simultaneously is small. In addition, even if both conditions are satisfied simultaneously, the polarization rate is not dramatically faster than in a two-step process. In a static sample, the two-step cross effect process could occur if time-dependent local magnetic field fluctuations from nearby electrons and nuclei cause a given biradical to sweep through the two conditions, so that both conditions are satisfied, but at different times when the local fields are different. Alternatively, electron spin diffusion could transport partial saturation of electron polarization from radicals that are resonant with the microwaves to biradicals that satisfy the three-spin transition condition. In these two ways, the cross effect might proceed by two steps even in a static sample.

CONCLUSIONS

Using a three-spin model, we have shown that, for wide-line biradicals with MAS at high magnetic field and with T_1e > 1/ω_r, cross effect DNP can occur through spin transitions at two separate avoided energy level crossings. When an ESR frequency crosses ω_m (electron-microwave crossing), the polarization of one of the electrons is reduced, creating or altering the polarization difference between the two electron spins. In this three-spin model, the electron polarization difference is primarily determined by the balance of the microwave field strength and T_1e. Beyond the three-spin model, electron spin diffusion may reduce the electron polarization difference. In the second step, the polarization difference between the electron spins in a biradical is partially transferred to the nucleus, through a three-spin level crossing where the ESR frequency difference equals the NMR frequency. The probability of polarization transfer, proportional to the square of both the electron-electron dipole coupling and the hyperfine coupling, is small at any single three-spin level crossing for typical experimental conditions. However, large nuclear polarization can develop over many three-spin crossings. For efficient cross effect DNP when T_1e > 1/ω_r, it is also important that the polarization difference between higher- and lower-frequency electrons of the biradical be maintained over the MAS rotor period. This requires that the electron-electron dipole coupling be large enough relative to ω_r, so that electrons exchange polarization with high probability when their ESR frequencies cross. Under MAS, a majority of random nitroxide biradical orientations contribute to DNP in our calculations. However, in principle, cross effect DNP could be significantly improved by using a hypothetical narrow-line biradical dopant, with two ESR frequencies separated by the NMR frequency.