Abstract
The molecular origin of the action of the F0 proton gradient-driven rotor presents a major puzzle despite significant structural advances. Although important conceptual models have provided guidelines of how such systems should work, it has been challenging to generate a structure-based molecular model using physical principles that will consistently lead to the unidirectional proton-driven rotational motion during ATP synthesis. This work uses a coarse-grained (CG) model to simulate the energetics of the F0-ATPase system in the combined space defined by the rotational coordinate and the proton transport (PTR) from the periplasmic side (P) to the cytoplasmic side (N). The model establishes the molecular origin of the rotation, showing that this effect is due to asymmetry in the energetics of the proton path rather than only the asymmetry of the interaction of the Asp on the c-ring helices and Arg on the subunit-a. The simulation provides a clear conceptual background for further exploration of the electrostatic basis of proton-driven mechanochemical systems.
Keywords: molecular motors, bioenergetics, chemiosmotic, F0F1-ATP synthase
The F0F1-ATPase is a ubiquitous nanomotor in all living cells that generate the ATP molecules essential for maintaining large gamut of cellular functions (1). This system is comprised of two rotary motors; the mechanochemical F1-ATPase that synthesizes or hydrolyzes ATP, utilizing the mechanical torque generated from the rotation of the stalk, and the membrane-bound F0-ATPase that drives the mechanical rotation utilizing the ion-motive force established across the membrane. The detailed nature of the conversion and the utility of energy by the F0F1-ATPase has long been one of the fundamental questions in biology. Significant progress has been achieved in understanding the mechanochemical coupling in the F1-ATPase, utilizing information from several high-resolution crystal structures and a wealth of biochemical and single-molecule spectroscopic data (2–6). Recently, the molecular nature of the coupling between chemical and conformational coordinates in the F1-ATPase has been elucidated using coarse-grained (CG) theoretical modeling approaches (7). In contrast, the molecular basis of the conversion of the pH gradient across the membrane producing directional rotation of the F0-ATPase is less understood, despite significant conceptual progress (3). The problems are partially due to the limited structural information about the complete membrane-bound F0-ATPase complex and also reflects the inherent difficulty in modeling coupled long-range biological processes, such as proton transfer and mechanical rotation.
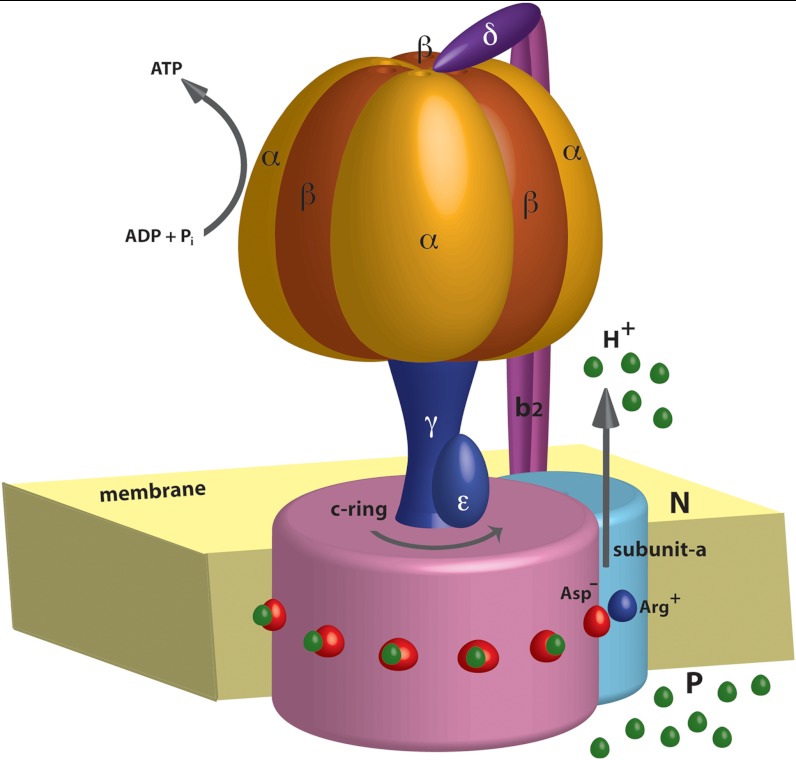
The F0 motor is consisted of a rotor part, known as the c-ring, connected with the stator subunit-a and dimer subunits-b. The c-ring is a tightly packed ring-like structure composed of several α-helical hairpins whose number varies in different species (3, 8). Most of the central part of the c-ring is embedded in the membrane, except for the cytoplasmic loops and the periplasmic termini. Each c-ring helices consists of a highly conserved ionizable Asp or Glu residue that most probably bind the proton or the sodium ion (depending on the organism) (9). The stator subunit-a is located adjacent to the c-ring and is a predominantly hydrophobic protein consisting of 5–6 transmembrane helices. The interface formed between the rotating c-ring and the subunit-a is known to play a dominant role in the torque generation of the motor. Several biochemical and mutational studies have highlighted the role of a conserved Arg residue in mediating the functional ion translocation pathways through the a/c interface. This Arg is located almost at the same position as the H+(Na+) binding Asp/Glu residues in the c-ring (10, 11). A schematic model of the entire F0-ATPase motor is shown in Fig. 1.
Fig. 1.
A schematic diagram of the F0F1-ATPsynthase system. During ATP synthesis, the protomotive force due to PTR from the P to the N side drives the F0 rotation, which in turn rotates the F1 stalk and leads to ATP synthesis in the catalytic α/β subunits.
Instructive phenomenological and simulation studies have utilized the available experimental data in attempts to generate a workable model for the action of F0-ATPase (3, 12–17). Out of these, the most notable idea has been the assumption that different channels lead to the release and uptake of the proton to the N (cytoplasmic) and P (periplasmic) side of the membrane (3, 12, 15). It has then been postulated in a phenomenological way that the directionality of c-ring rotation is enforced by the coupling of the pH-driven proton transport to the protonation/deprotonation events of the Asp residues (12, 15). Recent experiments have also suggested that the Arg residues is working to block the uptake of protons from the low pH reservoir (P) once the Asp comes close to the Arg and thus forces the proton to escape to the high pH side (N) (11). However, in spite of the above reasonable assumptions, it is still unclear as to how exactly the pH gradient is tied to the molecular events of protonation and deprotonation of the Asp residues or whether there is an asymmetry in proton transport (PTR), and how this asymmetry can lead to the unidirectional rotation.
In our view, a detailed understanding of the action of F0 must involve a conversion of the molecular structure of the system to a free energy map, which then can be used to determine the factors leading to the required vectorial process. Unfortunately, at present it is not practical to use full microscopic simulations to generate the relevant free energy surface for the proton gradient with the tentative structure of the c-ring rotor/subunit-a stator complex. Fortunately, the use of CG model offers the best current option for providing the needed landscape, as has been successfully demonstrated for the F1-ATPase mechanochemical coupling (7) and DNA helicases (18). The power of CG models in studying other macromolecular systems is further illustrated in recent works (19, 20). Thus we used our CG model with specialized electrostatic treatment (21) and explored the molecular origin of the rotational motion of F0. Remarkably, it is found that the rotation is due to asymmetry in the energetics of the proton path rather than just the asymmetry of the interaction between the Asp and Arg ions. The ability to explore this issue and to examine the nature of the vectorial motion reflects the fact that the CG model captures consistently the energy balance of the system. This includes accounting for the free energy of the proton movement through the protein/membrane system under the effect of the pH gradient, as well as the changes in the electrostatic interactions between the charges of the system along the rotational coordinate of the rotor.
The structural information about F0 includes recent high-resolution crystal structures of the c-ring (9), where information on the subunit-a is still lacking, and the NMR solution structure (22), which provides a rather hypothetical model for the a/c complex. All the crystal structures of the c-ring show the centrally located Asp residue in a locked conformation facing inwards towards the membrane helices, which is probably in its protonated form. The solution NMR structure (which is based on several assumptions about the a/c interface) indicates that the Asp containing c-ring helix facing the subunit-a is rotated outside forming an open conformation (22). There have been some recent concerns regarding the drastic rotation of the c-ring helix, since such a structural perturbation is inconsistent with the high-resolution crystal structures (9, 23). However, the helix rotation upon facing the Arg of subunit-a has been implicated to be important for the functionality of the F0 motor in other studies (24). At any rate, the relationship between the c-ring helix rotation and the motor functionality will be assessed in the present work (see Results and Discussion and SI Text).
Oster and coworkers (16, 17) modeled the F0 rotation while using phenomenological parameters for the energy of the ionized groups. These models have not been based on validated electrostatic studies of charges in proteins [for discussion of the proper dielectric, see ref. (25)], but nevertheless provide interesting insights. A more explicit extension of these concepts into an actual structural model (13) has provided additional insights, but unfortunately used the above electrostatic treatment without proper validation. More importantly, the above models have not considered the crucial barriers for the PTR path and the how those might be coupled to the rotary path. Furthermore, the directional motion of the F0 system has been obtained by imposing the torque arising due to ATP hydrolysis occurring on the catalytic subunits of F1-ATPase. Of course, the situation becomes much more challenging if one tries to model the effect of the proton gradient on the rotational process without using any phenomenological parameter. A recent work (23) has also attempted to provide a molecular insight to the action of F0, while using microscopic free energy calculations to evaluate the energetics of the Asp residue. This was done with a very tentative model of the membrane and the a/c interface; by inserting explicit water molecules in the largely hydrophobic a/c interface without attempting to evaluate the energy of creating such an assumed solvent environment (such a treatment is particularly problematic when it is done on a microscopic level).
At any rate, models that focused on the interaction between the Asp and the Arg residues have not considered the asymmetry of the PTR path. The role of such an asymmetry was envisioned to be the cause behind the directional rotation (12) and will be shown here to be crucial for the rotation of F0. In other words, we will show that the energetics of the ionizable Asp and Arg alone cannot account for the vectorial action of the F0-ATPase. Furthermore, we will point out that a proper description of the process must be reproduced based on the actual free energy surface rather than described (or discussed) by qualitative statements. It is important to emphasize that previous attempts to model the asymmetry were not based on a validated experience in modeling charges in protein interiors or on familiarity with the corresponding issue. This is exactly the issue that has been extensively studied by us (26) and has led to the electrostatic features of our CG model (21). At present, the CG is far more reliable in assessing pKa and electrostatic free energies in nonpolar regions of protein/membrane systems than the standard FEP calculations [e.g., of the type used in ref. (23)] that do not involve specialized treatment of water penetration (27) or extremely long simulations of the complete atomistic system.
Results and Discussion
Generating the F0-ATPase Rotary Landscape.
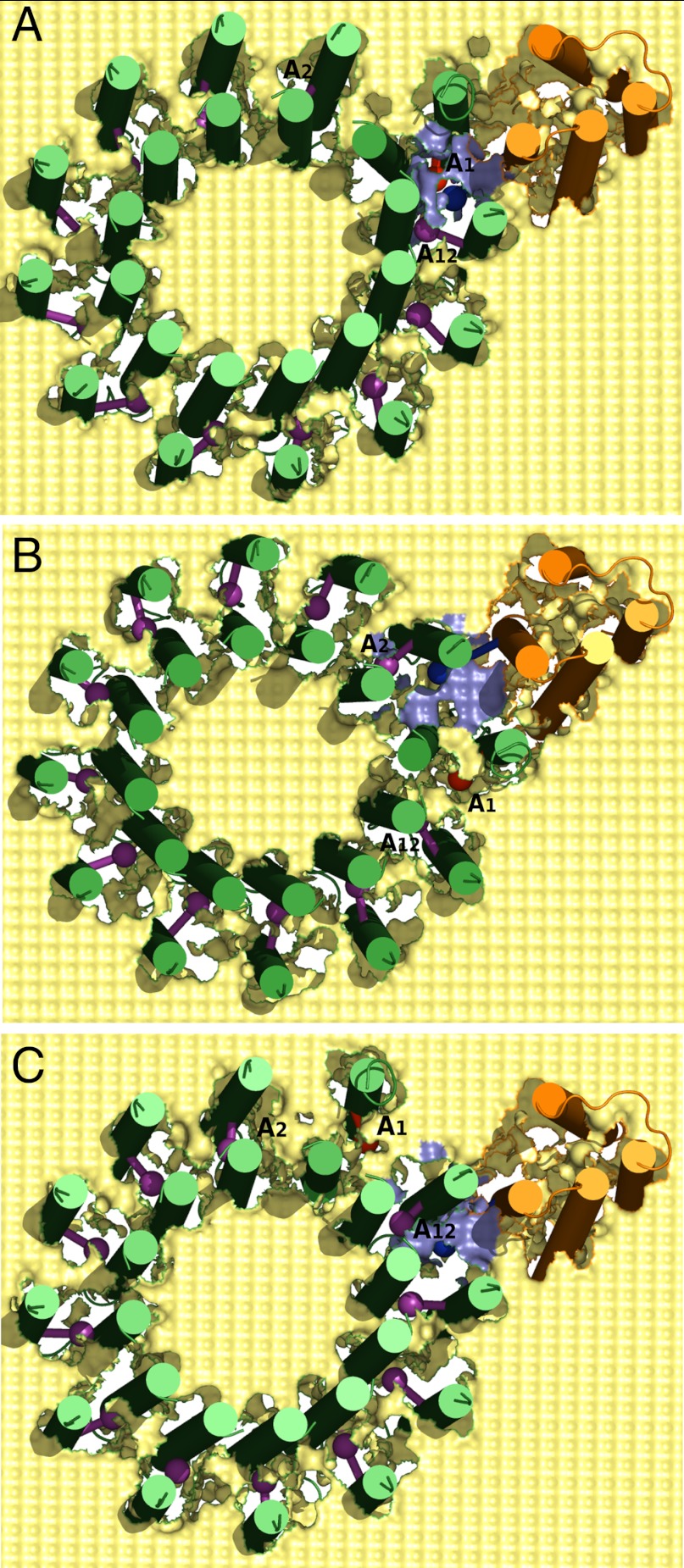
Our objective is to generate a structure-based free energy landscape that will reproduce the unidirectional rotation of the c-ring in the ATP synthesis direction (due to the PTR from the P to the N side). In order to explore the landscape, we started by generating a tentative structural model based on the solution structure (22). We have embedded the system in a rectangular membrane where both the protein and the lipid were represented by our CG model. The protein residues were represented with explicit backbone atoms and the side chains were represented with a single united atom (21), while the membrane was represented through a grid of effective atoms with a 3 Å spacing. The membrane block has a width of about 30 Å and the central Asp residues of the c-ring were placed almost at the middle of the membrane. Experimental evidences have suggested the presence of proton channels on the P and N side of the a/c interface that has access to the hydrophilic environment (28, 29). In order to explore this effect in our CG model, we removed part of the membrane environment from the vicinity of the Asp-Arg pair in the interfacial regions. The removal was done with a cutoff of 8 Å around the center of the Arg side chain. However, this treatment was then validated by obtaining similar results using a smaller cutoff of up to 6 Å. The relative insensitivity to the exact cutoff is one of the useful properties of the CG model. Several intermediate frames were created by rotating the c-ring gradually in the synthesis direction, while the subunit-a was kept fixed. The rotation started with the Asp residue on the left side of the Arg and then moved past the Arg towards the right side, when viewed from the N side. Typical frames of the resulting CG model of the F0-ATPase embedded in the membrane are shown in Fig. 2.
Fig. 2.
The CG model of the F0-ATPase shown from the P side, where rotation in the synthesis direction corresponds to the clockwise direction. The light yellow surface represents the CG membrane; subunit-a and c-ring are shown in orange and green, respectively. The CG side chain centers of the Arg(+) is shown as blue sphere, while the Asp(-) (A1) is shown as red sphere. All other protonated Asp residues on the c-ring helices are shown as magenta spheres. (A) The starting structure where A1 is closest to the Arg(+); (B) The c-ring is rotated in synthesis direction so that A1 enters the membrane phase and A2 is closest to the Arg(+); (C) The c-ring is rotated in opposite direction so that A1 enters the membrane phase and A12 is closest to the Arg(+).
With the structural model of Fig. 2, we started to explore the nature of the rotary landscape. First, we examined whether the contribution from the Asp(-) Arg(+) ion pair is the only reason for directional rotation of F0. This was done by calculating the free energy of the Asp(-) and Arg(+) while rotating the c-ring gradually from left to right in the synthesis direction (without considering the energy of the protons). The result (Fig. S1) shows that the Asp(-) Arg(+) ion pair free energy is asymmetric on both sides of the Arg position. The energy of the system when Asp is deprotonated on the left side of the central Arg is higher, due to destabilization by the membrane environment. The energy decreases as the deprotonated Asp moves to the right of the Arg, due to the more polar environment of the a/c interface. The free energy rises again as the Asp(-) moves further to the right and enters the membrane environment. Previous theoretical studies (13, 23) have implied that this energy difference reflects the change in the membrane and polar environment and is a sufficient reason for unidirectional rotation of the c-ring. However, these studies have not examined the PTR barriers related to the energetics of the rotating Asp(-) Arg(+) pair. At this stage it should be noted that any attempt to understand the reason for the functionality should also account for the actual PTR under the relevant pH gradient, and not just the asymmetry in the ion-pair free energy.
Generating the Coupled PTR/Rotation Landscape.
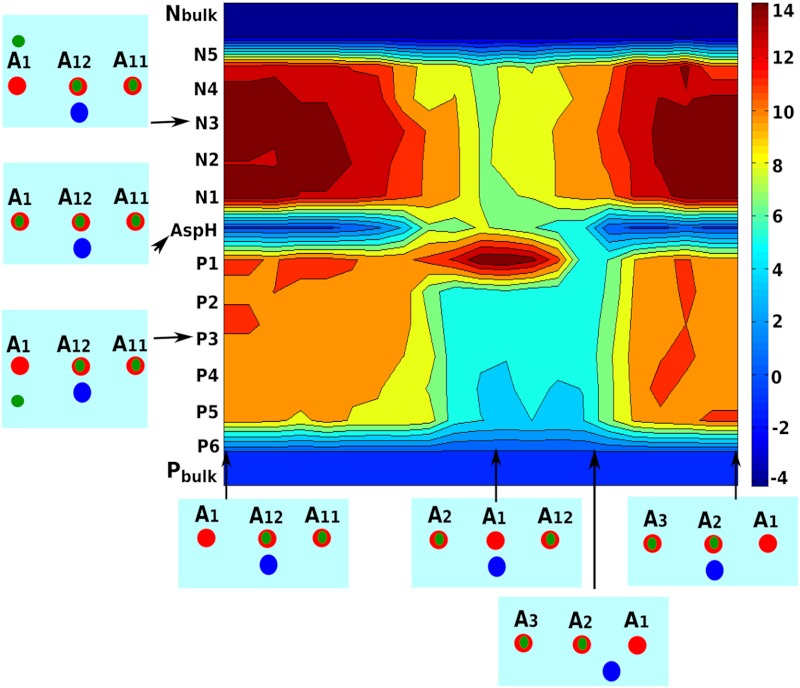
To obtain the full picture of the molecular basis of the F0 rotation, it is important to generate the functional vectorial motion from the energy landscape. Thus it is essential to have a clear description of the landscape in the key variables of the system (namely, the rotation of the c-ring and the PTR coordinates). Obviously, it is imperative to move from the rather simple focus on the energy of only Asp(-) Arg(+) ion pair to a model that also considers the coupling of the c-ring rotation to the PTR process. The PTR process can be described by a full EVB or a simplified EVB treatment (30), where we consider the proton transfer between any possible water sites along the N and P channels on the a/c interface and also the transfer between protonated water to ionized acidic groups on the c-ring α-helices. However, we can still obtain a reasonable approximation by following the energy of the localized states as demonstrated in ref. (30), and this approach has been adopted here (see SI Text, Fig. S2). We note in this respect that we actually check the energy of PTR through feasible paths along the membrane on the N and P sides. This is done by evaluating the energetics of inserting an H3O(+) ion at each of the feasible regions (see Fig. S3) for all of the frames generated by rotating the c-ring against the stator subunit-a. This reflects the energetics of the corresponding PTR along those paths, and is much more relevant in providing the electrostatic barriers than just looking at the possible water channels (see 30). The free energy profile calculated for the different rotated frames and proton positions is shown in Fig. 3. As indicated by the map, the positive potential from the Arg(+) residue blocks the protonation from P side and decouples the two proton channels on the P and N side. The role of Arg seems to be consistent with experimental findings (3, 11) and also with the implications of some models (12, 13, 16, 17). As the Asp(-) comes close to Arg(+), the only way for the proton exit is through the N channel, as the proton on the P side faces very high electrostatic barrier. This barrier is reduced quickly as the Asp rotates further to the right, and thus the channel on the P side becomes accessible to the Asp. Our calculated landscape also produces asymmetry in the protonation paths on both sides. Protonating the Asp(-) from the left involves significantly higher barrier than protonating from the right (see more in the SI Text). Moreover, the barrier for deprotonating through the N channel is higher by almost 3 kcal compared to that of protonating through the P channel.
Fig. 3.
The electrostatic map in kcal/mol for the rotation/PTR. The X axis represents the c-ring rotational coordinates and the Y axis represents the proton positions throughout the PTR from the Pbulk to the Nbulk (maintained at pH 5 and 8, respectively). The boxes along the X and Y axis depict the positions of the Asp and protons with respect to the Arg. The deprotonated Asp (A1) is indicated in red and all other Asp are protonated. The Arg is shown as a blue circle. The proton positions are shown as green dots where P1, …, P6 represents proton positions inside the a/c interface on the P-side and N1,…, N5 represents the same on the N-side of the centrally located Asp(-) Arg(+) pair.
While Fig. 3 depicts the basic landscape, it still cannot be used to describe the rotational process of the c-ring. That is, the figure involves only one round of ionizing and protonating a single acid, and cannot be used as a landscape depicting the continuous functional rotation. Thus, we describe in Fig. 4 the landscape generated by considering the energetics of protonation and deprotonation of two consecutive Asp groups (namely A1 and A2 shown in Fig. 2 and the X axis of Fig. 3). Now we can see in Fig. 4 a clear vectorial path where the PTR from P to N side drives the rotation. That is, the Asp closest to the Arg(+) (i.e., A1) is in a position to deprotonate through the N channel and it releases the proton to the Nbulk (kept at pH 8). The system then rotates to the right (state B → C) as rotating to the left is of higher energy. Once it reaches state C, Asp(-) can be protonated through the P channel by taking a proton from Pbulk (kept at pH 5). Now the system with the protonated A1 can only rotate further to the right and enter the membrane phase. This further rotation brings the next Asp group (i.e., A2) closest to the Arg(+). Thus, another cycle of deprotonation through N channel followed by subsequent rotation and protonation through the P channel is followed. Of course, for further rotation we have to superimpose the surfaces where additional acids are ionized; however, the results are simply a duplication of what we have in Fig. 4. Using the free energies of the PTR in the key states shown in Fig. 4, we generated in Fig. 5 a pathway depicting rotation from left to right (synthesis direction) and also from right to left (hydrolysis direction) under the pH conditions of 5 and 8 for the P and N sides, respectively. The energies and barriers along the rotational/PTR pathway indicates that moving to the right is advantageous as the barrier for the rotation to the right is about 5 kcal/mol, whereas that of the left motion is more than 11 kcal/mol. Additionally, we have conducted the same analysis for a mechanism where two Asp residues can be ionized simultaneously. In this case it was found that the rotational barriers are still favoring a vectorial motion from left to right; however, the overall PTR barriers are significantly higher and thus unlikely to be used by the system. We would like to emphasize that what drives the vectorial process is the decrease in free energy upon movement of the proton from the P to N side (which is of course included in our landscape). We also like to clarify the difference between our treatment and the ideas presented on F0-ATPase rotation (12). That is, although there have been pioneering and insightful ideas about the relationship between the PTR path and the rotational motion, the lack of energy-based landscape makes it very hard to examine the relationship between such vectorial proposals and the actual molecular system.
Fig. 4.
The rotational/PTR path in the synthesis direction is shown when only one Asp is protonated during the cycle. The cycle start by releasing a proton from the Asp (A1) closest to the Arg(+) to the Nbulk (lower free energy map). This is followed by rotation to the right side and then taking up a proton from the Pbulk. As the Asp(-) becomes A1H, it rotates further to the right until it reaches a point where the next A2H on the left is closest to Arg(+) (middle free energy map). Finally, this A2H releases the proton to the Nbulk and the cycle repeats itself (top free energy map).
Fig. 5.
The rotation/PTR path for both synthesis and hydrolysis direction are shown schematically where the free energies and the barriers for the key states are denoted. The Arg(+), Asp(-) and the protons are denoted by blue, red, and green circles, respectively.
Simulating the Time Dependence of the Proton-Driven Rotation of F0-ATPase.
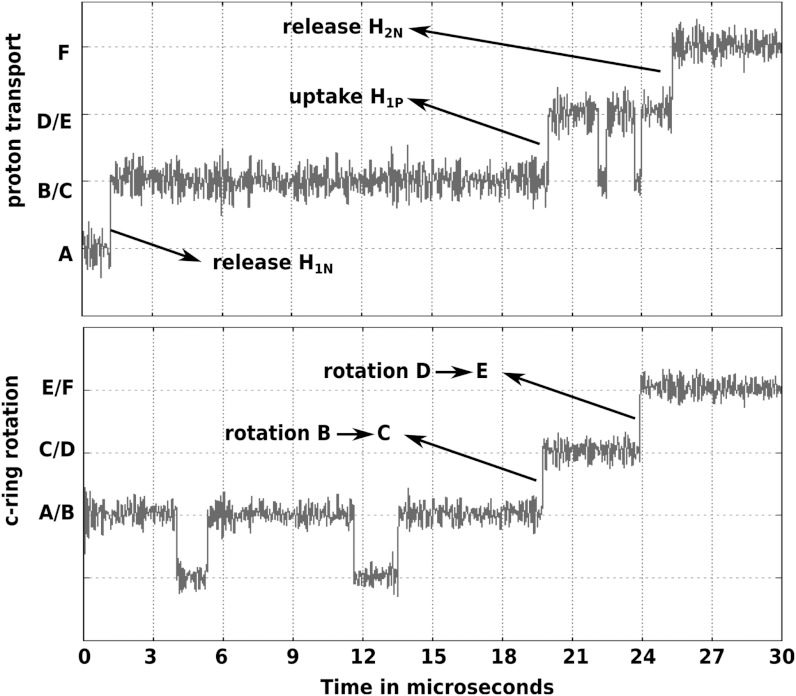
While the above analysis gives clear clues about the molecular origin of the rotational motion, it is important to further explore our findings by examining the time dependence of the system. This was done by adopting the same approach used in our study of F1-ATPase (7) and related systems (18), by converting the landscape of Fig. 4 to a general set of EVB-like surfaces and then running Langevin Dynamics (LD) simulations on the simplified surface. The constructed simplified surface (shown in Fig. S4) and the equations governing it along with the LD equations are discussed in the SI Text. The free energies of the key states (i.e., states A, B, …, F) along with the rotational and PTR barriers shown in Figs. 4 and 5 are used to generate the surface. All other regions apart from the functional path have higher free energies (approximately 35 kcal) compared to the functional surface. The parameters used for the LD are shown in Table S1. The simulation results are given in Fig. 6, where the upper and lower plots show the time evolutions of the PTR (the Q coordinate) and the c-ring rotation (the θ coordinate), respectively. The simulation starts from the state A and as soon as H1N is released to the Nbulk region, there is a sharp drop in free energy and the system rotates to state C in about 20 μs. Note that it is not possible for the c-ring to revert back to state A within relevant time scale (a barrier of approximately 12 kcal/mol) once state B rotates to C. The system now waits until H1P is absorbed from the Pbulk. This PTR drives the system to state E, which is accomplished by rotating further to the right, in about 4 μs. Further simulation would show that another proton (H2N) would be released to the Nbulk region, and the sharp drop in free energy would bias the system towards further rotation to the right. The results show that the PTR from P to N acts as the principal biasing force that drive the system towards unidirectional rotation, thus preventing back rotation. The total time of ionizing and protonating A1 along with the rotation of A1 away from the Arg(+) and bringing A2 closest to Arg(+) is approximately 24 μs. This corresponds to approximately 42000 protons transported per second. This rate of PTR is about 3 times higher than the experimental result of about 13000 protons transported per second at pH 8 and 200 mv membrane potential in the absence of the F1 part (31). At this point, we must clarify that our aim is not to reproduce the exact number of rotation per second for the F0F1-ATPase during the synthesis step. However, considering the fact that our results are not perfect in absence of a high-resolution X-ray structure of the a/c complex, it is still useful to re-emphasize that the study reproduces the F0 rotation based on the functional landscape evaluated from an actual atomistic structural model of the system. At present, the role of our model is to provide an understanding of the key barriers along the functional path, which can help in elucidating the trends in the effects of mutations and pH changes. The exact rotation time of the complete F0F1 complex also depends on the load exerted by the F1 part and is not considered in this work.
Fig. 6.
LD of the F0 rotation and PTR. The Upper plot represents the time evolution of the PTR coordinate (Q), while the Lower plot shows the time evolution of the c-ring rotation coordinate (θ). The system starts at step A (indicated in Fig. 4) and undergoes PTR to the N side within 1.2 μs. After H1N is released to the Nbulk region, the system rotates unidirectionally to the right (step B → C) in about 20 μs. This is followed by accepting the proton H1P from the Pbulk. Again, the system undergoes the next rotational step D → E, within 4 μs. Finally, another proton H2N is released to the Nbulk. The time evolution suggests that the PTR from P side to the N side along with the rotation takes up to 24 μs.
Concluding Remarks
Elucidating the molecular origin of the action of the proton-driven F0 rotor presents a major challenge despite significant advances. Some of the previous studies have provided viable theoretical models that can lead to the vectorial process. In particular, the directionality of the rotary proton conductor has been tentatively ascribed to two electrostatic constraints plus two non-colinear access channels to the Asp-Arg pair (12). However, the nature of the elusive asymmetric proton channels has not been established based on a structural model, nor validated through generation of a structure-based energy landscape that considers the coupling of the PTR to the F0 c-ring rotation. This challenge has been addressed here by the use of a CG model, which was able to account for the directionality of the rotor without imposing it through phenomenological parameters or by any external force mimicking the torque due to the rotation of the F1-ATPase. One of the key points in our treatment has been the effort to generate a complete functional landscape that actually describes the vectorial process. This philosophy, that started already in our earlier work (32, 33) and emphasized in several recent studies (7, 18), is in our view, an essential element in formulating and understanding the vectorial motion.
Although our initial model started from the tentative NMR structure, we note that the high degree of rotation of the c-ring helix predicted in the solution structure is not consistent with the recent x-ray structures (23). As clarified in the SI Text, we actually explored the possibility that the region of the c-ring in contact with the subunit-a Arg will be more similar to the rest of the c-ring helices. We show that this will not change the main features of our landscape. This further signifies that the c-ring helix rotation observed in the solution structure could not be the reason underlying the directionality in the rotation, as suggested by some studies (24). At this stage, it is useful to re-emphasize the interesting attempts (13) to account for the rotational motion during ATP hydrolysis, while attributing the vectorial driving force to the F1-ATPase. Such a model has avoided the challenge of understanding the actual vectorial motion of the F0 motor during ATP synthesis. We also mention that the works of Walz and Caplan (14) and that of Oster (16, 17) has tried to construct a phenomenological landscape, but the relationships of these landscapes to the actual structural features are not clear.
Insightful attempts to explore the nature and the energetics of the proton path were reported by Junge and coworkers (31). This work attempted to determine the pKas of the groups controlling the PTR by considering current-voltage relationships and pH effects and using a minimal rotary model. The model appeared to be consistent with two groups of pKas about 6 and 10 in both sides of the membrane. Now, as discussed in our recent study of the pKas in Cytocrome C oxidase (34), it is not simple to interpret apparent pKa of pumping processes even when the relevant sites are known. Furthermore, as discussed in our studies of proton conductance in gramicidin (35, 36) it is very hard to obtain unique information on the PTR profile using phenomenological fitting. However, combining the valuable experimental information of ref. (31) with the calculated profile using our CG treatment of external potentials (37) should provide instructive insights and lead to a significant advance in understanding the details of the protomotive action.
Our early finding that the EVB profile for PTR follows the electrostatic profile of the protonated water (30) has useful implications with regards to Na(+) activated motors. That is, the profile for the Na(+) transfer should be similar to that of the protonated water, with some modification for the difference between the Asp(-) Na(+) and the Asp(-) H(+) systems. It may be useful to point out here that a significant part of the calculated asymmetry in the PTR is due to the regions where the membrane was excluded and replaced by implicit water. Those who are familiar with water channels in proteins (34) may wonder how valid is our finding of the asymmetric PTR. We believe that this finding is quite robust since some of the a/c interfacial regions, in particular near the Asp-Arg pair, are clearly solvated, and the rest are likely to be accessible to water without major steric penalty (29). In fact, the overall results of the CG calculations appear not to be so sensitive to the exact cutoff value for the interfacial water region (tested for 6–8 Å). This stability is a reflection of the gradual change in moving from the membrane to the solvent/protein environment, and has been considered while parameterizing the CG model so that it represents the realistic effect of water penetration around charged groups. Obtaining such effects by microscopic models requires very long simulations, and it would be interesting to use here our new water flooding approach (38).
Overall, it seems clear that a proper analysis of the protomotive force induced action of the F0 motor must include the landscape in both dimensions, namely the c-ring rotation and the PTR. The barriers for PTR play a major role in the overall rate and directionality of the rotational motion. Providing the landscape for the F0 rotation and combining with our F1-ATPase model (7) gives hope for a complete molecular model of energy transduction in the F0F1-ATPsynthase.
Methods
The present work uses a CG model that describes the main chains by an explicit model and represents the side chains by a simplified united atom model. The model has a unique treatment of the electrostatic energy including the self-energy that gives its reliable features. The details of our model are given elsewhere (39) and is also described in the SI Text. Here we emphasized the evaluation of the proton energy and the PTR paths. The evaluation of the PTR energy is described in the SI Text.
In addition to the CG treatment, we also generated a simpler reduced dimension potential energy surface that could be used in Langevin Dynamics simulations of long time processes. The energy terms in the reduced dimension surface are similar to those used in our previous studies (18), and are described in detail in the SI Text. The corresponding LD equations are the same as those used in our previous studies (7, 18, 40) and are described in detail in the SI Text.
Supplementary Material
ACKNOWLEDGMENTS.
This work was supported by the National Institute of Health R01 GM 40283 and the National Science Foundation grant MCB-0836400. We also thank the University of Southern California High Performance Computing and Communication Center (HPCC) for computational resources.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1212841109/-/DCSupplemental.
References
- 1.Boyer PD. The ATP synthase—A splendid molecular machine. Annu Rev Biochem. 1997;66:717–749. doi: 10.1146/annurev.biochem.66.1.717. [DOI] [PubMed] [Google Scholar]
- 2.Abrahams JP, Leslie AG, Lutter R, Walker JE. Structure at 2.8 Å resolution of F1-ATPase from bovine heart mitochondria. Nature. 1994;370:621–628. doi: 10.1038/370621a0. [DOI] [PubMed] [Google Scholar]
- 3.Junge W, Sielaff H, Engelbrecht S. Torque generation and elastic power transmission in the rotary F(O)F(1)-ATPase. Nature. 2009;459:364–370. doi: 10.1038/nature08145. [DOI] [PubMed] [Google Scholar]
- 4.Weber J, Senior AE. Catalytic mechanism of F1-ATPase. Biochim Biophys Acta. 1997;1319:19–58. doi: 10.1016/s0005-2728(96)00121-1. [DOI] [PubMed] [Google Scholar]
- 5.Noji H, Yasuda R, Yoshida M, Kinosita K., Jr Direct observation of the rotation of F1-ATPase. Nature. 1997;386:299–302. doi: 10.1038/386299a0. [DOI] [PubMed] [Google Scholar]
- 6.Shimo-Kon R, et al. Chemo-mechanical coupling in F(1)-ATPase revealed by catalytic site occupancy during catalysis. Biophys J. 2010;98:1227–1236. doi: 10.1016/j.bpj.2009.11.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mukherjee S, Warshel A. Electrostatic origin of the mechanochemical rotary mechanism and the catalytic dwell of F1-ATPase. Proc Natl Acad Sci USA. 2011;108:20550–20555. doi: 10.1073/pnas.1117024108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dimroth P, von Ballmoos C, Meier T. Catalytic and mechanical cycles in F-ATP synthases. Fourth in the Cycles Review Series. EMBO Rep. 2006;7:276–282. doi: 10.1038/sj.embor.7400646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Meier T, Polzer P, Diederichs K, Welte W, Dimroth P. Structure of the rotor ring of F-Type Na+-ATPase from Ilyobacter tartaricus. Science. 2005;308:659–662. doi: 10.1126/science.1111199. [DOI] [PubMed] [Google Scholar]
- 10.Fillingame RH, Angevine CM, Dmitriev OY. Coupling proton movements to c-ring rotation in F(1)F(o) ATP synthase: Aqueous access channels and helix rotations at the a-c interface. Biochim Biophys Acta. 2002;1555:29–36. doi: 10.1016/s0005-2728(02)00250-5. [DOI] [PubMed] [Google Scholar]
- 11.Mitome N, et al. Essential arginine residue of the F(o)-a subunit in F(o)F(1)-ATP synthase has a role to prevent the proton shortcut without c-ring rotation in the F(o) proton channel. Biochem J. 2010;430:171–177. doi: 10.1042/BJ20100621. [DOI] [PubMed] [Google Scholar]
- 12.Junge W, Lill H, Engelbrecht S. ATP synthase: An electrochemical transducer with rotatory mechanics. Trends Biochem Sci. 1997;22:420–423. doi: 10.1016/s0968-0004(97)01129-8. [DOI] [PubMed] [Google Scholar]
- 13.Aksimentiev A, Balabin IA, Fillingame RH, Schulten K. Insights into the molecular mechanism of rotation in the Fo sector of ATP synthase. Biophys J. 2004;86:1332–1344. doi: 10.1016/S0006-3495(04)74205-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Walz D, Caplan SR. An electrostatic mechanism closely reproducing observed behavior in the bacterial flagellar motor. Biophys J. 2000;78:626–651. doi: 10.1016/S0006-3495(00)76622-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vik SB, Antonio BJ. A mechanism of proton translocation by F1F0 ATP synthases suggested by double mutants of the a subunit. J Biol Chem. 1994;269:30364–30369. [PubMed] [Google Scholar]
- 16.Dimroth P, Wang H, Grabe M, Oster G. Energy transduction in the sodium F-ATPase of Propionigenium modestum. Proc Natl Acad Sci USA. 1999;96:4924–4929. doi: 10.1073/pnas.96.9.4924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Xing J, Wang H, von Ballmoos C, Dimroth P, Oster G. Torque generation by the Fo motor of the sodium ATPase. Biophys J. 2004;87:2148–2163. doi: 10.1529/biophysj.104.042093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Liu H, Shi Y, Chen XS, Warshel A. Simulating the electrostatic guidance of the vectorial translocations in hexameric helicases and translocases. Proc Natl Acad Sci USA. 2009;106:7449–7454. doi: 10.1073/pnas.0900532106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hyeon C, Thirumalai D. Capturing the essence of folding and functions of biomolecules using coarse-grained models. Nat Commun. 2011;2:487. doi: 10.1038/ncomms1481. [DOI] [PubMed] [Google Scholar]
- 20.Hyeon C, Lorimer GH, Thirumalai D. Dynamics of allosteric transitions in GroEL. Proc Natl Acad Sci USA. 2006;103:18939–18944. doi: 10.1073/pnas.0608759103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Messer BM, et al. Multiscale simulations of protein landscapes: Using coarse-grained models as reference potentials to full explicit models. Proteins. 2010;78:1212–1227. doi: 10.1002/prot.22640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rastogi VK, Girvin ME. Structural changes linked to proton translocation by subunit c of the ATP synthase. Nature. 1999;402:263–268. doi: 10.1038/46224. [DOI] [PubMed] [Google Scholar]
- 23.Pogoryelov D, et al. Microscopic rotary mechanism of ion translocation in the F(o) complex of ATP synthases. Nat Chem Biol. 2010;6:891–899. doi: 10.1038/nchembio.457. [DOI] [PubMed] [Google Scholar]
- 24.Fillingame RH, Angevine CM, Dmitriev OY. Mechanics of coupling proton movements to c-ring rotation in ATP synthase. FEBS Lett. 2003;555:29–34. doi: 10.1016/s0014-5793(03)01101-3. [DOI] [PubMed] [Google Scholar]
- 25.Schutz CN, Warshel A. What are the dielectric “constants” of proteins and how to validate electrostatic models? Proteins. 2001;44:400–417. doi: 10.1002/prot.1106. [DOI] [PubMed] [Google Scholar]
- 26.Warshel A, Sharma PK, Kato M, Parson WW. Modeling electrostatic effects in proteins. Biochim Biophys Acta. 2006;1764:1647–1676. doi: 10.1016/j.bbapap.2006.08.007. [DOI] [PubMed] [Google Scholar]
- 27.Kato M, Warshel A. Using a charging coordinate in studies of ionization induced partial unfolding. J Phys Chem B. 2006;110:11566–11570. doi: 10.1021/jp061190o. [DOI] [PubMed] [Google Scholar]
- 28.Angevine CM, Herold KA, Fillingame RH. Aqueous access pathways in subunit a of rotary ATP synthase extend to both sides of the membrane. Proc Natl Acad Sci USA. 2003;100:13179–13183. doi: 10.1073/pnas.2234364100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Steed PR, Fillingame RH. Aqueous accessibility to the transmembrane regions of subunit c of the Escherichia coli F1F0 ATP synthase. J Biol Chem. 2009;284:23243–23250. doi: 10.1074/jbc.M109.002501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kato M, Pisliakov AV, Warshel A. The barrier for proton transport in aquaporins as a challenge for electrostatic models: The role of protein relaxation in mutational calculations. Proteins. 2006;64:829–844. doi: 10.1002/prot.21012. [DOI] [PubMed] [Google Scholar]
- 31.Feniouk BA, et al. The proton-driven rotor of ATP synthase: Ohmic conductance (10 fS), and absence of voltage gating. Biophys J. 2004;86:4094–4109. doi: 10.1529/biophysj.103.036962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Warshel A. Conversion of light energy to electrostatic energy in the proton pump of Halobacterium halobium. Photochem Photobiol. 1979;30:285. doi: 10.1111/j.1751-1097.1979.tb07148.x. [DOI] [PubMed] [Google Scholar]
- 33.Warshel A. Electrostatic basis of structure-function correlation in proteins. Acc Chem Res. 1981;14:284–290. [Google Scholar]
- 34.Chakrabarty S, Namslauer I, Brzezinski P, Warshel A. Exploration of the cytochrome c oxidase pathway puzzle and examination of the origin of elusive mutational effects. Biochim Biophys Acta. 2011;1807:413–426. doi: 10.1016/j.bbabio.2011.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Braun-Sand S, Burykin A, Chu ZT, Warshel A. Realistic simulations of proton transport along the gramicidin channel: Demonstrating the importance of solvation effects. J Phys Chem B. 2005;109:583–592. doi: 10.1021/jp0465783. [DOI] [PubMed] [Google Scholar]
- 36.Dryga A, Warshel A. Renormalizing SMD: The renormalization approach and its use in long time simulations and accelerated PMF calculations of macromolecules. J Phys Chem B. 2010;114:12720–12728. doi: 10.1021/jp1056122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dryga A, Chakrabarty S, Vicatos S, Warshel A. Realistic simulation of the activation of voltage-gated ion channels. Proc Natl Acad Sci USA. 2012;109:3335–3340. doi: 10.1073/pnas.1121094109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Chakrabarty S, Warshel A. Capturing the energetics of water insertion in biological systems: The water flooding approach. Proteins. 2012 doi: 10.1002/prot.24165. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dryga A, Chakrabarty S, Vicatos S, Warshel A. Coarse grained model for exploring voltage dependent ion channels. Biochim Biophys Acta. 2012;1818:303–317. doi: 10.1016/j.bbamem.2011.07.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pisliakov AV, Cao J, Kamerlin SC, Warshel A. Enzyme millisecond conformational dynamics do not catalyze the chemical step. Proc Natl Acad Sci USA. 2009;106:17359–17364. doi: 10.1073/pnas.0909150106. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.