Collective many-body van der Waals interactions in molecular systems

Abstract

Van der Waals (vdW) interactions are ubiquitous in molecules and condensed matter, and play a crucial role in determining the structure, stability, and function for a wide variety of systems. The accurate prediction of these interactions from first principles is a substantial challenge because they are inherently quantum mechanical phenomena that arise from correlations between many electrons within a given molecular system. We introduce an efficient method that accurately describes the nonadditive many-body vdW energy contributions arising from interactions that cannot be modeled by an effective pairwise approach, and demonstrate that such contributions can significantly exceed the energy of thermal fluctuations—a critical accuracy threshold highly coveted during molecular simulations—in the prediction of several relevant properties. Cases studied include the binding affinity of ellipticine, a DNA-intercalating anticancer agent, the relative energetics between the A- and B-conformations of DNA, and the thermodynamic stability among competing paracetamol molecular crystal polymorphs. Our findings suggest that inclusion of the many-body vdW energy is essential for achieving chemical accuracy and therefore must be accounted for in molecular simulations.

Atomistic simulations of molecular ensembles have greatly contributed to our understanding of the microscopic details of matter and its physical and chemical properties. To treat realistic molecular systems with thousands or even millions of atoms, these simulations are typically based on models of interatomic potentials that approximate the solution of the full quantum mechanical many-electron problem (1, 2). Almost all of these interatomic potentials utilize an effective interatomic pairwise approximation to account for nonbonded interactions, the notable exception being polarizable force fields, which treat induction (static) effects using mutually interacting sites (3, 4). Beyond static polarization effects, fluctuations in the electron density lead to dispersion, or van der Waals (vdW), interactions (5–7), that are dynamic in nature and are of paramount importance for seemingly different phenomena, including molecular crystal formation, protein folding, drug binding, self-assembly of supramolecular complexes, molecular recognition, and even the adhesion of gecko setae on glass surfaces (8). An accurate description of dispersion interactions represents a significant theoretical challenge because dispersion itself is an inherently quantum mechanical phenomenon, arising from collective many-body plasmonic excitations (9). As such, the role of many-body vdW interactions has been recognized and studied for model systems, such as chains, layers, and cubes (10–14), as well as for noble gas liquids (15–17). Despite this fact, the nonadditive many-body (beyond two-body) contributions to the vdW energy are not explicitly included in most molecular simulations, favoring instead an effective C₆/R⁶ interatomic pairwise summation (18–22). Here we demonstrate that many-body vdW interactions, which cannot be captured using an effective pairwise approach, are of substantial importance in the realistic modeling of molecular systems of biological and chemical significance.

Results and Discussion

To accurately compute the nonadditive many-body vdW energy, we begin by performing a self-consistent quantum mechanical calculation to generate the molecular electron density using semilocal density-functional theory (DFT) (23)—a method which accurately treats electrostatics, induction, and hybridization effects, but lacks the ability to describe dispersion interactions (24). We then utilize the Hirshfeld, or stockholder, partitioning of the molecular electron density to derive a set of atomic frequency dependent polarizabilities that reflect the local chemical environment surrounding each atom, as suggested by Tkatchenko and Scheffler (25). The resulting atomic polarizabilities yield C₆ coefficients that are accurate to ≈5% for a database of 1,225 atomic and molecular dimers with reference values experimentally determined from refractive index data. After representing the N atoms in a given molecular system as a collection of isotropic three-dimensional quantum harmonic oscillators (QHO), fully characterized by the aforementioned set of atomic frequency-dependent polarizabilities, we then directly solve the Schrödinger equation corresponding to N fluctuating and interacting QHOs within the dipole approximation (10–12). By only including interactions between dipoles, diagonalization of the 3N × 3N interaction Hamiltonian yields the long-range many-body vdW energy (vdW-MB) of the molecular system in terms of coupled many-body (many-atom) eigenmodes or collective plasmons (Fig. 1).

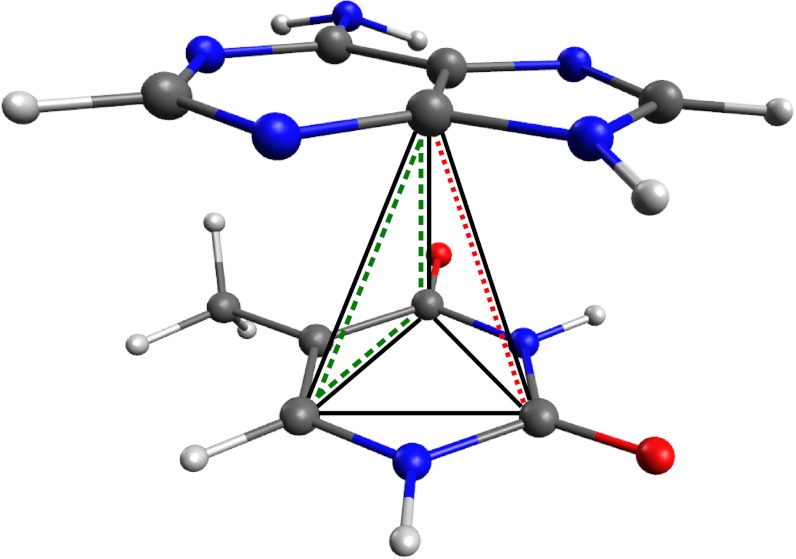
Fig. 1.

Graphical depiction of the coupled many-body vdW interactions present in the adenine-thymine dimer, a prototypical model of π–π stacking in DNA. Examples of two-, three-, and four-body contributions are illustrated by the dotted (red), dashed (green), and solid (black) lines, respectively.

A crucial aspect of our approach is that the vdW-MB Hamiltonian, and therefore the vdW-MB energy expression, directly follow from a rigorous derivation of the dipole-dipole interaction tensor from a range-separated Coulomb potential (see Methods). Therefore, the adjustment of a single physically motivated range-separation parameter allows the vdW-MB method to be coupled to a wide array of theoretical methods, ranging from classical force fields to higher level quantum chemical calculations (26). To accurately assess the underlying importance of the many-body vdW energy, we completed the coupling of the DFT and vdW-MB methods described above by utilizing a range-separation parameter obtained from global optimization of the total DFT+vdW-MB energy on the S22 test set, a widely employed benchmark database of noncovalent intermolecular interactions (27). Consisting of 22 dimers of common organic molecules, the S22 test set includes prototypes for hydrogen-bonded, dispersion-bound, and mixed electrostatic/dispersion stabilized complexes, with reference interaction energies computed using CCSD(T), the currently accepted “gold standard” quantum chemical method with an estimated accuracy of ≈1% (28, 29).

To elucidate the role of nonadditive many-body vdW energy contributions in the theoretical prediction of molecular properties, the following models were constructed:

1. vdW-MB—the full DFT+vdW-MB model as defined above, which includes all many-body energy contributions within the dipole approximation. It utilizes a range-separation parameter obtained via global optimization of the total DFT+vdW-MB energy on the S22 benchmark database.

2. vdW-NB—the N-body energy contribution in the full DFT+vdW-MB model, utilizes the same range-separation parameter as the DFT+vdW-MB model.

3. vdW-TB—an effective pairwise model, which computes the dispersion energy only via two-body interactions. To fairly represent the pairwise dispersion energy employed in atomistic force field simulations, we explicitly trained the vdW-TB model on the S22 benchmark database, which is the same database used for training the full DFT+vdW-MB model. Therefore, the vdW-TB model effectively mimics the shorter range many-body terms by using a larger value of the range-separation parameter than vdW-MB.

Comparisons made between the vdW-MB and vdW-TB models quantify higher-order correlation effects that can only be captured by explicitly including the nonadditive many-body vdW contributions beyond the two-body term and cannot be mimicked by an effective pairwise approach. Comparisons made between the vdW-MB and vdW-NB models distinguish contributions arising from different orders in the many-body vdW energy expansion. Furthermore, we also include comparisons with a different effective pairwise approach, namely the vdW-TS model (25), which has been extensively used in the literature for many molecular and condensed-matter systems. The vdW-TS method uses an empirical Fermi-type damping function, which distinguishes it from the range-separated Coulomb potential employed in the vdW-TB and vdW-MB models.

We first assessed the performance of the vdW-MB method on the aforementioned benchmark database of prototypical noncovalent dimers, the S22 test set (27). The mean absolute (relative) error of the vdW-MB model on the complete S22 database is 0.26 kcal/mol (6.2%) compared to 0.33 kcal/mol (7.9%) for the vdW-TB model. In comparison, the effective pairwise vdW-TS approach yields an error of 0.32 kcal/mol (10.3%). As one might expect, the vdW-MB and vdW-TB models yield essentially the same results for small hydrogen-bonded dimers and complexes bound by predominantly electrostatic interactions, and in most cases, the many-body effects were found to be repulsive. In fact, the deviation between these models is almost negligible at 0.1 kcal/mol, with the vdW-MB model yielding better overall agreement with the CCSD(T) reference binding energies. However, when considering only the dispersion-bound complexes in the S22 test set the deviation between the vdW-TB and vdW-MB models is indeed more significant. For example, the vdW-TB model underestimates the stability of the adenine-thymine stack (Fig. 1) by ≈1 kcal/mol, whereas inclusion of the nonadditive many-body effects at the vdW-MB level reduces this error by an order of magnitude, clearly illustrating both the limitations of an effective pairwise approach and the importance of higher-order correlation effects in one of the simplest prototypes for nonbonded stacking interactions in DNA. Taking the analysis one step further, we decomposed the vdW-MB energy for the adenine-thymine complex and the other π-π stacking dimers in the S22 test set, and found that the magnitude of the vdW-3B and vdW-4B contributions were ≈30% and ≈10% of the pairwise vdW-2B contribution, respectively.

We also extended our study to the larger S66 database, which was recently designed to provide a well-balanced representation of the intermolecular interactions found in bioorganic molecular systems by including benchmark energetics for a wider array of noncovalent binding motifs (30). In general, the same conclusions found above hold for the S66 database, in that both vdW-MB and vdW-TB are able to treat small electrostatically stabilized molecular dimers with an exceptional yet similar degree of accuracy. Again, we noticed a significant discrepancy between the performance of the vdW-MB and vdW-TB models when dealing with the expanded selection of dispersion-bound complexes present in the S66 database—vdW-MB consistently yields larger and more accurate interaction energies than the vdW-TB effective pairwise approach.

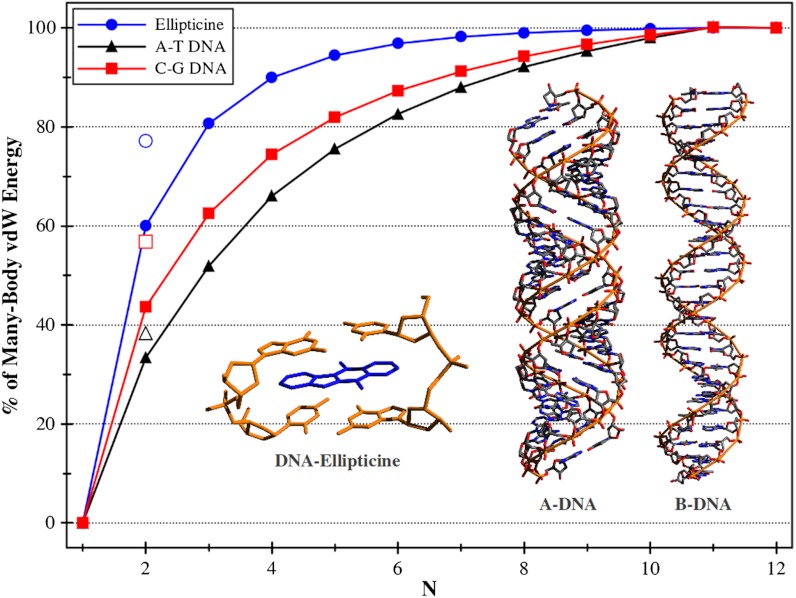
Having assessed the accuracy of the vdW-MB method for small organic molecules, we now examine the role of the many-body vdW energy in the theoretical prediction of binding affinities in larger biomolecular systems. For this purpose, we revisited ellipticine, an anticancer agent whose mode of action is based on DNA intercalation and inhibition of the topoisomerase II enzyme (31–33). In particular, we computed the many-body vdW energy contributions to the binding energy of a model of the DNA-intercalation complex consisting of ellipticine sandwiched between two Watson-Crick bonded cytosine-guanine base pairs linked by their phosphate sugar puckers. The resulting energetics (Table 1) confirm that vdW interactions are essential even for a qualitative prediction of the binding energy in this system, as the DNA-ellipticine complex is unbound at the DFT level of theory (ΔE_bind = +5.2 kcal/mol). Inclusion of vdW interactions using the vdW-TB model corrects the relative thermodynamic ordering and stabilizes the DNA-ellipticine complex by 44.3 kcal/mol, but once again, the effective pairwise approach underestimates the many-body vdW contribution to the binding energy. In fact, the contribution from the nonadditive many-body vdW interactions is quite significant in this system, increasing the overall binding strength of the DNA-ellipticine complex from -39.1 kcal/mol (vdW-TB) to -50.7 kcal/mol (vdW-MB). Furthermore, when using the effective pairwise vdW-TS method (25), the DNA–ellipticine binding energy is predicted to be -46.6 kcal/mol, still an underestimation of 4.1 kcal/mol compared to the full vdW-MB model. This additional stabilization of at least 4 kcal/mol, arising solely from nonadditive many-body vdW contributions, is a clear illustration of the increasingly important role played by these higher-order effects as molecular systems become larger and more structurally complex than the small organic molecular dimers considered before. In the context of predicting biomolecular ligand affinities, the difference between the DNA-ellipticine binding energies computed using the vdW-TB and vdW-MB models represents a marked discrepancy, as a decrease of about 1 kcal/mol in ΔG_bind, the binding free energy, corresponds to an order of magnitude decrease in the predicted equilibrium binding constant. In fact, to capture the vdW-MB energy with chemical accuracy, i.e., to within 1 kcal/mol, one needs to include the contributions from all terms up to vdW-7B in the many-body vdW energy expansion (Fig. 2). Although there is no high-level benchmark data currently available for ellipticine binding to DNA, our findings provide compelling evidence that nonadditive many-body vdW interactions play a substantial role in the binding of drugs to targets.

Table 1.

Binding energies for the DNA–ellipticine complex and DNA conformers

Level of theory	ΔEbind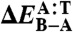
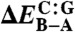DFT	+5.2	+4.2	+1.9
vdW-TS	−46.6	+2.5	−3.7
vdW-TB	−39.1	+2.6	−3.5
vdW-MB	−50.7	−0.1	−8.2

(Left) Binding energies (ΔE_bind) for the DNA–ellipticine complex in kcal/mol. (Right) Relative conformational energies of A-DNA and B-DNA (ΔE_B-A = E_B - E_A) consisting of pure adenine–thymine (A:T) and cytosine–guanine (C:G) sequences in kcal/mol per bp. All DFT calculations were performed using the PBE functional (37).

Fig. 2.

Percentagewise convergence of the individual vdW-NB contributions with respect to the vdW-MB energy. Displayed cases include the binding energy of the DNA-ellipticine complex (blue circles) and the relative binding energies of a single base pair in A-DNA and B-DNA consisting of pure adenine-thymine (black triangles) and pure cytosine-guanine (red squares) sequences. The unfilled markers at N = 2 correspond to the predictions of the vdW-TB effective pairwise model for each of the aforementioned systems.

To further elucidate the role of the many-body vdW energy in biological systems, we investigated the relative energetics between the A- and B-conformations of DNA. By modeling each conformer as a right-handed double-helix of fifteen Watson–Crick base pairs, consisting of either pure adenine-thymine (A:T) or pure cytosine-guanine (C:G) sequences, we computed the many-body vdW contributions to the cohesive energy of the central base pair in A-DNA vs. B-DNA conformations (see Methods). The resulting energetics (Table 1) reinforce the view that there is a need for including vdW interactions to obtain even qualitatively consistent results—in this case, DFT predicts A-DNA to be the more stable conformation by 4.2 and 1.9 kcal/mol/bp for the A:T and C:G sequences, respectively. However, using the effective pairwise approach to include vdW interactions is not enough to predict a consistent relative ordering among these DNA conformers; for both A:T and C:G DNA, the vdW-TB model destabilizes the A-DNA conformer by 1.6 and 5.4 kcal/mol/bp, respectively, but only in the C:G case is the B-DNA conformer now predicted to be lower in energy (in our DNA model). For these systems, the effective pairwise vdW-TS method yields essentially the same results as the vdW-TB model. Similar to the case of DNA–ellipticine binding, the energy contributions arising from the nonadditive vdW interactions were quite significant—the vdW-MB energy contribution was nearly 170% (A:T) and 90% (C:G) larger than the effective two-body vdW energy contribution. Hence, the vdW contributions to the relative DNA conformational energetics are dominated by many-body effects. Furthermore, the convergence of the many-body vdW contribution in predicting DNA conformational energetics was found to be remarkably slow. To capture 80% of the vdW-MB energy for the A:T and C:G DNA sequences, one needs to include all contributions up to vdW-6B and vdW-5B, respectively, whereas the same level of convergence is reached at the vdW-3B level in the prediction of the DNA–ellipticine binding energy (Fig. 2). With these findings in mind, we therefore conclude that although several other energetic contributions, e.g., thermal, solvent, and even nuclear quantum effects, are relevant for the modeling of DNA, it is evident that many-body vdW interactions, with energy contributions of nearly 3 kcal/mol/bp for A:T DNA and almost 5 kcal/mol/bp for C:G DNA, play an integral role in the conformational stability of DNA.

Having examined the many-body vdW energy contributions to binding affinities and relative conformational energetics, we now consider their role in predicting the relative thermodynamic stability among polymorphs of extended molecular crystals. The ability to characterize and distinguish competing molecular crystal polymorphs, which are often very close in energy (i.e., ΔE ≈ 0.1 kcal/mol per molecule), yet exhibit quite different physical and chemical properties, is of paramount importance in many fields, ranging from materials science and solid-state physics to biochemistry and pharmacology (34). In what follows, we focus our discussion on paracetamol (acetaminophen), an over-the-counter pharmaceutical agent used worldwide for its analgesic and antipyretic properties, which is experimentally known to have two polymorphs, P-I and P-II, that are essentially degenerate in lattice energy competing for the global minimum (35). To complicate matters, a recent computational study using DFT with an empirically parameterized effective pairwise vdW correction, identified a new polymorph, P-IV, and predicted it to lie energetically between P-I and P-II, thereby challenging experimentalists to search for this new form of paracetamol (36). Once again, we find that the inclusion of higher-order nonadditive many-body vdW contributions makes a significant difference; at the vdW-MB level, the P-IV polymorph is actually destabilized with respect to P-I and P-II by 0.79 and 0.92 kcal/mol/paracetamol molecule, respectively. Under the assumption that an essential condition for the accessibility of a given molecular crystal polymorph is that its energy lies within thermal energy (≈0.6 kcal/mol) of the global minimum, this destabilization of P-IV due to the many-body vdW energy contributions would make it virtually inaccessible to experimental determination, as there are many other possible metastable structures with similar energies (36). We also note that the nonadditive many-body vdW energy contributions to the energy difference between the experimentally observed P-I and P-II polymorphs amounts to a mere 0.14 kcal/mol, which is consistent with the fact that both forms were identified as stable polymorphs. These findings reiterate the limitations of an effective pairwise approach and further demonstrate the importance of the many-body vdW energy in the theoretical prediction of molecular properties; because the nonadditive many-body vdW energy contributions can be significantly larger than kT, our ability to make reliable predictions about the thermodynamic stability among competing molecular crystal polymorphs requires an accurate treatment of these energetically important contributions.

Previous studies of noble gas clusters and fluids (11, 15–17) found repulsive many-body vdW contributions when compared to the pairwise vdW energy. These findings contrast with our result that the nonadditive many-body energy stabilizes the ellipticine–DNA complex with respect to the effective pairwise model. We explain this difference by the relatively complex molecular geometries and higher polarizability densities utilized herein when compared to the noble gas cluster and liquid systems previously reported. In fact, previous work assumed a bare dipole–dipole interaction potential between all atoms, leading to a nondivergent many-body vdW energy only when relatively low atomic polarizabilities were utilized. In the vdW-MB method, the short-range contributions to the energy are treated by the underlying DFT functional, permitting the use of an attenuated Coulomb potential. As a result, the vdW-MB energy is nondivergent and real for all molecular systems studied herein. Interestingly, we find that the many-body vdW energy can be attractive or repulsive, with a subtle dependence upon the given molecular geometry and the nature of the intermolecular binding (i.e., whether the complex is predominantly electrostatic or dispersion bound).

In conclusion, we have introduced the vdW-MB model, which accurately captures the long-range many-body vdW energy in large molecular systems, to illustrate both the limitations of the effective pairwise approach as well as the crucial role played by the higher-order nonadditive vdW contributions in the prediction of several molecular properties of interest. We note that more work is needed to gain a deeper understanding of the binding situations and molecular geometries in which many-body vdW effects can be effectively described using a pairwise approach, which has been the predominant approach for a wide variety of systems to date (18–22). However, our findings provide compelling evidence that the many-body vdW energy contribution cannot always be mimicked with an effective pairwise model; instead, it is a complex physical quantity that depends on the overall molecular system size, the inherent structural motifs defining the underlying topology of the chemical environment, as well as the molecular property being investigated (Fig. 2). The many-body vdW energy described herein can be computed quite efficiently, thus it can realistically be incorporated into current model interatomic potentials.

Methods

Description of the vdW-MB Method.

The vdW-MB energy is calculated by exact diagonalization of the Hamiltonian corresponding to a set of N coupled isotropic three-dimensional quantum harmonic oscillators (11, 12):

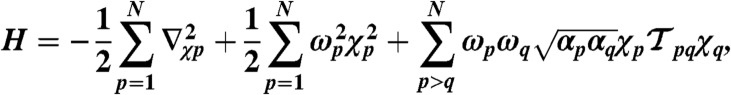[1]

in which 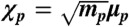is defined in terms of μ_p, the displacement of a given oscillator p from its equilibrium position, and 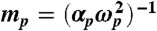. In the above equation, the first two terms correspond to the kinetic and potential energy for the individual oscillators, respectively. The last term in the Hamiltonian describes the coupling between oscillators via the dipole-dipole interaction tensor [, where W(r_pq) will be defined below]. The input parameters α_p and ω_p for each oscillator are defined as functionals of the self-consistent electron density, using the Tkatchenko–Scheffler method (25). For all DFT calculations, we used the Perdew–Burke–Ernzerhof functional (37) and the FHI-aims all-electron code (38).

The vdW-MB interaction energy for the full many-body system is then computed as the difference between the zero-point energies of the coupled and uncoupled oscillators, i.e.,

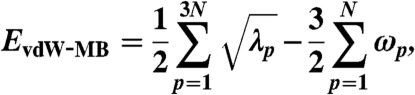[2]

in which λ_p are the vdW-MB Hamiltonian matrix eigenvalues. In the standard formulation of Eq. 1, in which the classical expression for the dipole-dipole interaction tensor is used, the vdW-MB energy would have an imaginary component due to the fact that the dipole-dipole interaction diverges at short distances, i.e., the well-known polarization catastrophe. Because we are only interested in computing the long-range many-body vdW energy, we utilize a dipole-dipole interaction tensor derived from the following Coulomb potential, which is attenuated at short interoscillator distances, namely, (26)

[3]

where r_pq is the distance between oscillators p and q, β is a range-separation parameter that controls how quickly W(r_pq) reaches the long-range 1/r_pq asymptote, and 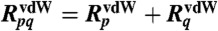defines the vdW correlation length in terms of the individual vdW radii, also defined as functionals of the density (25). Utilizing this modified dipole-dipole interaction tensor in Eq. 1 allows us to avoid the near-field divergence, and as a result, all of the vdW-MB energy components reported herein are real. The optimized values of the β parameter were found as 2.56 and 2.76 for the vdW-MB and vdW-TB models, respectively.

Construction of DNA Structures.

The A- and B-DNA structures were generated with 15 A-T and G-C base pairs using the TINKER DNA generation module available at: http://dasher.wustl.edu/ffe/. The negatively charged phosphate groups were protonated to yield overall neutral molecules. All conformer geometries were optimized at the vdW-TS level of theory (25) subject to the constraint of fixed phosphate atom positions in order to maintain the overall helix conformation. To compute the base pair binding energy contribution, we utilized an isodesmic replacement of the central base pair with hydrogen atoms that were relaxed while keeping the rest of the molecule fixed in order to ensure conservation of molecular charge and number of covalent bonds.